The Evolution Characteristics of Twisted Hermite–Gaussian Schell-Model Beams Propagating in a Uniaxial Crystal
Abstract
1. Introduction
2. The Cross-Spectral Density Function of THGSM Beams Propagating in Uniaxial Crystals Orthogonal to the Optical Axis
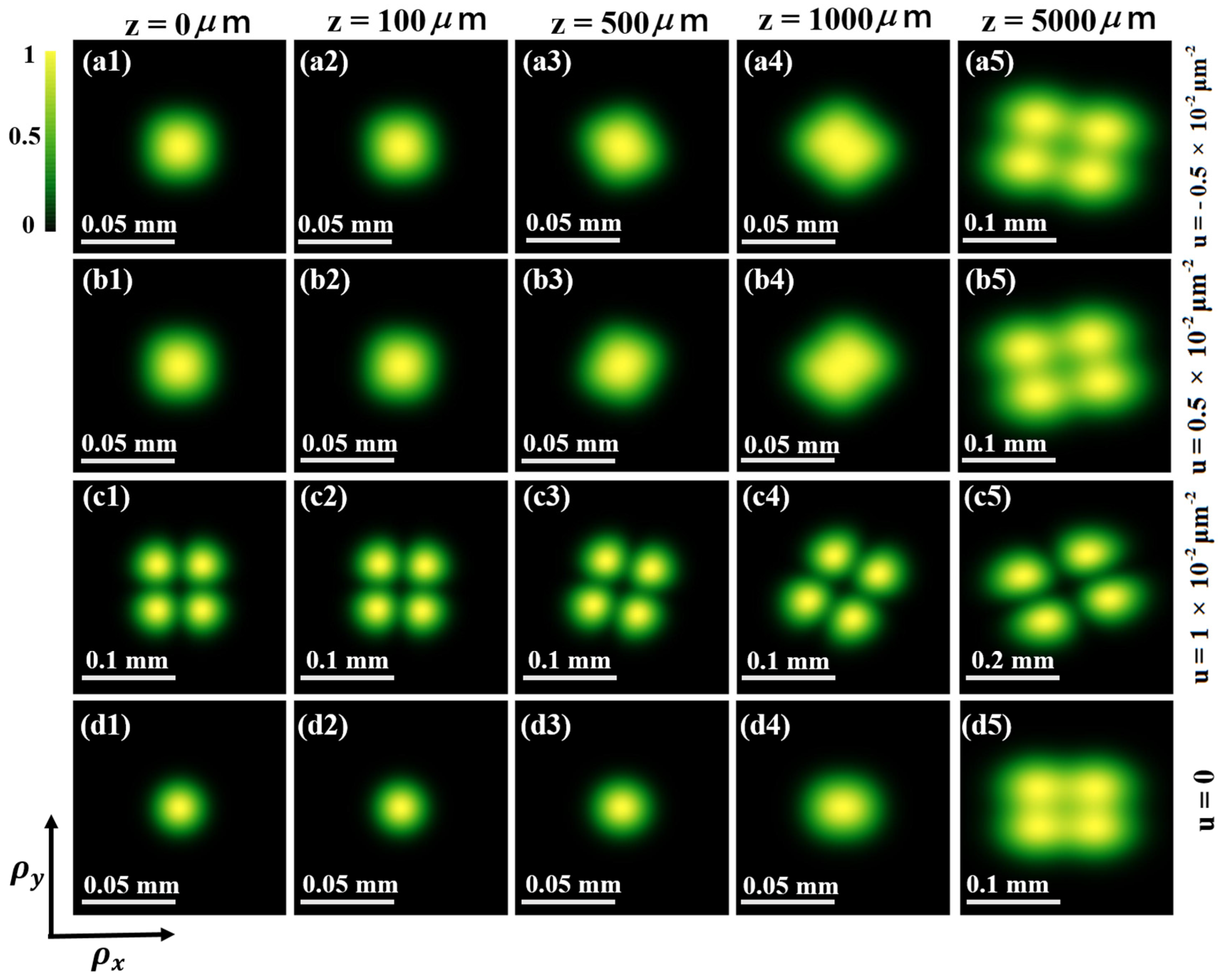
3. The Propagation Characteristics of THGSM Beams Propagating in Uniaxial Crystal Orthogonal to the Optical Axis
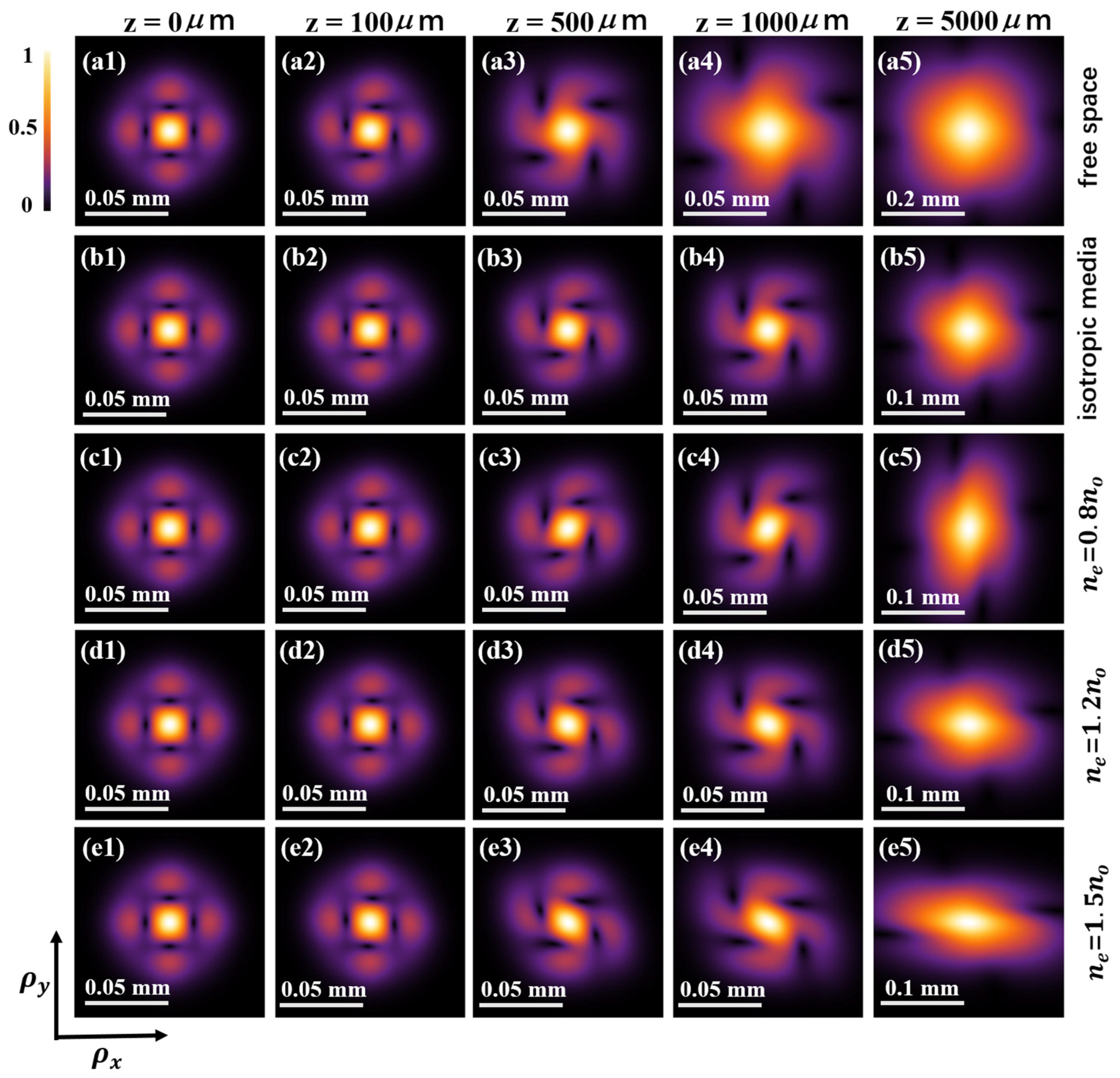
4. The Distribution of the DOC of THGSM Beams Propagating in Uniaxial Crystals Orthogonal to the Optical Axis
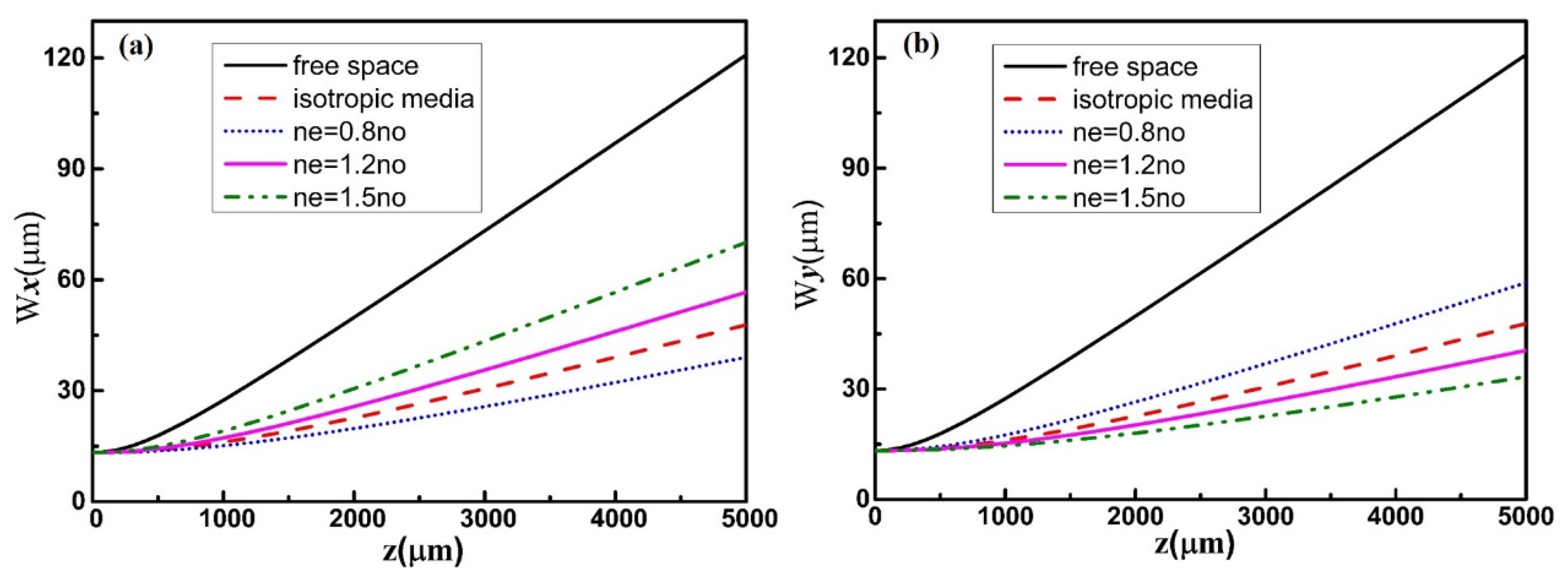
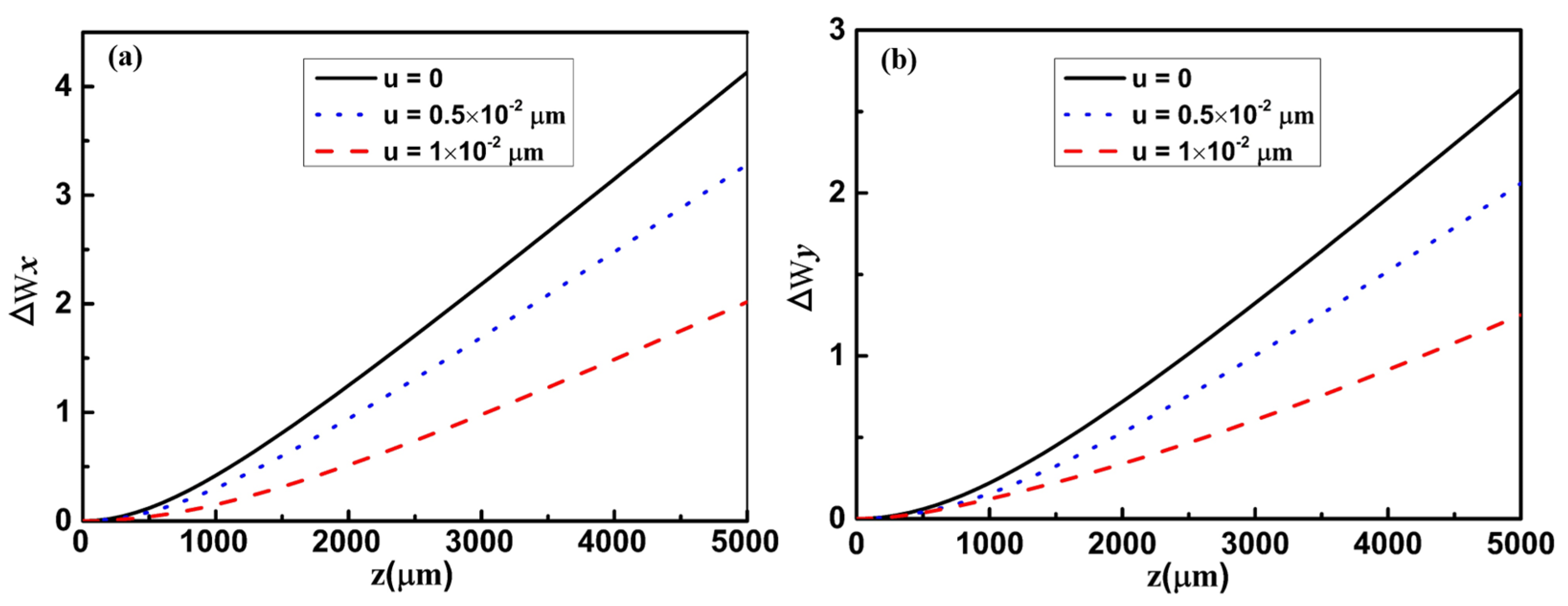
5. The Effective Beam Width of THGSM Beams Propagating in Uniaxial Crystal
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University: Cambridge, MA, USA, 2007; pp. 174–197. [Google Scholar]
- Cai, Y.; Wang, F. Tensor Method for Treating the Propagation of Scalar and Electromagnetic Gaussian Schell-Model Beams: A Review. Open Opt. J. 2010, 4, 1–20. [Google Scholar] [CrossRef]
- Gbur, G. Partially coherent beam propagation in atmospheric turbulence. J. Opt. Soc. Am. A. 2014, 31, 2038–2045. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, X.; Dong, Z.; Peng, D.; Chen, Y.; Wang, F.; Cai, Y. Robust Far-Field Optical Image Transmission with Structured Random Light Beams. Phys. Rev. Appl. 2022, 17, 024043. [Google Scholar] [CrossRef]
- Peng, D.; Huang, Z.; Liu, Y.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Optical coherence encryption with structured random light. PhotoniX 2021, 2, 6. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef]
- Gori, F.; Ramírez-Sánchez, V.; Santarsiero, M.; Shirai, T. On genuine cross-spectral density matrices. J. Opt. A Pure Appl. Opt. 2009, 11, 085706. [Google Scholar] [CrossRef]
- Sahin, S.; Korotkova, O. Light sources generating far fields with tunable flat profiles. Opt. Lett. 2012, 37, 2970–2972. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Cai, Y. Generation of a controllable optical cage by focusing a Laguerre–Gaussian correlated Schell-model beam. Opt. Lett. 2014, 39, 2549–2552. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, J.; Wang, F.; Cai, Y. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam. Phys. Rev. A 2015, 91, 013823. [Google Scholar] [CrossRef]
- Ponomarenko, S.A. A class of partially coherent beams carrying optical vortices. J. Opt. Soc. Am. A 2001, 18, 150–156. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Ponomarenko, S.A. Optical coherence gratings and lattices. Opt. Lett. 2014, 39, 6656–6659. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Zhu, X.; MI, C.; Peng, X.; Wang, F.; Cai, Y.; Ponomarenko, S.A. High-quality partially coherent Bessel beam array generation. Opt. Lett. 2018, 43, 3188–3191. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Ponomarenko, S.A. Free-space propagation of optical coherence lattices and periodicity reciprocity. Opt. Express 2015, 23, 1848–1856. [Google Scholar] [CrossRef]
- Lin, R.; Yu, H.; Zhu, X.; Liu, L.; Gbur, G.; Cai, Y.; Yu, J. The evolution of spectral intensity and orbital angular momentum of twisted Hermite Gaussian Schell model beams in turbulence. Opt. Express 2020, 28, 7152–7164. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Z.; Xu, H.; Zhou, Z.; Han, Y.; Yuan, Y.; Qu, J. Evolution properties of twisted Hermite Gaussian Schell-model beams in non-Kolmogorov turbulence. Opt. Express 2022, 30, 4071–4083. [Google Scholar] [CrossRef]
- Deng, D.; Yu, H.; Xu, S.; Shao, J.; Fan, Z. Propagation and polarization properties of hollow Gaussian beams in uniaxial crystals. Opt. Commun. 2008, 281, 202–209. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, R.; Chu, X. Propagation of Airy beams in uniaxial crystals orthogonal to the optical axis. Opt. Express 2012, 20, 2196–2205. [Google Scholar] [CrossRef]
- Deng, D.; Chen, C.; Zhao, X.; Li, H. Propagation of an Airy vortex beam in uniaxial crystals. Appl. Phys. B 2013, 110, 433–436. [Google Scholar] [CrossRef]
- Lian, M.; Gu, B.; Zhang, Y.; Rui, G.; He, J.; Zhan, Q.; Cui, Y. Polarization rotation of hybridly polarized beams in a uniaxial crystal orthogonal to the optical axis: Theory and experiment. J. Opt. Soc. Am. A 2017, 34, 1–6. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, G.; Wang, X. Nonparaxial propagation of Hermite–Laguerre Gaussian beams in uniaxial crystal orthogonal to the optical axis. Chin. Phys. B 2013, 22, 064101. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, Z. Propagation of partially coherent flat topped beams in uniaxial crystals orthogonal to the optical axis. J. Opt. Soc. Am. A 2009, 26, 924–930. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Cai, Y. Statistical properties of a nonparaxial Gaussian Schell-model beam in a uniaxial crystal. Opt. Express 2011, 19, 13312–13325. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Peng, X.; Chen, Y.; Guo, L.; Cai, Y. Statistical properties of a radially polarized twisted Gaussian Schell-model beam in a uniaxial crystal. J. Mod. Optic. 2016, 64, 1–11. [Google Scholar] [CrossRef]
- Lu, X.; Shen, Y.; Zhu, X.; Zhao, C.; Cai, Y. Evolution properties of multi-Gaussian Schell model beams propagating in uniaxial crystal orthogonal to the optical axis. Opt. Appl. 2016, 146, 19–34. [Google Scholar]
- Liu, H.; Xia, J.; Lu, Y. Evolution properties of partially coherent standard and elegant Hermite–Gaussian beams in uniaxial crystals. J. Opt. Soc. Am. A 2017, 34, 2102–2109. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, L.; Wang, F.; Cai, Y. Evolution properties of a Laguerre–Gaussian correlated Schell-model beam propagating in uniaxial crystals orthogonal to the optical axis. J. Opt. Soc. Am. A 2015, 32, 374–380. [Google Scholar] [CrossRef]
- Su, J.; Xu, C.; Xu, H.; Qu, J. Evolution properties of the radially polarized Laguerre-Gaussian-correlated Schell-model beams propagating in uniaxial crystals. J. Opt. Soc. Am. A 2020, 37, 529–539. [Google Scholar] [CrossRef]
- Lin, R.; Chen, M.; Liu, Y.; Zhang, H.; Gbur, G.; Cai, Y.; Yu, J. Measuring refractive indices of a uniaxial crystal by structured light with non-uniform correlation. Opt. Lett. 2021, 46, 2268–2271. [Google Scholar] [CrossRef]
- Ciattoni, A.; Palma, C. Optical propagation in uniaxial crystals orthogonal to the optical axis: Paraxial theory and beyond. J. Opt. Soc. Am. A 2003, 20, 2163–2171. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Y.; Yu, J.; Liu, X.; Liu, L. Generation of partially coherent beams. Prog. Opt. 2017, 62, 157–223. [Google Scholar]
- Carter, W.H. Spot size and divergence for Hermite Gaussian beams of any order. Appl. Opt. 1980, 19, 1027–1029. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, R.; Sun, H.; Zhang, H.; Liu, Y.; Wu, J.; Yu, J.; Cai, Y.; Zhu, X. The Evolution Characteristics of Twisted Hermite–Gaussian Schell-Model Beams Propagating in a Uniaxial Crystal. Photonics 2023, 10, 507. https://doi.org/10.3390/photonics10050507
Lin R, Sun H, Zhang H, Liu Y, Wu J, Yu J, Cai Y, Zhu X. The Evolution Characteristics of Twisted Hermite–Gaussian Schell-Model Beams Propagating in a Uniaxial Crystal. Photonics. 2023; 10(5):507. https://doi.org/10.3390/photonics10050507
Chicago/Turabian StyleLin, Rong, Hongyan Sun, Hui Zhang, Yonglei Liu, Jidong Wu, Jiayi Yu, Yangjian Cai, and Xinlei Zhu. 2023. "The Evolution Characteristics of Twisted Hermite–Gaussian Schell-Model Beams Propagating in a Uniaxial Crystal" Photonics 10, no. 5: 507. https://doi.org/10.3390/photonics10050507
APA StyleLin, R., Sun, H., Zhang, H., Liu, Y., Wu, J., Yu, J., Cai, Y., & Zhu, X. (2023). The Evolution Characteristics of Twisted Hermite–Gaussian Schell-Model Beams Propagating in a Uniaxial Crystal. Photonics, 10(5), 507. https://doi.org/10.3390/photonics10050507






