Dynamics of Gas Ionization by Laser Pulses with Different Envelope Shapes
Abstract
1. Introduction
2. Model
3. Results and Discussion
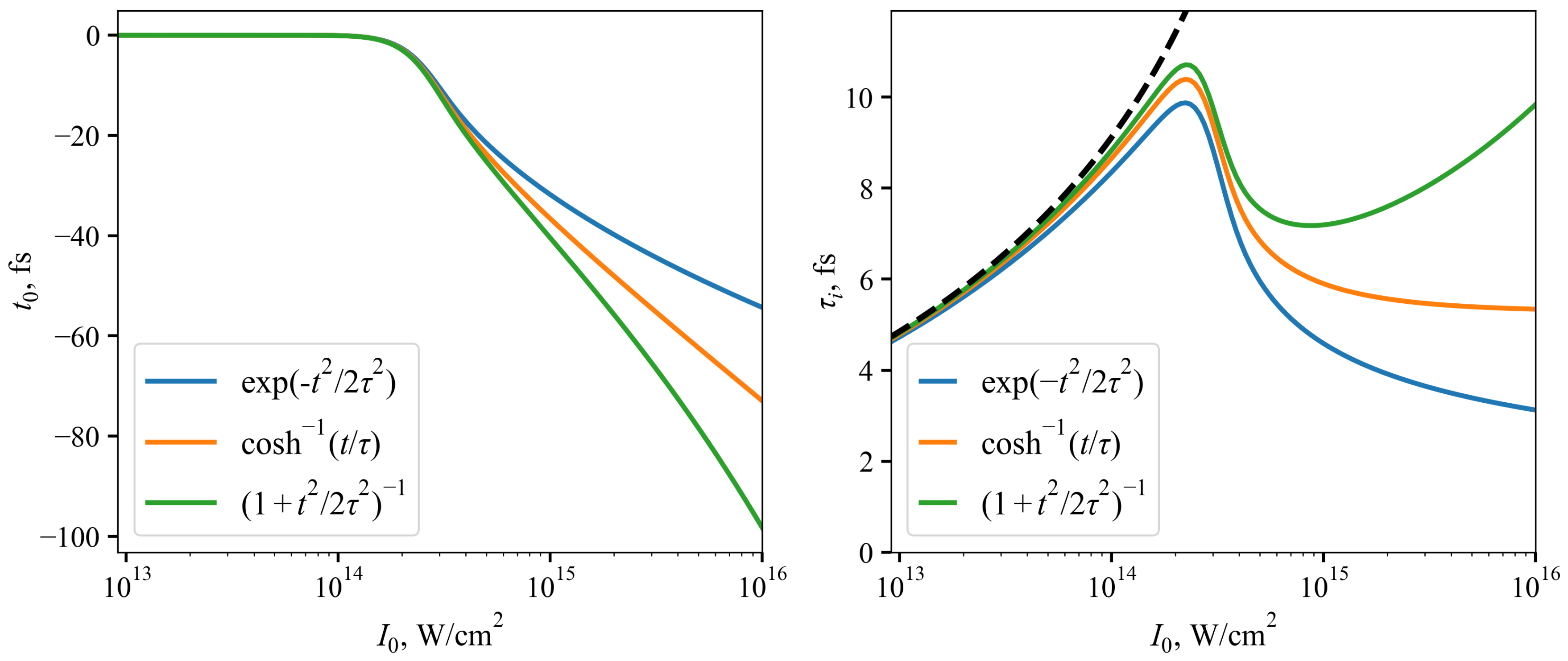
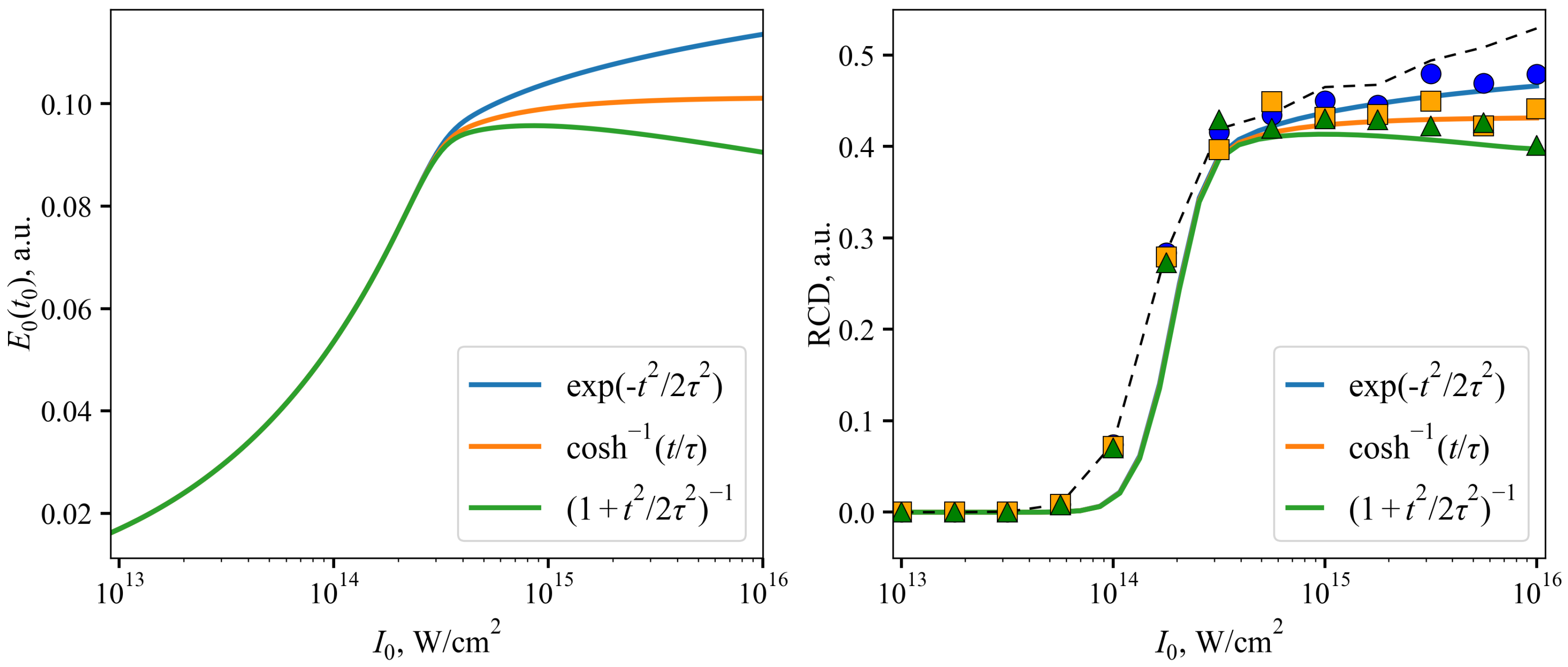
3.1. Analytical Solutions
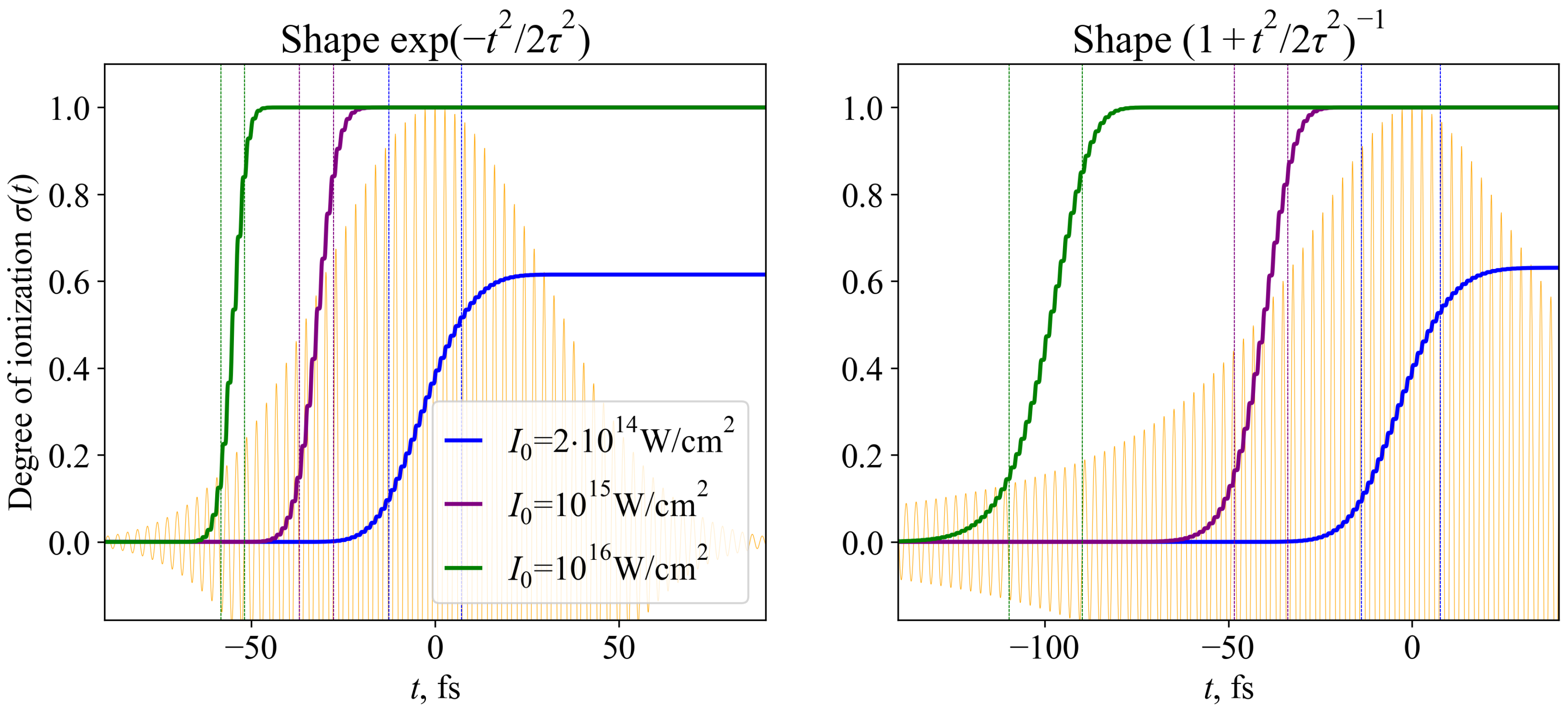
3.2. Numerical Calculations
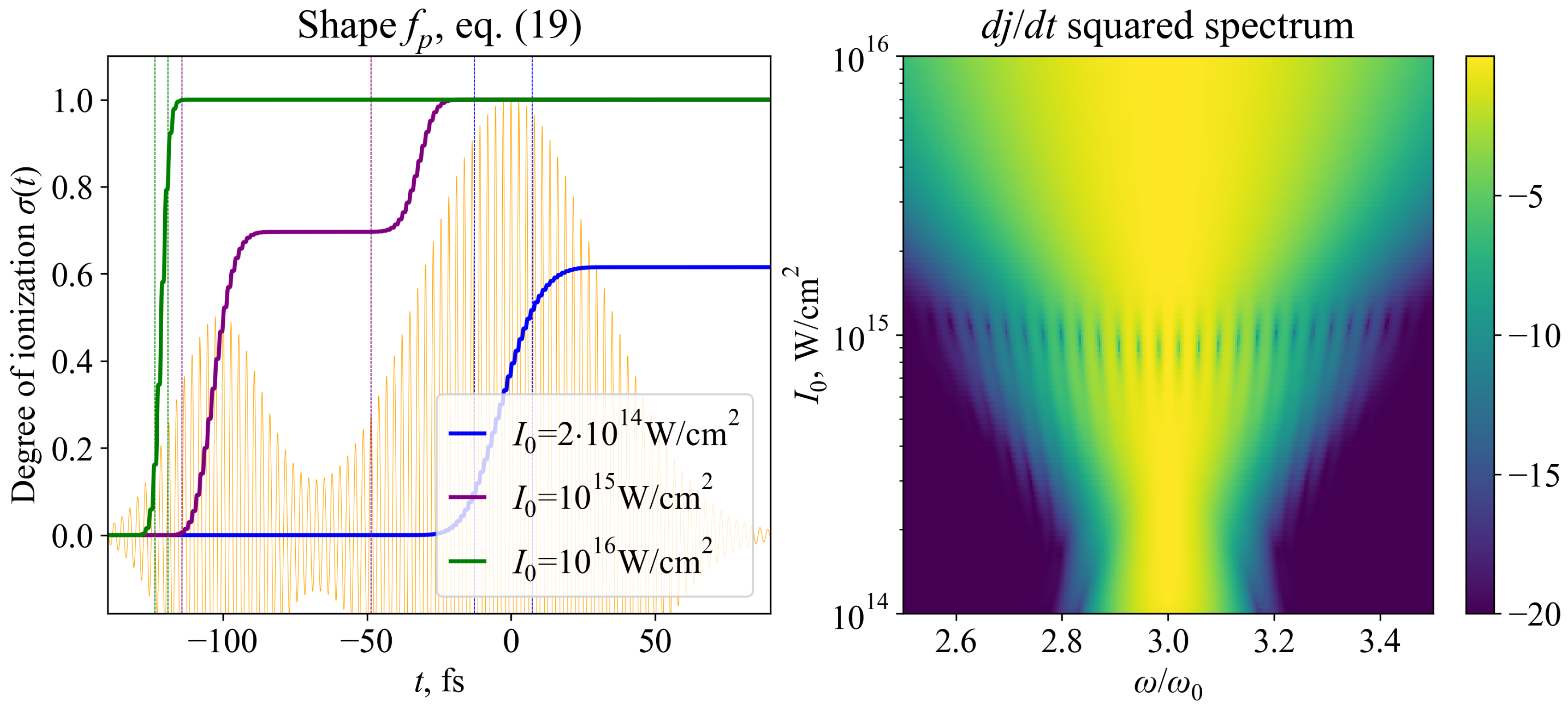
3.3. Presence of a Prepulse
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RCD | residual current density |
| TDSE | time-dependent Schrödinger equation |
| FWHM | full width at half maximum |
| TIPTOE | tunneling ionization with a perturbation for the time-domain observation of an electric field |
References
- Brunel, F. Harmonic generation due to plasma effects in a gas undergoing multiphoton ionization in the high-intensity limit. J. Opt. Soc. Am. B 1990, 7, 521–526. [Google Scholar] [CrossRef]
- Cook, D.; Hochstrasser, R. Intense terahertz pulses by four-wave rectification in air. Opt. Lett. 2000, 25, 1210–1212. [Google Scholar] [CrossRef] [PubMed]
- Geissler, M.; Tempea, G.; Scrinzi, A.; Schnürer, M.; Krausz, F.; Brabec, T. Light propagation in field-ionizing media: Extreme nonlinear optics. Phys. Rev. Lett. 1999, 83, 2930. [Google Scholar] [CrossRef]
- Jang, D.; Schwartz, R.M.; Woodbury, D.; Griff-McMahon, J.; Younis, A.H.; Milchberg, H.M.; Kim, K.Y. Efficient terahertz and Brunel harmonic generation from air plasma via mid-infrared coherent control. Optica 2019, 6, 1338–1341. [Google Scholar] [CrossRef]
- González de Alaiza Martínez, P.; Babushkin, I.; Bergé, L.; Skupin, S.; Cabrera-Granado, E.; Köhler, C.; Morgner, U.; Husakou, A.; Herrmann, J. Boosting terahertz generation in laser-field ionized gases using a sawtooth wave shape. Phys. Rev. Lett. 2015, 114, 183901. [Google Scholar] [CrossRef] [PubMed]
- Voronin, A.; Zheltikov, A. Laser-driven tunneling photocurrent as a source of midinfrared to microwave multidecade supercontinua yoked to high-order harmonics. Phys. Rev. A 2020, 101, 043813. [Google Scholar] [CrossRef]
- Silaev, A.A.; Vvedenskii, N.V. Analytical description of generation of the residual current density in the plasma produced by a few-cycle laser pulse. Phys. Plasmas 2015, 22, 053103. [Google Scholar] [CrossRef]
- Vvedenskii, N.V.; Kostin, V.A.; Laryushin, I.D.; Silaev, A.A. Excitation of low-frequency residual currents at combination frequencies of an ionising two-colour laser pulse. Quantum Electron. 2016, 46, 419. [Google Scholar] [CrossRef]
- Laryushin, I.; Romanov, A. Analysis of Combination Frequencies Arising from the Ionization of Gases by Multicolor Femtosecond Pulses. Photonics 2022, 9, 444. [Google Scholar] [CrossRef]
- Emelina, A.; Emelin, M.Y.; Ryabikin, M.Y. Wavelength scaling laws for high-order harmonic yield from atoms driven by mid-and long-wave infrared laser fields. JOSA B 2019, 36, 3236–3245. [Google Scholar] [CrossRef]
- Romanov, A.A.; Silaev, A.A.; Sarantseva, T.S.; Frolov, M.V.; Vvedenskii, N.V. Study of high-order harmonic generation in xenon based on time-dependent density-functional theory. New J. Phys. 2021, 23, 043014. [Google Scholar] [CrossRef]
- Emelina, A.; Emelin, M.Y.; Ryabikin, M.Y. Subattosecond keV beats of the high-harmonic x-ray field produced with few-cycle mid-IR laser pulses: Magnetic-field effects. Phys. Rev. A 2016, 93, 043802. [Google Scholar] [CrossRef]
- Silaev, A.A.; Vvedenskii, N.V. Residual-current excitation in plasmas produced by few-cycle laser pulses. Phys. Rev. Lett. 2009, 102, 115005. [Google Scholar] [CrossRef] [PubMed]
- Park, S.B.; Kim, K.; Cho, W.; Hwang, S.I.; Ivanov, I.; Nam, C.H.; Kim, K.T. Direct sampling of a light wave in air. Optica 2018, 5, 402–408. [Google Scholar] [CrossRef]
- Cho, W.; Hwang, S.I.; Nam, C.H.; Bionta, M.R.; Lassonde, P.; Schmidt, B.E.; Ibrahim, H.; Légaré, F.; Kim, K.T. Temporal characterization of femtosecond laser pulses using tunneling ionization in the UV, visible, and mid-IR ranges. Sci. Rep. 2019, 9, 16067. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Zhang, D.; Liu, J.; Zhao, Z.; Lin, C.D. Searching for optimal THz generation through calculations of the asymmetry of photoelectron momentum distributions by an improved strong-field-approximation method. Phys. Rev. A 2023, 107, 013106. [Google Scholar] [CrossRef]
- Tong, X.M.; Lin, C.D. Empirical formula for static field ionization rates of atoms and molecules by lasers in the barrier-suppression regime. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2593. [Google Scholar] [CrossRef]
- Silaev, A.A.; Romanov, A.A.; Vvedenskii, N.V. Multi-hump potentials for efficient wave absorption in the numerical solution of the time-dependent Schrödinger equation. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 065005. [Google Scholar] [CrossRef]
- Täschler, P.; Bertrand, M.; Schneider, B.; Singleton, M.; Jouy, P.; Kapsalidis, F.; Beck, M.; Faist, J. Femtosecond pulses from a mid-infrared quantum cascade laser. Nat. Photonics 2021, 15, 919–924. [Google Scholar] [CrossRef] [PubMed]
- Rampur, A.; Spangenberg, D.M.; Stępniewski, G.; Dobrakowski, D.; Tarnowski, K.; Stefańska, K.; Paździor, A.; Mergo, P.; Martynkien, T.; Feurer, T.; et al. Temporal fine structure of all-normal dispersion fiber supercontinuum pulses caused by non-ideal pump pulse shapes. Opt. Express 2020, 28, 16579–16593. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emelina, A.; Laryushin, I.; Romanov, A. Dynamics of Gas Ionization by Laser Pulses with Different Envelope Shapes. Photonics 2023, 10, 499. https://doi.org/10.3390/photonics10050499
Emelina A, Laryushin I, Romanov A. Dynamics of Gas Ionization by Laser Pulses with Different Envelope Shapes. Photonics. 2023; 10(5):499. https://doi.org/10.3390/photonics10050499
Chicago/Turabian StyleEmelina, Anna, Ivan Laryushin, and Alexander Romanov. 2023. "Dynamics of Gas Ionization by Laser Pulses with Different Envelope Shapes" Photonics 10, no. 5: 499. https://doi.org/10.3390/photonics10050499
APA StyleEmelina, A., Laryushin, I., & Romanov, A. (2023). Dynamics of Gas Ionization by Laser Pulses with Different Envelope Shapes. Photonics, 10(5), 499. https://doi.org/10.3390/photonics10050499




