1. Introduction
In recent years, metasurface technology has gained increasing development and application in microwave circuit and antenna design due to its complete planar structure. As in [
1,
2], metasurfaces are used for antenna gain enhancement and environmental sensing. In [
2,
3], metasurfaces are also used to design microwave component such as spatial filters and transmitting array antennas. In [
4], metasurfaces based on graphene-based structures are presented for reconfigurability of electromagnetic devices and so on. As another important application of metasurfaces, the design of slow-wave substrate-integrated waveguide devices is also receiving increasing attention.
Substrate-integrated waveguide (SIW) technology enables the realization of a rectangular waveguide in planar form using cost-effective processing solutions such as printed-circuit-board techniques. This popular technology has provided a great design platform to implement system integration and packaging [
5]. However, the practical applications of SIW is usually limited by physical size, particularly at low frequencies since the cutoff frequency is mainly determined by the SIW’s width. To overcome this hurdle, various methods, including substrate-integrated folded waveguide (SIFW), half-mode SIW (HMSIW) and ridge SIW (RSIW) among many others, have been proposed and studied in order to reduce the size of SIWs [
6,
7,
8]. In 2014, a slow-wave SIW (SW-SIW) concept was reported [
9]. In this SW-SIW scheme, periodically patterned blind-via arrays are formed, which can effectively enhance the equivalent ground capacitance of the SIW, thus decreasing its phase velocity and cutoff frequency and eventually realizing size miniaturization. Compact microwave filters have also been developed in this technology [
10]. However, the SIFW, RSIW and blind-via-patterned SW-SIW are all realized through multilayer structures, which increases the complexity of fabrication.
Recently, another type of SW-SIW patterned with nonuniform metasurface unit cells has been studied and demonstrated [
11]. The periodically patterned nonuniform metasurface unit cells can enlarge the equivalent inductance in the SW-SIW structures but exert little influence on the equivalent capacitance. Therefore, the equivalent permeability of the SW-SIW can be enhanced effectively, while the equivalent permittivity remains nearly unchanged, so that the product value of the equivalent permeability and permittivity is eventually augmented. In this way, the phase velocity and cutoff frequency of the SW-SIW can be decreased. That is to say, the guided-wave properties are changed and a slow-wave effect is manifested. Hence, a polyline-patterned SW-SIW can realize good size reduction on the premise of keeping a simple structure and easy fabrication. Based on this concept, a partially patterned slow-wave HMSIW (SW-HMSIW) and miniaturized SW-HMSIW coupler have been developed [
12,
13]. Moreover, an inductor-loaded anisotropic SW-SIW has also been studied and designed [
14]. By loading lumped inductors of various values along both the transverse and longitudinal directions, the equivalent relative permeability and permittivity in connection with these two directions is different, so that the property of anisotropy can be obtained. Meanwhile, patterning with lumped inductors can release the interrelationship between the phase velocity and cutoff frequency of the SW-SIW. This feature is very useful in the design of matching networks for SIW circuits and leaky-wave antennas. It becomes apparent that this class of emerging guided-wave structures holds promise and should be further explored and studied for spurring its potential applications.
In this work, an SW-SIW patterned with nonuniform metasurface unit cells is investigated in detail. The influence of rotating the proposed nonuniform cross-unit cells on the guided-wave properties of SW-SIW is studied. Particularly, it is significantly essential to separate the proposed work from the previous research reported in [
9,
10,
11,
12,
13,
14]. Firstly, in [
9,
10], blind-vias are utilized to enhance the effective permittivity of the SW-SIW. Obviously, they are different from the proposed work structurally and theoretically, as well as those of [
11,
12,
13,
14]. For this method, only the height and density of the blind-vias can be tuned to control the guided-wave properties of the SW-SIW, which is limited. Secondly, a SW-SIW and its half-mode version with polyline unit cells, as well as a demonstrated application, are reported in [
11,
12,
13]. However, since the polyline unit cells patterned in this SW-SIW are uniformly geometric on the metasurface, their guided-wave properties can only be controlled by changing the quantity or topology of the uniform metasurface unit cells. Moreover, there is an interrelationship between the metasurface’s phase velocity and cutoff frequency. With this interrelationship, the phase velocity and cutoff frequency cannot be controlled independently but will influence each other accordingly. Thirdly, to release this interrelationship, lumped inductors with various values are utilized to replace the polyline in the SW-SIW, as reported in [
14]. Nevertheless, the strong parasitic effect of lumped inductors restrains the applications of the inductor-loaded SW-SIW at high frequencies. According to the investigation in [
14], the parasitic effect of lumped inductors causes a notch-filtering phenomenon. Meanwhile, the design flexibility of this method is also limited, since only values of the lumped inductors can be tuned. Obviously, all three methods mentioned above have several limitations, especially regarding design flexibility. Moreover, the guided-wave properties of the SW-SIW with nonuniform polyline unit cells have not been investigated comprehensively. The influence of rotating the nonuniform unit cells on the guided-waves’ properties are unstudied as well. These three issues will be explored in this work. Actually, there is still an insufficiency in the systematic summary of the polyline-patterned SW-SIW. Fortunately, both the SW-SIW with uniform polyline unit cells in [
11] and the SW-SIW with lumped inductors in [
14] can be regarded as exceptional cases of the SW-SIW with nonuniform polyline unit cells. Investigation of a SW-SIW with nonuniform metasurface unit cells can cover most aspects of the polyline-patterned SW-SIW.
This paper is organized as follows. The geometric configuration and equivalent-circuit model of the SW-SIW patterned with the proposed nonuniform cross-unit cell, as well as the corresponding theoretical analyses, are presented in
Section 2.
Section 3 describes in detail the extraction method and procedures of the equivalent parameters of the proposed unit cell. The guided-wave properties of the SW-SIW with nonuniform metasurface unit cells rotating at different angles are studied in
Section 4; experimental results and the discussion are shown in
Section 5. Finally, the conclusions are given.
2. SW-SIW with Non-Uniform Cross-Unit Cells
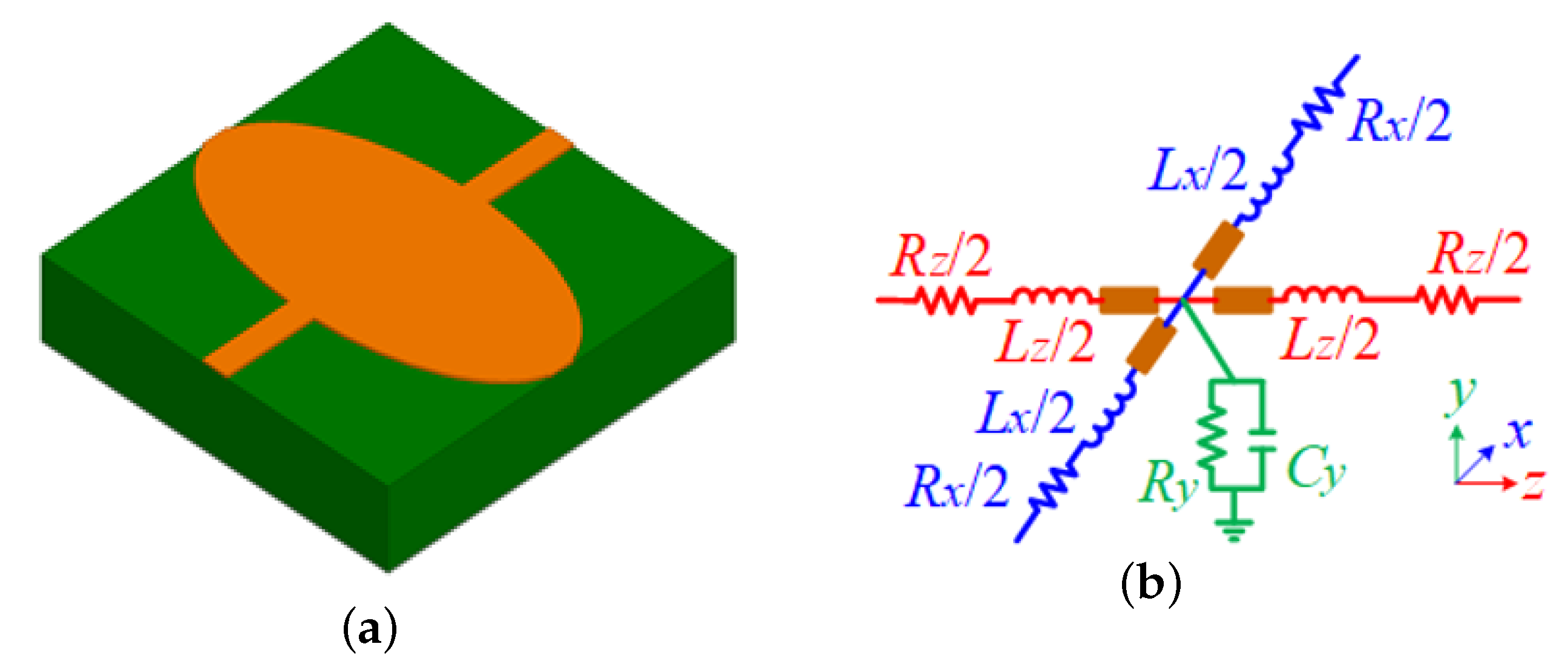
Figure 1 shows the structural geometry and equivalent circuit of the proposed nonuniform cross-metasurface unit cell along with the two-dimensional (2D) transmission line model utilized in the analysis of the SW-SIW. Obviously, the proposed unit cell consists of two perpendicularly crossing microstrip lines, of which one is uniformly shaped and the other is ellipsoid. As shown in
Figure 1a, the two perpendicular microstrip line branches are different from each other. Hence, for the simplification of description, the proposed unit cell is called a nonuniform cross-metasurface unit cell. Based on the equivalent-circuit-modeling method utilized in [
15,
16], the simplified equivalent circuit of the proposed unit cell can be expressed as a 2D transmission line model, as shown in
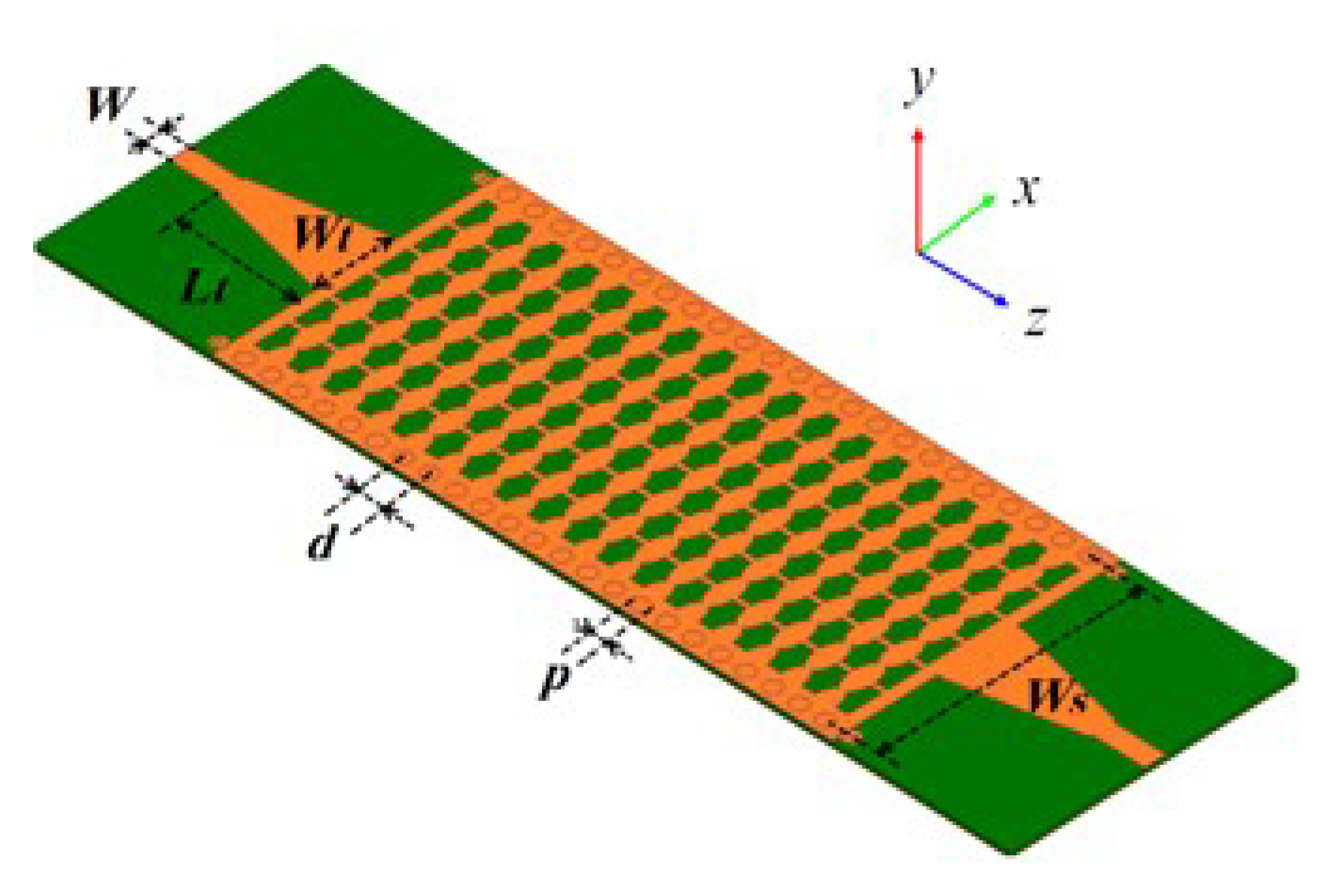
Figure 1b. Moreover, by patterning this proposed unit cell periodically into the metal top cover of a conventional SIW section, a SW-SIW is created, with its three-dimensional (3D) schematic description as shown in
Figure 2, in which two tapered transitions are also included.
For the proposed SW-SIW structure, as depicted in [
11,
12,
13,
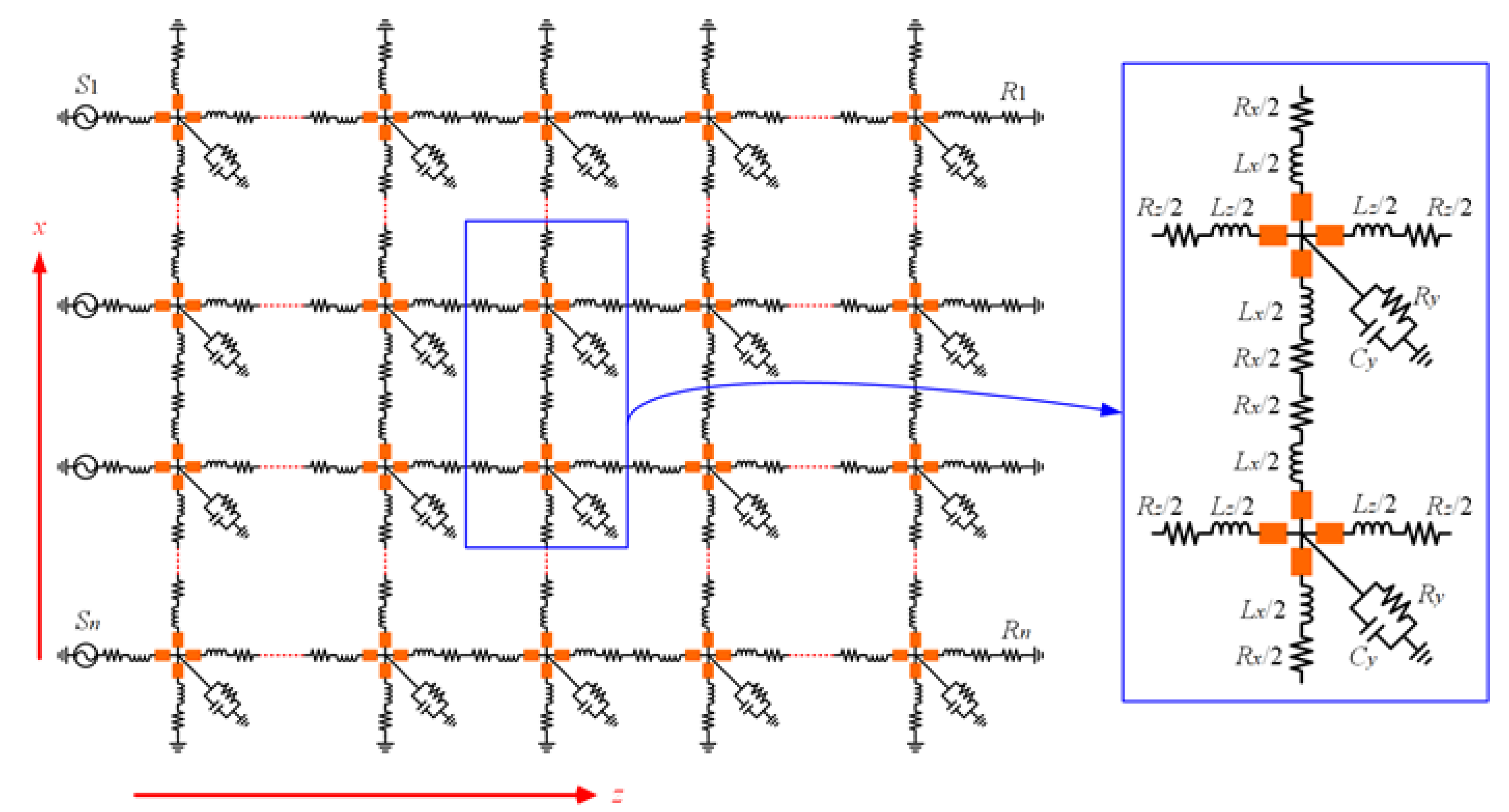
14], with the nonuniform cross-metasurface unit-cell patterning, the equivalent relative permeability of the SW-SIW can be enhanced remarkably while the change to its equivalent relative permittivity is barely visible, so that the product of its equivalent permittivity and permeability can be increased effectively. In this way, the phase velocity and cutoff frequency of the SW-SIW can also be decreased effectively, and the slow-wave effect can be exhibited demonstrably. Furthermore, to analyze the slow-wave effect of the proposed structure, an equivalent-circuit model based on a 2D transmission line network is developed by using the periodic analysis method introduced in [
17,
18,
19], as sketched in
Figure 3.
Here, the
x-axis represents the transverse standing wave direction and the
z-axis denotes the traveling wave direction. As shown in
Figure 3, at each node, inductors
/2 and
/2 represent the equivalent inductances contributed by the uniformly shaped and ellipsoid microstrip lines in the proposed unit cell.
represents the equivalent grounded capacitance between the nonuniform cross-metasurface microstrip and the ground plane.
Considering a linear, uniformly anisotropic medium through a diagonal permeability tensor, the two sub-equations of Maxwell’s equations can be respectively written in terms of Cartesian field components as:
and
For the quasi-TEM analysis in a microstrip line, the longitudinal fields are negligible and
dominates
. As such, for wave propagation along the
z-direction, the non-zero field components are
and
. Therefore, (
1) and (
2) can be simplified as:
By eliminating
, (
3) can be represented in the form of
as follows:
For a microstrip line, the voltage
between the ground and the microstrip can be captured by integrating (
4) along the substrate thickness. In the time–harmonic steady-state electromagnetic field, the integration yields:
Meanwhile, the Telegrapher’s equations for a transmission line with distributed inductance
(H/m) and capacitance
(F/m) can be expressed as:
where
,
are the distributed resistance and conductance along the
z- and
y-directions, respectively.
By eliminating
I(z), the second-order differential equation for the voltage along the transmission line is expressed as:
Based on the Analogy thought, two equivalences can be set up by comparing (
3) with (
6) and (
5) with (
7) separately:
Similarly, by applying the same procedures to the wave propagation along the
x-direction, another equivalence can be set up as:
By considering these relative permittivity and permeability values, the phase constant and phase velocity along the
z-direction can be obtained as [
20,
21,
22]:
Once
= 0, the cutoff frequency is:
Obviously, the phase constant and phase velocity along the z-direction mainly depend on the effective permeability along the z-direction and the effective permittivity along the y-direction .
According to the derived formulations,
and
can be used to determine the phase constant and phase velocity along the
z-direction of the proposed SW-SIW. Hence, to realize some required guided-wave properties, it is essential to further investigate the proposed nonuniform cross-metasurface unit cell and extract its equivalent material parameter tensors, i.e., its permittivity and permeability tensors.
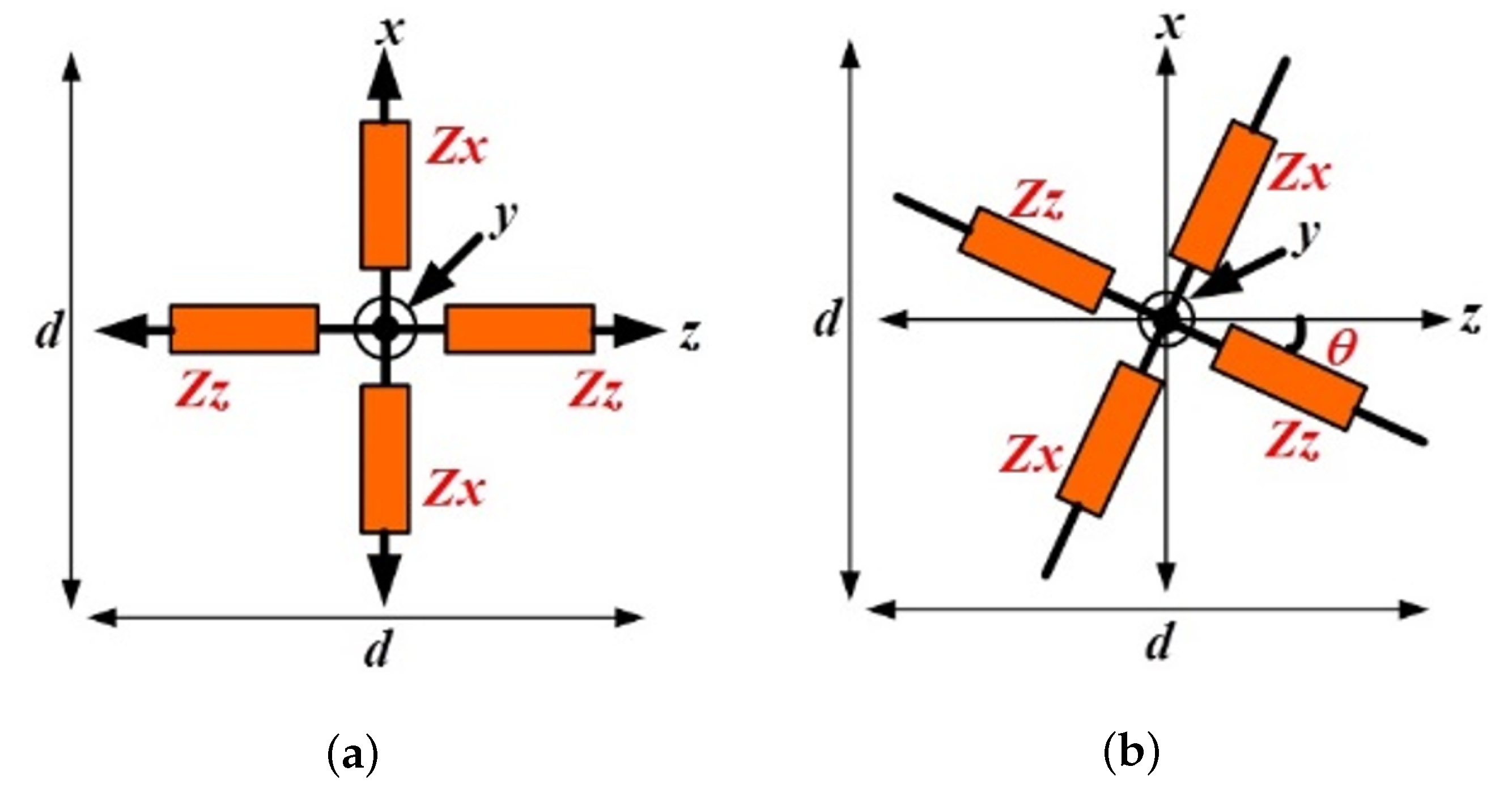
Figure 4 shows a simulated model of the proposed unit cell for parameter extraction, as well as the related Cartesian coordinate system. Once this unit cell is a sub-wavelength structure, the effect from the patterned microstrip lines can be regarded as an influence related to the material parameters of the substrate.
For the
mode in an SIW, its electric coefficients are considered along the
y-direction, while the magnetic coefficients are considered along the
x- and
z-directions. Therefore, the effective material parameter tensors of the proposed unit cell can be simplified as:
Then, the dispersion equation in this guided-wave medium can be expressed as [
23]:
where
is equal to
due to the reciprocity of the proposed unit cell, and
is the permittivity of the substrate.
By considering (
8)–(
10), (
14) and (
15) together, the coefficients of the simplified effective permeability and permeability tensors for
Figure 5b can be calculated as [
24]:
By considering (
8), (
9) and (
15) together, it can be obtained that the coefficients of the effective permeability tensor are:
4. Numerical Simulation of Guided-Wave Properties of SW-SIW
As shown in [
11,
18], since the proposed sub-wavelength unit cells, whether rotating or not, are periodically patterned into the metal top cover of the SIW, the equivalent material effect and equivalent circuit parameters in the unit cell can be generalized to the whole SW-SIW uniformly. That is to say, the whole SW-SIW is characterized by similar equivalent material and circuit parameters as a single unit cell, which is also given in
Figure 3. Hence, by combining this property with the extraction of parameter tensors, the equivalent permeability and permittivity tensors given in Section III can also be generalized to the whole SW-SIW patterned with the proposed unit cells that rotate at arbitrary angles. Therefore, for an SW-SIW patterned with rotary unit cells, its equivalent permeability and permittivity tensors can also be simply calculated by using (
16).
Furthermore, to verify the accuracy of these results, some 3D full-wave electromagnetic simulations are carried out for comparison by using the HFSS software. In the simulation, the substrate is set to a thickness of 0.508 mm, a relative permittivity of 2.94, a relative permeability of 1.0, a dielectric loss tangent of 0.0012 and a magnetic loss tangent of 0.0. Moreover, the substrate is covered with a 0.035 mm-thick conductor.
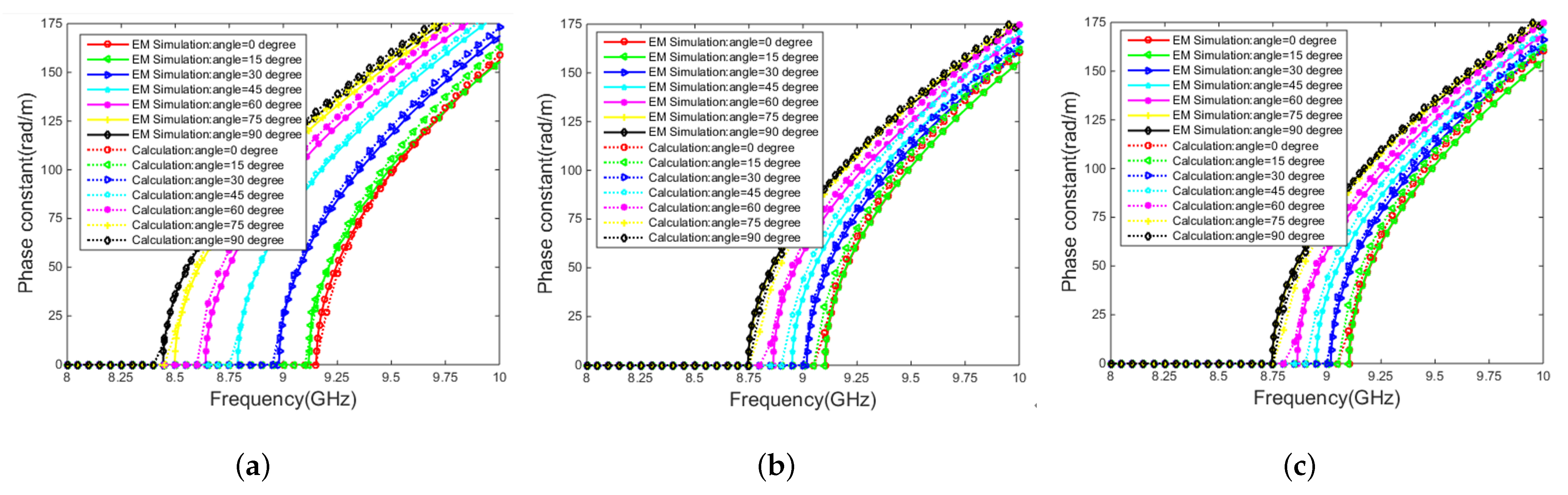
Figure 8 shows the calculated and simulated phase constants of the proposed SW-SIW with various substrate thicknesses h as well as different angles of rotation. In order to make the comparison more reasonable, all substrate thicknesses have been normalized to the first thickness
. According to
Figure 8a, for the proposed SW-SIW with substrate thickness ratio h/
= 100%, the cutoff frequency can be decreased from 9.12 GHz to 8.4 GHz as the patterned unit cells rotate from 0° to 90°. Once the substrate thickness is doubled, i.e., h/
= 200%, the cutoff frequency can only decrease from 9.12 GHz to 8.75 GHz with the patterned unit cells rotating from 0° to 90°. Moreover, for the case of h/
= 300%, the cutoff frequency can only vary from 9.12 GHz to 8.88 GHz with the angle of rotation swinging between 0° and 90°. Thus, it can be summarized that the slow-wave effect of the SW-SIW due to rotation of the patterned unit cells weakens as the substrate thickness increases. Therefore, in practical applications, using a substrate with a relatively low thickness is preferred for the purpose of prominent control of the slow-wave effect by rotating the patterned unit cell.
Figure 9a,b show the magnitude of the current and electric field distributions of the
mode at 10 GHz in the SW-SIW. The electric fields are mainly concentrated at the center region of SW-SIW—similar to the the conventional SIW—while the current distribution is diffused due to the loaded nonuniform metasurface elements on the metal surface of the SW-SIW. This behavior is a typical phenomenon for slow-wave SIW and increases the loss of the SW-SIW.
5. Experimental Results and Discussion
To demonstrate the influence on guided-wave properties from rotating the nonuniform metasurface unit cells in the SW-SIW, a series of SW-SIW transmission lines patterned with polyline unit cells with different angles of rotation are designed, optimized and fabricated. For simplification of the comparison in our experiments, the angles of rotation (
in
Figure 10) are selected as 0°, 30°, 60° and 90°. All of the structures with the selected angles of rotation are modeled, simulated and optimized using the ANSYS HFSS software.
By using the standard printed-circuit-board (PCB) process, four prototypes of the SW-SIW transmission lines patterned with the proposed nonuniform cross-unit cells with various angles of rotation are fabricated. Rogers/Duroid 6002 substrate with thickness of 0.508 mm, relative permittivity of 2.94 ± 0.02, dielectric loss tangent of 0.0023 and relative permeability of 1.0 is used for fabrication.
Figure 11 shows photographs of the fabricated prototypes. Finally, subminiature version A (SMA) connectors are silver-soldered at the input/output ports of each fabricated prototype for the convenience of connection with coaxial cables for measurement.
The four fabricated prototypes, with their photographs shown in
Figure 10, are measured by using a Keysight N5242A vector network analyzer and a self-designed test fixture. To remove the influence of insertion loss and phase constant from the tapered transitions and the 50-ohm microstrip lines, the thru-reflection-line (TRL) method is utilized for calibration before measurements.
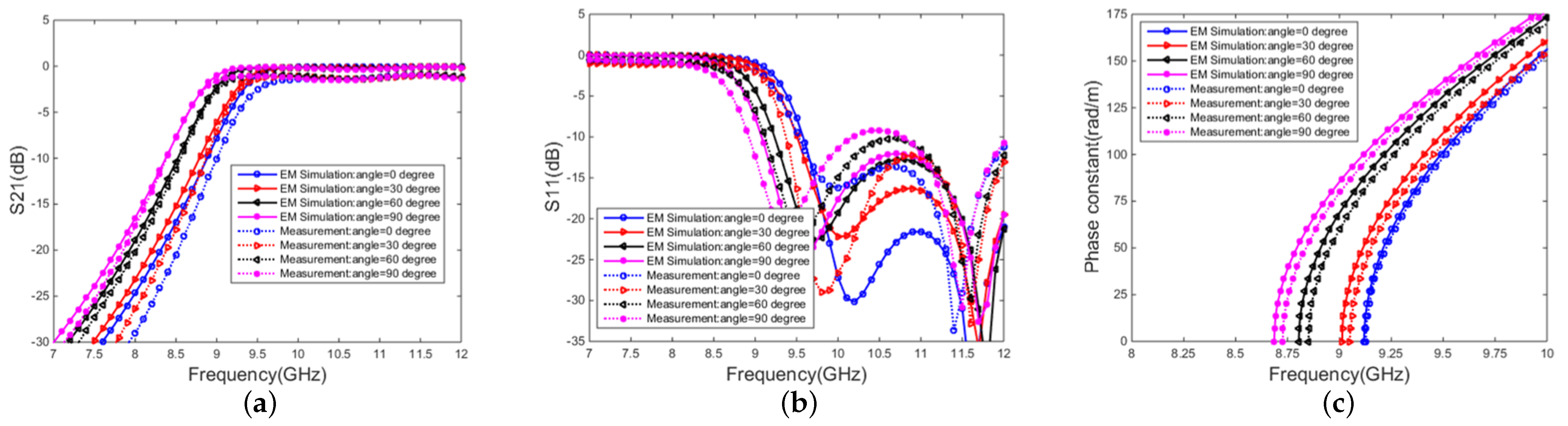
Figure 11 shows comparison between the measured and simulated results of the fabricated SW-SIW structures. It can be easily obtained from
Figure 11a that all four prototypes achieve insertion losses less than 2 dB from 9.2 GHz to 12 GHz. Moreover, the cutoff frequencies of the 0°, 30°, 60° and 90° prototypes are 9.1 GHz, 9.0 GHz, 8.85 GHz and 8.75 GHz, respectively. Meanwhile, as shown in
Figure 11b, the measured return losses of the fabricated prototypes are all better than 10 dB over 9–12 GHz, which is a bit worse than the simulated ones. Moreover, the phase constants of the four fabricated SW-SIWs are listed in
Figure 11c, in which the measured results are in good agreement with their simulated counterparts.
6. Conclusions
This work studied guided-wave properties of an SW-SIW patterned with the proposed nonuniform metasurface unit cells comprehensively to provide a systematical summary of a polyline-patterned SW-SIW. The influence of rotating the patterned nonuniform unit cells on the guided-wave properties of the SW-SIW was investigated theoretically and experimentally as well. By rotating the proposed nonuniform cross-unit cell in the SW-SIW through various angles, different phase constants, cutoff frequencies and phase velocities can be generated. Particularly, as the branch with a stronger equivalent inductance effect in the unit cell rotates to be parallel with the transverse direction of the SW-SIW, the slow-wave effect is stronger and the cutoff frequency is smaller. A series of prototypes of the proposed SW-SIW with various angles of rotation are fabricated for verification, and their measured results agree with their simulations quite well. Moreover, by rotating the patterned unit cells from 0° to 90°, the cutoff frequency can be decreased by 10%. These results illustrate that, besides using the quantity and geometry of patterned unit cells, the guided-wave properties of the proposed SW-SIW can be controlled flexibly by rotating the patterned unit cells through arbitrary angles, which will be useful in the development of controllable microwave guiding-wave structures and component applications.
Finally,
Table 1 summarizes some comparisons between the proposed SW-SIW and some reported similar size-miniaturized SIW structures. In these comparisons, the percentage of size reduction (PSR) is defined as:
where
denotes the circuit size of the size-miniaturized SIW structures, including the SIFW, RSIW and SW-SIW. SSIW represents the circuit size of their corresponding conventional SIW counterparts.
According to
Table 1, the SIFW and RSIW can achieve higher PSR than the proposed SW-SIW since the SIFW can utilize more layers and the RSIW can employ more ridges for size reduction. However, using more layers in SIFW or more ridges in RSIW both increase the fabrication complexity and cost. Meanwhile, it is more difficult to guarantee their transmission performance as well. As compared with all the works in [
9,
11,
12,
14], the proposed SW-SIW has similar size reduction. Nevertheless, the SW-SIW reported in [
11,
12,
14], as well as the conventional SIW, SIFW and RSIW, have only one or two options for design flexibility, whereas the SW-SIW with blind-vias in [
9] and the proposed one each have three different options for design flexibility, which means that they are promising for realizing more functions and better performance. Finally, the blind-vias-patterned SW-SIW requires a multilayer fabrication process, which is much more complex than that of the proposed SW-SIW. Hence, in practical applications, the proposed SW-SIW with rotating nonuniform unit cells is much more preferred than other similar work due to its increased design flexibility and decreased complexity as well as similar size reduction.