On Performance Analysis of Cooperative Horizontal and Vertical Underwater VLC Systems with Best Relay Selection
Abstract
1. Introduction
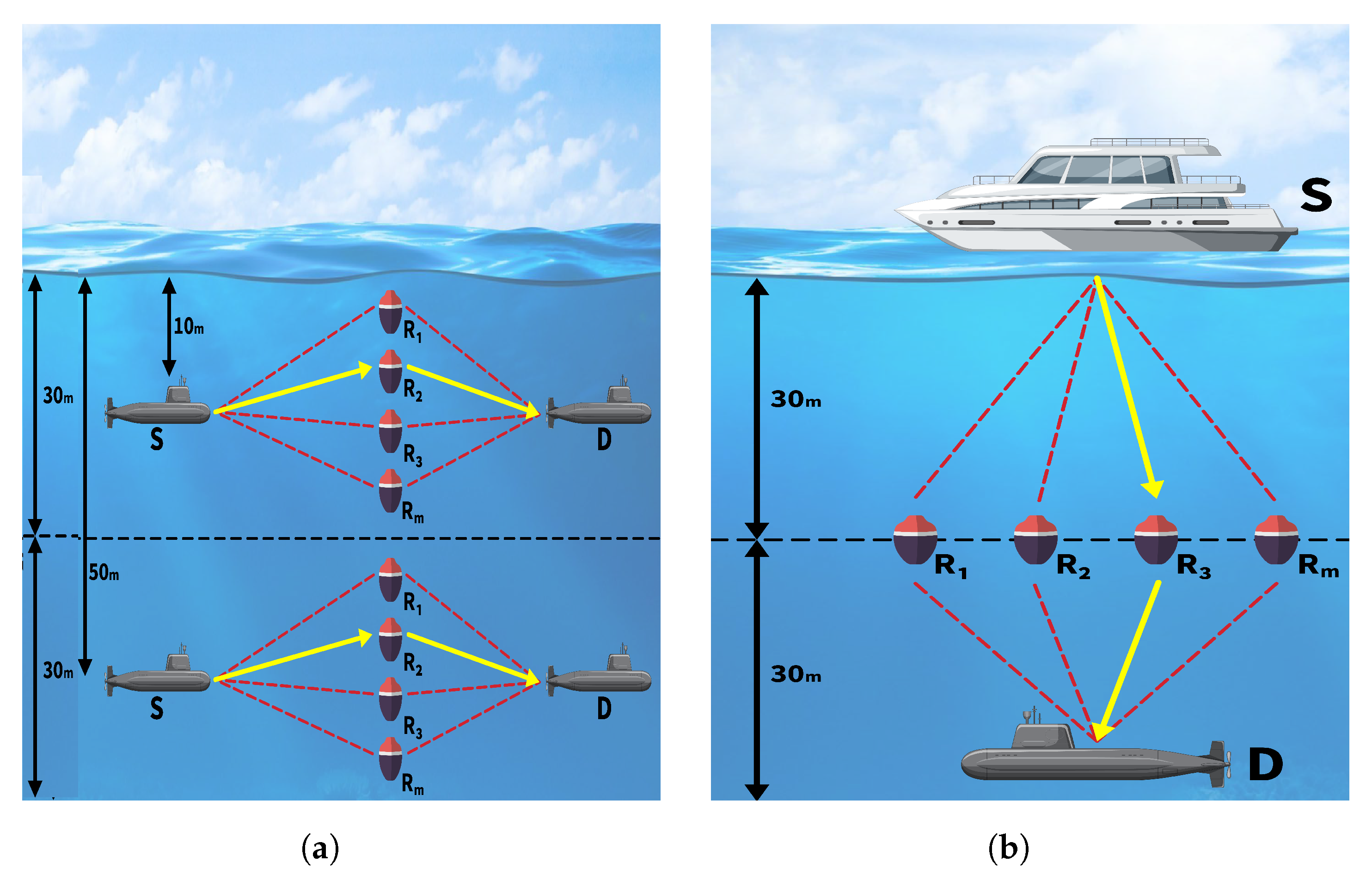
2. System and Channel Model
3. Performance Analysis
3.1. Outage Probability
3.2. Ergodic Capacity
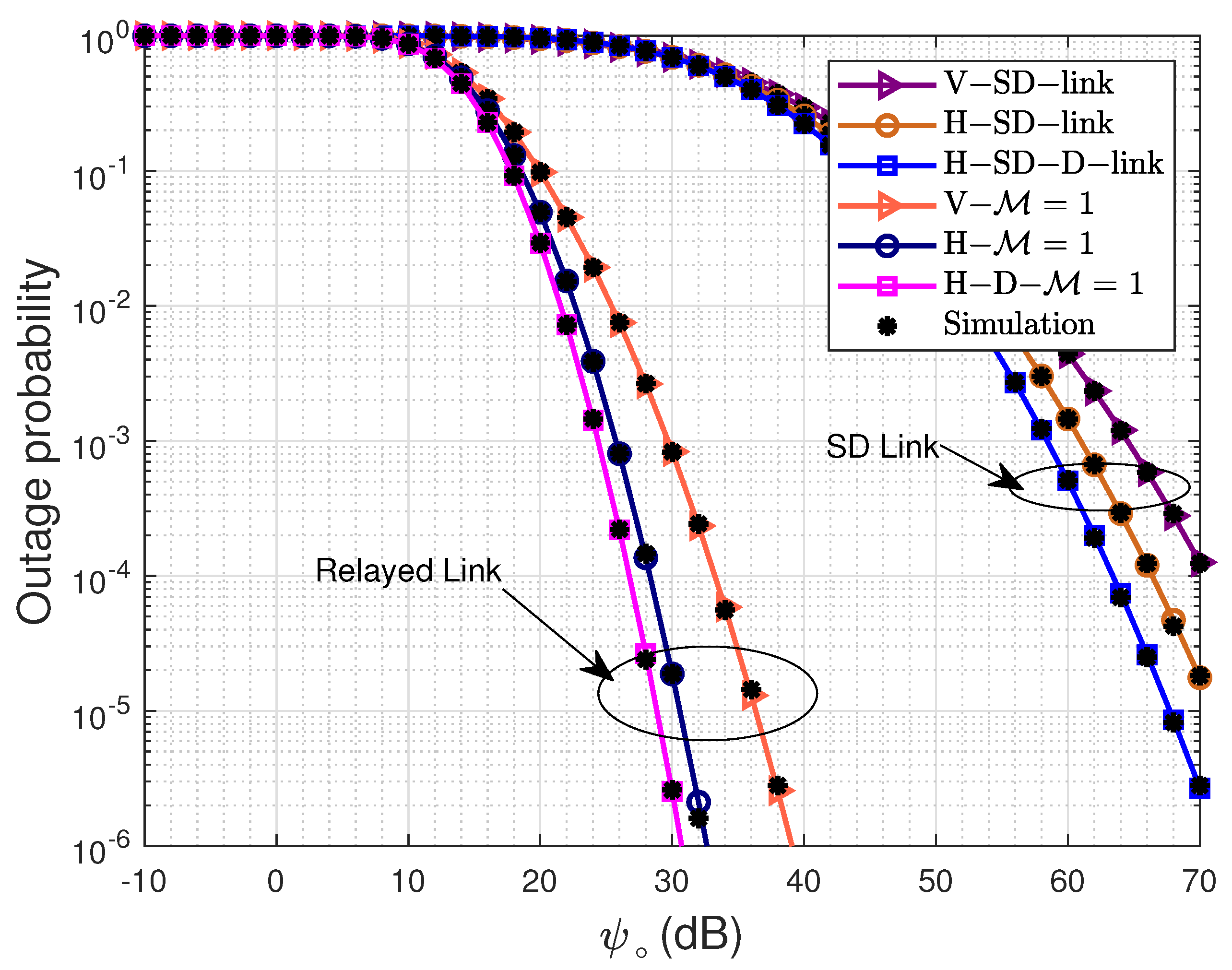
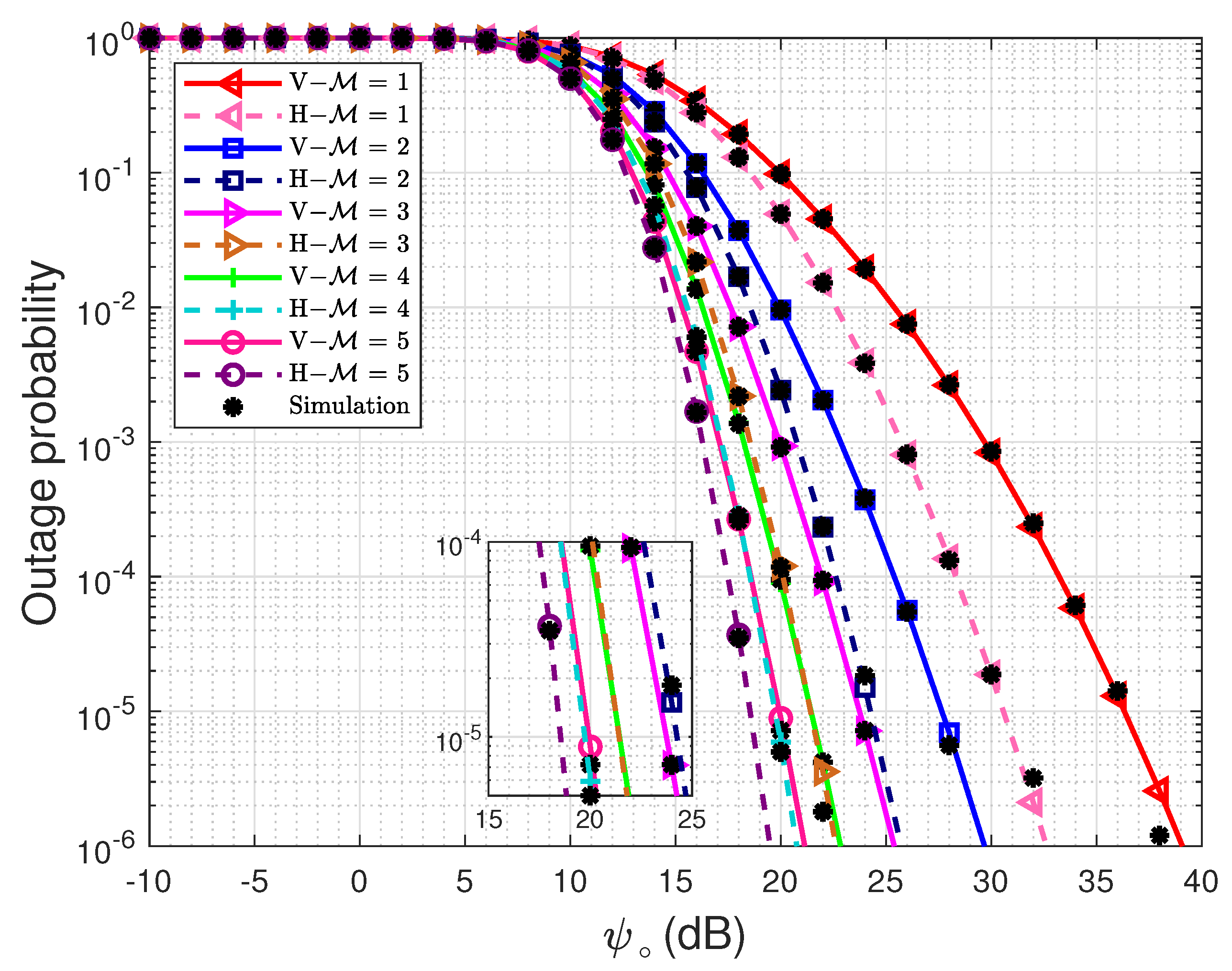
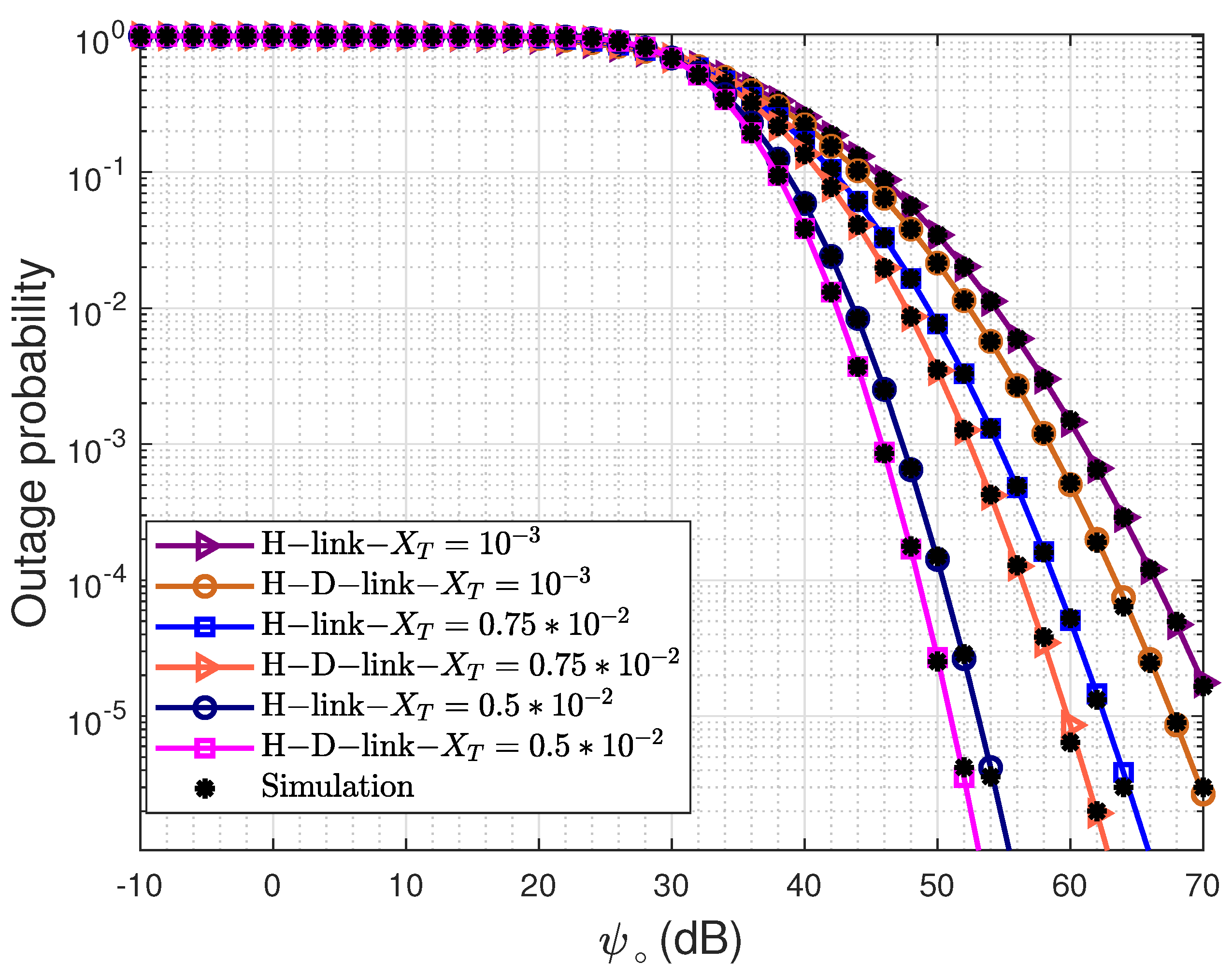
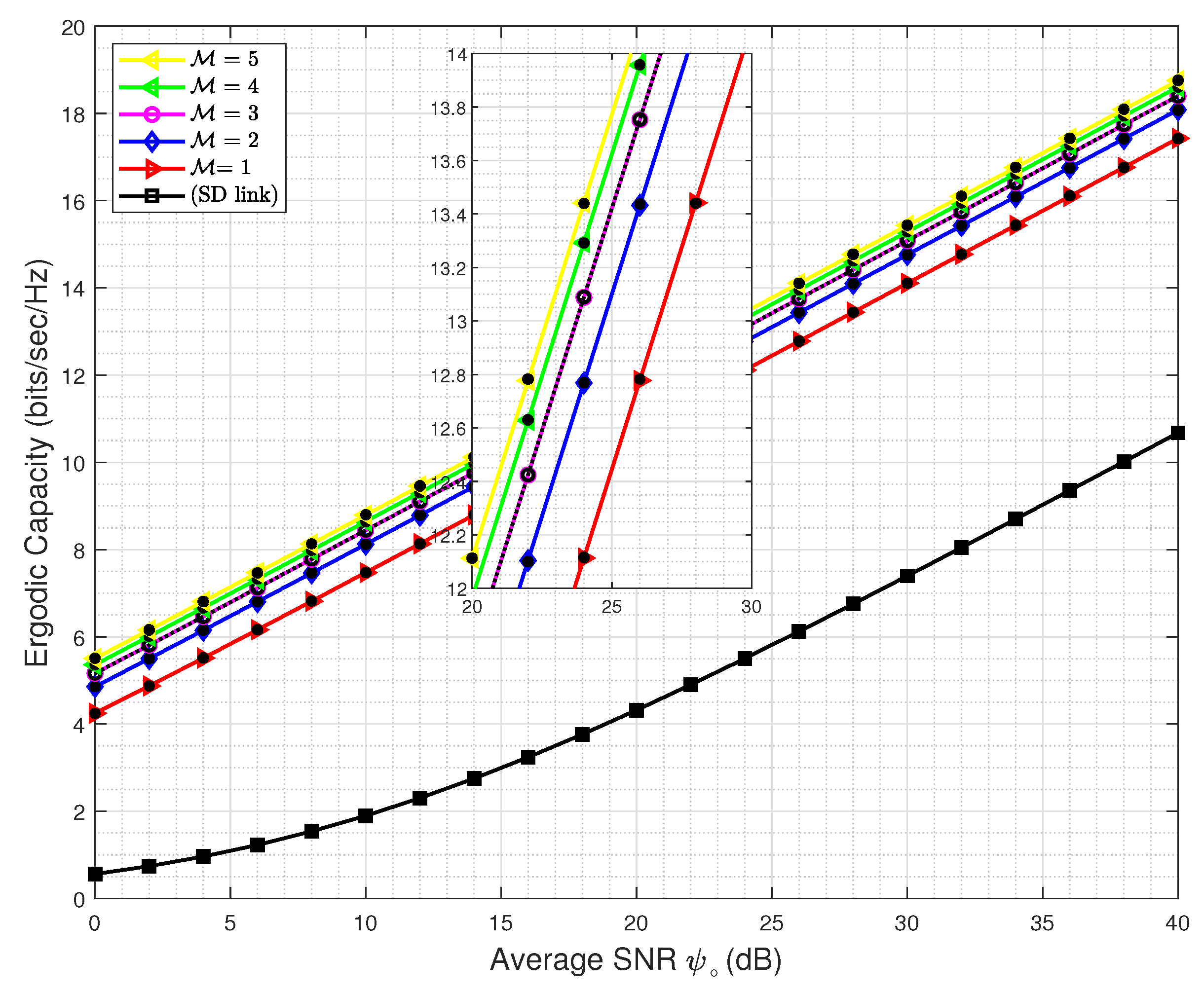
4. Numerical and Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A survey of underwater optical wireless communications. IEEE Commun. Surv. Tuts. 2016, 19, 204–238. [Google Scholar] [CrossRef]
- Gussen, C.M.; Diniz, P.S.; Campos, M.; Martins, W.A.; Costa, F.M.; Gois, J.N. A survey of underwater wireless communication technologies. J. Commun. Inf. Syst. 2016, 31, 242–255. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, M.; Wang, X.; Ren, X. Design and Implementation of More Than 50m Real-Time Underwater Wireless Optical Communication System. J. Light. Technol. 2022, 40, 3654–3668. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, G.; Li, X.; Liao, Q.; Guo, Y. Performance Improvement of Underwater Continuous-Variable Quantum Key Distribution via Photon Subtraction. Entropy 2019, 21, 1011. [Google Scholar] [CrossRef]
- Shin, H.; Kim, Y.; Baek, S.; Song, Y. Distributed Learning for Dynamic Channel Access in Underwater Sensor Networks. Entropy 2020, 22, 992. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Underwater Optical Wireless Communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
- Baykal, Y.; Ata, Y.; Gökçe, M.C. Underwater turbulence, its effects on optical wireless communication and imaging: A review. Opt. Laser Tech. 2022, 156, 108624. [Google Scholar] [CrossRef]
- Corporation, S. Bluecomm Underwater Optical Communication. 2020. Available online: https://www.sonardyne.com/products/bluecomm-200-wireless-underwater-link/ (accessed on 19 February 2023).
- Shen, C.; Guo, Y.; Sun, X.; Liu, G.; Ho, K.; Ng, T.K.; Alouini, M.; Ooi, B.S. Going beyond 10-meter, Gbit/s underwater optical wireless communication links based on visible lasers. In Proceedings of the 2017 Opto-Electronics and Communications Conference (OECC) and Photonics Global Conference (PGC), Singapore, 31 July 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Jiang, H.; He, N.; Liao, X.; Popoola, W.; Rajbhandari, S. The BER Performance of the LDPC-Coded MPPM over Turbulence UWOC Channels. Photonics 2022, 9, 349. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, G.; Zhang, Q.; Song, Z. Scintillation Index for Spherical Wave Propagation in Anisotropic Weak Oceanic Turbulence with Aperture Averaging under the Effect of Inner Scale and Outer Scale. Photonics 2022, 9, 458. [Google Scholar] [CrossRef]
- Millard, R.; Seaver, G. An index of refraction algorithm for seawater over temperature, pressure, salinity, density and wavelength. Deep Sea Res. Part A Oceanogr. Res. Pap. 1990, 37, 1909–1926. [Google Scholar] [CrossRef]
- Chester, R.; Jickells, T.D. Marine Geochemistry, 3rd ed.; Wiley Black Well: Hoboken, NJ, USA, 2012. [Google Scholar]
- Korotkova, O. Light propagation in a Turbulent Ocean. In Progress in Optics; Elsevier: Amsterdam, The Netherlands, 2019; Volume 64, pp. 1–43. [Google Scholar]
- Jamali, M.V.; Mirani, A.; Parsay, A.; Abolhassani, B.; Nabavi, P.; Chizari, A.; Khorramshahi, P.; Abdollahramezani, S.; Salehi, J.A. Statistical studies of fading in underwater wireless optical channels in the presence of air bubble, temperature, and salinity random variations. IEEE Trans. Commun. 2018, 66, 4706–4723. [Google Scholar] [CrossRef]
- Yao, J.R.; Elamassie, M.; Korotkova, O. Spatial power spectrum of natural water turbulence with any average temperature, salinity concentration, and light wavelength. JOSA A 2020, 37, 1614–1621. [Google Scholar] [CrossRef] [PubMed]
- Elamassie, M.; Miramirkhani, F.; Uysal, M. Performance Characterization of Underwater Visible Light Communication. IEEE Trans. Commun. 2019, 67, 543–552. [Google Scholar] [CrossRef]
- Elamassie, M.; Uysal, M. Asymptotic Performance of Generalized Transmit Laser Selection Over Lognormal Turbulence Channels. IEEE Commun. Lett. 2020, 24, 1762–1766. [Google Scholar] [CrossRef]
- Jamali, M.V.; Chizari, A.; Salehi, J.A. Performance analysis of multi-hop underwater wireless optical communication systems. IEEE Photon. Technol. Lett. 2017, 29, 462–465. [Google Scholar] [CrossRef]
- Elamassie, M.; Sait, S.M.; Uysal, M. Underwater visible light communications in cascaded gamma-gamma turbulence. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab, 9–13 December 2018; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Elamassie, M.; Uysal, M. Performance Characterization of Vertical Underwater VLC Links in the Presence of Turbulence. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–6. [Google Scholar]
- Akhoundi, F.; Salehi, J.A.; Tashakori, A. Cellular underwater wireless optical CDMA network: Performance analysis and implementation concepts. IEEE Trans. Commun. 2015, 63, 882–891. [Google Scholar] [CrossRef]
- Anous, N.; Abdallah, M.; Uysal, M.; Qaraqe, K. Performance Evaluation of LOS and NLOS Vertical Inhomogeneous Links in Underwater Visible Light Communications. IEEE Access 2018, 6, 22408–22420. [Google Scholar] [CrossRef]
- Elamassie, M.; Uysal, M. Vertical Underwater Visible Light Communication Links: Channel Modeling and Performance Analysis. IEEE Trans. Wirel. Commun. 2020, 19, 6948–6959. [Google Scholar] [CrossRef]
- Peppas, K.P.; Boucouvalas, A.C.; Ghassemloy, Z. Performance of underwater optical wireless communication with multi-pulse pulse-position modulation receivers and spatial diversity. IET Opt. 2017, 11, 180–185. [Google Scholar] [CrossRef]
- Elamassie, M.; Al-Nahhal, M.; Kizilirmak, R.C.; Uysal, M. Transmit Laser Selection for Underwater Visible Light Communication Systems. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Jamali, M.V.; Salehi, J.A. On the BER of multiple-input multiple-output underwater wireless optical communication systems. In Proceedings of the 2015 4th International Workshop on Optical Wireless Communications (IWOW), Istanbul, Turkey, 7–8 September 2015; pp. 26–30. [Google Scholar] [CrossRef]
- Jamali, M.V.; Salehi, J.A.; Akhoundi, F. Performance Studies of Underwater Wireless Optical Communication Systems with Spatial Diversity: MIMO Scheme. IEEE Trans. Commun. 2017, 65, 1176–1192. [Google Scholar] [CrossRef]
- Safari, M.; Uysal, M. Cooperative diversity over log-normal fading channels: Performance analysis and optimization. IEEE Trans. Wirel. Commun. 2008, 7, 1963–1972. [Google Scholar] [CrossRef]
- Yilmaz, A.; Elamassie, M.; Uysal, M. Diversity Gain Analysis of Underwater Vertical MIMO VLC Links in the Presence of Turbulence. In Proceedings of the 2019 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Sochi, Russia, 3–6 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Rachna, S.; N, T.Y. Performance analysis of vertical multihop cooperative underwater visible light communication system with imperfect channel state information. Opt. Eng. 2022, 61, 046106. [Google Scholar]
- Garg, K.K.; Shaik, P.; Singya, P.K.; Bhatia, V. Performance of Multiple Relay DF NLOS UVC System With CSI Imperfections. IEEE Open J. Commun. Soc. 2021, 2, 602–616. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, X.; Pan, G.; Xie, Y. Secrecy Analysis for Multi-Relaying RF-FSO Systems with a Multi-Aperture Destination. IEEE Photon. J. 2020, 12, 1–11. [Google Scholar] [CrossRef]
- Torabi, M.; Mohammadi, N.; Nerguizian, C. Performance analysis of an asymmetric two-hop amplify-and-forward relaying RF–FSO system in a cognitive radio with partial relay selection. Opt. Commun. 2022, 505, 127478. [Google Scholar] [CrossRef]
- Nikishov, V.; Nikishov, V. Spectrum of turbulent fluctuations of the sea-water refraction index. Int. J. Fluid Mech. Res. 2000, 27, 82–98. [Google Scholar] [CrossRef]
- Ata, Y.; Yao, J.; Korotkova, O. BER variation of an optical wireless communication system in underwater turbulent medium with any temperature and salinity concentration. Opt Commun. 2021, 485, 126751. [Google Scholar] [CrossRef]
- Elamassie, M.; Uysal, M.; Baykal, Y.; Abdallah, M.; Qaraqe, K. Effect of eddy diffusivity ratio on underwater optical scintillation index. J. Opt. Soc. Am. 2017, 34, 1969–1973. [Google Scholar] [CrossRef]
- Garg, K.K.; Singya, P.K.; Bhatia, V. Performance Analysis of AF Relayed NLOS UV Communication Over Turbulent Channel. In Proceedings of the 2018 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Indore, India, 16–19 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Uysal, M. Cooperative Communications for Improved Wireless Network Transmission: Framework for Virtual Antenna Array Applications: Framework for Virtual Antenna Array Applications; IGI Global: Hershey, PA, USA, 2009. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions (National Bureau of Standards, Washington, DC, 1972), 10th ed.; Dover Publ.: Mineola, NY, USA, 1972. [Google Scholar]
- Andrews, L.C. Laser beam propagation through random media. In Proceedings of the SPIE-International Society for Optical Engineering; SPIE: San Diego, CA, USA, 2005. [Google Scholar]
| Parameters | Values | |
|---|---|---|
| Wavelength | 530 nm | |
| Extinction coefficients | c | |
| Correction coefficients | ||
| Transmitter beam divergence angle | ||
| Receiver aperture diameter | 5 cm | |
| Dissipation rate of mean square temperature | Ks | |
| Dissipation rate of turbulent kinetic energy | ms | |
| Relative strength of temperature and salinity fluctuation | ||
| Temperature | T | 15.6 °C to 16.4 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, R.; Trivedi, Y.N.; Garg, K.K.; Bhatia, V.; Abdel-Hafez, M. On Performance Analysis of Cooperative Horizontal and Vertical Underwater VLC Systems with Best Relay Selection. Photonics 2023, 10, 429. https://doi.org/10.3390/photonics10040429
Sharma R, Trivedi YN, Garg KK, Bhatia V, Abdel-Hafez M. On Performance Analysis of Cooperative Horizontal and Vertical Underwater VLC Systems with Best Relay Selection. Photonics. 2023; 10(4):429. https://doi.org/10.3390/photonics10040429
Chicago/Turabian StyleSharma, Rachna, Yogesh N. Trivedi, Kamal K. Garg, Vimal Bhatia, and Mohammed Abdel-Hafez. 2023. "On Performance Analysis of Cooperative Horizontal and Vertical Underwater VLC Systems with Best Relay Selection" Photonics 10, no. 4: 429. https://doi.org/10.3390/photonics10040429
APA StyleSharma, R., Trivedi, Y. N., Garg, K. K., Bhatia, V., & Abdel-Hafez, M. (2023). On Performance Analysis of Cooperative Horizontal and Vertical Underwater VLC Systems with Best Relay Selection. Photonics, 10(4), 429. https://doi.org/10.3390/photonics10040429






