Study on the Expansion Kinetics of Plasma and Absorption Wave Induced by Millisecond-Nanosecond Combined Pulse Lasers in Fused Quartz
Abstract
1. Introduction
2. Theory
3. Simulation Results and Analysis
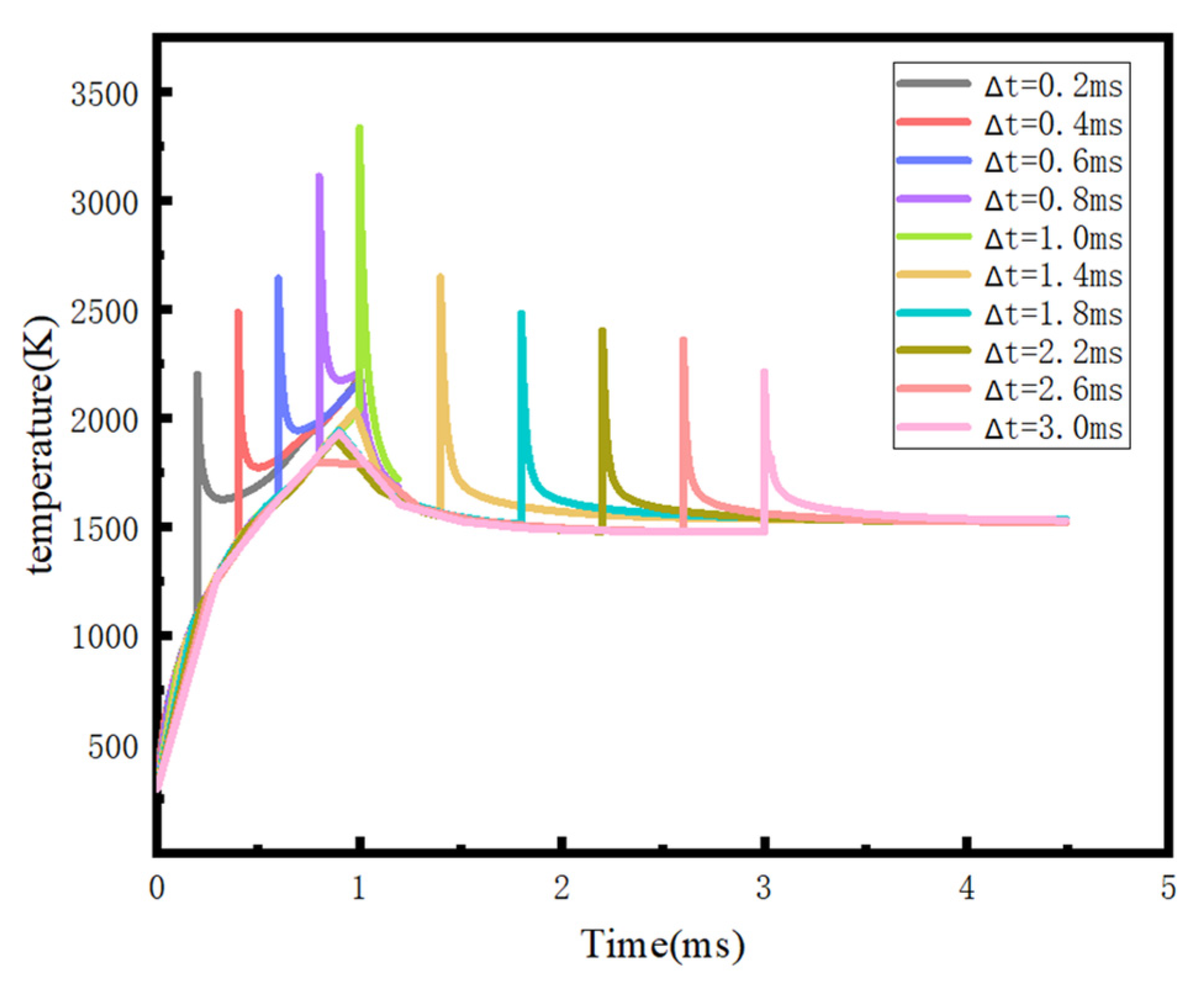
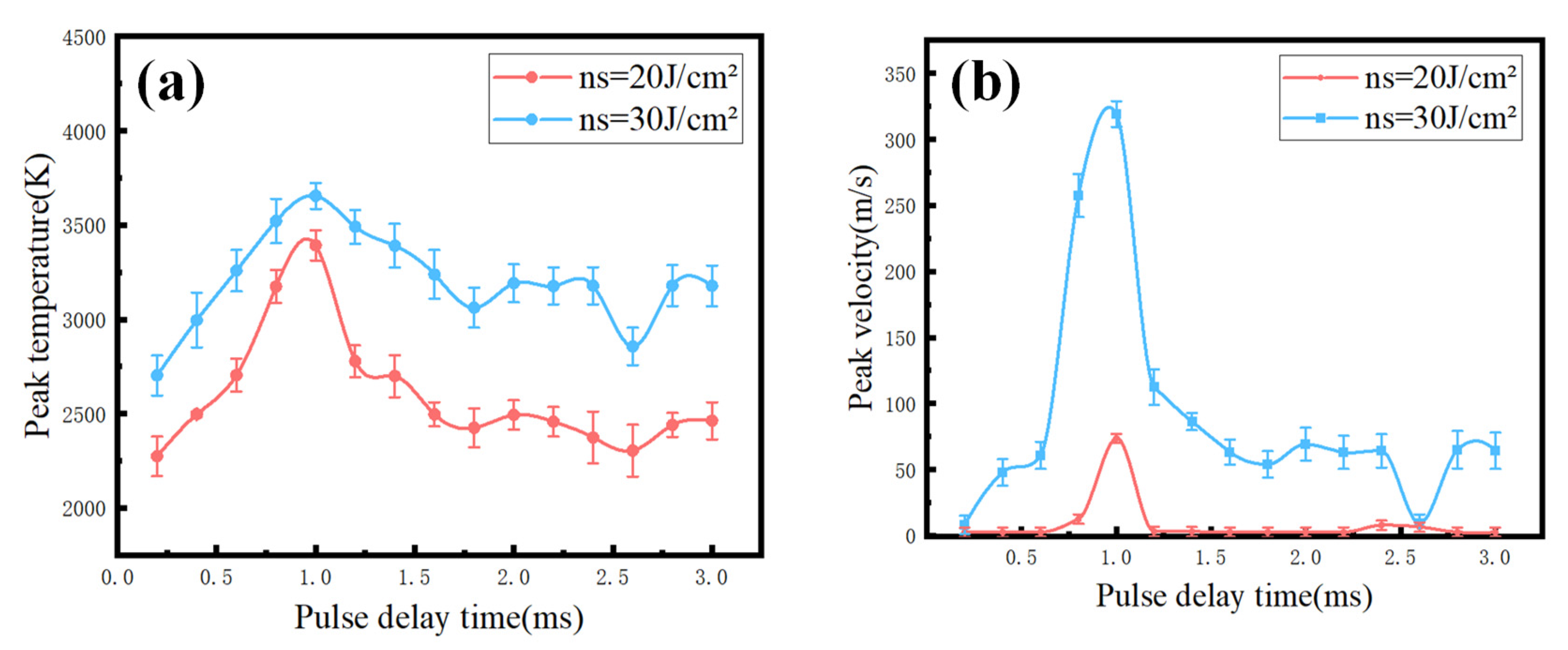
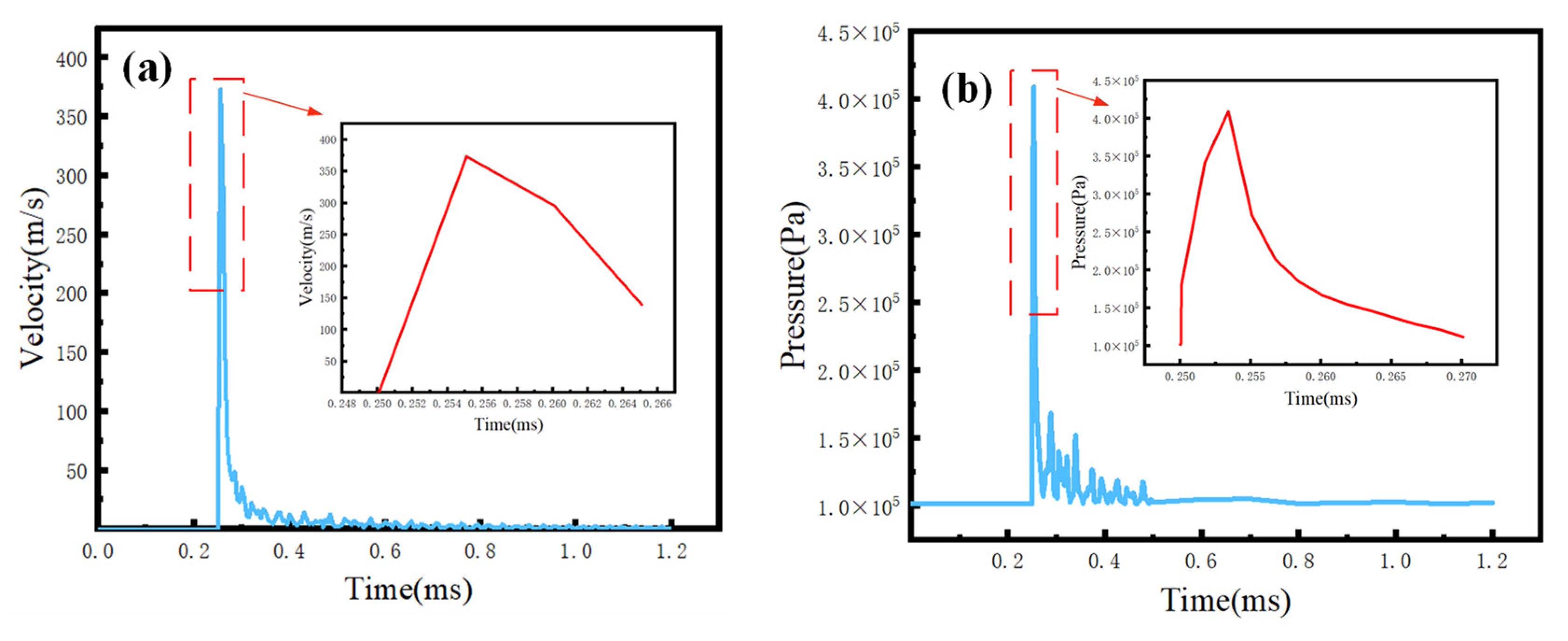
3.1. Temperature and Velocity Variations under Different Pulse Delay Conditions
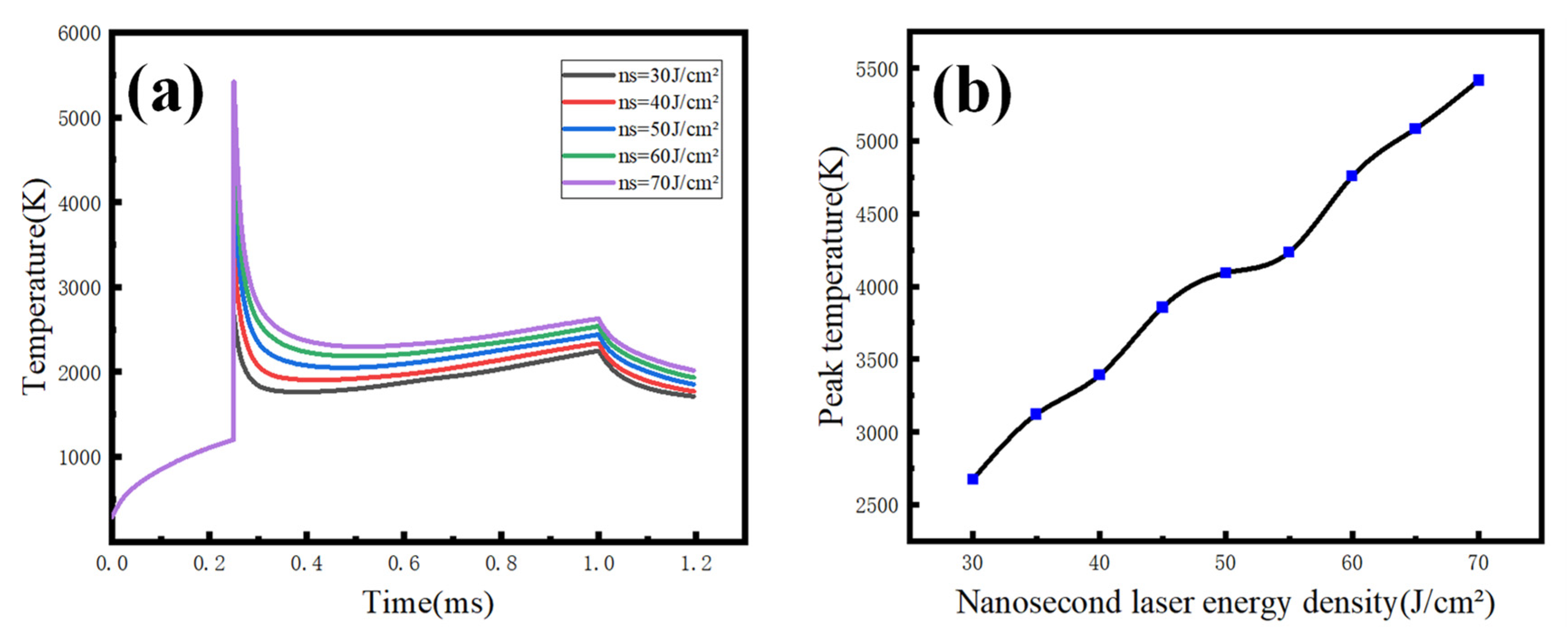
3.2. Temperature and Velocity Changes under Different Nanosecond Pulse Laser Energy Density
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nguyen, V.H.; Rehman, Z.U.; Janulewicz, K.A.; Suk, H. Dynamics of laser-induced phase transformation in bulk of monocrystalline sapphire. Results Phys. 2022, 40, 105848. [Google Scholar] [CrossRef]
- Ye, T.; Yang, L.; An, B.; Zhang, J.; Ding, M. Numerical simulation of the evolution of shock waves and plasma kernels of multi-point laser-induced plasma in supersonic flow. AIP Adv. 2022, 12, 095024. [Google Scholar] [CrossRef]
- Hamam, K.A.; Gamal, Y.E.E.D. Numerical analysis of breakdown dynamics dependence on pulse width in laser-induced damage in fused silica: Role of optical system. Results Phys. 2018, 9, 725–733. [Google Scholar] [CrossRef]
- Ly, S.; Shen, N.; Negres, R.A.; Carr, C.W.; Alessi, D.A.; Bude, J.D.; Rigatti, A.; Laurence, T.A. The role of defects in laser-induced modifications of silica coatings and fused silica using picosecond pulses at 1053 nm: I. Damage morphology. Opt. Express 2017, 25, 15161–15178. [Google Scholar] [CrossRef] [PubMed]
- Somayaji, M.; Bhuyan, M.K.; Bourquard, F.; Velpula, P.K.; D’Amico, C.; Colombier, J.P.; Stoian, R. Multiscale electronic and thermomechanical dynamics in ultrafast nanoscale laser structuring of bulk fused silica. Sci. Rep. 2020, 10, 15152. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Kumar, A.; Mishra, S.P.; Yadav, M.S.; Varma, A. Plasma wave aided heating of collisional nanocluster plasma by nonlinear interaction of two high power laser beams. Opt. Quantum Electron. 2022, 54, 753. [Google Scholar] [CrossRef]
- Joanni, E.; Kumar, R.; Fernandes, W.P.; Savu, R.; Matsuda, A. In situ growth of laser-induced graphene micro-patterns on arbitrary substrates. Nanoscale 2022, 14, 8914–8918. [Google Scholar] [CrossRef]
- Kumar, R.; Pérez del Pino, A.; Sahoo, S.; Singh, R.K.; Tan, W.K.; Kar, K.K.; Matsuda, A.; Joanni, E. Laser processing of graphene and related materials for energy storage: State of the art and future prospects. Progr. Energy Combust. Sci. 2022, 91, 100981. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, R.K.; Singh, D.P.; Joanni, E.; Yadav, R.M.; Moshkalev, S.A. Laser-assisted synthesis, reduction and micro-patterning of graphene: Recent progress and applications. Coord. Chem. Rev. 2017, 342, 34–79. [Google Scholar] [CrossRef]
- Mayi, Y.A.; Dal, M.; Peyre, P.; Bellet, M.; Metton, C.; Moriconi, C.; Fabbro, R. Laser-induced plume investigated by finite element modelling and scaling of particle entrainment in laser powder bed fusion. J. Phys. D Appl. Phys. 2020, 53, 075306. [Google Scholar] [CrossRef]
- Gilljohann, M.F.; Ding, H.; Döpp, A.; Götzfried, J.; Schindler, S.; Schilling, G.; Corde, S.; Debus, A.; Heinemann, T.; Hidding, B.; et al. Direct Observation of Plasma Waves and Dynamics Induced by Laser-Accelerated Electron Beams. Phys. Rev. X 2019, 9, 011046. [Google Scholar] [CrossRef]
- Kerrigan, H.; Masnavi, M.; Bernath, R.; Fairchild, S.R.; Richardson, M. Laser-plasma coupling for enhanced ablation of GaAs with combined femtosecond and nanosecond pulses. Opt. Express 2021, 29, 18481–18494. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, W.; Zhou, Y.; Yuan, B.; Cai, J.; Jin, G. The acceleration mechanism of shock wave induced by millisecond-nanosecond combined-pulse laser on silicon. Plasma Sci. Technol. 2021, 23, 055507. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhang, W.; Guo, L.P.; Zhang, X.Y.; Yuan, B.S.; Guo, M.; Jin, G.Y. Experimental study of different pulse delays on the phenomenon of double shock waves induced by a millisecond-nanosecond combined-pulse laser. Appl. Opt. 2020, 59, 7338–7342. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Zhou, Y.; Zhang, X.; Jin, G. Experimental study of the damage morphology induced by the millisecond-nanosecond combined-pulse laser with different pulse delay on silicon. Optik 2021, 226, 165904. [Google Scholar] [CrossRef]
- Yang, Z.; Wei, W.; Han, J.; Wu, J.; Li, X.; Jia, S. Experimental study of the behavior of two laser produced plasmas in air. Phys. Plasmas 2015, 22, 073511. [Google Scholar] [CrossRef]
- Cao, S.; Su, M.; Ma, P.; Wang, K.; Min, Q.; Sun, D.; Cheng, R.; Ying, Y.; Dong, C. Expansion dynamics and emission characteristics of nanosecond–picosecond collinear double pulse laser-induced Al plasma in air. J. Quant. Spectrosc. Radiat. Transf. 2020, 242, 106773. [Google Scholar] [CrossRef]
- Lv, X.M.; Pan, Y.X.; Jia, Z.C.; Li, Z.W.; Ni, X.W. Surface damage induced by a combined millisecond and nanosecond laser. Appl. Opt. 2017, 56, 5060–5067. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, L.; Zhou, D.; Liu, B.; Li, Q.; Shi, W.; Jin, Y. Experimental study on the dynamics and parameters of nanosecond laser-induced aluminum plasma. J. Phys. D Appl. Phys. 2022, 55, 325201. [Google Scholar] [CrossRef]
- Yuan, B.S.; Wang, D.; Dong, Y.; Zhang, W.; Jin, G.Y. Experimental study of the morphological evolution of the millisecond-nanosecond combined-pulse laser ablation of aluminum alloy. Appl. Opt. 2018, 57, 5743–5748. [Google Scholar] [CrossRef]
- Wang, M.; Wang, C.; Tao, X.; Zhou, Y. Numerical Study on Laser Shock Peening of Pure Al Correlating with Laser Shock Wave. Materials 2022, 15, 7051. [Google Scholar] [CrossRef]
- Protasov, C.E.; Khmyrov, R.S.; Grigoriev, S.N.; Gusarov, A.V. Selective laser melting of fused silica: Interdependent heat transfer and powder consolidation. Int. J. Heat Mass Transf. 2017, 104, 665–674. [Google Scholar] [CrossRef]
- Yang, G.; Sun, W.; Wan, F.; Ban, X.; Liu, Q.; Wang, Z.; Zhang, X.; Ma, M.; Zhang, J.; Zhao, B.; et al. Terahertz radiation enhanced by a laser-irradiating on a double-layer target. Eur. Phys. J. D 2022, 76, 189. [Google Scholar] [CrossRef]
- Chambonneau, M.; Lamaignere, L. Multi-wavelength growth of nanosecond laser-induced surface damage on fused silica gratings. Sci. Rep. 2018, 8, 891. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Lee, T.; Beresna, M.; Brambilla, G. Control of Laser Induced Cumulative Stress for Efficient Processing of Fused Silica. Sci. Rep. 2020, 10, 3819. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Su, J. Study of the length and influencing factors of air plasma ignition time. Open Phys. 2022, 20, 740–749. [Google Scholar] [CrossRef]
- Ikeda, Y.; Soriano, J.K. Microwave-enhanced laser-induced air plasma at atmospheric pressure. Opt. Express 2022, 30, 33756–33766. [Google Scholar] [CrossRef] [PubMed]
- Bidare, P.; Bitharas, I.; Ward, R.M.; Attallah, M.M.; Moore, A.J. Laser powder bed fusion in high-pressure atmospheres. Int. J. Adv. Manuf. Technol. 2018, 99, 543–555. [Google Scholar] [CrossRef]
- Bidare, P.; Bitharas, I.; Ward, R.M.; Attallah, M.M.; Moore, A.J. Fluid and particle dynamics in laser powder bed fusion. Acta Mater. 2018, 142, 107–120. [Google Scholar] [CrossRef]
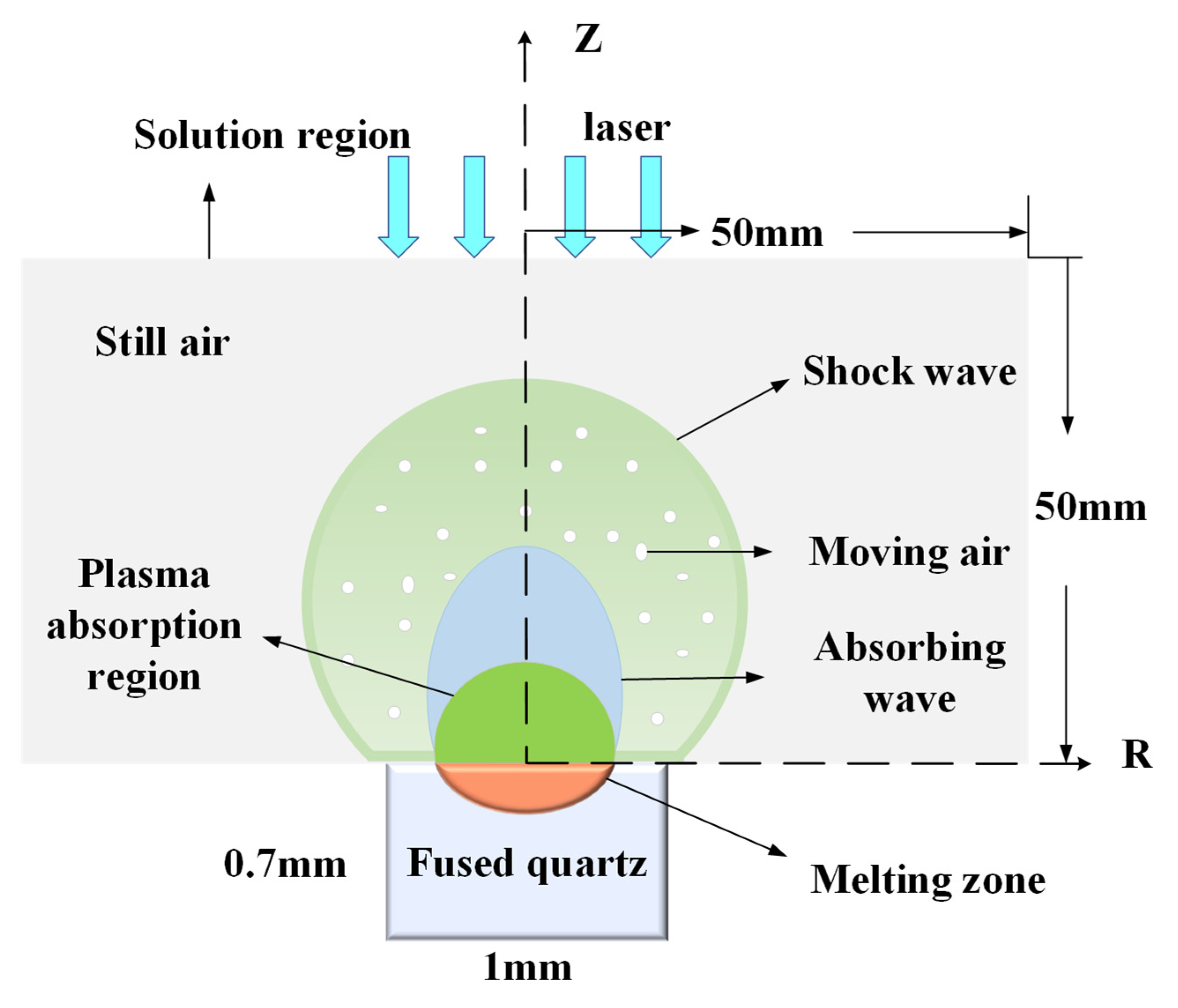



| Feature Parameter Name | Symbol | Dimension | Numerical Value |
|---|---|---|---|
| Plasma density | 3.49/T × 10−6 | ||
| Plasma thermal conductivity | −0.002 + 1.5 × 10−4 × T − 7.9 × 10−8 × T2 + 4.12 × 10−11 × T3 − 7.44 × 10−15 × T4 | ||
| Plasma heat capacity | 1047.27 + 9.45 × 10−4 × T2 − 6.02 × 10−7 × T3 + 1.29 × 10−10 × T4 | ||
| Plasma viscosity coefficient | −8.38 × 10−7 + 8.36 × 10−8 × T − 7.69 × 10−11 × T2 + 4.64 × 10−14 × T3 − 1.07 × 10−17 × T4 | ||
| Specific heat rate | 1 | 1 | |
| 1 | 1.4 | ||
| Relative permittivity | C2·N−1·M−2 | 1 | |
| Reflectivity | 1 | 0.3 | |
| Melting point | Tm | 1533 | |
| Boiling point | Tv | 3190 | |
| Absorptivity of 1064 nm | 354.67 × 10−4 × sqrt(−1.0 + 1.25 × 10−2 × T) | ||
| 354.67 × 10−4 × sqrt(10.7 + 1.45 × 10−2 × T) | |||
| Melting latent heat | 3.896 × 105 | ||
| Evaporative latent heat | 2.839 × 107 |
| Feature Parameter Name | Symbol | Dimension | Numerical Value |
|---|---|---|---|
| Laser wavelength | 1064 | ||
| Millisecond pulse laser energy density | 800 | ||
| Nanosecond pulse laser energy density | 20–70 | ||
| Millisecond pulse laser pulse width | 1 | ||
| Nanosecond pulse laser pulse width | 10 | ||
| Pulse delay | 0.2–3.0 | ||
| Absorption coefficient | 1.2992 × 106 | ||
| Laser spot diameter | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, C.; Cai, J.; Liu, Y.; Zhang, Z.; Mao, H.; Yu, H.; Wang, Y. Study on the Expansion Kinetics of Plasma and Absorption Wave Induced by Millisecond-Nanosecond Combined Pulse Lasers in Fused Quartz. Photonics 2023, 10, 411. https://doi.org/10.3390/photonics10040411
Geng C, Cai J, Liu Y, Zhang Z, Mao H, Yu H, Wang Y. Study on the Expansion Kinetics of Plasma and Absorption Wave Induced by Millisecond-Nanosecond Combined Pulse Lasers in Fused Quartz. Photonics. 2023; 10(4):411. https://doi.org/10.3390/photonics10040411
Chicago/Turabian StyleGeng, Congrui, Jixing Cai, Yubo Liu, Zequn Zhang, Hongtao Mao, Hao Yu, and Yunpeng Wang. 2023. "Study on the Expansion Kinetics of Plasma and Absorption Wave Induced by Millisecond-Nanosecond Combined Pulse Lasers in Fused Quartz" Photonics 10, no. 4: 411. https://doi.org/10.3390/photonics10040411
APA StyleGeng, C., Cai, J., Liu, Y., Zhang, Z., Mao, H., Yu, H., & Wang, Y. (2023). Study on the Expansion Kinetics of Plasma and Absorption Wave Induced by Millisecond-Nanosecond Combined Pulse Lasers in Fused Quartz. Photonics, 10(4), 411. https://doi.org/10.3390/photonics10040411




