Abstract
With the benefits of non–invasive and low radiation, terahertz radiation has shown great potential in biomedical imaging applications. However, the low spatial resolution of the imaging system significantly affects its application in these fields. Although immersion techniques and super–oscillation theory have achieved considerable success in improving the resolution of imaging systems, there are still problems with large focal spot sizes or large sidebands. Herein, a solid immersion lens based on super–oscillation is proposed to reduce the focal spot size when illuminated with circularly polarized light at a wavelength of 118.8 μm. The simulation results show that the lens can compress the full widths at half–maxima down to deep sub–wavelength scales, as small as 0.232 λ. At the same time, the maximum side–lobe ratio was 16.8%, which ensured that the device had a large field of view. The proposed method reveals new ideas in the field of super–resolution imaging.
1. Introduction
Owing to its high penetrability, low radiation and fingerprint characteristics, the application of terahertz (THz) (0.1 to 10 THz) imaging is paving the way for a new era in a wide range of fields [1], such as medical imaging and biological diagnosis [2,3,4]. These fields, specifically the differentiation and localization of health issues and malignant tumors of various diseases, have made great progress in the past decades [5,6]. The high penetration and low radiation of THz enable it to penetrate the epidermis of an animal to a depth of hundreds of microns without damaging the epidermis, so that the surface tissue can be imaged. However, THz imaging systems are often restricted in biological imaging because of their low resolution. Additionally, in order to obtain clearer medical images, deep sub–wavelength resolution is required.
Immersion techniques are commonly used to increase the spatial resolution of imaging systems by introducing a layer of liquid or solid material between the objective lens and the sample. Different from common liquid immersion microscopes, solid immersion microscopes choose solid immersion lenses made of higher refractive index materials instead of liquids to further improve the resolution of the microscope system. The traditional solid immersion technique uses a plano–convex lens as the objective lens, which has problems such as difficult processing, large volume, and difficulty in cascading [7,8]. With the advantages of easy processing, small volume, light weight, and easy integration, metasurface lenses have provided potential solutions to these problems [9,10,11,12]. The metasurface has unique advantages in phase, amplitude and polarization regulation [13,14,15,16,17]. Among them, studies on polynomial [18] and hyperboloid phase distributions [19] are also used in immersion techniques, respectively, and the minimum FWHM of the focal spot is 0.4 λ. However, their FWHM needs to be further compressed to obtain a clearer image of biological tissue. The super–oscillation, which can form arbitrarily small optical features, presents a new solution to this problem [20,21,22,23,24]. By combining it with the immersion technique, deep focusing in the subwavelength range should be achieved. Using this method, a focal spot with a FWHM of 0.289 λ in the focal plane was achieved [25]. However, the central peak of the focal spot is surrounded by a large side lobe, resulting in a field of view of ~0.6 λ. Conventionally, the immersion lenses have suffered from either a large focal spot or a large side lobe, which severely limits the focusing performance.
In the present work, the phase modulation structure is optimized to focus light from air into a dielectric material to create a super–oscillation immersion lens. The incident plane wave is modulated by the phase–modulation structure and propagates through the dielectric silicon, resulting in deep sub–wavelength focusing with a small side–lobe ratio (SLR) in air. To verify this proposal, a deep sub–wavelength–focusing metalens with a radius of 50 λ and a focal length of 21.43 λ was designed at a wavelength of λ = 118.8 μm. Numerical results showed that the FWHM of the focal spot is less than 0.25 λ and the maximum side–lobe ratio within 0.04 λ of the exit surface is 16.8%.
2. Design and Theoretical Analysis
The solid immersion lens optimized based on a super–oscillation for circularly polarized light is illustrated in Figure 1. Since the proposed metalens is planned to be applied in subsequent studies and the FIRL100 laser (Edinburgh Instruments Ltd., Edinburgh, UK) is available in the laboratory, its corresponding wavelength of 118.8 μm is chosen. Figure 1a shows the schematic diagram of the principle of operation of the solid immersion lens. The beam is focused in a dielectric column after passing through a super–oscillating phase mask and emitted into the air. The wavelength of the plane wave in the dielectric column theoretically equal to 1/n times that in air, as is the volume of the evanescent field behind it [26]. Therefore, at a small distance from the flat surface of the truncated silicon column, we can obtain a smaller terahertz beam. Rlens represents the radius of the solid immersion lens and H is the thickness of the dielectric column. High–resistance silicon was chosen as the material of the solid immersion lens because of its high refractive index and low absorption in the THz band.
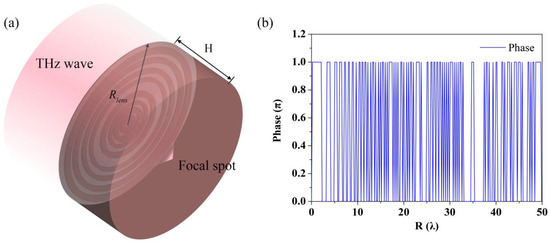
Figure 1.
(a) Schematic diagram of solid immersion lens with beam focused in air. (b) Binary phase distribution of the solid immersion lens.
According to the vectorial angular spectrum theory, the component of the electric field at any point of the plane z in the silicon column can be calculated as follows:
where and represent the angular spectrum. and are the spatial frequency of plane waves, , is the refractive index of the propagating medium. If , is imaginary. It means that the amplitude of these components decays exponentially in the z direction. If , then is real, thus representing the propagation factor of a plane wave. All of the above analysis revealed that the vector angular spectrum can express the transmission mode and evanescent mode, respectively. Obviously, the vector angular spectrum diffraction theory can accurately calculate the intensity distribution of the light field on the propagation plane after phase regulation.
Next, the focusing results of the solid immersion lens in a two–layer medium (Si–air) are investigated. The numerical aperture of the metalens is as large as possible while considering the lens performance, so the thickness of the silicon column is set to 21.43 λ. To conveniently describe the transverse electric field through the Si–air interface, we transform the transverse electric field along the axial direction of the Cartesian coordinate system into the corresponding components in the cylindrical coordinate system. The corresponding component of the angular spectrum is expressed as follows:
where is the angle of the wave vector of the beam in Si. The coordinates are defined under the condition , so that . As the beam propagates from the silicon column into the air, transmission and reflection of the beam may occur at the Si–air interface. Some beams have total reflection due to the transmission of a silicon medium with a high refractive index into the air. The Fresnel transmission coefficient ts tp and reflection coefficient rs rp of the electric field at the interface can be calculated. Then, the electric field in the air in Cartesian coordinate system can be obtained as:
The electric field reflected back into the silicon column can be written as:
where is the angle of the wave vector of the beam in air. According to Equations (2)–(4), the electric field distribution near the interface can be obtained. Based on E2x, E2y, and E2z, the electric field in the air after the light exiting from the silicon column can be calculated through the vector angle spectrum.
Combined with the above formula and particle swarm optimization algorithm [27], the intensity and FWHM of the focal spot were optimized. The light intensity distribution at the design position was calculated by Equations (1)–(4), and it was compared with the intensity distribution of the target light field to determine whether the optimal design of the metalens needs to be completed. Then, the corresponding super–oscillation phase distribution was obtained. Since super–oscillation is often accompanied by a large side–lobe ratio, we also add the side–lobe ratio to the optimization goal. After evaluating the focusing performance of the lens and the available high–resistance silicon–processing technology, we set the period of the ring to 25 μm. By optimizing the phase distribution of the lens, a deep sub–wavelength focusing lens with a small side–lobe ratio at λ = 118.8 μm is designed. The optimized structure of the lens with a radius of 50 λ and a focal length of 21.43 λ is shown in Figure 1a, which consists of a series of concentric silicon ring belts. Due to the existence of adjacent rings with the same phase, these rings can be combined so that the width of each ring band is an integer multiple of 25 μm. Combined with the existing microstructure–processing process, the desired structure can be achieved by UV lithography combined with dry etching. The etched rings are used to implement the optimized binary phase modulation shown in Figure 1b, and the depths 0 and h of the rings correspond to phase delays of π and 0. The h, which corresponds to the phase difference π, is calculated according to the following formula: , where Δφ is the phase difference π. The refractive index of silicon nSi at a wavelength of 118.8 μm is 3.418, and h is calculated as 24.56 μm.
Figure 2a illustrates the electric field intensity distribution of the focused beam formed by the solid immersion lens near the Si–air interface (rose dotted line), as calculated by Formulas (1)–(4). There are multiple spots inside the silicon column due to the coherent superposition of the incident beam and the reflection of the beam at the Si–air interface. By magnifying the light intensity distribution at the interface, as shown in Figure 2b, it is obvious that the beam exhibits the phenomenon of intensity attenuation. To further investigate the focusing performance of this lens, the normalized electric field intensity profile, FWHM, and the maximum side–lobe ratio corresponding to the propagation direction are plotted, as shown in Figure 2c. It can be clearly seen that the beam has significant attenuation as the distance from the interface of the truncated silicon column increases. Considering its application in subsequent research, its working distance is chosen to be half of its maximum intensity, i.e., 0.04 λ. The FWHM and side–lobe ratio of the beam are stable in this range and their values are less than 0.25 λ and 16.8%, respectively. Beyond this range, the FWHM of the THz beam increases significantly.
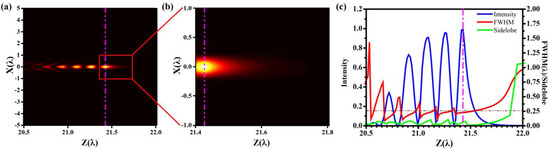
Figure 2.
The design results: characterization of solid immersion lens. (a) Intensity distribution of the light beam along the propagation direction. (b) Intensity distribution near the silicon–air interface. (c) Intensity (blue line), FWHM (red line) and side lobe (green line) electric field curves in the propagation direction.
3. Simulation Results and Discussion
To evaluate the performance of the designed lens, we simulated the device using finite–difference time–domain software (FDTD Solutions, Lumerical, Inc., Vancouver, BC, Canada.). Terahertz waves come in from the structure of the rings and out from the silicon column surface. The results of focusing on the XZ plane of the solid immersion lens are shown in Figure 3a. It can be seen that the distribution trend of the focal spot is close to the design result. For comparison, the electric field intensity distribution curves of the design (red line) and simulation (black line) are given in Figure 3b. Although there are some minor differences in the electric field intensity inside the dielectric column, the electric field intensity distribution in air obtained from the simulation is consistent with the design results, which implies the validity of our design method. To further illustrate this phenomenon, the intensity distributions related to the focal plane (XY plane) are shown in Figure 4. Figure 4a–c depict the intensity distribution of the focal spot in the XY plane at z = 21.43 λ, z = 21.46 λ, and z = 21.47 λ, respectively. Symmetric circular spots are generated in the figures. The intensity of the spots decreases significantly with the increase in the light propagation. In Figure 4d–f, the corresponding intensity curves are shown in the x–direction (black) and y–direction (red) through the centers of the hot spots. The FWHM is 0.218 λ, 0.228 λ, and 0.232 λ, and the corresponding side–lobe ratio is 13.65%, 14.94%, and 16.85%, respectively. This means that the deep sub–wavelength focusing can be realized with the small side lobe in air. At the same time, the electric intensity of the focal spot in the XY plane at z = 21.47 λ attenuates to half of the intensity at z = 21.43 λ. Considering the intensity of the focal spot, its working range is defined from 21.43 λ to 21.47 λ.
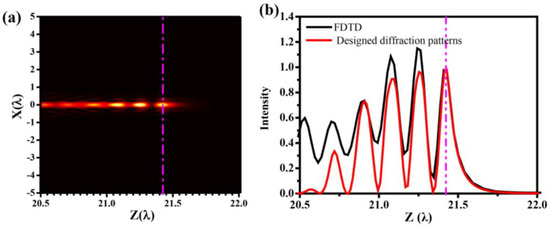
Figure 3.
The characterization of the propagation of the solid immersion lens. (a) Intensity distribution of light beam along the propagation direction. (b) Numerical simulation (red line) and FDTD simulation (blue line) of the intensity distribution curve of the electric field.
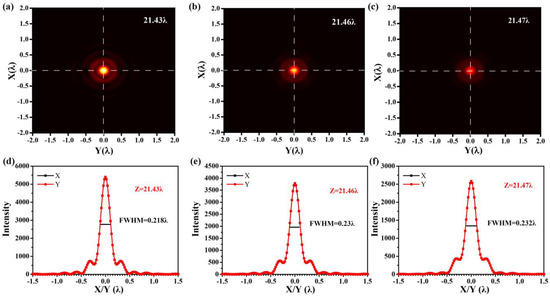
Figure 4.
The intensity obtained by FDTD in the focal plane at z = 21.43 λ (a), 21.46 λ (b), and 21.47 λ (c), respectively. The intensity curves obtained by FDTD at z = 21.43 λ (d), 21.46 λ (e), and 21.47 λ (f) on the x–axis and y–axis.
Since the linearly polarized wave is the superposition of the left– and right–circular polarized components described above, the as–designed solid immersion lens is also suitable for linearly polarized light. The focusing performance of the lens with x–polarized light and y–polarized light is shown in Figure 5. Figure 5a,b show the optical intensity distribution along the propagation plane under x–polarized and y–polarized incidence, respectively. They are consistent with the distribution trend of optical intensity under circularly polarized light. Figure 5c,d give the two–dimensional light intensity distribution on the focal plane at positions z = 21.43 λ, 21.46 λ, and 21.47 λ in air. As can be seen from the figures, the focused spots have distinct side lobes in the direction that coincides with the polarization. The corresponding intensity curves in x– and y– directions are presented in Figure 5e,f, and the corresponding parameters are listed in Table 1. The FWHMs in x–direction at z = 21.43 λ, 21.46 λ, and 21.47 λ are 0.24 λ, 0.25 λ, and 0.25 λ, respectively, which are slightly larger than the FWHM at the circular incidence. Additionally, the values in y–direction are 0.2 λ, 0.23 λ, and 0.232 λ, respectively, which are close to the FWHM at circular polarization. The FWHM in the x–direction is slightly larger than that in the y–direction, but it is still less than 0.25 λ. The side–lobe ratio of the x–axis is approximately three times that of the y–axis, 20.57% and 6.70%, 22% and 7.87%, and 24.19% and 9.50%, respectively. The same phenomenon occurs when the incident light is y–polarized, the direction with the larger side lobe of the focal spot is changed to the y direction. This result proves that we can use y–polarization or x–polarization in subsequent applications without polarization conversion, which further simplifies the application steps.
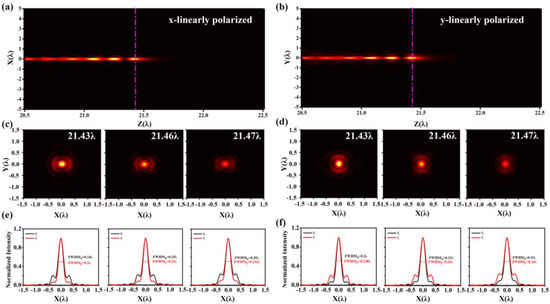
Figure 5.
Intensity distribution of the light field in the XZ plane when illuminated by x–linearly polarized plane wave (a) and y–linearly polarized plane wave (b). (c,d) are the intensity distribution of the light field in the XY plane when illuminated with the x–linearly polarized plane wave and y–linearly polarized plane wave, respectively. (e,f) are the intensity distribution curves in the x and y directions corresponding to (c,d).

Table 1.
Parameters of the focal spot on the focal plane at different z for x– and y–polarized light.
4. Conclusions
In summary, a solid immersion lens was designed based on super–oscillation at a wavelength of 118.8 μm. The lens consists of concentric rings on a silicon column that focus circularly polarized light to a deep sub–wavelength with a small side–lobe ratio. Numerical simulations showed that the maximum FWHM is about 0.232 λ, and the maximum side–lobe ratio is 16.85%. When the lens is irradiated with x– (or y–) polarization, the focal spot widens in the corresponding direction, but its FWHMs are still only about a quarter wavelength. The proposed solid immersion metalens can be used as an objective lens of microscopy, which provides a pathway for microscopic THz imaging and shows promise for applications in biomedicine.
Author Contributions
Conceptualization, M.Y.; methodology, M.Y.; software, M.Y.; validation, M.Y. and X.S.; writing—original draft preparation, M.Y.; writing—review and editing, M.Y., Z.W. and X.S.; supervision, Z.W. and X.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Chongqing, grant number cstc2019jcyj-msxmX0315.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ako, R.T.; Upadhyay, A.; Withayachumnankul, W.; Bhaskaran, M.; Sriram, S. Dielectrics for Terahertz Metasurfaces: Material Selection and Fabrication Techniques. Adv. Opt. Mater. 2019, 8, 1900750. [Google Scholar] [CrossRef]
- Woodward, R.M.; Cole, B.E.; Wallace, V.P.; Pye, R.J.; Arnone, D.D.; Linfield, E.H.; Pepper, M. Terahertz pulse imaging in reflection geometry of human skin cancer and skin tissue. Phys. Med. Biol. 2002, 47, 3853–3863. [Google Scholar] [CrossRef]
- Pickwell, E.; Wallace, V.P. Biomedical applications of terahertz technology. J. Phys. D Appl. Phys. 2006, 39, R301–R310. [Google Scholar] [CrossRef]
- Yu, C.; Fan, S.; Sun, Y. Pickwell-Macpherson, E. The potential of terahertz imaging for cancer diagnosis: A review of investigations to date. Quant. Imaging Med. Surg. 2012, 2, 33–45. [Google Scholar]
- Nikitkina, A.I.; Bikmulina, P.Y.; Gafarova, E.R.; Kosheleva, N.V.; Efremov, Y.M.; Bezrukov, E.A.; Butnaru, D.V.; Dolganova, I.N.; Chernomyrdin, N.V.; Cherkasova, O.P.; et al. Terahertz radiation and the skin: A review. J. Biomed. Opt. 2021, 26, 043005. [Google Scholar] [CrossRef]
- Peralta, X.G.; Lipscomb, D.; Wilmink, G.J.; Echchgadda, I. Terahertz spectroscopy of human skin tissue models with different melanin content. Biomed. Opt. Express 2019, 10, 2942. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Schadko, A.O.; Lebedev, S.P.; Tolstoguzov, V.L.; Kurlov, V.N.; Reshetov, I.V.; Spektor, I.E.; Skorobogatiy, M.; Yurchenko, S.O.; Zaytsev, K.I. Solid immersion terahertz imaging with sub–wavelength resolution. Appl. Phys. Lett. 2017, 110, 221109. [Google Scholar]
- Kurvits, J.A.; Jiang, M.; Zia, R. Comparative analysis of imaging configurations and objectives for Fourier microscopy. J. Opt. Soc. Am. A 2015, 32, 2082–2092. [Google Scholar] [CrossRef]
- Huo, P.; Zhang, S.; Liang, Y.; Lu, Y.; Xu, T. Hyperbolic Metamaterials and Metasurfaces: Fundamentals and Applications. Adv. Opt. Mater. 2019, 7, 1801616. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, H.; Li, Z.; Yuan, H.; Cao, L.; Luo, Z.; Zhang, K.; Zhang, Z.; Wen, Z.; Zhu, L.; et al. All–dielectric metalens for terahertz wave imaging. Opt. Express 2018, 26, 14132. [Google Scholar] [CrossRef] [PubMed]
- Hong, X.; Feng, S.; Guo, H.; Li, C. A small–spot–size and polarization–insensitive flat lens employing dielectric metasurface in the terahertz region. Opt. Commun. 2020, 459, 125083. [Google Scholar] [CrossRef]
- Chen, H.; Wu, Z.; Li, Z.; Luo, Z.; Jiang, X.; Wen, Z.; Zhu, L.; Zhou, X.; Li, H.; Shang, Z.; et al. Sub–wavelength tight–focusing of terahertz waves by polarization–independent high–numerical–aperture dielectric metalens. Opt. Express 2018, 26, 29817–29825. [Google Scholar] [CrossRef] [PubMed]
- Danila, O. Polyvinylidene Fluoride–Based Metasurface for High–Quality Active Switching and Spectrum Shaping in the Terahertz G–Band. Polymers 2021, 13, 1860. [Google Scholar] [CrossRef]
- Liang, Y.; Wei, Z.; Guo, J.; Wang, F.; Meng, H.; Liu, H. Metalenses Based on Symmetric Slab Waveguide and c–TiO2: Efficient Polarization–Insensitive Focusing at Visible Wavelengths. Nanomaterials 2018, 8, 699. [Google Scholar] [CrossRef]
- Dănilă, O.; Mănăilă-Maximean, D.; Bărar, A.; Loiko, V.A. Non–Layered Gold–Silicon and All–Silicon Frequency–Selective Metasurfaces for Potential Mid–Infrared Sensing Applications. Sensors 2021, 21, 5600. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, J.; Shu, Y.; Wu, L.; Lu, L.; Qi, K.; Che, Y.; Li, L.; Yin, H. High numerical aperture and large focusing efficiency metalens based on multilayer transmitarray elements. Opt. Laser. Eng. 2021, 147, 106734. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, H.; Wang, F.; Meng, H.; Guo, J.; Li, J.; Wei, Z. High–Efficiency, Near–Diffraction Limited, Dielectric Metasurface Lenses Based on Crystalline Titanium Dioxide at Visible Wavelengths. Nanomaterials 2018, 8, 288. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Khorasaninejad, M.; Shi, Z.; Sanjeev, V.; Capasso, F. Immersion Meta–Lenses at Visible Wavelengths for Nanoscale Imaging. Nano Lett. 2017, 17, 3188–3194. [Google Scholar] [CrossRef]
- Liang, H.; Lin, Q.; Xie, X.; Sun, Q.; Wang, Y.; Zhou, L.; Liu, L.; Yu, X.; Zhou, J.; Krauss, T.F.; et al. Ultrahigh Numerical Aperture Metalens at Visible Wavelengths. Nano Lett. 2018, 18, 4460–4466. [Google Scholar] [CrossRef]
- Yang, M.; Ruan, D.; Du, L.; Qin, C.; Li, Z.; Lin, C.; Chen, G.; Wen, Z. Subdiffraction focusing of total electric fields of terahertz wave. Opt. Commun. 2020, 458, 124764. [Google Scholar] [CrossRef]
- Ruan, D.; Li, Z.; Du, L.; Zhou, X.; Zhu, L.; Lin, C.; Yang, M.; Chen, G.; Yuan, W.; Liang, G.; et al. Realizing a terahertz far–field sub–diffraction optical needle with sub–wavelength concentric ring structure array. Appl. Optics. 2018, 57, 7905–7909. [Google Scholar] [CrossRef]
- Yuan, G.H.; Lin, Y.H.; Tsai, D.P.; Zheludev, N.I. Superoscillatory quartz lens with effective numerical aperture greater than one. Appl. Phys. Lett. 2020, 117, 021106. [Google Scholar] [CrossRef]
- Huang, K.; Liu, H.; Garcia-Vidal, F.J.; Hong, M.; Luk Yanchuk, B.; Teng, J.; Qiu, C. Ultrahigh–capacity non–periodic photon sieves operating in visible light. Nat. Commun. 2015, 6, 7059. [Google Scholar] [CrossRef]
- Rogers, E.T.F.; Lindberg, J.; Roy, T.; Savo, S.; Chad, J.E.; Dennis, M.R.; Zheludev, N.I. A super–oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 2012, 11, 432–435. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Li, H.; Zhu, Y.; Yu, Y. Controllable design of super–oscillatory lenses with multiple sub–diffraction–limit foci. Sci. Rep. 2017, 7, 1335. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, S.M.; Kino, G.S. Solid Immersion Microscopy. Appl. Phys. Lett. 1990, 57, 2615–2616. [Google Scholar] [CrossRef]
- Liu, T.; Tan, J.; Liu, J.; Wang, H. Vectorial design of super–oscillatory lens. Opt. Express 2013, 21, 15090. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).