Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity
Abstract
1. Introduction
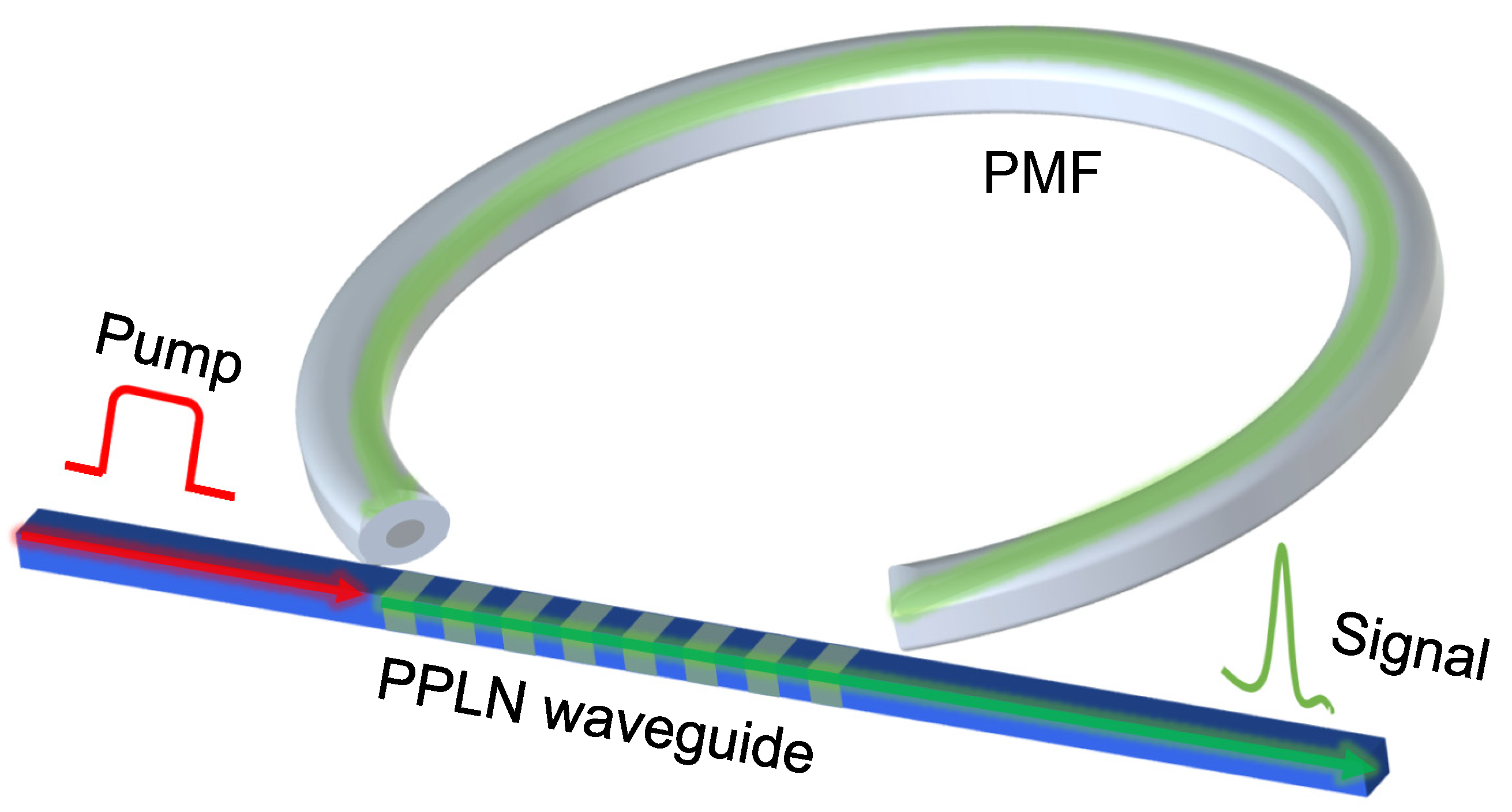
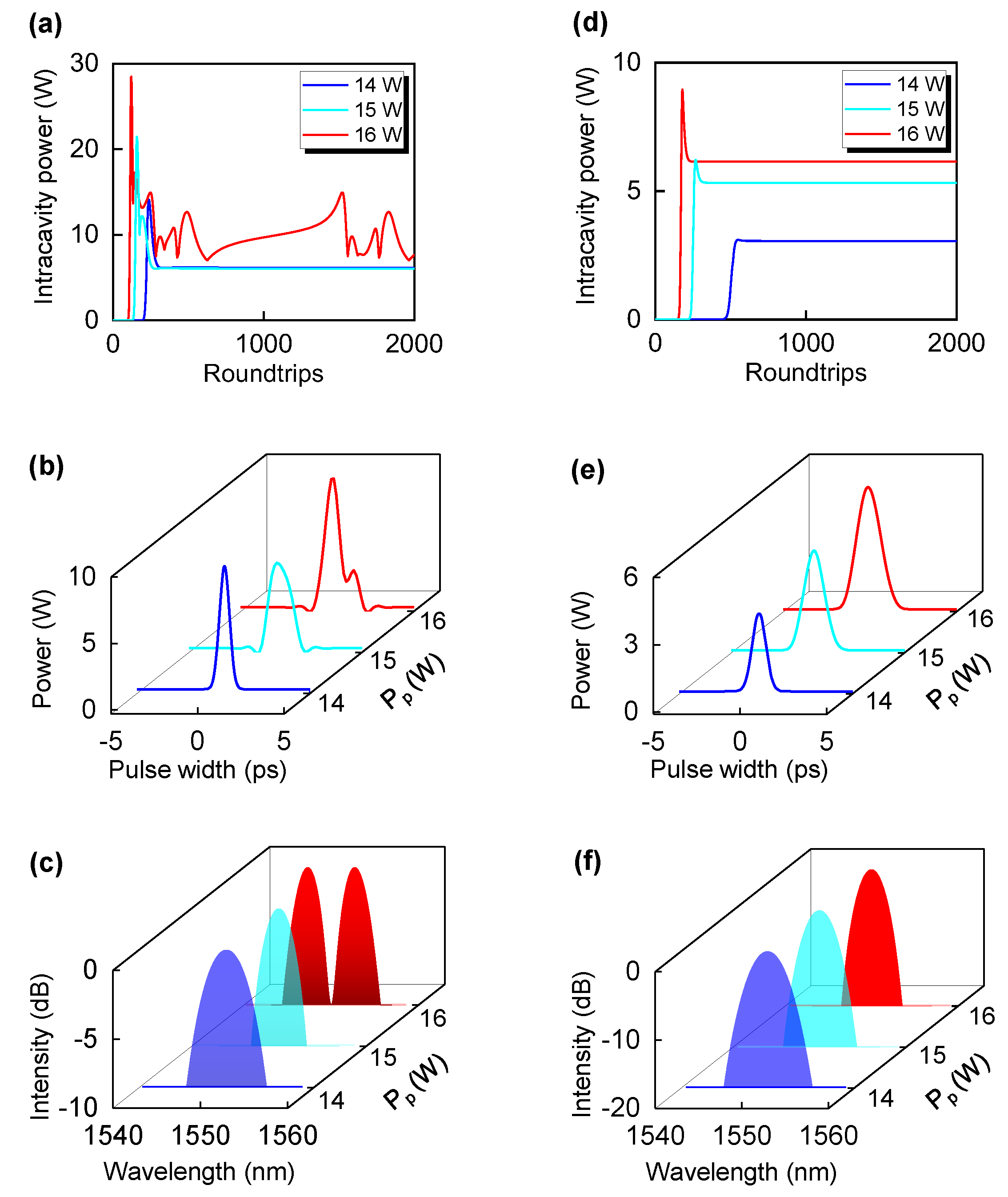
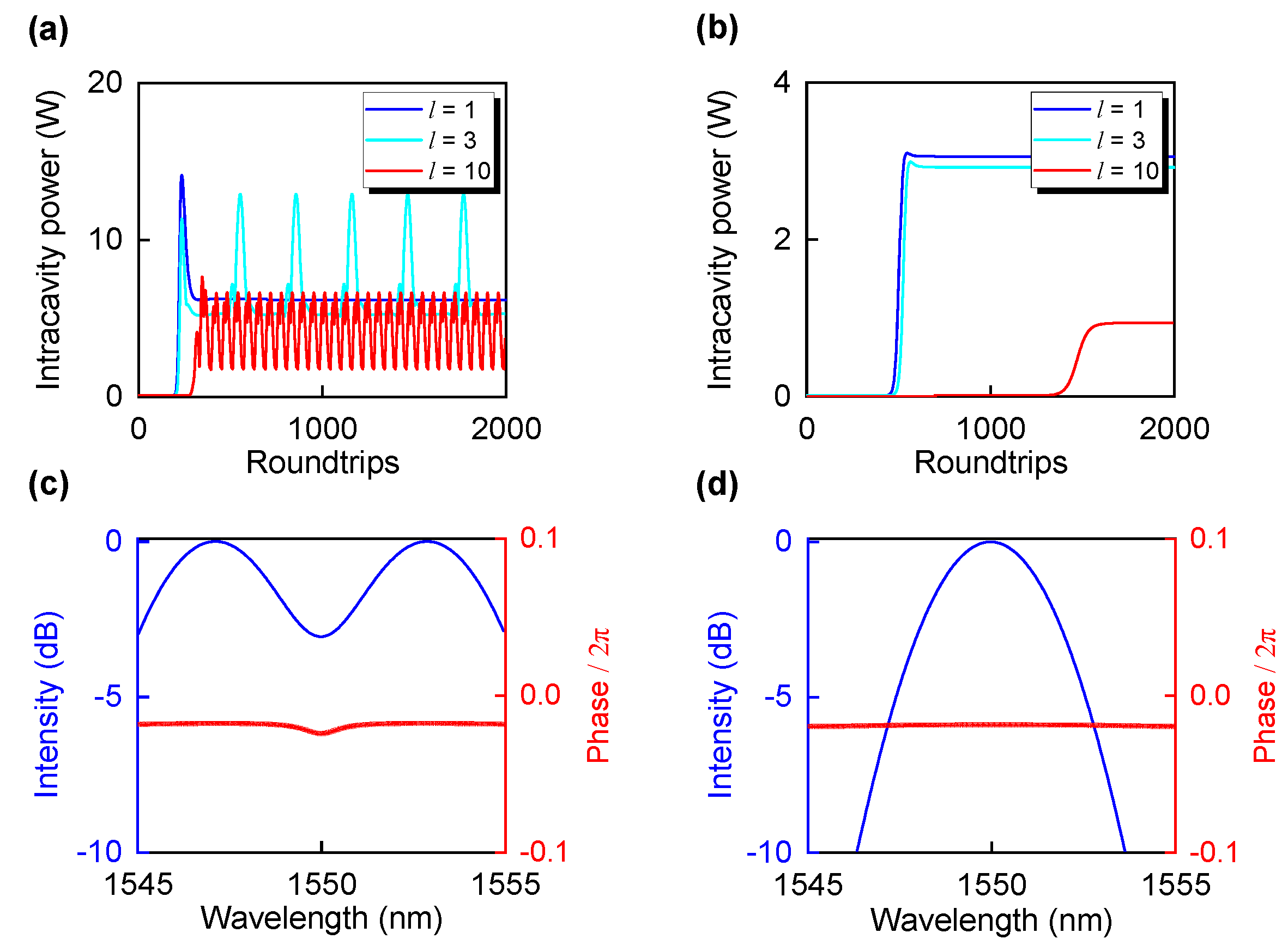
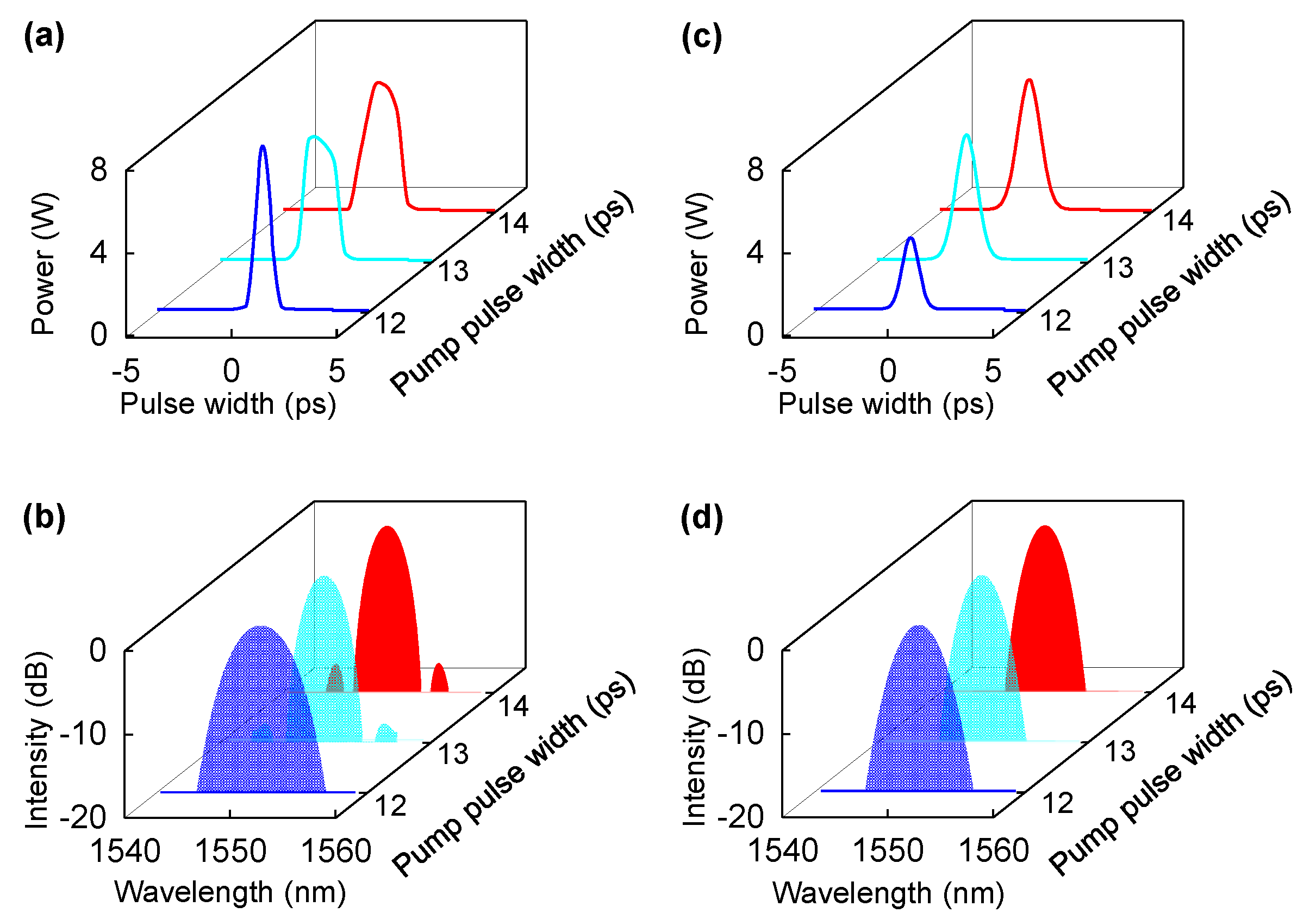
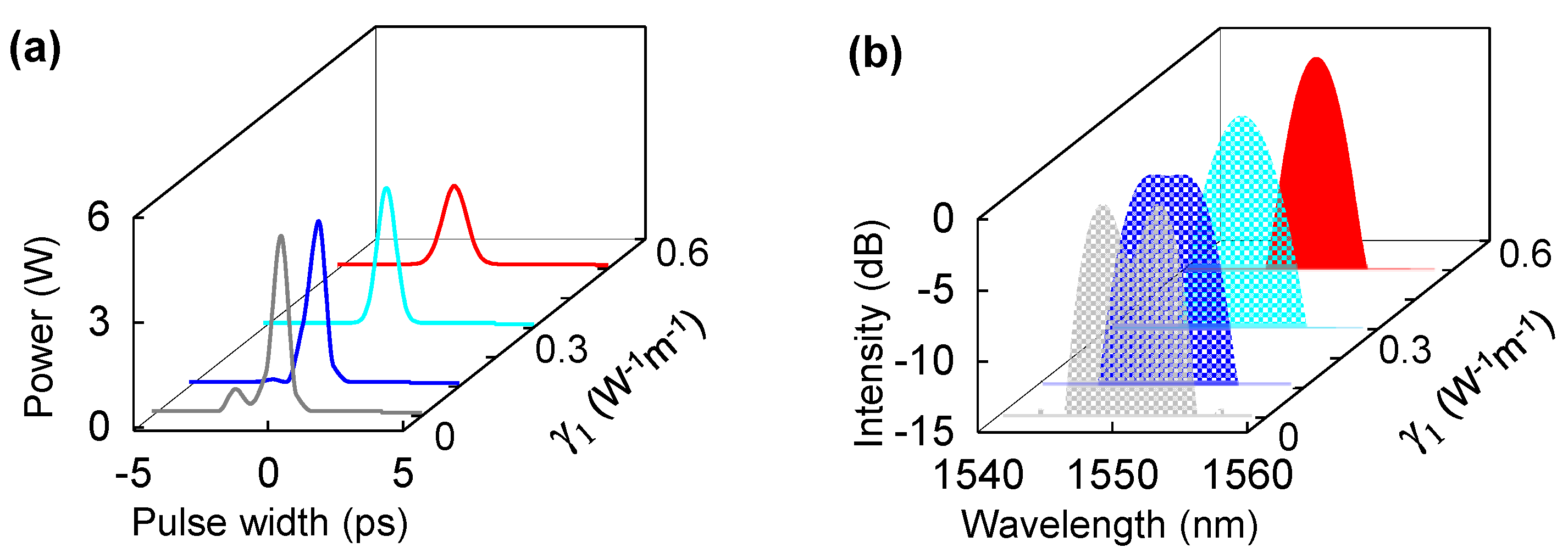
2. Theory and Simulation Results
3. Discussion and Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, L.; Liu, S.; Bowers, J.E. Integrated optical frequency comb technologies. Nat. Photonics 2022, 16, 95–108. [Google Scholar] [CrossRef]
- Gaeta, A.L.; Lipson, M.; Kippenberg, T.J. Photonic-chip-based frequency combs. Nat. Photonics 2019, 13, 158–169. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef]
- Marin-Palomo, P.; Kemal, J.N.; Karpov, M.; Kordts, A.; Pfeifle, J.; Pfeiffer, M.H.; Trocha, P.; Wolf, S.; Brasch, V.; Anderson, M.H.; et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 2017, 546, 274–279. [Google Scholar] [CrossRef]
- Pfeifle, J.; Brasch, V.; Lauermann, M.; Yu, Y.; Wegner, D.; Herr, T.; Hartinger, K.; Schindler, P.; Li, J.; Hillerkuss, D.; et al. Coherent terabit communications with microresonator Kerr frequency combs. Nat. Photonics 2014, 8, 375–380. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Schnatz, H.; Hollberg, L.W. Optical frequency combs: From frequency metrology to optical phase control. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1041–1058. [Google Scholar] [CrossRef]
- Collaboration, B.A.C.O.N.B. Frequency ratio measurements at 18-digit accuracy using an optical clock network. Nature 2021, 591, 564–569. [Google Scholar] [CrossRef]
- Papp, S.B.; Beha, K.; Del’Haye, P.; Quinlan, F.; Lee, H.; Vahala, K.J.; Diddams, S.A. Microresonator frequency comb optical clock. Optica 2014, 1, 10–14. [Google Scholar] [CrossRef]
- Suh, M.G.; Yi, X.; Lai, Y.H.; Leifer, S.; Grudinin, I.S.; Vasisht, G.; Martin, E.C.; Fitzgerald, M.P.; Doppmann, G.; Wang, J.; et al. Searching for exoplanets using a microresonator astrocomb. Nat. Photonics 2019, 13, 25–30. [Google Scholar] [CrossRef]
- Obrzud, E.; Rainer, M.; Harutyunyan, A.; Anderson, M.H.; Liu, J.; Geiselmann, M.; Chazelas, B.; Kundermann, S.; Lecomte, S.; Cecconi, M.; et al. A microphotonic astrocomb. Nat. Photonics 2019, 13, 31–35. [Google Scholar] [CrossRef]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Picqué, N.; Lipson, M.; Gaeta, A.L. Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat. Commun. 2018, 9, 1869. [Google Scholar] [CrossRef] [PubMed]
- Herr, T.; Hartinger, K.; Riemensberger, J.; Wang, C.; Gavartin, E.; Holzwarth, R.; Gorodetsky, M.; Kippenberg, T. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat. Photonics 2012, 6, 480–487. [Google Scholar] [CrossRef]
- Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal solitons in optical microresonators. Nat. Photonics 2014, 8, 145–152. [Google Scholar] [CrossRef]
- Szabados, J.; Sturman, B.; Breunig, I. Frequency comb generation threshold via second-harmonic excitation in χ (2) optical microresonators. APL Photonics 2020, 5, 116102. [Google Scholar] [CrossRef]
- Herr, S.J.; Brasch, V.; Szabados, J.; Obrzud, E.; Jia, Y.; Lecomte, S.; Buse, K.; Breunig, I.; Herr, T. Frequency comb up- and down-conversion in synchronously driven χ(2) optical microresonators. Opt. Lett. 2018, 43, 5745–5748. [Google Scholar] [CrossRef]
- Nie, M.; Huang, S.W. Quadratic Solitons in Singly Resonant Degenerate Optical Parametric Oscillators. Phys. Rev. Appl. 2020, 13, 044046. [Google Scholar] [CrossRef]
- Li, J.; Bao, C.; Ji, Q.X.; Wang, H.; Wu, L.; Leifer, S.; Beichman, C.; Vahala, K. Efficiency of pulse pumped soliton microcombs. Optica 2022, 9, 231–239. [Google Scholar] [CrossRef]
- Obrzud, E.; Lecomte, S.; Herr, T. Temporal solitons in microresonators driven by optical pulses. Nat. Photonics 2017, 11, 600–607. [Google Scholar] [CrossRef]
- Anderson, M.H.; Bouchand, R.; Liu, J.; Weng, W.; Obrzud, E.; Herr, T.; Kippenberg, T.J. Photonic chip-based resonant supercontinuum via pulse-driven Kerr microresonator solitons. Optica 2021, 8, 771–779. [Google Scholar] [CrossRef]
- Brasch, V.; Obrzud, E.; Lecomte, S.; Herr, T. Nonlinear filtering of an optical pulse train using dissipative Kerr solitons. Optica 2019, 6, 1386–1393. [Google Scholar] [CrossRef]
- Weng, W.; Kaszubowska-Anandarajah, A.; He, J.; Lakshmijayasimha, P.D.; Lucas, E.; Liu, J.; Anandarajah, P.M.; Kippenberg, T.J. Gain-switched semiconductor laser driven soliton microcombs. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Xu, Y.; Lin, Y.; Nielsen, A.; Hendry, I.; Coen, S.; Erkintalo, M.; Ma, H.; Murdoch, S.G. Harmonic and rational harmonic driving of microresonator soliton frequency combs. Optica 2020, 7, 940–946. [Google Scholar] [CrossRef]
- Diddams, S.A.; Vahala, K.; Udem, T. Optical frequency combs: Coherently uniting the electromagnetic spectrum. Science 2020, 369, eaay3676. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Nehra, R.; Jahani, S.; Ledezma, L.; Langrock, C.; Fejer, M.; Marandi, A. Temporal walk-off induced dissipative quadratic solitons. Nat. Photonics 2022, 16, 162–168. [Google Scholar] [CrossRef]
- Li, X.; Huang, X.; Chen, E.; Zhou, Y.; Han, Y. Dissipative-soliton-resonance and evolution in an all-normal dispersion Er-doped fiber laser. Opt. Laser Technol. 2022, 156, 108592. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Zhao, W.; Zhang, W.; Hu, X.; Gao, C.; Zhang, H.; Yang, Z.; Wang, H.; Wang, X.; et al. Numerical investigation of soliton molecules with variable separation in passively mode-locked fiber lasers. Opt. Commun. 2012, 285, 1356–1361. [Google Scholar] [CrossRef]
- Hansson, T.; Leo, F.; Erkintalo, M.; Coen, S.; Ricciardi, I.; De Rosa, M.; Wabnitz, S. Singly resonant second-harmonic-generation frequency combs. Phys. Rev. A 2017, 95, 013805. [Google Scholar] [CrossRef]
- Leo, F.; Hansson, T.; Ricciardi, I.; De Rosa, M.; Coen, S.; Wabnitz, S.; Erkintalo, M. Walk-Off-Induced Modulation Instability, Temporal Pattern Formation, and Frequency Comb Generation in Cavity-Enhanced Second-Harmonic Generation. Phys. Rev. Lett. 2016, 116, 033901. [Google Scholar] [CrossRef]
- Mosca, S.; Parisi, M.; Ricciardi, I.; Leo, F.; Hansson, T.; Erkintalo, M.; Maddaloni, P.; De Natale, P.; Wabnitz, S.; De Rosa, M. Modulation Instability Induced Frequency Comb Generation in a Continuously Pumped Optical Parametric Oscillator. Phys. Rev. Lett. 2018, 121, 093903. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Li, J.; Dai, F.; Wang, M.; Wang, C.; Wang, Q.; Tu, C.; Li, Y.; Wang, H.T. Kerr nonlinearity-assisted quadratic microcomb. Front. Phys. 2022, 10. [Google Scholar] [CrossRef]
- Li, Y.; Huang, S.W.; Li, B.; Liu, H.; Yang, J.; Vinod, A.K.; Wang, K.; Yu, M.; Kwong, D.L.; Wang, H.T.; et al. Real-time transition dynamics and stability of chip-scale dispersion-managed frequency microcombs. Light. Sci. Appl. 2020, 9, 52. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Al Sayem, A.; Gong, Z.; Surya, J.B.; Zou, C.L.; Tang, H.X. Ultralow-threshold thin-film lithium niobate optical parametric oscillator. Optica 2021, 8, 539–544. [Google Scholar] [CrossRef]
- Ledezma, L.; Sekine, R.; Guo, Q.; Nehra, R.; Jahani, S.; Marandi, A. Intense optical parametric amplification in dispersion-engineered nanophotonic lithium niobate waveguides. Optica 2022, 9, 303–308. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Li, J.; Dai, F.; Wang, M.; Wang, C.; Wang, Q.; Tu, C.; Li, Y.; Wang, H. Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity. Photonics 2023, 10, 155. https://doi.org/10.3390/photonics10020155
Wang K, Li J, Dai F, Wang M, Wang C, Wang Q, Tu C, Li Y, Wang H. Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity. Photonics. 2023; 10(2):155. https://doi.org/10.3390/photonics10020155
Chicago/Turabian StyleWang, Ke, Jing Li, Fan Dai, Mengshuai Wang, Chuanhang Wang, Qiang Wang, Chenghou Tu, Yongnan Li, and Huitian Wang. 2023. "Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity" Photonics 10, no. 2: 155. https://doi.org/10.3390/photonics10020155
APA StyleWang, K., Li, J., Dai, F., Wang, M., Wang, C., Wang, Q., Tu, C., Li, Y., & Wang, H. (2023). Robust Pulse-Pumped Quadratic Soliton Assisted by Third-Order Nonlinearity. Photonics, 10(2), 155. https://doi.org/10.3390/photonics10020155





