Thermal Sensitivity of Birefringence in Polarization-Maintaining Hollow-Core Photonic Bandgap Fibers
Abstract
1. Introduction
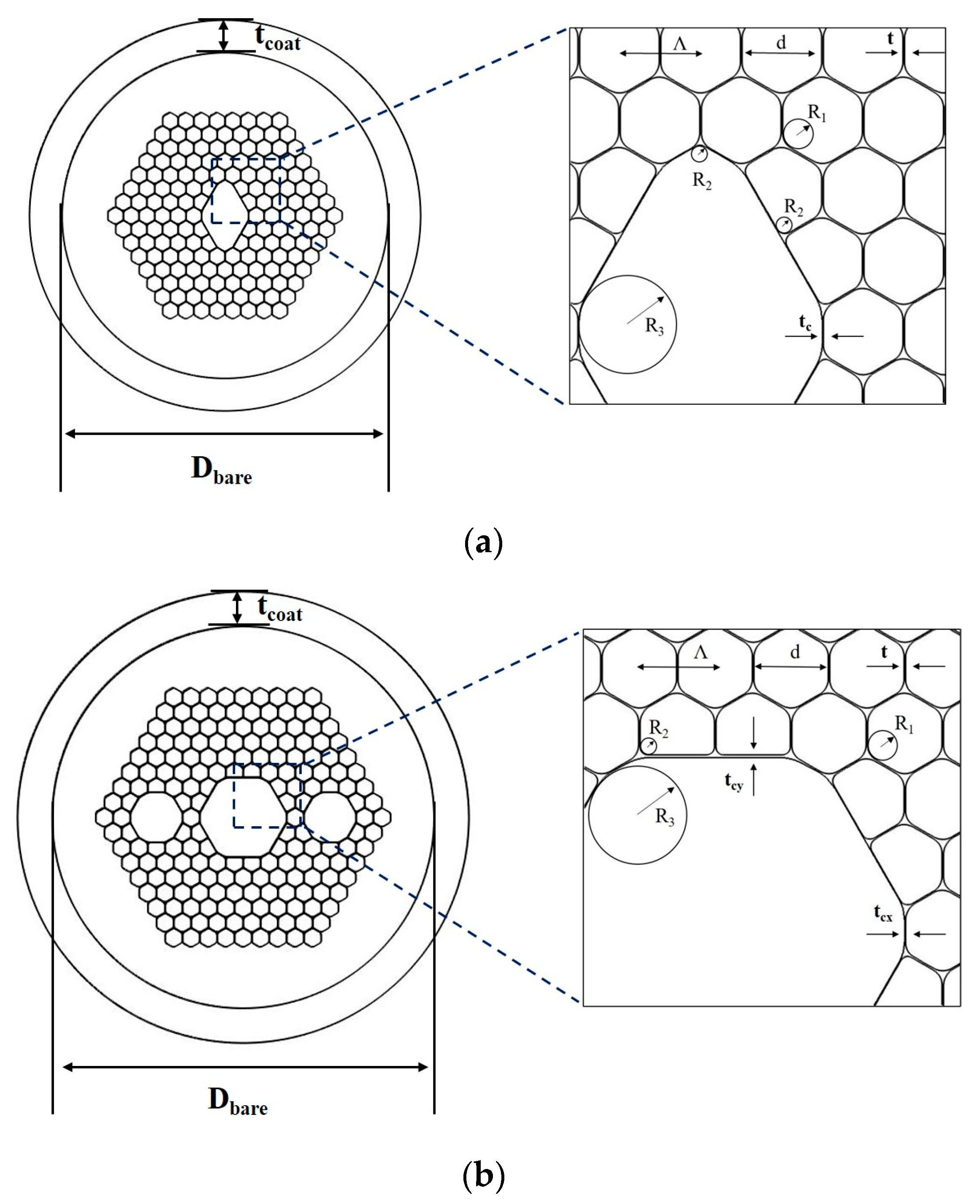
2. Fiber Structure and Fundamental Properties
2.1. Fiber Structure
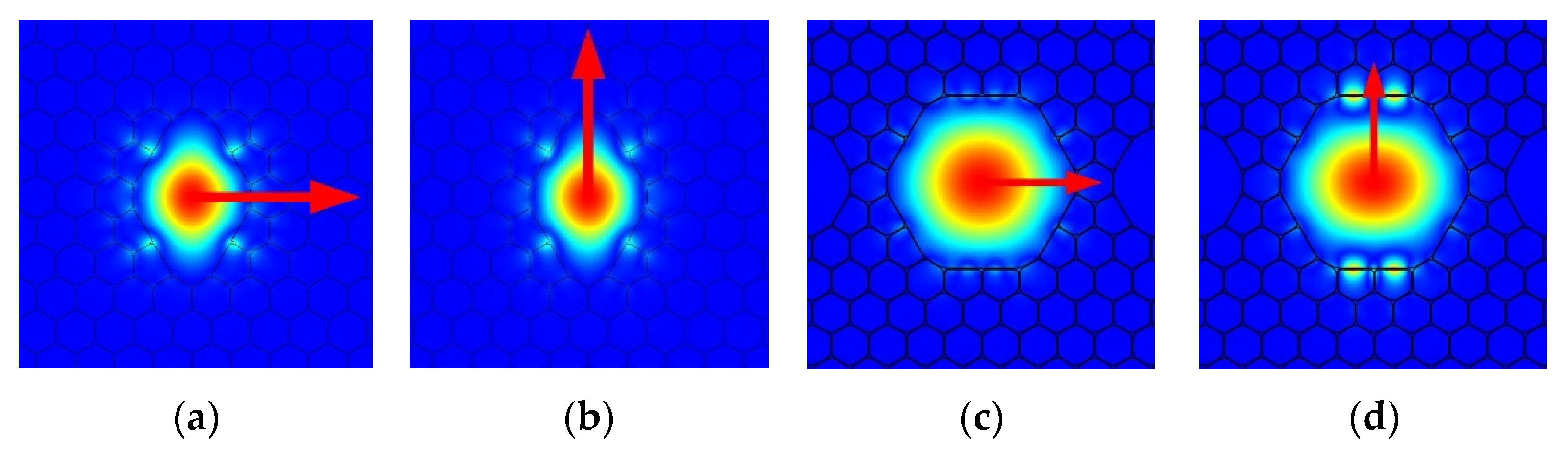
2.2. Fundamental Properties
3. Thermal Sensitivity of Birefringence of HC-PBGFs
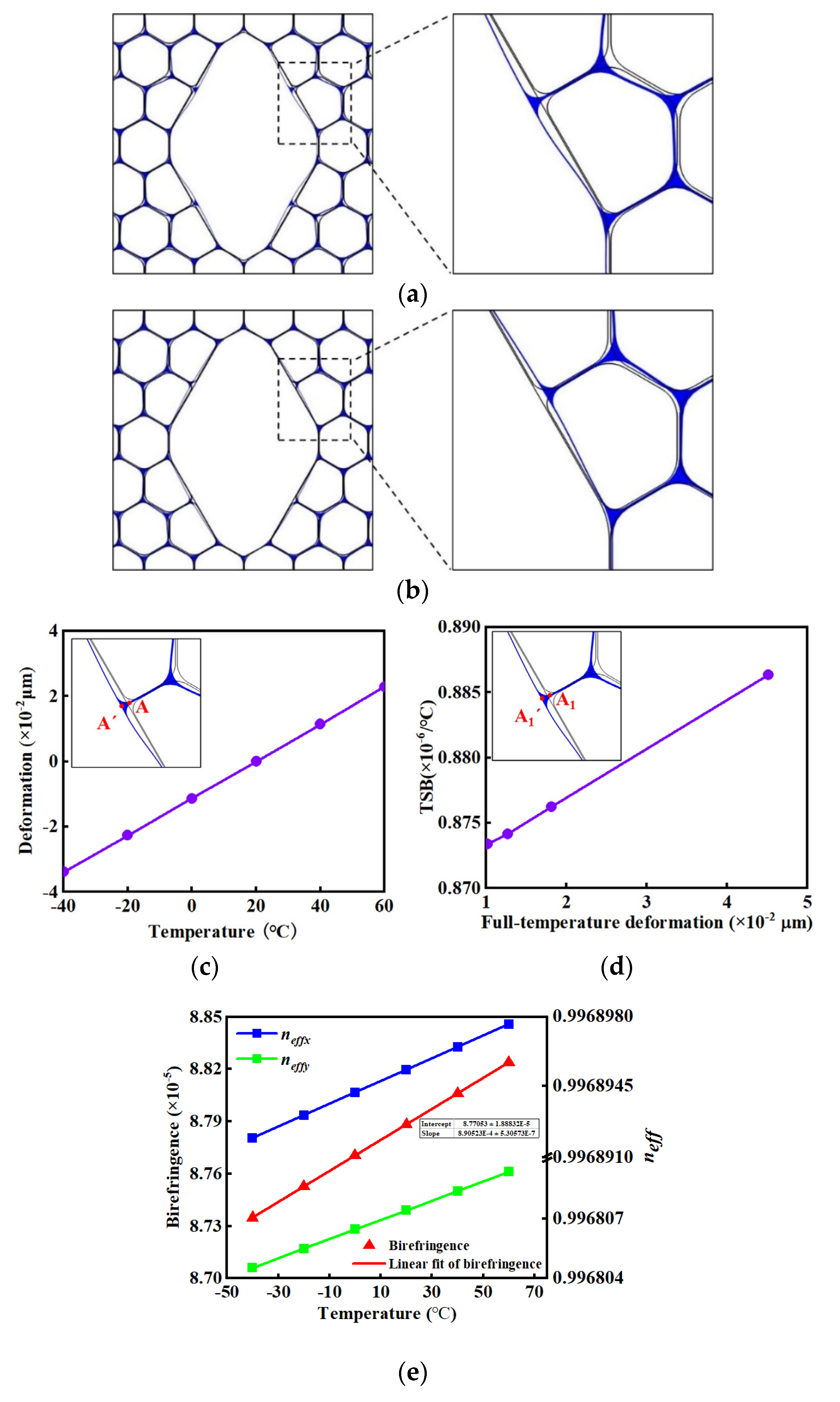
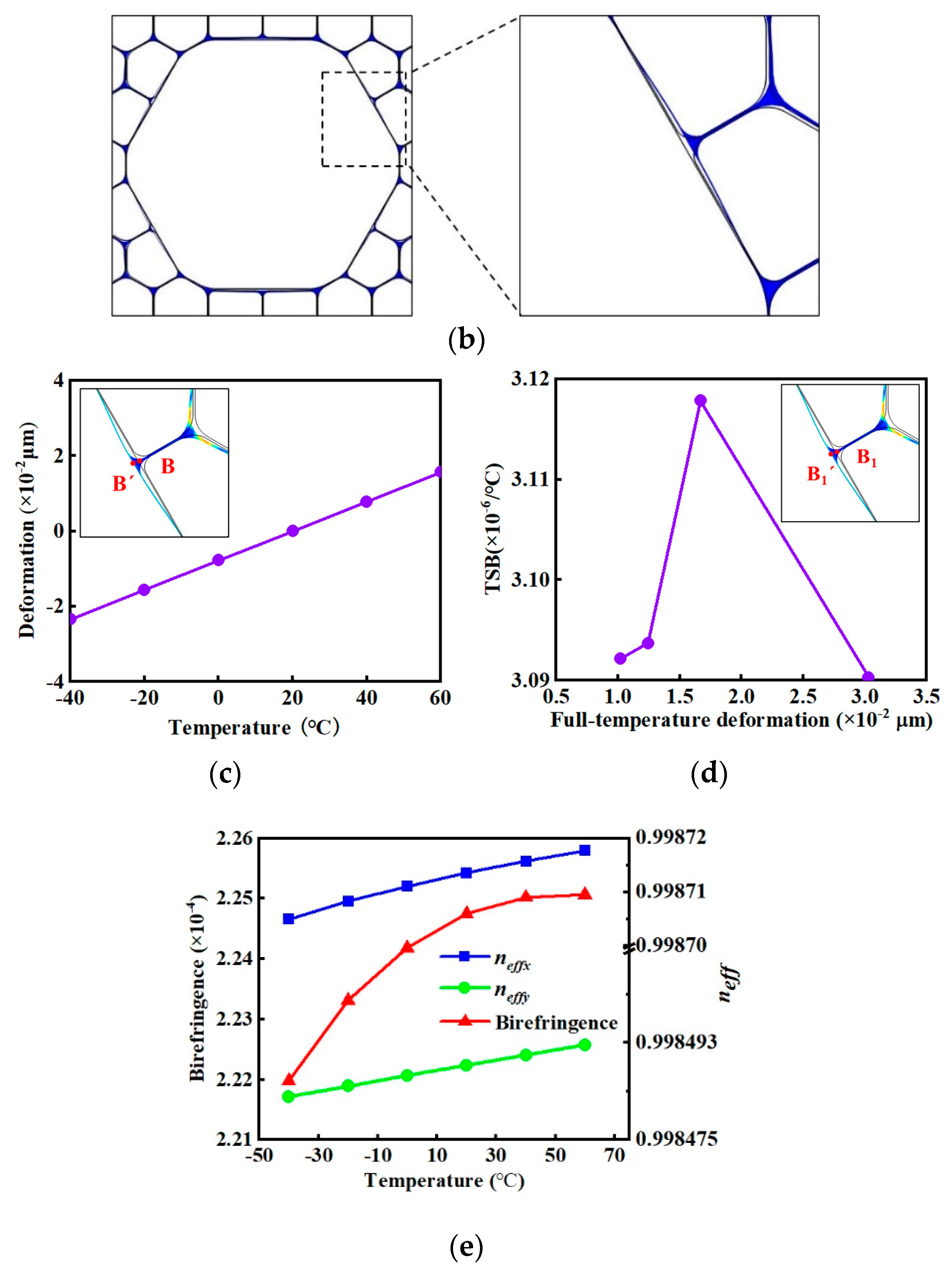
3.1. Thermal Deformation and Birefringence Variation in PM HC-PBGFs with Given Structure Parameters
3.2. TSB of PM HC-PBGFs with Different Structure Parameters
3.2.1. Different Periodic Microstructure Parameters
3.2.2. Different Glass Layer Thicknesses Parameters
3.2.3. Different Coating Thickness
4. Comparison of TSB between PM HC-PBGFs and Panda PM Fiber
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Post, E.J. Sagnac effect. Rev. Mod. Phys. 1967, 39, 475–494. [Google Scholar] [CrossRef]
- Arditty, H.J.; Lefèvre, H.C. Sagnac effect in fiber gyroscopes. Opt. Lett. 1981, 6, 401–403. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.X.; Liu, Q.W.; Liu, Y.Y.; Hui, H.L.; He, Z.Y. Navigation-grade resonant fiber-optic gyroscope using ultra-simple white-light multibeam interferometry. Photonics Res. 2022, 10, 542–549. [Google Scholar] [CrossRef]
- Lefèvre, H.C.; Steib, A.; Claire, A.; Couderette, A.; Pointel, A.-L.; Viltard, A.; Bonnet, A.; Frénois, A.; Gandoin, A.; Laurent, A.; et al. The fiber optic gyro ‘adventure’ at Photonetics, iXsea and now iXblue. SPIE Defense + Commercial Sensing. Opt. Waveguide Laser Sens. 2020, 11405, 791. [Google Scholar] [CrossRef]
- Pavlath, G.A. Fiber Optic Gyros: The Vision Realized. In Proceedings of the Optical Fiber Sensors, Cancun, Mexico, 23–27 October 2006. [Google Scholar]
- Zarinetchi, F.; Ezekiel, S. Observation of lock-in behavior in a passive resonator gyroscope. Opt. Lett. 1986, 11, 401–403. [Google Scholar] [CrossRef]
- Jin, J.; Zhang, T.; Kong, L.; Ma, K. In-Orbit Performance Evaluation of a Spaceborne High Precision Fiber Optic Gyroscope. Sensors 2018, 18, 106. [Google Scholar] [CrossRef]
- Digonnet, M.J.; Chamoun, J.N. Recent developments in laser-driven and hollow-core fiber optic gyroscopes. In Proceedings of the Fiber Optic Sensors and Applications XIII, Baltimore, MD, USA, 12 May 2016. [Google Scholar]
- Böhm, K.; Petermann, K.; Weidel, E. Sensitivity of a fiber-optic gyroscope to environmental magnetic fields. Opt. Lett. 1982, 7, 180–182. [Google Scholar] [CrossRef]
- Du, S.; Wang, X.; Lin, S.; Zhang, C. Gamma-radiation induced degradation random walk error in interferometer fiber optic gyroscope. Opt. Appl. 2011, 41, 953–959. [Google Scholar]
- Ma, H.; Yan, Y.; Chen, Y.; Jin, Z. Improving long-term stability of a resonant micro-optic gyro by reducing polarization fluctuation. IEEE Photon. J. 2012, 4, 2372–2381. [Google Scholar]
- Choi, W.S. Analysis of temperature dependence of thermally induced transient effect in interferometric fiber-optic gyroscopes. J. Opt. Soc. Korean 2011, 15, 237–243. [Google Scholar] [CrossRef]
- Fokoua, E.N.; Petrovich, M.N.; Bradley, T.; Poletti, F.; Richardson, D.J.; Slavík, R. How to make the propagation time through an optical fiber fully insensitive to temperature variations. Optica 2017, 4, 659. [Google Scholar] [CrossRef]
- Wang, C.G.; She, X.; Chen, K.; Yang, Z.; Chen, X.F.; Huang, T.C.; Liu, C. Analysis of thermal property in hollow-core polarization maintaining photonic crystal fibers. Opt. Rev. 2017, 24, 291–296. [Google Scholar] [CrossRef]
- Varnham, M.; Payne, D.; Barlow, A.; Birch, R. Analytic Solution for the Birefringence Produced by Thermal Stress in Polarization-Maintaining Optical Fibers. J. Light. Technol. 1983, LT-1, 332–339. [Google Scholar] [CrossRef]
- Rashleigh, S. Origins and control of polarization effects in single-mode fibers. J. Light. Technol. 1983, 1, 312–331. [Google Scholar] [CrossRef]
- Digonnet, M.J.F.; Kim, H.K.; Blin, S.; Dangui, V.; Kino, G.S. Sensitivity and Stability of an Air-Core Fiber Gyroscope. In Proceedings of the Optical Fiber Sensors, Cancun, Mexico, 23–27 October 2006. [Google Scholar]
- Kim, H.K.; Digonnet, M.J.F.; Kino, G.S. Air-Core Photonic-Bandgap Fiber-Optic Gyroscope. J. Light. Technol. 2006, 24, 3169. [Google Scholar]
- Zhang, Z.; Wang, Y.Y.; Zhou, M.; He, J.; Liao, C.R.; Wang, Y.P. Recent advance in hollow-core fiber high-temperature and high-pressure sensing technology. Chin Opt Lett. 2021, 19, 070601. [Google Scholar] [CrossRef]
- Blin, S.; Kim, H.K.; Digonnet, M.J.F.; Kino, G.S. Reduced Thermal Sensitivity of a Fiber-Optic Gyroscope Using an Air-Core Photonic-Bandgap Fiber. J. Light. Technol. 2007, 25, 861–865. [Google Scholar] [CrossRef]
- Dangui, V.; Kim, H.K.; Digonnet, M.J.F.; Kino, G.S. Phase sensitivity to temperature of the fundamental mode in air-guiding photonic-bandgap fibers. Opt. Express 2005, 13, 6669–6684. [Google Scholar] [CrossRef]
- Slavík, R.; Marra, G.; Fokoua, E.N.; Baddela, N.; Wheeler, N.V.; Petrovich, M.; Poletti, F.; Richardson, D.J. Ultralow thermal sensitivity of phase and propagation delay in hollow core optical fibres. Sci. Rep. 2015, 5, 15447. [Google Scholar] [CrossRef]
- Ma, H.H.; Liu, D.N.; Feng, C.K.; Feng, L.S. Thermal sensitivity of the birefringence of photonic-bandgap fiber. In Proceedings of the Applied Optics and Photonics China 2021, Beijing, China, 24 November 2021. [Google Scholar]
- Petrovich, M.N.; Poletti, F.; Brakel, A.V.; Richardson, D.J. Robustly single mode hollow core photonic bandgap fiber. Opt. Express 2008, 16, 4337–4346. [Google Scholar] [CrossRef]
- Amezcua-Correa, R.; Broderick, N.G.R.; Petrovich, M.N.; Poletti, F.; Richardson, D.J. Design of 7 and 19 cells core air-guiding photonic crystal fibers for low-loss, wide bandwidth and dispersion controlled operation. Opt. Express 2007, 15, 17577–17586. [Google Scholar] [CrossRef] [PubMed]

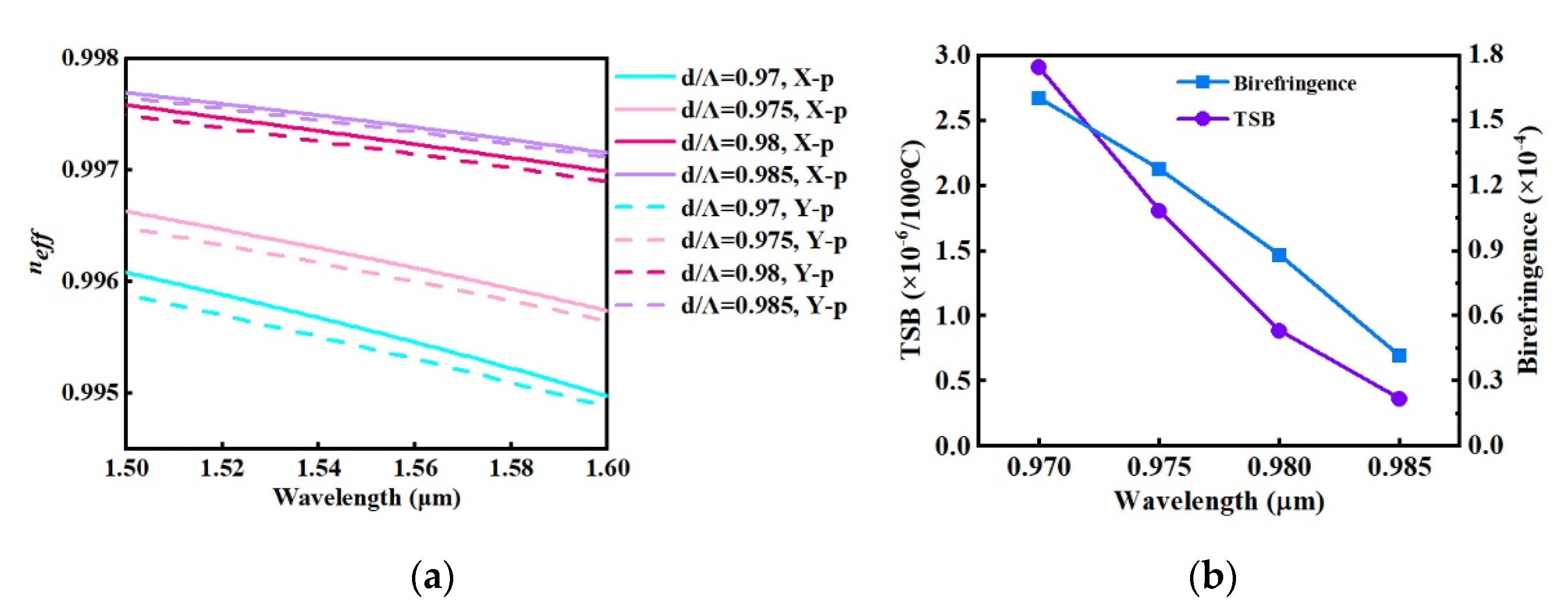
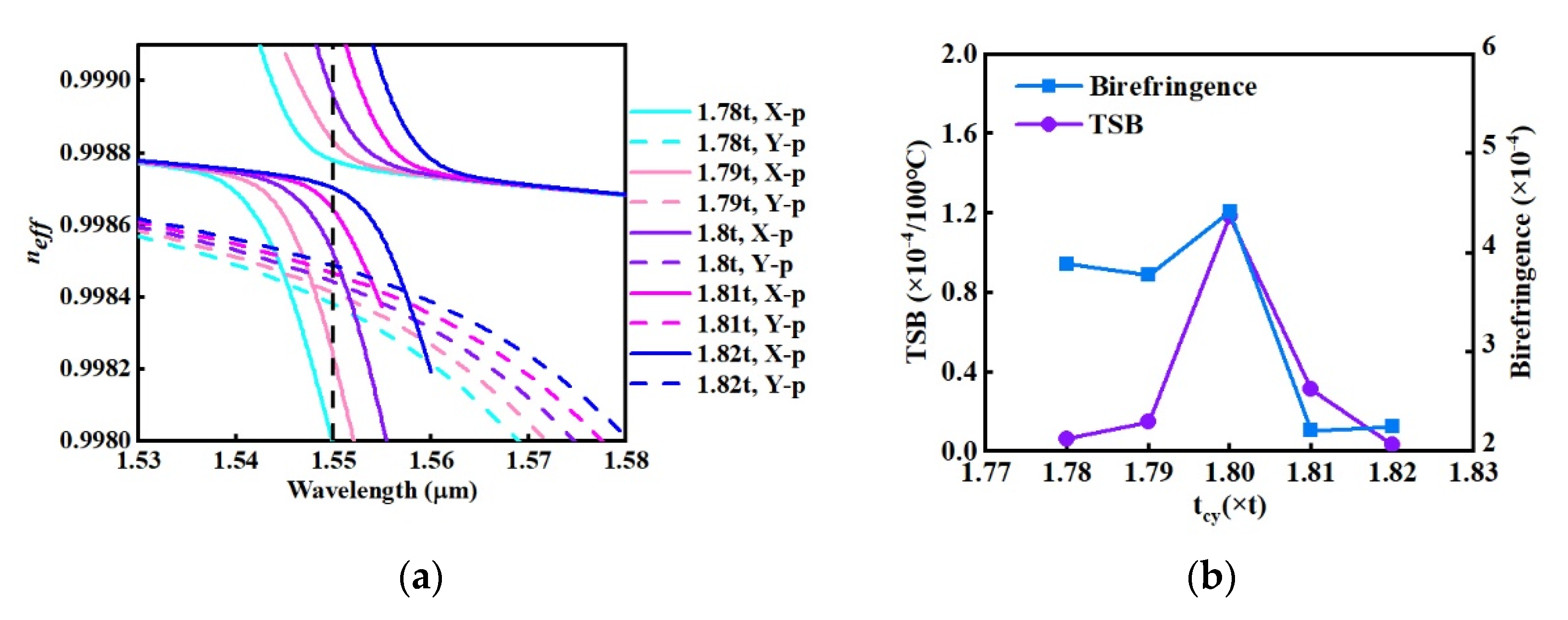

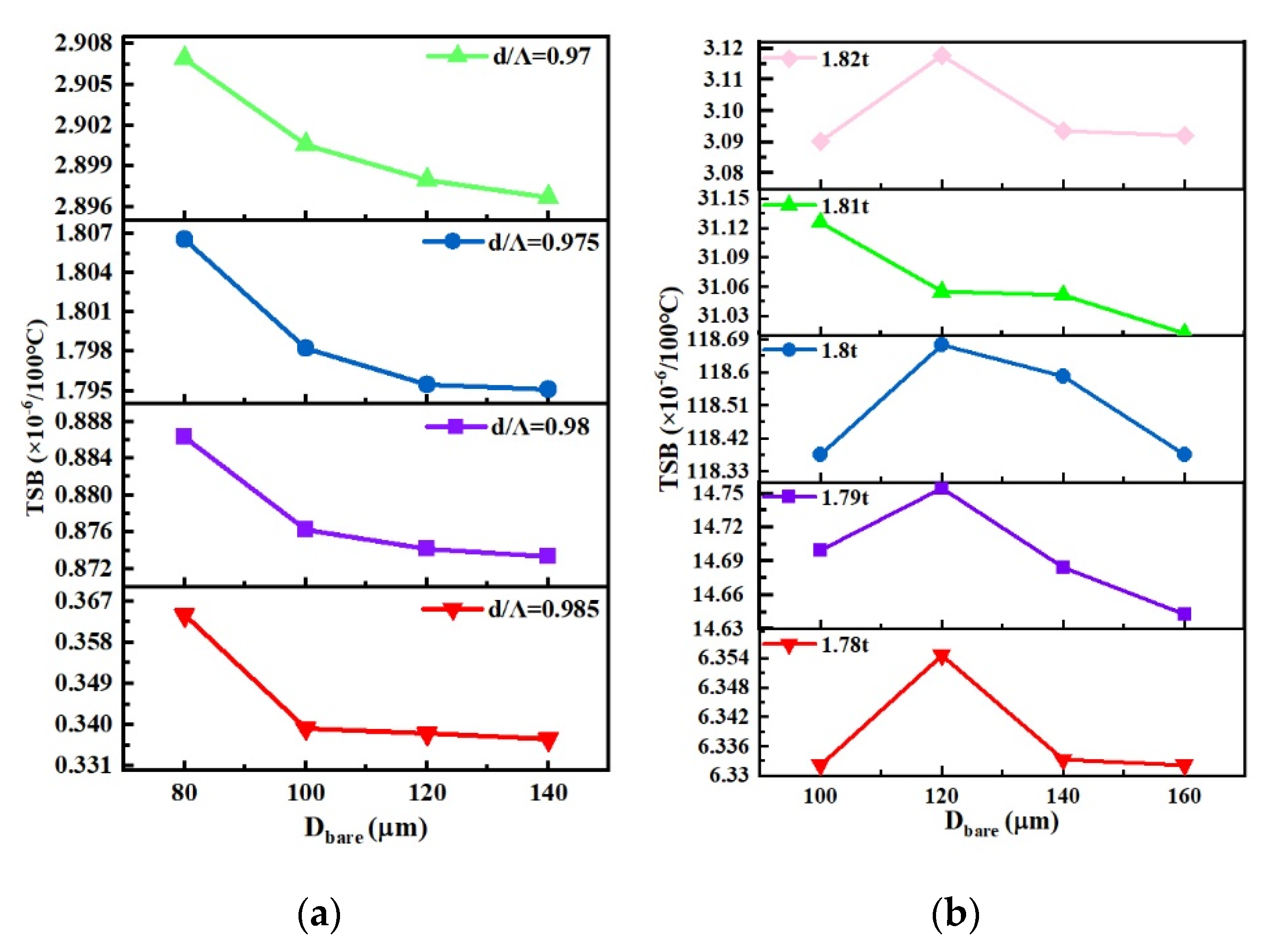

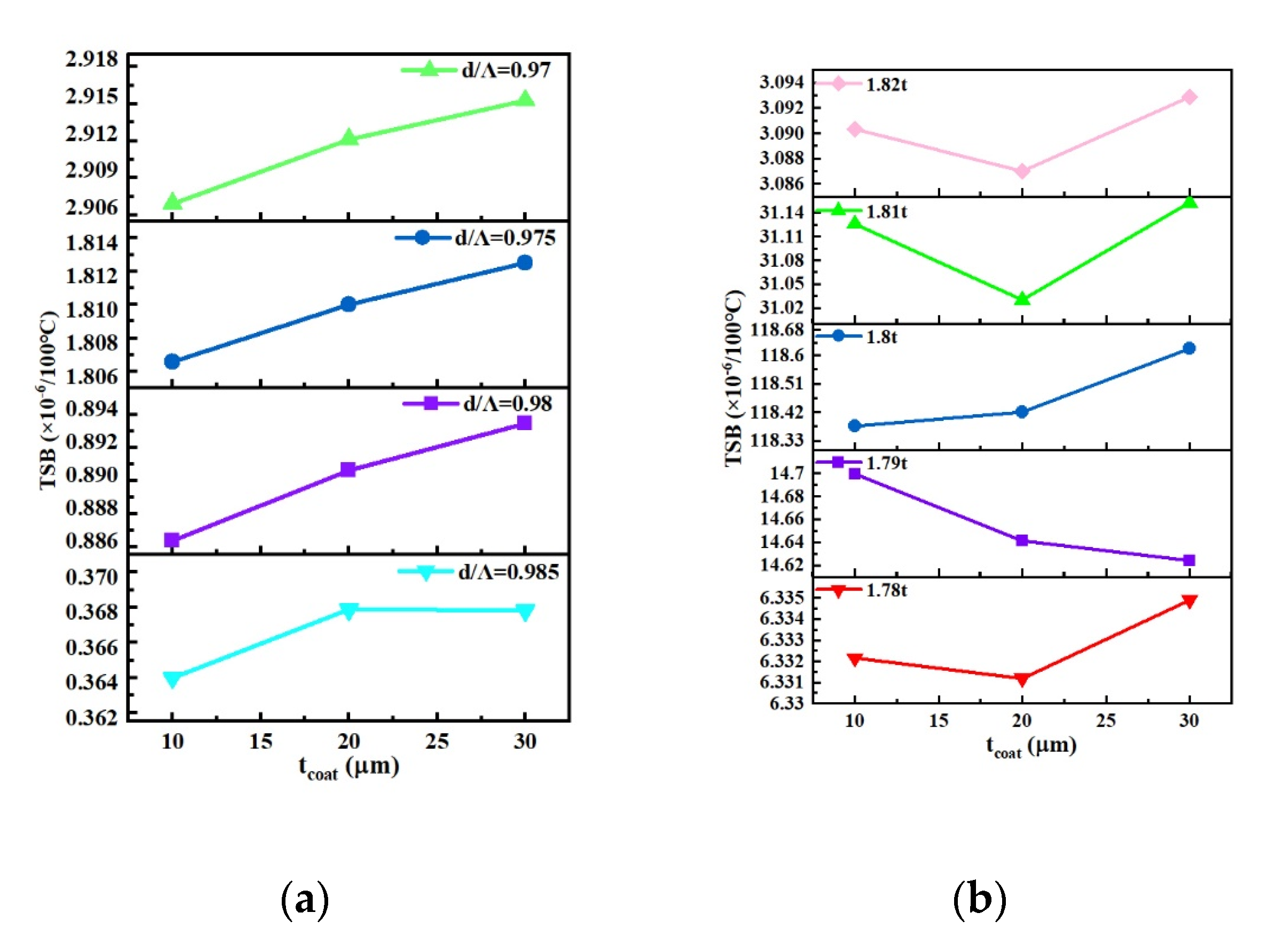
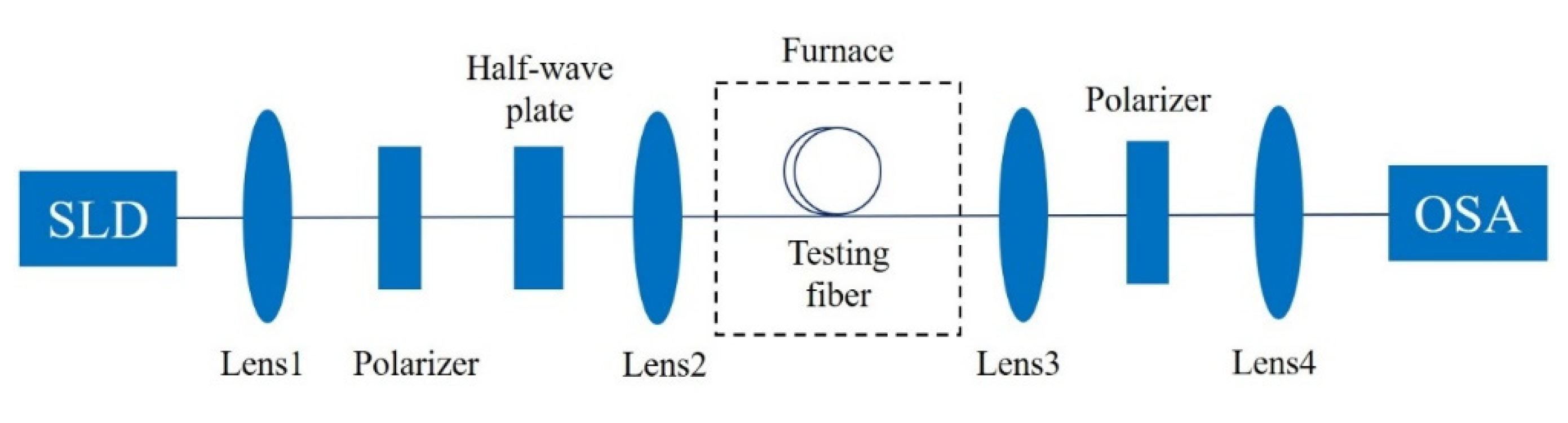
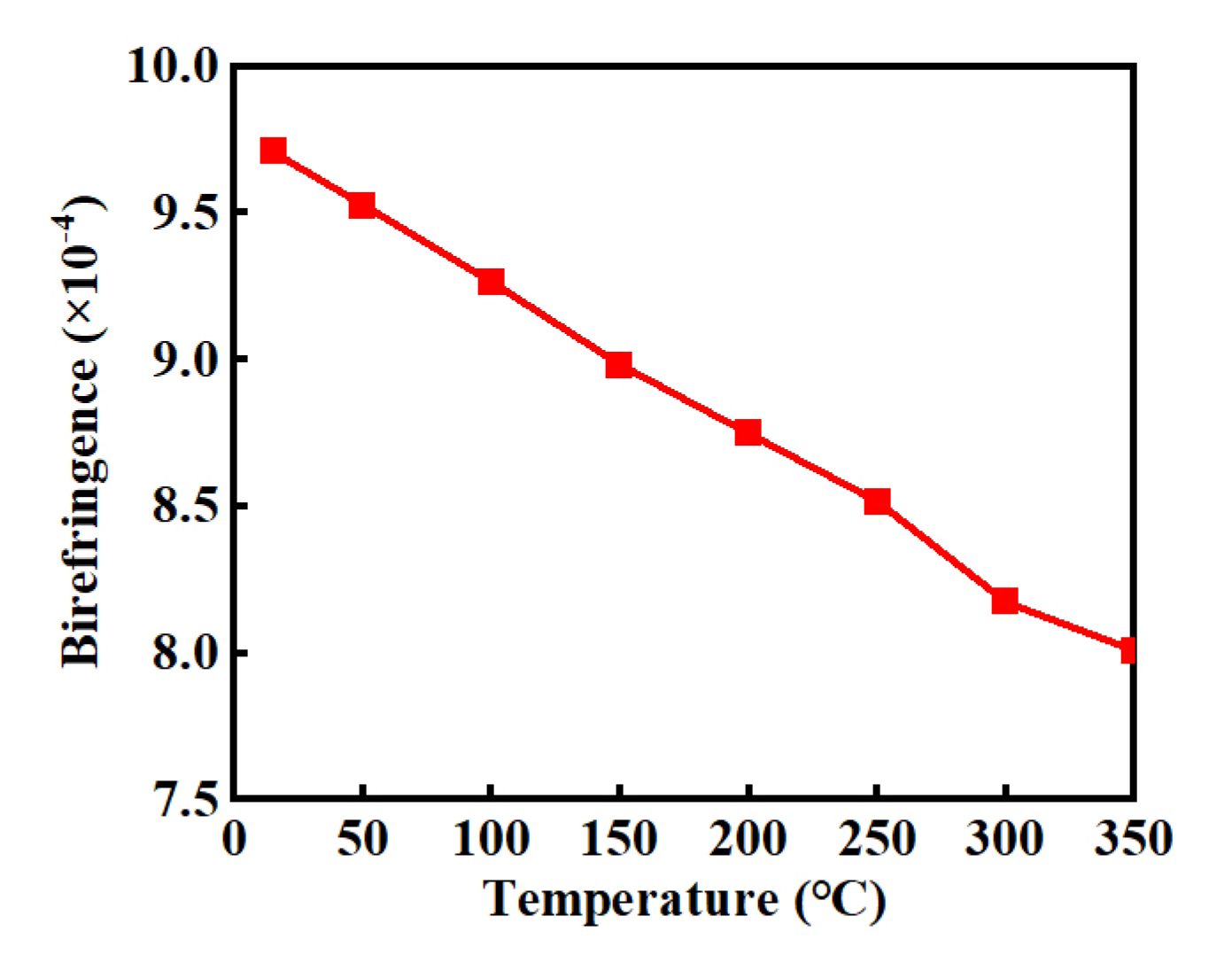
| d/Λ | 0.97 | 0.975 | 0.98 | 0.985 |
|---|---|---|---|---|
| Birefringence | 1.6 × 10−4 | 1.28 × 10−4 | 8.79 × 10−5 | 4.15 × 10−5 |
| tcy | 1.78 t | 1.79 t | 1.8 t | 1.81 t | 1.82 t |
|---|---|---|---|---|---|
| Birefringence | 3.88 × 10−4 | 3.77 × 10−4 | 4.41 × 10−4 | 2.21 × 10−4 | 2.25 × 10−4 |
| Fiber Types | Geometry Parameters | TSB | |
|---|---|---|---|
| Panda PM fiber | Dcore = 8.5 µm, Dbare = 125 µm | 5.07 × 10−5/100 °C | |
| Rhombic core fiber | d/Λ (Dbare = 80 μm, tcoat = 30 μm) | 0.97 | 2.92 × 10−6/100 °C |
| 0.975 | 1.81 × 10−6/100 °C | ||
| 0.98 | 8.93 × 10−7/100 °C | ||
| 0.985 | 3.68 × 10−7/100 °C | ||
| Hexagonal core fiber | tcy (Dbare = 120 μm, tcoat = 10 μm) | 1.78 t | 6.36 × 10−6/100 °C |
| 1.79 t | 1.48 × 10−5/100 °C | ||
| 1.8 t | 1.19 × 10−4/100 °C | ||
| 1.81 t | 3.11 × 10−5/100 °C | ||
| 1.82 t | 3.12 × 10−6/100 °C | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liao, M.; Yu, F.; Li, W.; Xu, J.; Hu, L.; Gao, W. Thermal Sensitivity of Birefringence in Polarization-Maintaining Hollow-Core Photonic Bandgap Fibers. Photonics 2023, 10, 103. https://doi.org/10.3390/photonics10020103
Wang L, Liao M, Yu F, Li W, Xu J, Hu L, Gao W. Thermal Sensitivity of Birefringence in Polarization-Maintaining Hollow-Core Photonic Bandgap Fibers. Photonics. 2023; 10(2):103. https://doi.org/10.3390/photonics10020103
Chicago/Turabian StyleWang, Lidong, Meisong Liao, Fei Yu, Weichang Li, Jiacheng Xu, Lili Hu, and Weiqing Gao. 2023. "Thermal Sensitivity of Birefringence in Polarization-Maintaining Hollow-Core Photonic Bandgap Fibers" Photonics 10, no. 2: 103. https://doi.org/10.3390/photonics10020103
APA StyleWang, L., Liao, M., Yu, F., Li, W., Xu, J., Hu, L., & Gao, W. (2023). Thermal Sensitivity of Birefringence in Polarization-Maintaining Hollow-Core Photonic Bandgap Fibers. Photonics, 10(2), 103. https://doi.org/10.3390/photonics10020103






