Investigation of the Space-Variance Effect of Imaging Systems with Digital Holography
Abstract
:1. Introduction
2. Materials and Methods
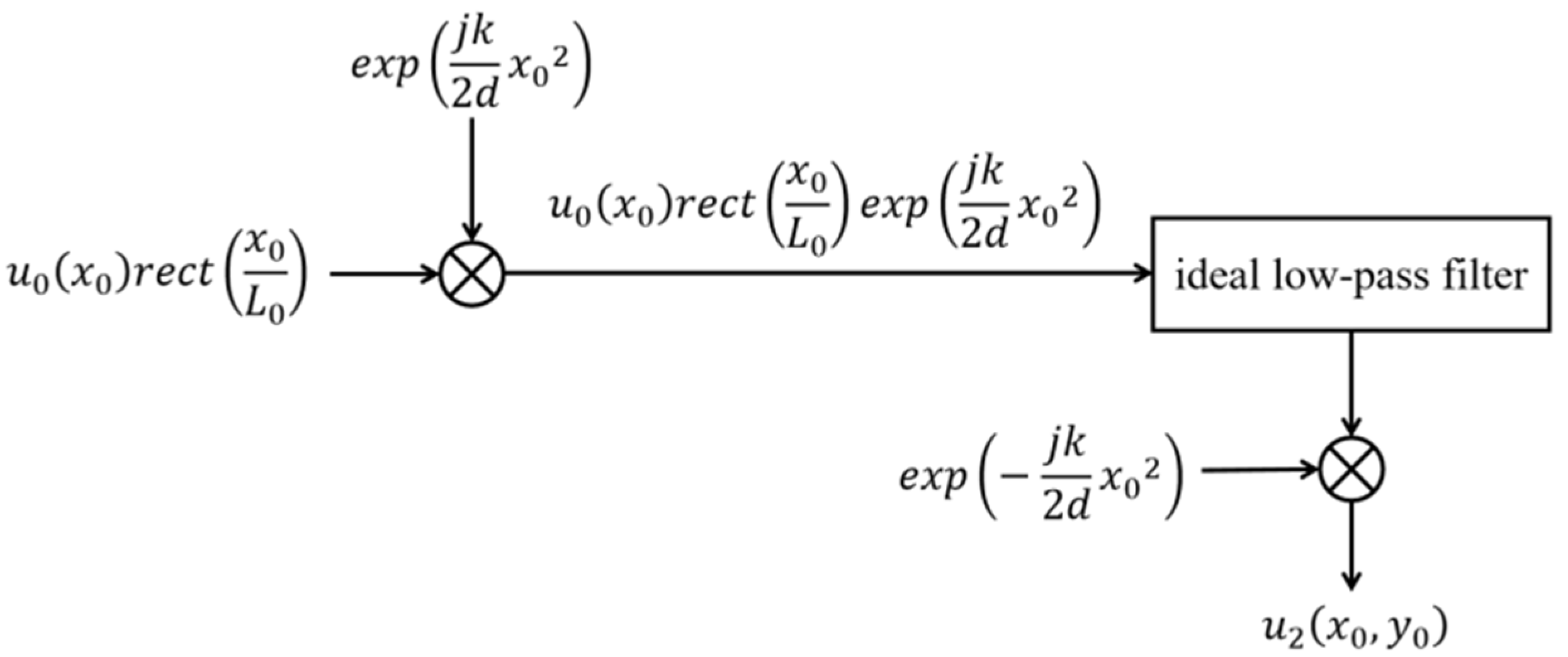
2.1. Mathematical Model of Space-Variant Fresnel Holographic Imaging Systems
- (1)
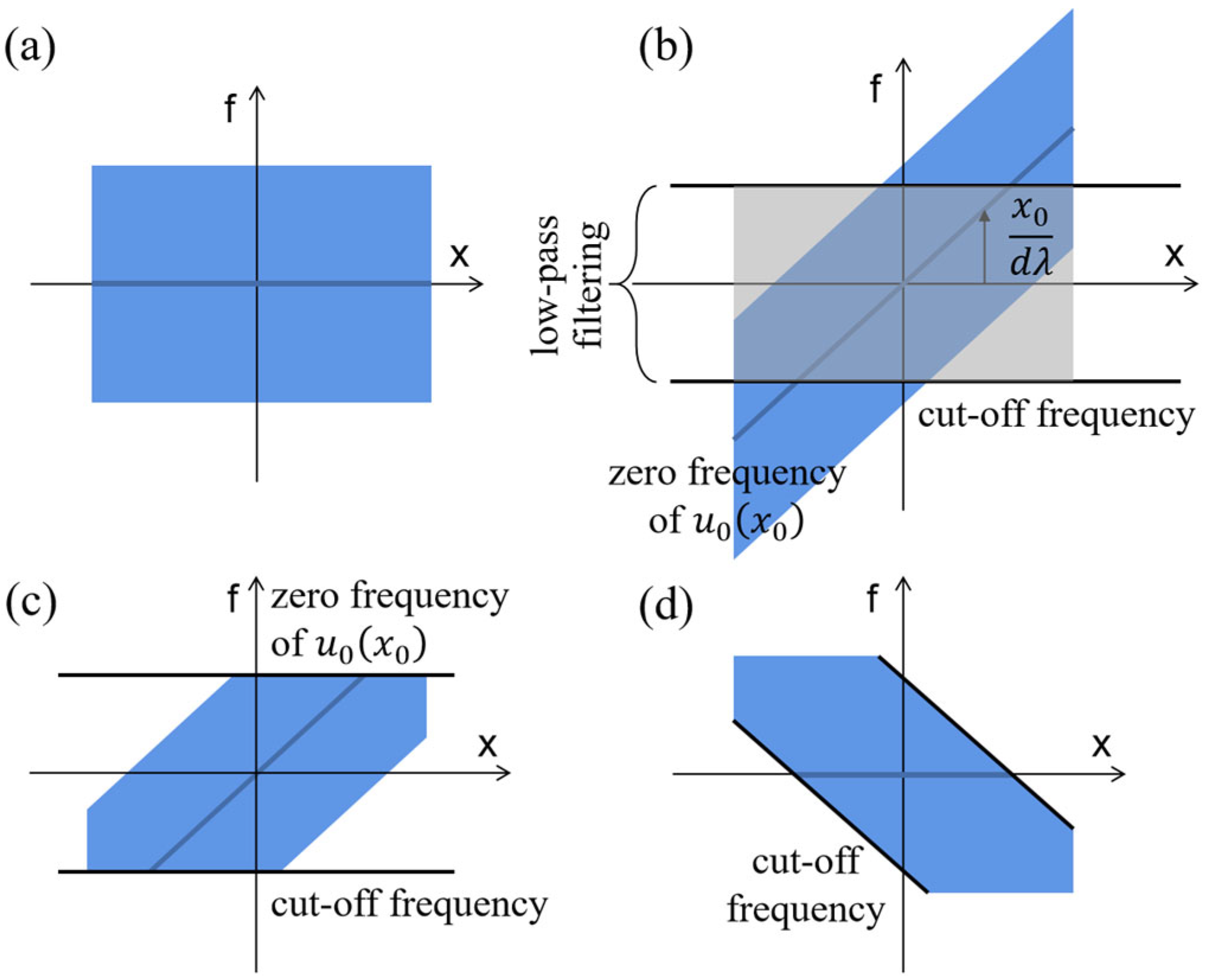
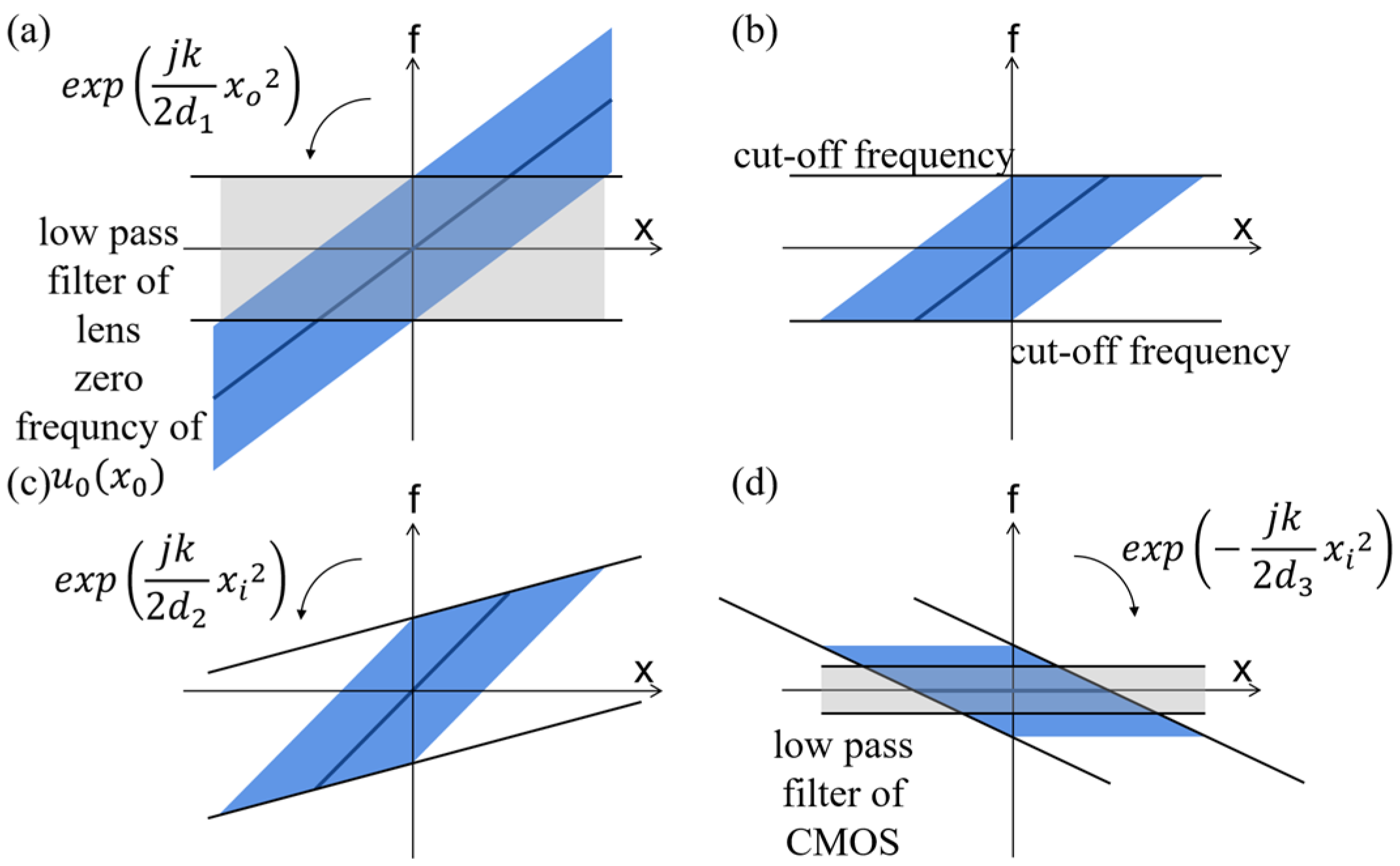
- Modulation of input signal by carrier signal . If , the frequency shift introduced by the carrier signal when applying the frequency shift theorem of the Fourier transform isEquation (6) shows that the frequency shift is dependent on the spatial coordinates, which indicates that this process is space-variant. The distribution of the modulated signal in phase space is shown in Figure 3b.
- (2)
- Ideal low-pass filtering of modulated signal . represents a rectangular ideal low-pass filter, as shown in Figure 4, whose passband is determined by the angular aperture of the CMOS target plane, namely, . As shown in Figure 3b,c, after the frequency shift of the modulation signal, the original low-frequency information becomes high-frequency. In this case, low-pass filtering will block the original low-frequency information of the modulation signal . The farther away it is from the optical axis, the more low-frequency information of the modulation signal that will be lost. Therefore, for the input signal of the system–object field , the aperture is not reflected as an ideal low-pass filter due to the frequency shift effect of Equation (6) but as a frequency-selective filter, with the constant passband width and center frequency changing with the position in the object plane. Such a filter presents different frequency responses with different spatial locations of the modulation signal ; that is, the filtering process is space-variant for the modulation signal .
- (3)
- Modulation of ideal low-pass-filtered signal by carrier signal . When the reconstruction distance is equal to the recording distance, the two carrier signals before and after filtering are conjugate and cancel each other, and the Fresnel holography reconstruction automatically completes the demodulation process. Therefore, the problem of quadratic phase aberration is not encountered in Fresnel holography. The distribution of the reconstructed wave field in phase space is shown in Figure 3d.
2.2. Three Stages of the Space-Variance Effect
- (1)
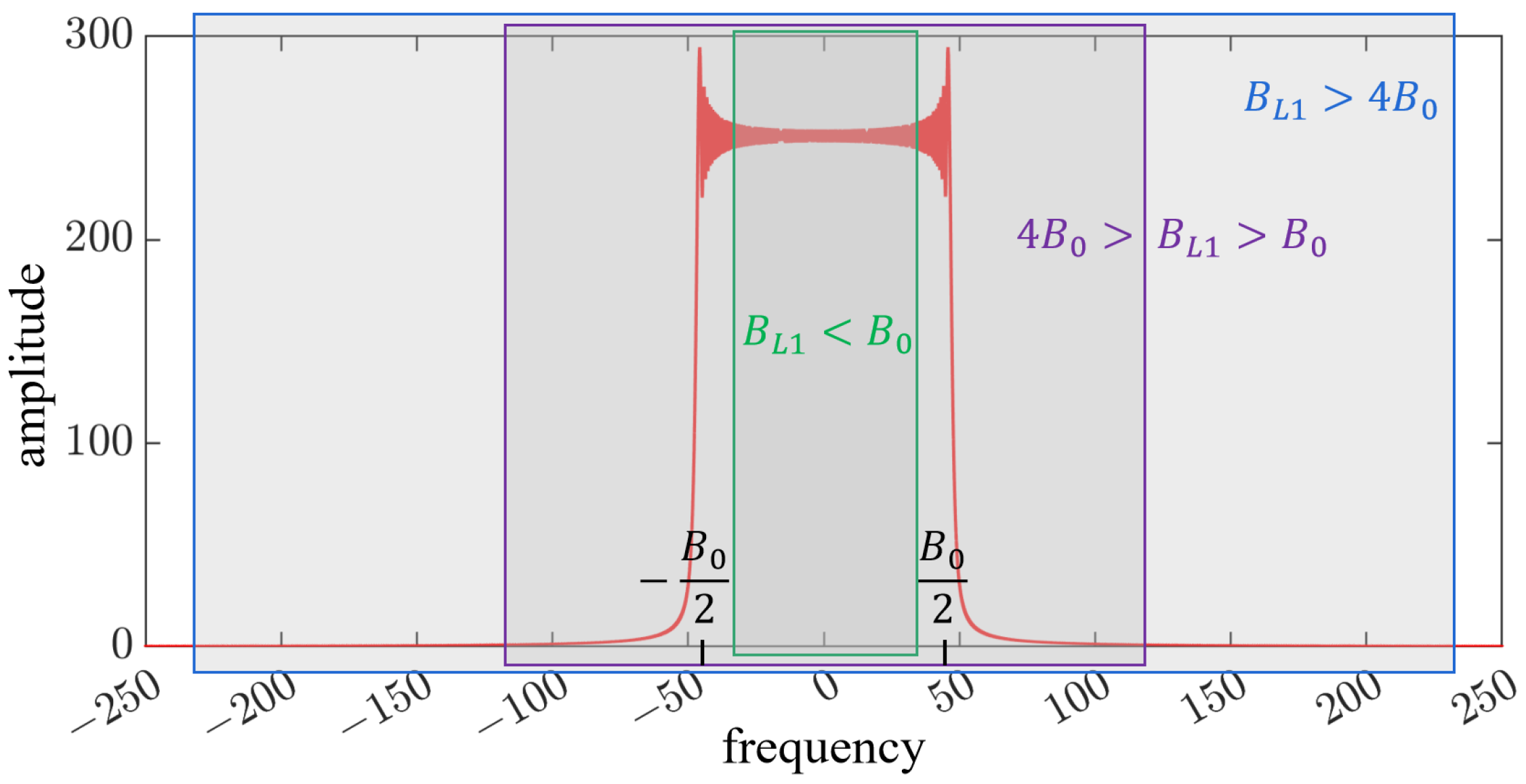
- Approximate space-invariance state. In this state, the filter passband width is much larger than the bandwidth of the LFM signal; that is, the width of the aperture is much larger than the width of the object field . The blue box in Figure 4 represents the passband of the low-pass filter in this case. Tichenor and Goodman [5] pointed out that when , the space-variance effect is negligible. The classical Fourier optical analysis of optical imaging systems rests on the assumption of approximate space invariance; in other words, only the case is considered.
- (2)
- High-frequency distortion state. The passband width of the filter in this state satisfies . The purple box in Figure 4 represents the passband of the low-pass filter in this case. The energy blocked by the filter is mainly from the high-frequency information of the object field far from the optical axis. The farther away the object wave field is from the optical axis, the higher the frequency modulated by the LFM signal is. Therefore, more information is lost in these areas after low-pass filtering, and the image quality is worse, which is mainly reflected in the distortion of the abrupt phase in the margin of the image wave field.
- (3)
- Boundary-diffraction state. The green box in Figure 4 represents the passband of the low-pass filter when . In this case, the high-frequency information and a mass of low-frequency information in the margin of the object wave field are filtered out. Because the main energy of the optical field is concentrated in the low-frequency information, high energy loss occurs in areas where low-frequency information is filtered out, which leads to a decrease in the signal-to-noise ratio, resulting in phase distortion.
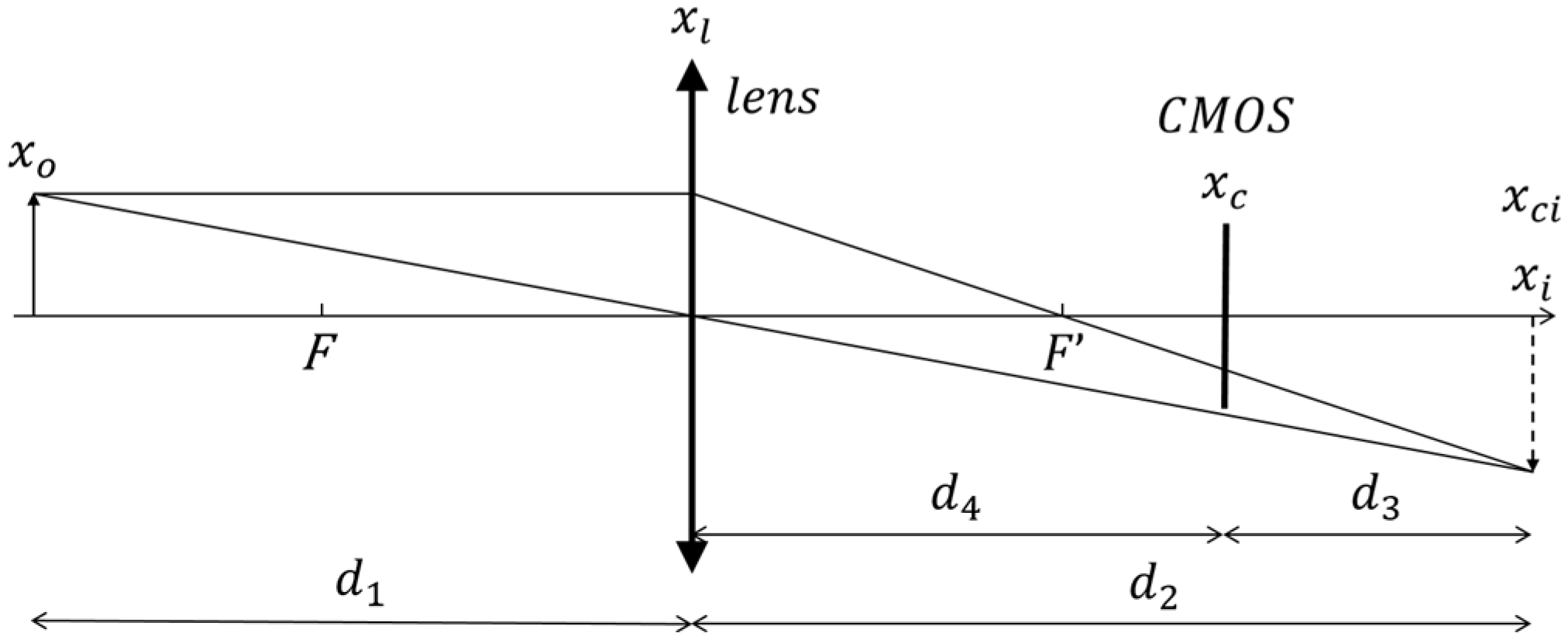
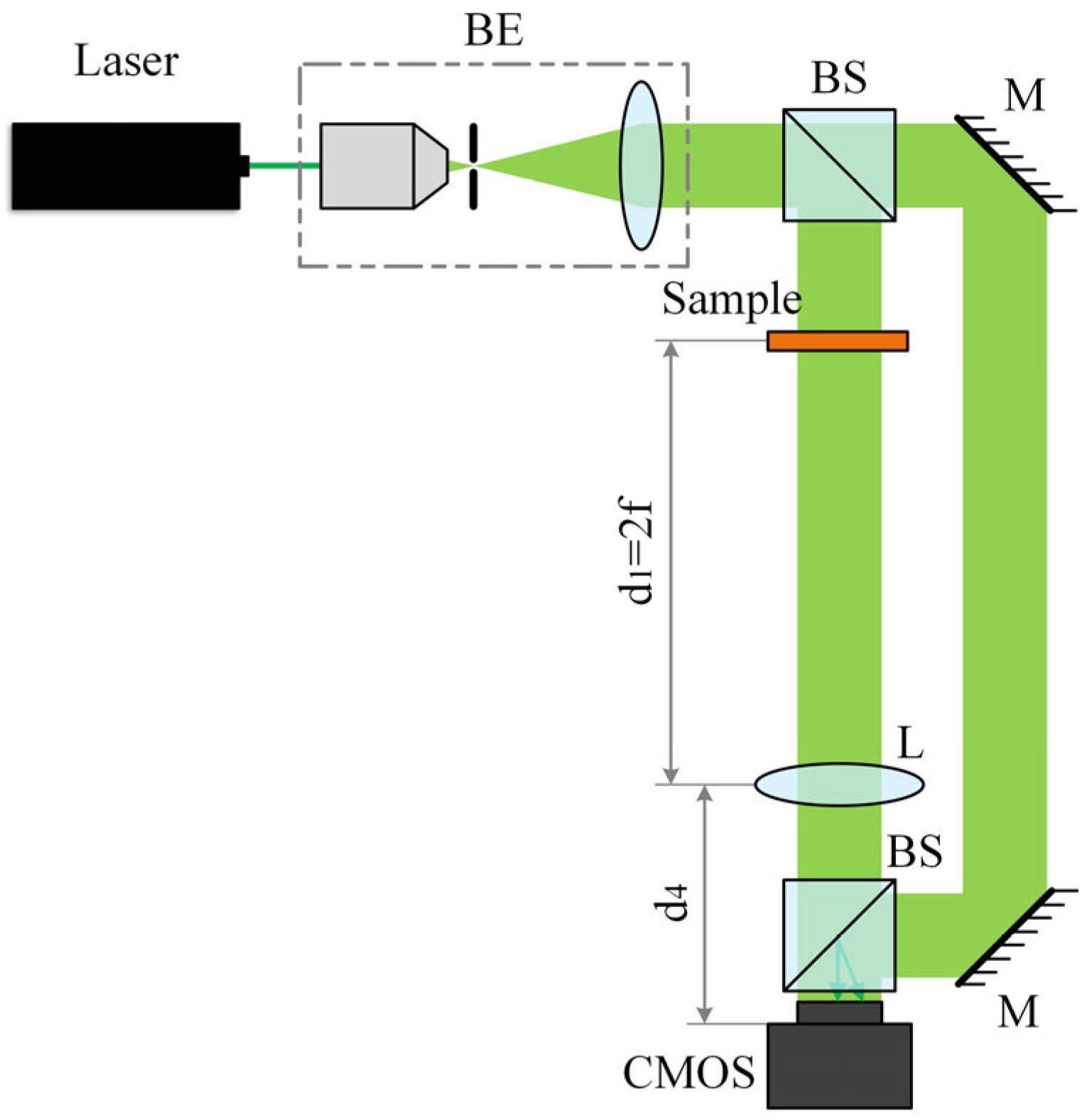
2.3. Eliminating the Space-Variance Effect by Recording Holograms at the Back Focal Plane of the Imaging Lens
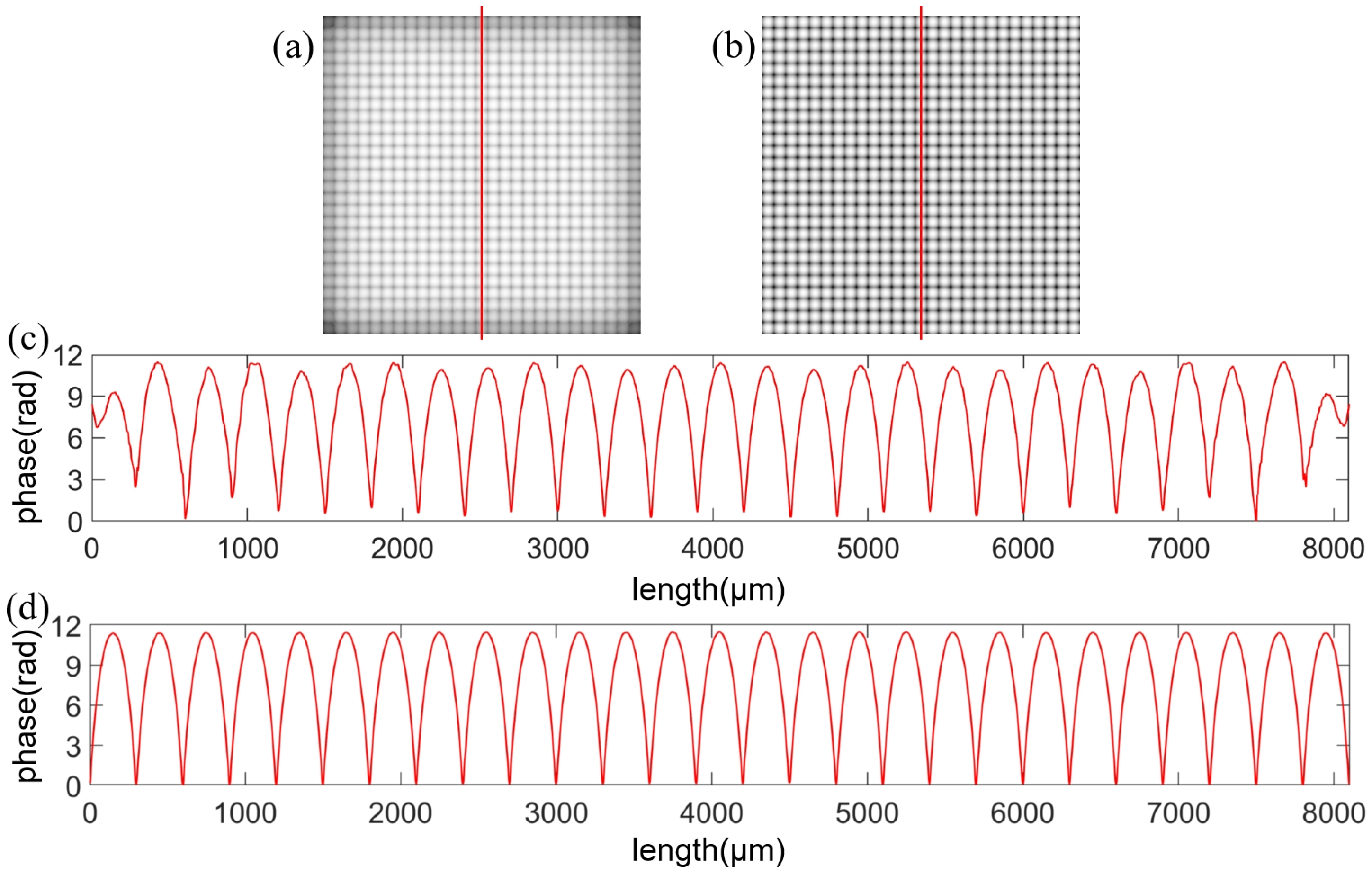
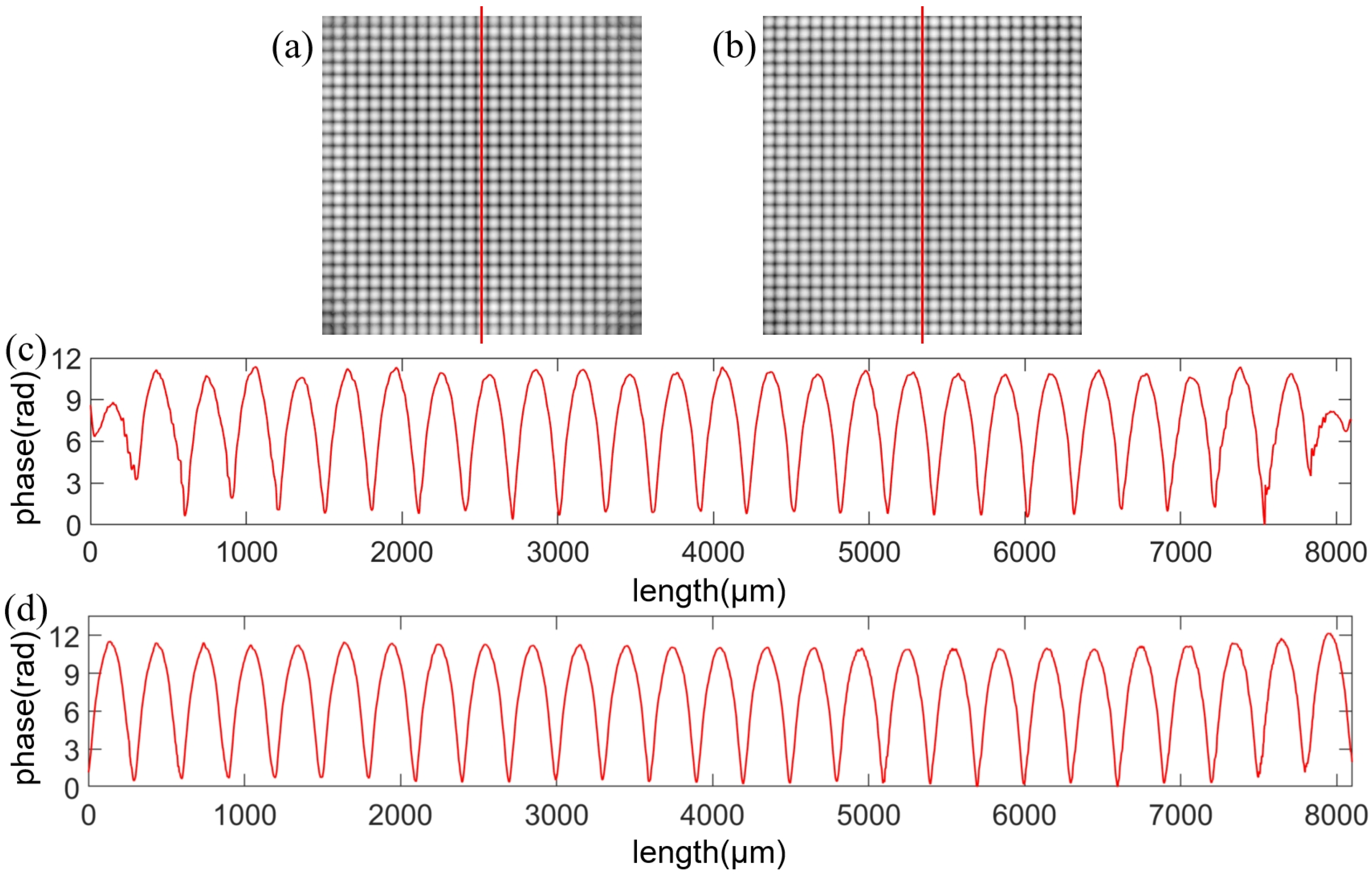
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goodman, J.W. Introduction to Fourier Optics, 4th ed.; W.H. Freeman: New York, NY, USA, 2017. [Google Scholar]
- Yan, H.; Liu, C.Y.; Jun, L.; Ping, C.; Qian, K.M.; Asundi, A. Investigation of the systematic axial measurement error caused by the space variance effect in digital holography. Opt. Lasers Eng. 2019, 112, 16–25. [Google Scholar] [CrossRef]
- Lohmann, A.W.; Paris, D.P. Space-Variant Image Formation. J. Opt. Soc. Am. 1965, 55, 1007–1013. [Google Scholar] [CrossRef]
- Brainis, E.; Muldoon, C.; Brandt, L.; Kuhn, A. Coherent imaging of extended objects. Opt. Commun. 2009, 282, 465–472. [Google Scholar] [CrossRef]
- Tichenor, D.A.; Goodman, J.W. Coherent Transfer-Function. J. Opt. Soc. Am. 1972, 62, 293–295. [Google Scholar] [CrossRef]
- Pan, A.; Zuo, C.; Xie, Y.G.; Lei, M.; Yao, B.L. Vignetting effect in Fourier ptychographic microscopy. Opt. Lasers Eng. 2019, 120, 40–48. [Google Scholar] [CrossRef]
- Girshovitz, P.; Shaked, N.T. Fast phase processing in off-axis holography using multiplexing with complex encoding and live-cell fluctuation map calculation in real-time. Opt. Express 2015, 23, 8773–8787. [Google Scholar] [CrossRef]
- Merola, F.; Memmolo, P.; Miccio, L.; Savoia, R.; Mugnano, M.; Fontana, A.; D’Ippolito, G.; Sardo, A.; Iolascon, A.; Gambale, A.; et al. Tomographic flow cytometry by digital holography. Light-Sci. Appl. 2017, 6, 7. [Google Scholar] [CrossRef]
- Tahara, T.; Quan, X.Y.; Otani, R.; Takaki, Y.; Matoba, O. Digital holography and its multidimensional imaging applications: A review. Microscopy 2018, 67, 55–67. [Google Scholar] [CrossRef]
- Katz, J.; Sheng, J. Applications of Holography in Fluid Mechanics and Particle Dynamics. Annu. Rev. Fluid Mech. 2010, 42, 531–555. [Google Scholar] [CrossRef]
- Miccio, L.; Memmolo, P.; Merola, F.; Fusco, S.; Embrione, V.; Paciello, A.; Ventre, M.; Netti, P.A.; Ferraro, P. Particle tracking by full-field complex wavefront subtraction in digital holography microscopy. Lab Chip 2014, 14, 1129–1134. [Google Scholar] [CrossRef]
- Chen, Y.; Guildenbecher, D.R.; Hoffmeister, K.N.G.; Cooper, M.A.; Stauffacher, H.L.; Oliver, M.S.; Washburn, E.B. Study of aluminum particle combustion in solid propellant plumes using digital in-line holography and imaging pyrometry. Combust. Flame 2017, 182, 225–237. [Google Scholar] [CrossRef]
- Khmaladze, A.; Restrepo-Martinez, A.; Kim, M.; Castaneda, R.; Blandon, A. Simultaneous dual-wavelength reflection digital holography applied to the study of the porous coal samples. Appl. Opt. 2008, 47, 3203–3210. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, J.; Charriere, F.; Colomb, T.; Cuche, E.; Montfort, F.; Emery, Y.; Marquet, P.; Depeursinge, C. Axial sub-nanometer accuracy in digital holographic microscopy. Meas. Sci. Technol. 2008, 19, 8. [Google Scholar] [CrossRef]
- Agour, M.; Falldorf, C.; Bergmann, R.B. Spatial multiplexing and autofocus in holographic contouring for inspection of micro-parts. Opt. Express 2018, 26, 28576–28588. [Google Scholar] [CrossRef] [PubMed]
- Kostencka, J.; Kozacki, T.; Kus, A.; Kemper, B.; Kujawinska, M. Holographic tomography with scanning of illumination: Space-domain reconstruction for spatially invariant accuracy. Biomed. Opt. Express 2016, 7, 4086–4101. [Google Scholar] [CrossRef] [PubMed]
- Balasubramani, V.; Kus, A.; Tu, H.Y.; Cheng, C.J.; Baczewska, M.; Krauze, W.; Kujawinska, M. Holographic tomography: Techniques and biomedical applications Invited. Appl. Opt. 2021, 60, B65–B80. [Google Scholar] [CrossRef] [PubMed]
- Cuche, E.; Bevilacqua, F.; Depeursinge, C. Digital holography for quantitative phase-contrast imaging. Opt. Lett. 1999, 24, 291–293. [Google Scholar] [CrossRef]
- Mann, C.J.; Yu, L.F.; Lo, C.M.; Kim, M.K. High-resolution quantitative phase-contrast microscopy by digital holography. Opt. Express 2005, 13, 8693–8698. [Google Scholar] [CrossRef]
- Mohammed, S.K.; Bouamama, L.; Bahloul, D.; Picart, P. Quality assessment of refocus criteria for particle imaging in digital off-axis holography. Appl. Opt. 2017, 56, F158–F166. [Google Scholar] [CrossRef]
- Yamagiwa, M.; Minamikawa, T.; Trovato, C.; Ogawa, T.; Ibrahim, D.G.A.; Kawahito, Y.; Oe, R.; Shibuya, K.; Mizuno, T.; Abraham, E.; et al. Multicascade-linked synthetic wavelength digital holography using an optical- comb-referenced frequency synthesizer. Opt. Express 2018, 26, 26292–26306. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms. Appl. Opt. 1999, 38, 6994–7001. [Google Scholar] [CrossRef] [PubMed]
- Colomb, T.; Cuche, E.; Charriere, F.; Kuhn, J.; Aspert, N.; Montfort, F.; Marquet, P.; Depeursinge, C. Automatic procedure for aberration compensation in digital holographic microscopy and applications to specimen shape compensation. Appl. Opt. 2006, 45, 851–863. [Google Scholar] [CrossRef]
- Hecht, E. Optics, Global, 5th ed.; Pearson: Boston, MA, USA, 2017. [Google Scholar]
- Stein, A.; Barbastathis, G. Axial imaging necessitates loss of lateral shift invariance. Appl. Opt. 2002, 41, 6055–6061. [Google Scholar] [CrossRef] [PubMed]
- Bastiaans, M.J. Application of the Wigner Distribution Function in Optics. In The Wigner Distribution—Theory and Applications in Signal Processing; Mecklenbräuker, W., Hlawatsch, F., Eds.; Elsevier: Amsterdam, The Netherlands, 1997; pp. 375–426. Available online: https://research.tue.nl/en/publications/application-of-the-wigner-distribution-function-in-optics (accessed on 29 November 2023).
- Oh, S.B.; Barbastathis, G. Axial imaging necessitates loss of lateral shift invariance: Proof with the Wigner analysis. Appl. Opt. 2009, 48, 5881–5888. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Pearson: New York, NY, USA, 2018; p. xvi. 1168p. [Google Scholar]
- Colomb, T.; Montfort, F.; Kuhn, J.; Aspert, N.; Cuche, E.; Marian, A.; Charriere, F.; Bourquin, S.; Marquet, P.; Depeursinge, C. Numerical parametric lens for shifting, magnification, and complete aberration compensation in digital holographic microscopy. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2006, 23, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Qu, W.J.; Asundi, A. Phase aberration compensation in digital holographic microscopy based on principal component analysis. Opt. Lett. 2013, 38, 1724–1726. [Google Scholar] [CrossRef] [PubMed]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; John Wiley & Sons, Inc: New York, NY, USA, 1991; p. xvii. 647p. [Google Scholar]
- Cuche, E.; Marquet, P.; Depeursinge, C. Aperture apodization using cubic spline interpolation: Application in digital holographic microscopy. Opt. Commun. 2000, 182, 59–69. [Google Scholar] [CrossRef]
- Kuhn, J.; Niraula, B.; Liewer, K.; Wallace, J.K.; Serabyn, E.; Graff, E.; Lindensmith, C.; Nadeau, J.L. A Mach-Zender digital holographic microscope with sub-micrometer resolution for imaging and tracking of marine micro-organisms. Rev. Sci. Instrum. 2014, 85, 6. [Google Scholar] [CrossRef]
- Wen, Y.F.; Qu, W.J.; Cheng, H.B.; Yan, H.; Asundi, A. Further investigation on the phase stitching and system errors in digital holography. Appl. Opt. 2015, 54, 266–276. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhang, X.C.; Xu, M.; Zhang, H.; Jiang, X.Q. Phase unwrapping in digital holography based on non-subsampled contourlet transform. Opt. Commun. 2018, 407, 367–374. [Google Scholar] [CrossRef]
- Ren, Z.B.; Zhao, J.L.; Lam, E.Y. Automatic compensation of phase aberrations in digital holographic microscopy based on sparse optimization. APL Photonics 2019, 4, 110808. [Google Scholar] [CrossRef]
- Liu, B.C.; Feng, D.Q.; Feng, F.; Tian, A.L.; Liu, W.G. Maximum a posteriori-based digital holographic microscopy for high-resolution phase reconstruction of a micro-lens array. Opt. Commun. 2020, 477, 126364. [Google Scholar] [CrossRef]
- Zheng, C.; Jin, D.; He, Y.P.; Lin, H.T.; Hu, J.J.; Yaqoob, Z.; So, P.T.C.; Zhou, R.J. High spatial and temporal resolution synthetic aperture phase microscopy. Adv. Photonics 2020, 2, 065002. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Zhao, H.J.; Shan, M.G.; Liu, B.; Lu, W.L.; Zhang, Y.B. Off-axis digital holographic microscopy with divided aperture. Opt. Lasers Eng. 2020, 127, 105954. [Google Scholar] [CrossRef]
- Fan, X.; Healy, J.J.; O’Dwyer, K.; Winnik, J.; Hennelly, B.M. Adaptation of the Standard Off-Axis Digital Holographic Microscope to Achieve Variable Magnification. Photonics 2021, 8, 264. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhao, R.; Chen, H.; Du, Y.; Fan, C.; Zhang, G.; Zhao, Z. Investigation of the Space-Variance Effect of Imaging Systems with Digital Holography. Photonics 2023, 10, 1350. https://doi.org/10.3390/photonics10121350
Yang X, Zhao R, Chen H, Du Y, Fan C, Zhang G, Zhao Z. Investigation of the Space-Variance Effect of Imaging Systems with Digital Holography. Photonics. 2023; 10(12):1350. https://doi.org/10.3390/photonics10121350
Chicago/Turabian StyleYang, Xingyu, Rong Zhao, Huan Chen, Yijun Du, Chen Fan, Gaopeng Zhang, and Zixin Zhao. 2023. "Investigation of the Space-Variance Effect of Imaging Systems with Digital Holography" Photonics 10, no. 12: 1350. https://doi.org/10.3390/photonics10121350
APA StyleYang, X., Zhao, R., Chen, H., Du, Y., Fan, C., Zhang, G., & Zhao, Z. (2023). Investigation of the Space-Variance Effect of Imaging Systems with Digital Holography. Photonics, 10(12), 1350. https://doi.org/10.3390/photonics10121350




