Abstract
We investigate the generation of optical third-harmonic frequency in quadratic crystals with a nonlinear domain lattice optimized with the aid of a random number generator. In the developed Monte Carlo algorithm and numerical experiments, we consider domain thicknesses to be taking either the values d1 or d2, with d1 and d2 being the coherence lengths for the cascaded parametric interactions and , respectively. We focus on the cases with single segments formed by equal and/or different domains, showing that frequency tripling can be achieved with high conversion efficiency from an arbitrary input wavelength. The presented approach allows one to accurately determine the optimized random alternation of domain thicknesses d1 and d2 along the propagation length.
1. Introduction
Following the attention paid to frequency conversion in non-centrosymmetric crystals in the early days of nonlinear optics [1,2,3], in recent years, cascaded quadratic processes have been proven to be able to mimic and implement cubic effects [4,5,6,7,8,9]. Among them, second-harmonic generation (SHG) and sum-frequency generation (SFG) can support third-harmonic generation (THG) (see e.g., [10] and references therein). Such parametric conversion cannot be implemented in homogeneous bulk crystals owing to dispersion, because the refractive index (i.e., phase–velocity) matching, n(ω) = n(2ω) = n(3ω), is not satisfied by the values at ω, 2ω, and 3ω, respectively [11,12].
The advent of quasi-phase-matching (QPM) through domain engineering in ferroelectric crystals has largely increased conversion efficiencies [13,14]. In periodic crystals, QPM at first [15] or higher grating orders [16] make SHG + SFG cascading possible for frequency tripling. It has been shown that an effective implementation of cascaded THG requires either an optimum ratio of fundamental and 2nd-harmonic amplitudes at the input of the periodic crystal [15], coupled nonlinear strengths [17,18,19,20], or Fourier optimization of the nonlinear lattice [21], etc. [22]. Notably, aperiodic crystals structured with either random domains [23], domains arranged in Fibonacci series [24], or the introduction of spatial inhomogeneities [25] can also allow for cascaded THG.
In this article, we introduce a design algorithm for the efficient tripling of arbitrary fundamental frequencies by engineering a nonlinear domain sequence in quadratic crystals. We specifically demonstrate the use of QPM lattices encompassing domains with opposite second-order susceptibilities and only two thicknesses, d1 and d2, with d1 = lc1 being the coherence length for the SHG process, and d2 = lc2 being the coherence length for the subsequent (cascaded) SFG process [11,12]. While genetic algorithms, simulated annealing, and optimal control based on Lagrange multipliers have been exploited earlier to design nonlinear optical lattices (see, e.g., [23] and references therein), the Monte Carlo based design presented hereby with reference to third-harmonic generation is an effective and convenient numerical approach to optimizing cascaded parametric interactions in quadratic crystals.
2. Materials and Methods
At variance with previously reported methods, in the approach presented hereby, a given QPM order in not required to operate towards the simultaneous generation of 2nd and 3rd harmonics. Only two domain types (thicknesses) are arranged along the propagation, in a random sequence optimized with the aid of a Monte Carlo algorithm and encompassing individual two-domain segments with equal or alternating thicknesses. Figure 1 is an artist’s rendering of the inhomogeneous nonlinear crystal under study.
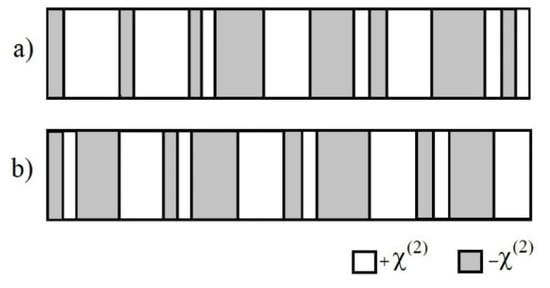
Figure 1.
Sketch of the QPM lattice with domains of thicknesses d1 and d2 and alternating sign of the nonlinear response (). Here, d1 and d2 are the coherence lengths of the interactions 2ω = ω + ω and 3ω = 2ω + ω, respectively. (a) QPM with unequal domain thicknesses in each segment, and (b) QPM with equal domains in each segment.
In order to introduce this approach and keep the design complexity at a minimum, we analyze the parametric interaction of plane waves of different wavelengths using coupled-mode theory in the usual slowly varying envelope approximation, assuming Kleinmann symmetry and Type 0 (ee-e) interactions between co-polarized extraordinary-wave components [10,13,14,16,17,23,24,25]:
with Aj and kj (j = 1, 2, 3) are the electric-field amplitudes and wave vectors at ω, 2ω, and 3ω, respectively; is the SHG wavevector mismatch; is the SFG wavevector mismatch; γSFG and γSHG are the corresponding nonlinear strengths ≈ ≈ ≈ ≈ (e.g., in Lithium Niobate); and δ(z) the sign-varying unity function with random size of either d1 or d2 along the propagation distance z.
To determine the optimal domain sequence along the crystal length, we used a Monte Carlo algorithm to generate random numbers 0 and 1 for positioning domains of size d1 or d2, respectively, with zeroes (ones) corresponding to d1 (d2) from the first up to the Nth domain over the total length. Then, we numerically integrated the system of ordinary differential Equation (1) and computed the resulting conversion efficiency η3 from the fundamental to the third-harmonic frequency.
The THG efficiency η3 was initially set to zero and updated to the value obtained after each randomization of the sequence, provided the latter η3 was higher than the former. Otherwise, when the last η3 result was lower than the previous one, the algorithm randomized the sequence by changing each subsequent (second, third, fourth etc.) domain type and repeating the procedure. By iterating the whole process, we increased the conversion efficiency until convergence was reached to a higher value than prescribed at the sample output or until a set number of iterations was completed.
Notably, the Monte Carlo algorithm proved to be quite successful and fast in converging to the “optimum randomly generated” sequence of the two domain types along the nonlinear crystal. Typical numerical runs, as reported below, involved one or a few thousand iterations and an overall time consumption of less than 90 min when using standard personal computers.
3. Results
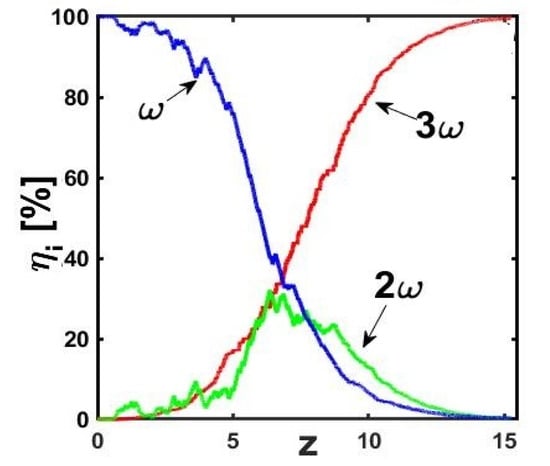
For the initial numerical experiments, we studied a dimensionless quadratic crystal with the following parameters: d1 = 0.01, d2 = 0.5 d1, γSHG = γSFG = γ = 1, ΔkSHG = π/d1, ΔkSFG = π/d2, A1 (z = 0) = 1, A2 (z = 0) = 0, and A3 (z = 0) = 0. The total number N of domains was set to 2000 (N/2 for d1 and N/2 for d2). We normally halted the algorithm within 5000 iterations. The typical results are displayed in Figure 2, showing the normalized intensities ηi (i = 1, 2, 3) at each frequency along the crystal after the 5000th iteration, for unequal domain types in each segment. Figure 3 displays the analog results for equal domain types in each segment. At the last iteration, the THG conversion efficiency reaches the value η3 ≈ 65% in the first case (Figure 2), whereas it is close to 100% in the second case (Figure 3). It is noteworthy that, although the numerical algorithm ran for several loops, the above conversion efficiencies from the fundamental to the 3rd harmonic were reached well before the iteration limit. For instance, 65% and 99% were obtained after ~2500 and ~300 iterations in the first and second cases, respectively.
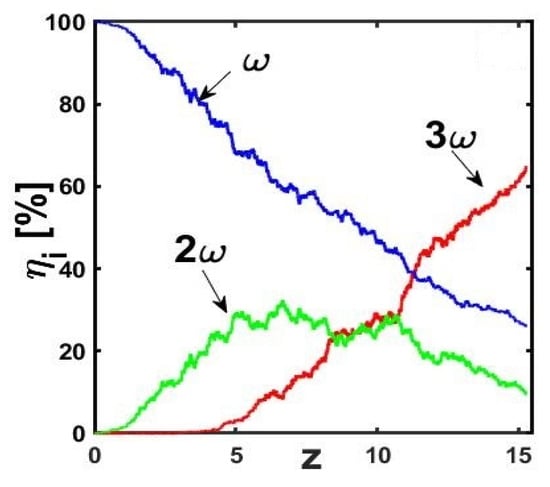
Figure 2.
Results of the numerical experiments after 5000 iterations in a dimensionless quadratic sample. Normalized intensities at the three frequencies along the propagation length when the QPM lattice has (see, e.g., Figure 1a) differently sized domains in each segment.
Next, we investigated the dynamics of the energy exchange between the three interacting waves in a realistic case of a 4 mm long aperiodically poled Lithium Niobate (APP-LN) crystal, using a fundamental wavelength λ = 1.52 µm, an input light intensity of 0.1 GW/cm2, a total number of domains N = 600, d33 = 26 pm/V, and d1 ≈ 9.07 µm, d2 ≈ 3.23 µm [26]. The iteration limit for the Monte Carlo procedure was set to 1000.
The results, graphed in Figure 4 and Figure 5, demonstrate the THG conversion efficiencies η3 ~85% (Figure 4) and η3 ~90% (Figure 5) in the two cases with segments of different or equal domain types, respectively. The efficiencies are initially as low as ~3% at the first iteration in both Figure 4 and Figure 5.
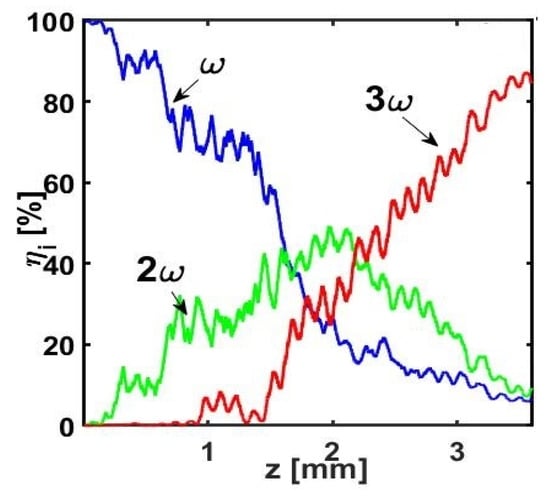
Figure 4.
Results of the numerical experiments after 1000 iterations with reference to an aperiodically poled (z-cut) Lithium Niobate crystal with a total length of 4 mm. Normalized intensities ηi (i = 1, 2, 3) at the three frequencies along the propagation distance z for different domain sizes in each segment.
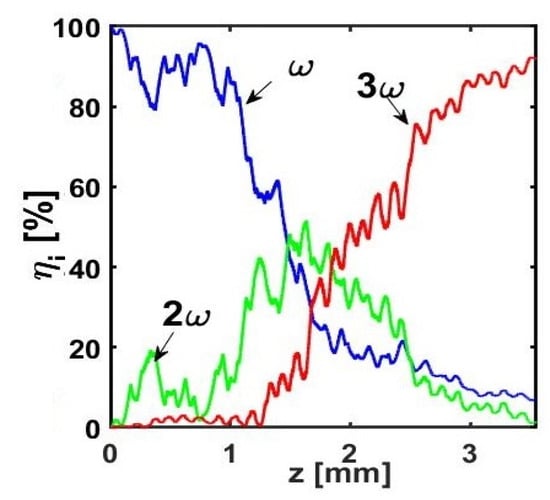
Figure 5.
Same as in Figure 4 but for equal domain sizes in each segment.
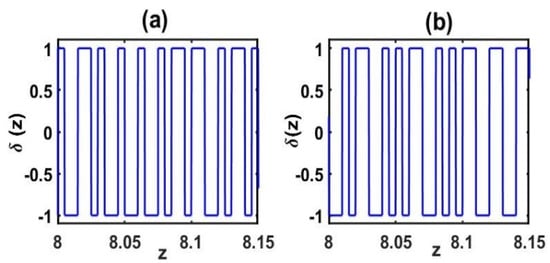
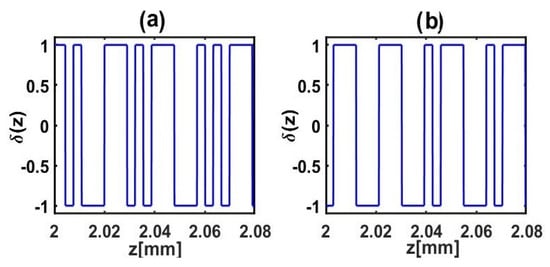
For illustrative purposes, Figure 6 displays the designed domain sequence in the central portion of the aperiodic nonlinear crystal, with reference to the dimensionless examples in Figure 2 and Figure 3 (Figure 6a,b, respectively) or to the realistic APP-LN crystal in Figure 4 and Figure 5 (Figure 7a,b, respectively). Remarkably, after converging to the optimal design for efficient THG, by reversing an arbitrarily positioned domain pair from d1-d2 to d2-d1, the resulting conversion efficiency η3 dropped dramatically, confirming the crucial role of each domain in the specific randomly generated sequence.
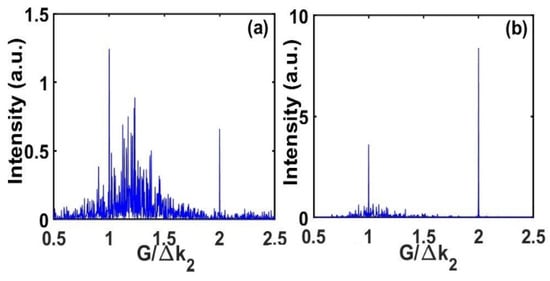
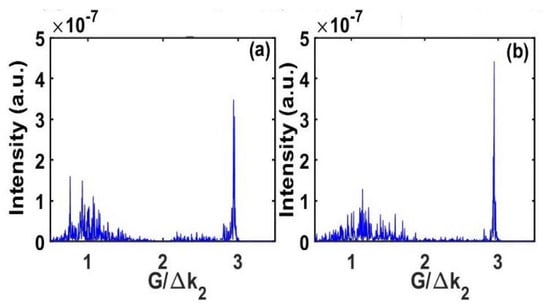
We also computed the Fourier transforms f(G) of the designed gratings (i.e., the sign-varying function δ(z)) in the cases above (Figure 2, Figure 3, Figure 4, Figure 5) through and plotted them in Figure 8 and Figure 9. The “optimum” spectra have normalized lattice wavenumbers around one and two for the dimensionless cases (Figure 8), and around one and three for the APP-LN crystal (Figure 9), as expected. As the nonlinear grating has to compensate the phase mismatch of both SHG and SFG, in the dimensionless example because d1/d2 = 2, while in the realistic case since d1/d2 ≈ 2.8.
Finally, we studied the dependence of the conversion efficiency η3 on the input intensity at the fundamental frequency, which is of relevance in view of actual experimental measurements. To this extent, we considered the realistic case of a QPM dual lattice in the APP−LN crystal with equal domain sizes in each segment, as discussed above (see Figure 5). Figure 10 shows some typical results for three values of input power densities, as specified on each line. Clearly, high conversion efficiencies to the third harmonic can be obtained despite intensity variations as large as 100% with respect to the nominal excitation (Figure 5).
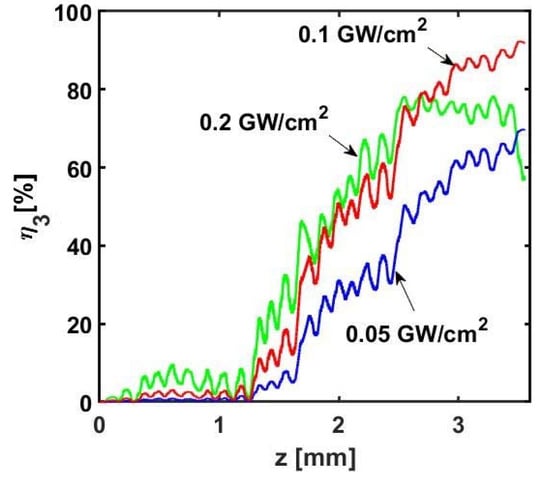
Figure 10.
Intensity conversion efficiency from the fundamental frequency to its 3rd harmonic, calculated for different input intensities (as marked) and the designed APP−LN lattice (Figure 5) with equal domain sizes in each segment.
4. Conclusions
In conclusion, using a randomized algorithm based on the Monte Carlo method, we numerically implemented an efficient cascaded generation from the fundamental to the second and third harmonics in QPM quadratic nonlinear crystals with aperiodically engineered domain structures, employing domain thicknesses corresponding to the SHG and SFG coherence lengths. Practical realization issues and fabrication tolerances of such domain lengths are not expected to be a problem using state-of-the-art technologies.
The designed frequency triplers can achieve conversion efficiencies above a prescribed value and even close to 100% from arbitrary input fundamental wavelengths. The presented design method could also be exploited towards other cascaded processes, as the realization of poled ferroelectric crystals with domains in the micrometer and sub-micrometer scales is no longer a critical issue [10,14]. For instance, the quadratic interactions, ωp = ωs + ωi (DFG) and ωi = ωs − ωi′ (SFG), with ωi′ as a secondary idler wave could lead to parametric amplification, with the idler ωi′ energy being fed back into the signal. This would take place with the simultaneous quasi-phase-matching of both DFG and SFG processes. For example, assuming λs ≈ 3.34 µm, λp ≈ 1.064 µm, λi ≈ 1.5486 µm, and λi′ ≈ 2.844 µm in a 5% MgO-doped APP-LN, [27], double QPM would require randomized optimum sequences with d1 ≈ 15.03 µm and d2 ≈ 0.33 µm.
Author Contributions
Conceptualization, O.I.S., U.K.S. and G.A.; methodology, O.I.S. and U.K.S.; software, O.I.S.; validation, G.A. and U.K.S.; writing—original draft preparation, O.I.S. and U.K.S.; writing—review and editing, U.K.S. and G.A. All authors have read and agreed to the published version of the manuscript.
Funding
U.K.S. acknowledges partial financial support from the projects Uzb-Ind-2021-96, Uzb-Ind-2021-83, and ATLANTIC-823897.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Armstrong, J.A.; Bloembergen, N.; Ducuing, J.; Pershan, P.S. Interactions between Light Waves in a Nonlinear Dielectric. Phys. Rev. 1962, 127, 1918–1939. [Google Scholar] [CrossRef]
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of Optical Harmonics. Phys. Rev. Lett. 1961, 7, 118–120. [Google Scholar] [CrossRef]
- Akhmanov, S.A.; Dmitriev, V.G.; Modenov, V.P. On the theory of frequency multiplication in nonlinear dispersive lines. Radio Eng. Electron. 1964, 9, 814–821. [Google Scholar]
- Stegeman, G.I.; Sheik-Bahae, M.; Van Stryland, E.W.; Assanto, G. Large nonlinear phase shifts in second-order nonlinear optical processes. Opt. Lett. 1993, 18, 13–15. [Google Scholar] [CrossRef]
- Assanto, G.; Stegeman, G.I.; Sheik-Bahae, M.; Van Stryland, E.W. All Optical Switching Devices Based on Large Nonlinear Phase Shifts from Second Harmonic Generation. Appl. Phys. Lett. 1993, 62, 1323–1325. [Google Scholar] [CrossRef]
- Hagan, D.J.; Sheik-Bahae, M.; Wang, Z.; Stegeman, G.I.; Van Stryland, E.W.; Assanto, G. Phase Controlled Transistor Action by Cascading of Second-Order Nonlinearities in KTP. Opt. Lett. 1994, 19, 1305–1307. [Google Scholar] [CrossRef] [PubMed]
- Assanto, G.; Stegeman, G.I.; Sheik-Bahae, M.; Van Stryland, E.W. Coherent interactions for all-optical signal processing via quadratic nonlinearities. IEEE J. Quantum Electron. 1995, 31, 673–681. [Google Scholar] [CrossRef]
- Stegeman, G.I.; Hagan, D.J.; Torner, L. χ(2) cascading phenomena and their applications to all-optical signal processing, mode-locking, pulse compression and solitons. Opt. Quantum Electron. 1996, 28, 1691–1740. [Google Scholar] [CrossRef]
- Assanto, G.; Stegeman, G.I. Nonlinear Optics Basics: Cascading. In Encyclopedia of Modern Optics; Guenther, R.D., Steel, D.G., Bayvel, L.D., Eds.; Elsevier: Oxford, UK, 2005; Volume 3, pp. 207–212. [Google Scholar]
- Chirkin, A.S.; Volkov, V.V.; Laptev, G.D.; Morozov, E.Y. Consecutive three-wave interactions in nonlinear optics of periodically inhomogeneous media. Quantum Electron. 2000, 30, 847. [Google Scholar] [CrossRef]
- Boyd, R. Nonlinear Optics, 3rd ed.; Academic Press: San Diego, MA, USA, 2008. [Google Scholar]
- Stegeman, G.I.; Stegeman, R. Nonlinear Optics, Phenomena, Materials and Devices, 1st ed.; J. Wiley & Sons: Ney York, NY, USA, 2012. [Google Scholar]
- Fejer, M.M.; Magel, G.A.; Jundt, D.H.; Byer, R.L. Quasi-phase-matched second harmonic generation: Tuning and tolerances. IEEE J. Quantum Electron. 1992, 28, 2631–2654. [Google Scholar] [CrossRef]
- Hum, D.S.; Fejer, M.M. Quasi-phase matching. Comptes Rendus Phys. 2007, 8, 180–198. [Google Scholar] [CrossRef]
- Wang, T.; Chen, P.; Xu, C.; Zhang, Y.; Wei, D.; Hu, X.; Zhu, S. Periodically poled LiNbO3 crystals from 1D and 2D to 3D. Sci. China Technol. Sci. 2020, 63, 1110–1126. [Google Scholar] [CrossRef]
- Sapaev, U.K.; Kulagin, I.A.; Satlikov, N.K.; Usmanov, T. Optimization of third harmonic generation for two coupled three-frequency interactions of waves with multiple frequencies in periodic crystals. Opt. Spectr. 2006, 101, 983–985. [Google Scholar] [CrossRef]
- Alexandrovsky, A.L.; Chirkin, A.S.; Volkov, V.V. Realization of quasi-phase-matched parametric interactions of waves of multiple frequencies with simultaneous frequency doubling. J. Russ. Laser Res. 1997, 18, 101–106. [Google Scholar] [CrossRef]
- Volkov, V.V.; Chirkin, A.S. Quasi-synchronous parametric amplification of waves at low-frequency pumping. Quantum Electron. 1998, 25, 101–102. [Google Scholar]
- Zhang, C.; Zhu, Y.-Y.; Yang, S.-X.; Qin, Y.-Q.; Zhu, S.-N.; Chen, Y.-B.; Liu, H.; Ming, N.-B. Crucial effects of coupling coefficients on quasi-phase-matched harmonic generation in an optical superlattice. Opt. Lett. 2000, 25, 436–438. [Google Scholar] [CrossRef] [PubMed]
- Komissarova, M.V.; Sukhorukov, A.P. On the properties of a parametric light amplifier with a multiple frequency ratio. Quantum Electron. 1993, 20, 1025–1027. [Google Scholar]
- Norton, A.H.; de Sterke, C.M. Aperiodic 1-dimensional structures for quasi-phase matching. Opt. Express 2004, 12, 841–846. [Google Scholar] [CrossRef]
- Yusupov, D.B.; Sapaev, U.K. Multistep third-harmonic generation of femtosecond laser pulses in periodically-poled and chirped-periodically-poled lithium niobate. J. Russ. Laser Res. 2009, 30, 321–326. [Google Scholar] [CrossRef]
- Sapaev, U.K.; Assanto, G. Engineered quasi-phase matching for multiple parametric generation. Opt. Express 2009, 17, 3765–3770. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, Y.; Ming, N. Quasi-phase-matched third-harmonic generation in a quasi-periodic optical superlattice. Science 1997, 278, 843–846. [Google Scholar] [CrossRef]
- Longhi, S. Third-harmonic generation in quasi-phase-matched media with missing second harmonic. Opt. Lett. 2007, 32, 1791–1793. [Google Scholar] [CrossRef] [PubMed]
- Dmitriev, V.G.; Gurzadyan, G.G.; Nikogosyan, D.N. Handbook of Nonlinear Optical Crystals, 3rd ed.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Sabirov, O.I.; Yusupov, D.B.; Akbarova, N.A.; Sapaev, U.K. On the theoretical analysis of parametric amplification of femtosecond laser pulses in crystals with a regular domain structure. Phys. Wave Phenom. 2022, 30, 277–282. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).