Demonstration of a Key Distribution Scheme Based on the Masking Effect of Fiber Channel Noise in Power Transmission System

Abstract

This paper proposes a novel key distribution method based on the masking effect of fiber channel noise in a power transmission system. The two physical layer signal processing technologies used in this solution are frame synchronization and resampling. The random data sent and received is digitally processed by these two techniques. An experimental platform is built, and the key performance is assessed by analyzing the measured bit error rate (BER) dynamic curve, setting different decision thresholds and the amplitude of the state basis. Experimental results show that the key distribution rate can reach 10 kbit/s with a key consistency rate of 98%. This is of great significance to the development of safe optical communication technology in power transmission systems. In the power communication system, a large number of optical fiber communication devices are used. The key distribution method proposed in this paper can effectively improve the security of optical fiber communication, which is of great significance.

1. Introduction

Optical fiber communication is closely related to our life and production, but it is vulnerable to various threats. Common attack methods include strong light attack, plaintext attack, light splitting eavesdropping, forgery attack and replay attack. To solve this problem, the transmitted data needs to be encrypted with a key [1,2,3]. In order to solve the security problem of optical fiber communication, it is necessary to study encryption technology and key distribution technology [4,5]. At present, the related research on the encryption technology of optical fiber communication systems includes: quantum noise flow encrypted optical communication, spread spectrum communication, covert optical communication and chaotic optical communication [6,7,8]. The related research on fiber channel key distribution technology includes: single-photon quantum key distribution, continuous variable quantum key distribution, polarization mode dispersion-based fiber key distribution and ultra-long fiber laser key distribution.

Quantum Key Distribution (QKD) is a technology that can improve the security level of 5G networks in the future, and will be used to ensure the distribution of symmetric encryption keys. It is produced by exchanging keys between two remote customers under absolute security. The European Commission plans to use QKD technology and Quantum Random Number Generator (QRNC) technology based on optical fiber links and satellite links to serve the Internet of Things and 5G networks in the next few years. At present, China, the United States, Japan and other countries have adopted similar methods for 5G network communication encryption [9]. In the existing methods of key distribution in the physical layer, only QKD protocols can achieve theoretically absolute security [10,11,12,13,14,15]. However, QKD has some limitations in terms of key distribution rate and transmission distance. Because it is impossible to amplify a single photon using an optical amplifier without changing the polarization state, its key transmission distance is seriously limited [16].

At present, quantum information processing is the research and development hotspot of quantum science, which aims to improve the speed and performance of smaller and smaller quantum information systems by using light states. In the past decade, there have been many ways to realize QKD, and quantum photonics has made a series of research achievements. In 2016, F. Mazeas reported a highly efficient energy time entangled photon pair source in a Complementary Metal Oxide Semiconductor (CMOS)-compatible silicon photonic ring resonator. This demonstrates the high purity of energy time entanglements, thus there is no photon noise and there is nearly perfect original visibility between different channel pairs in the telecommunications C-band, which produces a multiplexing system of continuous energy time entanglement [17]. An integrated weak coherent transmitter is proposed in [18]. The transmitter is based on a monolithic indium phosphide Indium Phosphide (InP) device and uses the reconfigurability of the device to demonstrate three QKD protocols-BB84. When these devices are used together with integrated single photon detectors, they pave the way for the successful integration of QKD into future telecommunications networks [18]. Reference [19] proposed an ultra-compact high-performance silicon on insulator pump stop filter with large rejection ratio, narrow bandwidth and low insertion loss, which is used to preserve single photons in photonic quantum systems. The device ensures the large suppression of the pump signal in a wide-ranging photonic system for quantum information processing, thereby improving the Spontaneous Four-Wave Mixing (SFWM) efficiency. In 2013, B. I. Akca et al. used integrated optical devices to assemble the central components of an optical coherence tomography (OCT) system on silicon chips. To further improve the coupling between the optical path and the dispersive element, the signal-to-noise ratio should also be improved [20]. The QKD equipment is incompatible with the existing communication system, and its deployment cost is very high. Therefore, it is necessary to explore a cost-effective key distribution method with a long transmission distance.

This paper proposes a key distribution method based on the masking effect of fiber channel noise. Although it is not absolutely secure, it is compatible with existing optical fiber transmission systems. As optical amplifiers can be used, the key distribution distance is much longer than the QKD scheme. Alice converts the random data using the random basis (A or B). Due to the channel noise, the eavesdropper cannot accurately distinguish the basis used by Alice. Alice measures the BER of the fiber channel loop. The comparison of the BER sampling value and the threshold value is conducted to determine whether the basis of both communication sides is consistent. If the basis is consistent, Basis A is coded as 1 and Basis B is coded as 0. Then, both sides of communication can get the same keys. Experimental results show that the key distribution rate of this scheme can reach 10 kbit/s when the key consistency rate is 98%. The key bit 0/1 proportion is always around 50%, which indicates that the key has good randomness. Eve cannot accurately distinguish the basis used by Alice and Bob, which means that the system has high security. In the power communication system, a large number of optical fiber communication devices are used. The security of communication equipment is related to the vital interests of the majority of the people. The key distribution method proposed in this paper can effectively improve the security of optical fiber communication, which is of great significance.

2. Key Distribution Scheme

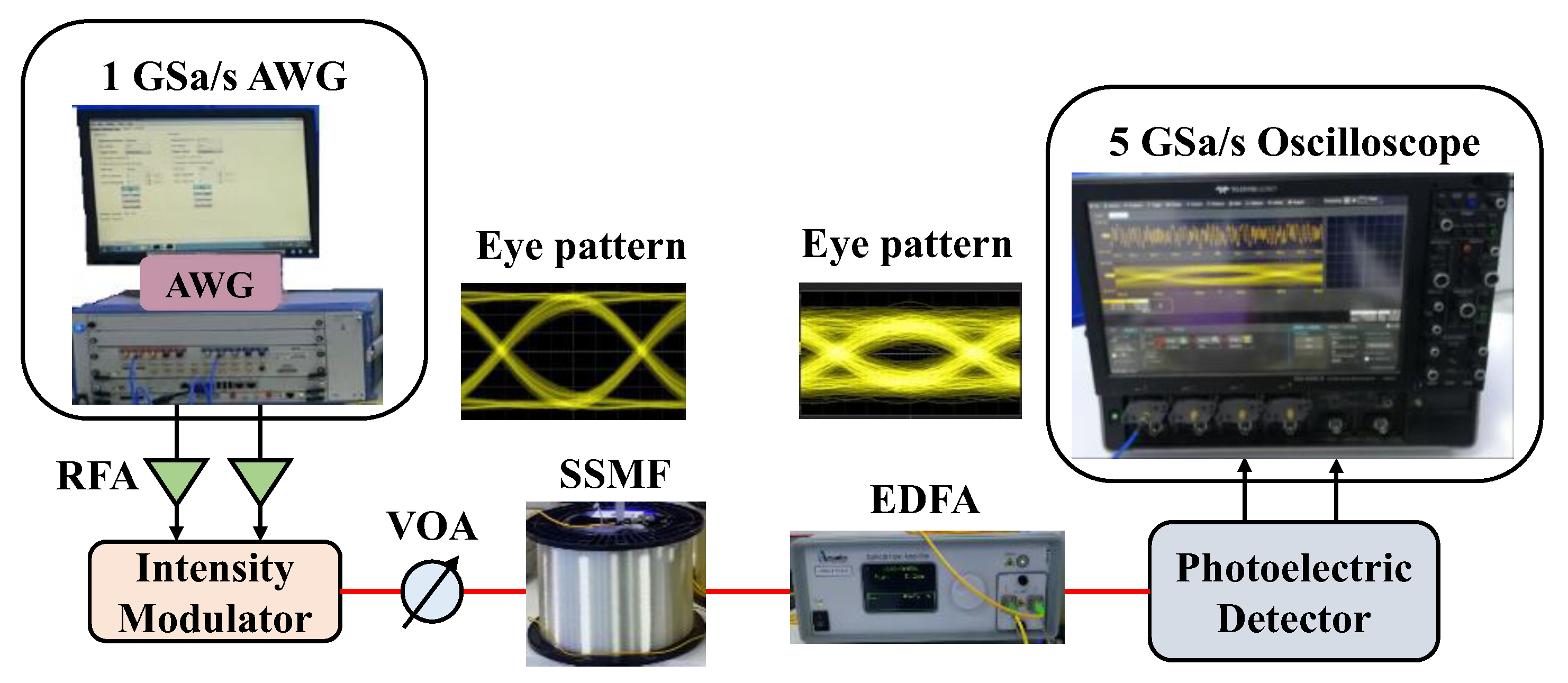
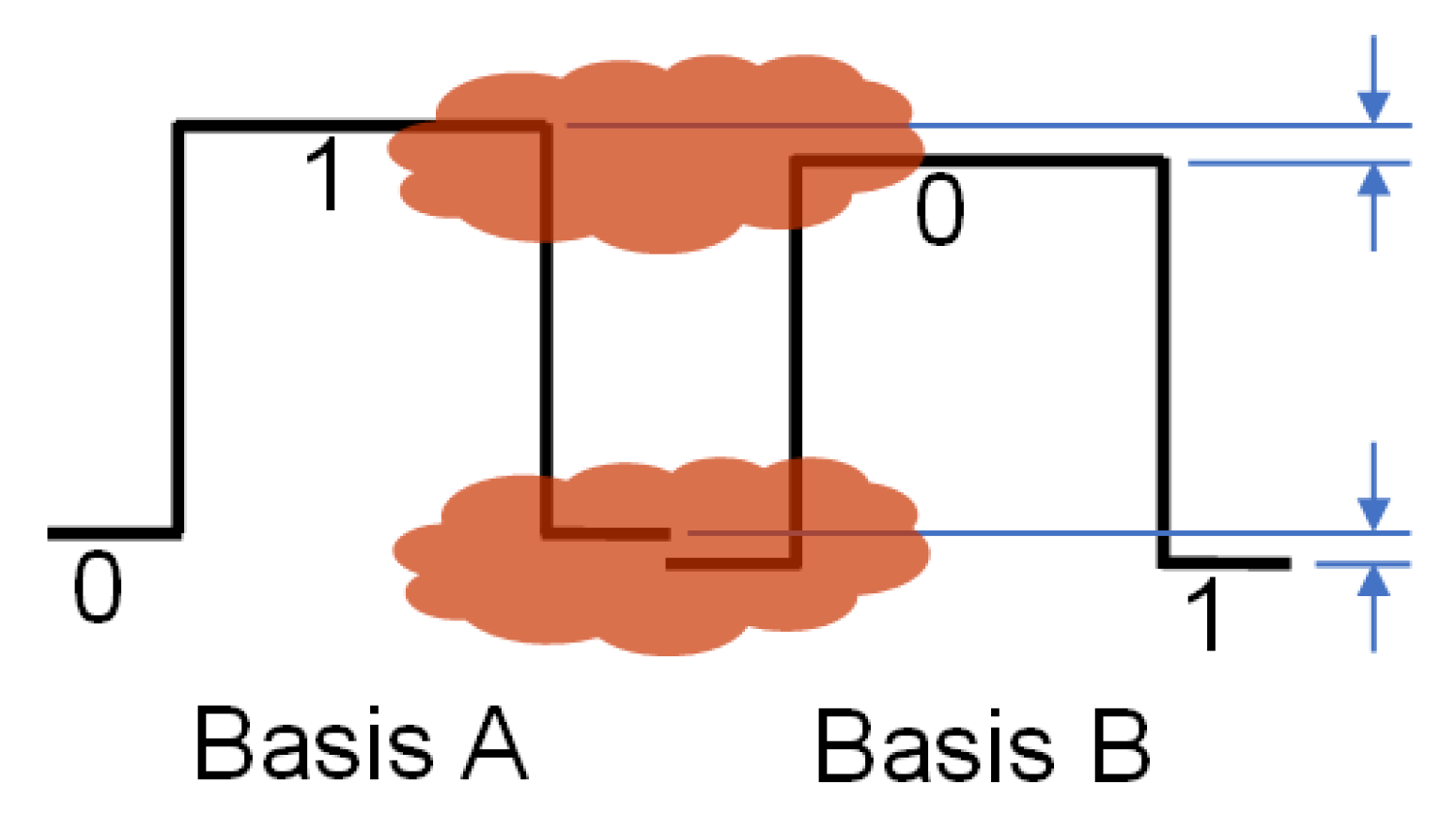
The scheme proposed in this paper is a single-ended measurement scheme. Firstly, Bob needs to use Basis B to solve the mapping and convert it into a digital signal; then, the digital signal is mapped to an electrical signal using Basis B; finally, it is modulated to an optical signal and sent to Alice. Figure 1 shows the comparison of the difference between Basis A and Basis B. The level in the figure is the level. The physical realization is that the 1 and 0 corresponding to Basis A respectively represent the high and low level, and the 0 and 1 corresponding to Basis B respectively represent the high and low level. The high and low level of Basis A are slightly different from the high and low level. This small difference is easily obscured by noise, and it is impossible to distinguish Basis A from Basis B simply by measuring levels. After transmission, states a and b are overwhelmed by noise and cannot be distinguished. Alice and Bob can quantify the differences between bases. Because the signals produced by Alice and Bob through the DA converter have no optical noise, this difference can be resolved and quantified. Alice and Bob can distinguish the difference. This signal difference is equivalent to the displacement of the signal. The larger the displacement of the signal, the greater the error rate. Because the signal is masked by noise after electro-optic conversion, Eve cannot tell the difference between the bases. Eve cannot quantify the difference between the bases. This small difference has an accumulated effect. Alice uses 10,000 bits to calculate a BER, and the accuracy of BER is relatively high. Therefore, BER can be affected by small differences.

The difference between high and low levels of Basis A and Basis B is very small. The quantum noise is completely random, and Basis A and Basis B are masked by quantum noise, thus they cannot be distinguished. Eve can only eavesdrop on the optical fiber. Eve eavesdrops by splitting the light. Even if he amplifies the signal, he does not have the key Basis, and thus he will introduce more quantum noise from the amplifier. Then, the eavesdropping results are different from Alice and Bob. This article assumes that Eve cannot send data. Eve can only eavesdrop on fiber signals in the middle and cannot send data because Alice and Bob will block Eve’s loopback measurements. Eve is unable to measure bases and the basis is masked. This basis is pre-defined and the basis is kept secret from Eve.

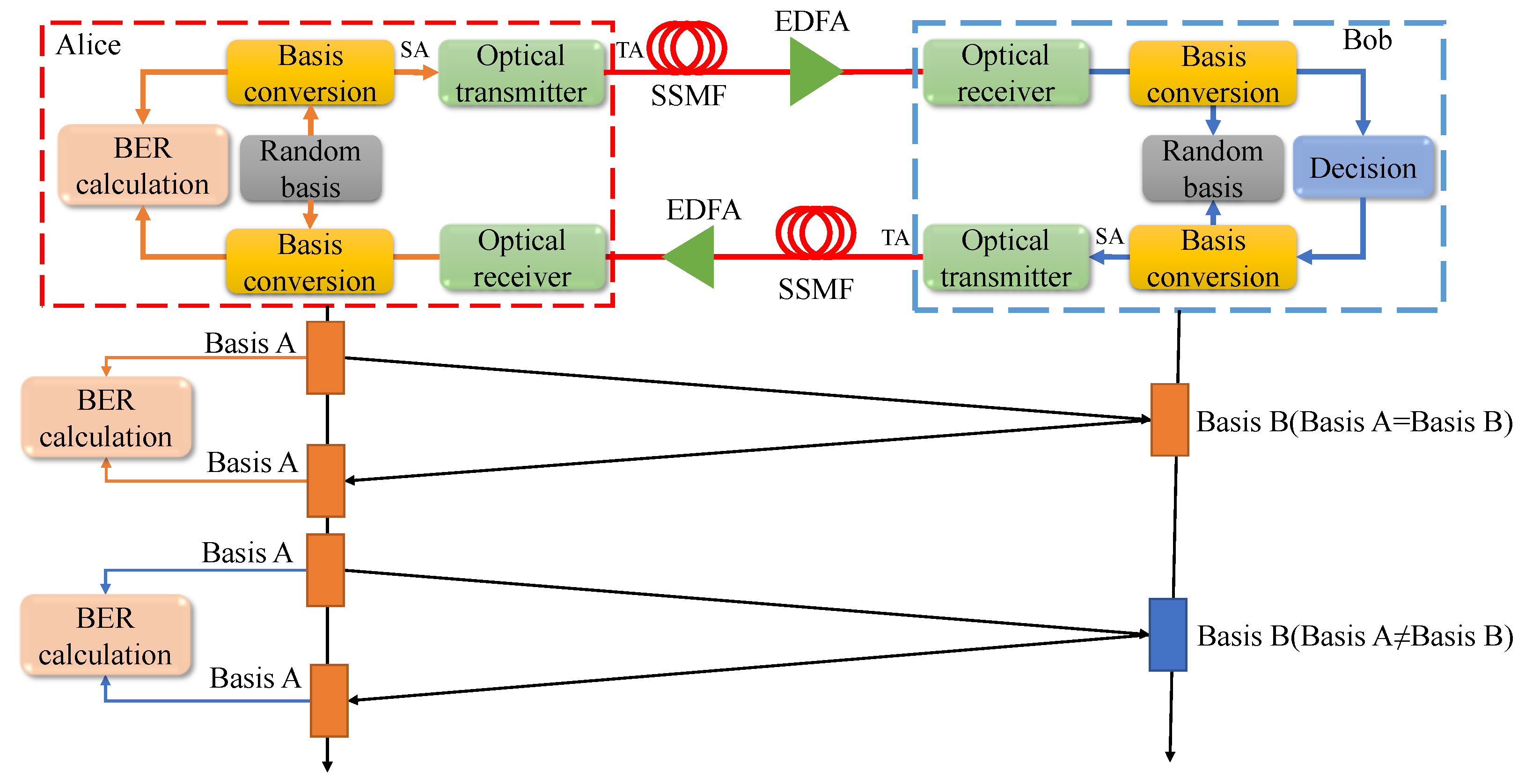
Figure 2 depicts the process of key distribution based on the masking effect of fiber channel noise. The original data is random and no information is transmitted. Alice generates random data DA and random basis SA. After basis conversion, the random data DA is converted to TA. TA is emitted by the optical transmitter and reaches the Erbium Doped Fiber Amplifier (EDFA) at the receiver side through the optical fiber. After being amplified by EDFA, the optical signal reaches the optical receiver. Bob uses the random basis SB to convert the received signal and make a decision. Then, Bob converts the decision using basis SB to get TB. After TB is transmitted, the optical signal passes through the optical fiber and EDFA and reaches the Alice side. Alice uses basis SA to convert the received data to get data DA’, and compares DA with DA’ to calculate the BER. The BER of the optical fiber loop can be measured by this method. Alice uses the masking effect to encrypt the data. The original data is a pseudorandom number, the copy sent is a 10,000-bit random number and the pseudo-random number is repeatedly sent; these data are different.

This paper negotiates the key by measuring the Alice and Bob channel characteristics BER of the optical channel transceiver. The specific steps are as follows:

Step 1. Alice and Bob randomly select a key, which is defined as Basis A or Basis B. The 0 and 1 levels corresponding to Basis A and Basis B are opposite, and there is a small difference between them.

Step 2. Alice encrypts the original data with Basis A and sends it to Bob. Bob uses Basis B to receive signals and send data to Alice. Alice uses Basis A to decrypt the signals after receiving them.

Step 3. If Basis A is equal to Basis B, the BER calculated by Alice is relatively low. If Basis A is not equal to Basis B, the calculated BER is higher.

Step 4. According to the aforementioned analysis, when the BER calculated by Alice is relatively low, it can be considered that Basis A is equal to Basis B. When the BER calculated by Alice is relatively high, it can be considered that Basis A is not equal to Basis B.

Step 5. Discard the case with high BER and select the case with low BER. At this time, Alice and Bob will quantize and encode the BER to reach a consensus key.

Alice and Bob must discard at the same time. They also discard the inconsistent positions of the basis. Alice will think that the BER obtained is low, which means that the basis is consistent. At the same time, Alice will tell Bob the location, and Bob will use the Basis B of the corresponding location as the key. Alice needs to measure through the communication loopback. Alice uses its local data and the data sent by Bob to calculate BER. If Basis A and Basis B are different, BER may be higher. SA and SB are a key base randomly selected by Alice and Bob. We define them as Basis A and Basis B. The corresponding 0 and 1 levels of Basis A and Basis B are opposite, and there is a small difference between them. Modify Figure 2, Basis B (Basis A = Basis B), Basis B (Basis A ≠ Basis B). TA is the encrypted signal sent from the Alice optical transmitter, and TB is the encrypted signal sent from the Bob optical transmitter.

There is quantum noise in the fiber channel, which is mainly generated by amplifiers and lasers. Because the amplitude difference between Basis A and Basis B is very small, it is easily covered by optical quantum noise. Because Eve at the unusual receiving end cannot distinguish Basis A from Basis B, the security of the system uses the masking effect of noise. Alice and Bob can distinguish Basis A and Basis B by measuring BER; Eve can only steal signals by splitting light. It cannot measure the loopback BER of the channel. Moreover, due to the masking effect of quantum noise, Eve cannot directly measure Basis A and Basis B, so the system is safe.

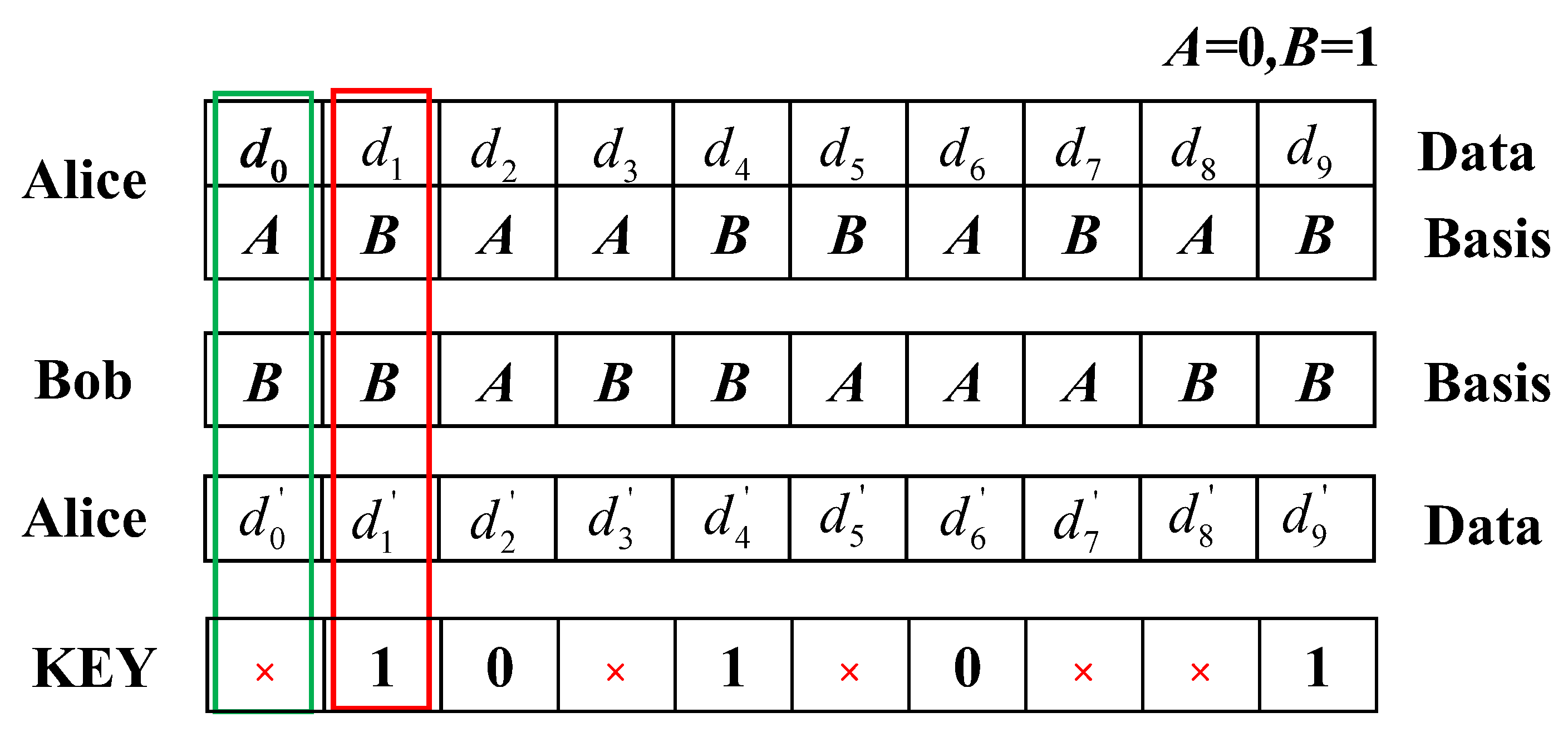
As shown in Figure 3, Alice uses the key base (ABAABBABAB) to send data ($d_0{d}_1{d}_2\cdots d_9$) to Bob, and Bob uses the randomly generated key base (BBABBAAABB) to receive signals, and then uses the key base to send signals to Alice. Since the bases of Alice and Bob are 0 and 1, suppose that Bob uses key base A when receiving signals and key base B when sending signals, which is equivalent to two reversals of 0 and 1, and has no effect on the signals. However, the difference between Alice and Bob will cause the BER of the signal to increase. Finally, Alice compares the received data ($d_0^{\prime }{d}_1^{\prime }{d}_2^{\prime }\cdots d_9^{\prime }$) with the sent data. For example, when BER > 0.3 is compared and calculated, we discard the position 0 at this time, as shown in the blue area in Figure 3. Because the basis is inconsistent, the BER increases. When BER < 0.3 is calculated by comparing $d_0$ and $d_0^{\prime }$, we retain the current position 1 and send the current position information to Bob. Each piece of position information corresponds to a base, as shown in the red area of Figure 3; Bob and Alice have the same base. They both know that the base is B, thus the key KEY = 1.

Alice and Bob do not need to declare a basis. The basis is randomly generated by Alice and Bob, and it is confidential. It will not go public and Eve cannot get it. Once you get to the right place, you can pick the corresponding basis. The location is public, the bases are random, and Eve has no way to get the selected bases. Since the bases do not exist to announce each other, Eve has no way to steal part of the optical signal.

Although Eve can measure the changing state of the signal, it can know the public location information. However, the key base reserved by Alice and Bob is unknown. Because Bob’s key base is random, the system is secure.

A BER is calculated from 10,000 bits and a key is generated. As shown in Figure 4, Alice gets BER of 0.2, which is the case of consistent basis. Alice gets a BER of 0.4, which is the base case. The average BER of consistent and inconsistent bases is 0.3. If it is less than 0.3, the basis is consistent; if it is greater than 0.3, the basis is inconsistent. Alice tells Bob the consistent location, and Bob gets the key. The base inconsistent position is discarded, and the base consistent position is retained. Bob uses the location to generate the key.

If BER is too small, assume it is 1E-5 BER, thus many data are required to calculate BER. If BER is set to 0.3, BER can be calculated with 10-bit data. If BER is set to 0.03, 100-bit data is required to calculate BER. In this way, set BER to get a high key rate, and the same data can get more keys. This data is only used to generate keys, and is not for communication.

Relatively high BER is a deliberate setting of this paper. By reducing signal amplitude and increasing optical noise, BER can be increased, which is convenient to generate a key when it is increased to a more appropriate BER. Only BER can be easily measured with less data. No error correction is required. Their BER is not caused by previous differences in the base, and is caused by reducing the signal amplitude and increasing the light noise, which is deliberately generated. Therefore, it is a high BER. The main reason is that the BER suitable for generating the key is artificially set. If BER is 0.3, data is discarded. If it is greater than 0.3, Basis One will not be; if it is less than 0.3, Basis One is consistent. Alice tells Bob the consistent location, and Bob gets the key. The positions with inconsistent bases are discarded and the positions with consistent bases are retained. Bob uses the location to generate the key: 10,000 bits for a BER, generate a key. The user can use this key as the seed key, and then use the key generated by the pseudo-random number generator to encrypt the data.

When Alice and Bob use the same random basis, the BER measured by Alice is lower. When different random bases are used at both sides, the BER is larger. The average BER is selected as the decision threshold. When the BER measured by Alice exceeds the threshold, it is considered that the two bases are inconsistent; when the BER measured is less than the threshold, it is considered that the two bases are consistent. If the basis is consistent, Basis A is coded as 1 and Basis B is coded as 0. Thus, a highly consistent key stream can be obtained.

3. Experimental Setup

Figure 5 shows the composition of the 200 km key distribution experiment system. The signal sampling rate of Arbitrary waveform generator (AWG) is set at 1 Gbit/s. The radio-frequency amplifier (RFA) has an amplification gain of 19 dB. The intensity modulator converts the electrical signal into optical signal. The output power of the intensity modulator is 5 dBm. The optical signal reaches the receiver after passing through the variable optical attenuator (VOA) and 200 km standard single-mode fiber (SSMF). The output power of EDFA is 0 dBm. The photoelectric detector converts optical signals into electrical signals. An oscilloscope with a sampling rate of 5G Sa/s samples the electrical signals. The figure also shows the eye patterns of optical signals collected by oscilloscope before and after 200 km SSMF.

DA is the original data before Alice sends it. The experiment in this paper is an equivalent experiment. A complete system—Alice to Bob, Bob to Alice—is a loop. The equivalent is transmitter to receiver, which means Alice to Bob and Bob to Alice. Simulate the loop system of Figure 5 through the data transmission experiment twice.

The two physical layer signal processing technologies used in this key distribution experiment are frame synchronization and resampling. The random data sent and received is digitally processed by these two techniques.

3.1. Frame Synchronization

In order to synchronize the keys generated by Alice and Bob, the accurate channel BER can be calculated, and then the consistent negotiated key can be obtained by quantizing and encoding. The frame synchronization technology mainly detects whether the signal has appeared by locating the starting point of the signal. Frame synchronization technology is the most important and basic technology in digital signal processing flow. During the frame synchronization estimation process, the digital signal received by the receiver may be affected by carrier phase noise, fiber channel response, carrier frequency offset, etc. The frame synchronization estimation algorithm needs to have the ability to estimate and compensate for the aforementioned interferences [21,22]. The position indicated by the arrow in Figure 6 is the starting point of the signal, and the signal before this is the optical noise in the link and the optical carrier that is not completely suppressed.

Frame synchronization estimation is performed based on the training sequence [23]. The position of the initial point of the signal is obtained by searching the training sequence. The accuracy of frame synchronization estimation depends on the design of the training sequence. The sender signal is:

$$a\left(t\right)={\displaystyle \sum _{n=-\infty }^{+\infty }{a}_{n}g\left(t-n{T}_s\right)}$$

(1)

where $T_s$ is the symbol period and $a_n$ is the training sequence. Assuming that both the channel and the carrier frequency offset have short-term invariance, after being affected by the response $a_n$, $g\left(t-n{T}_s\right)$ means gate function, the frequency offset $\Delta f$, and the additive noise $w_n$; the received signal is:

$$R\left(t\right)={\displaystyle \sum _{n=-\infty }^{n=+\infty }{a}_n}\ast h_n{e}^{j2\pi \Delta ft}+w_n$$

(2)

In general, frame synchronization technology is a process in which the sender gives the initial mark of each frame in the digital time division multiplexing system, and the receiver detects and extracts the mark. In a frame structure, the inserted frame synchronization code word is 400 consecutive 0 bits and 256 0/1 random bits, and the synchronization code is searched and identified from the received data stream for frame synchronization. As shown in Figure 6a, 400 zero bits are used for coarse synchronization. In order to quickly locate and find a general position and maintain synchronization, the peak position in the figure is the best coarse synchronization position. In Figure 6b, 256 randomly generated 0/1 bits are used for fine synchronization. The peak position in the figure is the exact fine tuning synchronization position. Using frame synchronization technology, the frame structure of the receiving end and the sending end is kept the same, ensuring that both parties of legal communication can work normally under the condition of synchronization and recognize the accurate transmission of information.

3.2. Resampling

In order to improve the sampling accuracy, improve the channel BER obtained by Alice calculation and improve the consistency of the key. Resampling is a commonly used statistical digital processing technique that makes the data in the sample more suitable for digital processing. In the experiment, the rate of the transmitter is 10 Gbps, and the sampling frequency of the oscilloscope is 40 Gbps. Therefore, it is necessary to use down-sampling technology to down-sample the four times oversampled data of the oscilloscope to make it more suitable for further data processing requirements.

Down-sampling technology is a way to reduce the sampling rate of a signal, which is usually applied in the scenario of down-speeding data signal transmission or reducing the data size. Down sampling and interpolation are complementary relationships, and interpolation is applied to scenarios where the sampling frequency is increased. Since signal aliasing will cause a certain degree of distortion, a filter is required to reduce signal aliasing during down sampling [24,25].

There are two types of down sampling techniques: integer down sampling and fractional down sampling. Integer down sampling is widely used, and its process can be decomposed into two parts. First, in order to prevent signal aliasing, a low-pass filter is used to filter out the high-frequency components of the signal. Afterwards, the sampling points with an interval of M in the middle of the original signal are retained, thus down-sampling M times. If only the second step is performed, the low-frequency signal in the process of reducing the sampling rate will be mixed with some high-frequency components. This distortion is called the aliasing effect. Therefore, in order to reduce the influence of the aliasing effect, it is necessary to use a low-pass filter to filter out the high-frequency components of the signal. Figure 7 shows the data spectrum before and after down sampling, respectively.

4. Results and Analysis

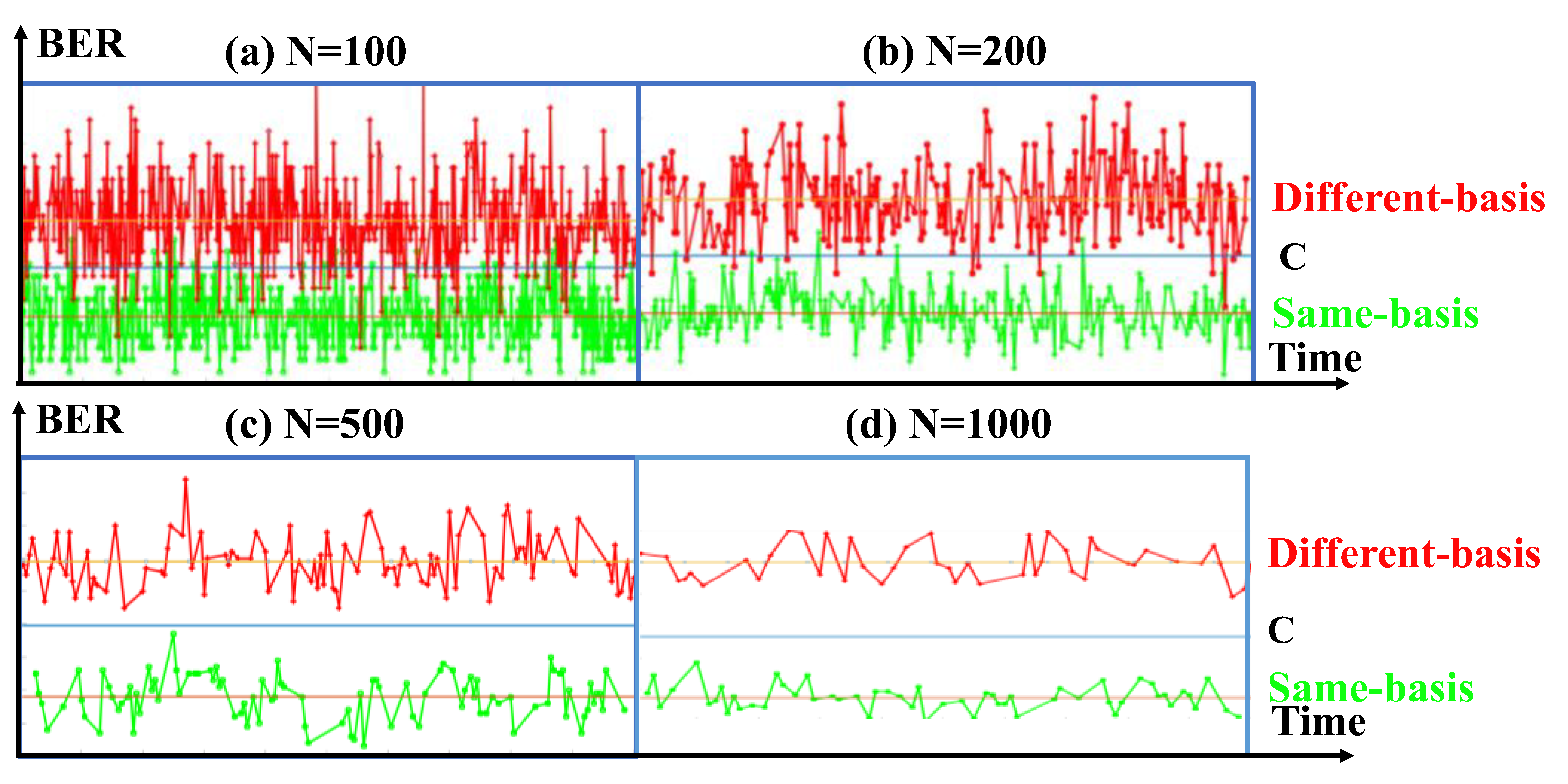
Figure 8 shows the variation curve of BER measured by Alice. The red curve represents the BER curve measured when the bases of Alice and Bob are inconsistent. The green curve represents the BER curve measured when both bases are consistent. The data length N for BER measurements are 100-bit, 200-bit, 500-bit and 1000-bit, respectively. It can be seen that the BER with consistency basis is significantly lower than the BER with inconsistency basis. The average BER of all data is expressed as C, which is taken as the judgment threshold. C is the average value of BER. When the BER is higher than C, the basis is considered consistent; when the BER is lower than C, the basis is considered inconsistent. For the case of consistent basis, Basis A is coded as 1 and Basis B is coded as 0. With the increase of N, the sampling points of BER become sparse, and the corresponding key encoding rate decreases. At this time, the BER is further away from the mean C and the key consistency rate rises. Since Eve only knows whether the bases of Alice and Bob are the same, it does not know the specific bases used by Alice and Bob. Therefore, Eve cannot get the key and the security of the system is guaranteed.

The meaning of not sending data is only a hypothesis made in this paper, and this paper does not consider the situation of sending data. If Eve can send data, it involves authentication-related fields. You can judge whether Eve has replaced Bob by measuring the strength change of the signal and other factors. If Alice and Bob declare a basis, doing so would make the generated key unsafe because Eve would have the correct key. Man-in-the-middle attacks, which must be resolved through authentication, are another area of research. The application scenario of this paper is only for the way of spectral eavesdropping, and other attack methods are not discussed in this article.

We followed the following steps: 10 kpbs = 1E9/1E5 = 1E4; divide 1E9 bit/s by 1000 bits to get the BER of 1E6. Because we use 1000 bits to calculate a BER, we can get 1E6 BERs. After quantization, encoding and key post-processing, the negotiated key needs to discard some invalid keys during the negotiation process, which reduces the key rate and finally obtains 1E4 keys. Figure 9a shows the relationship between the key distribution rate and the BER sampling interval. With the increase of the BER sampling interval, the key distribution rate decreases. When the BER sampling interval is 0.3 μs, the key distribution rate is 10 kbit/s. Figure 9b shows the relationship between key consistency rate and BER sampling interval. As the BER sampling interval increases, the key consistency rate increases gradually. When the BER sampling interval is 0.3 μs, the key consistency rate reaches 98%. Figure 9c shows the relationship between the 0/1 proportion of the key and the BER sampling interval. The 0/1 proportion of the key fluctuates around 50%, which indicates that the key has good randomness. When the segment length is greater than 0.3 μs, the key consistency rate is greater than 98%, and the error correction coding can be used to further improve the key consistency rate. The key negotiated in this scheme is random—mainly because the optical quantum noise itself is a truly random noise—the BER obtained is also random, and the key negotiated is also random.

5. Conclusions

This paper proposes a key distribution method based on the characteristics of the fiber channel, which uses the BER measured at both ends of the transmitter and receiver to generate a consistent key after quantization and coding. This scheme describes the process of the key agreement scheme with single end measurement in detail, and builds an experimental platform to verify the key performance. Finally, when the segment length is 1000 bits, the maximum achievable rate of the system is 10 kps, and the key consistency is higher than 98% of the security key. By setting different state base thresholds and analyzing different BER segment lengths, it can be seen that the higher the BER threshold, the higher the key generation rate, but the worse the consistency. When the segment length is longer, the key generation rate is smaller, and the consistency is higher. Therefore, we must appropriately adjust the threshold value and segment length value to make the consistency of generated keys and the coding rate meet the requirements of the transmission system.