Clinical Prediction and Spatial Statistical Analysis of Ascending Thoracic Aortic Aneurysm Structure

Abstract

This study presents an analysis of data from patients with ascending thoracic aortic aneurysms (ATAAs). Two databases of 87 patients were available: one containing clinical variables and the other consisting of measurements of the maximum diameter taken along the ascending aorta. For the clinical database, both a supervised and an unsupervised learning method were applied to explore patterns within the data. On the other hand, for the ascending aorta dataset, experimental variograms were calculated, from which key parameters of interest were extracted. These parameters were then analyzed over time to assess temporal patterns. This analysis aimed to assess the emergence of similar patterns or behaviour in patients with aneurysms of comparable sizes. Based on the analyses conducted, the clinical variables with the greatest importance in surgical decision-making were identified, while the spatial statistical analysis revealed patterns that may be related to elasticity, stiffness, or deformations of the aorta.

1. Introduction

Ascending Thoracic Aortic Aneurysm (ATAA) is a degenerative process of the thoracic aorta and a severe vascular disease characterized by the progressive dilation of the thoracic aorta due to the weakening of the aortic wall.

Central aortic stiffening in the absence of aortic dilatation has been well documented as a risk factor for a variety of adverse cardiovascular outcomes. In ATAA, localized wall stiffening within the aneurysm itself is common, largely due to the increased collagen content and its disorganization, combined with the accelerated fragmentation of elastin fibres [1].

The structure and function of the aorta can be affected by factors such as age, genetics, and lifestyle factors [2,3]. Aneurysm is one of the most common diseases associated with the aorta, and its rupture is a major cause of mortality in adults over 65 years old [4].

When rupture or dissection occurs, the situation is fatal for a large proportion of patients before they reach the hospital. Those who do arrive require an emergency surgical procedure, which carries a mortality risk of approximately 20%; in contrast, elective replacement of the ascending aorta involves a relatively low risk of mortality and morbidity [5].

Therefore, the aim of elective surgical intervention is to provide a survival benefit by replacing the aneurysmal segment of the ascending aorta before the occurrence of an acute aortic event. A comprehensive understanding of the natural history of ATAA is essential to determine the balance between risk and benefit in elective aortic surgery [5].

The size of the aneurysm is determined based on diameter measurements, which may vary slightly depending on the imaging technology used, such as ultrasound or computed tomography angiography (CTA). According to previous studies, elective repair was recommended when the maximum diameter (Dmax) exceeded 55 mm or when the lesion grew by more than 1 cm per year [6]. According to Czerny et al., who present one of the current clinical guidelines or recommendations, aneurysm repair is recommended in women for diameters greater than 50 mm and in men for diameters greater than 55 mm [7].

However, it has been observed that these parameters are not sufficient, as there are cases of patients with maximum diameters below the indicated threshold who suffer aneurysm rupture, as well as cases of patients with larger diameters who do not experience rupture [8,9].

One study showed that more than 80% of ascending aortic dissections may occur with a diameter smaller than 55 mm. Furthermore, another study indicated that the 55 mm criterion could exclude approximately 99% of patients from the possibility of preventive surgery [10].

In 2018, a systematic review and meta-analysis of twenty studies including a total of 8800 patients determined that the growth rate of ascending aortic aneurysms is slow and has implications for the imaging follow-up interval. Data on the risk of dissection, rupture, and death associated with ascending aortic aneurysm remain limited [5].

According to Tjahjadi et al. [11], the spatial and temporal relationships between stiffness, aortic size, and progressive growth in ATAA remain not yet fully understood. As a result, aortic stiffness has not become a key metric to determine disease severity or to estimate its progression in ATAA, despite frequent calls for biomechanical metrics to improve current diameter-based assessments.

The mechanical properties and morphological characteristics of aortic tissue are fundamental for maintaining cardiovascular health, whereas their dysfunction is related to the occurrence and development of cardiovascular diseases. In that study, it was found that age, sex, aortic valve diseases (insufficiency and stenosis), coronary artery disease, and the diameter of the ascending aortic wall had a statistically significant impact on aortic stiffness prior to rupture [12].

This study presents an exploratory analysis of the characteristics of ATAAs in a sample of patients using spatial statistics. Two databases are available: one containing the patients’ clinical data and another with measurements of the ascending aorta. For the clinical database, a predictive study is presented, highlighting the importance of different variables in the surgical decision-making process for aneurysm treatment. With the second database, an analysis was carried out using spatial statistical techniques to study the biomechanical characteristics of ascending aortic aneurysms. Specifically, the variogram and the parameters sill and range are used to characterize the maximum diameters of the ascending aortas.

2. Materials and Methods

The data for this study were collected from 87 patients diagnosed with ATAA at Hospital de Santa Marta in Lisbon, Portugal. Each patient underwent an electrocardiographically synchronized computed tomography scan (Cine CTA) and clinical consultations to assess the status of the ATAA.

There are two databases. One of them, the clinical database, includes information on the patients’ clinical variables, such as personal history, comorbidities, anthropometric data, and relevant clinical measurements, among others. The other database contains information related to each patient’s aneurysm. This was obtained through a segmentation process based on the CTA performed for each patient and includes various measurements, such as the maximum diameter, taken along the patient’s ascending aorta.

The anonymized image sets were obtained through ethically approved protocols within the framework of the project and authorized by the management of the São José Local Health Unit. These were used to extract anatomical and dynamic characteristics of the aorta. All participants provided written informed consent [13].

2.1. Clinical Variables

This section presents the clinical variables considered in the analysis of the present study. These variables were selected due to their medical relevance and their possible association with the cardiovascular conditions under investigation.

The clinical database used in this study comprises demographic, hemodynamic, anatomical, and comorbidity-related variables collected from patients with aortic conditions. Demographic information includes age, sex, weight, height, body mass index, and body surface area. Hemodynamic variables encompass systolic, diastolic, and mean blood pressure, as well as heart rate measurements. Anatomical assessment includes the maximum systolic aortic diameter, which is a key determinant in surgical decision-making. In addition, the dataset records comorbidities and risk factors such as hypertension, diabetes mellitus, dyslipidemia, chronic kidney disease, chronic obstructive pulmonary disease, smoking status, coronary artery disease, peripheral arterial disease, stroke, and hyperuricemia.

The selection of clinical variables was driven by their established relevance in the diagnosis, monitoring, and management of ascending thoracic aortic aneurysms, as supported by current clinical guidelines and prior literature [6,7]. Core variables such as maximum systolic aortic diameter and sex are directly incorporated into surgical decision criteria, while additional factors, including hypertension, dyslipidemia, smoking status, and family history, have been associated with aortic wall degeneration, altered biomechanical properties, and disease progression [1,10,11,12].

In the context of this study, machine learning was employed as a complementary analytical tool to assess how conventional clinical variables jointly contribute to the classification of surgical indication, rather than to infer causality or propose new clinical thresholds. Logistic regression was selected due to its transparency and interpretability, allowing the relative contribution of each variable to be quantified within a multivariate framework.

In the database, the variable ‘surgery’ was included, representing the surgical decision according to clinical and morphological criteria. This new variable was manually defined with the following criterion. Patients who, according to clinical guidelines [7], must undergo surgical intervention (i.e., their aneurysm should be operated on) were assigned the value 1; otherwise, the value 0 was assigned. As previously mentioned, surgical intervention is indicated when the aneurysm diameter exceeds certain parameters: in women, a diameter greater than 50 mm; in men, greater than 55 mm.

Data standardization and cleaning were performed: removal of identifiers, normalization of variable names, conversion of numeric variables with decimal commas to numeric format, and imputation of missing values by median (numeric variables) or mode (categorical variables). Categorical variables were transformed into dummy variables using one-hot encoding.

Since the objective is to perform a classification for a main qualitative and dichotomous variable, logistic regression was selected, as it is suitable for this type of classification. Logistic regression is a supervised classification method that considers the contribution of different factors to the occurrence of a single event. For model training and validation, the k-fold technique was applied [14,15]. This technique consists of cross-validation carried out k different times, each time using a different partition of the data for training and testing. Once this process was completed, the results were averaged. In this study, a value of k = 5 folds was used. That is, the data were partitioned into the following group sizes: (18, 69), (18, 69), (17, 70), (17, 70), and (17, 70). For example, in the first ordered pair, 69 participants were used for training and 18 for testing, and so on.

To evaluate this type of model, the confusion matrix is used, which is a contingency table with two dimensions, “actual/observed value” and “predicted value” [14,15]. It allows for the visualization of an algorithm’s performance, typically in the context of supervised learning. In addition, the F1-score, accuracy, and the Area Under the Curve (AUC) of the Receiver Operating Characteristic (ROC) curve also help assess the model.

Moreover, the ROC curve facilitates the visualization of the model’s behaviour; the larger the area under the curve, the better the classifier. Both the confusion matrix, the ROC curve, and the aforementioned metrics were applied in the analysis of the clinical data.

On the other hand, hidden patterns within the data were also explored through an unsupervised method. For this purpose, the k-means clustering algorithm was applied. This is an unsupervised learning method that partitions the dataset into k non-overlapping groups based on distance [14,15]. The number of groups is a predefined parameter for which the silhouette method can be used as an indicator.

For visualization purposes, dimensionality reduction was applied using Principal Component Analysis (PCA), which is a method for reducing dimensionality by retaining a smaller number of dimensions that explain the greatest variability in the data [14,15].

For the analysis of the clinical data, the Python libraries pandas, numpy, matplotlib, seaborn, and sklearn were used [16].

2.2. Aortic Data

Each patient has variables that vary across spatial and temporal dimensions. The first step involved segmenting the aorta in the images using a Multiview 2D U-Net. The rings were selected based on the normal to the centreline (see Figure 1). The largest diameter is defined as the distance between the two points that determine the maximum diameter at systole [13].

Spatially, the variables are measured in rings distributed uniformly along the centreline (at different lengths: 0.2, 0.3, 0.4, 0.5, depending on aorta size), and temporally, they represent different moments of the cardiac cycle, measured in 5% increments associated with each time step in the CTA.

The analysis presented focuses on three patients, as they represent three distinct patient groups discussed in Section 3.2.

2.3. Empirical Variogram and Model Fitting

The variogram is a tool from geostatistics that allows analyzing the spatial relationship present in the data. To define it, it is necessary to define the regionalized variable [17,18]. A regionalized variable is a random variable for each region used. It is denoted by

$$\{Z\left(s\right):s\in D\subset R^n\}.$$

Each $Z\left(s\right)$ is a random variable. The variogram $\gamma$ is defined as

$$\gamma \left(h\right)={\displaystyle \frac{1}{2}}E\left[{\left(Z\left(s\right)-Z\left(s+h\right)\right)}^2\right]$$

where $h$ is the vector (distance and direction) separating the values of the points (illustrated in Figure 2). The variogram $\gamma$ can be estimated by the empirical variogram $\widehat{\gamma }$, defined as

$$\widehat{\gamma }\left(h\right)={\displaystyle \frac{1}{2\left|N\left(h\right)\right|}}\sum _{\left(i,j\right)\in N\left(h\right)}{\left(Z\left(i\right)-Z\left(j\right)\right)}^2$$

where $N\left(h\right)=\left\{\right(i,j):\Vert i-j\Vert =h\}$, that is, the number of pairs with separation vector $h$.

It stores information about how the properties of data change with distance and direction between sample points. The variogram helps to identify spatial relationships, revealing trends or uniformities in the data. It can be used to classify areas with similar behaviours. This ability to detect spatial patterns makes the variogram useful not only in geostatistics but also in any data analysis where spatial structure is important, helping to better understand and model the phenomena being studied.

Once the empirical variogram has been calculated, model fitting can be performed using well-known parametric models. In this work, the skgstat library in Python will be used, which provides a variety of variogram models [17,19] such as those listed below:

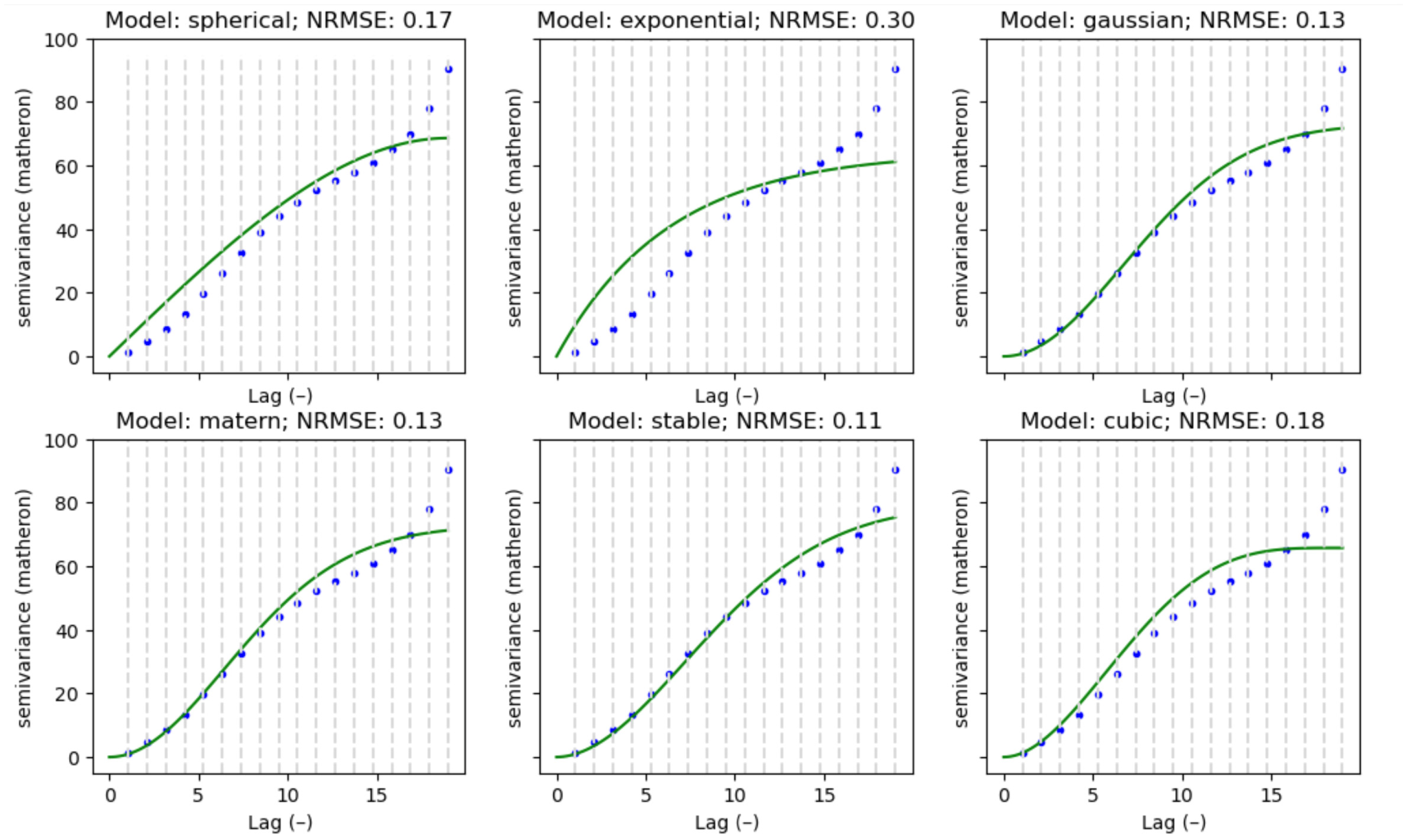
• Spherical: This model describes a gradual increase in variability with distance, until it stabilizes at a maximum range.
• Exponential: The exponential model describes variability that increases continuously and more rapidly with distance.
• Gaussian: Similarly to the exponential model, but with a smoother decrease.
• Matern: This model is a generalization of the earlier ones and includes an additional parameter that controls the smoothness of the function.
• Stable: The stable model is used for phenomena that show irregular variability, even at large distances.
• Cubic: Variability increases or decreases cubically with distance.

2.4. Aortic Data Processing

The data processing for this study involved the calculation of experimental variograms for each patient, with measurements taken at multiple time points. In this work, only the maximum diameters were considered, which were used to assess spatial dependencies and quantify variability across different distances. The following steps were carried out to compute the variogram and its parameters:

• Data collection: For each patient, the data was read from their corresponding file. Each dataset contained a series of observations taken over time, which included various spatial measurements of the region of interest. These data points served as the foundation for the subsequent analysis.
• Distance setup: A predefined set of distances, ranging from 0 to 19 units, was selected to characterize the spatial relationship between the measurement points. These distances represent the intervals over which the differences in the data points were calculated and compared.
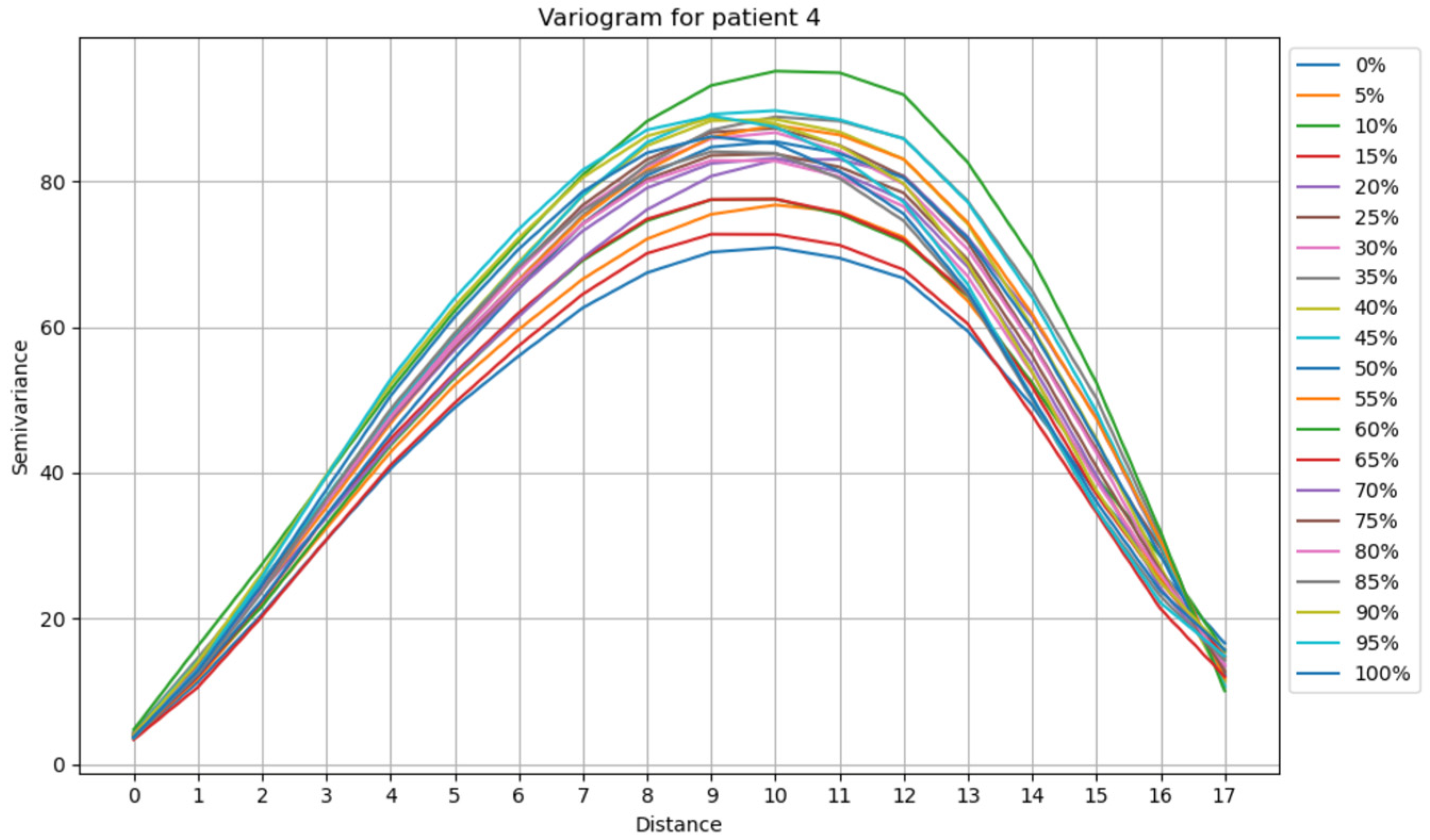
• Variogram calculation: For each observation, the experimental variogram was computed using the selected distances. The variogram quantifies the spatial correlation between the measurements at different distances by calculating the squared differences between the values and their spatial lag. The variogram also provides insights into the spatial structure and dependencies of the data.
• Parameter estimation: In addition to calculating the experimental variogram, key parameters of the variogram model were estimated. Twenty experimental variograms were calculated (one for each time point: 0%, 5%,10%, etc.) for each patient. Then, the models mentioned in the previous subsection were used to construct 21 theoretical variograms for each patient with each model. The goal was to determine which model best fits the experimental variograms for each patient (Figure 3). To achieve this, the Normalized Root Mean Squared Error (NRMSE) was calculated for each patient and each model. NRMSE is a metric used to assess the accuracy of a model’s predictions while accounting for the scale of the data. It is a variation in the Root Mean Squared Error (RMSE) but normalized to make it more interpretable across different datasets [20].

As a result, each patient had 21 NRMSE values per model. These NRMSE values were then averaged to determine which model best fit the data for each patient, and the model with the lowest average was selected as the best fit for that patient. Finally, a database was created, listing each patient along with the best-fitting model and the parameters. These parameters include the following:

• Nugget: This parameter represents the small-scale variation or noise in the data, typically reflecting measurement error or fine-scale variability. It corresponds to the value of the variogram at distance zero.
• Sill: The sill represents the plateau level of the variogram, indicating the point at which the spatial correlation between measurements becomes negligible, and further increases in distance no longer influence the variance.
• Range: The range is the distance at which the variogram reaches the sill, indicating the effective spatial distance over which measurements are correlated.

For the analysis of the aortic database, the libraries numpy, pandas, skgstat, and matplotlib were used.

3. Results and Discussion

3.1. Description of Clinical Data

This section presents the results of the analysis carried out on the clinical data of the patients. The sample consisted of 87 patients, of whom 25 (28.7%) were classified as having a surgical indication (surgical_eligibility = 1). The distribution of the dependent variable showed a higher proportion of patients without a surgical indication (71.3%), as illustrated in Figure 4.

In addition, Figure 5 presents the distribution of maximum systolic diameters of patients with and without surgical indication. Among patients without surgical indication, the diameters follow a nearly symmetric distribution, and 100% are below 55 mm (in accordance with international parameters). In the group of patients with surgical indication, the maximum diameters reveal a negative skew, with 50% of values equal to or greater than 55 mm. Moreover, greater variability is observed in the central 50% of diameters in the group requiring surgery.

In the supervised analysis, the logistic regression model showed satisfactory performance, with an accuracy of 85.1% and an F1-score of 0.748. The confusion matrix (Figure 6) indicated good performance in the non-surgical class (surgical_eligibility = 0) and moderate performance in the surgical class (surgical_eligibility = 1). This can also be observed in the ROC curve (Figure 7).

Analyzing Figure 8, the variables most strongly associated with the surgical decision were the maximum systolic diameter (max_diam_sys, absolute importance = 2.27), male sex (sex_M, absolute importance = 0.94), and hypertension (hypertension, absolute importance = 0.64). These results reinforce that, in addition to the established criteria (diameter and sex), other clinical variables such as hypertension, family history, and smoking may contribute to explaining the surgical decision in patients with ascending aortic aneurysm.

In the unsupervised analysis, the k-means algorithm identified two distinct clusters. Cluster 1 showed a balanced distribution between surgical and non-surgical patients (6 vs. 6), whereas Cluster 2 included most of the patients, with a predominance of non-surgical cases (57 vs. 18) (see Figure 9).

The projection of the data in the two-dimensional PCA space revealed a partial separation between the groups, suggesting heterogeneity in the patients’ clinical profiles. The first two principal components explained approximately 21% of the total data variance, indicating that this two-dimensional plane retains a relevant portion of the original information and allows the observation of general trends and groupings within the dataset.

Among the two clusters, cluster 2 included slightly younger patients (mean age 64.7 years), a higher proportion of operated cases (76%), and marginally larger aortic diameters. Cluster 1, in contrast, comprised older patients (mean age 68.1 years), with higher blood pressure and predominantly non-surgical management. Although no statistically significant differences were found (p > 0.05), trends were observed in the maximum aortic diameter (p = 0.08).

These findings support the presence of two clinically plausible yet overlapping subgroups, consistent with the moderate silhouette coefficient (0.257), indicating that while the separation between clusters is not sharp, it reflects meaningful heterogeneity within the patients.

3.2. Analysis of the Empirical Variogram

The first observation is that the variogram is a useful tool for identifying patient groups. Initially, a group of patients was identified whose variogram exhibits an increasing trend (Figure 10). This suggests that the aneurysm is located at one of the extremes of the studied area or, less commonly, tends to concentrate towards one of those extremes.

On the other hand, the following variogram (Figure 11) shows a curvature at medium distances, which may indicate that the aneurysm is located at the centre of the ascending aorta.

This confirms that the variogram preserves the spatial information of the aneurysm in the aorta; however, this is not such a relevant finding since it is easy to observe with tomography and by measuring the maximum diameters.

It can also be observed that there are important threshold values. It could be said that from 0 to 15, the variogram can be considered constant, which would indicate a uniform distribution along the ascending aorta. Values between 15 and 120 could be considered indicative of a more notable or evident aneurysm, depending on the previously discussed groups. Finally, values between 120 and 200 could indicate corrupted data. Regarding the latter, there were instances where some corrupted data were found, which were subsequently corrected.

Analysis of the Variograms Parameters

Once the variogram model is set for each patient, a range study is conducted, as it can provide information on elasticity or deformation depending on the distance. This is because the range indicates how much influence one sample has over another (correlated measures), and the sill gives the trend of the variogram for distances quite large. An explanation will be given regarding the interpretation of the range and sill over time.

If the range is low, this suggests that the aorta does not easily propagate its deformation during systole, which may indicate local stiffness. If the range is high, the deformation of the aorta propagates over a greater distance, which may suggest a more elastic aorta, contributing to the propagation of deformation at higher ranges. That is, if one part of the aorta deforms, this deformation influences more distant sections. This is a typical behaviour of a structure with low resistance to stress and a high capacity to distribute tensions.

There are cases where both high and low ranges may occur over time. This could indicate a time-dependent elastic response. If the fluctuations follow a pattern, it may be possible to analyze whether the aorta shows signs of fatigue or stress depending on time.

To complement the interpretation of the variogram, a clinical validation was carried out using an established metric for aortic wall stiffness, the area distensibility [13].

$$D={\displaystyle \frac{A_{syst}-A_{diast}}{A_{dist}\left(P_{syst}-P_{diast}\right)}}$$

Here, $A_{syst}$ and $A_{diast}$ represent the cross-sectional area at systole and diastole, respectively. $P_{syst}$ and $P_{diast}$ represent the arterial pressure during systole and diastole, respectively.

Low distensibility values indicate an increase in aortic wall stiffness. This metric was compared with the range and sill parameters, and several specific cases are presented.

Now, the sill and range of some cases of patients will be analyzed. First, we will look at patient 2, who has a small aneurysm but large deformations (Figure 12). Then, patient 18, who has a large aneurysm (Figure 13). Finally, patient 30, who has a small aneurysm with minor deformations (Figure 14).

In the case of patient 2, despite having a small aneurysm, there is low variability (see sill, Figure 5) due to the large deformation. Additionally, the variability fluctuates, indicating that the aorta exhibits some complexity in its structure. On the other hand, the range suggests correlation at short ranges, specifically in the time intervals from 0 to 40 and 65 to 100, indicating greater stiffness in the ascending aorta. There is total correlation in the time interval from 45 to 60, suggesting that blood pressure during the cardiac cycle affects all maximum diameters.

When calculating the distensibility for the maximum aortic area at the moments of systole and diastole, a value of 0.293 was obtained for patient 2. According to the literature, this indicates stiffness, which is consistent with the findings derived from the variogram parameters [21].

Patient 18 has a large aneurysm and high maximum variability (see sill, Figure 6). Additionally, it has long ranges, indicating that at almost all-time intervals, most of the diameters are correlated.

For patient 18, the area distensibility was 0.1822, indicating stiffness in the ascending aorta.

Patient 30 has a small aneurysm with a minor deformation. The maximum variability is not very high, and the ranges are large, indicating that this patient has a more elastic aorta.

For patient 30, the area distensibility was 0.3604, showing greater elasticity in this patient’s aorta.

4. Conclusions

The analysis of the clinical variables showed that, in addition to the maximum diameter, other variables may play an important role in surgical decision-making, such as sex, hypertension, family history, and smoking habits.

This study provides an initial approach to analyzing ATAAs using spatial statistics. The findings suggest that spatial statistics can be a valuable tool for identifying patterns in aneurysms, such as their location in the ascending aorta through variograms.

On the other hand, the analysis of the variogram parameters allows the observation of fluctuations or variations in the aorta across the 21 time points of the cardiac cycle.

The maximum diameter remains the primary criterion for clinical decision-making in aneurysms, and our results confirm its continued relevance. However, the dynamic analysis provided by variograms shows that this measure does not fully capture the biomechanical complexity of the vascular wall. Variograms enable the characterization of internal heterogeneity and its variation throughout the cardiac cycle, revealing local changes that may become more pronounced during systole than during diastole. Such temporal differences may indicate variations in the mechanical response of the tissue, which are not reflected in static morphometric metrics.

In an aneurysm whose size would traditionally be considered non-critical, for example, around 45 mm, the presence of localized areas of stiffness or irregularity that intensify under systolic load could suggest a reduced capacity of the wall to distribute stress. These dynamic patterns may have clinical implications, as a wall exhibiting decreased elasticity at moments of peak pressure could be more vulnerable, even when the diameter does not exceed the usual intervention threshold.

It is important to note that this hypothesis cannot be evaluated with the data available. The dataset is not longitudinal, and no information is provided on whether patients underwent surgical intervention or on their subsequent vital status. Consequently, although variogram analysis offers valuable insights into the dynamic behaviour of the aortic wall, it is not possible to establish relationships with clinical outcomes or therapeutic decisions. Future longitudinal studies will be required to determine the actual predictive value of these metrics.

This approach opens the door to future research aimed at identifying cases in which aneurysms below established diameter thresholds exhibit atypical mechanical behaviour or relevant structural complexities.

Although this study does not propose clinical criteria, it does suggest that the spatial properties of deformation could, in future research, offer valuable information to better understand the regional vulnerability of the aortic wall and its potential relevance in risk assessment. However, further exploration is needed to assess the effectiveness of the sill and range parameters in studying elasticity and stiffness.

Also, based on the analyses conducted, it is suggested that future research could extend the use of spatial statistical techniques, such as kriging, to generate an interpolation of the spatiotemporal data, thereby obtaining more accurate estimates.