A Mean-Risk Multi-Period Optimization Model for Cooperative Risk in the Shipbuilding Supply Chain

Abstract

This study addresses the cooperative development problem between shipbuilding enterprises and suppliers under supply risk by improving and optimizing the Markowitz model. A mean-risk multi-period linear programming decision model and a nonlinear programming decision model are constructed under uncertain conditions. First, the connotation of supply chain cooperation risks in shipbuilding enterprises is analyzed, and key risk characteristics are identified. Then, based on lifecycle theory, the cooperation process is examined, and corresponding risk prevention strategies are proposed. Finally, an enhanced mean-risk multi-period linear programming model is developed, and a nonlinear programming decision model is introduced. Numerical experiments and sensitivity analysis using real-world shipbuilding enterprise data validate the correctness and effectiveness of the proposed models. The results demonstrate that, compared to linear programming models, nonlinear programming models achieve a lower risk for equivalent returns. The findings suggest that the proposed approach can effectively optimize cooperative decision-making under uncertainty, providing valuable insights for risk management in the shipbuilding supply chain.

1. Introduction

The shipbuilding industry is a cornerstone of global trade and economic development, characterized by its capital intensity, extended project lifecycles, and highly complex supply chain networks. This supply chain is a multi-layered system encompassing a wide array of stakeholders, from raw material suppliers and equipment manufacturers to shipyards and ship owners. The inherently globalized nature of this network, as noted by Alfnes et al. [1], renders it particularly susceptible to a multitude of risks, including geopolitical instability, material shortages, and logistical delays.

The shipbuilding supply chain is a multi-layered and complex network. The relationship between shipbuilding enterprises and suppliers is crucial to the cooperation risk management of shipbuilding enterprises. From the perspective of the formation of the value chain, suppliers upstream of the shipbuilding supply chain have a greater impact on shipbuilding costs. Therefore, this paper mainly studies the cooperation risks between shipbuilding enterprises and suppliers.

At present, there are relatively few studies on cooperative risk management in the shipbuilding supply chain. In order to comprehensively, objectively, and reasonably analyze cooperative risk management, we can learn from the relevant cooperative risk management experience and models of other industries. Risk management is a set of management theories to achieve optimal production with a scientific guarantee. Its general steps are to identify risks first, then analyze risks, and finally evaluate risks. The introduction of risk management by enterprises can reduce risks to the greatest extent and improve benefits. Risk management follows the purpose of “pre-prevention and continuous improvement”, and it has a system of self-discipline, self-improvement, and self-motivation. Risk management is an indispensable part of corporate culture, the core competitiveness of enterprises in participating in global games, and the organic unity of economic, environmental, and social issues. Risk assessment is an important step in implementing risk management.

At present, scholars have adopted many risk assessment methods to explore it. Some researchers have constructed a risk management research model for risk identification, risk assessment, and risk control and prevention in response to the risk problems in shipbuilding logistics. They analyzed several core risk elements such as interruption management, disaster and emergency management, and logistics delays, and concluded that the risks of shipbuilding logistics come from four main factors: external environment, internal enterprise conditions, management and operation processes, and information transmission processes [2,3]. Beasley et al. [4] used a questionnaire survey method to collect data, analyze, and identify the risks of logistics outsourcing, and finally obtained a survey result in which logistics outsourcing may cause seven major risks to enterprises: market risk, operational risk, financial risk, human resource risk, technology leakage risk, legal risk, and credit risk. The engineering team of the procurement office of the US Air Force Electronic Systems Center (ESC) applied the risk matrix method to identify risks in the procurement of US defense materials. The risk matrix method is a structural method that distinguishes the relative importance of risk sources (risk sets) in the project management process. It can also be used to evaluate the potential role of project risk sources (risk sets) [5].

Haimes et al. [6] constructed a risk holographic model (HHM) and a risk filtering, ranking and management framework (RFRMF) to address the risk issues in high-tech projects and conducted quantitative analysis. Schank [7] first mentioned the case-based reasoning method (CBR) in his monograph. The CBR method is an inference method in the field of artificial intelligence and has been widely used to identify logistics risks. Giaglis [8] pointed out that logistics risks should be identified from the following four aspects: external environment, internal enterprise situation, management and operation process, and information transmission process. The evaluation indicators of logistics risk warning should be determined based on the actual situation of these four aspects, and the fuzzy comprehensive evaluation method should be used for evaluation. Tao [9] summarized the characteristics of the shipbuilding industry and created a supply chain structure and numerical model based on the symbiotic cooperation form, based on the characteristics of the shipbuilding supply chain. He analyzed the supply chain structure risk and gave opinions and methods for managing and controlling the supply chain structure risk.

He [10] proposed a comprehensive evaluation method based on principal component analysis and linear regression for the risk measurement of the credit index system of supply chain finance. Zhou [11] studied the inherent characteristics of supply chain cooperation risk management in shipbuilding enterprises and proposed targeted measures and treatment methods for the deficiencies caused by supply chain cooperation risks and the risk factors in managing supply chain node enterprises. According to Alfnes et al. [1], these conditions characterize the shipbuilding industry’s globalized supply chain structure, making it susceptible to risks of geopolitical instability, material shortages, and logistical delays. Recent empirical studies show that inefficient collaboration between shipbuilders and suppliers can considerably increase these risks. For example, a study of Norwegian shipyards found that poor supplier relationships contributed to a 30% higher disruption rate than integrated relationships. Comparative analysis among Asian shipbuilders indicated that formalized supplier development and joint R&D significantly improved resilience to demand shocks, with South Korean firms instituting such programs demonstrating 25% greater resilience than their peers relying on non-structured arrangements [12].

Ramirez-Peña et al. [13] proposed the shipbuilding 4.0 Index as a framework to evaluate the digital transformation level of shipbuilding supply chains. Their study identified key enabling technologies of Industry 4.0 and emphasized the supply chain’s pivotal role in enhancing sustainability and guiding the structured adoption of advanced technologies within the shipbuilding industry. However, the shift in the industry toward modular construction also came with new risks, such as design misalignment between shipbuilders and suppliers, which required new, more dynamic contract frameworks [14]. For instance, Tao [9] studied Chinese shipyards and found that symbiotic supplier alliances with nonlinear cost-sharing contracts reduced bullwhip by 22% relative to the linear ones. Chen et al. [15] found that cascading delays in shipbuilding projects could be predicted using Bayesian networks with a prediction accuracy of 89%, outperforming traditional linear regression models significantly. Shipbuilders employing adaptive inventory buffers can reduce operational risk during volatile market conditions, highlighting how flexible response mechanisms enhance supply chain resilience [16]. Despite these advances, major challenges remain. Data scarcity in engineer-to-order supply chains was identified as a key constraint to the application of Artificial Intelligence by Fatouh and Rego [17], whilst Kuiti et al. [18] developed new cap-and-trade policies that could serve as a solution to both environmental and financial risks for sustainable shipbuilding projects.

There are very limited studies on the cooperation between shipbuilding enterprises and suppliers under supply risk. At present, there are two main research methods. (1) The subjective scoring method: Experts score single risks based on their intuitive judgment, for example, a number between 0 and 10. It can be defined that 0 means no risk, 10 means a particularly large risk, and then all risks are cumulatively added according to certain standards. (2) The fuzzy comprehensive evaluation method: Many factors affect supply chain risks, some of which can be obtained, while others cannot. Therefore, it is impossible to accurately describe the risk level in the risk assessment process. At the same time, given that the supply chain is a dynamic network alliance created around core enterprises, its risk-based inference lacks original data in many cases, and the corresponding probability distribution cannot be determined. In most cases, it relies on personal subjective judgment, which is relatively vague. Therefore, for the overall evaluation of supply chain risks, the fuzzy comprehensive evaluation method is used more. These two methods, the subjective scoring method and the fuzzy comprehensive evaluation method, both use expert scoring to assess risks. In essence, they are qualitative studies. Their evaluation results include the subjective factors of the evaluator. The evaluation results produced are not intuitive and have certain cognitive errors. Furthermore, the engineer-to-order nature of shipbuilding creates data scarcity, complicating the application of advanced analytical techniques like Artificial Intelligence [17]. The industry’s shift towards modular construction also introduces new risks like design misalignment between shipbuilders and suppliers, necessitating more dynamic contract frameworks [14].

This paper uses a quantitative method to study and improve the Markowitz model and applies it to the study of the cooperation risk between shipbuilding enterprises and suppliers. The main contributions of this paper are as follows:

• This paper makes a quantitative study of the cooperative risk of shipbuilding enterprises. At present, risk management is mainly analyzed in three steps: risk identification, risk evaluation, and risk control. There is little literature on cooperative risk management of shipbuilding enterprises, and most of the risk assessment models are in the active scoring stage, lacking objectivity and pertinency. The multi-period linear programming decision model and the nonlinear programming decision model established in this paper are both quantitative research models.
• A multi-period nonlinear programming decision model based on mean risk is established to study the risk of shipbuilding supply chain cooperation. This paper constructs a multi-period planning decision model in which the expected return and the investment amount have a nonlinear relationship, which is more in line with the actual situation, and is compared with the results of the linear decision model. The calculation results show that the nonlinear decision model can reduce the risk at the same level of return.
• Enriched the research on cooperative risk in the shipbuilding supply chain. Aiming at the cooperative development work between shipbuilding enterprises and suppliers under supply risk, the mean-risk model was improved, and the mean-risk multi-period linear programming decision model and nonlinear programming decision model were constructed and applied to the research on cooperative risk in the shipbuilding supply chain for the first time.

The structure of this paper is as follows. Section 2 is the literature review of this paper. Section 3 constructs a multi-period linear and nonlinear programming decision model based on mean risk. Section 4 presents the empirical analysis and results. Section 5 is the conclusion of this paper.

2. Literature Review

2.1. Overview of Shipbuilding Supply Chain Cooperation Risks

A supply chain partnership can be defined as a partnership formed between two or more node enterprises within the supply chain to achieve a set goal. The risk of shipbuilding supply chain cooperation exists in the supporting factories, raw material factories, ship intermediaries, cooperative factories, shipowners, and other enterprises in the shipbuilding supply chain. When they form a cooperative relationship with each other, due to the differences between the two parties on some issues, the shipbuilding supply chain will produce many uncertainties in the process of cooperation, which will cause the probability and possibility of inconsistency between the expected results and the actual results of the shipbuilding supply chain of the entire system. Shipbuilding is closely related to related industries such as production and transportation, import and export trade, finance, and insurance, and is also a capital-intensive and high-risk industry.

If the supply chain cooperation is based on the cooperation of various enterprises with independent interests, such cooperation contains established risks. There is no doubt that the supply chain of shipbuilding enterprises must first cooperate because if various module factories and assembly plants do not cooperate in division of labor, there will be no improvement in the shipbuilding model and the improvement of the large-scale customized shipbuilding model; if the assembly shipyard, raw material factory, supporting factory, module factory, etc., do not cooperate closely and fully, the module shipyard and the assembly shipyard will have to use the method of gradually replenishing inventory to ensure production; if all enterprises in the supply chain lack cooperation, the significant advantages of large-scale customized shipbuilding cannot be manifested; in summary, if continuous and efficient cooperation cannot last for a long time, the shipbuilding supply chain of the entire system will appear fragile. Therefore, the closer the cooperation between node enterprises, the better the overall benefit of the shipbuilding supply chain. However, cooperation also has some inherent risks, which are more common and cumbersome than the risks of a single shipyard independently building ships.

Any production and operation accident caused by any of the cooperative node enterprises will more or less cause some obstacles to the supply chain of the entire system. If the platform and channel for communication between cooperative node enterprises suddenly stagnate, it may cause blockage and chain breakage of the entire system supply chain. Improper actions of a certain node partner enterprise will have a certain impact on the positions and activities of other node enterprises, and then endanger the maintenance of the relationship between the node partners of the supply chain and the acquisition of collaborative effects.

2.2. Risk Characteristics of Shipbuilding Supply Chain Cooperation

The cooperation risks in the shipbuilding supply chain have the usual characteristics of cooperation risks, but due to the complexity and particularity of the industry, they also have their distinctive characteristics:

• Globally. Compared with the supply chains of other manufacturing industries, the shipbuilding supply chain involves a larger number of cooperative enterprises, and the number of foreign cooperative node enterprises is also larger, with a particularly wide geographical span. There are both domestic suppliers and overseas suppliers. Suppliers are geographically diverse and more susceptible to exchange rates and energy price fluctuations, cultural and language differences, trade regulations, and political and economic stability. Shipbuilding is a complex project involving a large number of different types of parts. Many domestic and foreign suppliers are involved in inbound logistics, and different parts have different logistics requirements. If a supplier fails to deliver on time, it may cause a chain reaction. Therefore, the cooperation risk of the shipbuilding supply chain has global characteristics.
• Uncertainty. Based on the characteristics of the shipbuilding industry and the production logistics of the shipbuilding industry, it is known that the process of manufacturing ships is extremely arduous and complex, and the architecture of the shipbuilding supply chain is also particularly cumbersome. In the shipbuilding supply chain, there is not only cooperation between node enterprises but also a lot of collaboration between sub-chains. This extremely cumbersome collaboration has many uncontrollable or uncertain elements and is, therefore, more prone to uncertain cooperation risks.
• Uncertainty. From the perspective of the cooperative node enterprises in the supply chain, there is always some sudden unpredictability in terms of cooperation risks, and it is quite obvious. In the shipbuilding supply chain, whether it is the production and transportation of parts and the assistance of cooperative manufacturers, or the step-by-step assembly of shipbuilding enterprises, there are many links and steps involved in the middle, which are particularly complicated. These links and steps will interfere with the attention of the cooperative node enterprises in the supply chain to a certain extent. Shipbuilding enterprises cannot accurately predict and calculate these unpredictable cooperation risks, so they will not perceive the cooperation risks until they occur, which will catch the node enterprises off guard and make them feel the suddenness of the cooperation risks.
• Dynamicity. The cooperation risk of the shipbuilding supply chain is not always constant but is in a dynamic development process. Sometimes, the cooperation risk becomes weaker and weaker due to the implementation of risk model management. Sometimes, the cooperation risk becomes worse due to the disruption of internal and external factors of the supply chain.

2.3. Shipbuilding Supply Chain Cooperation Risk Assessment Model

Risk management assessment models can be divided into probability models, fuzzy comprehensive evaluation models, mean-risk models, and Bayesian network models.

• Probabilistic decision model. The international engineering standard ISO 14971 defines risk as R, the product of the probability and harmfulness of $R=P_e\times S_e$ a risk source event: $e$, where $P_e$ represents $e$ the probability of the risk event, and $S_e$ represents the loss of $e$ cost, quality, and time caused by the risk event. The main purpose of supply chain risk assessment is to estimate the adverse impact of the probability of the risk event on the entire supply chain. It is often difficult to quantify the probability and harmfulness $S_e$ of risk events $P_e$ because it is almost impossible to accurately assess the possibility of occurrence and its impact; however, as a qualitative method, it is desirable to evaluate the identified risks. The probability decision matrix is a qualitative risk assessment tool with two dimensions: “probability” (from low to high) and “impact” (from weak to severe) based on the scale. In the risk assessment of the supply chain, the probability decision matrix is a widely used risk assessment model.
• Fuzzy comprehensive evaluation model. Many factors affect supply chain risks, some of which can be obtained, while others cannot be obtained, which is a kind of gray information. Therefore, it is impossible to accurately describe the risk level in the risk assessment process. At the same time, given that the supply chain is a dynamic network alliance created around core enterprises, the risk-based inference lacks original data in many cases, and the corresponding probability distribution cannot be determined. In many cases, it relies on personal subjective inference, which is relatively vague. Therefore, for the overall evaluation of supply chain risks, fuzzy comprehensive evaluation methods are widely used [19,20].
• Bayesian network model. The Bayesian network model takes into account the advantages of probability theory and graph theory. It combines the two organically and can handle uncertainty problems very clearly. It has been widely used in decision support, machine learning, and data mining.
• Mean-risk model. Also called Markowitz model, or mean-risk (risk) analysis, also known as modern portfolio theory (MPT), it was established by economist Harry Markowitz in the 1950s. The author was later awarded the Nobel Prize in Economics. In the initial version of the mean-risk theory model, investment return is defined as the expected value of the rate of return, that is, the average return of the asset, and investment risk is defined as the volatility of the rate of return, that is, the risk of the asset return [21,22]. In the existing literature, it is assumed that the return and investment amount are in a linear relationship, and nonlinear situations are not considered. Based on the existing literature, the main risk assessment models and their related characteristics are listed in

  Table 1. Risk assessment models and characteristics.

  Evaluation Model	Characteristic	References
  LEC evaluation model	Easy to understand and operate, but strong subjectivity, limited ability to assess complex risks.	[23]
  Mean-risk model	Can quantify risk, concise and intuitive, but accurate data acquisition is difficult.	[21,22]
  Bayesian network model	The model is simple and interpretable, but it needs to collect a lot of data.	[24]
  Network analysis model (ANP)	It is presented graphically, but the modeling of the relationship between each factor requires a lot of data support.	[25]
  Risk matrix model	The graphical presentation is intuitive and easy to understand, but ignoring some potential risks makes the assessment incomprehensive and subjective.	[26]

  .

Synthesis and Identified Research Gap

The preceding analysis outlines a suite of established risk assessment models, from qualitative matrices to quantitative frameworks like the Bayesian network [24] and the Mean-Risk model [21,22]. While these models provide a foundational toolkit, their application to the specific context of cooperative risk in the shipbuilding supply chain remains superficial. The literature reveals a heavy reliance on qualitative or semi-quantitative methods, such as the fuzzy comprehensive evaluation [19,20], for assessing cooperation risks. These methods, while valuable for initial screening, are inherently limited by evaluator subjectivity and cannot provide the precise, optimized investment decisions required for strategic supplier portfolio management under uncertainty.

Furthermore, a critical gap exists in the evolution from assessment to decision-making. Even in the limited quantitative applications, a key simplifying assumption persists: the relationship between the investment amount and return is linear. However, real-world supplier relationships often involve economies of scale, volume discounts, and other factors that create a nonlinear return structure. Research in other supply chain domains has demonstrated that assuming linearity can lead to suboptimal risk-return outcomes compared to models that capture these nonlinear realities [27]. Therefore, the principal research gaps this study addresses is the lack of a multi-period, quantitative decision model for shipbuilding supply chain cooperation that moves beyond linear assumptions to incorporate more realistic nonlinear relationships between investment and return, thereby enabling superior risk-return optimization.

3. Risk Model of Shipbuilding Supply Chain Cooperation

3.1. Markowitz Model Theory

The Markowitz Mean-Variance (MV) model provides a foundational mathematical framework for optimizing a portfolio of assets by quantifying the trade-off between expected return (mean) and risk (variance) [21,28]. In the mean-risk model, Markowitz defines return as the expected value of the rate of return, that is, the average return of an asset, and defines risk as the volatility of the rate of return, that is, the risk value of the asset return. The core concept of this model is that investors need to avoid risks on the one hand and achieve a satisfactory level of return on the other hand. In this case, in order to obtain the best resource allocation plan, the goal is to minimize risk under the expected return level limit or to maximize return under the expected risk level limit. This model makes full use of mathematical formulas to describe the configuration of asset portfolios and quantify the minimum risk level (defined as risk). It can be described in mathematical language as follows:

Suppose there are $n$ risky assets in the market, each with a positive expected return but subject to certain risks (i.e., no risk-free asset exists). Let the asset vector be $A=\left(A_1, A_2, \cdots , A_n\right)$, its corresponding rate of return vector be $R=\left(R_1,R_2,\cdots ,R_n\right)$, and its corresponding configuration weight vector be $\omega =\left({\omega }_1, {\omega }_2, \cdots , {\omega }_n\right)$, where ${\omega }_1+{\omega }_2+\cdots +{\omega }_n=1$. Let ${\rho }_{ij}$ be the correlation coefficient between assets $A_i$ and $A_j$ returns ($i\ne j$), the rate of return risk of any two assets is recorded as ${\sigma }_{ij}=\mathrm{cov}\left(R_i,R_j\right),i,j\in \left\{1,2,\cdots n\right\}$, and the corresponding risk matrix is recorded as $H={\left({\sigma }_{ij}\right)}_{n\times n}$, that is,

$$H=\left[\begin{array}{l}{\sigma }_{11} {\sigma }_{12} \cdots {\sigma }_{1n}\\ {\sigma }_{21} {\sigma }_{22} \cdots {\sigma }_{2n}\\ \cdots \cdots \cdots \cdots \\ {\sigma }_{n1} {\sigma }_{n2} \cdots {\sigma }_{nn}\end{array}\right]$$

(1)

where ${\sigma }_{ii}={\sigma }_i^2, {\sigma }_{ij}={\sigma }_{ji}={\rho }_{ij}{\sigma }_i{\sigma }_j\left(i\ne j\right)$.

${\omega }^T$ represents the transpose of the weight vector $\omega$, so the expected return of the asset portfolio configuration is

$$E\left(R\right)={\displaystyle \sum _{i=1}^n{\omega }_i{R}_i}={\omega }^{T}R$$

(2)

The total risk of the portfolio is the risk

$$Var\left[E\left(R\right)\right]=\omega \mathrm{H} {\omega }^T={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\omega }_i{\omega }_j{\sigma }_{ij}}}$$

(3)

3.2. Analysis of Cooperation Process in Shipbuilding Supply Chain

3.2.1. Collaborative Process of Shipbuilding Supply Chain

The shipbuilding supply chain is a multi-level and complex network, and the relationship between shipbuilding enterprises and suppliers is crucial for the cooperative risk management of shipbuilding enterprises. Take the cooperation risk between shipbuilding enterprises and suppliers as an example for process analysis. Suppliers in this article refer to raw material suppliers and ship supporting enterprises, collectively referred to as suppliers. In the cooperation process between shipbuilding enterprises and suppliers, the shipbuilding enterprise issues a procurement list of raw materials or ship supporting equipment and materials to the supplier, and then the supplier produces the raw materials and ship supporting equipment and materials based on the received orders. After production, they are delivered according to the agreed time to meet the needs of the shipbuilding enterprise for the required materials.

3.2.2. Lean Control of Cooperative Risk Based on the Whole Life Cycle Theory

The survival and development of enterprises have a certain periodicity, which can generally be divided into stages such as germination, development, maturity, and decline. The cooperation between shipbuilding enterprises and suppliers is constantly evolving, and the full life cycle theory can be used to divide the cooperation change cycle into three stages: the establishment, operation, maintenance, and optimization stages of the cooperative relationship. Targeted control measures can be taken for the risks in these three stages, taking the cooperation risks between shipbuilding enterprises and suppliers as an example.

• Establishment stage and control of cooperative relationship

The responsibility of the cooperation relationship formation stage is to choose the appropriate and correct cooperative enterprise. Shipbuilding enterprises analyze the requirements of ship owners, and based on their own objective reality, search for qualified candidate cooperative enterprises in each type of enterprise, and then select qualified category suppliers from a relatively large number of supporting product factories, raw material factories, and cooperative factories. The selection of a cooperative enterprise indicates that the cooperative relationship has been established. At this stage, the main risk of cooperation comes from both parties themselves, which is caused by their own reasons. For example, risks such as inadequate supplier capabilities, material quality, motivation, and ethics. A supplier list can be established to avoid blindly selecting partners. In Section 3, all selected suppliers can be included in the supplier list library of the shipbuilding enterprise. The shipbuilding enterprise only needs to find similar suppliers in the library, and then analyze the quality level, delivery timeliness, actual and expected revenue of each supplier’s historical cycle data to select suitable category suppliers.

2.

Operation stage and control of cooperative relationships

This stage belongs to the second stage of cooperation, where both parties are fully engaged. During this stage, the partners are required to perform the tasks specified in the agreement, continuously manage, execute, and re-manage. The risk at this stage comes from the risk factors faced by both parties during the cooperative operation process. For example, risks related to non-implementation of contracts or incomplete and thorough fulfillment of agreements and logistics transportation. The risks at this stage can basically be attributed to poor logistics and delayed information exchange. Therefore, it is crucial to establish a strong logistics and information flow platform to prevent operational risks. Therefore, great efforts must be made in logistics and information flow to reduce the occurrence of uncertain factors.

3.

Maintenance and optimization stages and control of cooperative relationships

This stage is the third stage of cooperation risk, defined as retaining good successful experiences and continuing them. Optimization is the process of adjusting partners, retaining those who perform well overall and discarding those who perform poorly overall. The risks at this stage mainly include the risk of distributing benefits and the risk of conflicting goals. Shipbuilding companies should pay special attention to and consider the interests of cooperative enterprises and not bully the weak. At the same time, it is necessary to establish an incentive and supervision system to promote all cooperative enterprises to maintain good cooperative relationships.

In Section 3.3, a cooperation risk model between shipbuilding enterprises and suppliers was established, which can effectively prevent cooperation risks. In response to supply risk, shipbuilding companies can determine how to optimize the allocation of investment amounts among multiple suppliers while minimizing risk and maintaining expected return levels.

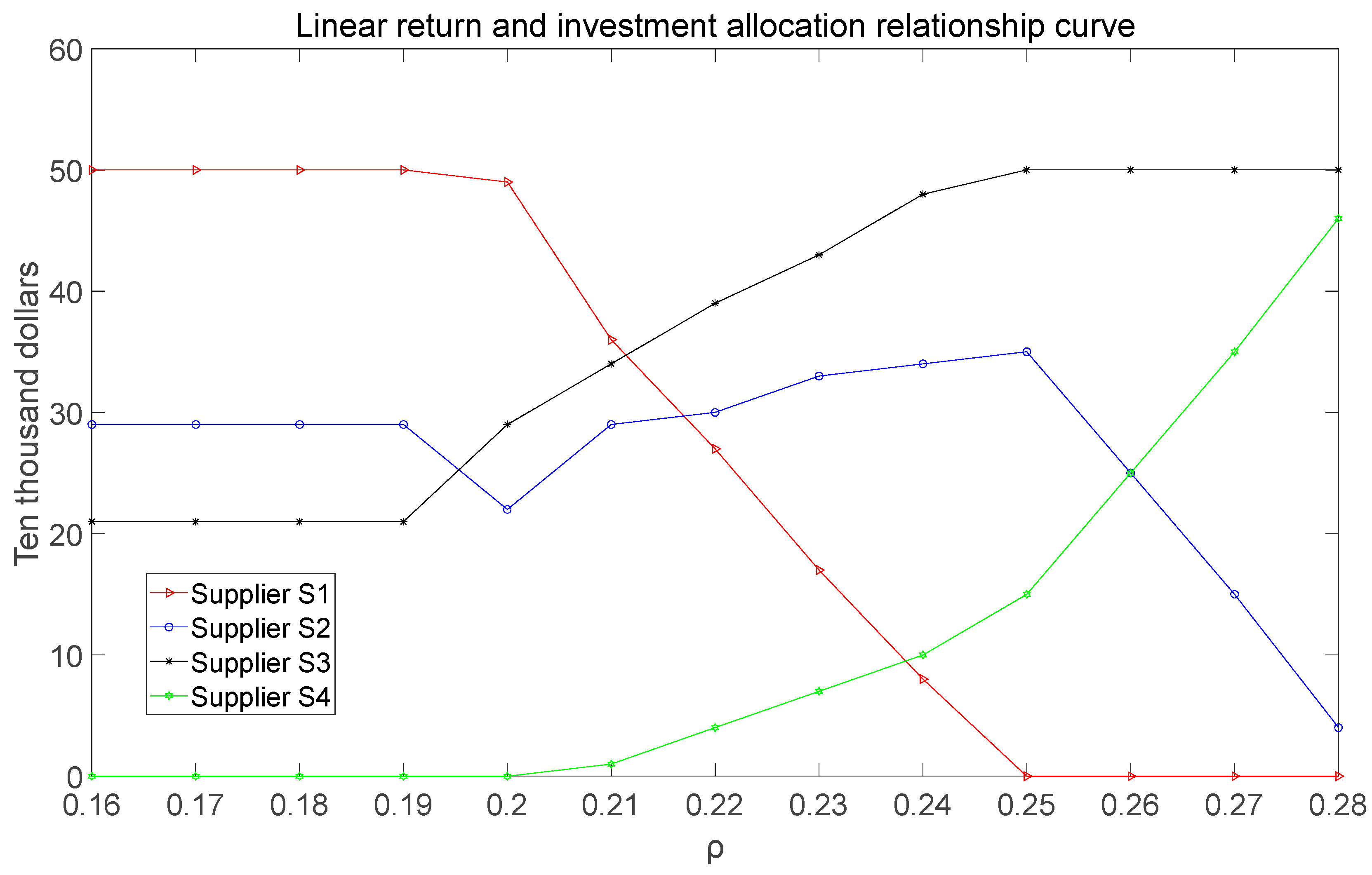
3.3. Multi-Period Linear Programming Decision Model Based on Mean-Risk

3.3.1. Problem Description and Model Assumptions

Regarding supply risk, consider the situation of a shipbuilding company cooperating with multiple suppliers for development. The shipbuilding company has limited budget funds for cooperating with suppliers and needs to allocate limited funds to multiple suppliers. Due to the different production and execution capabilities of suppliers, the return and risk of investing in each supplier are different. The investment goal of the shipbuilding company is to reasonably allocate the investment amount and minimize the risk while achieving the established expected return level. In order to avoid the risk of single procurement, the investment amount of each supplier has an upper and lower limit. The cooperative development work between the shipbuilding company and the supplier may involve a single product or several products of the supplier. Therefore, the return on investment of the shipbuilding company is an overall return.

Assume the following:

• The total budget amount for each period includes not only procurement costs but also other related costs.
• The data of the $T$ historical cycles are reliable and there are no major market fluctuations. The returns and risks of this period are estimated based on the data of the $T$ historical cycles.
• The return on investment in each supplier is linearly related to the investment amount, and the returns are all positive.
• This model considers the case of a single product and multiple cycles.
• After fitting, the $T$ historical period data of each supplier obeys a certain probability distribution of mathematical statistics.
• The investment amount allocated by the shipbuilding enterprise to the supplier is an integer.

3.3.2. Linear Decision Model Construction

The parameters are defined as follows:

• $X$: It indicates the total budget amount invested by the shipbuilding enterprise in suppliers.
• $x_i$: Indicates the investment amount allocated to the supplier $i$.
• $n$: Indicates the number of suppliers.
• $\rho$: Represents the overall expected minimum rate of return required by the shipbuilding enterprise.
• $L_i$: Indicates the minimum amount allocated to the supplier $i$.
• $U_i$: Indicates the maximum amount allocated to the supplier $i$.
• $R_i$: Represents the rate of return of shipbuilding enterprises’ investment in supplier $i$.
• $T$: Indicates the total number of time cycles.
• $r_{i,t}$: The actual rate of return of the supplier $i$ in the period $t$.
• $r_i$: Represents the expected rate of $R_i$.
• ${\sigma }_{ij}$: The covariance between the expected rates of return $r_i$ and $r_j$ for any two suppliers, i.e., ${\sigma }_{ij}=\mathrm{cov}\left(r_i,r_j\right),i,j\in \left\{1,2,\cdots n\right\}$.

Based on the above assumptions and parameter definitions, the Markowitz mean-risk model is improved, and a multi-period linear programming decision model for cooperative development of a single shipbuilding enterprise and multiple suppliers is established under supply risk:

$$\mathrm{Objective} \mathrm{function}: Min Var\left({\displaystyle \sum _{i=1}^n{x}_i{R}_i}\right)$$

(4)

$$\mathrm{Constraints}: {\displaystyle \sum _{i=1}^n{x}_i=X}$$

(5)

$${\displaystyle \sum _{i=1}^n{x}_i{r}_i\ge }X \rho$$

(6)

$$L_i\le x_i\le U_i, i\in \left\{1, 2, \cdots ,n\right\}$$

(7)

$$x_i\in N$$

(8)

Among them, Formula (4) can be written as

$$\begin{array}{l} Var\left({\displaystyle \sum _{i=1}^n{x}_i{R}_i}\right)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_i{x}_j{\sigma }_{ij}}}\\ ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_i{x}_j\left[\frac{1}{T}{\displaystyle \sum _{k=1}^T\left(r_{i,k}-r_i\right)\left(r_{j,k}-r_j\right)}\right]}}\\ ={\displaystyle \frac{1}{T}}{\displaystyle \sum _{k=1}^T\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_i{x}_j\left(r_{i,k}-r_i\right)\left(r_{j,k}-r_j\right)}}\right]}\\ ={\displaystyle \frac{1}{T}}{\displaystyle \sum _{k=1}^T{\left[{\displaystyle \sum _{i=1}^n\left(r_{i,k}-r_i\right)x_i}\right]}^2}\end{array}$$

(9)

Among them, Formula (4) indicates that the risk level is minimized while meeting the expected return level. Formula (5) indicates that the total investment budget of the shipbuilding enterprise is equal to the sum of the amount invested in each supplier. Formula (6) indicates the total return level expected by the shipbuilding enterprise, indicating that the overall expected return of the shipbuilding enterprise must reach the established return target level. Formula (7) indicates the investment constraints that the shipbuilding enterprise imposes on suppliers, namely the maximum amount and minimum amount constraints. Formula (8) indicates that the amount invested by the shipbuilding enterprise in suppliers is an integer.

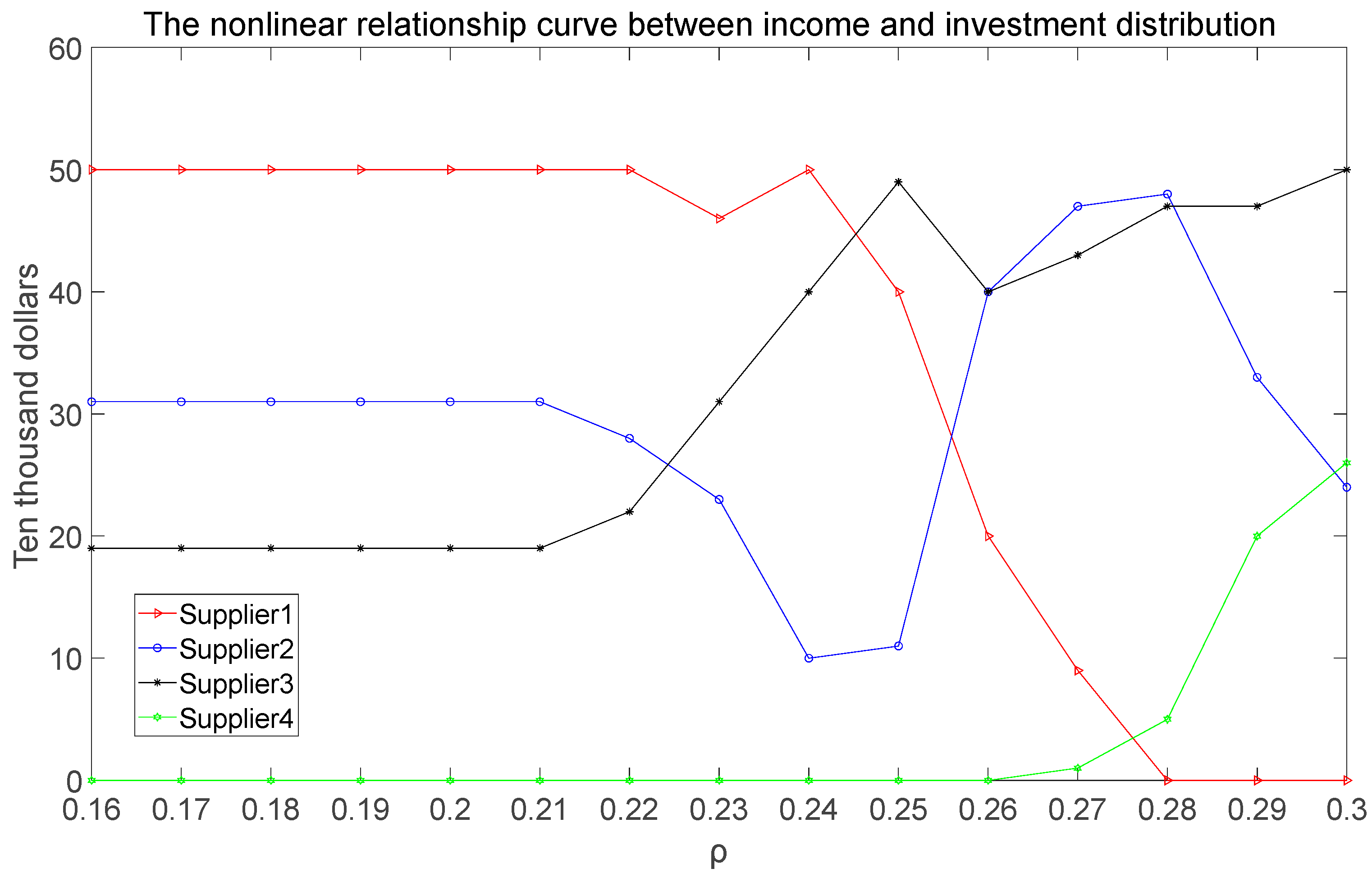
3.4. Multi-Period Nonlinear Programming Decision Model Based on Mean Risk

The above model assumes that the return on investment of a shipbuilding enterprise in any supplier is linearly related to the investment amount. However, in reality, in most cases, the return on investment is nonlinearly related to the investment amount. For example, if the investment amount in a supplier is large, the supplier will give certain discounts, which will also increase the shipbuilding enterprise’s profit level. This section modifies and optimizes the linear model in the previous section, proposes an investment plan in which the return on investment is nonlinearly related to the investment amount, studies how to optimize the allocation of resources under supply risk, and then compares the results with the model results of the linear relationship.

3.4.1. Problem Description and Model Assumptions

Under supply risk, consider the nonlinear relationship between the amount invested by shipbuilding companies in suppliers and their returns, as shown in Figure 1. In Figure 1, the horizontal axis represents the amount invested in suppliers, and the vertical axis represents the revenue of shipbuilding enterprises. Assuming that the rate of return on investment to the supplier $i$ starts at $y_1$, and the investment amount increases to a fixed value $x_1$, due to an increase in the order quantity, the supplier provides a discount, and the shipbuilding enterprise’s rate of return increases, resulting in a rate of return of $y_2$. Continuing to increase to a fixed value $x_2$, the rate of return also increases $y_3$. Equation (10) can be used to represent the nonlinear relationship between the rate of return and the investment amount.

$$y=\left\{\begin{array}{l}{y}_1, x\in \left[0, x_1\right)\\ y_2, x\in \left[x_1, x_2\right)\\ y_3, x\in \left[x_2, x_3\right)\\ y_4. x\in \left[x_3, +\infty \right)\end{array}\right.$$

(10)

In order to construct the mean-risk multi-period nonlinear programming decision model and ensure the rationality and effectiveness of the model, the following assumptions are made:

• The total budget amount for each period includes not only procurement costs but also other related costs.
• The data of the $T$ historical cycles are reliable and there are no major market fluctuations. The returns and risks of this period are estimated based on the data of the $T$ historical cycles.
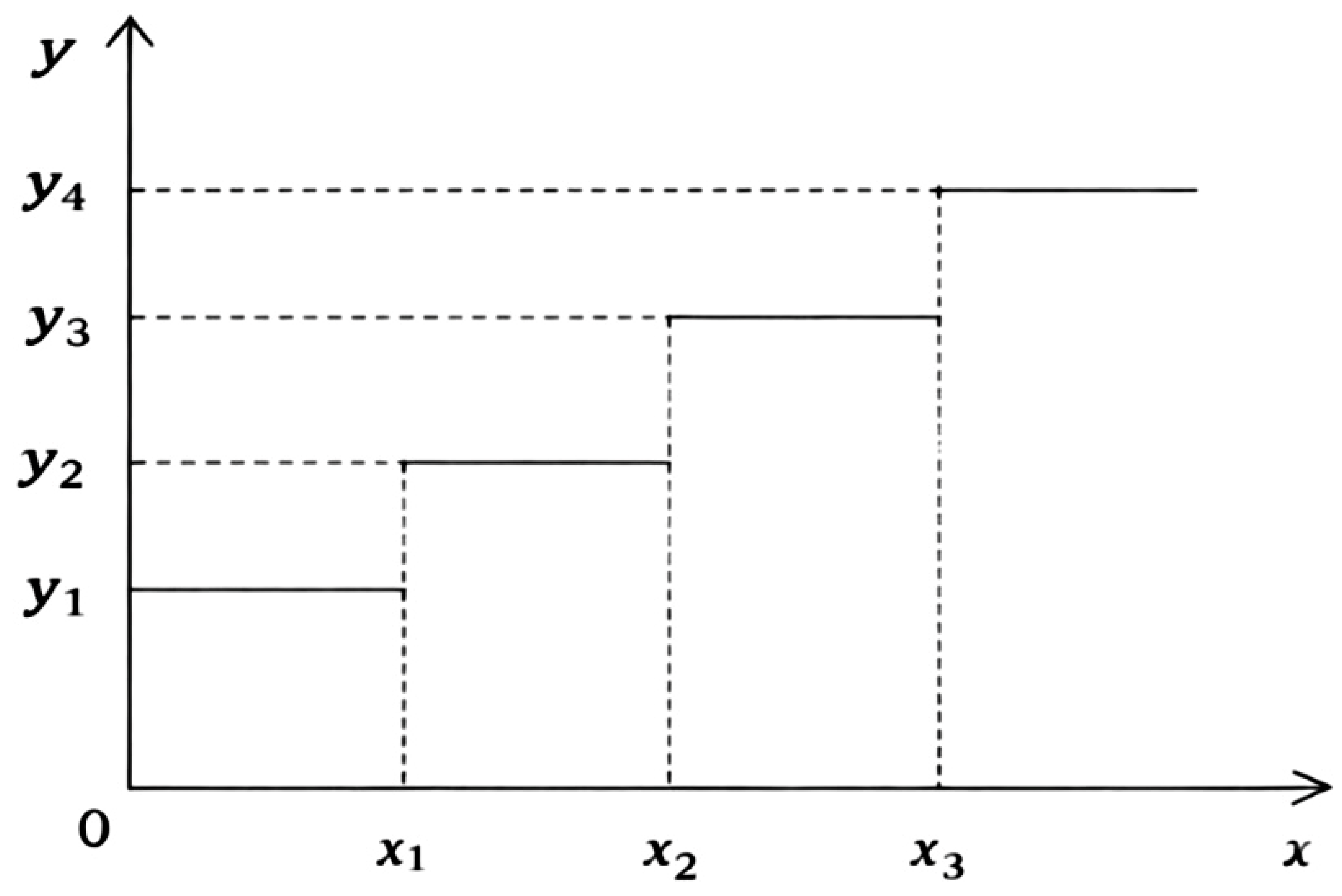
• The return on investment in each supplier is nonlinearly related to the investment amount. The higher the investment amount, the higher the rate of return, and the rate of return is always positive.
• This model considers the case of a single product and multiple cycles.
• After fitting, the historical period data of each supplier $T$ obeys a certain probability distribution of mathematical statistics.
• The investment amount allocated by the shipbuilding enterprise to the supplier is an integer.

3.4.2. Construction of a Nonlinear Decision Model

The parameters are defined as follows:

• $X$: It indicates the total budget amount invested by the shipbuilding enterprise in suppliers.
• $x_i$: Indicates the investment amount allocated to the supplier $i$.
• $e_i$: Indicate the highest investment level of the supplier $i$.
• $x_{ij}$: Indicate the investment amount of the supplier $i$ at level $j$, where $j\in \left\{1, 2, \cdots , e_i\right\}$.
• $y_{ij}$: If the investment amount of the supplier $i$ is at level $j$, it is 1; otherwise, it is 0.
• $n$: Indicates the total number of suppliers.
• $\rho$: Represents the overall expected minimum rate of return required by the shipbuilding enterprise.
• $L_i$: Indicate the minimum investment amount for the supplier $i$.
• $U_i$: Indicate the maximum investment amount for the supplier $i$.
• $L_{ij}$: The minimum investment amount of the supplier $i$ at the first level $j$.
• $U_{ij}$: The maximum investment amount of the supplier $i$ at the first level $j$.
• $R_i$: Represents the rate of return of shipbuilding enterprises’ investment in supplier $i$.
• $T$: Indicates the total number of time cycles.
• $r_{i,j,k}$: Indicates the actual rate of return of the Supplier $i$ at the $j$-th level during the $k$-th cycle.
• $r_{i,j}$: Indicate the expected return rate $R_i$ at level $j$.
• ${\sigma }_{ij}$: The covariance between the expected rates of return $r_i$ and $r_j$ for any two suppliers, i.e., ${\sigma }_{ij}=\mathrm{cov}\left(r_i,r_j\right),i,j\in \left\{1,2,\cdots n\right\}$.

Based on the above assumptions and parameter definitions, a multi-period nonlinear programming decision model for a single shipbuilding enterprise and multiple suppliers’ cooperative development is established under supply risk:

$$\mathrm{Objective} \mathrm{function}: Min Var\left({\displaystyle \sum _{i=1}^n{x}_i{R}_i}\right)$$

(11)

$$\mathrm{Constraints}: {\displaystyle \sum _{i=1}^n{x}_i=X}$$

(12)

$${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{e_i}{r}_{ij}{x}_{ij}}}\ge \rho X$$

(13)

$$L_{ij}{y}_{ij}\le x_{ij}\le U_{ij}{y}_{ij}, i\in \left\{1,2,\cdots ,n\right\},j\in \left\{e_1,e_2,\cdots ,e_n\right\}$$

(14)

$${\displaystyle \sum _{j=1}^{e_i}{y}_{ij}}=1 \forall i\in \left\{1,2,\cdots ,n\right\}$$

(15)

$$y_{ij}=\left\{\begin{array}{l}1, \mathrm{If} \mathrm{the} \mathrm{investment} \mathrm{amount} \mathrm{of} \mathrm{supplier} \mathrm{is} \mathrm{at} \mathrm{level} \\ 0. \mathrm{Other} \mathrm{situations}\end{array}\right. \forall i,j$$

(16)

$${\displaystyle \sum _{j=1}^{e_i}{x}_{ij}}=x_i \forall i\in \left\{1,2,\cdots ,n\right\}$$

(17)

$$x_{ij}=\left\{\begin{array}{l}{x}_i, \mathrm{If} \mathrm{Supplier} \mathrm{has} \mathrm{an} \mathrm{investment} \mathrm{amount} \mathrm{at} \mathrm{Level} \\ 0. \mathrm{Other} \mathrm{situations}\end{array}\right. \forall i,j$$

(18)

$$L_i\le x_i\le U_i x_i\in N, x_{ij}\in N \forall i,j$$

(19)

In order to facilitate the calculation of the objective function (11), we can obtain

$$Min Var\left({\displaystyle \sum _{i=1}^n{x}_i{R}_i}\right)={\displaystyle \frac{1}{T}}{\displaystyle \sum _{k=1}^T{\left[{\displaystyle \sum _{i=1}^n{D}_{ik}{x}_i}\right]}^2}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{k=1}^T{\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{e_i}{x}_{ij}\left(r_{ijk}-r_{ij}\right)}}\right]}^2}$$

(20)

This is proved below.

Proof. In the above formula,

$$D_{ik}={\displaystyle \sum _{j=1}^{e_i}{y}_{ij}\left(r_{ijk}-r_{ij}\right)}$$

So,

$$\begin{gathered} {\displaystyle \sum _{i=1}^n{D}_{ik}{x}_i}={\displaystyle \sum _{i=1}^n\left[{\displaystyle \sum _{j=1}^{e_i}{y}_{ij}\left(r_{ijk}-r_{ij}\right)}{\displaystyle \sum _{j=1}^{e_i}{x}_{ij}}\right]} \\ {\displaystyle \sum _{j=1}^{e_i}{y}_{ij}\left(r_{ijk}-r_{ij}\right)}{\displaystyle \sum _{j=1}^{e_i}{x}_{ij}}=\left[y_{i1}\left(r_{i1k}-r_{i1}\right)+y_{i2}\left(r_{i2k}-r_{i2}\right)+\cdots +y_{i{e}_i}\left(r_{i{e}_{i}k}-r_{i{e}_i}\right)\right]\left(x_{i1}+x_{i2}+\cdots +x_{i{e}_i}\right) \end{gathered}$$

(21)

According to Formula (15), we have

$$y_{ij}{x}_{i{j}^{\prime }}=\left\{\begin{array}{l}{x}_{i{j}^{\prime }} j=j^{\prime }\\ 0 j\ne j^{\prime } \end{array}\right.$$

(22)

So, we can obtain

$$\begin{array}{l}{\displaystyle \sum _{j=1}^{e_i}{y}_{ij}\left(r_{ijk}-r_{ij}\right)}{\displaystyle \sum _{j=1}^{e_i}{x}_{ij}}=x_{i1}\left(r_{i1k}-r_{i1}\right)+x_{i2}\left(r_{i2k}-r_{i2}\right)+\cdots +x_{i{e}_i}\left(r_{i{e}_{i}k}-r_{i{e}_i}\right)\\ ={\displaystyle \sum _{j=1}^{e_i}{x}_{ij}\left(r_{ijk}-r_{ij}\right)}\end{array}$$

(23)

Therefore, the objective Function (11) can be written as

$$Min Var\left({\displaystyle \sum _{i=1}^n{x}_i{R}_i}\right)={\displaystyle \frac{1}{T}}{\displaystyle \sum _{k=1}^T{\left[{\displaystyle \sum _{i=1}^n{D}_{ik}{x}_i}\right]}^2}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{k=1}^T{\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{e_i}{x}_{ij}\left(r_{ijk}-r_{ij}\right)}}\right]}^2}$$

(24)

□

Among them, Formula (11) represents the objective function of minimizing the risk level under a certain expected return level. Formula (12) indicates that the total investment budget of the shipbuilding enterprise is equal to the sum of the amounts invested in each supplier. Formula (13) represents the total return level expected by the shipbuilding enterprise, indicating that the overall expected return of the shipbuilding enterprise must reach the established return target level. Formula (14) represents the upper and lower limits of each supplier’s investment at different investment levels. Formula (15) indicates that the investment amount of a supplier can only belong to a certain investment level. Formula (16) represents the value range of $y_{ij}$. Formula (17) indicates that the investment amount of a supplier is equal to the sum of the investment amounts of all its investment levels. Formula (17) represents the value range of $x_{ij}$. Formula (19) represents the upper and lower limits of the supplier’s investment and the value range of the investment amount.

4. Empirical Research and Results Analysis

Both the mean-risk multi-period linear programming decision model and the nonlinear decision model can be regarded as a standard resource allocation problem. The resource allocation problem is to reasonably allocate a certain number of resources (such as machinery and equipment, funds, raw materials, manpower, etc.) to several users so that the total objective function value can reach the optimal value. The shipbuilding enterprise allocates the total budget amount to suppliers to minimize the risk value while meeting certain benefits.

This paper uses MATLAB R2021a software to solve this problem. In order to illustrate the effectiveness of the model application, a Chinese shipbuilding enterprise decides to purchase a common material for ships, for example. According to the total budget amount, it cooperates with four suppliers to optimize the investment portfolio strategy, achieve the expected benefits, and minimize the risk. Based on the survey interviews and empirical data analysis during the internship at the shipbuilding enterprise, it can be concluded that although the total exact amount of each order for the product may be difficult to obtain, it is feasible for the shipbuilding enterprise to obtain a reasonable and estimated total budget amount. The total budget amount of the model not only includes the procurement cost (the fee received by each supplier) but also includes the remaining related costs (the costs and expenses related to it consumed by the shipbuilding enterprise). The costs and expenses related to it consumed by the shipbuilding enterprise can give a reasonable budget amount. For example, the investment costs related to factors such as facilities and training can be obtained from the financial accounting system.

The investment costs (time value cost, travel cost, on-site technical support cost) related to the shipbuilding company’s employees participating in the purchase and contacting suppliers can also be calculated. The cost of related quality can be estimated based on the number of defective products, returns, and repairs in each supplier’s historical data. The delivery performance of the product can also be assessed based on the on-time delivery rate, the number of delayed deliveries, out-of-stock frequency, etc., in each supplier’s historical cycle data.

Consider a randomly generated data set with a certain probability distribution to analyze and apply the model in this paper. In this example, the shipbuilding company selected 4 suppliers for cooperative development. According to the budget, it is assumed that the total investment amount is exactly 1 million US dollars. In the past 8 historical data cycles, the yield of each supplier is available and presents a certain probability distribution. It is assumed that the yield data of each supplier follows a normal distribution after fitting. Therefore, the normal distribution of supplier S1 can be set to N(0.16, 0.02), the normal distribution of supplier S2 to N(0.21, 0.04), the normal distribution of supplier S3 to N(0.26, 0.06), and the normal distribution of supplier S4 to N(0.31, 0.10). The normal distribution N(0.16, 0.02) of supplier S1 indicates that the expected return of supplier S1 is 0.16, and the actual rate of return generated by supplier S1 in the past 8 historical data periods is fitted to a normal distribution with a mean of ${\mu }_1=0.16$ and a risk of ${\sigma }_1=0.02$, that is $S_1\sim N\left({\mu }_1, {\sigma }_1\right)$.

The normal distribution of suppliers S2, S3, and S4 is explained in the same way. The specific data of the actual and expected rates of return of the four suppliers in the past 8 historical periods are shown in

Table 2. Actual and expected returns of shipbuilding enterprises and each supplier in the historical period data.

Supplier	P1	P2	P3	P4	P5	P6	P7	P8	${\mathit{r}}_{\mathit{i}}$
S1	0.17	0.18	0.16	0.15	0.17	0.13	0.17	0.14	0.16
S2	0.22	0.24	0.25	0.16	0.20	0.17	0.19	0.22	0.21
S3	0.25	0.32	0.22	0.19	0.21	0.32	0.26	0.25	0.26
S4	0.41	0.37	0.42	0.21	0.26	0.25	0.38	0.28	0.31

, where P1 to P8 represent the actual rate of return in each period and $r_i$ represent the expected rate of return of the supplier $i$. The expected rate of return of the shipbuilding enterprise ranges from $\left[0.16, 0.28\right]$, with a historical period of 8 periods, and the maximum investment amount for each supplier shall not exceed 500,000 US dollars. Therefore, the relevant parameter data are as follows:

$$X=100, n=4, \rho \in \left[0.16, 0.28\right], L_1=L_2=L_3=L_4=0, U_1=U_2=U_3=U_4=50, T=8.$$

The calculation steps are divided into two steps. The first step is to calculate the mean-risk multi-period linear programming decision model (hereinafter referred to as the linear decision model). The second step is to calculate the mean-risk multi-period nonlinear programming decision model (hereinafter referred to as the nonlinear decision model) and then compare and analyze the solution results of the nonlinear decision model and the linear decision model.

Based on the Grey Wolf algorithm and validated using the branch and bound method [29,30], the computational results of the linear decision-making model are presented in Figure 2, solved with MATLAB software.

The nonlinear decision model is solved below. The parameters related to the nonlinear decision model are the same as those related to the linear decision model. The nonlinear return is related to the allocation amount of each supplier. The investment amount is set to three levels: if the investment amount is at the first level, the expected rate of return and the actual rate of return remain unchanged; if the investment amount is at the second level, the expected rate of return and the actual rate of return are both multiplied by 1.1; if the investment amount is at the third level, the expected rate of return and the actual rate of return are both multiplied by 1.2. The specific multiples of investment amount level, investment range, and return multiplication are shown in

Table 3. Correspondence between the investment amount and investment amount level.

Investment Amount (Unit: Ten Thousand US Dollars)	Investment Amount Level	Multiple Rates of Return
0–19	1	1.0
20–39	2	1.1
40–50	3	1.2

. The calculation results of the nonlinear model are shown in Figure 3.

After calculation, when the rate of return is $\rho =0.18$, the allocation amount of the linear decision model is S1 = 50, S2 = 29, S3 = 21, S4 = 0, and the risk level value is 3.0225. When the rate of return is $\rho =0.18$, the allocation amount of the nonlinear decision model is shown in

Table 4. Fund allocation of nonlinear investment ($\rho =0.18$).

Supplier	Investment Amount	Investment Amount Level
S1	50	3
S2	31	2
S3	19	1
S4	0	1

, and it can be obtained that S1 = 50, S2 = 31, S3 = 19, and S4 = 0. According to Table 3, since the investment allocation amount of S1 is in the third investment amount level, the corresponding S1 expected return and actual return should be calculated by multiplying 1.2 times based on Table 2, and since the investment allocation amount of S2 is in the second investment amount level, the corresponding S2 expected return and actual return should be calculated by multiplying 1.1 times based on Table 2.

After the calculation, the risk level value is 3.7364. At that time $\rho =0.20$, after calculation, the risk level value calculated by the linear decision model was 3.2221, and the risk level value calculated by the nonlinear decision model was 3.7363. At that time $\rho =0.21$, after calculation, the risk level value calculated by the linear decision model was 4.1694, and the risk level value calculated by the nonlinear decision model was 3.7363. At that time $\rho =0.22$, after calculation, the risk level value calculated by the linear decision model was 5.3569, and the risk level value calculated by the nonlinear decision model was 3.8692. The risk level values calculated by the linear decision model and the nonlinear decision model for the shipbuilding enterprise yield $\rho$ from 0.23 to 0.27 are shown in

Table 5. Comparison of risk values between the linear decision model and nonlinear decision model.

Yield	Linear Model Value at Risk	Nonlinear Model Value at Risk	Risk Reduction Percentage
0.16–0.19	3.0225	3.7364 (−0.7139)
0.20	3.2221	3.7363 (−0.5142)
0.21	4.1694	3.7363 (0.4331)	10.39%
0.22	5.3569	3.8692 (1.4877)	22.77%
0.23	6.7660	4.3163 (2.4497)	36.20%
0.24	8.3956	5.5237 (2.8719)	34.21%
0.25	10.2778	6.7284 (3.5494)	34.53%
0.26	12.7578	7.7543 (5.0035)	39.22%
0.27	15.9403	9.4019 (6.8384)	42.90%

Note: The values in brackets are the risk values of nonlinearity reduced relative to linearity.

. As can be seen from Table 5, when the yield increases from 0.16 to 0.20, the risk level value of the linear decision model is smaller than the risk level value of the nonlinear decision model.

However, when the yield increases from 0.21 to 0.27, at the same yield level, the risk level value of the linear decision model is greater than the risk level value of the nonlinear decision model, and the higher the yield, the more obvious the difference in risk level value. Therefore, when the yield is high, at the same yield level, the risk value calculated by the nonlinear decision model is smaller than that of the linear decision model. The specific risk value comparison is shown in Table 5, which illustrates the practicality and effectiveness of the nonlinear decision model.

Figure 2 shows the return and investment of the linear decision model, and Figure 3 shows the return and investment of the nonlinear decision model. Figure 2 and Figure 3 show the investment allocation of four suppliers at different expected returns $\rho$, where the upper limit of investment for each supplier is fifty thousand dollars. According to Figure 2, in the linear decision model, when the value $\rho$ is low, the shipbuilding enterprise should consider allocating more funds to suppliers S1 and S2 and investing less in suppliers S3 and S4. However, as the value $\rho$ increases, the shipbuilding enterprise should consider investing more in suppliers S3 and S4, and less in suppliers S1 and S2. The meaning of cooperative risk management for shipbuilding enterprises is that when a higher overall expected return is difficult to achieve or not feasible, the shipbuilding enterprise can reduce the expected return or adjust the investment allocation according to the analysis of Figure 2. According to Figure 3, in the nonlinear decision model, the investment returns have a similar trend to the returns in Figure 2, but the performance $\rho$ is different.

For example, in the linear return, when $\rho \in \left[0.16, 0.19\right]$, the allocation amount of the investment supplier remains unchanged; in the nonlinear return, when $\rho \in \left[0.16, 0.21\right]$, the allocation amount of the investment supplier remains unchanged. In the case of linear returns, at that time, the investment allocation amount of supplier S1 $\rho \ge 0.25$ is 0; while in the case of nonlinear returns, at that time $\rho \ge 0.28$, the investment allocation amount of supplier S1 is 0. According to Figure 3, the risk value of S2 first decreases, then increases, and then decreases, while the risk value of S3 first increases, then decreases, and then increases. The investment allocation amounts of S2 and S3 fluctuate, indicating that under the condition that the return is met, S4 with a higher risk is not given priority; and adjustments are made from S2 and S3 first, which not only meets the expected rate of return but also meets the minimum risk value. This means that under the condition of high overall expected returns $\rho$, the risk value of nonlinear returns is smaller than that of linear returns, which is completely consistent with the calculation results in Table 5.

5. Conclusions

The shipbuilding supply chain is a multi-level complex network, so the relationships between supply chain members are crucial for collaborative risk management. Based on scientific analysis of the connotation of cooperative risks in the shipbuilding supply chain, this article improves Markowitz’s mean risk model for cooperative development between shipbuilding enterprises and suppliers under supply risk and applies it to the cooperative development of shipbuilding enterprises’ suppliers. A mean risk multi-period linear programming decision model and a nonlinear programming decision model for shipbuilding enterprises and suppliers are established to address supply risk. The risk research of shipbuilding enterprises is mostly conducted from a qualitative perspective, and even if a small number of scholars conduct quantitative research, they assume that the investment amount of suppliers is linearly related to expected returns. However, in reality, it does not conform to the objective situation. Based on this, this article constructs a nonlinear relationship model between expected returns and investment amount, applies it to a shipbuilding enterprise, and compares the results with linear decision models. The calculation results indicate that the nonlinear decision model can reduce risk at the same level of return.

The issue of cooperation risks in shipbuilding enterprises is a dynamic process, and risks can change over time rather than remain constant. Therefore, shipbuilding enterprises should regularly organize safety experts, senior management personnel, or team leaders to conduct risk monitoring and control.

Research Prospects

While this study provides a quantitative framework for managing cooperative risk, several avenues for future research remain unexplored. These include the following: First, the reasonable and scientific calculation method for the total budget, which includes associated costs beyond pure procurement, requires further demonstration and refinement. Second, the nonlinear scenarios considered in this model are relatively singular; subsequent research could extend to more complex nonlinear relationships and stochastic parameters. Finally, integrating dynamic risk assessment that updates over time with real-time supply chain data could enhance the model’s responsiveness and practical utility in managing the evolving risk landscape of shipbuilding projects.