Type-2 Backstepping T-S Fuzzy Control Based on Niche Situation

Abstract

The niche situation can reflect the advantages and disadvantages of biological individuals in the ecosystem environment as well as the overall operational status of the ecosystem. However, higher-order niche systems generally exhibit complex nonlinearities and parameter uncertainties, making it difficult for traditional Type-1 fuzzy control to accurately handle their inherent fuzziness and environmental disturbances in complex environments. To address this, this paper introduces the backstepping control method based on Type-2 T-S fuzzy control, incorporating the niche situation function as the consequent of the T-S backstepping fuzzy control. The stability analysis of the system is completed by constructing a Lyapunov function, and the adaptive law for the parameters of the niche situation function is derived. This design reflects the tendency of biological individuals to always develop in a direction beneficial to themselves, highlighting the bio-inspired intelligent characteristics of the proposed method. The results of case simulations show that the Type-2 backstepping T-S fuzzy control has significantly superior comprehensive performance in dealing with the complexity and uncertainty of high-order niche situation systems compared with the traditional Type-1 control and Type-2 T-S adaptive fuzzy control. These results not only verify the adaptive and self-development capabilities of biological individuals, as well as their efficiency in environmental utilization, but also endow this control method with a solid practical foundation.

1. Introduction

The niche, as a core concept in ecology, provides crucial guidance for ecological management and conservation. Within ecosystems, the survival and development of biological organisms are intimately tied to their niche status. This status not only intuitively reflects the adaptive advantages or disadvantages of individuals in their environment but also serves as a key indicator for assessing the overall health and dynamics of the ecosystem [1]. With the continuous process of biological evolution, higher-order niche systems have increasingly demonstrated complex nonlinear characteristics and significant uncertainties. This dual complexity renders conventional linear or simple nonlinear modeling methods inadequate to accurately describe and effectively control such systems. While Type-1 fuzzy control can handle certain types of imprecise information, its reliance on fixed and precise membership functions limits its ability to capture the inherent fuzziness and uncertainty in niche perception and environmental disturbances. As a result, it falls short of meeting the precision required for dynamic ecosystem regulation.

Li et al. pioneered a fuzzy control method based on niche modeling [2,3]. By integrating the “state” and “potential” theory of niches into the T-S fuzzy framework, they replaced the traditional linear or constant consequent parts in fuzzy rules with niche-based variables. This innovation allowed the fuzzy rules to directly embody the adaptive principle that “biological organisms always develop in a self-beneficial direction” [4]. However, as this method was built on Type-1 fuzzy sets, its predetermined membership functions could not fully represent the dual complex characteristics of niche systems.

In contrast, Type-2 fuzzy sets extend the capabilities of Type-1 fuzzy sets by handling uncertainties in membership degrees themselves, which significantly broadens their application range and enhances robustness against disturbances and uncertainties. The use of interval Type-2 fuzzy sets for fuzzifying inputs or outputs can also reduce computational complexity, improving practicality for real-time control [5,6]. The experimental results in [7] demonstrated that interval Type-2 T-S fuzzy models achieve an accuracy improvement of over 30% compared to Type-1 models when fitting uncertain parameters. Studies [8,9] further confirmed the superior performance of interval Type-2 fuzzy models in managing complex systems and uncertainties. Additionally, the study in [10] combined evolutionary and adaptive biological characteristics with direct Type-2 T-S fuzzy control to develop a bio-inspired control strategy. Comparative simulations revealed that Type-2 controllers outperform Type-1 in stability and convergence. Nevertheless, existing Type-2 fuzzy methods predominantly address “single uncertainty” and remain insufficiently optimized for the “high-order nonlinearity” of niche systems. As system order increases beyond two, control errors accumulate and convergence time lengthens [5,6,7].

The backstepping control method, proposed by Krstic [11] in 1995, is a nonlinear control approach that eliminates the traditional requirement for nonlinear functions to satisfy “matching conditions”. When systems exhibit complexities such as parametric uncertainties, unknown nonlinearities, and structural uncertainties, the adaptive fuzzy backstepping control method effectively addresses these challenges: fuzzy systems approximate unknown nonlinear functions, ensuring the system output asymptotically and stably tracks the desired reference signal while maintaining uniform boundedness of all closed-loop signals, thereby significantly enhancing robustness and stability [12,13]. In addition to handling general nonlinearities, the backstepping control method has also been successfully applied in other fields requiring high-precision control; for example, reference [14] applied this method to high-order trajectory tracking in quadrotor unmanned aerial vehicles (UAVs), reducing convergence time by 40%; the authors of [15] developed a nonlinear strategy for pneumatic manipulators by integrating an adaptive extended state observer (AESO) with a backstepping integral sliding mode controller (BISMC), validating its effectiveness and superiority through comparative experiments. The authors of [16] designed a novel fast fixed-time backstepping method that further improves convergence speed and system stability. However, these methods have not been integrated with the “state-potential” characteristics of ecological niches and thus fail to reflect the biological principle of “development toward beneficial conditions”.

In recent years, many scholars have integrated the backstepping control into Type-2 fuzzy systems for research. In [17], the authors incorporated backstepping into a Type-2 T-S fuzzy control framework. They employed an exponential symmetric function composed of ecological factors as the consequent part of the backstepping controller. This integration of “ecological factor + control method” provides a design reference for using niche state-potential functions as consequents in fuzzy rules. For uncertain discrete nonlinear systems, Boukhalfa and Khettab [18] proposed a hybrid backstepping Type-2 fuzzy adaptive control (HBT2AC) scheme, and they designed an adaptive Type-2 fuzzy controller that uses a derived weighted simplified least squares (WSLS) estimator to approximate unmeasurable states and adjustable parameters. The study in [19] combined backstepping with artificial intelligence (Type-1 and Type-2 fuzzy logic) in wind energy conversion systems, achieving high-precision power control and demonstrating the complementary advantages of “Type-2 handling uncertainty + backstepping handling nonlinearity”. For SISO nonlinear systems with unmeasurable states, Chouelkn and Kermani [20] proposed fuzzy adaptive backstepping control (FABC) and fuzzy adaptive backstepping sliding mode control (FABSMC), with comparative analysis of these adaptive schemes providing valuable insights for optimizing Type-2 fuzzy and backstepping control.

To further reduce system errors and enhance stability and anti-interference capabilities, researchers have in recent years explored the integration of intelligent optimization algorithms with fuzzy control. The study in [21] proposed an improved variable-step MPPT method based on the grey wolf optimizer (GWO) and whale optimization algorithm (WOA), which was combined with a PID controller in photovoltaic systems, effectively optimizing output power. The study in [22] introduced the grey wolf optimizer (GWO) into the direct torque control of double-star induction motors, improving control accuracy and dynamic response speed. The study in [23] confirmed through comparative validation that the variable-step MPPT algorithm optimized by GWO and WOA significantly enhances the power tracking efficiency and stability of photovoltaic systems. These research results on intelligent optimization algorithms not only provide novel tools for improving the control performance of complex nonlinear systems but also offer new insights for algorithm optimization and performance improvement, supporting subsequent studies—including the integration of Type-2 T-S backstepping fuzzy control with niche state-potential properties as proposed in this paper.

Therefore, building on Type-2 T–S fuzzy control, this paper introduces the backstepping control method, adopts the niche state-potential function as the consequent of the backstepping fuzzy controller, derives adaptive laws for the ecological factors within the function, and performs stability analysis using Lyapunov theory.

The main innovations of this paper are as follows: (1) To address the high-order complex nonlinearity and parametric uncertainties exhibited by evolved high-order niche systems, this study overcomes the limitations of Type-1 T–S fuzzy control and proposes a composite control method that integrates Type-2 T–S fuzzy control with backstepping control. This approach leverages both the ability of Type-2 fuzzy systems to handle membership function uncertainties and the layered design advantages of backstepping control for nonlinear systems, enabling effective regulation of high-order complex nonlinear systems. (2) The niche state-potential function is adopted as the consequent part of the T–S backstepping fuzzy controller, replacing traditional linear or constant output forms. This establishes a direct relationship between the control rules and the “state-potential” characteristics of the ecosystem. Meanwhile, the stability of the system is analyzed via the construction of a Lyapunov function, and adaptive laws for the parameters of the niche state-potential function are derived, ensuring asymptotic stability of the system. (3) The derived adaptive laws for the niche state-potential function parameters embody the ecological principle of “self-beneficial development”, highlighting the bio-inspired intelligent nature of the proposed method. (4) Multi-dimensional comparative verification is conducted through case simulations to confirm the effectiveness of the proposed composite control method: On one hand, by comparing the Type-2 and Type-1 backstepping control methods, it is quantitatively concluded that the Type-2 control shortens the convergence time by approximately 13.3% and reduces the dynamic error by about 40%, which verifies the advantages of the composite method in stability and convergence. On the other hand, through the comparison of reference signal tracking and the verification of anti-interference performance between the Type-2 backstepping control (the proposed method) and the Type-2 T-S adaptive fuzzy control, the comprehensive performance advantages of the proposed method in complex scenarios are further highlighted. At the same time, combined with all simulation results, the adaptive and self-development capabilities of biological individuals as well as their efficiency in environmental utilization are verified, endowing this control method with a more solid practical physical background.

The paper is organized as follows: Section 2 introduces the theory and inference mechanism of Type-2 bio-inspired fuzzy systems and presents the structure and design algorithm of Type-2 backstepping T–S control. Section 3 describes the design of the Type-2 backstepping T-S fuzzy controller for niche state-potential and the corresponding adaptive laws. Section 4 validates the effectiveness of the method through numerical simulations. Section 5 summarizes the research conclusions.

2. System Description and Type-2 Fuzzy Modeling

For clarity, the main mathematical notations and definitions used in this paper are summarized in

Table A2. Symbol table (aligned with article sections).

Symbol	Definition	Description
$s_k^i,$$p_k^i$	The k-th “state/potential” component of niche in the i-th rule	In the fuzzy rule definition in Section 2.1, they describe, respectively, the niche state and development potential in one dimension under a single rule.
$C$	Dimension coordination factor	In the fuzzy rule output formula section of Section 2.1, the dimensions of $s_k^i$ and $p_k^i$ are coordinated to enable addition.
$x={\left[x_1,x_2,\dots ,x_n\right]}^T$	System state vector	At the beginning of the system model in Section 2, the set of measurable state variables of the system is represented.
$f_i\left(X_i\right),g_i\left(X_i\right)$	Bounded unknown nonlinear functions/Control gain functions	Equation (1): $f_i\left(X_i\right)$ describes the intrinsic nonlinear dynamics of the systems; $g_i\left(X_i\right)$ characterizes the influence intensity of the control input $u$ on the state $x_i$.
${\upsilon }_i,{\upsilon }_i^{\ast }$	The i-th virtual controller/its ideal form	Section 3: ${\upsilon }_i$ is the actual intermediate control variable in the hierarchical backstepping design; ${\upsilon }_i^{\ast }$ is the ideal form designed based on known nonlinearities, used for stability analysis derivation.
${\dot{e}}_i$	The derivative of the tracking error $e_i$	Used to analyze the dynamic change process of the error and is an important part in deriving the system stability conditions.
$s_{gijl},s_{gijr},s_{fijl},s_{fijr}$	Parameters of niche situation function	These are parameters related to the ”state” of the niche, updated in the consequent part of fuzzy rules to reflect the bionic development characteristics of biological individuals.
$p_{gijl},p_{gijr},p_{fijl},p_{fijr}$	Parameters of niche situation function	These are parameters related to the ”potential” of the niche, used to quantify the dynamic potential of biological individuals in utilizing niche resources.
${\mathrm{\Omega }}_f,{\mathrm{\Omega }}_g,{\mathrm{\Omega }}_X,{\mathrm{\Omega }}_{\overline{X}}$	The bounded compact set number	Define the value range of parameters and state variables to prevent parameter overrun during updates.
${\mathsf{{\rm Y}}}_{fijl},{\mathsf{{\rm Y}}}_{fijr},{\mathsf{{\rm Y}}}_{gijl},{\mathsf{{\rm Y}}}_{gijr}$	Given positive real numbers	Used to constrain parameter ranges and adjust gains in fuzzy systems or adaptive laws.
${\theta }_{fijl},{\theta }_{fijr},{\theta }_{gijl},{\theta }_{gijr}$  ${\xi }_{fijl},{\xi }_{fijr},{\xi }_{gijl},{\xi }_{gijr}$	Type-2 T-S fuzzy system parameters (unified indexing)	Section 3: Used to approximate unknown nonlinear functions in the system. Indexing Rule: Type(f/g)-Step(i)-Sequence(j)-Endpoint(l/r). For example, ${\theta }_{f11l}$ represents the left endpoint parameter for the f function, Step 1, Parameter Set 1.
${\theta }_{fl}^{\ast },{\theta }_{fr}^{\ast },{\theta }_{gr}^{\ast },{\theta }_{gl}^{\ast }$	The optimal parameters	Ideal parameter standard in the adaptive law, used to reduce approximation errors of the system and improve control accuracy.
${\xi }_{fi}^T\left(X_i\right){\theta }_{fi},{\xi }_{gi}^T\left(X_i\right){\theta }_{gi}$	Type-2 T-S fuzzy logic systems	Used to approximate unknown nonlinear function in the system, supporting controller design and stability analysis

of the Appendix A.

Consider the following form of an n-th order SISO nonlinear system:

$$\left\{\begin{array}{l}{\dot{x}}_i=f_i\left(X_i\right)+g_i\left(X_i\right)x_{i+1},1\le i\le n-1\\ {\dot{x}}_n=f_n\left(X_i\right)+g_n\left(X_i\right)u,n\ge 2\\ y=x_1\end{array}\right.$$

(1)

where $X={\left(x_1,\dots ,x_n\right)}^T={\left(x,\dots ,x^{\left(\mathrm{n}-1\right)}\right)}^T\in R^n$ is the measurable state vector; $f\left(X\right)$ and $g\left(X\right)$ are unknown continuously nonlinear functions; $u\in R$ is the continuously differentiable control input; and $y\in R$ is the output of the system.

To ensure the stability of the control system, this paper introduces the following assumption:

Assumption 1. 

The control gain function $g_n\left(X\right)$ is strictly positive, and there exist known positive constants $g_{\min }$ and $g_{\max }$ such that 0 < $g_{\min }\le g_n\left(X\right)\le g_{\max }$ holds for all state vectors $X\in R^n$.

2.1. Rules for a Type-2 Bionic Fuzzy Inference System

When modeling $u(X)$ in system (1), the niches are represented by the variable $x_1,x_2,\dots ,x_n$, with the niche fuzzy sets serving as the antecedent of the fuzzy rules and the overall “state and potential” serving as the consequent of the fuzzy rules. The following fuzzy rules are established:

$$R_u^i: \mathrm{If} x_1\mathrm{is} A_1\mathrm{and} x_2\mathrm{is} A_2\mathrm{and} ... \mathrm{and} x_n\mathrm{is} A_n, \mathrm{then} {\widehat{u}}_i=N^i,i=1,2,\dots ,M.$$

(2)

Among them, $R^i$ denotes the i-th fuzzy rule; $A_k$ is the Type-2 ecological niche fuzzy set of the k-th individual organism; ${\widehat{u}}^i$ is the output of the i-th rule; $N^i$ is determined by the “state” and “potential” of the niche of the biological individual, representing the total ”state and potential” of the biological individual.

Here, we define $N^i={\displaystyle \sum _{k=1}^n{s}_k^i}+C{\displaystyle \sum _{k=1}^n{p}_k^i}$, $k=1,2,\dots ,n.$ Among them, $s_k^i$ represents the component of the k-th “state” in the i-th rule, $p_k^i$ represents the component of k-th “potential” in the i-th rule, and $C$ is a dimension coordination factor that coordinates the dimensions of the two to achieve additivity.

2.2. Bionic Fuzzy Inference System

The steps to build a Type-2 fuzzy system are as follows:

$${\mu }_{\tilde{X}\circ {\tilde{A}}_1^i\times {\tilde{A}}_2^i\times \cdot \cdot \cdot \times {\tilde{A}}_n^i}\left(X\right)=\left[{\displaystyle \underset{x_1\in {\tilde{x}}_1}{\cap }{\mu }_{{\tilde{x}}_1}\left(x_1\right)}\cap {\mu }_{{\tilde{A}}_1^i}\left(x_1\right)\right]\cap \cdot \cdot \cdot \cap \left[{\displaystyle \underset{x_n\in {\tilde{x}}_n}{\cap }{\mu }_{{\tilde{x}}_n}}\left(x_n\right)\cap {\mu }_{{\tilde{A}}_n^i}\left(x_n\right)\right]$$

(3)

Using single-point fuzzification for the system input $x$, Equation (3) can be changed into

$${\mu }_{\tilde{X}\circ {\tilde{A}}_1^i\times {\tilde{A}}_2^i\times \cdot \cdot \cdot \times {\tilde{A}}_n^i}\left(X\right)={\mu }_{{\tilde{A}}_1^i\times {\tilde{A}}_2^i\times \cdot \cdot \cdot \times {\tilde{A}}_n^i}\left(X\right)={\displaystyle \underset{x_1\in {\tilde{x}}_1}{\cap }{\mu }_{{\tilde{A}}_1^i}\left(x_1\right)}\cap \cdot \cdot \cdot \cap {\mu }_{{\tilde{A}}_n^i}\left(x_n\right)={\displaystyle \underset{k=1}{\overset{n}{\cap }}{\mu }_{{\tilde{A}}_k^i}}\left(x_k\right)$$

(4)

The output Type-2 fuzzy sets can be represented by $U$, where $i=1,2,\dots ,M,$ using the center-of-sets reducer, it can be expressed as:

$$U_D\left({\tilde{U}}^1,\dots ,{\tilde{U}}^M\right)={\displaystyle \underset{w_u^1}{\int }\cdot \cdot \cdot {\displaystyle \underset{w_u^M}{\int }{\tau }_{i=1}^M{\mu }_{{\tilde{U}}^i}}}\left({\tilde{w}}_u^i\right)/{\displaystyle \frac{{\displaystyle \sum _{i=1}^M{w}_u^i{\widehat{u}}^i\left(X\right)}}{{\displaystyle \sum _{i=1}^M{w}_u^i}}}$$

(5)

Using the Type-2 affiliation function to $A_k^i$, Equation (5) can be transformed into

$$\widehat{U}\left({\tilde{W}}_u^1,\dots ,{\tilde{W}}_u^M\right)={\displaystyle \underset{w_u^1}{\int }\cdot \cdot \cdot {\displaystyle \underset{w_u^M}{\int }1}}/{\displaystyle \frac{{\displaystyle \sum _{i=1}^M{w}_u^i{\widehat{u}}^i\left(X\right)}}{{\displaystyle \sum _{i=1}^M{w}_u^i}}}$$

(6)

where $\widehat{U}=\left[{\widehat{u}}_1,{\widehat{u}}_2\right]$, $w_u^i\in {\tilde{W}}_u^i=\left[{\underset{¯}{w}}_u^i,{\overline{w}}_u^i\right]$.

To obtain the crisp value of the type-reduced interval, this paper employs the KM iteration method [24] to calculate the left and right endpoints, $u_l$ and $u_r$, respectively. The specific calculation process is as follows:

$$\begin{gathered} u_l={\displaystyle \frac{{\displaystyle \sum _{i=1}^L{\overline{w}}_u^i{\widehat{u}}^i+{\displaystyle \sum _{j=L+1}^M{\underset{¯}{w}}_u^i{\widehat{u}}^j}}}{{\displaystyle \sum _{i=1}^L{\overline{w}}_u^i{\widehat{u}}^i+{\displaystyle \sum _{j=L+1}^M{\underset{¯}{w}}_u^i}}}}={\displaystyle \sum _{\mathrm{i}=1}^L{q}_l^i}{\widehat{u}}^i+{\displaystyle \sum _{j=L+1}^M{q}_l^j}{\widehat{u}}^j={\displaystyle \sum _{\mathrm{i}=1}^L{q}_l^i}\left({\theta }_{1l}^i+C{\theta }_{2l}^i\right)+{\displaystyle \sum _{j=L+1}^M{q}_l^j}\left({\theta }_{1l}^j+C{\theta }_{2l}^j\right) \\ {u}_r={\displaystyle \frac{{\displaystyle \sum _{i=1}^R{\underset{¯}{w}}_u^i{\widehat{u}}^i+{\displaystyle \sum _{j=R+1}^M{\overline{w}}_u^j{\widehat{u}}^j}}}{{\displaystyle \sum _{i=1}^R{\underset{¯}{w}}_u^i+{\displaystyle \sum _{j=R+1}^M{\overline{w}}_u^j}}}}={\displaystyle \sum _{\mathrm{i}=1}^R{q}_r^i}{\widehat{u}}^i+{\displaystyle \sum _{j=R+1}^M{q}_r^j}{\widehat{u}}^j={\displaystyle \sum _{\mathrm{i}=1}^R{q}_r^i}\left({\theta }_{1r}^i+C{\theta }_{2r}^i\right)+{\displaystyle \sum _{j=R+1}^M{q}_r^j}\left({\theta }_{1r}^j+C{\theta }_{2r}^j\right) \\ =\left(\begin{array}{cc}{\overline{Q}}_r& {\underset{¯}{Q}}_r\end{array}\right)\left[\left(\begin{array}{c}{\overline{\theta }}_{1r}\\ {\underset{¯}{\theta }}_{1r}\end{array}\right)+C\left(\begin{array}{c}{\overline{\theta }}_{2r}\\ {\underset{¯}{\theta }}_{2r}\end{array}\right)\right]={\xi }_r\left({\theta }_{1r}+C{\theta }_{2r}\right) \end{gathered}$$

(7)

Assumption 2. 

In order to adjust the parameters in the fuzzy logic system, the optimal parameters ${\theta }_{fl}^{\ast }$, ${\theta }_{fr}^{\ast }$, ${\theta }_{gr}^{\ast }$ and ${\theta }_{gl}^{\ast }$ are defined as follows:

$$\begin{array}{c}{\theta }_{fl}^{\ast }=arg\underset{{\theta }_{fl}\in {\mathrm{\Omega }}_f}{min}\left[\underset{X_i\in {\mathrm{\Omega }}_X,{\overline{X}}_i\in {\mathrm{\Omega }}_{\overline{X}}}{sup}\left|{\widehat{f}}_l\left({\displaystyle \frac{{\overline{X}}_i}{{\theta }_{fl}}}\right)-f\left(X_i\right)\right|\right]\\ {\theta }_{fr}^{\ast }=arg\underset{{\theta }_{fr}\in {\mathrm{\Omega }}_f}{min}\left[\underset{X_i\in {\mathrm{\Omega }}_X,{\overline{X}}_i\in {\mathrm{\Omega }}_{\overline{X}}}{sup}\left|{\widehat{f}}_r\left({\displaystyle \frac{{\overline{X}}_i}{{\theta }_{fr}}}\right)-f\left(X_i\right)\right|\right]\\ {\theta }_{gl}^{\ast }=arg\underset{{\theta }_{gl}\in {\mathrm{\Omega }}_f}{min}\left[\underset{X_i\in {\mathrm{\Omega }}_X,{\overline{X}}_i\in {\mathrm{\Omega }}_{\overline{X}}}{sup}\left|{\widehat{g}}_l\left({\displaystyle \frac{{\overline{X}}_i}{{\theta }_{gl}}}\right)-g\left(X_i\right)\right|\right]\\ {\theta }_{gr}^{\ast }=arg\underset{{\theta }_{gr}\in {\mathrm{\Omega }}_g}{min}\left[\underset{X_i\in {\mathrm{\Omega }}_X,{\overline{X}}_i\in {\mathrm{\Omega }}_{\overline{X}}}{sup}\left|{\widehat{g}}_r\left({\displaystyle \frac{{\overline{X}}_i}{{\theta }_{gr}}}\right)-g\left(X_i\right)\right|\right]\end{array}$$

(8)

Here, ${\mathrm{\Omega }}_f$, ${\mathrm{\Omega }}_g$, ${\mathrm{\Omega }}_X$, and ${\mathrm{\Omega }}_{\overline{X}}$ are at the boundary compact sets. ${\theta }_{fl}^{\ast }$, ${\theta }_{fr}^{\ast }$, ${\theta }_{gr}^{\ast }$, ${\theta }_{gl}^{\ast }$, $X_i$, and ${\overline{X}}_i$ are defined as:

$$\begin{array}{c}{\mathrm{\Omega }}_f=\left\{{\theta }_{fl}^i,{\theta }_{fr}^i:‖{\theta }_{fl}^i‖\le M_f,‖{\theta }_{fr}^i‖\le M_f\right\},\\ {\mathrm{\Omega }}_g=\left\{{\theta }_{gl}^i,{\theta }_{gr}^i:‖{\theta }_{gl}^i‖\le M_g,‖{\theta }_{gr}^i‖\le M_g\right\}\\ {\mathrm{\Omega }}_X=\left\{X_i:‖X_i‖\le M_X\right\}, {\mathrm{\Omega }}_{\overline{X}}=\left\{{\overline{X}}_i:‖{\overline{X}}_i‖\le M_{\overline{X}}\right\}\end{array}$$

Here, $M_f$, $M_{\mathrm{g}}$, $M_{\mathrm{D}}$, $M_{\mathrm{X}}$, and $M_{\overline{\mathrm{X}}}$ are all positive constants.

3. Design Type-2 Controller with Backstepping

The following is the specific design process and proof:

Step 1: Define the system tracking error:

$$e_1=x_1-y_1$$

(9)

where $y_1={\left(y_{1l},y_{1r}\right)}^T$.

With the derivation of Equation (9) with respect to time, we obtain ${\dot{e}}_1={\dot{x}}_1-{\dot{y}}_1$.

Substitute ${\dot{x}}_1=f_1\left(X_1\right)+g_1\left(X_1\right)x_2$ (from Equation (1) when $i=1$) into the above formula ${\dot{e}}_1=f_1\left(X_1\right)+g_1(X_1)x_2-{\dot{y}}_1$.

To facilitate the design of the virtual controller, rearrange the terms by factoring out $g_1\left(X_1\right)$ (using $g_1\left(X_1\right)$ > $0$ from Assumption 1, the sign of $g_1\left(X_1\right)$ remains unchanged during rearrangement):

$${\dot{e}}_1=g_1\left(X_1\right)\left({\displaystyle \frac{1}{g_1\left(X_1\right)}}{f}_1\left(X_1\right)+x_2-{\displaystyle \frac{1}{g_1\left(X_1\right)}}{\dot{y}}_1\right)$$

(10)

To stabilize the error $e_1$, we treat $x_2$ as a virtual controller and define its ideal form as:

$${\upsilon }_1^{\ast }=-k_1{e}_1-{\displaystyle \frac{1}{g_1\left(X_1\right)}}\left(f_1\left(X_1\right)-{\dot{y}}_1\right)$$

(11)

where $k_1$ is a normal number.

Substitute $x_2={\upsilon }_1^{\ast }$ into Equation (10), and Equation (10) becomes ${\dot{e}}_1=g_1\left(X_1\right)\left(-k_1{e}_1\right),$ since $g_1\left(X_1\right)$ > $0$ (Assumption 1) and $k_1$ > $0$, the error derivative ${\dot{e}}_1$ satisfies the convergence trend: when $e_1$ > $0$, ${\dot{e}}_1$ < $0$; when $e_1$ < $0$, ${\dot{e}}_1$ > $0$.

Because $f_1\left(X_1\right)$ is an unknown function, the $g_1\left(X_1\right)$ function, although bounded, is also an unknown and imprecise function, making it difficult to obtain an ideal controller. To solve this problem, Type-2 T-S fuzzy logic systems ${\xi }_{f1}{\theta }_{f1}$ and ${\xi }_{g1}{\theta }_{g1}$ can be used to approximate the unknown function $-{\displaystyle \frac{1}{g_1\left(X_1\right)}}\left(f_1\left(X_1\right)-{\dot{y}}_1\right)$, obtaining

$${\upsilon }_1^{\ast }=-k_1{e}_1-{\xi }_{f1}{\theta }_{f1}-{\xi }_{g1}{\theta }_{g1}-{\omega }_{f1}-{\omega }_{g1},$$

Let ${\omega }_{f1}+{\omega }_{g1}={\omega }_1$, then we have

$$\begin{array}{c}{\upsilon }_1^{\ast }=-k_1{e}_1-{\xi }_{f1}{\theta }_{f1}-{\xi }_{g1}{\theta }_{g1}-{\omega }_1\\ {\xi }_{f1}={\left[{\xi }_{f11},{\xi }_{f12}\right]}^T, {\theta }_{f1}={\left[{\theta }_{f11},{\theta }_{f12}\right]}^T, {\theta }_{g1}={\left[{\theta }_{g11},{\theta }_{g12}\right]}^T\end{array}$$

(12)

Let $x_2$$=e_2+{\upsilon }_1$ (where $e_2=x_2-{\upsilon }_1$ denotes the error between the actual $x_2$ and the approximate virtual controller ${\upsilon }_1$) and define as follows:

$$\begin{array}{c}{\upsilon }_1=-k_1{e}_1-{\xi }_{f11}{\theta }_{f11}-{\xi }_{f12}{\theta }_{f12}-{\xi }_{g11}{\theta }_{g11}-{\xi }_{g12}{\theta }_{g12}\\ \begin{array}{l}=-k_1{e}_1-{\xi }_{f11l}{\theta }_{f11l}-{\xi }_{f11r}{\theta }_{f11r}-{\xi }_{g11l}{\theta }_{g11l}-{\xi }_{g11r}{\theta }_{g11r}\\ -{\xi }_{f12l}{\theta }_{f12l}-{\xi }_{f12r}{\theta }_{f12r}-{\xi }_{g12l}{\theta }_{g12l}-{\xi }_{g12r}{\theta }_{g12r}\end{array}\end{array}$$

(13)

Then Equation (10) is updated to the complete error dynamic equation considering approximation errors and parameter uncertainties:

$$\begin{array}{c}{\dot{e}}_1=f_1\left(X_1\right)+g_1\left(X_1\right)\left(e_2+{\upsilon }_1\right)-{\dot{y}}_1=g_1\left(X_1\right)\left(e_2-k_1{e}_1-{\xi }_{f1}{\theta }_{f1}-{\xi }_{g1}{\theta }_{g1}+{\omega }_1\right)\\ =g_1\left(X_1\right)\left(\begin{array}{l}{e}_2-k_1{e}_1-{\xi }_{f11l}{\tilde{\theta }}_{f11l}-{\xi }_{f11r}{\tilde{\theta }}_{f11r}-{\xi }_{g11l}{\tilde{\theta }}_{g11l}-{\xi }_{g11r}{\tilde{\theta }}_{g11r}\\ -{\xi }_{f12l}{\tilde{\theta }}_{f12l}-{\xi }_{f12r}{\tilde{\theta }}_{f12r}-{\xi }_{g12l}{\tilde{\theta }}_{g12l}-{\xi }_{g12r}{\tilde{\theta }}_{g12r}+{\omega }_1\end{array}\right)\end{array}$$

(14)

where

$$\begin{array}{c}{\tilde{\theta }}_{f11l}={\theta }_{f11l}-{\theta }_{f11l}^{\ast }, {\tilde{\theta }}_{f11r}={\theta }_{f11r}-{\theta }_{f11r}^{\ast }, {\tilde{\theta }}_{g11r}={\theta }_{g11r}-{\theta }_{g11r}^{\ast }, {\tilde{\theta }}_{g11l}={\theta }_{g11l}-{\theta }_{g11l}^{\ast }\\ {\tilde{\theta }}_{f12l}={\theta }_{f12l}-{\theta }_{f12l}^{\ast }, {\tilde{\theta }}_{f12r}={\theta }_{f12r}-{\theta }_{f12r}^{\ast }, {\tilde{\theta }}_{g12r}={\theta }_{g12r}-{\theta }_{g12r}^{\ast }, {\tilde{\theta }}_{g12l}={\theta }_{g12l}-{\theta }_{g12l}^{\ast }\end{array}$$

Consider the following Lyapunov function:

$$\begin{array}{c}{V}_1={\displaystyle \frac{1}{2g_1\left(X_1\right)}}{e}_1^2+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f1}}}{\tilde{\theta }}_{f1}^T{\tilde{\theta }}_{f1}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g1}}}{\tilde{\theta }}_{g1}^T{\tilde{\theta }}_{g1}\\ ={\displaystyle \frac{1}{2g_1\left(X_1\right)}}{e}_1^2+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f11l}}}{\tilde{\theta }}_{f11l}^T{\tilde{\theta }}_{f11l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f11r}}}{\tilde{\theta }}_{f11l}^T{\tilde{\theta }}_{f11r}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g11l}}}{\tilde{\theta }}_{g11l}^T{\tilde{\theta }}_{g11l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g11r}}}{\tilde{\theta }}_{g11r}^T{\tilde{\theta }}_{g11r}\\ +{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f12l}}}{\tilde{\theta }}_{f12l}^T{\tilde{\theta }}_{f12l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f12r}}}{\tilde{\theta }}_{f12l}^T{\tilde{\theta }}_{f12r}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g12l}}}{\tilde{\theta }}_{g12l}^T{\tilde{\theta }}_{g12l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g12r}}}{\tilde{\theta }}_{g12r}^T{\tilde{\theta }}_{g12r}\end{array}$$

(15)

Then the derivative of $V_1$ is

$$\begin{array}{c}{\dot{V}}_1={\displaystyle \frac{e_1{\dot{e}}_1}{g_1\left(X_1\right)}}-{\displaystyle \frac{{\dot{g}}_1\left(X_1\right)}{2g_1^2\left(X_1\right)}}{e}_1^2+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{f1}}}{\tilde{\theta }}_{f1}^T{\dot{\theta }}_{f1}+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{g1}}}{\tilde{\theta }}_{g1}^T{\dot{\theta }}_{g1}\\ ={\displaystyle \frac{e_1{\dot{e}}_1}{g_1\left(X_1\right)}}-{\displaystyle \frac{{\dot{g}}_1\left(X_1\right)}{2g_1^2\left(X_1\right)}}{e}_1^2+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f11l}}}{\tilde{\theta }}_{f11l}^T{\dot{\theta }}_{f11l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f11r}}}{\tilde{\theta }}_{f11r}^T{\dot{\theta }}_{f11r}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g11l}}}{\tilde{\theta }}_{g11l}^T{\dot{\theta }}_{g11l}\\ +{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g11r}}}{\tilde{\theta }}_{g11r}^T{\dot{\theta }}_{g11r}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f12l}}}{\tilde{\theta }}_{f12l}^T{\dot{\theta }}_{f12l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f12r}}}{\tilde{\theta }}_{f12r}^T{\dot{\theta }}_{f12r}\\ +{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g12l}}}{\tilde{\theta }}_{g12l}^T{\dot{\theta }}_{g12l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g12r}}}{\tilde{\theta }}_{g12r}^T{\dot{\theta }}_{g12r}\\ =e_1{e}_2-k_1{e}_1^2-e_1\left({\tilde{\theta }}_{f1}^T{\xi }_{f1}+{\tilde{\theta }}_{g1}^T{\xi }_{g1}\right)+e_1{\omega }_1-{\displaystyle \frac{{\dot{g}}_1\left(X_1\right)}{2g_1^2\left(X_1\right)}}{e}_1^2\\ +{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{f11l}}}{\tilde{\theta }}_{f11l}^T{\dot{\theta }}_{f11l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g1l}}}{\tilde{\theta }}_{g1l}^T{\dot{\theta }}_{g1l}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{g1r}}}{\tilde{\theta }}_{g1r}^T{\dot{\theta }}_{g1r}\\ =e_1{e}_2-k_1{e}_1^2-e_1\left({\tilde{\theta }}_{f1}^T{\xi }_{f1}+{\tilde{\theta }}_{g1}^T{\xi }_{g1}\right)+e_1{\omega }_1+{\tilde{\theta }}_{f11l}^T\left[-e_1{\xi }_{f11l}^T+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{f11l}}}{\dot{\theta }}_{f11l}\right]\\ +{\tilde{\theta }}_{f11r}^T\left[-e_1{\xi }_{f11r}^T+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{f11r}}}{\dot{\theta }}_{f11r}\right]+{\tilde{\theta }}_{g11r}^T\left[-e_1{\xi }_{g11r}^T+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{g11r}}}{\dot{\theta }}_{g11r}\right]+{\tilde{\theta }}_{g11l}^T\left[-e_1{\xi }_{g11l}^T+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{g11l}}}{\dot{\theta }}_{g11l}\right]\\ +{\tilde{\theta }}_{f12l}^T\left[-e_1{\xi }_{f12l}^T+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{f12l}}}{\dot{\theta }}_{f12l}\right]+{\tilde{\theta }}_{f12r}^T\left[-e_1{\xi }_{f12r}^T+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{f12r}}}{\dot{\theta }}_{f12r}\right]\\ +{\tilde{\theta }}_{g12r}^T\left[-e_1{\xi }_{g12r}^T+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{g12r}}}{\dot{\theta }}_{g12r}\right]+{\tilde{\theta }}_{g12l}^T\left[-e_1{\xi }_{g12l}^T+{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{g12l}}}{\dot{\theta }}_{g12l}\right]\end{array}$$

(16)

The adaptive laws are designed as follows:

$$\begin{array}{c}{\dot{\theta }}_{f11l}={\dot{\tilde{\theta }}}_{f11l}={\mathrm{\Gamma }}_{f11l}\left(e_1{\xi }_{f11l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11l}{\theta }_{f11l}\right),\\ {\dot{\theta }}_{f11r}={\dot{\tilde{\theta }}}_{f11r}={\mathrm{\Gamma }}_{f11r}\left(e_1{\xi }_{f11r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11r}{\theta }_{f11r}\right),\\ {\dot{\theta }}_{g11l}={\dot{\tilde{\theta }}}_{g11l}={\mathrm{\Gamma }}_{g11l}\left(e_1{\xi }_{g11l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{g11l}{\theta }_{g11l}\right),\\ {\dot{\theta }}_{g11r}={\dot{\tilde{\theta }}}_{g11r}={\mathrm{\Gamma }}_{g11r}\left(e_1{\xi }_{g11r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{g11r}{\theta }_{g11r}\right),\\ {\dot{\theta }}_{f12l}={\dot{\tilde{\theta }}}_{f12l}={\mathrm{\Gamma }}_{f12l}C\left(e_1{\xi }_{f12l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12l}{\theta }_{f12l}\right),\\ {\dot{\theta }}_{f12r}={\dot{\tilde{\theta }}}_{f12r}={\mathrm{\Gamma }}_{f12r}C\left(e_1{\xi }_{f12r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12r}{\theta }_{f12r}\right),\\ {\dot{\theta }}_{g12l}={\dot{\tilde{\theta }}}_{g12l}={\mathrm{\Gamma }}_{g12l}C\left(e_1{\xi }_{g12l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{g12l}{\theta }_{g12l}\right),\\ {\dot{\theta }}_{g12r}={\dot{\tilde{\theta }}}_{g12r}={\mathrm{\Gamma }}_{g12r}C\left(e_1{\xi }_{g12r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{g12r}{\theta }_{g12r}\right)\end{array}$$

(17)

where ${\mathsf{{\rm Y}}}_{f11l},{\mathsf{{\rm Y}}}_{f11r},{\mathsf{{\rm Y}}}_{g11r},{\mathsf{{\rm Y}}}_{g11l}$, ${\mathsf{{\rm Y}}}_{f12l},{\mathsf{{\rm Y}}}_{f12r},{\mathsf{{\rm Y}}}_{g12r},{\mathsf{{\rm Y}}}_{g12l}$ are given positive real numbers.

$$\begin{gathered} {\mathrm{\Gamma }}_{f11}=\left[\begin{array}{cc}{\mathrm{\Gamma }}_{f11l}& {\mathrm{\Gamma }}_{f11r}\end{array}\right], {\mathrm{\Gamma }}_{f11l}=\left[\begin{array}{ccc}{\tau }_{f11l0}& & \\ & \ddots & \\ & & {\tau }_{f11ln}\end{array}\right], {\mathrm{\Gamma }}_{g11} \text{can be similarly expressed.} \\ {\mathrm{\Gamma }}_{f12}=\left[\begin{array}{cc}{\mathrm{\Gamma }}_{f12l}& {\mathrm{\Gamma }}_{f12r}\end{array}\right], {\mathrm{\Gamma }}_{f12l}=\left[\begin{array}{ccc}{\tau }_{f12l0}& & \\ & \ddots & \\ & & {\tau }_{f12ln}\end{array}\right], {\mathrm{\Gamma }}_{g12} \text{can be similarly expressed.} \end{gathered}$$

Substituting the adaptive law of Equation (17) into the derivative of the Lyapunov function yields the simplified result:

$$\begin{gathered} {\left({\dot{\theta }}_{f11l}\right)}^T=\left(\begin{array}{c}{a}_{f11l0}\\ ⋮\\ a_{f11ln}\end{array}\right)=\left(e_1{\xi }_{f11l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11l}{\theta }_{f11l}\right)\left(\begin{array}{c}{\tau }_{f11l0}^k\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{f11r}\right)}^T=\left(\begin{array}{c}{a}_{f11r0}\\ ⋮\\ a_{f11rn}\end{array}\right)=\left(e_1{\xi }_{f11r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11r}{\theta }_{f11r}\right)\left(\begin{array}{c}{\tau }_{f11r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{g11l}\right)}^T=\left(\begin{array}{c}{a}_{g11l0}\\ ⋮\\ a_{g11ln}\end{array}\right)=\left(e_1{\xi }_{g11l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{g11l}{\theta }_{g11l}\right)\left(\begin{array}{c}{\tau }_{g11l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{g11r}\right)}^T=\left(\begin{array}{c}{a}_{g11r0}\\ ⋮\\ a_{g11rn}\end{array}\right)=\left(e_1{\xi }_{g11r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{g11r}{\theta }_{g11r}\right)\left(\begin{array}{c}{\tau }_{g11r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{f12l}\right)}^T=\left(\begin{array}{c}{a}_{f12l0}\\ ⋮\\ a_{f12ln}\end{array}\right)=\left(e_1{\xi }_{f12l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12l}{\theta }_{f12l}\right)\left(\begin{array}{c}{\tau }_{f12l0}^k\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{f12r}\right)}^T=\left(\begin{array}{c}{a}_{f12r0}\\ ⋮\\ a_{f12rn}\end{array}\right)=\left(e_1{\xi }_{f12r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12r}{\theta }_{f12r}\right)\left(\begin{array}{c}{\tau }_{f12r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{g12l}\right)}^T=\left(\begin{array}{c}{a}_{g12l0}\\ ⋮\\ a_{g12ln}\end{array}\right)=\left(e_1{\xi }_{g12l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{g12l}{\theta }_{g12l}\right)\left(\begin{array}{c}{\tau }_{g12l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{g12r}\right)}^T=\left(\begin{array}{c}{a}_{g12r0}\\ ⋮\\ a_{g12rn}\end{array}\right)=\left(e_1{\xi }_{g12r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{g12r}{\theta }_{g12r}\right)\left(\begin{array}{c}{\tau }_{g12r0}\\ 0\\ ⋮\\ 0\end{array}\right) \end{gathered}$$

(18)

The adaptive law of ecological factor parameters in the niche situation function is derived using the gradient descent method. These parameters are specifically updated for the niche situation function (serving as the consequent part of fuzzy rules) to reflect the bionic characteristic of biological individuals “developing in directions beneficial to themselves”. The specific forms include the following:

$$\begin{array}{c}{s}_{f11l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f11l0}\left(e_1{\xi }_{f11l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11l}{\theta }_{f11l}\right)\\ s_{f11r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f11r0}\left(e_1{\xi }_{f11r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11r}{\theta }_{f11r}\right)\\ s_{f12l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f12l0}\left(e_1{\xi }_{f12l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12l}{\theta }_{f12l}\right)\\ s_{f12r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f12r0}\left(e_1{\xi }_{f12r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12r}{\theta }_{f12r}\right)\end{array}$$

(19)

$$\begin{array}{c}{p}_{f11l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f11l0}\left(e_1{\xi }_{f11l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11l}{\theta }_{f11l}\right)\\ p_{f11r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f11l0}\left(e_1{\xi }_{f11r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11r}{\theta }_{f11r}\right)\\ p_{f12l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f12l0}\left(e_1{\xi }_{f12l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12l}{\theta }_{f12l}\right)\\ p_{f12r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f12r0}\left(e_1{\xi }_{f12r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12r}{\theta }_{f12r}\right)\end{array}$$

(20)

A similar expression can be obtained for the $g$ function.

Using the methodology of the literature of [25], it is proved out:

$$\begin{array}{c}{\dot{V}}_1\le e_1{e}_2-d_{11}{e}_1^2+{\displaystyle \frac{{\epsilon }_1^2}{4d_{12}}}-{\displaystyle \frac{{\mathsf{{\rm Y}}}_{f11l}{‖{\tilde{\theta }}_{f11l}‖}^2}{2}}-{\displaystyle \frac{{\mathsf{{\rm Y}}}_{f11r}{‖{\tilde{\theta }}_{f11r}‖}^2}{2}}-{\displaystyle \frac{{\mathsf{{\rm Y}}}_{f12l}{‖{\tilde{\theta }}_{f12l}‖}^2}{2}}\\ -{\displaystyle \frac{{\mathsf{{\rm Y}}}_{g11l}{‖{\tilde{\theta }}_{g11l}‖}^2}{2}}-{\displaystyle \frac{{\mathsf{{\rm Y}}}_{f12r}{‖{\tilde{\theta }}_{f12r}‖}^2}{2}}-{\displaystyle \frac{{\mathsf{{\rm Y}}}_{g12l}{‖{\tilde{\theta }}_{g12l}‖}^2}{2}}-{\displaystyle \frac{{\mathsf{{\rm Y}}}_{g12r}{‖{\tilde{\theta }}_{g12r}‖}^2}{2}}-{\displaystyle \frac{{\mathsf{{\rm Y}}}_{g11r}{‖{\tilde{\theta }}_{g11r}‖}^2}{2}}\\ +{\displaystyle \frac{{\mathsf{{\rm Y}}}_{f11l}{‖{\theta }_{f11l}^{\ast }‖}^2}{2}}+{\displaystyle \frac{{\mathsf{{\rm Y}}}_{f11r}{‖{\theta }_{f11r}^{\ast }‖}^2}{2}}+{\displaystyle \frac{{\mathsf{{\rm Y}}}_{g11l}{‖{\theta }_{g11l}^{\ast }‖}^2}{2}}+{\displaystyle \frac{{\mathsf{{\rm Y}}}_{g11r}{‖{\theta }_{g11r}^{\ast }‖}^2}{2}}+{\displaystyle \frac{{\mathsf{{\rm Y}}}_{f12l}{‖{\theta }_{f12l}^{\ast }‖}^2}{2}}\\ +{\displaystyle \frac{{\mathsf{{\rm Y}}}_{f12r}{‖{\theta }_{f12r}^{\ast }‖}^2}{2}}+{\displaystyle \frac{{\mathsf{{\rm Y}}}_{g12l}{‖{\theta }_{g12l}^{\ast }‖}^2}{2}}+{\displaystyle \frac{{\mathsf{{\rm Y}}}_{g12r}{‖{\theta }_{g12r}^{\ast }‖}^2}{2}}\end{array}$$

(21)

where $d_{11}$ and $d_{12}$ are positive real numbers.

The parameters of the niche equality index function are derived, and the adaptive law of the parameters is obtained using the gradient descent method. Equations (9)–(21) utilize the adaptive law to adjust the parameters by defining the error, the virtual controller, and introducing the Lyapunov function to ensure the stability and tracking performance of the system; these are the key steps of the backstepping control method.

Step $i$ $\left(2\le i\le n-1\right)$: As with the method in the first step, define

$$e_i=x_i-{\upsilon }_{i-1}$$

(22)

By differentiating $e_i$, we obtain

$${\dot{e}}_i={\dot{x}}_i-{\dot{\upsilon }}_{i-1}=f_i\left(X_i\right)+g_i\left(X_i\right)x_{i+1}-{\dot{\upsilon }}_{i-1}$$

(23)

Consider $x_{i+1}$ as a virtual controller and define

$${\upsilon }_i^{\ast }=-e_{i-1}-k_i{e}_i-{\displaystyle \frac{1}{g_i\left(X_i\right)}}\left(f_i\left(X_i\right)-{\dot{\upsilon }}_{i-1}\right)$$

(24)

where $k_i$ is a normal number.

$$\begin{array}{c}{\dot{\upsilon }}_{i-1}={\displaystyle \sum _{k=1}^{i-1}\frac{\mathsf{\partial }{\upsilon }_{i-1}}{\mathsf{\partial }{x}_k}}\left(g_k{x}_{k+1}+f_k\right)+{\displaystyle \frac{\mathsf{\partial }{\upsilon }_{i-1}}{\mathsf{\partial }{y}_i}}{y}_i+{\displaystyle \sum _{k=1}^{i-1}\frac{\mathsf{\partial }{\upsilon }_{i-1}}{\mathsf{\partial }{\theta }_{fkl}}}\left[{\mathrm{\Gamma }}_{fkl}\left(e_k{\xi }_{fkl}^T-{\mathsf{{\rm Y}}}_{fkl}{\theta }_{fkl}\right)\right]\\ +{\displaystyle \sum _{k=1}^{i-1}\frac{\mathsf{\partial }{\upsilon }_{i-1}}{\mathsf{\partial }{\theta }_{fkr}}}\left[{\mathrm{\Gamma }}_{fkr}\left(e_k{\xi }_{fkr}^T-{\mathsf{{\rm Y}}}_{fkr}{\theta }_{fkr}\right)\right]+{\displaystyle \sum _{k=1}^{i-1}\frac{\mathsf{\partial }{\upsilon }_{i-1}}{\mathsf{\partial }{\theta }_{gkr}}}\left[{\mathrm{\Gamma }}_{gkr}\left(e_k{\xi }_{gkr}^T-{\mathsf{{\rm Y}}}_{gkr}{\theta }_{gkr}\right)\right]\\ +{\displaystyle \sum _{k=1}^{i-1}\frac{\mathsf{\partial }{\upsilon }_{i-1}}{\mathsf{\partial }{\theta }_{gkl}}}\left[{\mathrm{\Gamma }}_{gkl}\left(e_k{\xi }_{gkl}^T-{\mathsf{{\rm Y}}}_{gkl}{\theta }_{gkl}\right)\right]\end{array}$$

(25)

Using Type-2 T-S fuzzy logic systems ${\xi }_{fi}^T\left(X_i\right){\theta }_{fi}$ and ${\xi }_{gi}^T\left(X_i\right){\theta }_{gi}$ to approximate the unknown function $-{\displaystyle \frac{1}{g_i\left(X_i\right)}}\left(f_i\left(X_i\right)-{\dot{\upsilon }}_{i-1}\right)$, we obtain

$${\upsilon }_i=-e_{i-1}-k_i{e}_i-{\xi }_{fi}^T\left(X_i\right){\theta }_{fi}-{\xi }_{gi}^T\left(X_i\right){\theta }_{gi}$$

(26)

Considering $x_{i+1}$ as $x_{i+1}=e_{i+1}+{\upsilon }_i$, then Equation (23) reads as follows:

$${\dot{e}}_i=g_i\left(X_i\right)\left(e_{i+1}-e_{i-1}-k_i{e}_i-{\xi }_{fi}^T\left(X_i\right){\tilde{\theta }}_{fi}-{\xi }_{gi}^T\left(X_i\right){\tilde{\theta }}_{gi}+{\omega }_i\right)$$

(27)

where ${\omega }_i={\omega }_{fi}+{\omega }_{gi}$, ${\tilde{\theta }}_{fi}={\theta }_{fi}-{\theta }_{fi}^{\ast }$, ${\tilde{\theta }}_{gi}={\theta }_{gi}-{\theta }_{gi}^{\ast }$.

Consider the following Lyapunov function:

$$\begin{array}{c}{V}_i=V_{i-1}+{\displaystyle \frac{1}{2g_i\left(X_i\right)}}{e}_i^2+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{fi}}}{\tilde{\theta }}_{fi}^T{\tilde{\theta }}_{fi}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{gi}}}{\tilde{\theta }}_{gi}^T{\tilde{\theta }}_{gi}\\ =V_{i-1}+{\displaystyle \frac{1}{2g_i\left(X_i\right)}}{e}_i^2+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{fil}}}{\tilde{\theta }}_{fil}^T{\tilde{\theta }}_{fil}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{fir}}}{\tilde{\theta }}_{fir}^T{\tilde{\theta }}_{fir}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{gil}}}{\tilde{\theta }}_{gil}^T{\tilde{\theta }}_{gil}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{gir}}}{\tilde{\theta }}_{gir}^T{\tilde{\theta }}_{gir}\end{array}$$

(28)

Adopt a method completely similar to the first step, take the derivative of $V_i$ with respect to time, and we have

$$\begin{array}{c}{\dot{V}}_i={\dot{V}}_{i-1}-e_{i-1}{e}_i+e_i{e}_{i+1}-{\displaystyle \frac{{\dot{g}}_i\left(X_i\right)}{2g_i^2\left(X_i\right)}}{e}_i^2+e_i{\omega }_i-{\tilde{\theta }}_{fil}^T\left[e_i{\xi }_{fil}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fil}}}{\dot{\theta }}_{fil}\right]\\ -{\tilde{\theta }}_{fir}^T\left[e_i{\xi }_{fir}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fir}}}{\dot{\theta }}_{fir}\right]-{\tilde{\theta }}_{gir}^T\left[e_i{\xi }_{gir}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gir}}}{\dot{\theta }}_{gir}\right]-{\tilde{\theta }}_{gil}^T\left[e_i{\xi }_{gil}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gil}}}{\dot{\theta }}_{gil}\right]\\ ={\dot{V}}_{i-1}-e_{i-1}{e}_i+e_i{e}_{i+1}-{\displaystyle \frac{{\dot{g}}_i\left(X_i\right)}{2g_i^2\left(X_i\right)}}{e}_i^2+e_i{\omega }_i-{\tilde{\theta }}_{fi1l}^T\left[e_i{\xi }_{fi1l}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fi1l}}}{\dot{\theta }}_{fi1l}\right]\\ -{\tilde{\theta }}_{fi1r}^T\left[e_i{\xi }_{f1ir}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fi1r}}}{\dot{\theta }}_{fi1r}\right]-{\tilde{\theta }}_{gi1r}^T\left[e_i{\xi }_{gi1r}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gi1r}}}{\dot{\theta }}_{gi1r}\right]\\ -{\tilde{\theta }}_{gi1l}^T\left[e_i{\xi }_{gi1l}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gi1l}}}{\dot{\theta }}_{gi1l}\right]-{\tilde{\theta }}_{fi2l}^T\left[e_i{\xi }_{fi2l}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fi2l}}}{\dot{\theta }}_{fi2l}\right]\\ -{\tilde{\theta }}_{fi2r}^T\left[e_i{\xi }_{fi2r}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fi2r}}}{\dot{\theta }}_{fi2r}\right]-{\tilde{\theta }}_{gi2r}^T\left[e_i{\xi }_{gi2r}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gi2r}}}{\dot{\theta }}_{gi2r}\right]\\ -{\tilde{\theta }}_{gi2l}^T\left[e_i{\xi }_{gi2l}^T\left(X_i\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gi2l}}}{\dot{\theta }}_{gi2l}\right]\end{array}$$

(29)

Select the following adaptive rate:

$$\begin{array}{c}{\dot{\theta }}_{fi1l}={\dot{\tilde{\theta }}}_{fi1l}={\mathrm{\Gamma }}_{fi1l}\left(e_i{\xi }_{fi1l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi1l}{\theta }_{fi1l}\right), {\dot{\theta }}_{fi1r}={\dot{\tilde{\theta }}}_{fi1r}={\mathrm{\Gamma }}_{fi1r}\left(e_i{\xi }_{fi1r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi1r}{\theta }_{fi1r}\right)\\ {\dot{\theta }}_{gi1r}={\dot{\tilde{\theta }}}_{gi1r}={\mathrm{\Gamma }}_{gi1r}\left(e_i{\xi }_{gi1r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi1r}{\theta }_{gi1r}\right), {\dot{\theta }}_{gi1l}={\dot{\tilde{\theta }}}_{gi1l}={\mathrm{\Gamma }}_{gi1l}\left(e_i{\xi }_{gi1l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi1l}{\theta }_{gi1l}\right)\\ {\dot{\theta }}_{fi2l}={\dot{\tilde{\theta }}}_{fi2l}={\mathrm{\Gamma }}_{fi2l}\left(e_i{\xi }_{fi2l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi2l}{\theta }_{fi2l}\right), {\dot{\theta }}_{fi2r}={\dot{\tilde{\theta }}}_{fi2r}={\mathrm{\Gamma }}_{fi2r}\left(e_i{\xi }_{fi2r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi2r}{\theta }_{fi2r}\right)\\ {\dot{\theta }}_{gi2r}={\dot{\tilde{\theta }}}_{gi2r}={\mathrm{\Gamma }}_{gi2r}\left(e_i{\xi }_{gi2r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi2r}{\theta }_{gi2r}\right), {\dot{\theta }}_{gi2l}={\dot{\tilde{\theta }}}_{gi2l}={\mathrm{\Gamma }}_{gi2l}\left(e_i{\xi }_{gi2l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi2l}{\theta }_{gi2l}\right)\end{array}$$

(30)

where ${\mathsf{{\rm Y}}}_{fi1l},{\mathsf{{\rm Y}}}_{fi1r},{\mathsf{{\rm Y}}}_{gi1r},{\mathsf{{\rm Y}}}_{gi1l}$, ${\mathsf{{\rm Y}}}_{fi2l},{\mathsf{{\rm Y}}}_{fi2r},{\mathsf{{\rm Y}}}_{gi2r},{\mathsf{{\rm Y}}}_{gi2l}$ are given positive real numbers. ${\mathrm{\Gamma }}_{fi}=\left[\begin{array}{cc}{\mathrm{\Gamma }}_{fil}& {\mathrm{\Gamma }}_{fir}\end{array}\right]$, ${\mathrm{\Gamma }}_{fil}=\left[\begin{array}{ccc}{\tau }_{fil0}& & \\ & \ddots & \\ & & {\tau }_{fi\ln }\end{array}\right]$, ${\mathrm{\Gamma }}_{gi}$, and others can be similarly expressed.

According to the adaptive law obtained from (30), there are

$$\begin{gathered} {\left({\dot{\theta }}_{fi1l}\right)}^T=\left(\begin{array}{c}{a}_{fi1l0}\\ ⋮\\ a_{fi1ln}\end{array}\right)=\left(e_i{\xi }_{fi1l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi1l}{\theta }_{fi1l}\right)\left(\begin{array}{c}{\tau }_{fi1l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{fi1r}\right)}^T=\left(\begin{array}{c}{a}_{fi1r0}\\ ⋮\\ a_{fi1rn}\end{array}\right)=\left(e_i{\xi }_{fi1r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{f1ir}{\theta }_{f1ir}\right)\left(\begin{array}{c}{\tau }_{fi1r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{gi1l}\right)}^T=\left(\begin{array}{c}{a}_{gi1l0}\\ ⋮\\ a_{gi1ln}\end{array}\right)=\left(e_i{\xi }_{gi1l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi1l}{\theta }_{gi1l}\right)\left(\begin{array}{c}{\tau }_{gi1l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{gi1r}\right)}^T=\left(\begin{array}{c}{a}_{gi1r0}\\ ⋮\\ a_{gi1rn}\end{array}\right)=\left(e_i{\xi }_{gi1r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi1r}{\theta }_{gi1r}\right)\left(\begin{array}{c}{\tau }_{gi1r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{fi2l}\right)}^T=\left(\begin{array}{c}{a}_{fi2l0}\\ ⋮\\ a_{fi2ln}\end{array}\right)=\left(e_i{\xi }_{fi2l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi2l}{\theta }_{fi2l}\right)\left(\begin{array}{c}{\tau }_{fi2l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{fi2r}\right)}^T=\left(\begin{array}{c}{a}_{fi2r0}\\ ⋮\\ a_{fi2rn}\end{array}\right)=\left(e_i{\xi }_{fi2r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi2r}{\theta }_{fi2r}\right)\left(\begin{array}{c}{\tau }_{fi2r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{gi2l}\right)}^T=\left(\begin{array}{c}{a}_{gi2l0}\\ ⋮\\ a_{gi2ln}\end{array}\right)=\left(e_i{\xi }_{gi2l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi2l}{\theta }_{gi2l}\right)\left(\begin{array}{c}{\tau }_{gi2l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{gi2r}\right)}^T=\left(\begin{array}{c}{a}_{gi2r0}\\ ⋮\\ a_{gi2rn}\end{array}\right)=\left(e_i{\xi }_{gi2r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi2r}{\theta }_{gi2r}\right)\left(\begin{array}{c}{\tau }_{gi2r0}\\ 0\\ ⋮\\ 0\end{array}\right) \end{gathered}$$

(31)

Adopt a method similar to the first step, take the derivative of the parameters of the niche situation function and use the gradient descent method to obtain the parameter adaptive law of the niche situation function:

$$\begin{array}{c}{s}_{fi1l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{fi1l0}\left(e_i{\xi }_{fi1l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi1l}{\theta }_{fi1l}\right)\\ s_{fi1r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{fi1r0}\left(e_i{\xi }_{fi1r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi1r}{\theta }_{fi1r}\right)\\ s_{gi1l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{gi1l0}\left(e_i{\xi }_{gi1l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi1l}{\theta }_{gi1l}\right)\\ s_{gi1r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{gi1r0}\left(e_i{\xi }_{gi1r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi1r}{\theta }_{gi1r}\right)\end{array}$$

(32)

$$\begin{array}{c}{p}_{fi2l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{fi2l0}\left(e_i{\xi }_{fi2l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi2l}{\theta }_{fi2l}\right)\\ p_{fi2r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{fi2r0}\left(e_i{\xi }_{fi2r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{fi2r}{\theta }_{fi2r}\right)\\ p_{gi2l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{gi2l0}\left(e_i{\xi }_{gi2l}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi2l}{\theta }_{gi2l}\right)\\ p_{gi2r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{gi2r0}\left(e_i{\xi }_{gi2r}^T\left(X_i\right)-{\mathsf{{\rm Y}}}_{gi2r}{\theta }_{gi2r}\right)\end{array}$$

(33)

Bringing Equation (30) to Equation (29) gives

$$\begin{array}{c}{\dot{V}}_i\le e_i{e}_{i+1}-{\displaystyle \sum _{k=1}^i{d}_{k1}}{e}_k^2+{\displaystyle \sum _{k=1}^i\frac{{\epsilon }_k^2}{4k_{k2}}}-{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{fk1l}{‖{\tilde{\theta }}_{fk1l}‖}^2}{2}}-{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{fk1r}{‖{\tilde{\theta }}_{fk1r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{gk1r}{‖{\tilde{\theta }}_{gk1r}‖}^2}{2}}\\ -{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{gk1l}{‖{\tilde{\theta }}_{gk1l}‖}^2}{2}}-{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{fk2r}{‖{\tilde{\theta }}_{fk2r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{gk2r}{‖{\tilde{\theta }}_{gk2r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{gk2l}{‖{\tilde{\theta }}_{gk2l}‖}^2}{2}}\\ -{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{fk2l}{‖{\tilde{\theta }}_{fk2l}‖}^2}{2}}+{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{fk1l}{‖{\theta }_{fk1l}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{fk1r}{‖{\theta }_{fk1r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{gk1r}{‖{\theta }_{gk1r}^{\ast }‖}^2}{2}}\\ +{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{fk2l}{‖{\theta }_{fk2l}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{fk2r}{‖{\theta }_{fk2r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{gk2r}{‖{\theta }_{gk2r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{gk1l}{‖{\theta }_{gk1l}^{\ast }‖}^2}{2}}\\ +{\displaystyle \sum _{k=1}^i\frac{{\mathsf{{\rm Y}}}_{gk2l}{‖{\theta }_{gk2l}^{\ast }‖}^2}{2}}\end{array}$$

(34)

Similarly, the parameters of the niche equality index function are derived, and the adaptive law of the parameters is obtained using the gradient descent method. The subsequent steps are similar to the first step, which is gradually derived, and the parameter adaptive law is adjusted by continuously defining new errors, virtual controllers, and introducing Lyapunov functions, so as to gradually construct the complete controller to achieve the effective control of the system. Every step is taken on the premise of guaranteeing the stability of the system to advance towards the final controller design.

Step n: This is the last step and will derive the actual controller $u$ for this method.

Define $e_n=x_n-{\upsilon }_{n-1}$, and take the derivative:

$${\dot{e}}_n={\dot{x}}_n-{\dot{\upsilon }}_{n-1}=f_n\left(X_n\right)+g_n\left(X_n\right)u-{\dot{\upsilon }}_{n-1}$$

(35)

According to Assumption 1, the control gain function $g_n\left(X\right)$ > 0 and has a lower bound $g_{\min }$ > 0; so the actual controller is defined as follows:

$$u=-e_{n-1}-k_n{e}_n-{\xi }_{fn}^T\left(X_n\right){\tilde{\theta }}_{fn}-{\xi }_{gn}^T\left(X_n\right){\tilde{\theta }}_{gn}$$

(36)

where $k_n>0$, ${\tilde{\theta }}_{fn}={\theta }_{fn}-{\theta }_{fn}^{\ast }$, ${\tilde{\theta }}_{gn}={\theta }_{gn}-{\theta }_{gn}^{\ast }$.

Choose the final Lyapunov function as:

$$\begin{array}{c}V=V_{n-1}+{\displaystyle \frac{1}{2g_n\left(X_n\right)}}{e}_n^2+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{fn}}}{\tilde{\theta }}_{fn}^T{\tilde{\theta }}_{fn}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{gn}}}{\tilde{\theta }}_{gn}^T{\tilde{\theta }}_{gn}\\ =V_{n-1}+{\displaystyle \frac{1}{2g_n\left(X_n\right)}}{e}_n^2+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{fnl}}}{\tilde{\theta }}_{fnl}^T{\tilde{\theta }}_{fnl}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{fnr}}}{\tilde{\theta }}_{fnr}^T{\tilde{\theta }}_{fnr}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{gnr}}}{\tilde{\theta }}_{gnr}^T{\tilde{\theta }}_{gnr}+{\displaystyle \frac{1}{2{\mathrm{\Gamma }}_{gnl}}}{\tilde{\theta }}_{gnl}^T{\tilde{\theta }}_{gnl}\end{array}$$

(37)

where ${\tilde{\theta }}_{fnl}=\left[{\tilde{\theta }}_{fn1l},{\tilde{\theta }}_{fn2l}\right]$, ${\mathrm{\Gamma }}_{fnl}=\left[{\mathrm{\Gamma }}_{fn1l},{\mathrm{\Gamma }}_{fn2l}\right]$, ${\mathrm{\Gamma }}_{gnl}$, and ${\tilde{\theta }}_{gnl}$ similar expressions.

Deriving the above Equation (37), we have

$$\begin{array}{c}\dot{V}={\dot{V}}_{n-1}-e_{n-1}{e}_n-k_n{e}_n^2-{\displaystyle \frac{g_n\left(X_n\right)}{2g_n^2\left(X_n\right)}}{e}_n^2+e_n{\omega }_n-{\tilde{\theta }}_{fn1l}^T\left[e_n{\xi }_{fn1l}^T\left(X_n\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fn1l}}}{\dot{\theta }}_{fn1l}\right]\\ -{\tilde{\theta }}_{fn1r}^T\left[e_n{\xi }_{fn1r}^T\left(X_n\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fn1r}}}{\dot{\theta }}_{fn1r}\right]-{\tilde{\theta }}_{gn1r}^T\left[e_n{\xi }_{gn1r}^T\left(X_n\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gn1r}}}{\dot{\theta }}_{gn1r}\right]\\ -{\tilde{\theta }}_{gn1l}^T\left[e_n{\xi }_{gn1l}^T\left(X_n\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gn1l}}}{\dot{\theta }}_{gn1l}\right]-{\tilde{\theta }}_{fn2l}^T\left[e_n{\xi }_{fn2l}^T\left(X_n\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fn2l}}}{\dot{\theta }}_{fn2l}\right]\\ -{\tilde{\theta }}_{fn2r}^T\left[e_n{\xi }_{fn2r}^T\left(X_n\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{fn2r}}}{\dot{\theta }}_{fn2r}\right]-{\tilde{\theta }}_{gn2r}^T\left[e_n{\xi }_{gn2r}^T\left(X_n\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gn2r}}}{\dot{\theta }}_{gn2r}\right]\\ -{\tilde{\theta }}_{gn2l}^T\left[e_n{\xi }_{gn2l}^T\left(X_n\right)-{\displaystyle \frac{1}{{\mathrm{\Gamma }}_{gn2l}}}{\dot{\theta }}_{gn2l}\right]\end{array}$$

(38)

Select the adaptive rate as follows:

$$\begin{array}{c}{\dot{\theta }}_{fn1l}={\dot{\tilde{\theta }}}_{fn1l}={\mathrm{\Gamma }}_{fn1l}\left(e_n{\xi }_{fn1l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn1l}{\theta }_{fn1l}\right), {\dot{\theta }}_{fn1r}={\dot{\tilde{\theta }}}_{fn1r}={\mathrm{\Gamma }}_{fn1r}\left(e_n{\xi }_{fn1r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn1r}{\theta }_{fn1r}\right)\\ {\dot{\theta }}_{gn1r}={\dot{\tilde{\theta }}}_{gn1r}={\mathrm{\Gamma }}_{gn1r}\left(e_n{\xi }_{gn1r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn1r}{\theta }_{gn1r}\right), {\dot{\theta }}_{gn1l}={\dot{\tilde{\theta }}}_{gn1l}={\mathrm{\Gamma }}_{gn1l}\left(e_n{\xi }_{gn1l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn1l}{\theta }_{gn1l}\right)\\ {\dot{\theta }}_{fn2l}={\dot{\tilde{\theta }}}_{fn2l}={\mathrm{\Gamma }}_{fn2l}\left(e_n{\xi }_{fn2l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn2l}{\theta }_{fn2l}\right), {\dot{\theta }}_{fn2r}={\dot{\tilde{\theta }}}_{fn2r}={\mathrm{\Gamma }}_{fn2r}\left(e_n{\xi }_{fn2r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn2r}{\theta }_{fn2r}\right)\\ {\dot{\theta }}_{gn2r}={\dot{\tilde{\theta }}}_{gn2r}={\mathrm{\Gamma }}_{gn2r}\left(e_n{\xi }_{gn2r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn2r}{\theta }_{gn2r}\right), {\dot{\theta }}_{gn2l}={\dot{\tilde{\theta }}}_{gn2l}={\mathrm{\Gamma }}_{gn2l}\left(e_n{\xi }_{gn2l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn2l}{\theta }_{gn2l}\right)\end{array}$$

(39)

where ${\mathsf{{\rm Y}}}_{fn1l},{\mathsf{{\rm Y}}}_{fn1r},{\mathsf{{\rm Y}}}_{gn1r},{\mathsf{{\rm Y}}}_{gn1l}$, ${\mathsf{{\rm Y}}}_{fn2l},{\mathsf{{\rm Y}}}_{fn2r},{\mathsf{{\rm Y}}}_{gn2r},{\mathsf{{\rm Y}}}_{gn2l}$ are given positive real numbers. ${\mathrm{\Gamma }}_{fn}=\left[\begin{array}{cc}{\mathrm{\Gamma }}_{fnl}& {\mathrm{\Gamma }}_{fnr}\end{array}\right]$, ${\mathrm{\Gamma }}_{fnl}=\left[\begin{array}{cc}{\mathrm{\Gamma }}_{fn1l}& {\mathrm{\Gamma }}_{fn2l}\end{array}\right]$, ${\mathrm{\Gamma }}_{fnl}=\left[\begin{array}{ccc}{\tau }_{fnl0}& & \\ & \ddots & \\ & & {\tau }_{fnln}\end{array}\right]$. Other parameters such as ${\mathrm{\Gamma }}_{gn}$ can be expressed similarly.

According to the adaptive law obtained from (39), there are

$$\begin{gathered} {\left({\dot{\theta }}_{fn1l}\right)}^T=\left(\begin{array}{c}{a}_{fn1l0}\\ ⋮\\ a_{fn1ln}\end{array}\right)=\left(e_n{\xi }_{fn1l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn1l}{\theta }_{fn1l}\right)\left(\begin{array}{c}{\tau }_{fn1l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{fn1r}\right)}^T=\left(\begin{array}{c}{a}_{fn1r0}\\ ⋮\\ a_{fn1rn}\end{array}\right)=\left(e_n{\xi }_{fn1r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn1r}{\theta }_{fn1r}\right)\left(\begin{array}{c}{\tau }_{fn1r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{gn1l}\right)}^T=\left(\begin{array}{c}{a}_{gn1l0}\\ ⋮\\ a_{gn1ln}\end{array}\right)=\left(e_n{\xi }_{gn1l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn1l}{\theta }_{gn1l}\right)\left(\begin{array}{c}{\tau }_{gn1l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{gn1r}\right)}^T=\left(\begin{array}{c}{a}_{gn1r0}\\ ⋮\\ a_{gn1rn}\end{array}\right)=\left(e_n{\xi }_{gn1r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn1r}{\theta }_{gn1r}\right)\left(\begin{array}{c}{\tau }_{gn1r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{fn2l}\right)}^T=\left(\begin{array}{c}{a}_{fn2l0}\\ ⋮\\ a_{fn2ln}\end{array}\right)=\left(e_n{\xi }_{fn2l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn2l}{\theta }_{fn2l}\right)\left(\begin{array}{c}{\tau }_{fn2l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{fn2r}\right)}^T=\left(\begin{array}{c}{a}_{fn2r0}\\ ⋮\\ a_{fn2rn}\end{array}\right)=\left(e_n{\xi }_{fn2r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn2r}{\theta }_{fn2r}\right)\left(\begin{array}{c}{\tau }_{fn2r0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{gn2l}\right)}^T=\left(\begin{array}{c}{a}_{gn2l0}\\ ⋮\\ a_{gn2ln}\end{array}\right)=\left(e_n{\xi }_{gn2l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn2l}{\theta }_{gn2l}\right)\left(\begin{array}{c}{\tau }_{gn2l0}\\ 0\\ ⋮\\ 0\end{array}\right) \\ {\left({\dot{\theta }}_{gn2r}\right)}^T=\left(\begin{array}{c}{a}_{gn2r0}\\ ⋮\\ a_{gn2rn}\end{array}\right)=\left(e_n{\xi }_{gn2r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn2r}{\theta }_{gn2r}\right)\left(\begin{array}{c}{\tau }_{gn2r0}\\ 0\\ ⋮\\ 0\end{array}\right) \end{gathered}$$

(40)

Then the parameters of the niche situation function are derived, and the gradient descent method is used to obtain the parameter adaptive rate of the niche situation function:

$$\begin{array}{c}{s}_{fn1l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{fn1l0}\left(e_n{\xi }_{fn1l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn1l}{\theta }_{fn1l}\right)\\ s_{fn1r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{fn1r0}\left(e_n{\xi }_{fn1r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn1r}{\theta }_{fn1r}\right)\\ s_{gn1l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{gn1l0}\left(e_n{\xi }_{gn1l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn1l}{\theta }_{gn1l}\right)\\ s_{gn1r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{gn1r0}\left(e_n{\xi }_{gn1r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn1r}{\theta }_{gn1r}\right)\end{array}$$

(41)

$$\begin{array}{c}{p}_{fn2l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{fn2l0}\left(e_n{\xi }_{fn2l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn2l}{\theta }_{fn2l}\right)\\ p_{fn2r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{fn2r0}\left(e_n{\xi }_{fn2r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{fn2r}{\theta }_{fn2r}\right)\\ p_{gn2l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{gn2l0}\left(e_n{\xi }_{gn2l}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn2l}{\theta }_{gn2l}\right)\\ p_{gn2r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{gn2r0}\left(e_n{\xi }_{gn2r}^T\left(X_n\right)-{\mathsf{{\rm Y}}}_{gn2r}{\theta }_{gn2r}\right)\end{array}$$

(42)

Substituting (39) into (38) yields

$$\begin{array}{c}\dot{V}\le -{\displaystyle \sum _{k=1}^n{d}_{k1}}{e}_k^2+{\displaystyle \sum _{k=1}^n\frac{{\epsilon }_k^2}{4k_{k2}}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1l}{‖{\tilde{\theta }}_{fk1l}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1r}{‖{\tilde{\theta }}_{fk1r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1l}{‖{\tilde{\theta }}_{gk1l}‖}^2}{2}}\\ -{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1r}{‖{\tilde{\theta }}_{gk1r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1l}{‖{\tilde{\theta }}_{fk1l}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1r}{‖{\tilde{\theta }}_{fk1r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1l}{‖{\tilde{\theta }}_{gk1l}‖}^2}{2}}\\ -{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1r}{‖{\tilde{\theta }}_{gk1r}‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1l}{‖{\theta }_{fk1l}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1r}{‖{\theta }_{fk1r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk2l}{‖{\theta }_{fk2l}^{\ast }‖}^2}{2}}\\ +{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1l}{‖{\theta }_{gk1l}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1r}{‖{\theta }_{gk1r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk2r}{‖{\theta }_{fk2r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk2l}{‖{\theta }_{gk2l}^{\ast }‖}^2}{2}}\\ +{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk2r}{‖{\theta }_{gk2r}^{\ast }‖}^2}{2}}\end{array}$$

(43)

Choose an appropriate $d_{k1}$ such that $d_{k1}>\left(\rho /2g_k\right)$, then

$$d_{k1}>\left(\rho /2g_k\right)+\left({\dot{g}}_k/2g_k^2\right)k=\left(1,2,\dots ,n\right)$$

where $\rho$ is a positive constant, and

$$\begin{array}{c}\delta \le {\displaystyle \sum _{k=1}^n\frac{{\epsilon }_k^2}{4k_{k2}}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1l}{‖{\theta }_{fk1l}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1r}{‖{\theta }_{fk1r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk2l}{‖{\theta }_{fk2l}^{\ast }‖}^2}{2}}\\ +{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1l}{‖{\theta }_{gk1l}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1r}{‖{\theta }_{gk1r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk2r}{‖{\theta }_{fk2r}^{\ast }‖}^2}{2}}+{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk2r}{‖{\theta }_{gk2r}^{\ast }‖}^2}{2}}\end{array}$$

(44)

Then it can be deduced from (44) that

$$\begin{array}{c}\dot{V}\le -{\displaystyle \sum _{k=1}^n{d}_{k1}}{e}_k^2+\delta -{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1l}{‖{\tilde{\theta }}_{fk1l}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk1r}{‖{\tilde{\theta }}_{fk1r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1l}{‖{\tilde{\theta }}_{gk1l}‖}^2}{2}}\hfill \\ -{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk1r}{‖{\tilde{\theta }}_{gk1r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk2l}{‖{\tilde{\theta }}_{fk2l}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{fk2r}{‖{\tilde{\theta }}_{fk2r}‖}^2}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk2l}{‖{\tilde{\theta }}_{gk2l}‖}^2}{2}}\hfill \\ -{\displaystyle \sum _{k=1}^n\frac{{\mathsf{{\rm Y}}}_{gk2r}{‖{\tilde{\theta }}_{gk2r}‖}^2}{2}}\hfill \\ <-{\displaystyle \sum _{k=1}^n\frac{\rho }{2g_k}}{e}_k^2+\delta -{\displaystyle \sum _{k=1}^n\frac{\rho {\tilde{\theta }}_{fk1l}^T{\tilde{\theta }}_{fk1l}}{2}}-{\displaystyle \sum _{k=1}^n\frac{\rho {\tilde{\theta }}_{fk1r}^T{\tilde{\theta }}_{fk1r}}{2}}-{\displaystyle \sum _{k=1}^n\frac{\rho {\tilde{\theta }}_{gk1l}^T{\tilde{\theta }}_{gk1l}}{2}}-{\displaystyle \sum _{k=1}^n\frac{\rho {\tilde{\theta }}_{gk1r}^T{\tilde{\theta }}_{gk1r}}{2}}\hfill \\ -{\displaystyle \sum _{k=1}^n\frac{\rho {\tilde{\theta }}_{gk2l}^T{\tilde{\theta }}_{gk2l}}{2}}-{\displaystyle \sum _{k=1}^n\frac{\rho {\tilde{\theta }}_{gk2r}^T{\tilde{\theta }}_{gk2r}}{2}}-{\displaystyle \sum _{k=1}^n\frac{\rho {\tilde{\theta }}_{fk2l}^T{\tilde{\theta }}_{fk2l}}{2}}-{\displaystyle \sum _{k=1}^n\frac{\rho {\tilde{\theta }}_{fk2r}^T{\tilde{\theta }}_{fk2r}}{2}}\hfill \\ <\left(\rho \right.{\displaystyle \sum _{k=1}^n\frac{1}{2g_k}}{e}_k^2-{\displaystyle \sum _{k=1}^n\frac{{\tilde{\theta }}_{fk1l}^T{\tilde{\theta }}_{fk1l}}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\tilde{\theta }}_{fk1r}^T{\tilde{\theta }}_{fk1r}}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\tilde{\theta }}_{gk1l}^T{\tilde{\theta }}_{gk1l}}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\tilde{\theta }}_{gk1r}^T{\tilde{\theta }}_{gk1r}}{2}}\hfill \\ -{\displaystyle \sum _{k=1}^n\frac{{\tilde{\theta }}_{fk2l}^T{\tilde{\theta }}_{fk2l}}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\tilde{\theta }}_{fk2r}^T{\tilde{\theta }}_{fk2r}}{2}}\left.-{\displaystyle \sum _{k=1}^n\frac{{\tilde{\theta }}_{gk2l}^T{\tilde{\theta }}_{gk2l}}{2}}-{\displaystyle \sum _{k=1}^n\frac{{\tilde{\theta }}_{gk2r}^T{\tilde{\theta }}_{gk2r}}{2}}\right)+\delta \hfill \\ <-\rho V+\delta \hfill \end{array}$$

(45)

According to (45), we can obtain

$$V\left(t\right)<V\left(t_0\right)e^{-\rho \left(t-t_0\right)}+{\displaystyle \frac{\delta }{\rho }}$$

(46)

It can be seen that the signals $x_2$, $H_{\infty }$, ${\theta }_{fk1l}$, ${\theta }_{fk1r}$, ${\theta }_{gk1l}$, ${\theta }_{gk1r}$, ${\theta }_{fk2l},{\theta }_{fk2r}$, ${\theta }_{gk2l}$, ${\theta }_{gk2r}$, and $u\left(t\right)$ are all globally uniformly ultimately bounded, and $\left|y_n(t)-y_r(t)\right|\le \sqrt{2V(t)}{e}^{(\rho /2)\left(t-t_0\right)}+\sqrt{2\delta /\rho }$. To make the tracking error converge to a small neighborhood around zero, the parameters ρ and δ must take appropriate values such that $\sqrt{2\delta /\rho }$ is sufficiently small. Let $\varphi >\sqrt{2\delta /\rho }$. Since $t\to \infty$, $e^{-(\delta /2)\left(t-t_0\right)}\to 0$, there exists T, when t ≥ T, $\left|y(t)-y_r(t)\right|\le \varphi$, and thus $V\left(t\right)<0$.

4. Example Simulation

Equation for cerebral aneurysms with damping terms:

$$\ddot{x}+\phi \dot{x}+\alpha x-\beta x^2+\gamma x^3=F\cos \omega t$$

In the equation, $x$ denotes the blood flow velocity within the cerebral aneurysm, $\dot{x}$ denotes the rate of change of blood flow, $\alpha ,\beta ,\gamma$ denote the resistance to blood flow, $F$ denotes the amplitude of the blood flow impulse, and $\omega$ represents heartbeat frequency.

Let ${\dot{x}}_1=y_1$, then the driving system is

$$\left\{\begin{array}{l}{\dot{x}}_1=y_1\\ {\dot{y}}_1=-\phi y_1-{\alpha }_1{x}_1+3x_1^2-2x_1^3+0.1\cos t\end{array}\right.$$

Let ${\dot{x}}_2=y_2$, the response system is

$$\left\{\begin{array}{l}{\dot{x}}_2=y_1+u_1\\ {\dot{y}}_2=-{\phi }_2{y}_2-{\alpha }_2{x}_2+3x_2^2-2x_2^3+0.1\cos t+u_2\end{array}\right.$$

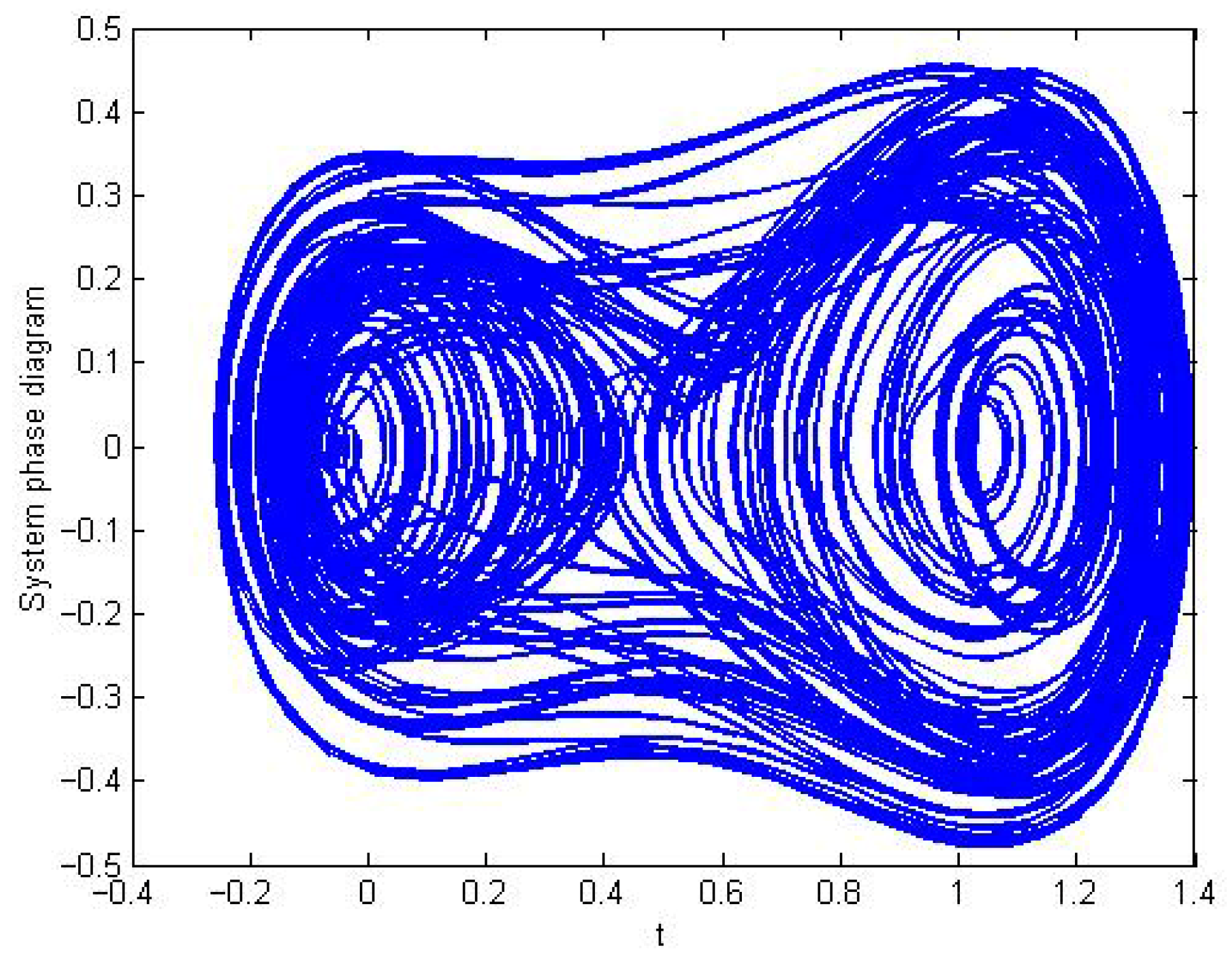
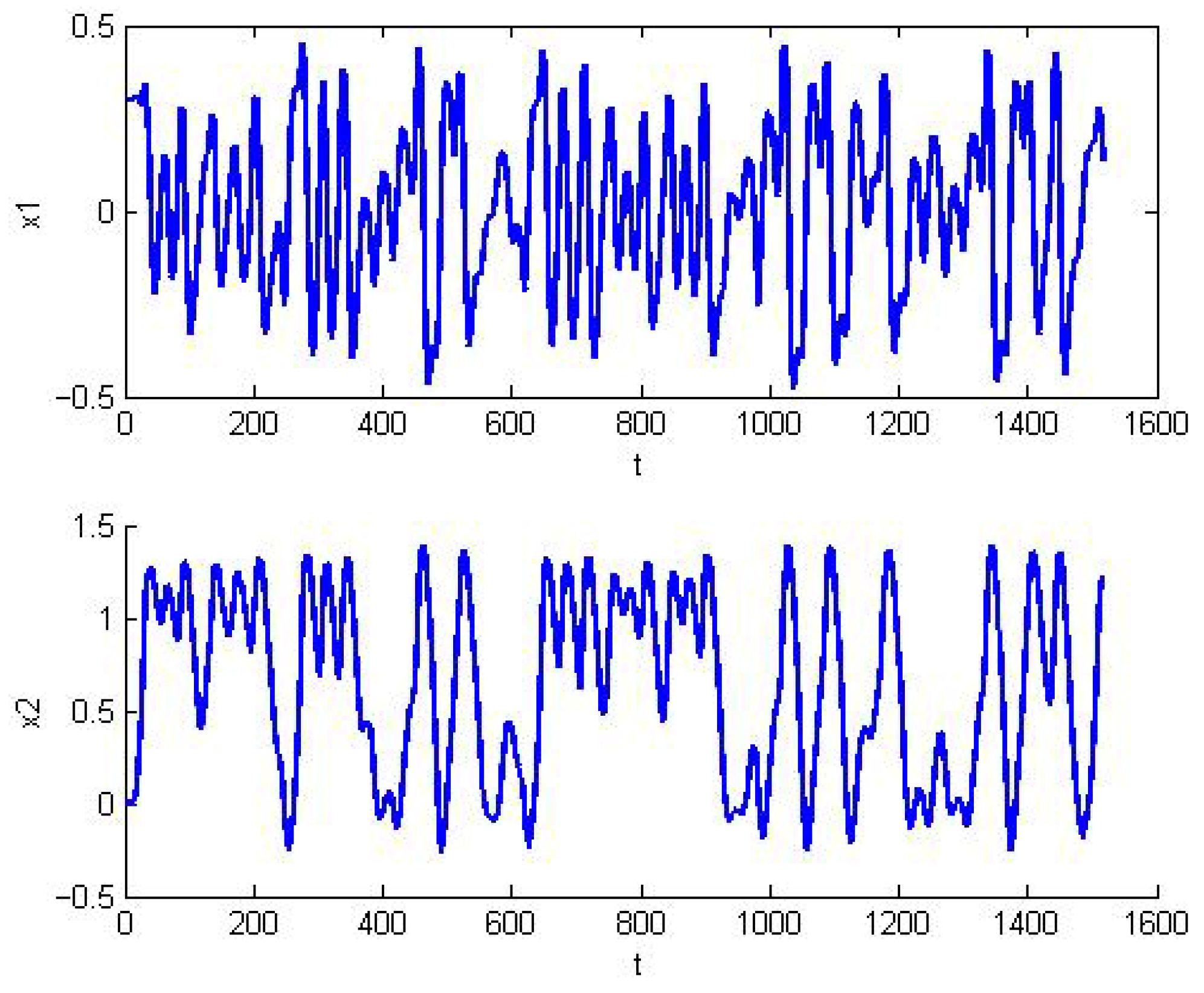
When the parameters ${\alpha }_1=0.09, {\mu }_1=0.06$ and the initial values are taken as $x_1=0.3, x_2=0.01$, the system exhibits a chaotic state, as shown in Figure 1, and the two-variable operating curves are shown in Figure 2.

Figure 1 indicates that the system exhibits chaotic behavior in the absence of control. Figure 2 shows large fluctuations in the two variables, with significant oscillations present in the uncontrolled system. The system fails to maintain stability, possibly due to external disturbances. Throughout the observed duration, the state variables do not converge and continue to fluctuate. The Type-2 adaptive backstepping fuzzy control design process is specified as follows:

Step 1: Define the Type-2 affiliation function:

$$\begin{gathered} {\mu }_{M_1}^1\left(x_1\right)=e^{-{\left({\displaystyle \frac{x_1-50\ast \left(1\pm 10\%\right)}{10}}\right)}^2}, {\mu }_{M_1}^2\left(x_1\right)=e^{-{\left({\displaystyle \frac{x_1-60\ast \left(1\pm 10\%\right)}{10}}\right)}^2} \\ {\mu }_{M_2}^1\left(x_2\right)=e^{-{\left({\displaystyle \frac{x_2-50*\left(1\pm 10\%\right)}{10}}\right)}^2}, {\mu }_{M_2}^2\left(x_2\right)=e^{-{\left({\displaystyle \frac{x_2-60*\left(1\pm 10\%\right)}{10}}\right)}^2} \end{gathered}$$

The fuzzy basis function is

$$\begin{array}{c}{\xi }_{1l}=\left[{\displaystyle \frac{{\underset{¯}{\mu }}_{M_1}^1}{A}},{\displaystyle \frac{{\overline{\mu }}_{M_1}^2}{A}}\right], A={\underset{¯}{\mu }}_{M_1}^1+{\overline{\mu }}_{M_1}^2\\ {\xi }_{1r}=\left[{\displaystyle \frac{{\overline{\mu }}_{M_1}^1}{B}},{\displaystyle \frac{{\underset{¯}{\mu }}_{M_1}^2}{B}}\right], B={\overline{\mu }}_{M_1}^1+{\underset{¯}{\mu }}_{M_1}^2\\ {\xi }_{2l}=\left[{\displaystyle \frac{{\underset{¯}{\mu }}_{M_1}^1*{\underset{¯}{\mu }}_{M_2}^1}{C}},{\displaystyle \frac{{\underset{¯}{\mu }}_{M_1}^1*{\overline{\mu }}_{M_2}^2}{C}}\right.,{\displaystyle \frac{{\underset{¯}{\mu }}_{M_1}^2*{\underset{¯}{\mu }}_{M_2}^1}{C}},\left.{\displaystyle \frac{{\underset{¯}{\mu }}_{M_1}^2\ast {\overline{\mu }}_{M_2}^2}{C}}\right]\\ {\xi }_{2r}=\left[{\displaystyle \frac{{\overline{\mu }}_{M_1}^1*{\overline{\mu }}_{M_2}^1}{D}},{\displaystyle \frac{{\overline{\mu }}_{M_1}^1*{\underset{¯}{\mu }}_{M_2}^2}{D}},\right.{\displaystyle \frac{{\overline{\mu }}_{M_1}^2*{\overline{\mu }}_{M_2}^1}{D}},\left.{\displaystyle \frac{{\overline{\mu }}_{M_1}^2*{\underset{¯}{\mu }}_{M_2}^2}{D}}\right]\\ D={\overline{\mu }}_{M_1}^1*{\overline{\mu }}_{M_2}^1+{\overline{\mu }}_{M_1}^1*{\underset{¯}{\mu }}_{M_2}^2+{\overline{\mu }}_{M_1}^2*{\overline{\mu }}_{M_2}^1+{\overline{\mu }}_{M_1}^2*{\underset{¯}{\mu }}_{M_2}^2\\ {\xi }_{1l}={\left[{\xi }_{1l}^1,{\xi }_{1l}^2\right]}^T, {\xi }_{1r}={\left[{\xi }_{1r}^1,{\xi }_{1r}^2\right]}^T, {\xi }_{2l}={\left[{\xi }_{21l}^1,{\xi }_{22l}^2\right]}^T, {\xi }_{2r}={\left[{\xi }_{21r}^1,{\xi }_{22r}^2\right]}^T\end{array}$$

Step 2: We assume that the following language rules exist for the unknown functions 1, 2, respectively:

$$\mathrm{Unknown} \mathrm{function} 1: {\displaystyle \frac{1}{\frac{r}{K}+\lambda }}\left[r{x}_1\left(1-{\displaystyle \frac{x_1}{K}}\right)-{\dot{y}}_r\right]$$

$$\mathrm{Unknown} \mathrm{function} 2: {\displaystyle \frac{x_2+a}{m{x}_2}}\left(\lambda x_1{x}_2-\mu x_2-{\dot{\alpha }}_1\right)$$

The fuzzy rule for the unknown function 1 is as follows:

$$\begin{array}{c}{R}_{f1}^i: \mathrm{If} x_1\mathrm{is} {\tilde{A}}_1^i\mathrm{and} x_2\mathrm{is} {\tilde{A}}_2^i\mathrm{and} ... \mathrm{and} x_n\mathrm{is} {\tilde{A}}_n^i, \mathrm{then} N_{g1}^i={\displaystyle \sum _{i=1}^n\left(s_i+c_i{p}_i\right)}\\ R_{g1}^i: \mathrm{If} x_1\mathrm{is} {\tilde{A}}_1^i\mathrm{and} x_2\mathrm{is} {\tilde{A}}_2^i\mathrm{and} ... \mathrm{and} x_n\mathrm{is} {\tilde{A}}_n^i, \mathrm{then} N_{f1}^i={\displaystyle \sum _{i=1}^n\left(s_i+c_i{p}_i\right)}\end{array}$$

The fuzzy rule for the unknown function 2 is as follows:

$$\begin{array}{c}{R}_{f2}^i: \mathrm{If} x_1\mathrm{is} {\tilde{A}}_1^i\mathrm{and} x_2\mathrm{is} {\tilde{A}}_2^i\mathrm{and} ... \mathrm{and} x_n\mathrm{is} {\tilde{A}}_n^i, \mathrm{then} N_{g2}^i={\displaystyle \sum _{i=1}^n\left(s_i+c_i{p}_i\right)}\\ R_{g2}^i: \mathrm{If} x_1\mathrm{is} {\tilde{A}}_1^i\mathrm{and} x_2\mathrm{is} {\tilde{A}}_2^i\mathrm{and} ... \mathrm{and} x_n\mathrm{is} {\tilde{A}}_n^i, \mathrm{then} N_{f2}^i={\displaystyle \sum _{i=1}^n\left(s_i+c_i{p}_i\right)}\end{array}$$

Step 3: Design parameters are specified as follows:

$$\begin{array}{c}{k}_1=k_2=0.5, {\gamma }_{1l}={\gamma }_{2l}={\gamma }_{1r}={\gamma }_{2r}=1, {\gamma }_{f11r}={\gamma }_{f11l}={\gamma }_{g11l}={\gamma }_{g11r}=1\\ c_{1l}=c_{2l}=0.5, c_{1r}=c_{2r}=0.6, {\gamma }_{f12l}={\gamma }_{f12r}={\gamma }_{g12l}={\gamma }_{g12r}=3\\ {\gamma }_{f21r}={\gamma }_{f21l}={\gamma }_{g21l}={\gamma }_{g21r}=5, {\gamma }_{f22r}={\gamma }_{f22l}={\gamma }_{g22l}={\gamma }_{g22r}=7\end{array}$$

The first intermediate controller is designed as follows:

$${\alpha }_1=-k_1{e}_1-\left({\xi }_{1l}^T\left({\overline{x}}_1\right){\widehat{\mathrm{\Theta }}}_{1l}+{\xi }_{1r}^T\left({\overline{x}}_1\right){\widehat{\mathrm{\Theta }}}_{1r}\right)$$

The first intermediate adaptive law is designed as follows:

$$\begin{array}{c}{\dot{\widehat{\mathrm{\Theta }}}}_{1l}={\dot{\tilde{\mathrm{\Theta }}}}_{1l}={\gamma }_{1l}\left(e_1{\xi }_{1l}^T\left({\overline{x}}_1\right)-c_{1l}{\widehat{\mathrm{\Theta }}}_{1l}\right)\\ {\dot{\widehat{\mathrm{\Theta }}}}_{1r}={\dot{\tilde{\mathrm{\Theta }}}}_{1r}={\gamma }_{1r}\left(e_1{\xi }_{1r}^T\left({\overline{x}}_1\right)-c_{1r}{\widehat{\mathrm{\Theta }}}_{1r}\right)\\ s_{f11l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f11l0}\left(e_1{\xi }_{f11l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11l}{\theta }_{f11l}\right)\\ s_{f11r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f11r0}\left(e_1{\xi }_{f11r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11r}{\theta }_{f11r}\right)\\ s_{f12l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f12l0}\left(e_1{\xi }_{f12l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12l}{\theta }_{f12l}\right)\\ s_{f12r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f12r0}\left(e_1{\xi }_{f12r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12r}{\theta }_{f12r}\right)\\ p_{f11l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f11l0}\left(e_1{\xi }_{f11l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11l}{\theta }_{f11l}\right)\\ p_{f11r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f11l0}\left(e_1{\xi }_{f11r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f11r}{\theta }_{f11r}\right)\\ p_{f12l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f12l0}\left(e_1{\xi }_{f12l}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12l}{\theta }_{f12l}\right)\\ p_{f12r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f12r0}\left(e_1{\xi }_{f12r}^T\left(X_1\right)-{\mathsf{{\rm Y}}}_{f12r}{\theta }_{f12r}\right)\end{array}$$

The second intermediate controller is designed as follows:

$${\alpha }_2=-e_1-k_2{e}_2-\left({\xi }_{2l}^T\left({\overline{x}}_2\right){\widehat{\mathrm{\Theta }}}_{2l}+{\xi }_{2r}^T\left({\overline{x}}_2\right){\widehat{\mathrm{\Theta }}}_{2r}\right)$$

The second intermediate adaptive law is designed as follows:

$$\begin{array}{c}{\dot{\widehat{\mathrm{\Theta }}}}_{2l}={\dot{\tilde{\mathrm{\Theta }}}}_{2l}={\gamma }_{2l}\left(e_2{\xi }_{2l}^T\left({\overline{x}}_2\right)-c_{2l}{\widehat{\mathrm{\Theta }}}_{2l}\right)\\ {\dot{\widehat{\mathrm{\Theta }}}}_{2r}={\dot{\tilde{\mathrm{\Theta }}}}_{2r}={\gamma }_{2r}\left(e_2{\xi }_{2r}^T\left({\overline{x}}_2\right)-c_{2r}{\widehat{\mathrm{\Theta }}}_{2r}\right)\\ s_{f21l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f21l0}\left(e_2{\xi }_{f21l}^T\left(X_2\right)-{\mathsf{{\rm Y}}}_{f21l}{\theta }_{f21l}\right)\\ s_{f21r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f21r0}\left(e_2{\xi }_{f21r}^T\left(X_2\right)-{\mathsf{{\rm Y}}}_{f21r}{\theta }_{f21r}\right)\\ s_{g21l}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{g21l0}\left(e_2{\xi }_{g21l}^T\left(X_2\right)-{\mathsf{{\rm Y}}}_{g21l}{\theta }_{g21l}\right)\\ s_{g21r}\left(\eta +1\right)={\displaystyle \frac{{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)-s_i}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{g21r0}\left(e_2{\xi }_{g21r}^T\left(X_2\right)-{\mathsf{{\rm Y}}}_{g21r}{\theta }_{g21r}\right)\\ p_{f22l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f22l0}\left(e_2{\xi }_{f22l}^T\left(X_2\right)-{\mathsf{{\rm Y}}}_{f22l}{\theta }_{f22l}\right)\\ p_{f22r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{f22r0}\left(e_2{\xi }_{f22r}^T\left(X_2\right)-{\mathsf{{\rm Y}}}_{f22r}{\theta }_{f22r}\right)\\ p_{g22l}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{g22l0}\left(e_2{\xi }_{g22l}^T\left(X_2\right)-{\mathsf{{\rm Y}}}_{g22l}{\theta }_{g22l}\right)\\ p_{g22r}\left(\eta +1\right)={\displaystyle \frac{c_i\left(1-p_i\right){\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}}{{\left[{\displaystyle \sum _{m=1}^n\left(s_m+c_m{p}_m\right)}\right]}^2}}.{\tau }_{g22r0}\left(e_2{\xi }_{g22r}^T\left(X_2\right)-{\mathsf{{\rm Y}}}_{g22r}{\theta }_{g22r}\right)\end{array}$$

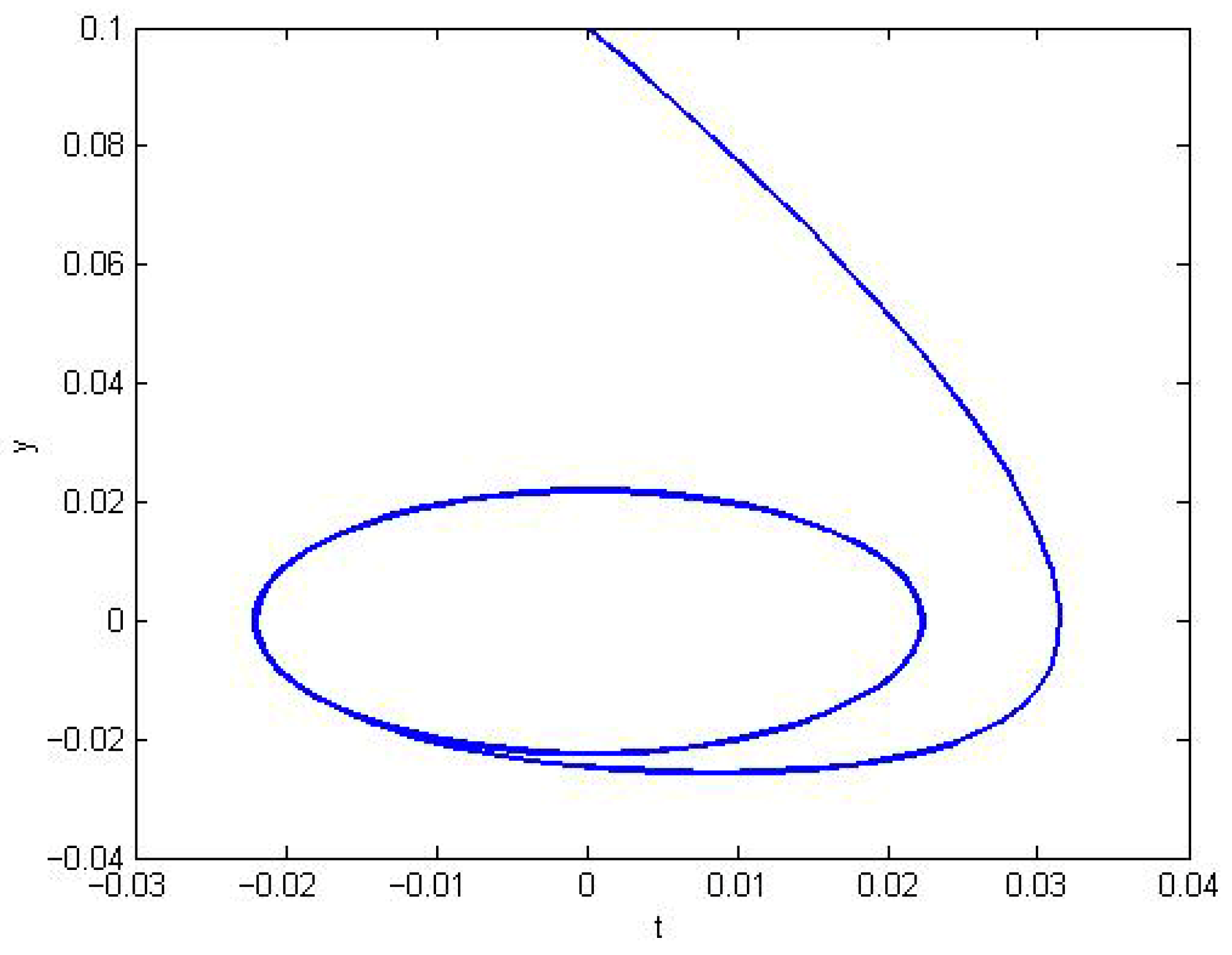
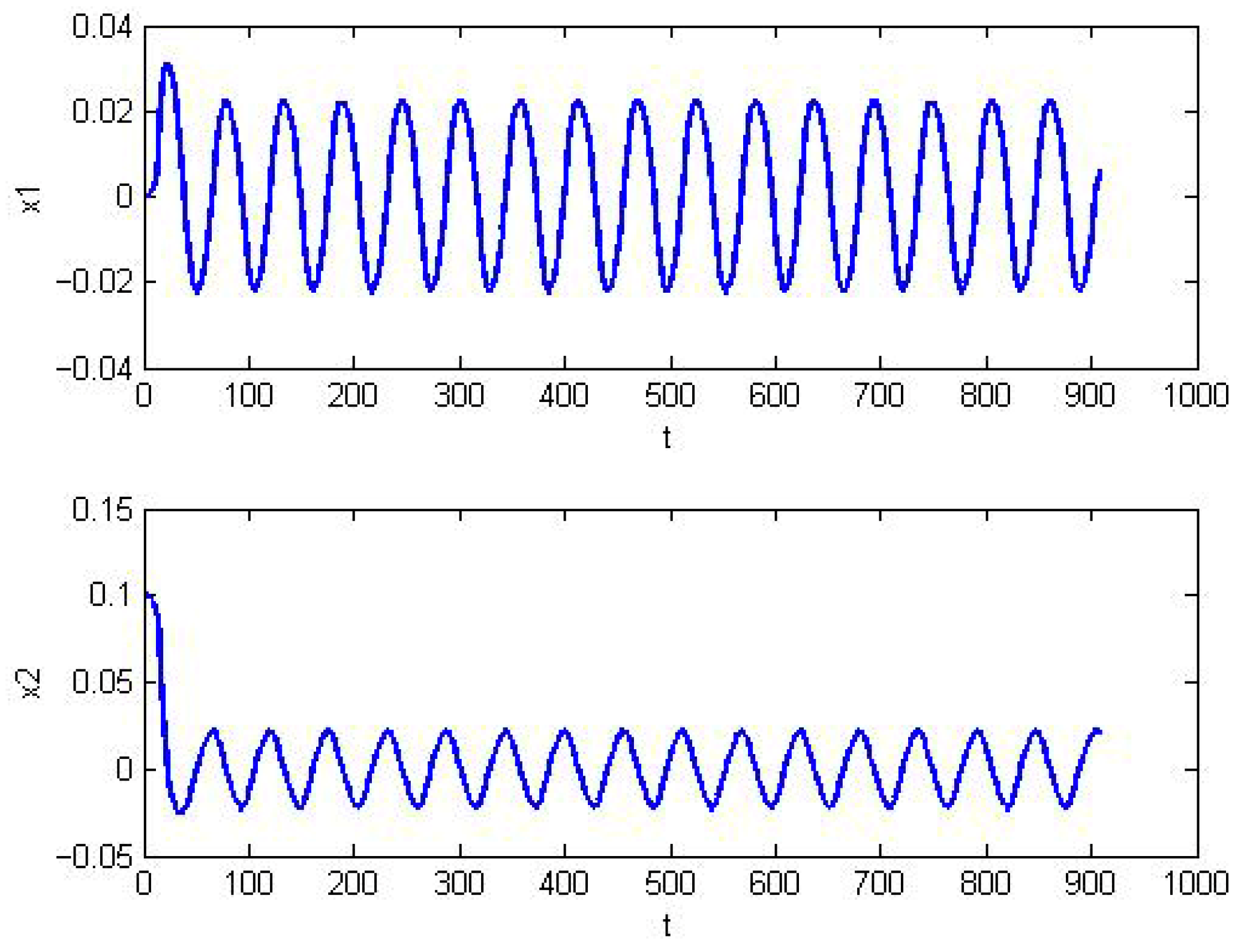
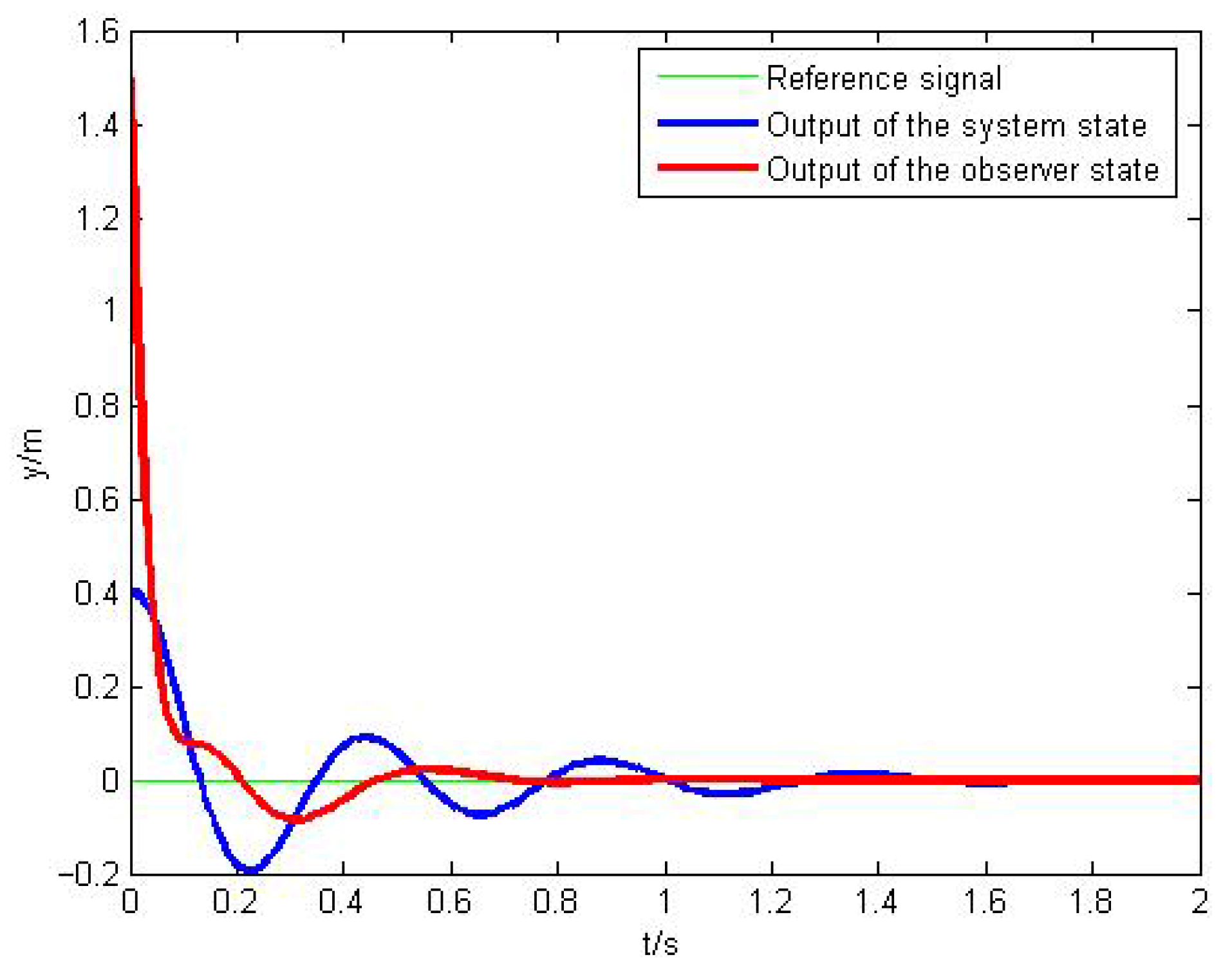
It can be seen from Figure 3 that after the system incorporates the Type-2 adaptive backstepping fuzzy controller, it undergoes a fundamental transformation, rapidly changing from a chaotic state to a stable and convergent state. The control method effectively suppresses chaotic oscillations. Figure 4 shows that the state variables quickly converge to near zero, which proves the excellent convergence and robustness of the controller.

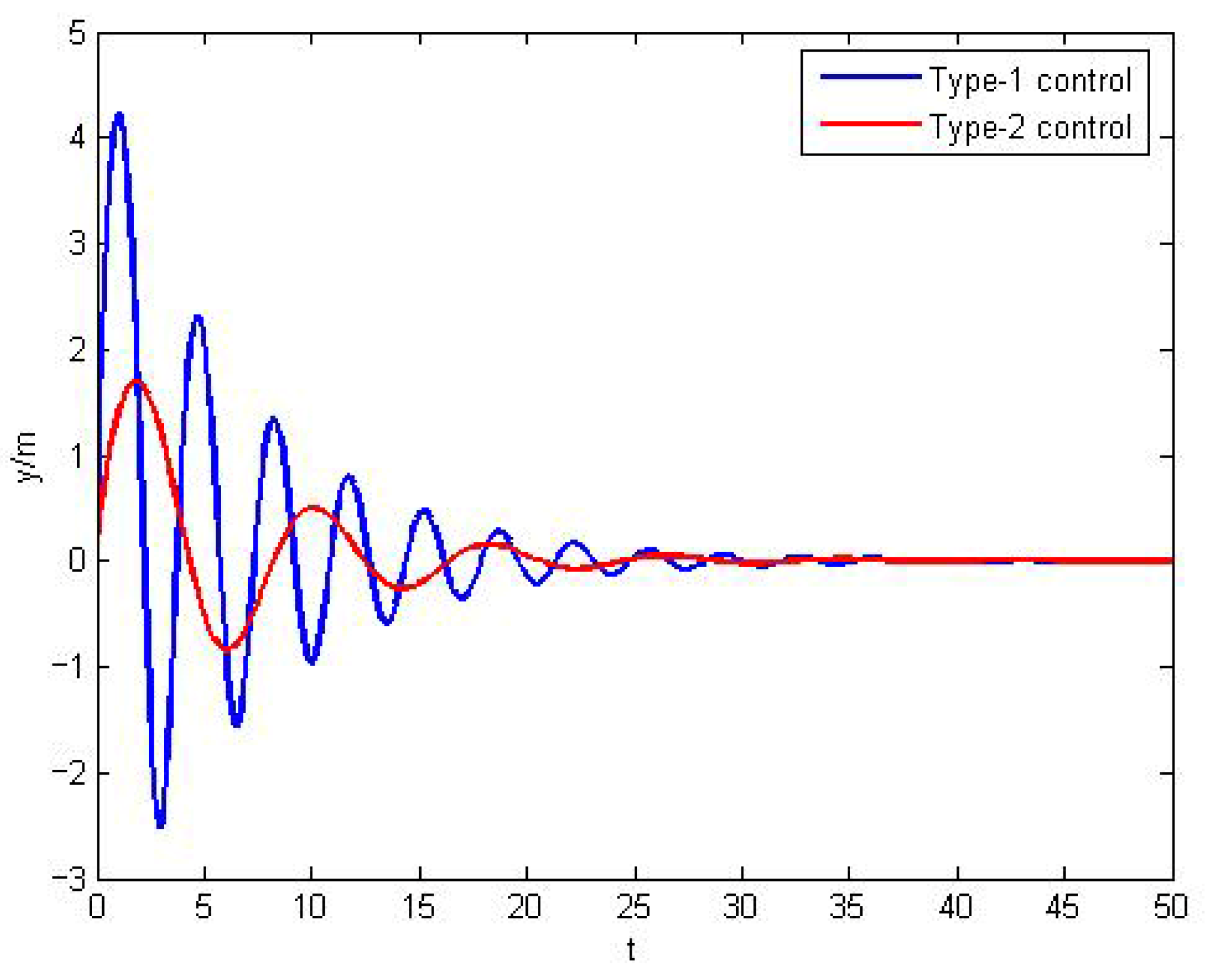
Figure 5 presents a comparative analysis of the control performance between the Type-2 and Type-1 adaptive backstepping controllers. The analysis shows the following: 1. Compared with the Type-1 controller, the Type-2 controller exhibits superior convergence performance. Its response curve can approach and stabilize near the target value more quickly. Quantitative analysis indicates that its convergence time is approximately 13.3% shorter than that of the Type-1 controller, demonstrating better convergence speed. 2. In terms of oscillation suppression and steady-state maintenance, the Type-2 controller performs significantly better, with a smaller fluctuation amplitude and smoother control effect. The dynamic error (peak–valley deviation) is reduced by about 40% compared with the Type-1 controller. Overall, the Type-2 adaptive backstepping control strategy demonstrates stronger robustness and a better control effect than the Type-1 strategy in handling system uncertainties. The quantitative data of the above qualitative analysis have been organized in

Table A1. Comparison of Type-2 and Type-1 fuzzy control.

Comparison Dimension	Conventional Type-1 Backstepping Control	Proposed Type-2 Backstepping T-S Fuzzy Control	Cost vs. Performance Analysis
Computational Complexity/Time Cost	Lower, due to the simpler Type-1 fuzzy inference.	Medium-high, primarily due to type-reduction (e.g., KM algorithm) and more online parameters.	The cost is necessary for higher robustness and better handling of uncertainties.
Convergence Time (Dynamic Performance)	Baseline (slower convergence).	Approximately 13.3% shorter (see Figure 5 and analysis).	Faster response improves dynamic stability.
Dynamic Error/Steady-state Accuracy	Baseline (larger oscillations).	Approximately 40% reduction (see Figure 5 and analysis).	Complex adaptation laws suppress oscillations and improve accuracy.
Reference Signal Tracking Performance	Poor, with long settling time and fluctuations (see Figure 7)	Fast, smooth tracking with short settling time (see Figure 7).	The combined method greatly enhances tracking accuracy and smoothness.
Disturbance Rejection Capability	Generally weaker (inferred from comparative studies)	Strong. Under disturbance, the system recovers and stabilizes quickly.	Extra computation enables real-time disturbance compensation.

.

Figure 6 shows that the controller and adaptive law designed based on Lyapunov stability theory can indeed ensure the global stability of the entire closed-loop system, and all signals are uniformly ultimately bounded.

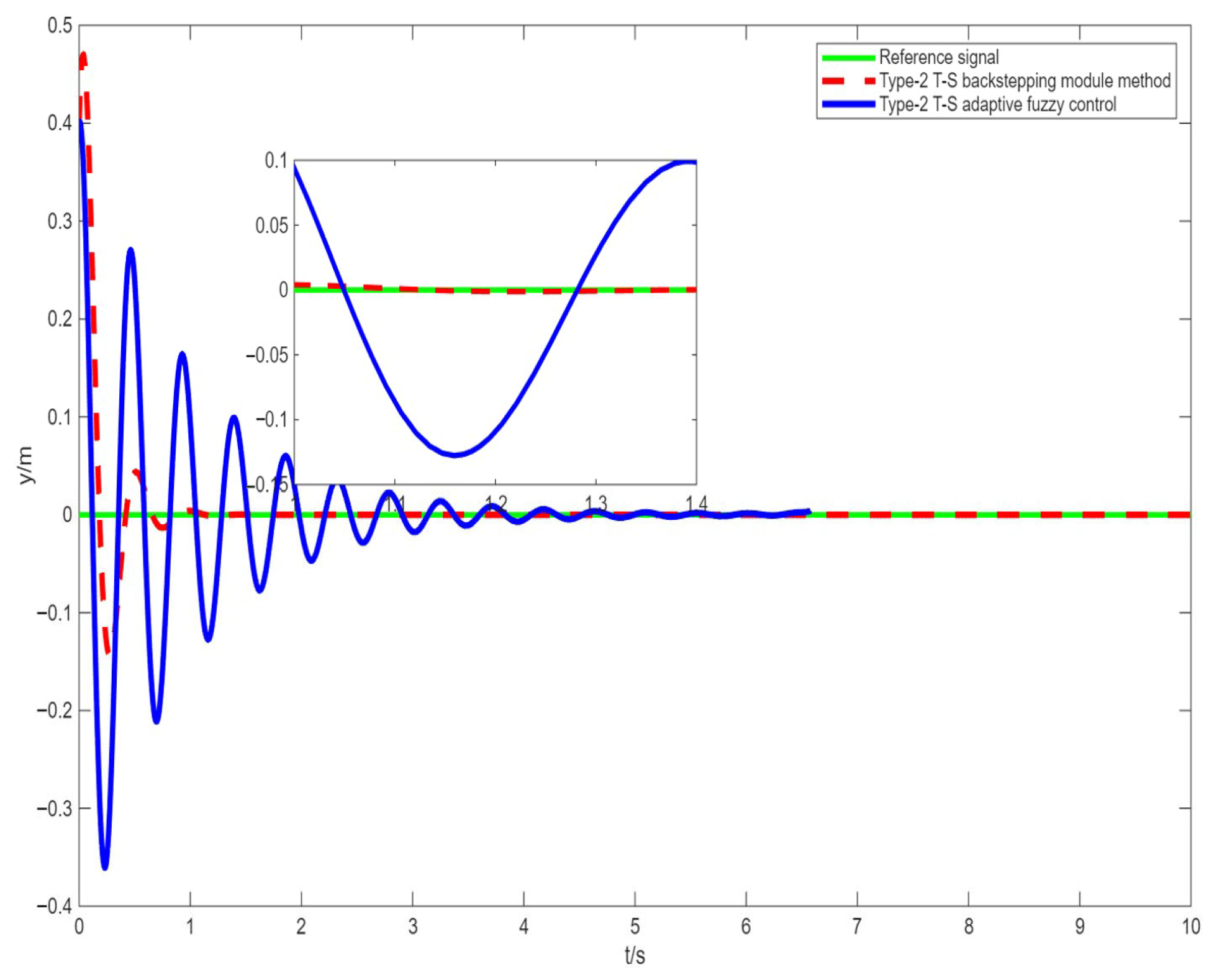
To further verify the effectiveness of the Type-2 T-S backstepping control method, an analytical comparison was conducted between the Type-2 T-S backstepping control and the Type-2 T-S adaptive fuzzy control, as shown in Figure 7. Among them, the green solid line represents the reference signal, the red dashed line represents the Type-2 T-S backstepping control, and the blue solid line represents the Type-2 T-S adaptive fuzzy control. It can be seen from Figure 7 that the Type-2 T-S backstepping control method can track the reference signal quickly and stably, approaching the reference signal and maintaining stability within a short period of time. In contrast, the Type-2 T-S adaptive fuzzy control exhibits large fluctuations in the initial stage, and it takes a long time to adjust before gradually stabilizing, with a large fluctuation range during the adjustment process.

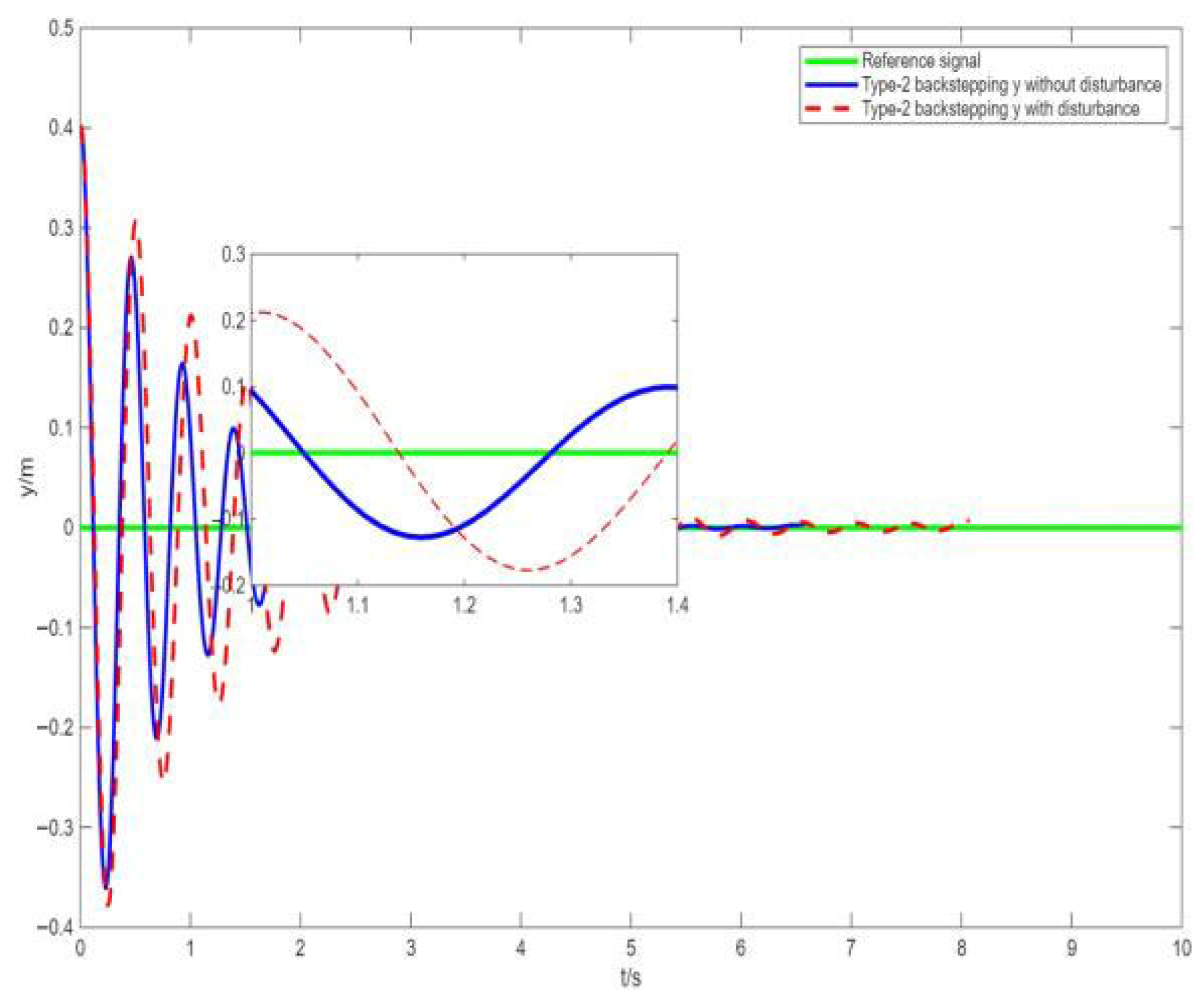
Figure 8 shows the variation in the system output over time under Type-2 backstepping control with and without interference. The blue line represents the system output based on Type-2 backstepping control in the absence of interference: there is oscillation in the initial stage, but the oscillation amplitude is relatively small, and the system output can quickly approach the reference signal. The red dashed line represents the system output under Type-2 backstepping control in the presence of interference; although the oscillation amplitude increases in the initial stage, it gradually approaches the reference signal afterward, indicating that this control method can still function effectively even when interference exists.

5. Conclusions

This study has addressed the challenge of controlling higher-order niche systems, which are characterized by complex nonlinearities and significant parametric uncertainties. To this end, a novel bio-inspired intelligent control strategy was developed by synergistically integrating interval Type-2 T-S fuzzy logic with the backstepping control framework. The key innovation lies in adopting the niche state-potential function as the consequent of the fuzzy rules, thereby directly embedding the ecological principle of “self-beneficial development” into the controller’s core. The global stability of the closed-loop system was rigorously guaranteed via Lyapunov theory, with corresponding adaptive laws derived for the controller parameters.

Comprehensive simulation results on a chaotic system model convincingly demonstrate the superiority of the proposed method. (1) In a comparative analysis, the Type-2 backstepping controller achieved a 13.3% reduction in convergence time and a 40% decrease in dynamic error compared to its Type-1 counterpart, confirming its enhanced performance in convergence speed and steady-state maintenance. (2) Furthermore, when compared to a standard Type-2 T-S adaptive fuzzy controller, the proposed method exhibited significantly better reference signal tracking accuracy and robustness against disturbances. These performance metrics not only validate the control efficacy but also reflect the adaptive and self-optimizing capabilities of biological systems that the method aims to emulate.

While the proposed method entails higher computational complexity than conventional approaches, its significant performance gains in precision and stability make it highly suitable for applications where these factors are critical, such as in ecological system management and other complex nonlinear systems.

In summary, this research contributes both a theoretically sound and practically effective solution for complex system control and provides valuable insights into bio-inspired intelligent design. Future work will focus on streamlining the computational algorithms for real-time implementation and exploring its potential in burgeoning fields like medical robotics and smart energy microgrids.