HGREncoder: Enhancing Real-Time Hand Gesture Recognition with Transformer Encoder—A Comparative Study
Abstract
1. Introduction
1.1. Research Objective
1.2. Specific Objectives
- 1.
- Analyze the literature on neural network architectures for HGR, focusing on models that have employed transformer neural networks over the past five years, in order to gain a deeper understanding of the existing scientific literature on this topic.
- 2.
- Develop a real-time HGR model for five right-hand gestures using a transformer neural network, using the EMG-EPN-612 dataset to address generalization challenges, remove spurious labels, and improve recognition accuracy.
- 3.
- Compare the performance of the proposed model with existing models in the HGR field, evaluating their classification and recognition accuracy.
1.3. Hypothesis
1.4. Problems Addressed by the Study
2. Literature Review
- Invasive methods stand out for their ability to detect the electromyographic signal of a specific muscle, which allows muscle movements to be monitored with great precision. Invasive methods necessitate the insertion of intramuscular electrodes, which demands specialized skills from the installer [19,20].
- Non-invasive methods are those that do not require penetrating the person’s skin. Unlike invasive methods, non-invasive methods are easy to use and apply, making them easy to use even for people with little knowledge [19].
2.1. Machine Learning Models for Hand Gesture Recognition
2.2. Transformers in Hand Gesture Recognition
2.3. Research Gap
3. Materials and Methods
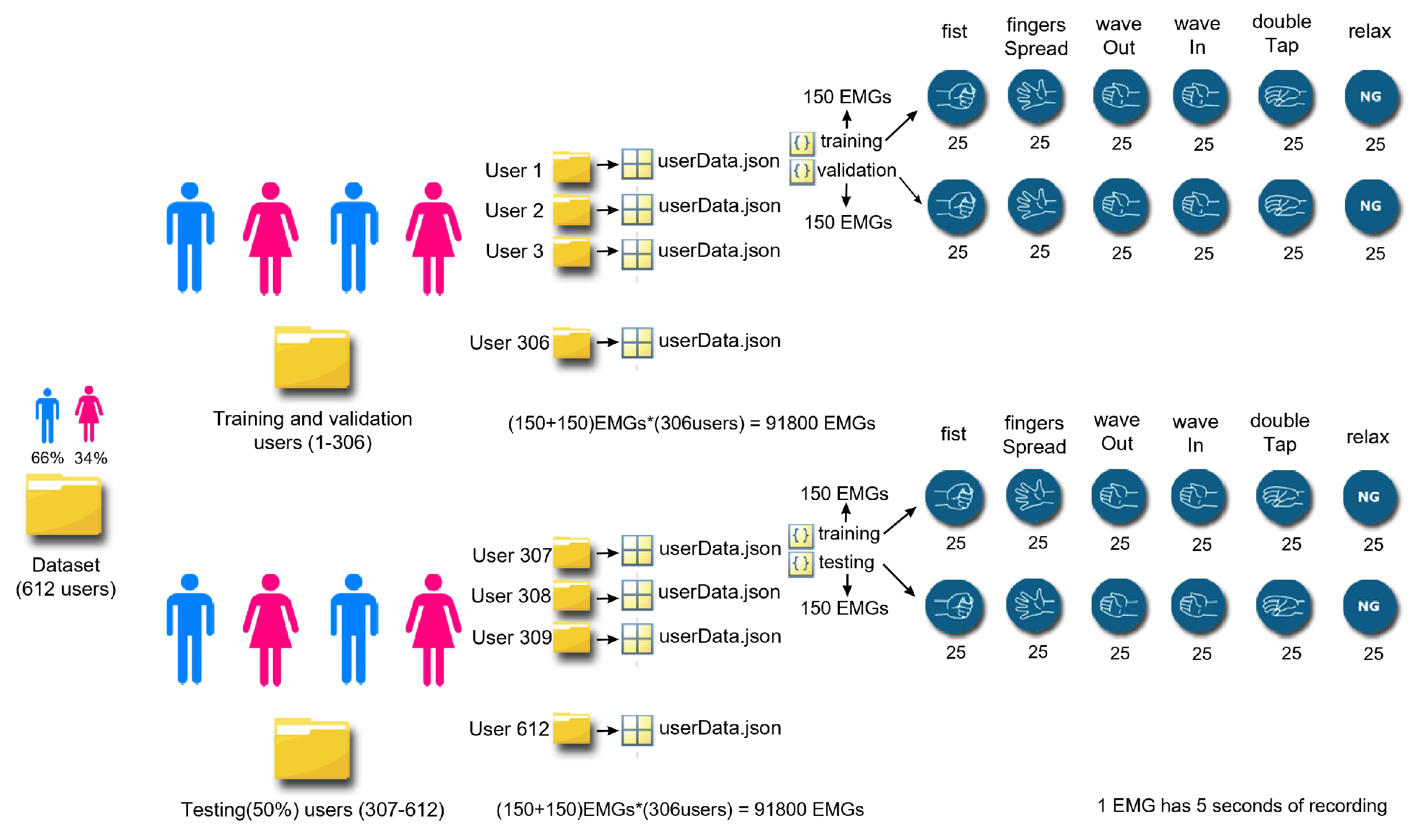
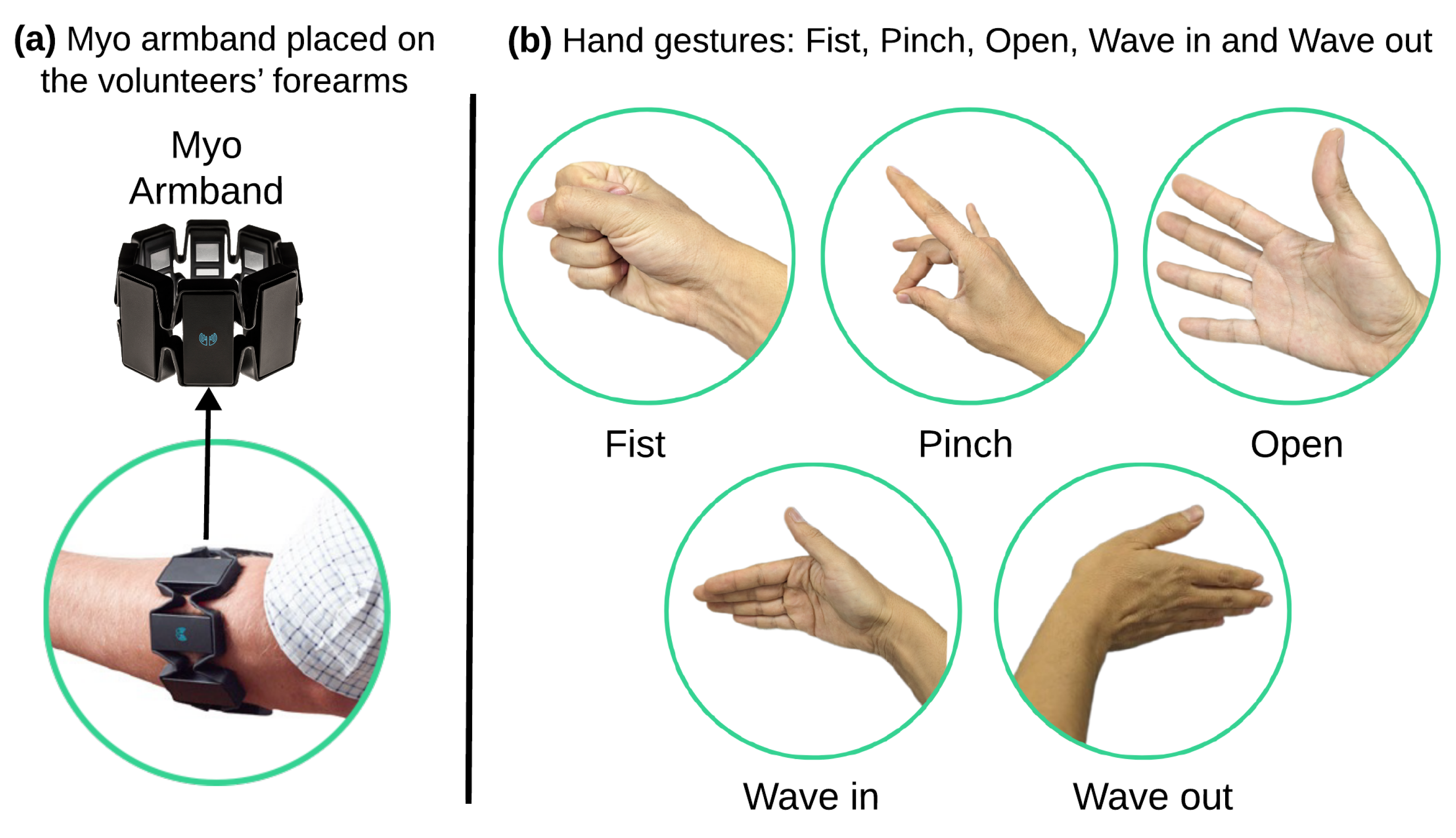
3.1. Dataset
3.1.1. Origin of the Dataset
3.1.2. Characteristics of the Dataset
3.1.3. Comparison with Other Datasets
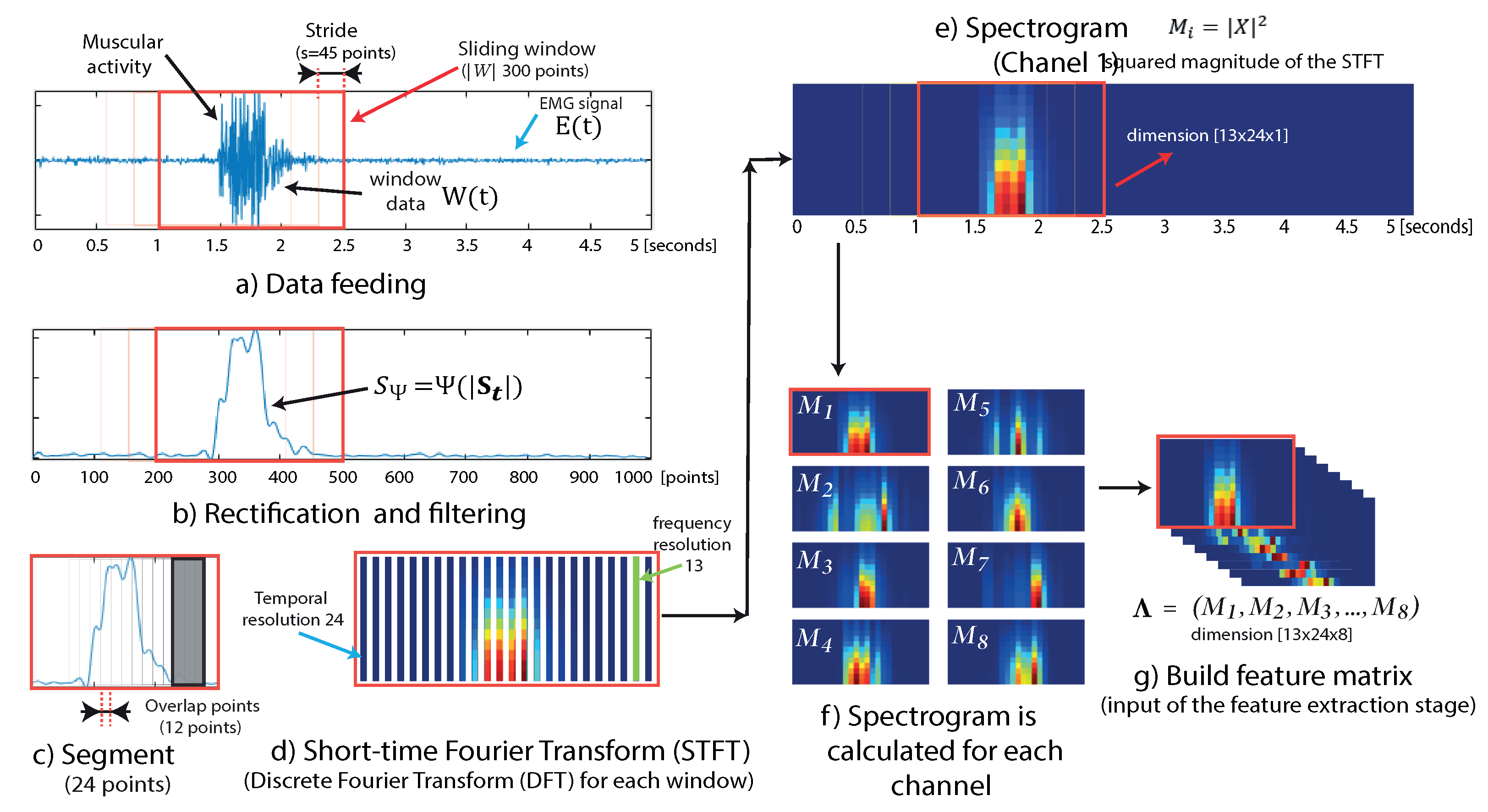
3.2. Data Preprocessing
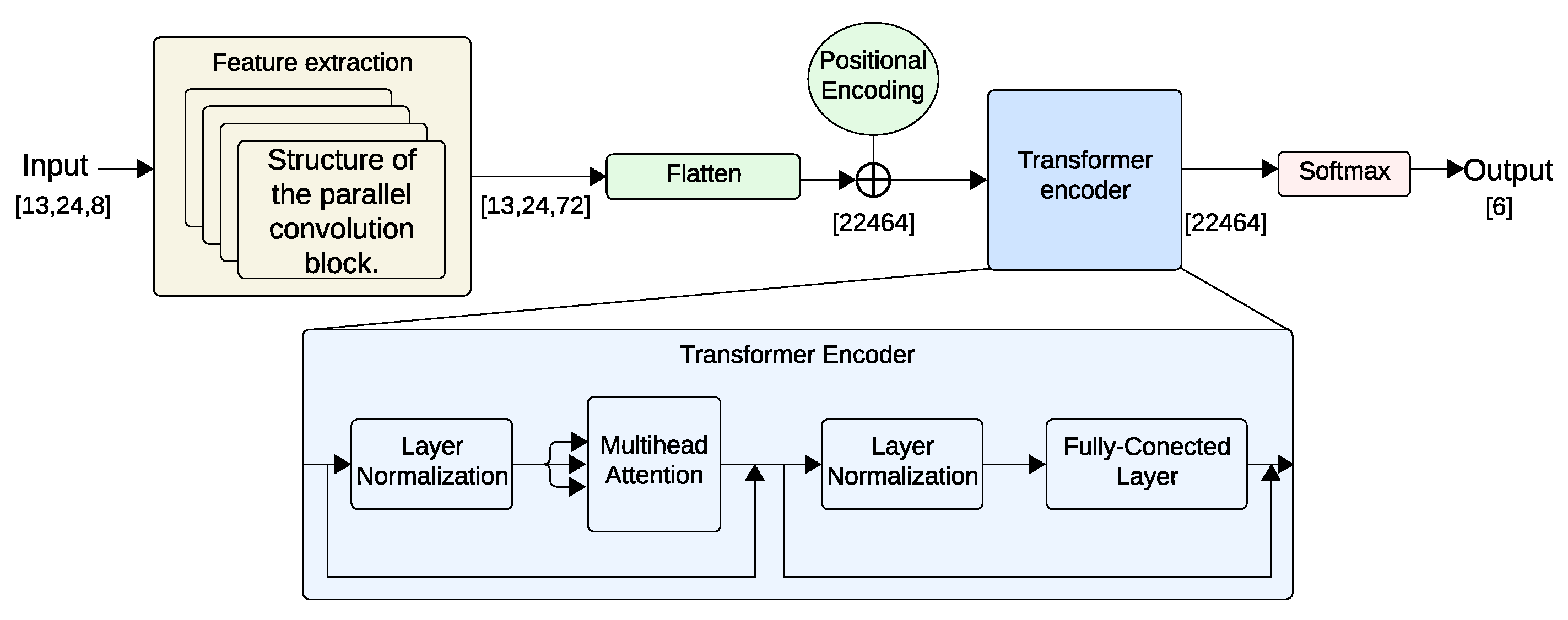
3.3. Feature Extraction
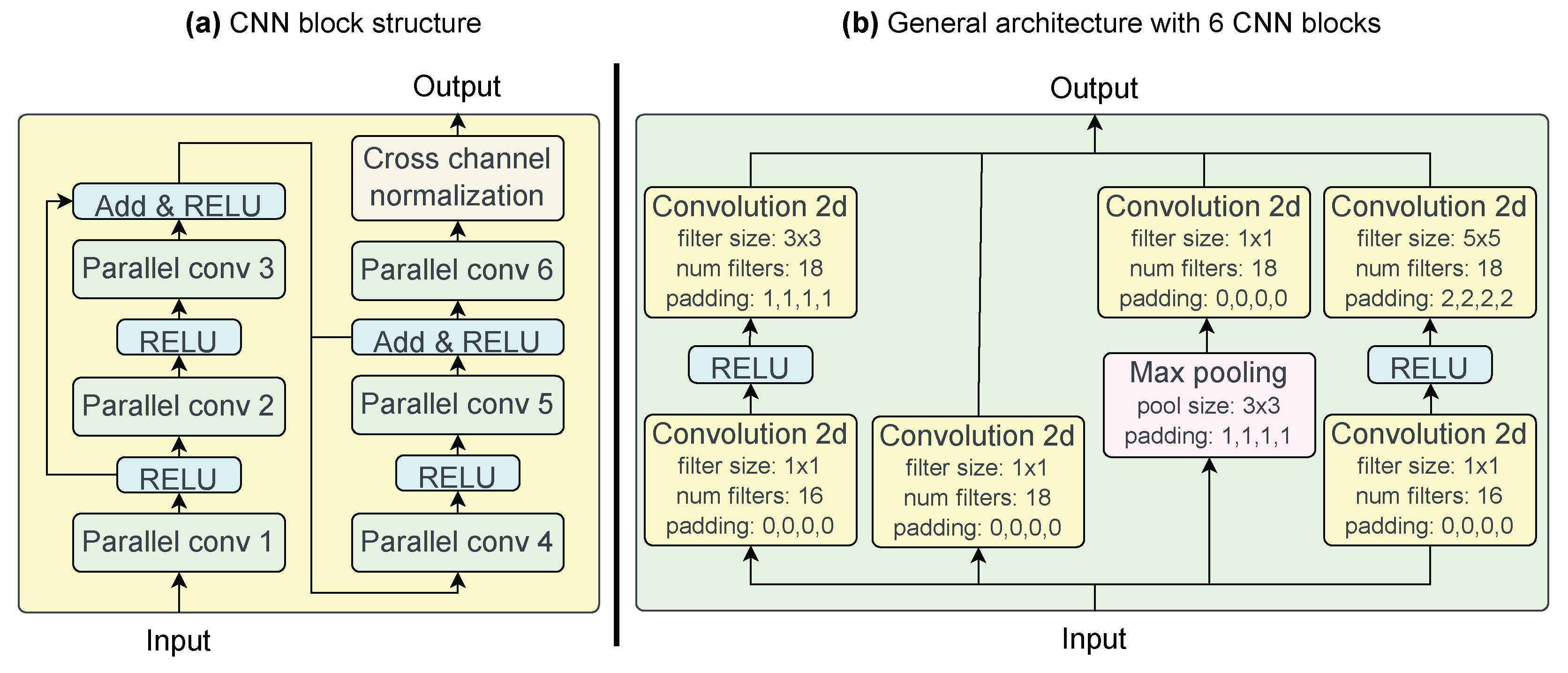
3.4. Architecture
3.4.1. Overview of Transformer Architecture
- •
- Input Embedding: Involves representing input tokens as vectors in a high-dimensional space.
- •
- Positional Encoding: Adds positional information to the input sequence.
- •
- The Encoder: Processes the signal and transforms it into an abstract representation.
- •
- The Decoder: Uses this representation to generate an output sequence.

3.4.2. Positional Encoding
3.4.3. Encoder
3.4.4. Multi-Head Attention
3.5. Customization for Hand Gesture Recognition
- 1.
- A positional encoding layer that assigns an additional value to each position in the sequence.
- 2.
- The processed sequence then passes through 8 heads (multi-head attention). The different details of the sequence will be attended simultaneously by each attention head.
- 3.
- After the attention stage, the sequence moves through a fully connected layer.
- 4.
- Between the layers of multi-head attention and fully connected layer, normalization is applied to both the inputs and outputs of these layers, mitigating issues such as overflow and gradient vanishing, ensuring more efficient convergence.
- 5.
- Finally, a Softmax function is applied to the 6 possible gesture categories, including the “noGesture” class.
3.6. Training and Validation
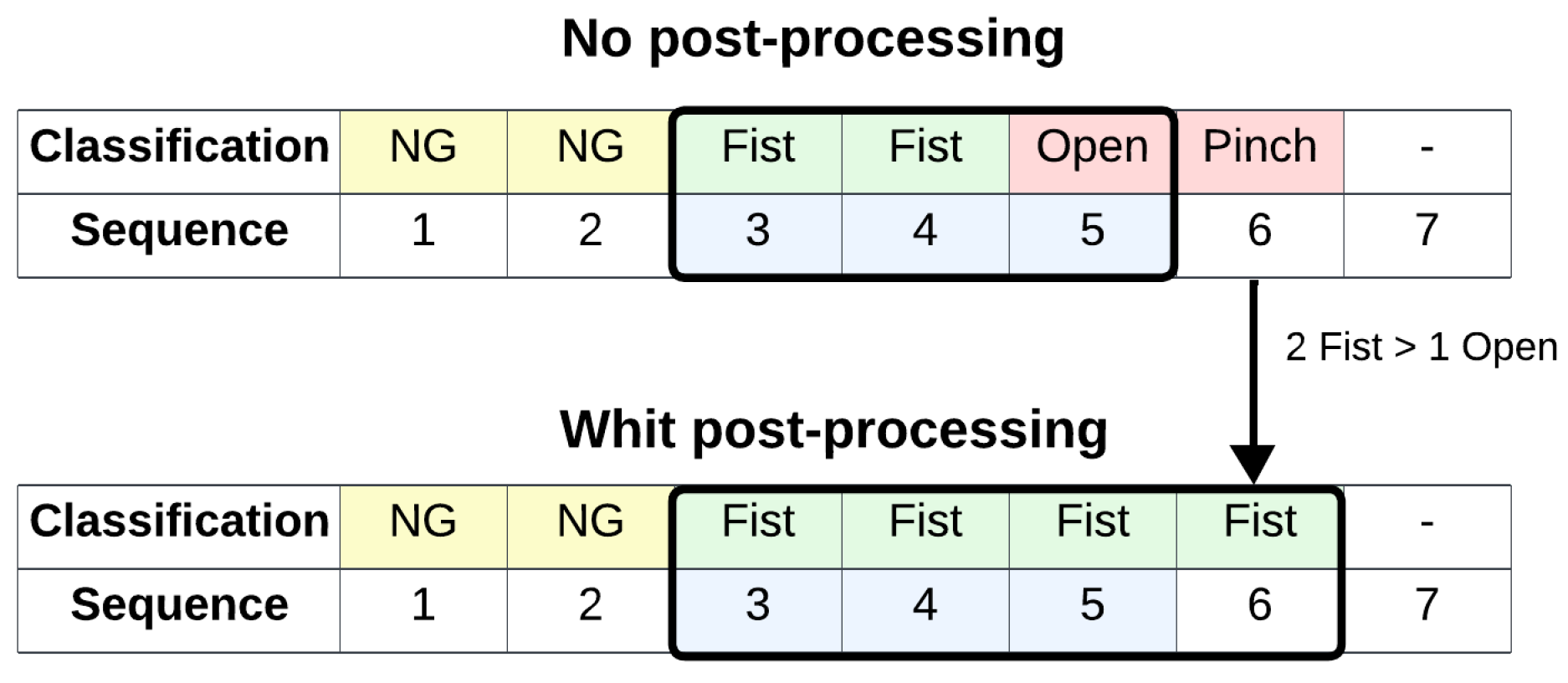
3.7. Post-Processing
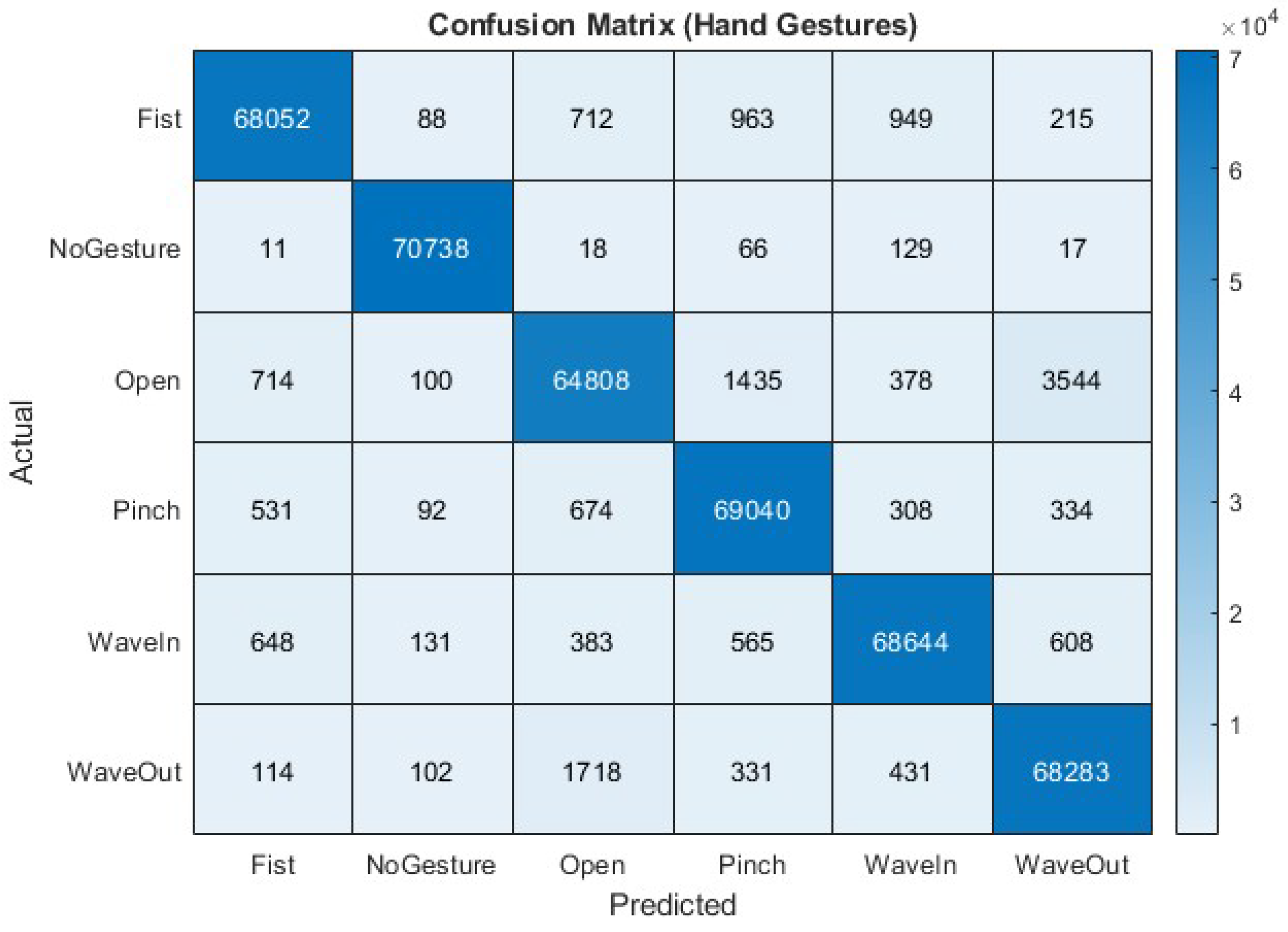
4. Results
4.1. Evaluation Metrics
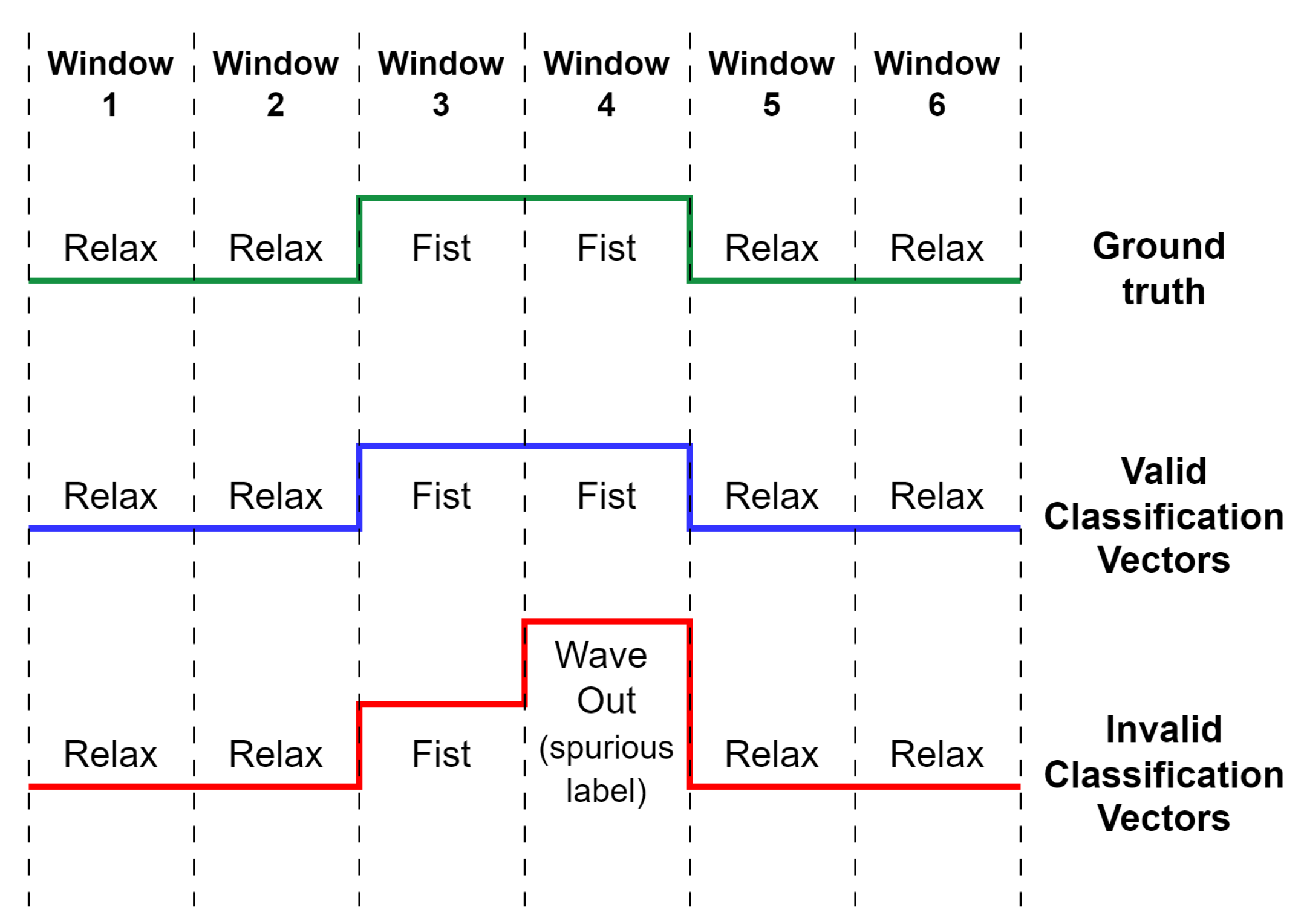
- Prediction Vector Validity: The prediction vector is considered valid only when it does not present discontinuities throughout its classification. That is, it does not have spurious labels.
- Classification Accuracy: Classification accuracy refers to the proportion of gestures correctly classified by the model.
- Recognition Accuracy: Recognition accuracy goes beyond classification. Recognition is based on the presence of a valid prediction vector, which maintains a single designated label over time.
- Standard Deviation: It is a statistical measure of dispersion used to understand the variability present in a dataset. In this case, the standard deviation refers to the variability between the users’ mean values.
- Overlap: The overlap is a percentage value. This value represents the percentage by which the prediction vector overlaps with the ground truth at a given time. Ground truth refers to the manually labeled actual values that serve as a reference for evaluating the accuracy of the model’s predictions.
- Processing Time: Records the time it takes for the model to process and assign a label to a gesture. This metric is essential to evaluate the model in real-time. In this work, a model must respond in less than 300 ms for its response to be considered real-time according to [47].
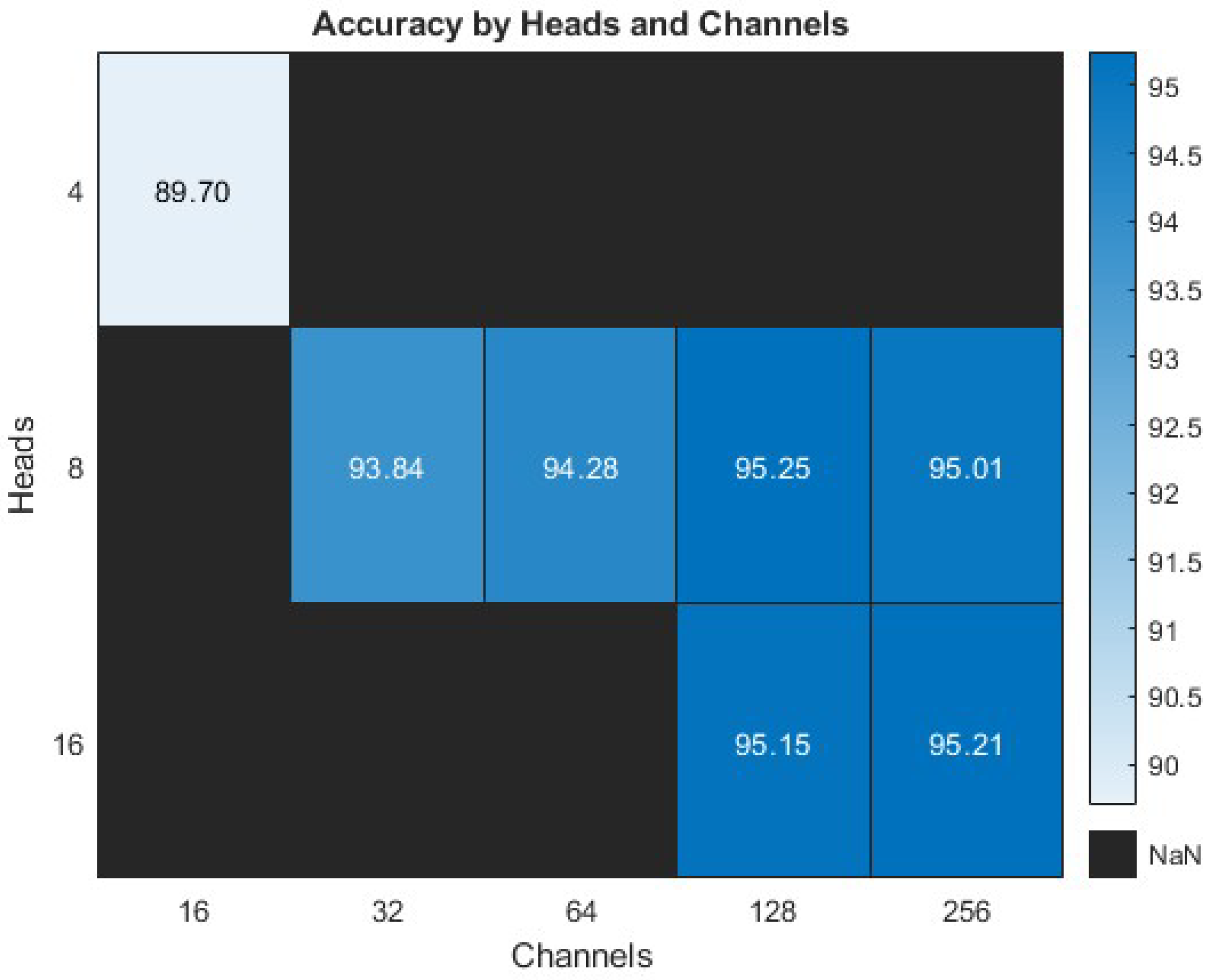
4.2. Training Results
- •
- Precision: Proportion of true positive predictions among all positive predictions. Measures accuracy when the model predicts a positive class.
- •
- Recall: Proportion of true positive predictions among all actual positives. Measures the model’s ability to capture all positive instances.
- •
- F1 Score: Harmonic mean of precision and recall. Balances precision and recall, providing a single metric.
- •
- Specificity: Proportion of true negative predictions among all actual negatives. Measures accuracy when the model predicts a negative class.
| Class | Precision | Recall | F1 Score | Specificity |
|---|---|---|---|---|
| Fist | 97.12% | 95.88% | 96.49% | 99.43% |
| NoGesture | 99.28% | 99.66% | 99.47% | 99.86% |
| Open | 94.87% | 91.31% | 93.05% | 99.01% |
| Pinch | 95.36% | 97.27% | 96.30% | 99.05% |
| WaveIn | 96.90% | 96.71% | 96.81% | 99.38% |
| WaveOut | 93.54% | 96.20% | 94.85% | 98.67% |
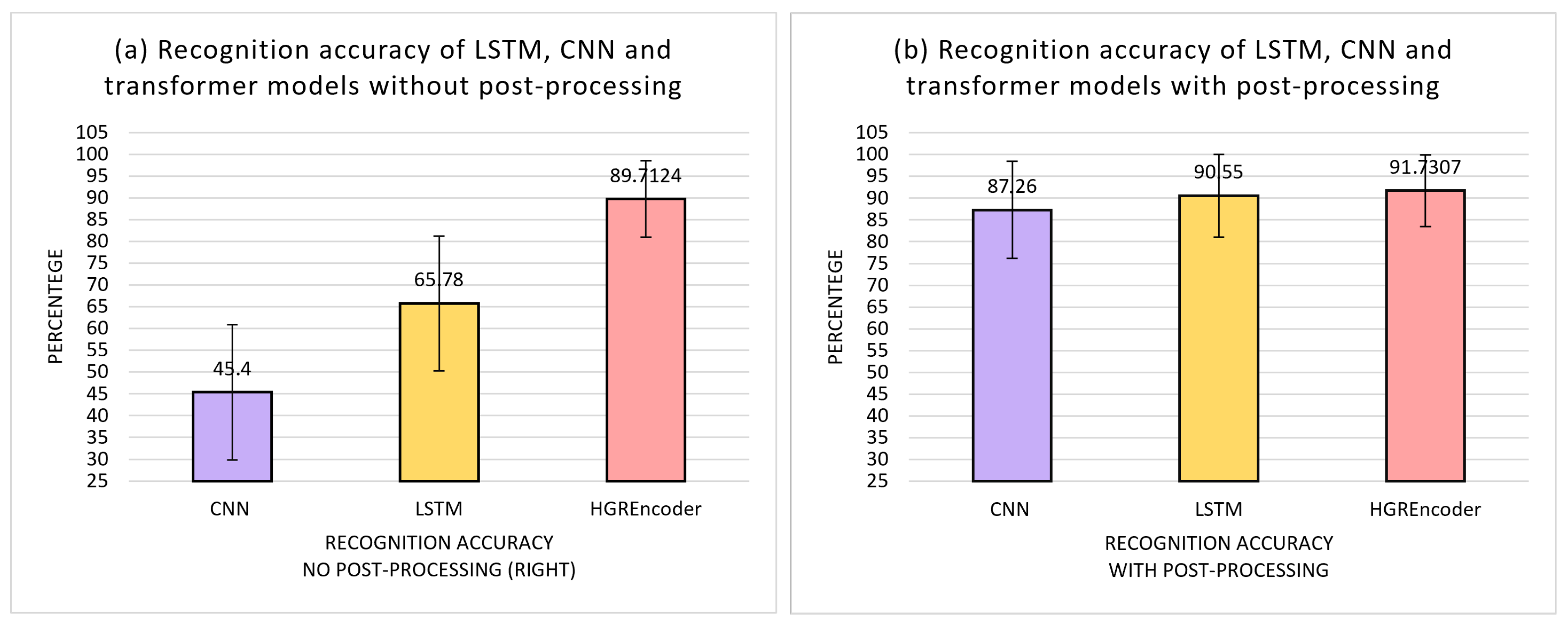
4.3. Test Results
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saggio, G.; Cavallo, P.; Ricci, M.; Errico, V.; Zea, J.; Benalcázar, M.E. Sign language recognition using wearable electronics: Implementing K-nearest neighbors with dynamic time warping and convolutional neural network algorithms. Sensors 2020, 20, 3879. [Google Scholar] [CrossRef]
- Koh, J.I.; Cherian, J.; Taele, P.; Hammond, T. Developing a hand gesture recognition system for mapping symbolic hand gestures to analogous emojis in computer-mediated communication. ACM Trans. Interact. Intell. Syst. 2019, 9, 1–35. [Google Scholar] [CrossRef]
- Simon, A.M.; Turner, K.L.; Miller, L.A.; Dumanian, G.A.; Potter, B.K.; Beachler, M.D.; Hargrove, L.J.; Kuiken, T.A. Myoelectric prosthesis hand grasp control following targeted muscle reinnervation in individuals with transradial amputation. PLoS ONE 2023, 18, e0280210. [Google Scholar] [CrossRef] [PubMed]
- Godoy, R.V.; Dwivedi, A.; Liarokapis, M. Electromyography Based Decoding of Dexterous, In-Hand Manipulation Motions With Temporal Multichannel Vision Transformers. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2207–2216. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.K.; Lim, K.M.; Chang, R.K.Y.; Lee, C.P.; Alqahtani, A. HGR-ViT: Hand Gesture Recognition with Vision Transformer. Sensors 2023, 23, 5555. [Google Scholar] [CrossRef] [PubMed]
- Montazerin, M.; Zabihi, S.; Rahimian, E.; Mohammadi, A.; Naderkhani, F. ViT-HGR: Vision Transformer-based Hand Gesture Recognition from High Density Surface EMG Signals. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, Scotland, UK, 11–15 July 2022; pp. 5115–5119. [Google Scholar] [CrossRef]
- Birkeland, S.; Fjeldvik, L.J.; Noori, N.; Yeduri, S.R.; Cenkeramaddi, L.R. Thermal video-based hand gestures recognition using lightweight CNN. J. Ambient Intell. Humaniz. Comput. 2024, 15, 3849–3860. [Google Scholar] [CrossRef]
- Ahmed, I.T.; Gwad, W.H.; Hammad, B.T.; Alkayal, E. Enhancing Hand Gesture Image Recognition by Integrating Various Feature Groups. Technologies 2025, 13, 164. [Google Scholar] [CrossRef]
- Jaramillo-Yánez, A.; Benalcázar, M.E.; Mena-Maldonado, E. Real-time hand gesture recognition using surface electromyography and machine learning: A systematic literature review. Sensors 2020, 20, 2467. [Google Scholar] [CrossRef]
- Vásconez, J.P.; López, L.I.B.; Ángel Leonardo Valdivieso Caraguay; Benalcázar, M.E. Hand Gesture Recognition Using EMG-IMU Signals and Deep Q-Networks. Sensors 2022, 22, 9613. [Google Scholar] [CrossRef]
- Benalcázar, M.E.; Motoche, C.; Zea, J.A.; Jaramillo, A.G.; Anchundia, C.E.; Zambrano, P.; Segura, M.; Benalcázar Palacios, F.; Pérez, M. Real-time hand gesture recognition using the Myo armband and muscle activity detection. In Proceedings of the 2017 IEEE Second Ecuador Technical Chapters Meeting (ETCM), Salinas, Ecuador, 16–20 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Valdivieso Caraguay, A.L.; Vásconez, J.P.; Barona López, L.I.; Benalcázar, M.E. Recognition of Hand Gestures Based on EMG Signals with Deep and Double-Deep Q-Networks. Sensors 2023, 23, 3905. [Google Scholar] [CrossRef]
- Anastasiev, A.; Kadone, H.; Marushima, A.; Watanabe, H.; Zaboronok, A.; Watanabe, S.; Matsumura, A.; Suzuki, K.; Matsumaru, Y.; Nishiyama, H.; et al. A Novel Bilateral Data Fusion Approach for EMG-Driven Deep Learning in Post-Stroke Paretic Gesture Recognition. Sensors 2025, 25, 3664. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zabihi, S.; Rahimian, E.; Asif, A.; Mohammadi, A. TraHGR: Transformer for Hand Gesture Recognition via ElectroMyography. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 4211–4224. [Google Scholar] [CrossRef] [PubMed]
- Barona López, L.I.; Ferri, F.M.; Zea, J.; Ángel Leonardo Valdivieso Caraguay; Benalcázar, M.E. CNN-LSTM and post-processing for EMG-based hand gesture recognition. Intell. Syst. Appl. 2024, 22, 200352. [Google Scholar] [CrossRef]
- Jiang, Y.; Song, L.; Zhang, J.; Song, Y.; Yan, M. Multi-Category Gesture Recognition Modeling Based on sEMG and IMU Signals. Sensors 2022, 22, 5855. [Google Scholar] [CrossRef]
- Benalcázar, M.; Barona, L.; Valdivieso, L.; Aguas, X.; Zea, J. EMG-EPN-612 Dataset. 2020. Available online: http://dx.doi.org/10.5281/zenodo.4421500 (accessed on 18 July 2025).
- Merletti, R. Electromyography: Physiology, Engineering, and Non-Invasive Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 11. [Google Scholar] [CrossRef]
- Péter, A.; Andersson, E.; Hegyi, A.; Finni, T.; Tarassova, O.; Cronin, N.J.; Grundström, H.; Arndt, A. Comparing Surface and Fine-Wire Electromyography Activity of Lower Leg Muscles at Different Walking Speeds. Front. Physiol. 2019, 10, 1283. [Google Scholar] [CrossRef]
- Kyranou, I.; Vijayakumar, S.; Erden, M.S. Causes of performance degradation in non-invasive electromyographic pattern recognition in upper limb prostheses. Front. Neurorobotics 2018, 12, 58. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, D.; Jiang, L.; Zhang, H.; Liu, H.; Kotani, K. A Novel Unsupervised Adaptive Learning Method for Long-Term Electromyography (EMG) Pattern Recognition. Sensors 2017, 17, 1370. [Google Scholar] [CrossRef]
- Schulte, R.V.; Prinsen, E.C.; Buurke, J.H.; Poel, M. Adaptive Lower Limb Pattern Recognition for Multi-Day Control. Sensors 2022, 22, 6351. [Google Scholar] [CrossRef]
- Jiang, N.; Muceli, S.; Graimann, B.; Farina, D. Effect of arm position on the prediction of kinematics from EMG in amputees. Med Biol. Eng. Comput. 2013, 51, 143–151. [Google Scholar] [CrossRef]
- Zhai, X.; Jelfs, B.; Chan, R.H.; Tin, C. Self-recalibrating surface EMG pattern recognition for neuroprosthesis control based on convolutional neural network. Front. Neurosci. 2017, 11, 379. [Google Scholar] [CrossRef]
- He, J.; Zhang, D.; Jiang, N.; Sheng, X.; Farina, D.; Zhu, X. User adaptation in long-term, open-loop myoelectric training: Implications for EMG pattern recognition in prosthesis control. J. Neural Eng. 2015, 12, 046005. [Google Scholar] [CrossRef] [PubMed]
- Côté-Allard, U.; Fall, C.L.; Drouin, A.; Campeau-Lecours, A.; Gosselin, C.; Glette, K.; Laviolette, F.; Gosselin, B. Deep Learning for Electromyographic Hand Gesture Signal Classification Using Transfer Learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 760–771. [Google Scholar] [CrossRef] [PubMed]
- Unanyan, N.; Belov, A. Case Study: Influence of Muscle Fatigue and Perspiration on the Recognition of the EMG Signal. Adv. Syst. Sci. Appl. 2021, 21, 58–70. [Google Scholar] [CrossRef]
- Espinoza, D.L.; Velasco, L.E.S. Comparison of EMG Signal Classification Algorithms for the Control of an Upper Limb Prosthesis Prototype; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; Volume 11. [Google Scholar] [CrossRef]
- Zhou, H.; Thanh Le, H.; Zhang, S.; Lam Phung, S.; Alici, G. Hand Gesture Recognition From Surface Electromyography Signals With Graph Convolutional Network and Attention Mechanisms. IEEE Sens. J. 2025, 25, 9081–9092. [Google Scholar] [CrossRef]
- Barona López, L.I.; Valdivieso Caraguay, A.L.; Vimos, V.H.; Zea, J.A.; Vásconez, J.P.; Álvarez, M.; Benalcázar, M.E. An Energy-Based Method for Orientation Correction of EMG Bracelet Sensors in Hand Gesture Recognition Systems. Sensors 2020, 20, 6327. [Google Scholar] [CrossRef]
- Chung, E.A.; Benalcázar, M.E. Real-Time Hand Gesture Recognition Model Using Deep Learning Techniques and EMG Signals. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), A Coruña, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Jaramillo-Yanez, A.; Unapanta, L.; Benalcázar, M.E. Short-Term Hand Gesture Recognition using Electromyography in the Transient State, Support Vector Machines, and Discrete Wavelet Transform. In Proceedings of the 2019 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Guayaquil, Ecuador, 11–15 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Alaparthi, S.; Mishra, M. Bidirectional Encoder Representations from Transformers (BERT): A sentiment analysis odyssey. arXiv 2020, arXiv:2007.01127. [Google Scholar] [CrossRef]
- Llinet Benavides, C.; Manso-Callejo, M.A.; Cira, C.I. BERT (Bidirectional Encoder Representations from Transformers) for Missing Data Imputation in Solar Irradiance Time Series. Eng. Proc. 2023, 39, 26. [Google Scholar]
- Montazerin, M.; Rahimian, E.; Naderkhani, F.; Atashzar, S.; Yanushkevich, S.; Mohammadi, A. Transformer-based hand gesture recognition from instantaneous to fused neural decomposition of high-density EMG signals. Sci. Rep. 2023, 13, 11000. [Google Scholar] [CrossRef]
- Benalcázar, M.E.; Ángel Leonardo Valdivieso Caraguay; López, L.I.B. A user-specific hand gesture recognition model based on feed-forward neural networks, emgs, and correction of sensor orientation. Appl. Sci. 2020, 10, 8604. [Google Scholar] [CrossRef]
- Laboratorio de Investigación en Inteligencia y Visión Artificial. Escuela Politécnica Nacional, 2024. Available online: https://laboratorio-ia.epn.edu.ec/es/ (accessed on 15 August 2025).
- Atzori, M.; Gijsberts, A.; Castellini, C.; Caputo, B.; Hager, A.G.; Elsig, S.; Giatsidis, G.; Bassetto, F.; Müller, H. Electromyography data for non-invasive naturally-controlled robotic hand prostheses. Sci. Data 2014, 1, 140053. [Google Scholar] [CrossRef]
- Eddy, E.; Campbell, E.; Bateman, S.; Scheme, E. Big data in myoelectric control: Large multi-user models enable robust zero-shot EMG-based discrete gesture recognition. Front. Bioeng. Biotechnol. 2024, 12, 2024. [Google Scholar] [CrossRef]
- Vásconez, J.P.; Barona López, L.I.; Ángel Leonardo Valdivieso Caraguay; Benalcázar, M.E. A comparison of EMG-based hand gesture recognition systems based on supervised and reinforcement learning. Eng. Appl. Artif. Intell. 2023, 123, 106327. [Google Scholar] [CrossRef]
- Benalcázar, M.E.; Jaramillo, A.G.; Jonathan; Zea, A.; Páez, A.; Andaluz, V.H. Hand gesture recognition using machine learning and the Myo armband. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 1040–1044. [Google Scholar] [CrossRef]
- Tsai, A.C.; Luh, J.; Lin, T.T. A novel STFT-ranking feature of multi-channel EMG for motion pattern recognition. Expert Syst. Appl. 2015, 42, 44. [Google Scholar] [CrossRef]
- Jiang, W.; Ren, Y.; Liu, Y.; Wang, Z.; Wang, X. Recognition of Dynamic Hand Gesture Based on Mm-Wave Fmcw Radar Micro-Doppler Signatures. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 4905–4909. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Los Alamitos, CA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Rahimi, N.; Eassa, F.; Elrefaei, L. An Ensemble Machine Learning Technique for Functional Requirement Classification. Symmetry 2020, 12, 1601. [Google Scholar] [CrossRef]
- Farrell, T.R.; Weir, R.F. The Optimal Controller Delay for Myoelectric Prostheses. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 111–118. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2011, arXiv:2010.16061. [Google Scholar]

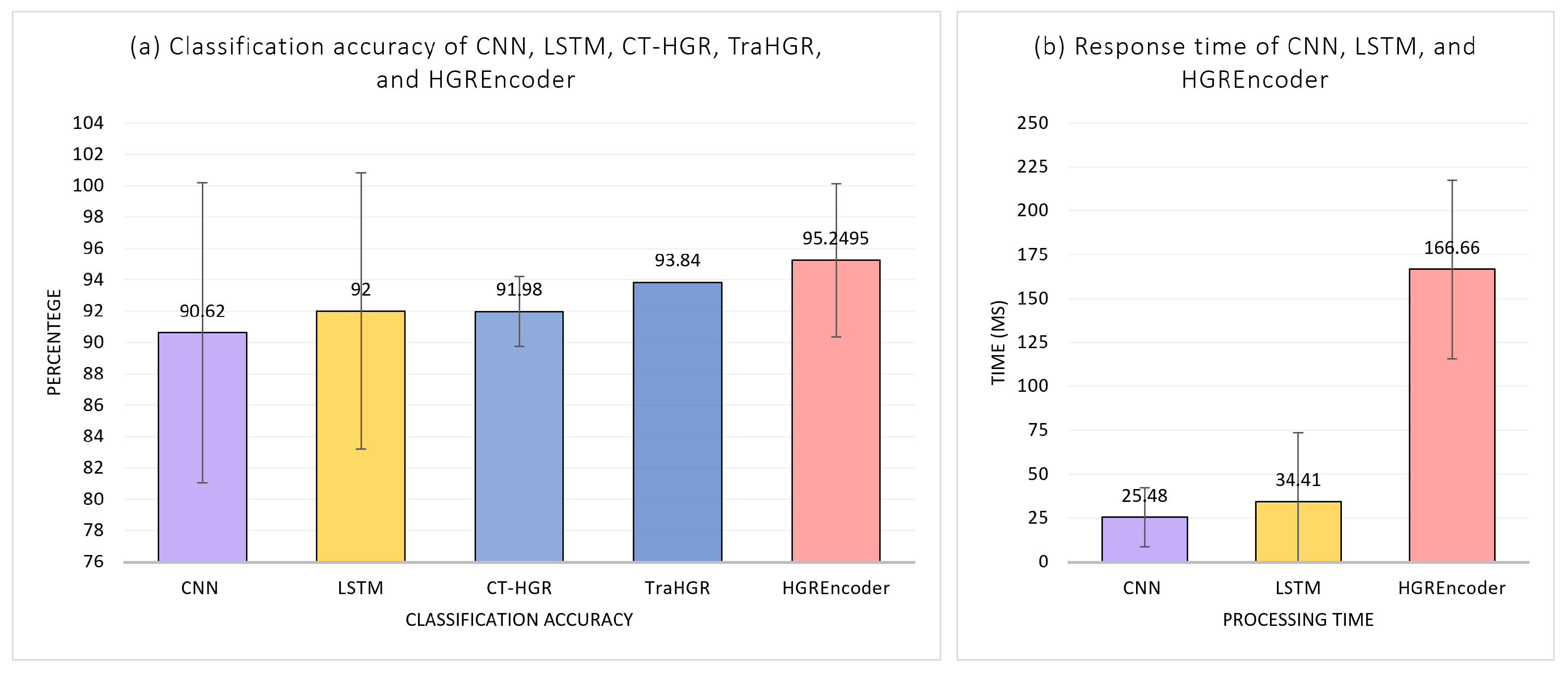

| Model | Recognition Accuracy | Variability | Number of Weights |
|---|---|---|---|
| ANN | 85.08% | ±15.21 | 70.9 K |
| SVM | 87.5% | – | – |
| CNN | 87.26% | ±11.14 | 219.1 K |
| LSTM | 90.55% | ±9.45 | 11.7 M |
| Parameter | Value |
|---|---|
| Initial Learning Rate | 0.001 |
| Learning Rate Scheduling | piecewise |
| Learning Rate Drop Factor | 0.2 |
| Learning Rate Drop Period | 8 |
| MiniBatch Size | 64 |
| Number of Epochs | 10 |
| Metric | No Post-Processing | With Post-Processing |
|---|---|---|
| Classification | 95.25 ± 4.9% | |
| Recognition | 89.7 ± 8.77% | 91.7 ± 8.2% |
| Overlapping | 49.8 ± 8.27% | 50.5 ± 8.35% |
| Time (ms) | 151 ± 49.2 | 167 ± 50.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macías, L.G.; Zea, J.A.; Barona, L.I.; Valdivieso, Á.L.; Benalcázar, M.E. HGREncoder: Enhancing Real-Time Hand Gesture Recognition with Transformer Encoder—A Comparative Study. Math. Comput. Appl. 2025, 30, 101. https://doi.org/10.3390/mca30050101
Macías LG, Zea JA, Barona LI, Valdivieso ÁL, Benalcázar ME. HGREncoder: Enhancing Real-Time Hand Gesture Recognition with Transformer Encoder—A Comparative Study. Mathematical and Computational Applications. 2025; 30(5):101. https://doi.org/10.3390/mca30050101
Chicago/Turabian StyleMacías, Luis Gabriel, Jonathan A. Zea, Lorena Isabel Barona, Ángel Leonardo Valdivieso, and Marco E. Benalcázar. 2025. "HGREncoder: Enhancing Real-Time Hand Gesture Recognition with Transformer Encoder—A Comparative Study" Mathematical and Computational Applications 30, no. 5: 101. https://doi.org/10.3390/mca30050101
APA StyleMacías, L. G., Zea, J. A., Barona, L. I., Valdivieso, Á. L., & Benalcázar, M. E. (2025). HGREncoder: Enhancing Real-Time Hand Gesture Recognition with Transformer Encoder—A Comparative Study. Mathematical and Computational Applications, 30(5), 101. https://doi.org/10.3390/mca30050101







