Energy Management and Power Distribution for Battery/Ultracapacitor Hybrid Energy Storage System in Electric Vehicles with Regenerative Braking Control
Abstract
1. Introduction
1.1. Related Works
1.2. Research Gap and Contribution
- Updating the state of the art and related works concerning the research topic.
- Providing a more detailed analysis of power flow operational modes between the BP, UC, and load.
- Expanding experimental studies on IM braking at different speeds.
- Experimentally integrating the BP and UC with a 4 kW static load.
- Analyzing the performance of the hybrid energy storage system under different operational modes using experimental results.
- Presenting detailed calculations of energy efficiency across various operational modes.
- 1.
- Regenerative Braking Control:
- A control strategy is developed for an induction motor to maximize kinetic energy recovery during regenerative braking.
- The braking energy is strategically distributed between the UC and battery to enhance overall system efficiency.
- 2.
- Power Flow Management in HESS:
- During motoring (discharge mode), an optimal power distribution strategy is implemented, balancing power delivery between the battery and UC using a distribution factor.
- The distribution factor is dynamically adjusted to maximize system efficiency, with UC discharge current actively controlled.
- During braking (charge mode), a DC link voltage control mechanism prioritizes UC charging over the battery, improving energy recovery efficiency.
- 3.
- Theoretical, Simulation-based, and Experimental-based Validation:
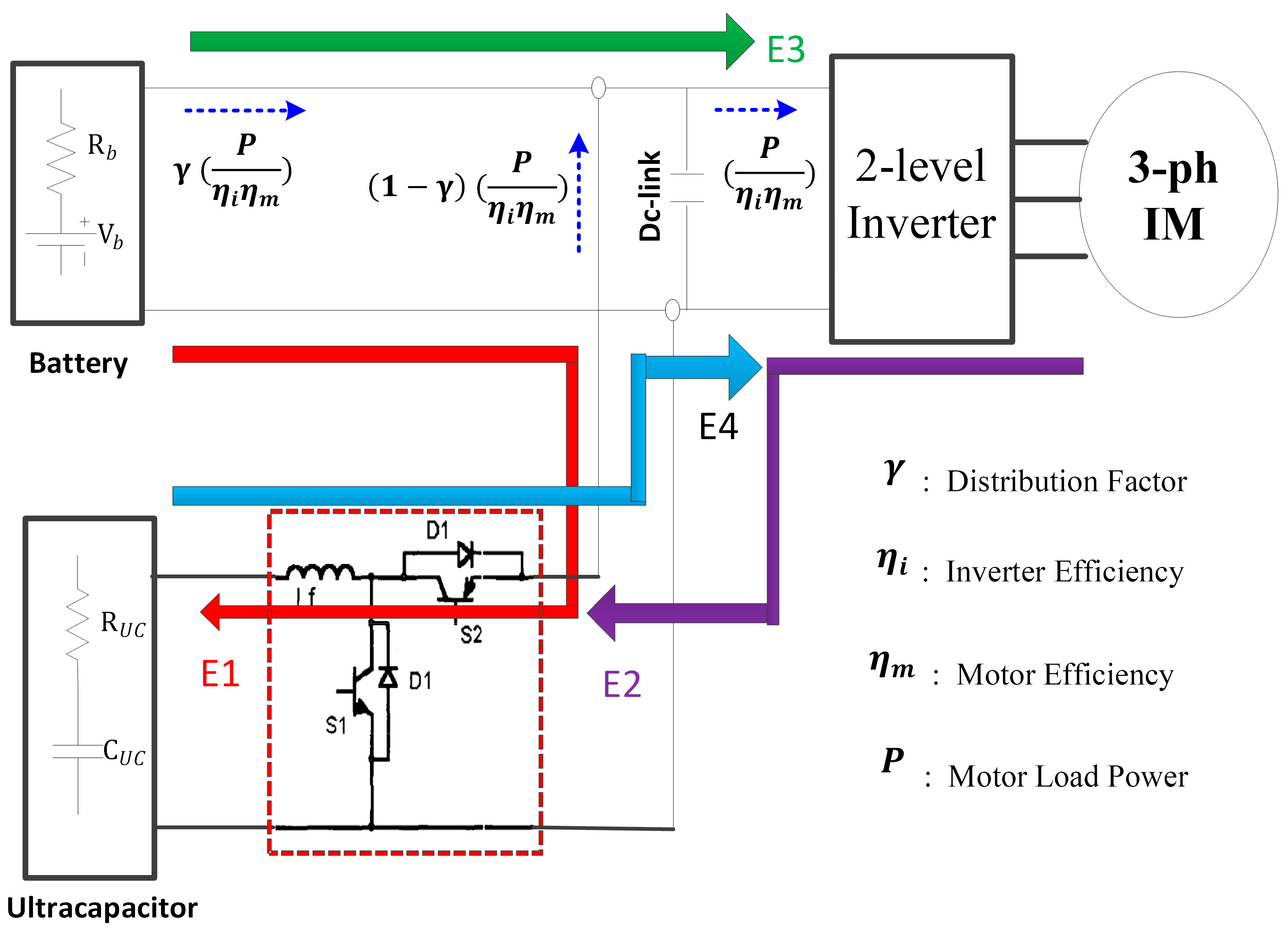
2. System Description and Operational Modes
- Mode 1: Charging the UC from the battery at light loads (Path E1): During this mode, the load is powered by the BP (Path E3), while the UC is charged. The chopper operates in buck mode, with switch S2 turned ON.
- Mode 2: Charging the UC from the load during regenerative braking (Path E2): In this mode, the chopper remains in buck mode, with switch S2 ON, to store recovered energy in the UC.
- Mode 3: Simultaneous charging of the UC from both the BP and the load (Paths E1 and E2). In Mode 3, the ultracapacitor is charged simultaneously from the regenerative braking system and the battery pack. This mode is enabled only when the energy recovered from braking is insufficient to meet the UC charging demand. A dedicated DC-DC converter allows supplementary power from the battery under controlled conditions. The energy management system monitors braking intensity, battery state-of-charge, and UC voltage to ensure safe operation, prevent overcharging, and optimize power flow efficiency.
- Mode 4: Power sharing at heavy loads: The load current is drawn from both the battery (Path E3) and the UC (Path E4) through diode D2, following a load power sharing strategy, which will be explained in the next section.
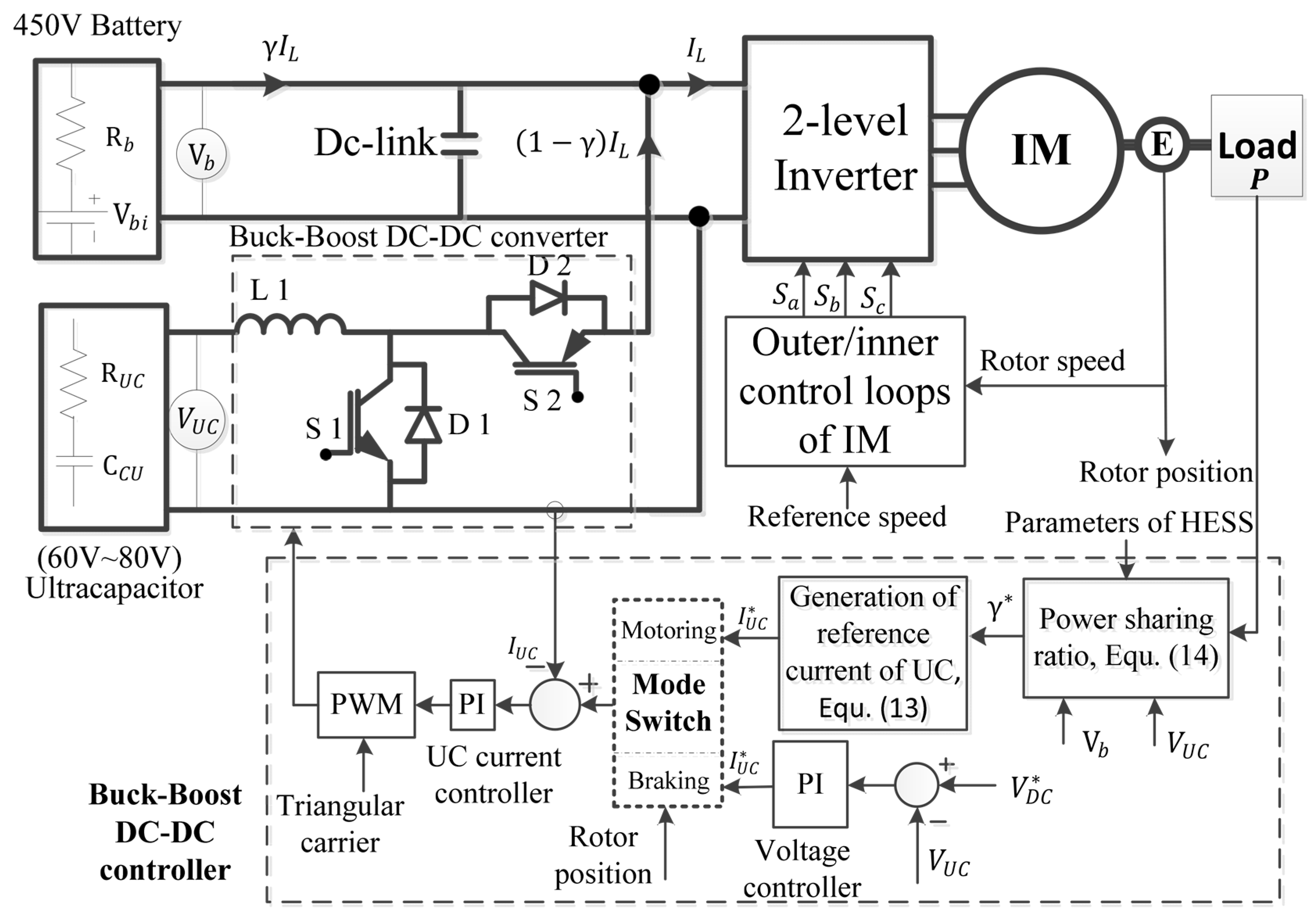
3. Control Strategy for Hybrid Energy Storage System
3.1. Motoring Operation (Boost Mode, Current Control, Discharge Mode)
3.2. Braking Operation (Buck Mode, Voltage Control, Charging Operation)
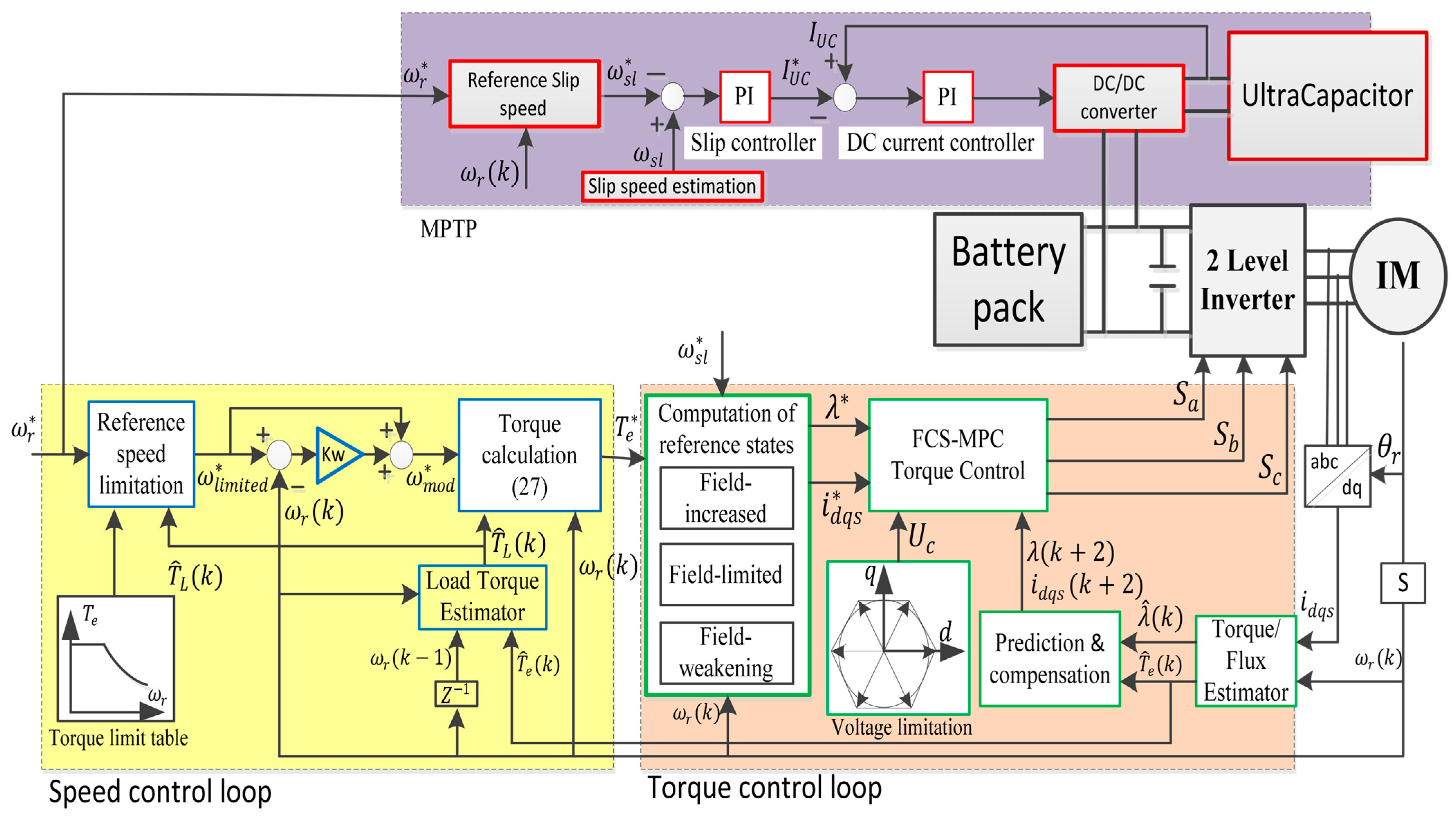
- Outer loop: Responsible for speed control, relying on an individual MPC cost function.
Generation of Reference Torque for IM
Reference Slip Speed
Reference Rotor Flux
Reference Current Components
4. Results and Analysis
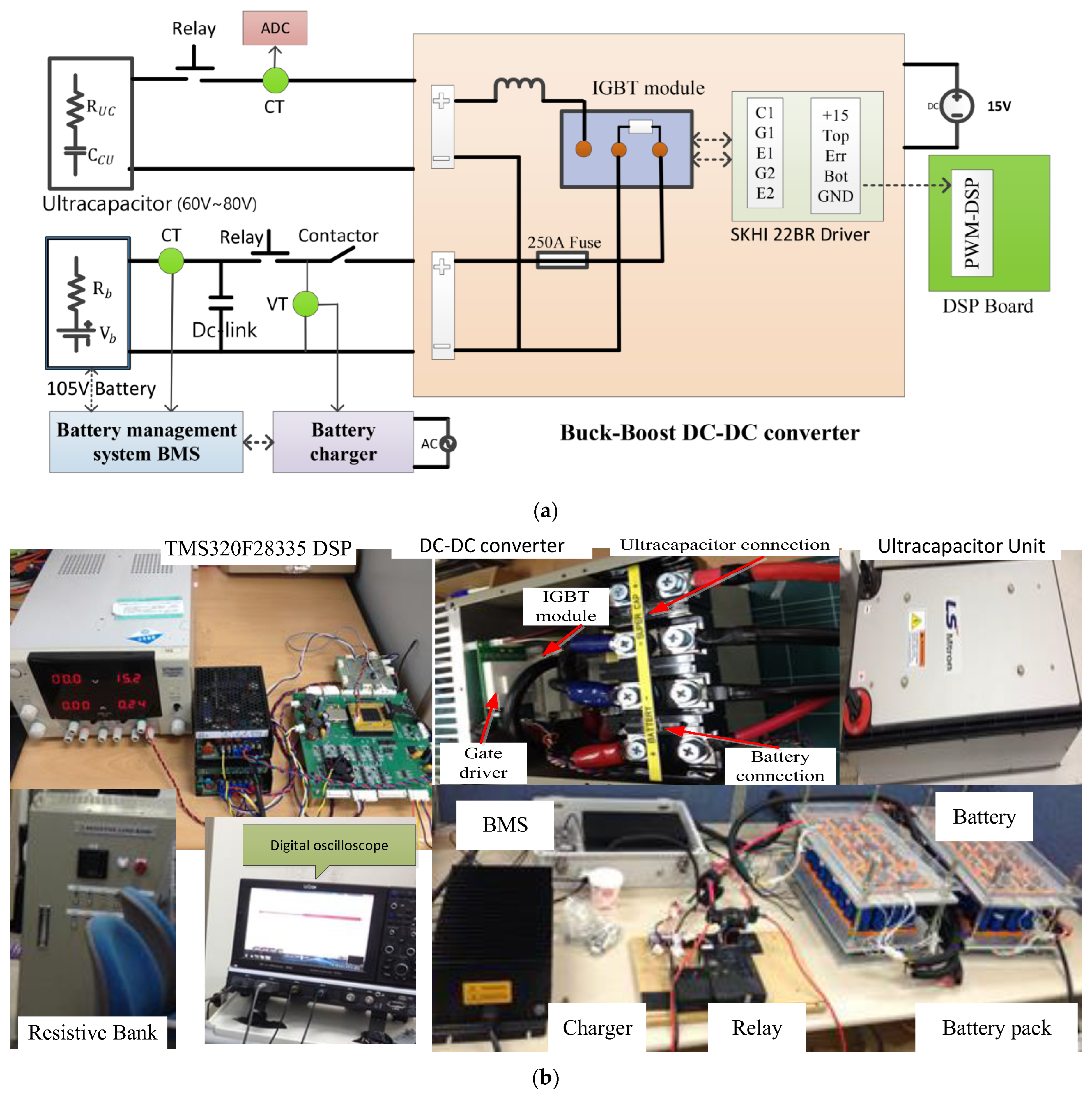
4.1. Integration of Battery–Ultracapacitor HESS
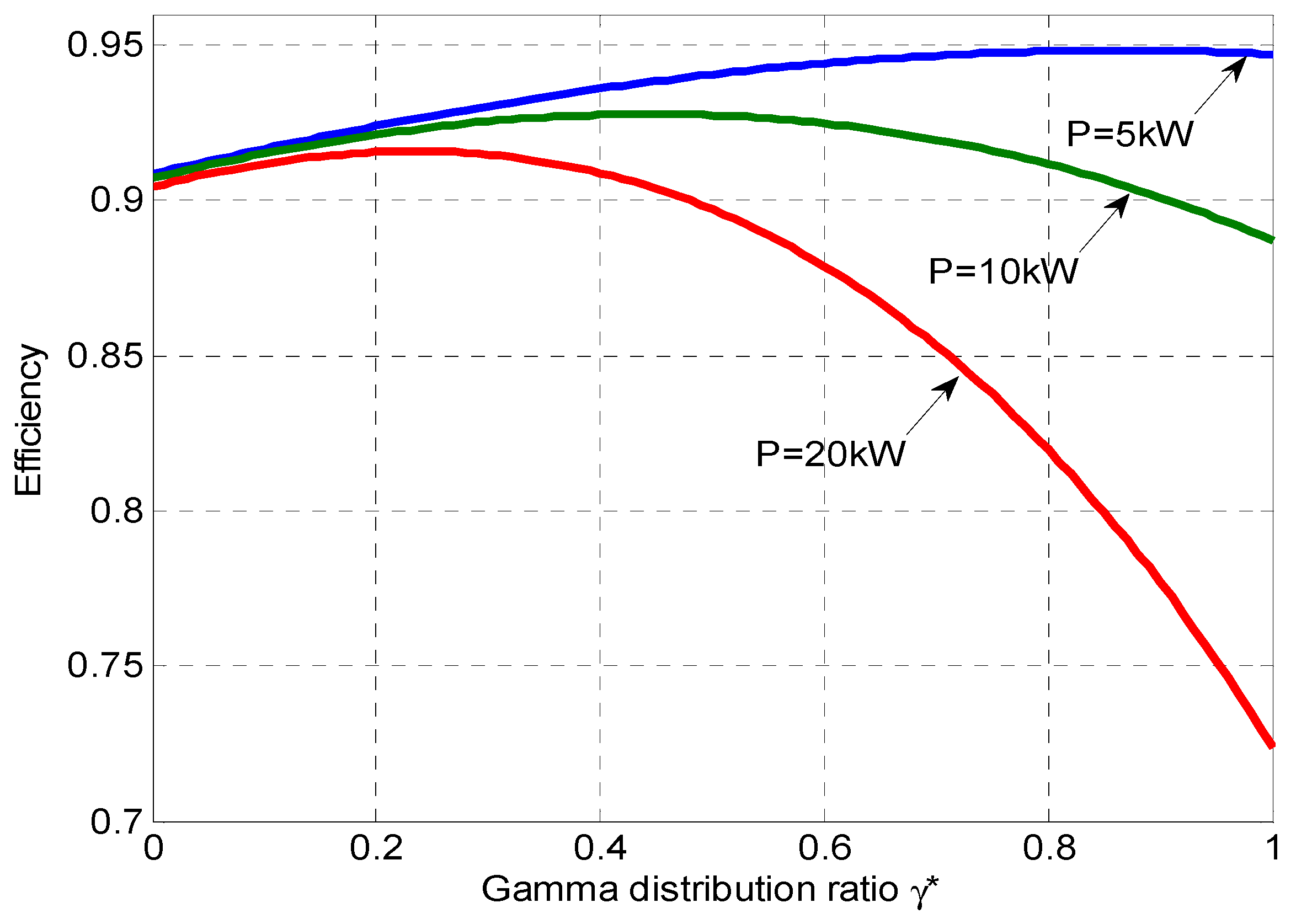
4.2. Relationship Between Distribution Factor, Efficiency, and Load Power
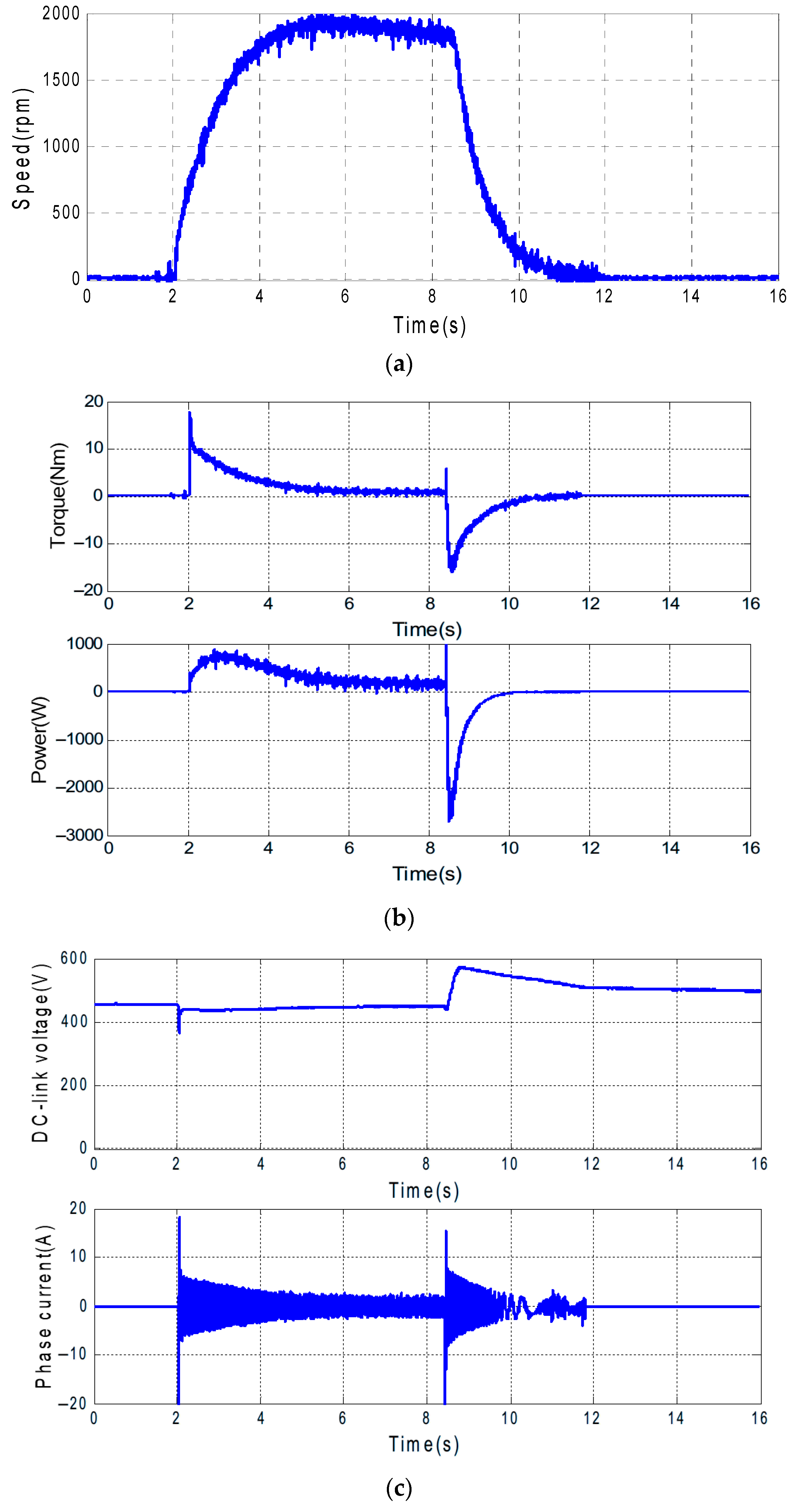
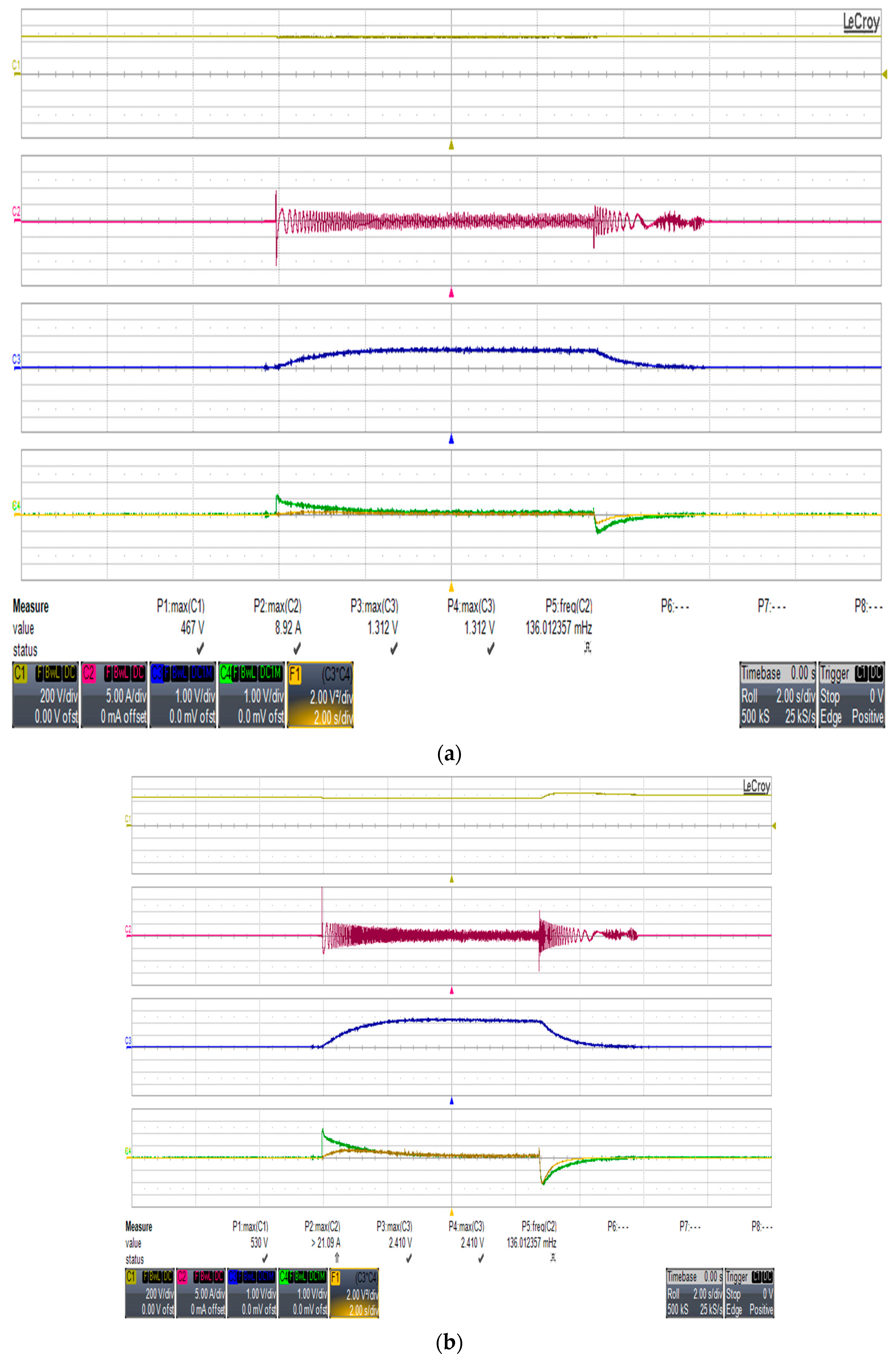
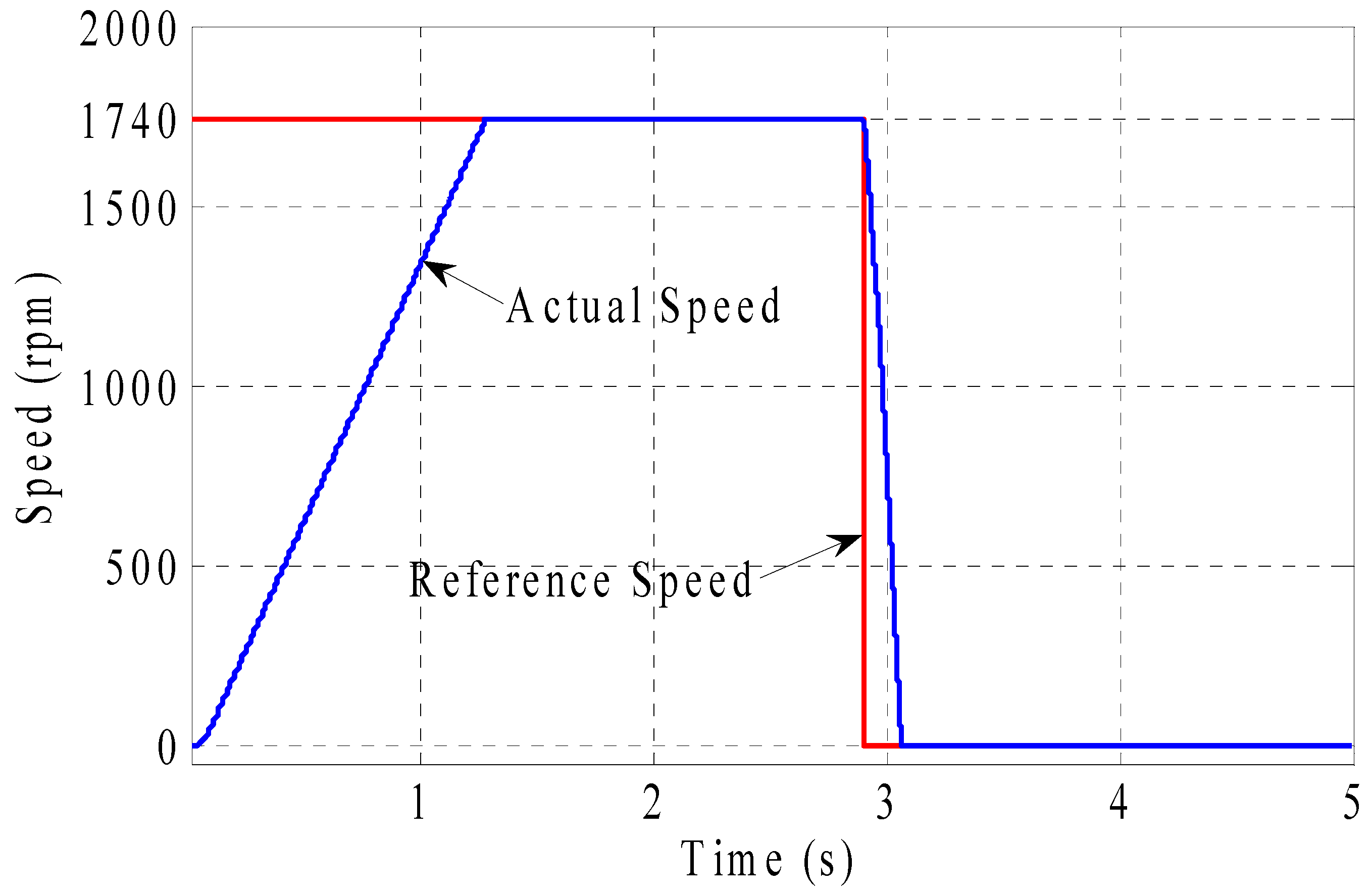
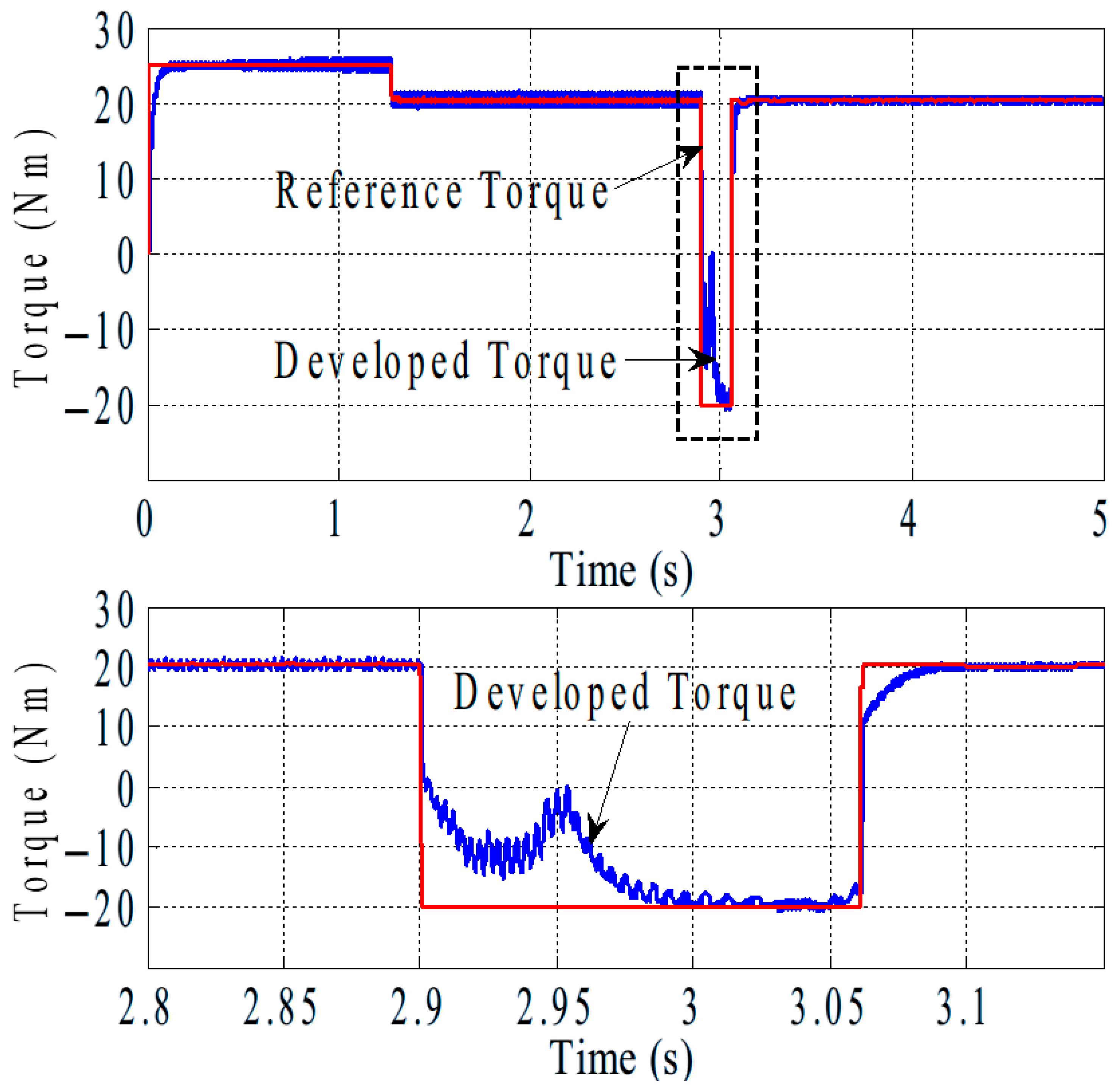
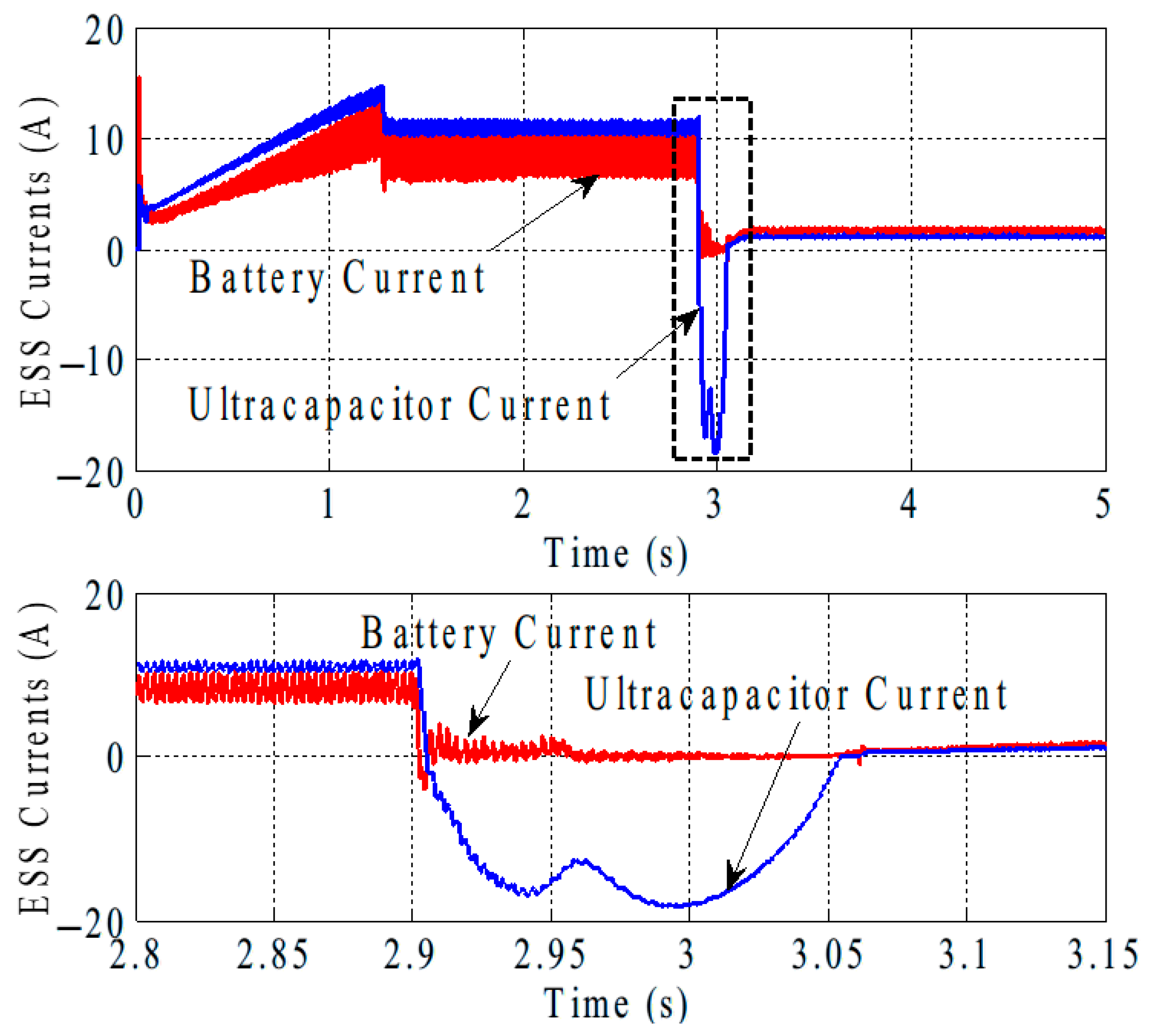
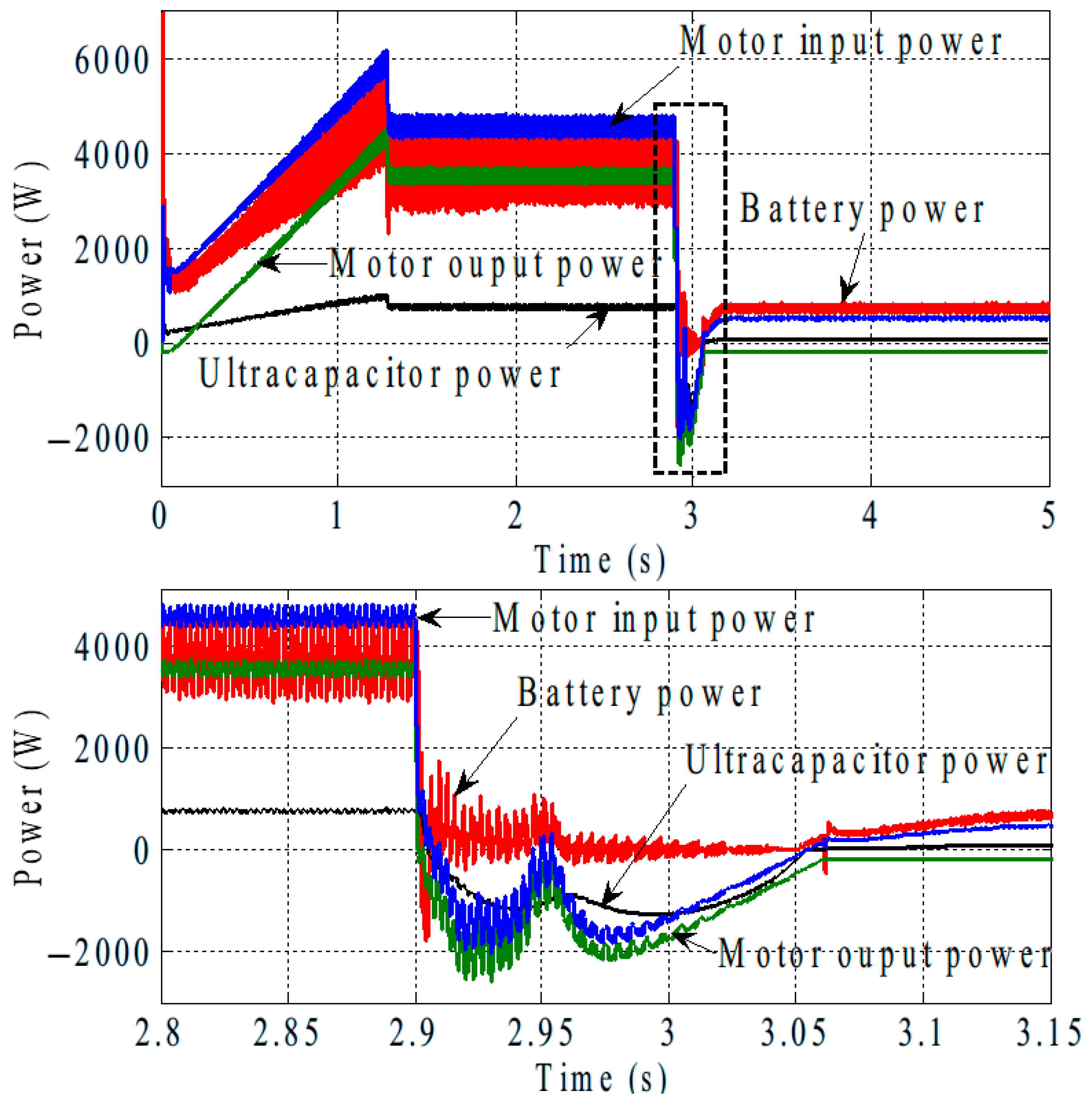
4.3. Experimental Validation of Slip Control of IM for Regenerative Braking
- 1.
- Induction Motor (IM):
- 2.
- Battery Pack (BP):
- 3.
- Ultracapacitor (UC) Module:
- 4.
- DC Link Capacitor:
- 5.
- Power Electronics (DC-DC Converters):
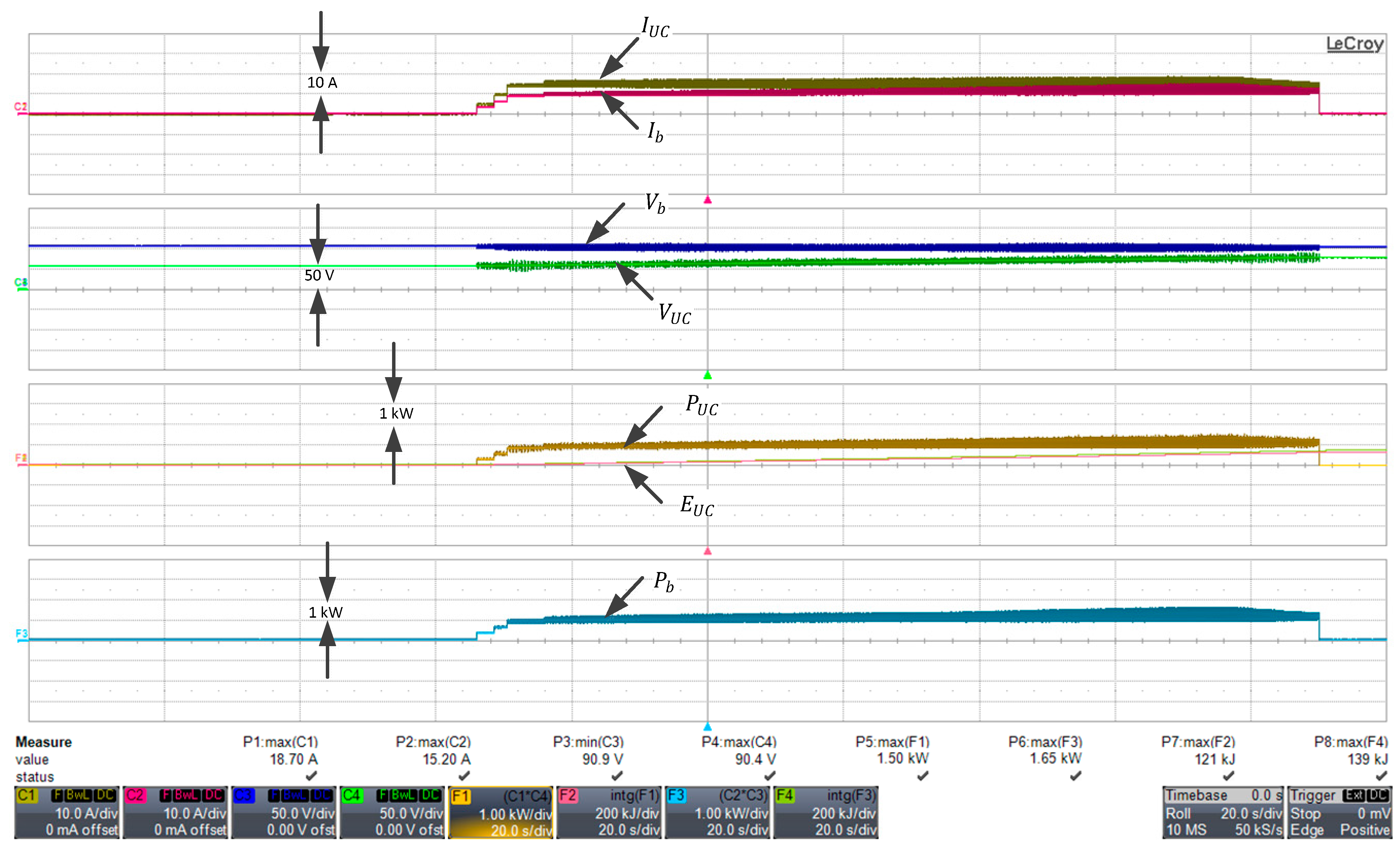
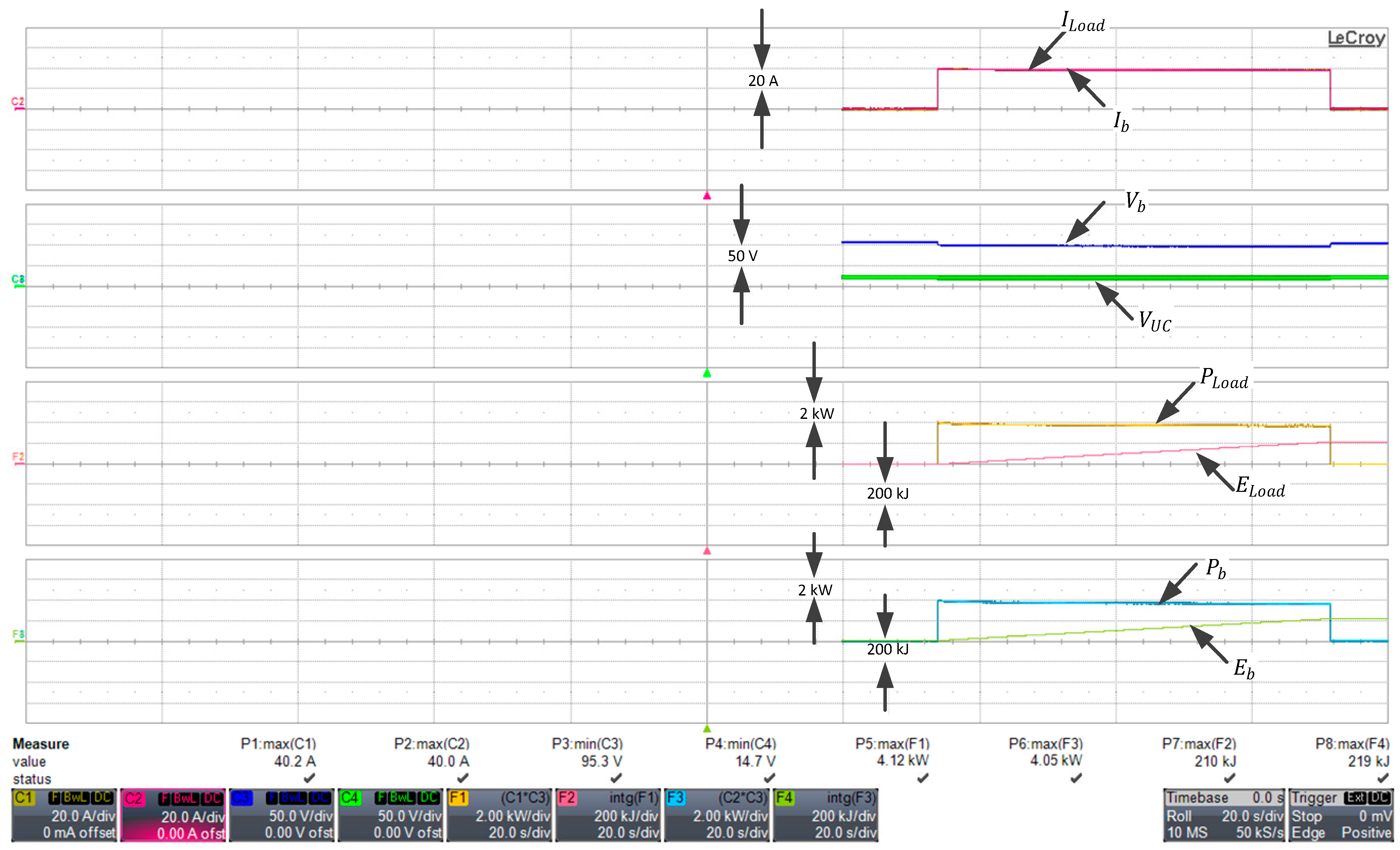
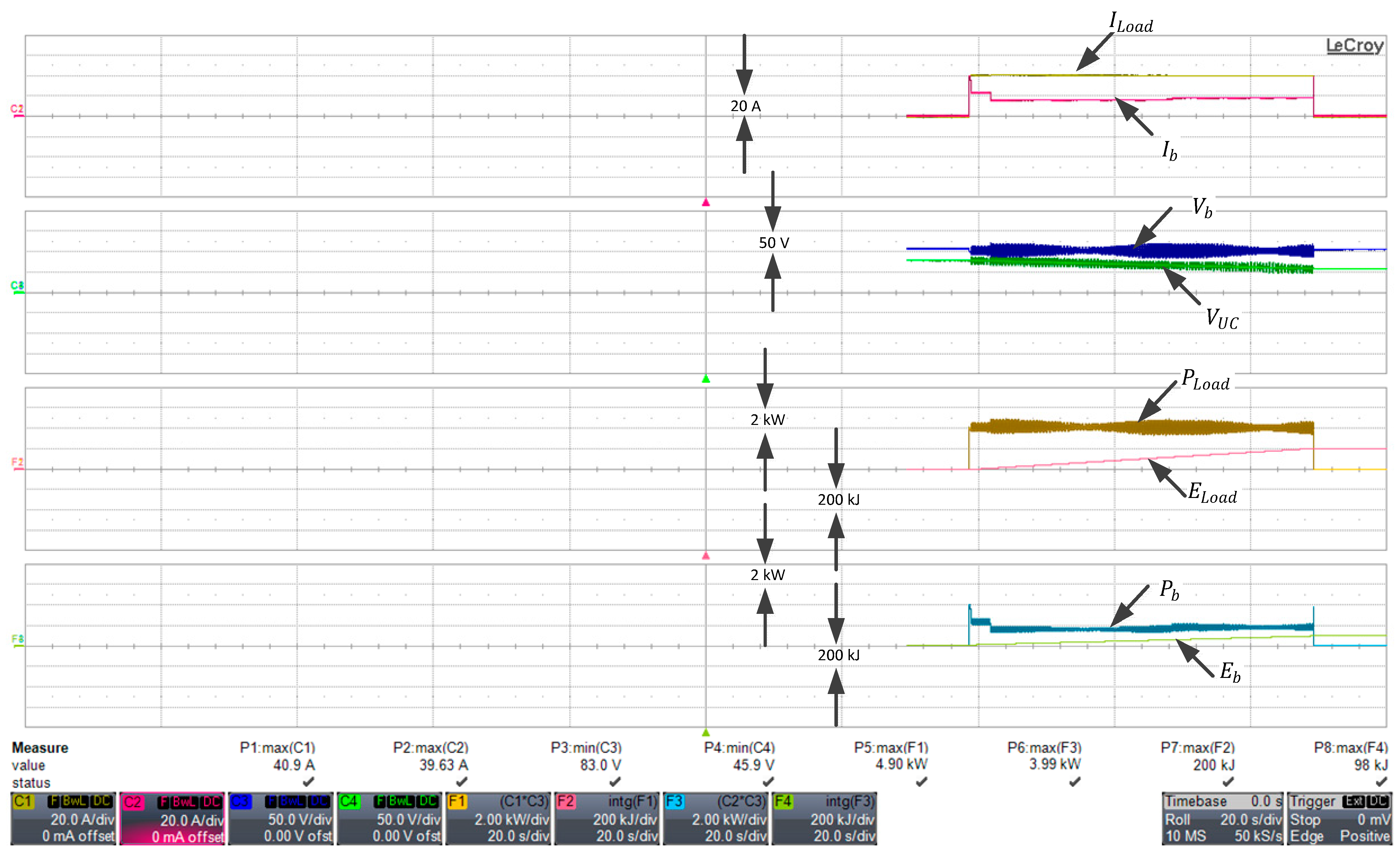
4.4. Performance Assessment of HESS with a Static Load
Efficiency of Charge/Discharge in HESS
Charging of Ultracapacitor from Battery (Path E1)
Discharging of Battery to Load (Path 3)
Discharging of BP and UC to Load (Path 3 + Path 4)
4.5. Dynamic Performance with Regenerative Braking
5. Conclusions
- The proposed control technique efficiently utilizes excess energy to charge the UC.
- For higher load demands the UC plays a crucial role in power distribution, optimizing efficiency and system performance.
- The DC-DC converter achieves 87% efficiency during UC charging, demonstrating effective energy transfer.
- Compared to a battery-only configuration (82%), incorporating a UC improves discharge efficiency (92%) and enhances energy savings in frequent discharge operations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eftekhari, A. Low voltage anode materials for lithium-ion batteries. Energy Storage Mater. 2017, 7, 157–180. [Google Scholar] [CrossRef]
- Burke, A.; Miller, M. The power capability of ultracapacitors and lithium batteries for electric and hybrid vehicle applications. J. Power Sources 2011, 196, 514–522. [Google Scholar] [CrossRef]
- Emadi, A.C. 8: Hybrid Energy Storage Systems. In Advanced Electric Drive Vehicles; Taylor & Francis Group, LLC: Boca Raton, FL, USA, 2015; pp. 285–286. [Google Scholar]
- Camara, M.B.; Gualous, H.; Gustin, F.; Berthon, A.; Dakyo, B. DC/DC converters design for supercapacitors and battery power management in hybrid vehicle applications-polynomial control strategy. IEEE Trans. Ind. Electron. 2010, 57, 587–597. [Google Scholar] [CrossRef]
- Bian, Y.; Zhu, L.; Lan, H.; Li, A.; Xu, X. Regenerative braking strategy for motor hoist by ultracapacitor. Chin. J. Mech. Eng. 2012, 25, 377–384. [Google Scholar] [CrossRef]
- Xiang, C.; Wang, Y.; Hu, S.; Wang, W. A New Topology and Control Strategy for a Hybrid Battery-Ultracapacitor Energy Storage System. Energies 2014, 7, 2874–2896. [Google Scholar] [CrossRef]
- Awerbuch, J.J.; Sullivan, C.R. Control of Ultracapacitor-Battery Hybrid Power Source for Vehicular Applications. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008. [Google Scholar]
- Chau, K.T.; Wong, Y.S. Hybridization of energy sources in electric vehicles. Energy Convers. Manag. 2001, 42, 1059–1069. [Google Scholar] [CrossRef]
- Miller, J.R. Engineering electrochemical capacitor applications. J. Power Sources 2016, 326, 726–735. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Emadi, A. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles: Fundamentals, Theory, and Design, 2nd ed.; Power Electronics and Applications Series; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- So, K.M.; Wong, Y.S.; Hong, G.S.; Lu, W.F. An improved energy management strategy for a Battery/Ultracapacitor Hybrid Energy Storage System in Electric Vehicles. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–6. [Google Scholar]
- Ahmed, A.; Cui, S. Control and analysis of regenerative power distribution on electrical variable transmission using fuzzy logic on HEV system. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Beijing, China, 20–23 August 2011. [Google Scholar]
- Mahapatra, A.A.; Gopalakrishna, S. Regenerative braking in induction motor drives in applications to electric vehicles. In Proceedings of the 2014 IEEE Students’ Conference on Electrical, Electronics and Computer Science, Bhopal, India, 1–2 March 2014. [Google Scholar]
- Li, Z.; Pan, Y. On steering regenerative brake torque control of dual-motor drive for electric tracked vehicle. In Proceedings of the IEEE International Conference on Automation and Logistics, Beijing, China, 29–31 August 2010. [Google Scholar]
- Kouchachvili, L.; Yaïci, W.; Entchev, E. Hybrid battery/supercapacitor energy storage system for the electric vehicles. J. Power Sources 2018, 374, 237–248. [Google Scholar] [CrossRef]
- Chen, S.; Yang, Q.; Zhou, J.; Chen, X. Hybrid energy storage system control method based on model predictive control. CSEE J. Power Energy Syst. 2020, 7. [Google Scholar] [CrossRef]
- Punna, S.; Behera, P.; Lamba, A. A Power Management Scheme for Electric Vehicles with Hybrid Energy Storage Systems. In Proceedings of the 2024 IEEE 4th International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 31 July–3 August 2024; pp. 1–5. [Google Scholar]
- Ahmed, A.A.; Mousa, M.G.; Lee, Y.I. Regenerative braking control of IM with battery/ultracapacitor hybrid ESS in electric vehicles. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 320–325. [Google Scholar]
- Ahmed, A.A.; Koh, B.K.; Park, H.S.; Lee, K.-B.; Lee, Y.I. Finite control set model predictive control method for torque control of induction motors using a state tracking cost index. IEEE Trans. Ind. Electron. 2017, 64, 1916–1928. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Koh, B.K.; Lee, Y.I. A Comparison of Finite Control Set and Continuous Control Set Model Predictive Control Schemes for Speed Control of Induction Motors. IEEE Trans. Ind. Inform 2017, 14, 1334–1346. [Google Scholar] [CrossRef]
- Orion BMS. Available online: http://www.orionbms.com/ (accessed on 22 July 2025).
- Boglou, V.; Karavas, C.-S.; Karlis, A.; Arvanitis, K.G.; Palaiologou, I. An optimal distributed RES sizing strategy in hybrid low voltage networks focused on EVs’ integration. IEEE Access 2023, 11, 16250–16270. [Google Scholar] [CrossRef]
- Karavas, C.-S.; Arvanitis, K.G.; Papadakis, G. Optimal technical and economic configuration of photovoltaic powered reverse osmosis desalination systems operating in autonomous mode. Desalination. 2019, 466, 97–106. [Google Scholar] [CrossRef]
- Boglou, V.; Karavas, C.; Karlis, A.; Arvanitis, K. An intelligent decentralized energy management strategy for the optimal electric vehicles’ charging in low-voltage islanded microgrids. Int. J. Energy Res. 2022, 46, 2988–3016. [Google Scholar] [CrossRef]
- Rimpas, D.; Kaminaris, S.D.; Piromalis, D.D.; Vokas, G.; Arvanitis, K.G.; Karavas, C.-S. Comparative review of motor technologies for electric vehicles powered by a hybrid energy storage system based on multi-criteria analysis. Energies 2023, 16, 2555. [Google Scholar] [CrossRef]
- Loukatos, D.; Arapostathis, V.; Karavas, C.-S.; Arvanitis, K.G.; Papadakis, G. Power consumption analysis of a prototype lightweight autonomous electric cargo robot in agricultural field operation scenarios. Energies 2024, 17, 1244. [Google Scholar] [CrossRef]

| Specification [unit] | Value | Specification [unit] | Value |
|---|---|---|---|
| Rated voltage [V] | 86.4 | Maximum current [A] | 80 |
| Capacitance [F] | 93 | Max. stored energy [Wh/kg] | 3.7 |
| Resistance [ | 11.3 | Weight [kg] | 26 |
| Quantity | Symbol | Value |
|---|---|---|
| DC-bus volt | 450 | |
| Number of Poles | 4 | |
| Rated voltage [V] | 220/380 | |
| Rated current [A] | 14.2/8.2 | |
| Stator Resistance | 1.77 | |
| Rotor Resistance | 1.275 | |
| Stator Inductance | 0.157 | |
| Rotor Inductance | 0.158 | |
| Mutual Inductance | 0.15 | |
| Inertia coefficient [Kg·m2] | J | 0.00006 |
| Rated Motor Speed | 1740 | |
| Rated Power | 3.7 |
| Parameter | Specification |
|---|---|
| Configuration | 32s4p LiFePO4 cells |
| Cell Voltage/Capacity | 3.2 V/10 Ah |
| Total Pack Voltage | 100 V |
| Total Pack Capacity | 40 Ah |
| Total Energy | 4.0 kWh |
| Max Charge Current | 18 A (via onboard charger) |
| Parameter | Specification |
|---|---|
| Model | LS Mtron LSUM 086R4C 0093F EA |
| Rated Voltage | 86.4 V |
| Capacitance | 93 F |
| Maximum Current | 80 A |
| Internal Resistance | 11.3 mΩ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.A.; Lee, Y.I.; Al Dawsari, S.; Diab, A.A.Z.; Ezzat, A.A. Energy Management and Power Distribution for Battery/Ultracapacitor Hybrid Energy Storage System in Electric Vehicles with Regenerative Braking Control. Math. Comput. Appl. 2025, 30, 82. https://doi.org/10.3390/mca30040082
Ahmed AA, Lee YI, Al Dawsari S, Diab AAZ, Ezzat AA. Energy Management and Power Distribution for Battery/Ultracapacitor Hybrid Energy Storage System in Electric Vehicles with Regenerative Braking Control. Mathematical and Computational Applications. 2025; 30(4):82. https://doi.org/10.3390/mca30040082
Chicago/Turabian StyleAhmed, Abdelsalam A., Young Il Lee, Saleh Al Dawsari, Ahmed A. Zaki Diab, and Abdelsalam A. Ezzat. 2025. "Energy Management and Power Distribution for Battery/Ultracapacitor Hybrid Energy Storage System in Electric Vehicles with Regenerative Braking Control" Mathematical and Computational Applications 30, no. 4: 82. https://doi.org/10.3390/mca30040082
APA StyleAhmed, A. A., Lee, Y. I., Al Dawsari, S., Diab, A. A. Z., & Ezzat, A. A. (2025). Energy Management and Power Distribution for Battery/Ultracapacitor Hybrid Energy Storage System in Electric Vehicles with Regenerative Braking Control. Mathematical and Computational Applications, 30(4), 82. https://doi.org/10.3390/mca30040082







