Extracting Flow Characteristics from Single and Multi-Point Time Series Through Correlation Analysis
Abstract
1. Introduction
2. The Bluff Body Experiment
3. Spectral Analyses of Single and Multi-Point Time Series and Correlation Analysis
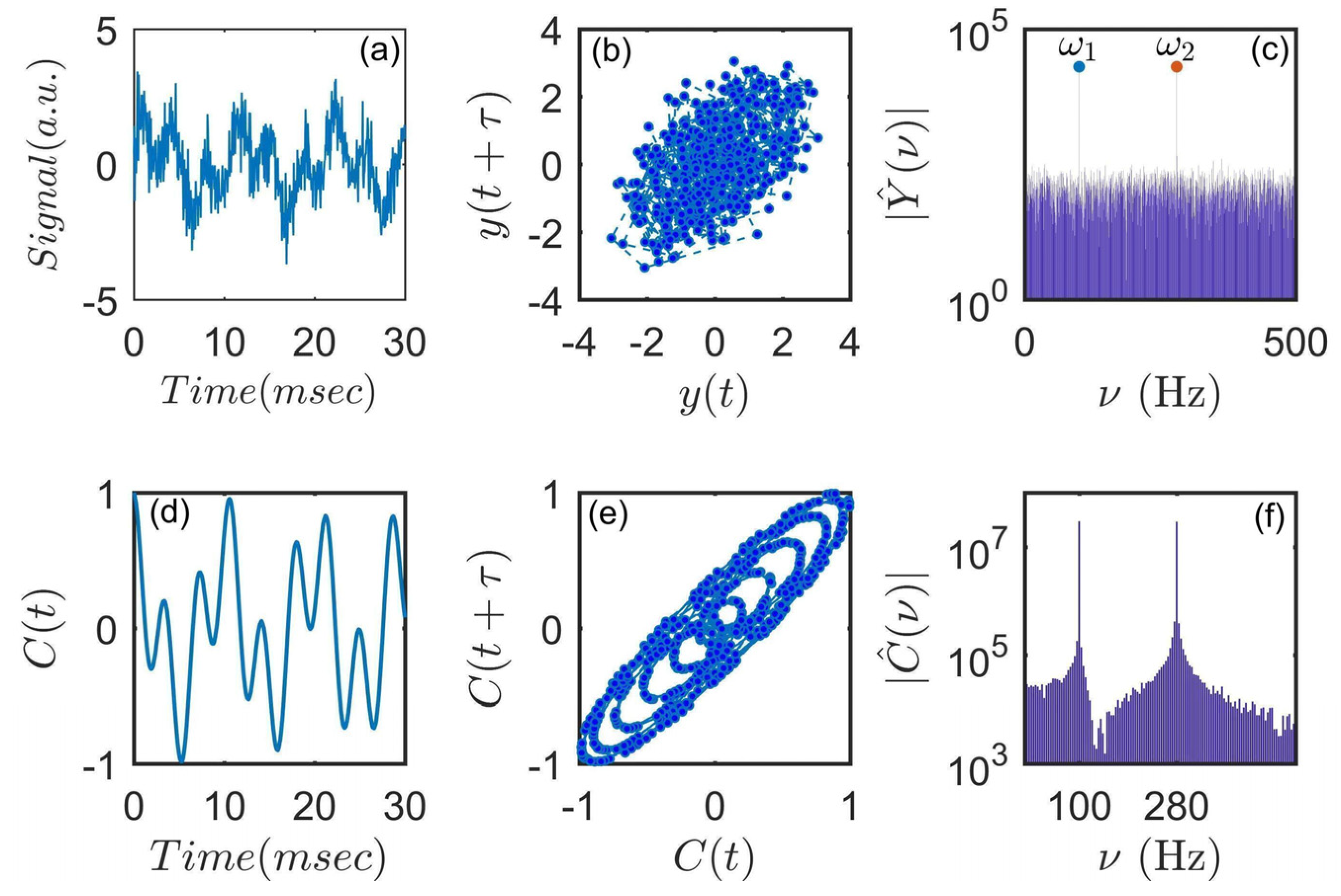
3.1. Introduction to Correlation Analysis
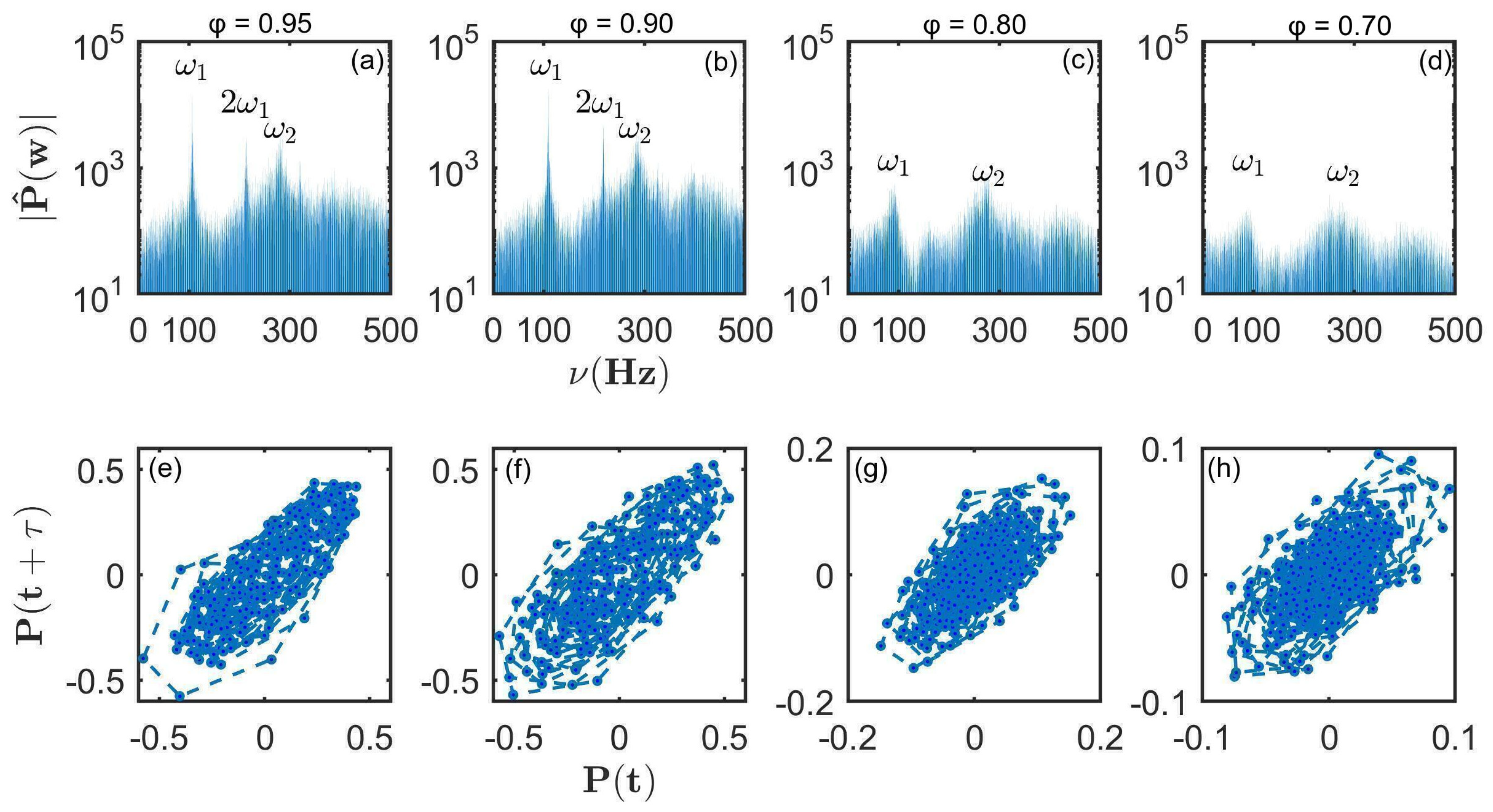
3.2. Autocorrelation Function of Bluff Body Pressure Time Series
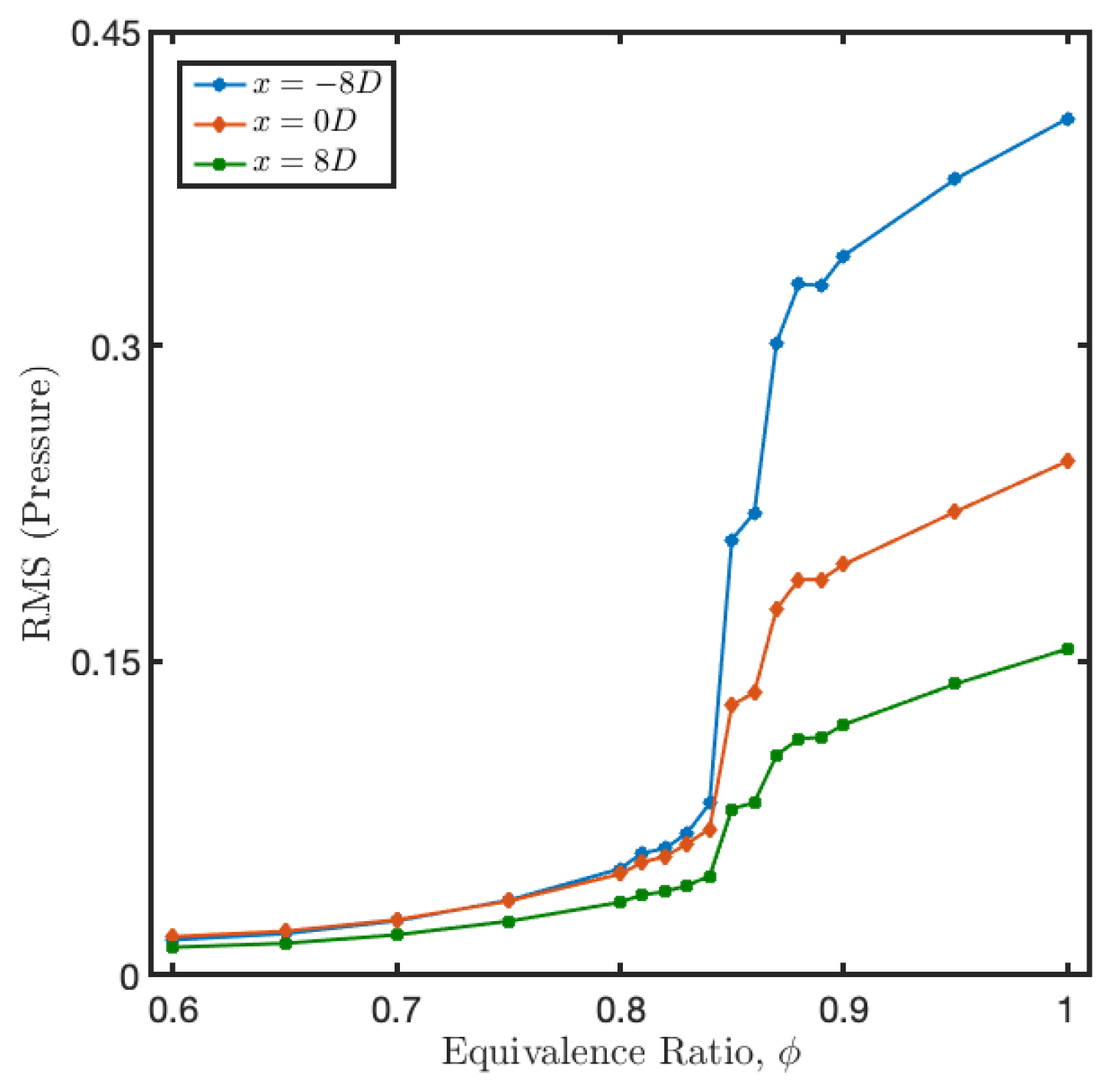
3.3. Growth of the Asymmetric Mode with Equivalence Ratio at Various Inlet Temperature Conditions
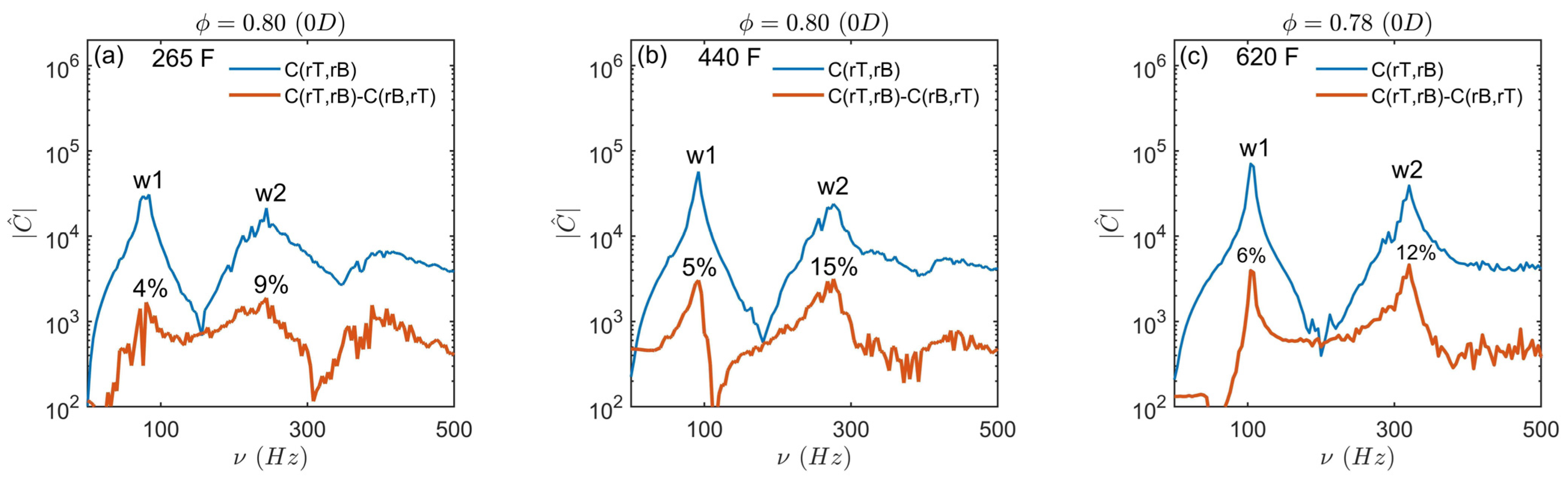
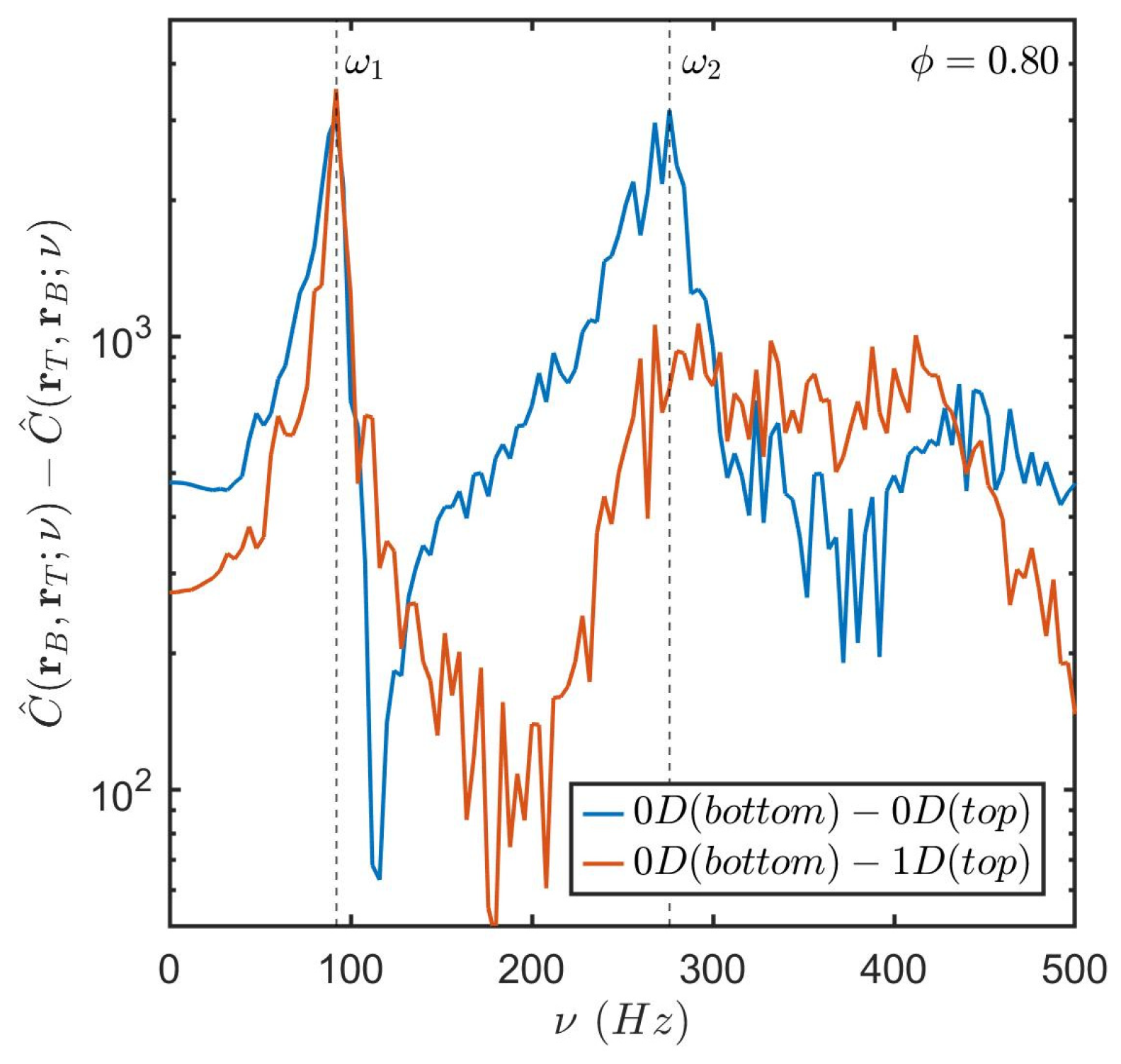
4. Cross-Correlation Functions of Bluff-Body Pressure Time Series
5. Discussion
6. Conclusive Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Differentiating Symmetric and Time-Delayed Anti-Symmetric Constituents
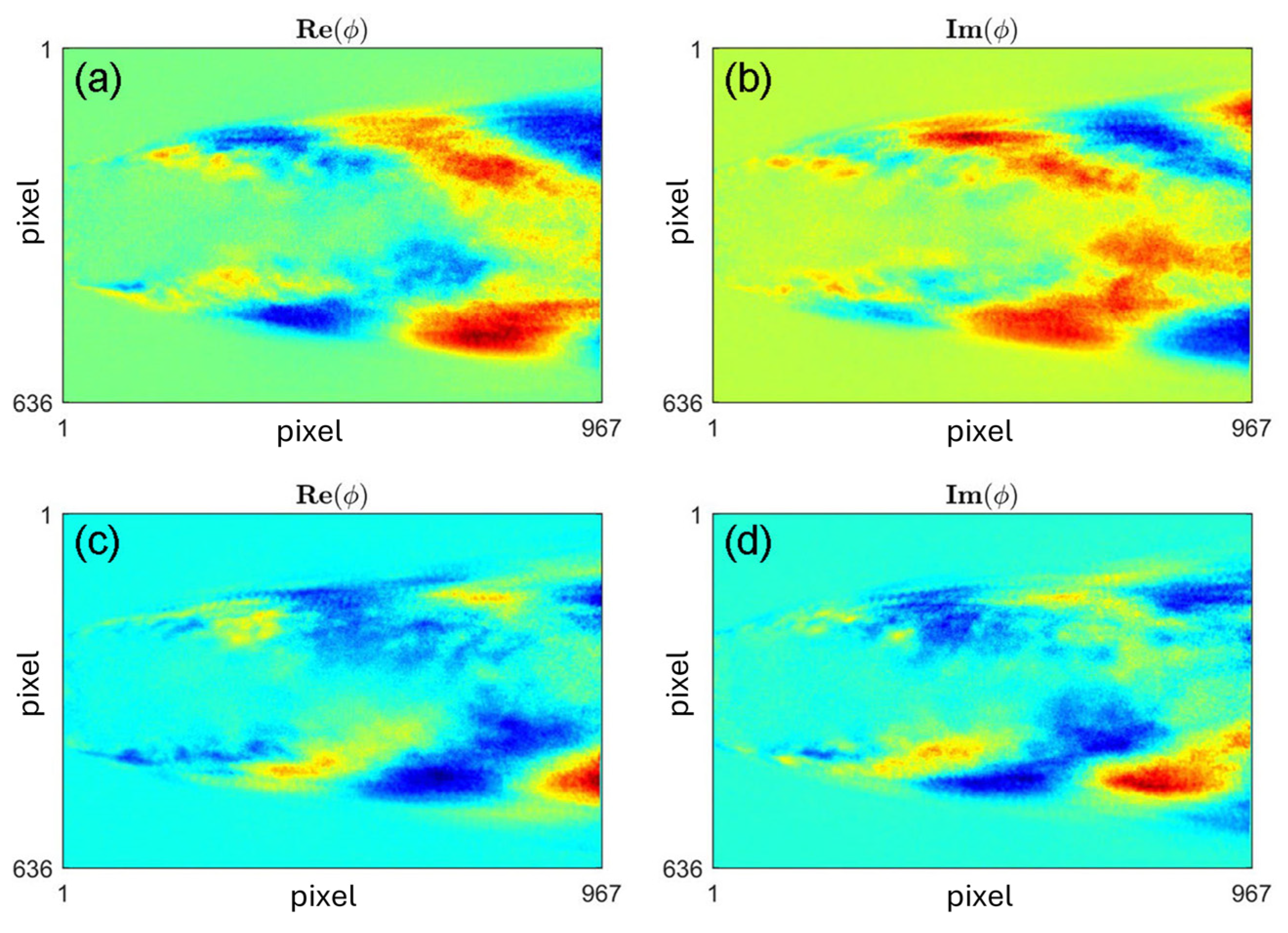
Appendix B. Dynamic Mode Decomposition Applied to Spatio-Temporal Data
References
- Lieuwen, T.C. Unsteady Combustor Physics; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Seshadri, A.; Pavithran, I.; Unni, V.R.; Sujith, R.I. Predicting the Amplitude of Limit-Cycle Oscillations in Thermoacoustic Systems with Vortex Shedding. AIAA J. 2018, 56, 3507–3514. [Google Scholar] [CrossRef]
- Pavithran, I.; Unni, V.R.; Varghese, A.J.; Sujith, R.; Saha, A.; Marwan, N.; Kurths, J. Universality in the emergence of oscillatory instabilities in turbulent flows. EPL (Europhys. Lett.) 2020, 129, 24004. [Google Scholar] [CrossRef]
- Dupe`re, I.D.J.; Dowling, A.P. The Use of Helmholtz Resonators in a Practical Combustor. J. Eng. Gas Turbines Power 2005, 127, 268–275. [Google Scholar] [CrossRef]
- Dawson, J.R.; Worth, N.A. The effect of baffles on self-excited azimuthal modes in an annular combustor. Proc. Combust. Inst. 2015, 35, 3283–3290. [Google Scholar] [CrossRef]
- Waesche, R.H.W. Mechanisms and Methods of Suppression of Combustion Instability by Metallic Additives. J. Propuls. Power 1999, 15, 919–922. [Google Scholar] [CrossRef]
- Lieuwen, T.; Shanbhogue, S.; Khosla, S.; Smith, C. Dynamics of bluff body flames near blowoff. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Shanbhogue, S.J.; Husain, S.; Lieuwen, T. Lean blowoff of bluff body stabilized flames: Scaling and dynamics. Prog. Energy Combust. Sci. 2009, 35, 98–120. [Google Scholar] [CrossRef]
- Kostka, S.; Lynch, A.C.; Huelskamp, B.C.; Kiel, B.V.; Gord, J.R.; Roy, S. Characterization of flame-shedding behavior behind a bluff-body using proper orthogonal decomposition. Combust. Flame 2012, 159, 2872–2882. [Google Scholar] [CrossRef]
- Shanbhogue, S.; Plaks, D.; Lieuwen, T. The KH instability of reacting, acoustically excited bluff body shear layers. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. [Google Scholar]
- Kandlikar, S.G.; Joshi, S.; Tian, S. Effect of Surface Roughness on Heat Transfer and Fluid Flow Characteristics at Low Reynolds Numbers in Small Diameter Tubes. Heat Transf. Eng. 2003, 24, 4–16. [Google Scholar] [CrossRef]
- Kim, D.E.; Kim, M.H. Experimental study of the effects of flow acceleration and buoyancy on heat transfer in a supercritical fluid flow in a circular tube. Nucl. Eng. Des. 2010, 240, 3336–3349. [Google Scholar] [CrossRef]
- Kabiraj, L.; Sujith, R. Nonlinear self-excited thermoacoustic oscillations: Intermittency and flame blowout. J. Fluid Mech. 2012, 713, 376–397. [Google Scholar] [CrossRef]
- Chiam, Z.L.; Lee, P.S.; Singh, P.K.; Mou, N. Investigation of fluid flow and heat transfer in wavy micro-channels with alternating secondary branches. Int. J. Heat Mass Transf. 2016, 101, 1316–1330. [Google Scholar] [CrossRef]
- Kunze, K.; Hirsch, C.; Sattelmayer, T. Transfer Function Measurements on a Swirl Stabilized Premix Burner in an Annular Combustion Chamber; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2008; pp. 21–29. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.G.; Quay, B.D.; Santavicca, D.A.; Kim, K.; Srinivasan, S. Effect of Flame Structure on the Flame Transfer Function in a Premixed Gas Turbine Combustor. J. Eng. Gas Turbines Power 2009, 132, 021502. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Xie, Y.; Wei, Z.; Jin, W.; Huang, Z.; Kobayashi, H. Measurement on instantaneous flame front structure of turbulent premixed CH4/H2/air flames. Exp. Therm. Fluid Sci. 2014, 52, 288–296. [Google Scholar] [CrossRef]
- Fojtlín, M.; Planka, M.; Fišer, J.; Pokorný, J.; Jícha, M. Airflow Measurement of the Car HVAC Unit Using Hot-Wire Anemometry. EPJ Web Conf. 2016, 114, 02023. [Google Scholar] [CrossRef]
- Kalpakli Vester, A.; Sattarzadeh, S.S.; Örlü, R. Combined hot-wire and PIV measurements of a swirling turbulent flow at the exit of a 90° pipe bend. J. Vis. 2016, 19, 261–273. [Google Scholar] [CrossRef]
- Kwon, S.Y.; Lee, S. Precise measurement of thermal conductivity of liquid over a wide temperature range using a transient hot-wire technique by uncertainty analysis. Thermochim. Acta 2012, 542, 18–23. [Google Scholar] [CrossRef]
- Minakov, A.V.; Rudyak, V.Y.; Guzei, D.V.; Pryazhnikov, M.I.; Lobasov, A.S. Measurement of the Thermal-Conductivity Coefficient of Nanofluids by the Hot-Wire Method. J. Eng. Phys. Thermophys. 2015, 88, 149–162. [Google Scholar] [CrossRef]
- Azarfar, S.; Movahedirad, S.; Sarbanha, A.A.; Norouzbeigi, R.; Beigzadeh, B. Low cost and new design of transient hot-wire technique for the thermal conductivity measurement of fluids. Appl. Therm. Eng. 2016, 105, 142–150. [Google Scholar] [CrossRef]
- Li, F.; Shi, S.; Ma, W.; Zhang, X. A switched vibrating-hot-wire method for measuring the viscosity and thermal conductivity of liquids. Rev. Sci. Instrum. 2019, 90, 075105. [Google Scholar] [CrossRef]
- Mylona, S.K.; Yang, X.; Hughes, T.J.; White, A.C.; McElroy, L.; Kim, D.; Al Ghafri, S.; Stanwix, P.L.; Sohn, Y.H.; Seo, Y.; et al. High-Pressure Thermal Conductivity Measurements of a (Methane + Propane) Mixture with a Transient Hot-Wire Apparatus. J. Chem. Eng. Data 2020, 65, 906–915. [Google Scholar] [CrossRef]
- Saha, A.; Crosmer, J.; Roy, S.; Meyer, T.R. Spatio-temporal dynamics of an acoustically forced cryogenic coaxial jet injector. Int. J. Multiph. Flow 2024, 170, 104627. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- da Cunha Lima, A.T.; da Cunha Lima, I.C.; de Almeida, M.P. Analysis of turbulence power spectra and velocity correlations in a pipeline with obstructions. Int. J. Mod. Phys. C 2016, 28, 1750019. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851. [Google Scholar] [CrossRef]
- Kabiraj, L.; Saurabh, A.; Wahi, P.; Sujith, R. Route to chaos for combustion instability in ducted laminar premixed flames. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 023129. [Google Scholar] [CrossRef] [PubMed]
- Basarab, M.A.; Konnova, N.S.; Basarab, D.A.; Matsievskiy, D.D. Digital signal processing of the Doppler blood flow meter using the methods of nonlinear dynamics. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium—Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017. [Google Scholar] [CrossRef]
- Fric, T.F.; Roshko, A. Vortical structure in the wake of a transverse jet. J. Fluid Mech. 1994, 279, 1–47. [Google Scholar] [CrossRef]
- Lee, I.; Sung, H.J. Multiple-arrayed pressure measurement for investigation of the unsteady flow structure of a reattaching shear layer. J. Fluid Mech. 2002, 463, 377–402. [Google Scholar] [CrossRef]
- Hudy, L.M.; Naguib, A.; Humphreys, W.M. Stochastic estimation of a separated-flow field using wall-pressure-array measurements. Phys. Fluids 2007, 19, 024103. [Google Scholar] [CrossRef]
- Sherry, M.; Jacono, D.; Sheridan, J.; Mathis, R.; Marusic, I. Flow separation characterisation of a forward facing step immersed in a turbulent boundary layer. In Proceedings of the 6th International Symposium on Turbulence and Shear Flow Phenomena, Seoul, Republic of Korea, 22–24 June 2009. [Google Scholar] [CrossRef]
- Awasthi, M.; Devenport, W.J.; Glegg, S.A.L.; Forest, J.B. Pressure fluctuations produced by forward steps immersed in a turbulent boundary layer. J. Fluid Mech. 2014, 756, 384–421. [Google Scholar] [CrossRef]
- Wu, S.J.; Miau, J.J.; Hu, C.C.; Chou, J.H. On low-frequency modulations and three-dimensionality in vortex shedding behind a normal plate. J. Fluid Mech. 2005, 526, 117–146. [Google Scholar] [CrossRef]
- Xu, S.J.; Zhou, Y.; Wang, M.H. A symmetric binary-vortex street behind a longitudinally oscillating cylinder. J. Fluid Mech. 2006, 556, 27–43. [Google Scholar] [CrossRef]
- Behera, N.; Agarwal, V.K.; Jones, M.; Williams, K.C. Power Spectral Density Analysis of Pressure Fluctuation in Pneumatic Conveying of Powders. Part. Sci. Technol. 2015, 33, 510–516. [Google Scholar] [CrossRef]
- Fugger, C.A.; Roy, S.; Caswell, A.W.; Rankin, B.A.; Gord, J.R. Structure and dynamics of CH2O, OH, and the velocity field of a confined bluff-body premixed flame, using simultaneous PLIF and PIV at 10 kHz. Proc. Combust. Inst. 2019, 37, 1461–1469. [Google Scholar] [CrossRef]
- Heitor, M.; Taylor, A.; Whitelaw, J. Influence of confinement on combustion instabilities of premixed flames stabilized on axisymmetric baffles. Combust. Flame 1984, 57, 109–121. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Timokha, A.N. Sloshing; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Saha, A.; Subramani, H.; Meyer, T.R.; Gunaratne, G.; Yi, T.; Roy, S. Analysis of Spatiotemporal Data. In Optical Diagnostics for Reacting and Non-Reacting Flows: Theory and Practice; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2022; pp. 1203–1288. [Google Scholar] [CrossRef]
- Bourgoin, M.; Baudet, C.; Kharche, S.; Mordant, N.; Vandenberghe, T.; Sumbekova, S.; Stelzenmuller, N.; Aliseda, A.; Gibert, M.; Roche, P.-E.; et al. Investigation of the small-scale statistics of turbulence in the Modane S1MA wind tunnel. CEAS Aeronaut. J. 2018, 9, 269–281. [Google Scholar] [CrossRef]
- Yanovych, V.; Duda, D.; Uruba, V.; Antoš, P. Anisotropy of turbulent flow behind an asymmetric airfoil. SN Appl. Sci. 2021, 3, 885. [Google Scholar] [CrossRef]
- Roy, S.; Hua, J.-C.; Barnhill, W.; Gunaratne, G.H.; Gord, J.R. Deconvolution of reacting-flow dynamics using proper orthogonal and dynamic mode decompositions. Phys. Rev. E 2015, 91, 013001. [Google Scholar] [CrossRef]
- Rowley, C.W.; Mezić, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391. [Google Scholar] [CrossRef]
- Roy, S.; Yi, T.; Jiang, N.; Gunaratne, G.; Chterev, I.; Emerson, B.; Lieuwen, T.; Caswell, A.; Gord, J. Dynamics of robust structures in turbulent swirling reacting flows. J. Fluid Mech. 2017, 816, 554–585. [Google Scholar] [CrossRef]
- Hua, J.-C.; Gunaratne, G.H.; Talley, D.G.; Gord, J.R.; Roy, S. Dynamic-mode decomposition based analysis of shear coaxial jets with and without transverse acoustic driving. J. Fluid Mech. 2016, 790, 5–32. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Combustion chamber size (mm) | 152.4 × 127 |
| Equivalence ratio ( | 0.6–1.0 |
| Inlet temperature (F) | 100, 265, 350, 440, 560, 620 |
| Transducer recording rate (kHz) | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, A.; Subramani, H. Extracting Flow Characteristics from Single and Multi-Point Time Series Through Correlation Analysis. Math. Comput. Appl. 2025, 30, 68. https://doi.org/10.3390/mca30040068
Saha A, Subramani H. Extracting Flow Characteristics from Single and Multi-Point Time Series Through Correlation Analysis. Mathematical and Computational Applications. 2025; 30(4):68. https://doi.org/10.3390/mca30040068
Chicago/Turabian StyleSaha, Anup, and Harish Subramani. 2025. "Extracting Flow Characteristics from Single and Multi-Point Time Series Through Correlation Analysis" Mathematical and Computational Applications 30, no. 4: 68. https://doi.org/10.3390/mca30040068
APA StyleSaha, A., & Subramani, H. (2025). Extracting Flow Characteristics from Single and Multi-Point Time Series Through Correlation Analysis. Mathematical and Computational Applications, 30(4), 68. https://doi.org/10.3390/mca30040068






