Common Attractor for Hutchinson θ-Contractive Operators in Partial Metric Spaces
Abstract
1. Introduction and Preliminaries
- (i)
- (ii)
- (iii)
- (i)
- If then
- (ii)
- (iii)
- θ is non-decreasing.
- For any sequence iff
- There exist and such thatMoreover, the class Θ is the collection of all such which are continuous as well.
2. Main Results
- (i)
- (ii)
- There exists an open set such that and
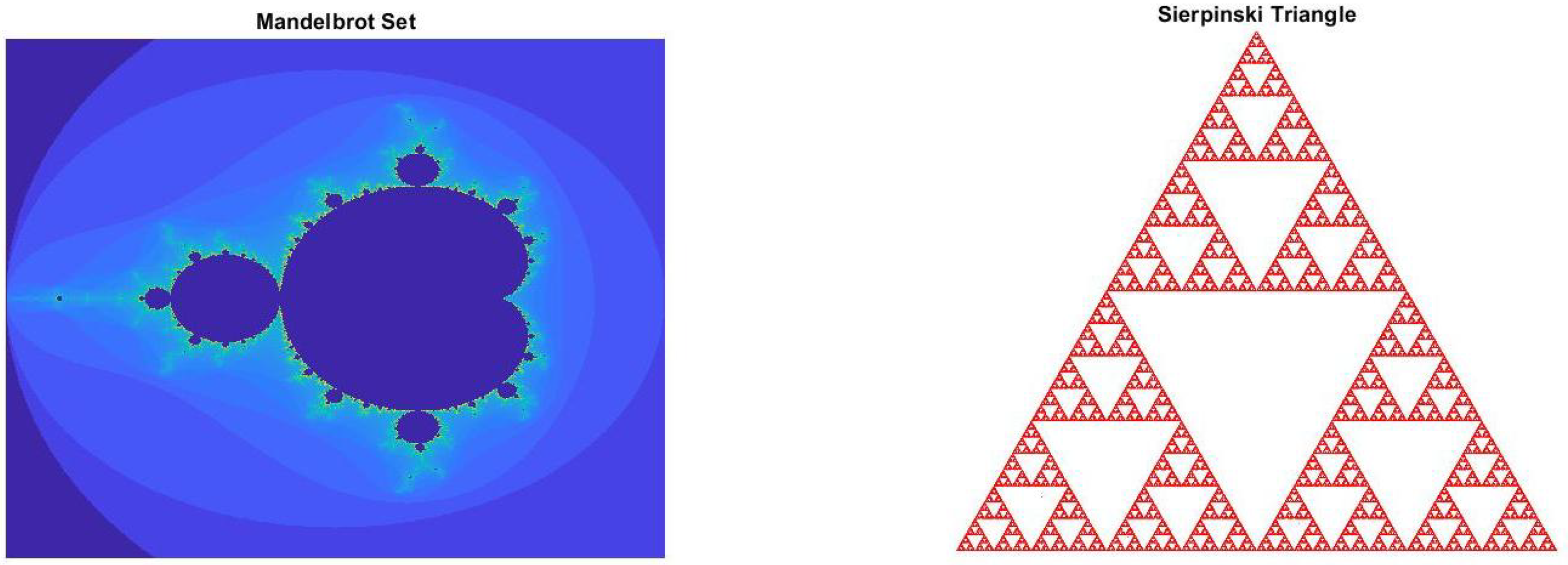
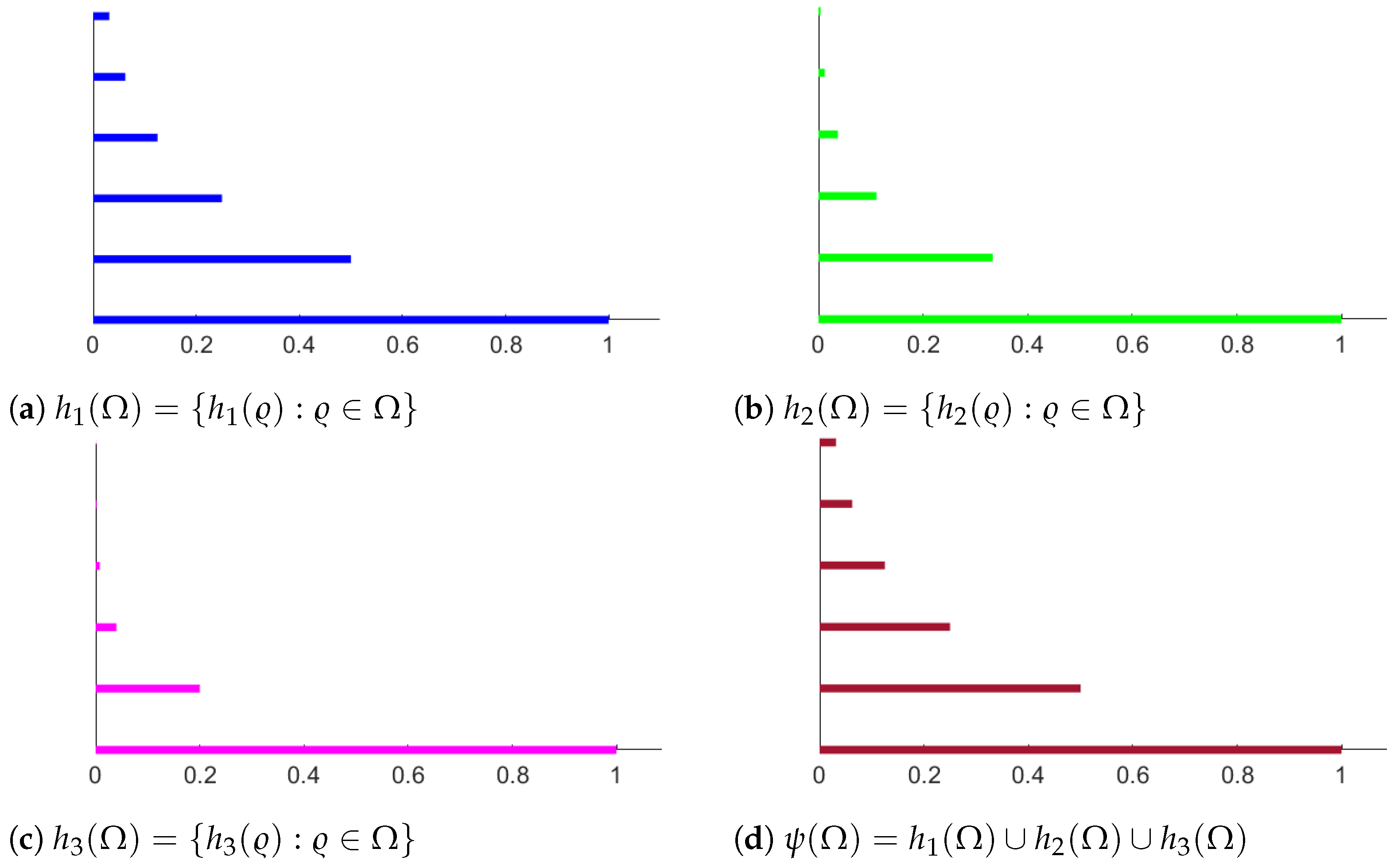
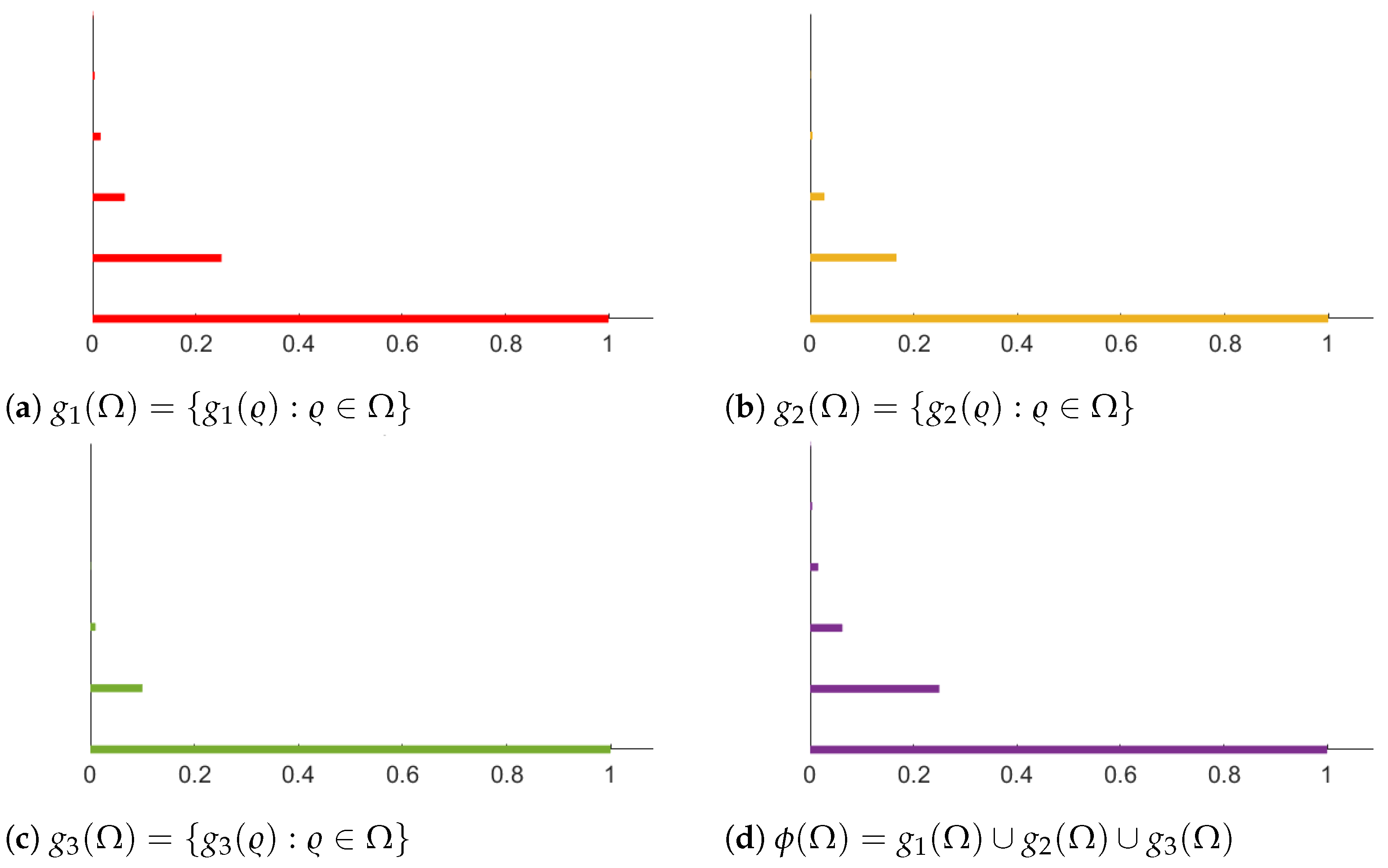
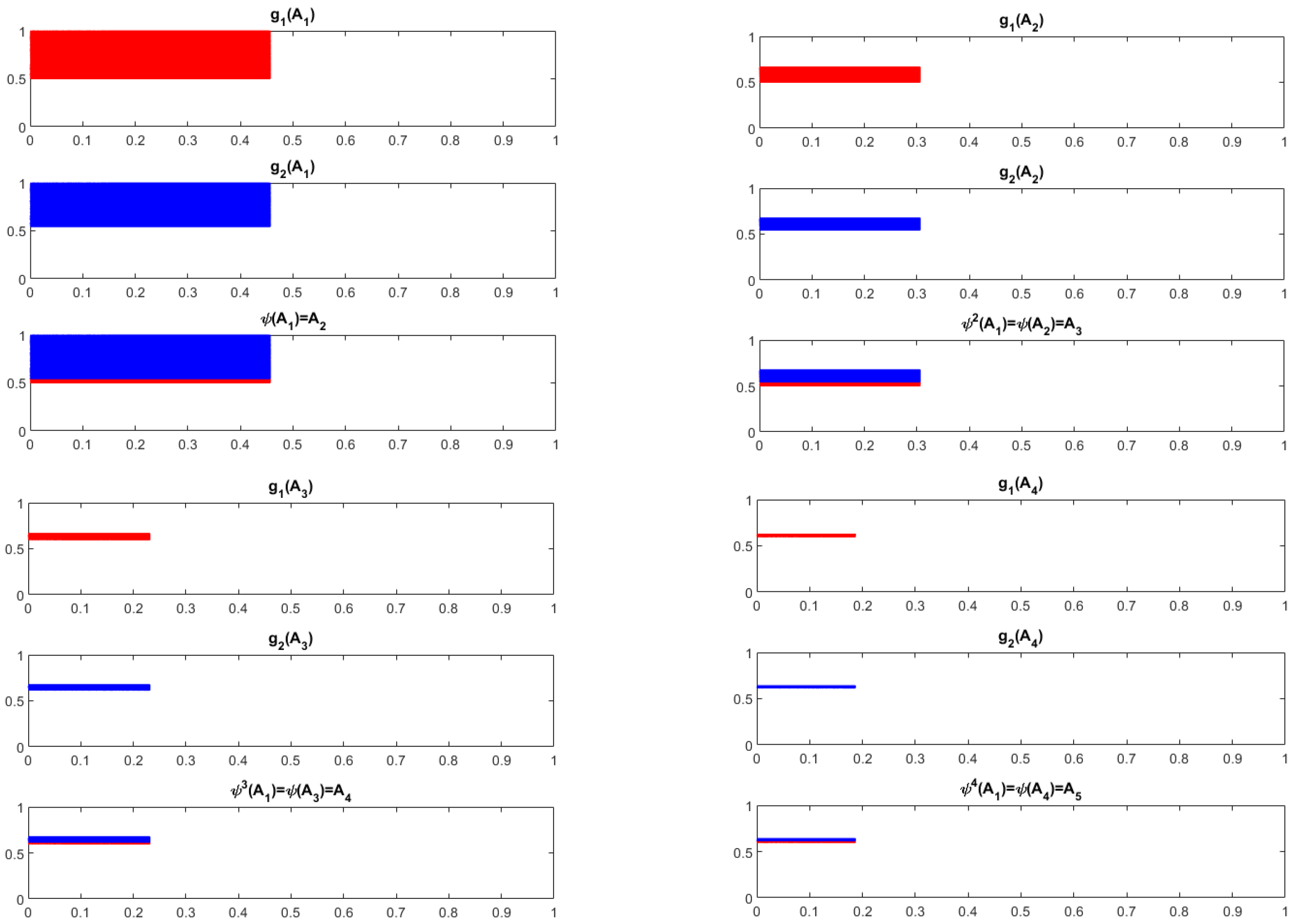
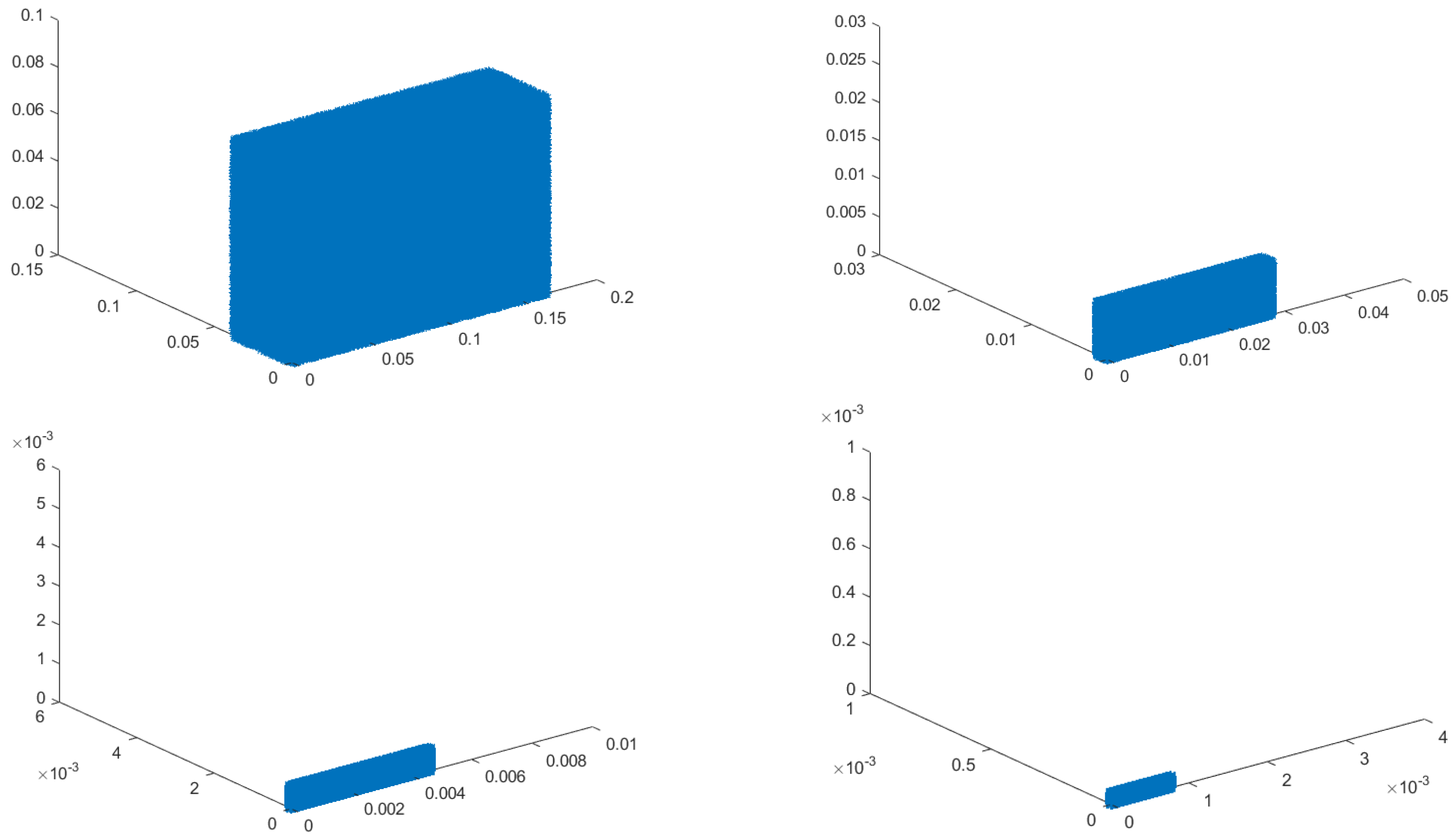
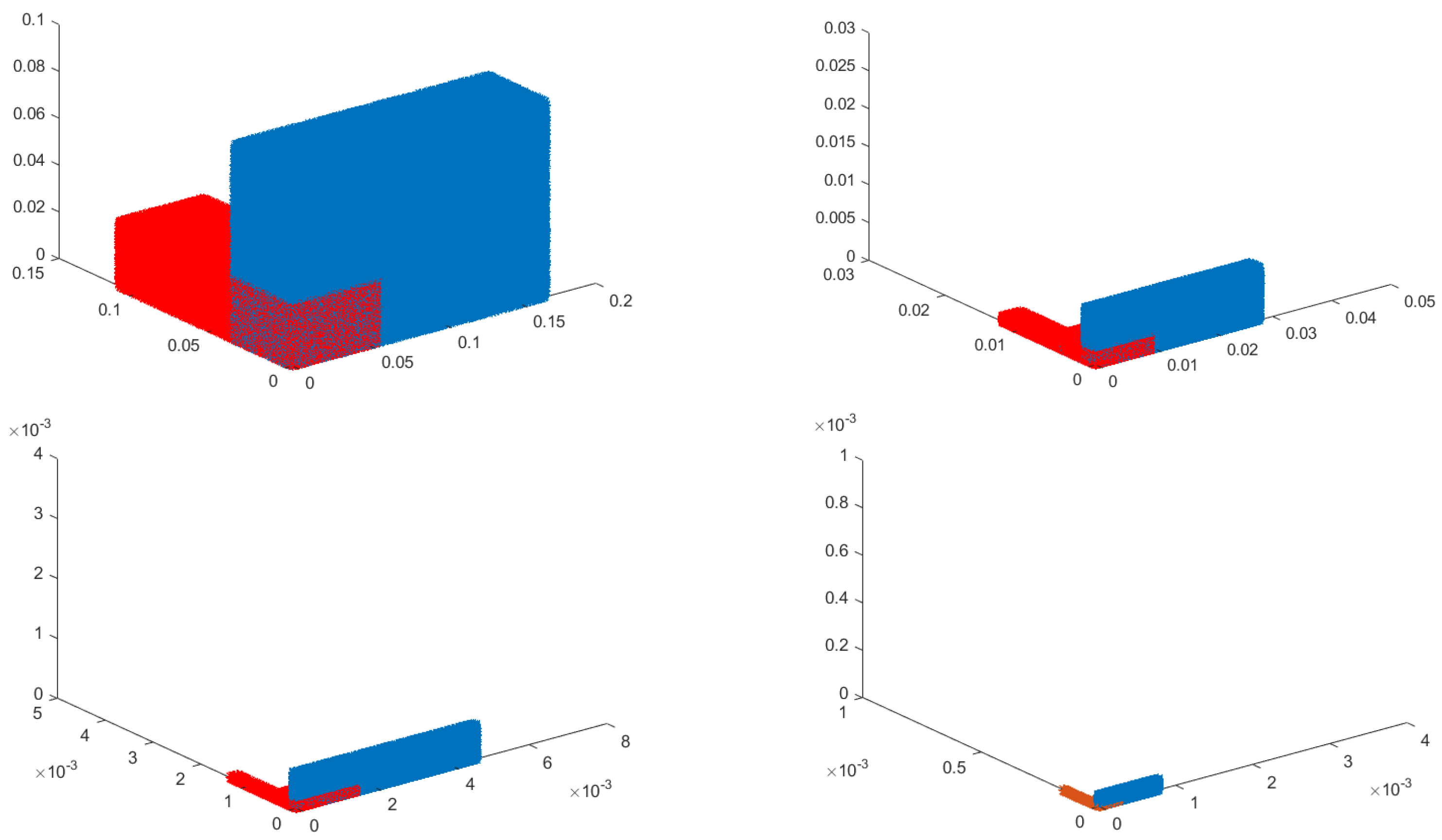
3. Examples
4. Application to Functional Equation
- , and are bounded and continuous.
- For and take as
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hutchinson, J.E. Fractals and self-similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Rising, H. Fractals Everywhere; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Iqbal, B.; Saleem, N.; Iqbal, I.; Aphane, M. Common Attractors of Generalized Hutchinson–Wardowski Contractive Operators. Fractal Fract. 2024, 8, 651. [Google Scholar] [CrossRef]
- Nazir, T.; Silvestrov, S. Common Attractors for Generalized F-Iterated Function Systems in G-Metric Spaces. Fractal Fract. 2024, 8, 346. [Google Scholar] [CrossRef]
- Ashwin, P.; Fadera, M.; Postlethwaite, C. Network attractors and nonlinear dynamics of neural computation. Curr. Opin. Neurobiol. 2024, 84, 102818. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Li, C.; Li, Y.; Ge, X.; Lei, T. Various patterns of coexisting attractors in a hyperchaotic map. Nonlinear Dyn. 2023, 111, 7807–7818. [Google Scholar] [CrossRef]
- Karatetskaia, E.; Kazakov, A.; Safonov, K.; Turaev, D. Analytic proof of the emergence of new type of Lorenz-like attractors from the triple instability in systems with Z4-symmetry. J. Differ. Equ. 2025. [Google Scholar] [CrossRef]
- Shaheryar, M.; Ud Din, F.; Hussain, A.; Alsulami, H. Fixed point results for fuzzy enriched contraction in fuzzy Banach spaces with applications to fractals and dynamic market equilibrium. Fractal Fract. 2024, 8, 609. [Google Scholar] [CrossRef]
- Tanveer, M.; Ahmed, I.; Raza, A.; Nawaz, S.; Lv, Y.P. New escape conditions with general complex polynomial for fractals via new fixed point iteration. AIMS Math. 2021, 6, 6. [Google Scholar] [CrossRef]
- Jleli, M.; Samet, B. A new generalization of the Banach contraction principle. J. Inequal. Appl. 2014, 2014, 38. [Google Scholar] [CrossRef]
- Pasupathi, R.; Miculescu, R. A very general framework for fractal interpolation functions. J. Math. Anal. Appl. 2024, 534, 128093. [Google Scholar] [CrossRef]
- Proinov, P.D. Fixed point theorems for generalized contractive mappings in metric spaces. J. Fixed Point Theory Appl. 2020, 22, 21. [Google Scholar] [CrossRef]
- Raza, A.; Abbas, M.; Hammad, H.A.; De la Sen, M. Fixed Point Approaches for Multi-Valued Prešić Multi-Step Iterative Mappings with Applications. Symmetry 2023, 15, 686. [Google Scholar] [CrossRef]
- Khumalo, M.; Nazir, T.; Makhoshi, V. Generalized iterated function system for common attractors in partial metric spaces. AIMS Math. 2022, 7, 13074–13103. [Google Scholar] [CrossRef]
- Ahmad, J.; Al-Mazrooei, A.E.; Rassias, T.M. Fractals of generalized Θ-Hutchinson operator. Int. J. Nonlinear Anal. Appl. 2022, 13, 1–12. [Google Scholar]
- Aydi, H.; Abbas, M.; Vetro, C. Partial Hausdorff metric and Nadler’s fixed point theorem on partial metric spaces. Topol. Appl. 2012, 159, 3234–3242. [Google Scholar] [CrossRef]
- Bellman, R. The theory of dynamic programming. Bull. Am. Math. Soc. 1954, 60, 503–515. [Google Scholar] [CrossRef]
- Bellman, R. Functional equations in the theory of dynamic programming. V. Positivity and quasi-linearity. Proc. Natl. Acad. Sci. USA 1955, 41, 743–746. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shabir, N.; Raza, A.; De la Sen, M.; Abbas, M.; Ahmad, S. Common Attractor for Hutchinson θ-Contractive Operators in Partial Metric Spaces. Math. Comput. Appl. 2025, 30, 27. https://doi.org/10.3390/mca30020027
Shabir N, Raza A, De la Sen M, Abbas M, Ahmad S. Common Attractor for Hutchinson θ-Contractive Operators in Partial Metric Spaces. Mathematical and Computational Applications. 2025; 30(2):27. https://doi.org/10.3390/mca30020027
Chicago/Turabian StyleShabir, Naila, Ali Raza, Manuel De la Sen, Mujahid Abbas, and Shahbaz Ahmad. 2025. "Common Attractor for Hutchinson θ-Contractive Operators in Partial Metric Spaces" Mathematical and Computational Applications 30, no. 2: 27. https://doi.org/10.3390/mca30020027
APA StyleShabir, N., Raza, A., De la Sen, M., Abbas, M., & Ahmad, S. (2025). Common Attractor for Hutchinson θ-Contractive Operators in Partial Metric Spaces. Mathematical and Computational Applications, 30(2), 27. https://doi.org/10.3390/mca30020027





