A Review on Large-Scale Data Processing with Parallel and Distributed Randomized Extreme Learning Machine Neural Networks

Abstract

The randomization-based feedforward neural network has raised great interest in the scientific community due to its simplicity, training speed, and accuracy comparable to traditional learning algorithms. The basic algorithm consists of randomly determining the weights and biases of the hidden layer and analytically calculating the weights of the output layer by solving a linear overdetermined system using the Moore–Penrose generalized inverse. When processing large volumes of data, randomization-based feedforward neural network models consume large amounts of memory and drastically increase training time. To efficiently solve the above problems, parallel and distributed models have recently been proposed. Previous reviews of randomization-based feedforward neural network models have mainly focused on categorizing and describing the evolution of the algorithms presented in the literature. The main contribution of this paper is to approach the topic from the perspective of the handling of large volumes of data. In this sense, we present a current and extensive review of the parallel and distributed models of randomized feedforward neural networks, focusing on extreme learning machine. In particular, we review the mathematical foundations (Moore–Penrose generalized inverse and solution of linear systems using parallel and distributed methods) and hardware and software technologies considered in current implementations.

1. Introduction

Feedforward neural networks with random weights (RWNNs) [1] and random vector functional link (RVFL) networks [2,3] were presented in 1992, introducing the randomized feedforward neural networks. Particularly, the extreme learning machine (ELM) is an algorithm that was initially proposed in 2004 for single-hidden-layer feedforward networks (SLFNs) [4]. ELM is a variant of RVFL neural networks that eliminates the direct connections between the input layer and the output layer [2,3]. The method randomly assigns the weights and biases of the hidden layer, and then, analytically calculates the weights of the output layer using the Moore–Penrose generalized inverse (MPGI) matrix [4,5]. ELM research has become highly relevant in the field of artificial neural networks (ANNs) due to its faster training speed and good performance compared to other traditional learning algorithms such as back-propagation (BP) and support vector machines (SVMs) [4].

Because of the evolution and great acceptance of ELM networks in the scientific community, several papers have reviewed the topic in the last decade. Previous review papers have mainly focused on the following: mathematical and computational theory of ELM networks, which includes the system of linear equations (SLEs) solution because of its direct relationship with the MPGI matrix; applications in different areas of science and technology; the evolution of ELM networks since their presentation in previous research [4]; variants of ELM networks for solving classification and regression problems in different contexts; strengths and weaknesses of ELM networks and their variants; and open challenges to the scientific community. Among the main limitations, processing large volumes of data remains a problem, and it is a major challenge due to high memory consumption and training time. To cope with the memory and training time issues, distributed and parallel computing is considered a suitable solution. The size of data sets processed with ELM has been steadily increasing; however, it is still a challenge to process large amounts of data on the order of millions of samples. In this paper, it is important to clarify that parallel computing refers to systems with a shared memory architecture; meanwhile, distributed computing points to systems with distributed memory architectures where different nodes are connected in a network.

In this sense, thoroughly addressing the advances of ELM based on parallel and distributed computing is the main objective of the present review, with more attention paid to working with large-scale data sets. This review brings the following contributions to the scientific community:

• An overview of the basic structure of ELM and the variants with parallel and distributed computing to solve problems with large-scale data sets.
• A discussion of advances in solving SLE using parallel and distributed computing to address high-dimensional arrays.
• A description of the parallel and distributed tools used to improve the performance of the ELM algorithm and its variants by solving problems associated with training time and memory capacity.
• A summary of the evolution in the last decade of the ELM algorithm and its variants combined with parallel and distributed tools.

Identifying the challenges of processing large-scale databases with ELM networks is the main scope of this review article. In this regard, the size of databases and computational architectures used with ELM are reviewed in this paper. In addition, a section to discuss the computing of MPGI with high-dimensional matrices is presented. Database size, computational architectures, and the MPGI matrix are the main focus of this review.

The remainder of this paper is as follows: Section 2 presents a discussion on the contributions of review articles published in the last decade. Section 3 describes the fundamentals of ELM and the variants adapted to parallel and distributed computing. Section 4 discusses parallel methods that have been used for the SLE solution and the improvements they can bring to the ELM algorithm. Section 5 reviews the parallel and distributed algorithms for ELM developed in the last decade and provides a brief description of the parallel and distributed tools used in these works. Section 6 discusses the findings. Finally, we present the conclusions in Section 7.

2. Related Reviews about Extreme Learning Machine

ANNs (artificial neural networks) have been widely accepted into the scientific community. New proposals constantly appear which combine various techniques and algorithms to address problems in different contexts. Considering the latter, some recent work includes a deep neural network (DNN) with fuzzy wavelet for predicting energy demand in Iran [6]. A hybrid method incorporating an inline particle swarm optimization (PSO) and a gradient-based algorithm is used in the training. The authors show that the PSO method improves model accuracy and reduces training time. The proposed deep neural network based on fuzzy wavelet (DNFW) outperformed other models in all simulations.

In addition, six classification methods for diagnosing fatigued foot from digital images of the footprint are used in one study [7]. K-nearest neighbors (KNNs) classifier, multilayer perceptron (MLP), SVM, naïve Bayesian (NB) learning, decision tree (DT), and convolutional neural network (CNN) architecture are used by the authors. The results show that CNN is the most accurate method, with 100% accuracy. In another study [8], a classifier based on fuzzy logic and wavelet transformation, in the form of a neural network (FWNNet), is presented for brain tumor diagnosis. The results show that the proposed FWNNet has an accuracy of 100%. Also, FWNNet is presented as the best classifier for brain tumor diagnosis.

An approach to identify breast cancer using machine learning and image processing is presented in another study [9]. The particle-swarm-optimized wavelet neural network (PSOWNN) method presented was proven to be more accurate than other machine learning algorithms such as SVM, KNNs, and CNN. In this direction, a method combining signal processing techniques and machine learning algorithms (MLP, KNNs, NB, and SVM) is presented in another study [10]. The method is proposed to suppress different types of electroencephalogram artifacts. The results show that the proposed method is fully automated and more accurate. However, this approach is computationally extensive, and fast processing machines are required.

As can be seen, ANN-based models have proven to be adequate to address problems widely studied by the scientific community. In this paper, we present a review of the advances in ANNs, with a focus on ELM networks and their variants to address large-scale database problems, as well as the associated mathematical and computational schemes. This section presents a discussion of previous review articles on randomized feedforward neural networks published in the last decade, focusing on ELM networks. Table 1 shows a brief description of these studies, including publication type, focus, some advantages and disadvantages, and the number of citations up to February 2024. The following review papers have been found using the WoS, Scopus, and Google Scholar databases.

Table 1. Summary of reviews on ELM in the last decade up to February 2024. The data were obtained from the databases Google Scholar, WoS, and Scopus.

Reference	Type	Focus	Advantages/Disadvantages	No. Citations *
				WoS	Scopus	Scholar
Huérfano-Maldonado et al. (2023) [11]	Journal: Neurocomputing	Medical image processing using ELM	ELM offers advantages such as fewer training parameters, fast learning speed, and high generalization ability. However, most publications focus on supervised learning, with fewer on unsupervised learning.	3	4	5
Patil and Sharma (2023) [12]	Conf: Int. Conf. on Computational Intelligence and Sustainable Engineering Solutions	Theories, algorithms, and applications of ELM	ELM exhibits fast training and efficient processing of large data sets; however, it is constrained by its limited capacity to learn complex patterns.	-	0	0
Kaur et al. (2023) [13]	Journal: Multimedia Tools and Applications	Multilayer ELM	The applications of ML-ELM in parallel and distributed computing are open. Also, its effectiveness for big data applications can be investigated further.	0	3	3
Vásquez-Coronel et al. (2023) [14]	Journal: Artificial Intelligence Review	Multilayer ELM	With the advancement of technology and the Internet, the amount of data continues to increase exponentially, giving rise to a current open problem in machine learning.	4	4	5
Wang et al. (2022) [15]	Journal: Multimed. Tools Appl.	ELM neural network	ELM has the potential of playing a more important role in big data.	120	138	241
Zheng et al. (2022) [16]	Journal: Big Data Research	Data-stream classification based on ELM	ELM-based algorithms have better generalization ability and less computation time. However, these algorithms are little focused on multi-label data-stream classification.	3	6	7
Martínez et al. (2022) [17]	Conf: Colombian Conf. Communications and Computing	Identification and classification of fingerprint databases	ELM-based algorithms are an economical and accessible alternative to reduce the penetration rate in fingerprint databases compared to traditional algorithms.	-	0	1
Kaur et al. (2022) [18]	Conf: Int. Conf. Machine Learning, Computer Systems, and Security	ELM on TF-IDF features for sentiment analysis	The need for a high number of hidden nodes in ELM is one of the drawbacks which needs to be addressed.	-	0	0
Nilesh and Sunil (2021) [19]	Journal: EAI Endorsed Transactions on Industrial Networks and Intelligent Systems	Optimization algorithms for ELM	The efficiency, accuracy, and easy implementation in various fields are advantages. However, ELM cannot handle massive high-dimensional information. It needs additional hidden nodes.	-	2	5
Mujal et al. (2021) [20]	Journal: Advanced Quantum Technologies	Quantum reservoir computing (QRC) and quantum ELM (QELM)	QRC and QELM are still taking their first steps, so it is premature to make quantitative comparisons with their much more advanced classical counterparts.	33	41	79
Nilesh and Sunil (2021) [21]	Conf.: Int. Conf. Advanced Computing and Communication Systems	Optimization algorithm for ELM	Parallel and transmitted processing of ELM will become the following focal point. Identifying the appropriate number of hidden layer neurons is a disadvantage.	-	7	9
Rodrigues et al. (2021) [22]	Journal: Informatics	Convolutional ELM (CELM)	The training time, test time, and accuracy are some advantages of CELM. However, when the number of layers increases, problems with increasing training time and a loss of generalization capacity emerge.	8	15	19
Saldaña et al. (2021) [23]	Conf.: Brazilian Technology Symposium	ELM for business sales forecasts	There exists little information on the subject because it is a new topic.	-	3	5
Wang et al. (2020) [24]	Journal: IEEE Access	Application of ELM in computer-aided diagnosis (CAD)	The research in this field has important medical and social value. ELM has a short processing time and also has good generalization performance.	9	11	12
Wang et al. (2020) [25]	Journal: IEEE Access	Distributed and parallel ELM for big data	The limitation of hardware is a disadvantage of distributed ELM. Distributed ELM does not apply well to specific problems.	4	7	9
Alaba et al. (2019) [26]	Journal: Neurocomputing	Advances and drawbacks of ELM	The adoption of parallel computing based on MapReduce and GPU acceleration has demonstrated better efficiency.	38	44	51
Yibo et al. (2019) [27]	Journal: J. Phys.: Conf. Ser.	Prediction model of ELM	A combination forecasting method is better than a single forecasting method in forecasting accuracy.	-	8	10
Li et al. (2019) [28]	Journal: Multimed. Tools Appl.	Improved ELM algorithms used for data stream	There is no ideal solution for determining the optimal number of hidden layer nodes. The application of improved ELM for data-stream classification is limited.	16	22	25
Eshtay et al. (2019) [29]	Journal: Int. J. Machi. Learn. and Cyber.	ELM based on metaheuristics	In real life specific problems are still at an early stage. There is still no work that has researched the performance of this type of model using large-scale data sets.	33	38	47
Ghosh et al. (2018) [30]	Conf.: Int. Conf. Recent Trends in Image Processing and Pattern Recognition	ELM and the evolution of its variants	ELM is well-defined in the field of pattern recognition, medical diagnosis, and forecasting areas. The applications of ELM are still open for parallel and distributed computing.	-	5	7
Zhang et al. (2018) [31]	Conf.: Int. Conf. Control, Decision and Information Technologies (CoDIT)	Online sequential extreme learning machine (OS-ELM)	OS-ELM is a faster and more accurate algorithm as compared to other online learning algorithms. The improved OS-ELM algorithms need to be network structure adjusted to improve learning prominence.	-	7	10
Alade et al. (2018) [32]	Conf.: Int. Conf. Reliable Information and Communication Technology	Advances in ELM techniques and their applications	The relevance of ELM in artificial intelligence has brought about great interest. The handling of high-dimensional data is a disadvantage.	-	19	26
Salaken et al. (2017) [33]	Journal: Neurocomputing	Transfer learning (TL) using ELM	The papers published to validate the effectiveness of ELM to solve transfer learning problems. However, these articles failed to compare their performance against existing algorithms.	65	78	98
Albadra and Tiun (2017) [34]	Journal: Int. J. Appl. Engineering Research	Advances in ELM techniques and their applications	ELM’s major strength is that the learning parameters do not have to be iterative. However, the classification boundary of the parameters may not be optimal because they remain the same during training.	-	86	111
Ali and Zolkipli (2016) [35]	Journal: ARPN Journal of Engineering and Applied Sciences	Integration of genetic algorithms (GAs) and ELM to function as an intrusion detection system (IDS)	Advantages of ELMs include ease of implementation and the ability to perform multi-class classification directly without using binary classification techniques in succession.	-	9	12
Huanh et al. (2015) [36]	Journal: Neural Networks	Trends in ELM	ELM and its variants are efficient, accurate, and easy to implement. High-dimensional data analysis is a challenging problem for ELM and its variants.	1240	1461	1839
Cao and Lin (2015) [37]	Journal: Mathematical Problems in Engineering	ELM on high-dimensional and large data applications	ELM has a fast data learning speed and easy implementation. Designing real-time processing systems and devices for applications is highly desired.	33	66	116
Ding et al. (2015) [38]	Journal: Artif. Intell. Rev.	ELM algorithms, theory, and applications	ELM generates a unique optimal solution with the advantages of fast learning speed and generalization performance. However, setting the number of nodes in the hidden layer is a disadvantage.	344	440	574
Deng et al. (2015) [39]	Journal: Sci. China Inf. Sci.	New trends and applications of ELM	Fast learning speed, ease of implementation, and minimal human intervention are significant advantages of ELM compared with traditional NNs and SVM.	103	123	154
Ding et al. (2014) [40]	Journal: Neural Computing and Applications	ELM and its applications	The generalization performance of ELM turns out to be stable. Parallel and distributed computing of ELM are some open problems.	163	213	283

* The references that are not indexed in these databases are represented by a hyphen (-).

In Ding et al. [40], a review of variants and applications of ELM is presented. The variants that focus on adjusting the number of nodes in the hidden layer include incremental ELM (I-ELM), pruned ELM (P-ELM), error-minimized ELM (EM-ELM), and two-stage ELM (TS-ELM). This review also presents online sequential ELM (OS-ELM) [41]. This model performs one-to-one or batch online learning, which makes the algorithm faster without losing accuracy. The model performs initial training with the first batch of data, and then, these results are used to train the next batches of data or individual data. Evolutionary ELM (E-ELM) manages to optimize the hidden layer weights and biases, obtaining good generalization performance. However, the method requires a longer training time because it requires constant iteration of the differential evolution (DE) algorithm. The fully complex ELM (C-ELM) extends the domain of the algorithm to complexes. Finally, the authors show that voting-based ELM (V-ELM), ordinal ELM, and symmetric ELM (S-ELM) improve the ELM algorithm to some extent.

Also, Ding et al. [40] mention that regression and classification problems require less training time and have better performance and generalization (compared to other conventional ANN algorithms), mainly in the following applications: pattern recognition, prediction, diagnosis, image processing, and reporting a good overall performance. In addition, the authors expose the following as open problems: computation of neurons in the hidden layer for good performance according to data characteristics, solving problems with big data, and parallel and distributed computing in ELM. Moreover, Ding et al. [38] reviewed the progress of ELM algorithms, theories, and applications. This study shows that the ELM algorithm still has some shortcomings that require further development and refinement. Among the improvements considered by the researchers are the following: (1) the model structure and generalization performance; (2) the combination of online learning, genetic algorithms, SVM, and ELM; and (3) the extension of ELM applications.

Subsequently, Cao and Lin [37] reviewed applications with large amounts of high-dimensional data. Applications with these characteristics are related to image, video, and medical signal processing. The exact number of neurons in the hidden layer and the design of real-time processing systems and devices are the open problems highlighted by the authors. Also, trends in ELM are discussed in Huang et al. [36], where they highlight the runtime difficulties faced by ELM when working with large data sets. In addition, the authors also highlight parallel computing as an alternative to address these difficulties. Although some researchers have implemented parallel computing, it is considered a field that needs to be further explored in ELM research with large-scale data sets. Ali and Zolkipli [35] reviewed ELM and genetic algorithms (GAs) to integrate them as an intrusion detection system (IDS) in cloud computing. Their proposal aimed to improve the speed and accuracy of the IDS. Two years later, the authors developed a hybrid model based on particle swarm optimization (PSO-ELM) [42] and showed that the model improves accuracy, with fewer neurons compared to the standard ELM algorithm.

The papers of Alade et al. [32], and Albadra and Tiun [34] present an updated view of ELM and describe its strengths and weaknesses. Among the advantages they highlight is that the parameters of the hidden layer do not need to be tuned. Furthermore, ELM can bridge the gap between biological learning machines and conventional learning machines. Despite the advantages of ELM, the authors highlight the importance of further research in finding the optimal number of hidden nodes, training with large data sets, and modifying the algorithm for distributed and parallel computation. In addition, Salaken et al. [33] study transfer learning (TL) using ELM. Their work considers kernel ELM (K-ELM), OS-ELM, and reduced kernel ELM (RK-ELM), providing an updated review for future TL research using ELM. In Zhang et al. [31], the authors study the OS-ELM model, and Ghosh et al. [30] review ELM variants. As in previous works, they highlight the importance of expanding research on the OS-ELM algorithm, as well as regarding the use of distributed and parallel computing for training ELM on massive data sets. In addition, Eshtay et al. [29] provides the first review of ELM based on metaheuristics. Their work shows that applications of ELM using metaheuristics are still in a very early and open stage for research, and no studies have implemented these models on large-scale data sets.

Li et al. [28] conducted a review of recently used algorithms for data mining. The authors consider it necessary to study the monolayer and multilayer ELM algorithms for data-stream classification due to the complexity of massive data labeling. In contrast, Yibo et al. [27] discussed ELM-based prediction algorithms, highlighting several advances in ELM prediction research, although this requires further research. Furthermore, Alaba et al. [26] reviewed the main advantages and disadvantages of ELM, where the main limitation is the determination of the hidden layer structure. They conclude that although the computation of the pseudo-inverse has been addressed with different methods, it requires further research. Their report shows that methods based on the MapReduce framework, GPU acceleration, and block training have shown better performance for parallel computing and large-scale data handling.

Wang et al. [24] reviewed the application of ELM in computer-aided diagnostics (CAD). The authors showed it is possible to apply ELM in the construction of CAD systems, so the perspective is broad and deserves further study. Moreover, Wang et al. [25] presented the research background of ELM and enhanced ELM, implementing a distributed ELM from matrix set operations. The authors highlight that the most computationally expensive computation is the MPGI multiplication operator. They conclude that the implementation of parallel and distributed ELM algorithms will become one of the key points of future research. At this point, it is important to highlight that, unlike the review by Wang et al. [25], our work, in addition to reviewing the distributed and parallel algorithms developed for ELM models, emphasizes observing and describing the parallel architectures and tools used and the size of the databases, because these are very important aspects to consider when analyzing the performance of ELM variants for large-scale databases. In addition, considering the high time required for the computation of the MPGI, an updated review of the solution of systems of linear equations through parallel methods is made, because these are important developments to improve the current ELM variants.

In Saldaña-Olivas and Huamán-Tuesta [23], a systematic review was carried out to identify the level of help that an ELM network provides to companies’ sales forecasts. The authors conclude that ELM models greatly improve the accuracy of sales forecasts compared to traditional techniques, so they suggest further research and studies with real data. In Rodrigues et al. [22], a systematic review is presented on the alternative architectures of convolutional ELM (CELM), a combination of deep learning and ELM networks. The authors focus their study on the solution of problems based on image analysis and highlight that CELM models present good accuracy, convergence, and computational performance. In the same year, Nilesh and Sunil [19,21] reviewed the different optimization algorithms developed to improve the performance of ELM networks. The authors note that optimization techniques in ELM still present certain drawbacks and emphasize that parallel processing will become the next focus of research on ELM and its variants. In Mujal et al. [20], a review of recent proposals, first experiments, and the potential of quantum devices for reservoir computing (RC) and ELM is performed. The results of this review show that several tasks can be successfully performed; however, these models are still at an early stage, so it is too early to make comparisons with classical models that today have much more progress in terms of efficiency or performance.

One year later, a review of data-stream classification based on ELM was realized by Zheng et al. [16]. The authors consider that little research has yet been conducted in this field. ELM for multi-label data-stream classification based on semi-supervised learning, high-dimensional data processing based on ELM, the random mechanism of ELM parameters, and the impact of the distribution of hidden layer parameters are considered open problems by the authors. Wang et al. [15] presented a theoretical analysis of the universal approximation and generalization of ELM. This review notes how interesting it could be to combine deep learning and ELM in big data problems. Additionally, ELM reviews for sentiment analysis [18] and fingerprint classification [17] have been presented at international conferences. These highlight the need to investigate further the number of neurons in the hidden layer in future studies. Recently, two reviews of multilayer ELM neural networks [13,14] have been presented, highlighting the importance of implementing parallel and distributed computing to address big data problems with this variant. Finally, Patil and Sharma [12] provide a review of theories, algorithms, and applications of ELM, while Huérfano-Maldonado et al. [11] present a comprehensive review of medical image processing with ELM. The authors highlight the large number of parameters, fast training, and efficiency in processing large-scale databases as advantages of these models. However, they also note disadvantages such as the limited ability to learn complex patterns and the high focus on supervised learning compared to unsupervised learning. A background on ELM and other randomized feedforward neural network models is presented in the following section.

3. Background

The ELM model was proposed in 2004 [4] as an SLFN learning scheme with high generalization capabilities that require less training time. This algorithm has similarities with RWNN [1] and RVFL [3], presented in 1992 and 1994, respectively. The algorithm consists of a pseudo-random initialization of the hidden layer weights and biases; thus, the weights of the output layer are calculated analytically using the MPGI. Below, we introduce the randomized feedforward neural networks, mainly by focusing on RWNN, RVFL, and the origin or inspiration of ELM and its variants. Additionally, we present the basics of the ELM and describe its parallel and distributed variants.

3.1. Moore–Penrose Generalized Inverse

In ELM networks and other randomized feedforward neural network models, the Moore–Penrose generalized inverse (MPGI) [43] is used for the analytical computing of the output layer weights. The MPGI is commonly known as the pseudo-inverse and is defined as follows. Let $\mathbf{A}\mathbf{x}=\mathbf{y}$ be a linear system where $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ with $m,n\in \mathbb{N}$, and $m>n$; its solution can be simplified with the MPGI matrix ${\mathbf{A}}^{†}\in {\mathbb{R}}^{n\times m}$. The MPGI matrix is unique and satisfies the following four conditions, which are usually called Moore–Penrose conditions:

$$\mathbf{A}{\mathbf{A}}^{†}\mathbf{A}=\mathbf{A},{\mathbf{A}}^{†}\mathbf{A}{\mathbf{A}}^{†}={\mathbf{A}}^{†},{\mathbf{A}}^{†}\mathbf{A}={\left({\mathbf{A}}^{†}\mathbf{A}\right)}^T,\mathrm{and}\mathbf{A}{\mathbf{A}}^{†}={\left(\mathbf{A}{\mathbf{A}}^{†}\right)}^T.$$

(1)

For a linear system $\mathbf{A}\mathbf{x}=\mathbf{y}$ that has no exact solution, the solution of the problem is by the method of least squares with Euclidean $min\left|\right|\mathbf{A}\mathbf{x}-\mathbf{y}\left|\right|$ norm. The solution of the linear system $\mathbf{A}\mathbf{x}=\mathbf{y}$ by the least squares method corresponds to the matrix form of the system ${\mathbf{A}}^T\mathbf{A}\mathbf{x}={\mathbf{A}}^T\mathbf{y}$ and can be written as follows:

$$\left\{\begin{array}{c}\mathbf{x}={\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\mathbf{y}\hfill \\ {\mathbf{A}}^{†}={\left({\mathbf{A}}^T\mathbf{A}\right)}^{-1}{\mathbf{A}}^T\hfill \end{array}\right.$$

(2)

where ${\mathbf{A}}^{†}$ is the MPGI of the matrix $\mathbf{A}$ [43]. The pseudo-inverse is a concept that has been useful for solving SLE in multiple contexts [43,44].

3.2. Standard Model of Extreme Learning Machine

The standard ELM model is composed of an input layer, a hidden layer, and an output layer, as shown in Figure 1. Given an arbitrary training set $\aleph =\{({\mathbf{x}}_i,{\mathbf{t}}_i)\mid {\mathbf{x}}_i\in {\mathbb{R}}^n,{\mathbf{t}}_i\in {\mathbb{R}}^m\}$, with $i=1,\dots ,N$, an activation function $g\left(x\right):{\mathbb{R}}^n\to {\mathbb{R}}^m$, and the number of hidden neurons $L\mid L\le N$, the training algorithm of an SLFN is defined as follows:

$$\sum _{i=1}^L{\mathit{\beta }}_{i}g({\mathbf{w}}_i·{\mathbf{x}}_j+b_i)={\mathbf{t}}_j,j=1,\dots ,N,$$

(3)

where ${\mathbf{w}}_i$ and $b_i$ are the i-th weight and bias of the hidden layer, respectively, ${\mathit{\beta }}_i$ is the i-th weight of the output layer, and ${\mathbf{w}}_i·{\mathbf{x}}_j$ represents the inner product of ${\mathbf{w}}_i$ and ${\mathbf{x}}_j$ [44]. Equation (3) can be written in matrix notation as $\mathbf{H}\mathit{\beta }=\mathbf{T}$, where

$$\begin{array}{c}\mathbf{H}={\left[\begin{array}{ccc}g({\mathbf{w}}_1{\mathbf{x}}_1+b_1)& \cdots & g({\mathbf{w}}_L{\mathbf{x}}_1+b_L)\\ ⋮& \ddots & ⋮\\ g({\mathbf{w}}_1{\mathbf{x}}_N+b_1)& \cdots & g({\mathbf{w}}_L{\mathbf{x}}_N+b_L)\end{array}\right]}_{N\times L}\end{array},\begin{array}{c}\mathit{\beta }={\left[\begin{array}{c}{\mathit{\beta }}_1\\ ⋮\\ {\mathit{\beta }}_L\end{array}\right]}_{L\times m}\end{array},\mathrm{and}\begin{array}{c}\mathbf{T}={\left[\begin{array}{c}{\mathbf{t}}_1\\ ⋮\\ {\mathbf{t}}_N\end{array}\right]}_{N\times m}\end{array}.$$

(4)

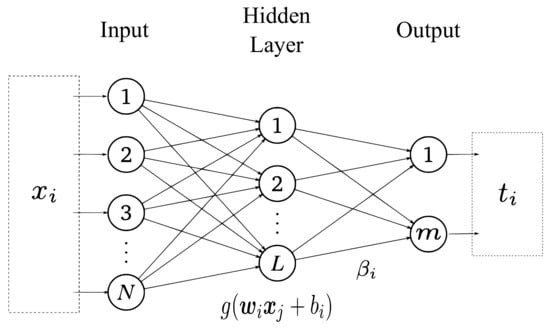
Figure 1. Basic structure of the standard ELM model.

The $\mathbf{H}$ matrix in (4) is called the output matrix of the hidden layer of the neural network [4,44]. Thus, the weights ${\mathit{\beta }}_i$ of the output layer are calculated analytically using the following:

$$\mathit{\beta }={\mathbf{H}}^{†}\mathbf{T},$$

(5)

where ${\mathbf{H}}^{†}$ is the MPGI of the matrix $\mathbf{H}$. A brief description of randomized feedforward neural networks is presented below. We focus on the similarity of ELM with RWNN and RVFL.

3.3. Randomized Feedforward Neural Networks and ELM’s Origin

Several randomization-based feedforward neural networks have been proposed in the literature. The similarities that RWNN and RVFL have with ELM are introduced in this section. In 1992, Schmidt et al. [1] proposed feedforward neural networks with random weights (RWNNs). In this work, random values were assigned to the weights in the hidden layer. The following represents the function computed by a network:

$$\sum _{i=1}^L{\mathbf{w}}_{i}g\left(\sum {\mathbf{m}}_i·{\mathbf{x}}_j\right)+{\mathbf{w}}_{L+1},j=1,\dots ,N,$$

(6)

Here, ${\mathbf{m}}_i$ and ${\mathbf{x}}_j$ are the weight and input vectors in the hidden layer, respectively. ${\mathbf{w}}_i$ is the weights in the output units and ${\mathbf{w}}_{L+1}$ is always multiplied by one and can be regarded as a threshold value. In this model, the network weights are optimized by using the well-known $L_2$ criterion. The parameters ${\mathbf{w}}_i$ and ${\mathbf{w}}_{L+1}$ are then optimized for a chosen set of weights ${\mathbf{m}}_i$, taken randomly. Furthermore, only one hidden layer is used.

Pao et al. [2,3] proposed a random vector functional link (RVFL) network. As shown in Figure 2, this model is a semi-random realization of the functional link neural networks with direct links from the input layer to the output layer [45,46]. The RVFL network performs a nonlinear transformation of the input pattern before it is fed to the input layer of the network. The essential action is, therefore, the generation of an enhanced pattern to be used instead of the original [3]. In this model, if the input data has K features and there are L enhancement (hidden) nodes, then there are in total $K+L$ inputs for each output node. The RVFL output layer weights are obtained by minimizing the following squared error:

$$E=\frac{1}{N}\sum _{i=1}^N{({\mathbf{t}}_i-{\mathit{\beta }}_j{\mathbf{d}}_i)}^2,j=1,\dots ,K+L,$$

(7)

where ${\mathbf{d}}_i$ is the concatenation of hidden features and original features via direct links. Using a generalized Moore–Penrose inverse matrix, the solution is given by $\mathit{\beta }={\mathbf{D}}^{†}\mathbf{T}$, where $\mathbf{D}=\left[\mathbf{H}\mathbf{X}\right]$.

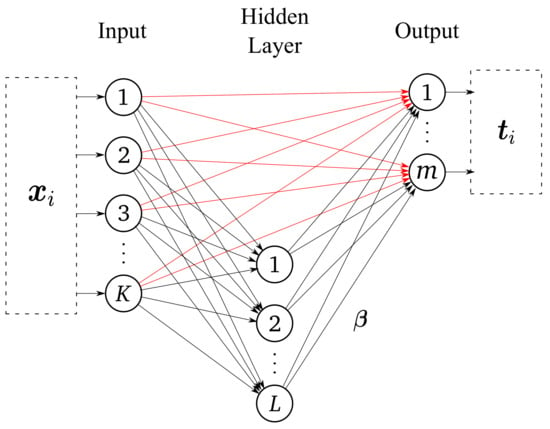
Figure 2. Basic structure of the RVFL model.

In the case of ELM, the direct link from the input layer to the output layer is eliminated, so it can be said that ELM is a simplified version of RVFL inspired by the different randomization-based feedforward neural networks reported in the literature before 2004. Reviews of randomization-based feedforward neural networks have been presented in a couple of previous studies [45,46]. The similarities between RVFL and ELM are also visible in the variants of both models. An updated review of recent developments, applications, and future directions of RVFL is presented in another study [47], where the authors present the RVFL network variants in detail and classify them as shallow RVFL, ensemble-learning-based RVFL, deep RVFL architectures, semi-supervised and unsupervised methods based on RVFL, and hyper-parameter optimization. A summary of RVFV applications is further presented in another study [47], where electricity load forecasting, solar power forecasting, wind power forecasting, and financial time-series forecasting are the highlighted applications.

Because our goal is to identify the challenges of processing large-scale databases with ELM, below we present a review of ELM variants implemented by using parallel and distributed computing.

3.4. ELM Variants Implemented by Using Distributed and Parallel Computing

To obtain better performance of the ELM algorithm, different variants have emerged to improve its training time, accuracy, and generalization capability. This section presents a brief description of the two variants of ELM that have been most widely implemented through distributed and parallel computing tools to solve regression and classification problems on large-scale data sets.

The most widely implemented variant for solving problems on large-scale data sets using distributed and parallel computing is called online sequential extreme learning machine (OS-ELM) [41]. This algorithm is presented as an alternative for those applications where new data are constantly being received. In this case, training the network with new data requires performing the entire training process, which requires a significant amount of time. Therefore, the OS-ELM algorithm allows training with new samples based on the previous training results through a sequential learning process without the need to retrain the entire network.

Figure 3 shows a general scheme of the OS-ELM algorithm, which consists of two phases: the initialization phase and the sequential training phase. During the initialization, an initial training set is provided ${\aleph }_0=\{({\mathbf{x}}_i,{\mathbf{t}}_i)\mid {\mathbf{x}}_i\in {\mathbb{R}}^n,{\mathbf{t}}_i\in {\mathbb{R}}^m\}$, with $i=1,\dots ,N_0$. Therefore, the initial matrix ${\mathbf{H}}_0$ is computed and the weights ${\mathit{\beta }}^{\left(0\right)}$ of the output layer are estimated using the standard ELM model algorithm. In the sequential training phase, a new set of samples is given ${\aleph }_1$ with corresponding labels ${\mathbf{T}}_1$, for which the output partial matrix of the hidden layer ${\mathbf{H}}_1$ is calculated. From this new output matrix ${\mathbf{H}}_1$, the new labels ${\mathbf{T}}_1$, previous weights ${\mathit{\beta }}^{\left(0\right)}$, and current weights ${\mathit{\beta }}^{\left(1\right)}$ are estimated. The sequential training phase is continuously repeated as sets of training samples, which are not necessarily the same size, are obtained.

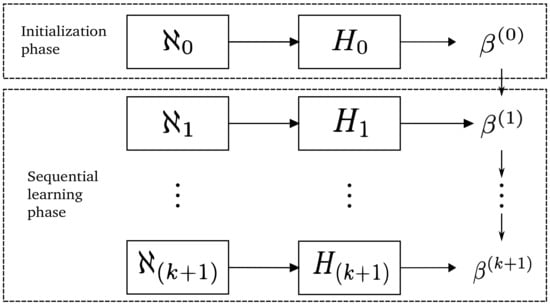
Figure 3. General scheme of the training process of the OS-ELM.

Because OS-ELM allows batch training, the database can be divided into smaller batches to be used for sequential training. Splitting the database is presented as a good alternative for those cases where the computational architecture does not allow processing the large size of the hidden layer output matrix, having as an alternative sequential training. In addition, it is possible to speed up the training time of each batch by combining this methodology with parallel methods to compute the MPGI. Among the most recent work using this algorithm with parallel and distributed computing is that presented in a system-on-a-chip field-programmable gate array (SoC-FPGA) study [48]. In another study [49], the authors implement a parallel OS-ELM algorithm for particulate matter prediction. In a study on the prediction of avionics [50], a core system of modern aircraft is made using ensemble-enhanced OS-ELM. Finally, in another study [51] a regularized mixed-norm OS-ELM (MRO-ELM) algorithm accelerated with a parallel GPU is proposed that outperforms the standard OS-ELM version.

K-ELM is also widely used for solving problems with distributed and parallel computing. This model is identical to kernel ridge regression (KRR) [52], was renamed in another study [53], and differs from the classical ELM and other randomized feedforward neural networks models because it uses a kernel function that does not take into account the weights $\mathbf{w}$, biases $\mathbf{b}$, and number of neurons L of the hidden layer. Equation (8) represents the kernel matrix, which only depends on the input data $x_i$ and the number of training samples.

$$\mathbf{H}{\mathbf{H}}^T={\mathrm{\Omega }}_{ELM}=\left[\begin{array}{ccc}\mathbf{K}(x_1,x_1)& \cdots & \mathbf{K}(x_1,x_N)\\ ⋮& \ddots & ⋮\\ \mathbf{K}(x_N,x_1)& \cdots & \mathbf{K}(x_N,x_N)\end{array}\right].$$

(8)

In this sense, the weights of the output layer $\mathit{\beta }$ are calculated as follows:

$$\mathit{\beta }={\left(\frac{\mathbf{I}}{C}+{\mathrm{\Omega }}_{ELM}\right)}^{-1}\mathbf{T},$$

(9)

where $\mathbf{I}$ is the identity matrix, C is a regularization parameter, and $\mathbf{T}$ is the vector of the labels of the training set. The features of the K-ELM algorithm have been used to propose online sequential algorithms (OS-RKELM) that, like OS-ELM, allow training samples to be split for one-to-one or block-by-block learning [54], enabling configurations for parallel training. A recent study using the K-ELM algorithm with parallel and distributed methods has also been presented [55]. The authors propose a new K-ELM model together with K-means clustering and firefly algorithms (Kmeans-FFA-KELM) to accurately and quickly estimate reference evapotranspiration, an important process for determining crop water requirements.

3.5. Other Variants

The Incremental ELM (I-ELM) algorithm utilizes an incremental approach for constructing the network, allowing for the gradual addition of hidden nodes. Before training, the network begins with no nodes in the hidden layer [56]. The addition of new hidden nodes occurs randomly, one at a time. While adding a new hidden node, the output weights of the existing hidden nodes are maintained without modification. This methodology not only enhances the efficiency of I-ELM for SLFN featuring continuous activation functions but also for those utilizing piecewise continuous activation functions like threshold functions. Pruned ELM(P-ELM) is a systematic and automated method for designing ELM classifier networks [57]. The use of an inappropriate number of hidden nodes can lead to issues of underfitting or overfitting in pattern classification. P-ELM addresses this by starting with a large number of hidden nodes, and then, removing those that are irrelevant or have low relevance to the class labels during the learning process. This automated approach to network design results in compact network classifiers that exhibit fast response times and robust prediction accuracy on unseen data. P-ELM is particularly well-suited for pattern classification tasks.

Evolutionary ELM (E-ELM) optimizes input weights and hidden biases, as well as determines output weights. The algorithm employs a modified differential evolutionary (DE) algorithm to optimize input weights and hidden biases, while the MPGI is used to analytically determine output weights [58]. Experimental results demonstrate that E-ELM achieves good generalization performance with more compact networks compared to other algorithms such as BP and the original ELM. An overview of these and other variants of ELM can be found in review articles reported in the literature [5,34,39,40]. Section 5 delves into the distributed and parallel systems that have been used to improve ELM variants in the last decade, with an emphasis on the architectures and tools used.

4. Methods for Solving Linear Systems with Parallel and Distributed Computing

In this section, we review the most relevant methods proposed to solve a system of linear equations in an accelerated manner by applying distributed and parallel computing. The reported works are classified as follows: (1) methods based on matrix operations, (2) methods based on matrix decomposition, and (3) iterative methods. This section is an update of the review in a previous study [59]. The works presented are related to the algebraic processes associated with ELM models and their variants. Parallel architectures and tools and the size of the databases used are also presented. In the following, let us consider a linear system (LS) as

$$\mathbf{A}\mathbf{X}=\mathbf{B},$$

(10)

where $\mathbf{A}\in {\mathbb{R}}^{n\times n}$ is a regular matrix and $\mathbf{B}\in {\mathbb{R}}^n$.

Matrix-operations-based methods represent a great variety of methods that combine matrix operations to solve (10). Among the most applied and performed with distributed and parallel computing is Gaussian elimination and its variants (Gauss–Jordan, Gauss–Huard). The methods based on Gaussian elimination used to solve (10) perform elementary operations to obtain the step form of $\mathbf{A}$ (diagonal or triangular). The sequence of equivalent linear systems is obtained by applying elementary operations (i.e., ${\mathbf{A}}^k\mathbf{X}={\mathbf{B}}^k$) for $k=1,\dots ,n$, where n is the smallest positive number for which ${\mathbf{A}}^n$ is the step form of $\mathbf{A}$. The reduced system ${\mathbf{A}}^n\mathbf{X}={\mathbf{B}}^n$ has solutions equivalent to solutions of (10), and obtaining its solution is easier [43]. Concerning matrix-decomposition-based methods, the effective algorithms to solve (10) are the methods based on singular value decomposition (SVD), Cholesky factorization, QR factorization, tensor product, and the conjugate process of Gram–Schmidt [60]. To apply Cholesky decomposition, let $\mathbf{A}$ be a positively defined Hermitian matrix in (10). Cholesky’s method is a decomposition of a positively defined Hermitian matrix into the product of a lower triangular matrix and its conjugate transpose. The method defines $\mathbf{L}$ as a lower triangular matrix (Cholesky factor) in such a way that $\mathbf{A}=\mathbf{L}{\mathbf{L}}^T$. Thus, Lu et al. [60] introduce the Cholesky factorization algorithm of a singular matrix as a fast method for ELM (Geninv-ELM).

In the case of oversized systems, that is, the matrix $\mathbf{A}$ in (10) is not a square matrix, other methods should be applied. For instance, the singular value decomposition (SVD) method, which consists of decomposing the matrix $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ with rank r as follows: $\mathbf{A}=\mathbf{U}\Sigma {\mathbf{V}}^T$, where $\mathbf{U}\in {\mathbb{R}}^{m\times m}$ y $\mathbf{V}\in {\mathbb{R}}^{n\times n}$ are unitary matrices [43]. Using SVD decomposition, the MPGI ${\mathbf{A}}^{†}$, which is defined by ${\mathbf{A}}^{†}=\mathbf{V}{\Sigma }^{†}{\mathbf{U}}^T$, is calculated. SVD decomposition is supported as an effective algorithm for estimating the MPGI in ELM [60]. In addition, $QR$ factorization is another widely used method in the ELM algorithm. This method consists of a matrix $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ with linearly independent columns, which decomposes in the form $\mathbf{A}=\mathbf{Q}\mathbf{R}$, where $\mathbf{Q}$ is a unit matrix with orthonormal columns and $\mathbf{R}$ an upper triangular matrix [43]. In the ELM model, $QR$ factorization is used to obtain $\mathbf{H}\mathbf{P}=\mathbf{Q}\mathbf{R}$, where $\mathbf{H}$ is the output matrix of the hidden layer and $\mathbf{P}\in {\mathbb{R}}^{L\times L}$ is a permutation matrix. The MPGI matrix of $\mathbf{H}$ is obtained by ${\mathbf{H}}^{†}=\mathbf{P}{\mathbf{R}}^{†}{\mathbf{Q}}^T$ [60].

Finally, an iterative method involves the selection of an initial approximation ${\mathbf{X}}_0$ of (10) and the sequence ${\mathbf{X}}_1$, ${\mathbf{X}}_2$, …, ${\mathbf{X}}_k$, defined by an approximation algorithm. Mathematical efforts are concentrated on finding the sequence $\left({\mathbf{X}}_k\right)$ that converges (in some sense) to the solution of (10) [61]. The advantage of using iterative methods to compute the solution of the system in (10) is that this type of algorithm does not alter the matrix $\mathbf{A}$ during the process. Therefore, the accumulation error is smaller than for other algorithms. However, many times, the size and density of $\mathbf{A}$ can affect the computational speed [61]. By defining an iterative method to solve (10), the sequence ${\mathbf{X}}_k$ converges to an approximation of the exact solution of (10) for any initial condition ${\mathbf{X}}_0$, where the iteration terminates upon satisfying a predefined stopping criterion related to the desired accuracy (tolerance). Among the most popular classical iterative methods for SLE solutions are the Jacobi, Gauss–Seidel, and successive over-relaxation (SOR) methods [43].

Table 2 presents a summary of proposed works for solving a linear system using parallel and distributed computing. As can be seen, the implementation of parallel and distributed computing provides better performance in solving the LS with matrix-operations-based methods, matrix-decomposition-based methods, and iterative methods.

Table 2. Summary of papers that have used matrix-operations-based methods, matrix-decomposition-based methods, and iterative methods with parallel and distributed computing to solve linear systems.

Reference	Application	Architecture	Parallel Tool	Data	Results	Limitations
Li (2024) [62]	Sparse Triangular Solver (SpTRSV)	Sunway many-core processors.	swSparse library	949 real square matrices and 32 complex square matrices from the SuiteSparse matrix data set.	Outperforms cuSparse on NVIDIA V100 GPUs and Intel MKL library, with better speedup for larger matrices (size > 10,000).	Further comparison is needed to determine how closely the observed performance matches the hardware peak.
Gelvez-Almeida et al. (2023) [63]	Strassen algorithm	Server, 2 × Intel Xeon Gold 6238R (56 cores), 128 GB RAM.	OpenMP	Full-rank matrices $m\times n$ with $Rank=n$, and $n=5000$ to $n=25,000$.	Superior computation time for the Moore–Penrose generalized inverse compared to previously reported algorithms.	High memory consumption.
Lukyanenko (2023) [64]	Conjugate gradient method	Supercomputer, Intel Xeon E5-2697 (14 cores) each node, 64 GB RAM, Tesla K40s GPU 11.56 GB.	MPI	Matrices of size $m\times n$ with $m=90,000$ and $n=70,000$.	The implementation provides a suitable approximate solution without increasing computational complexity.	The matrix dimensions are limited by the available memory.
Suzuki et al. (2023) [65]	Blocks into ILU preconditioning (ILUB)	Server, 2 × Intel Xeon Gold 6148 (20 cores/CPU), 384 GB RAM; Intel Xeon Phi 7250 (68 cores), 96 GB RAM.	OpenMP	Several data sets of dimensions $17,758$ to $1,602,111$.	Outperformed conventional ILU(0) preconditioning.	Future research should explore how ILUB performs when combined with others reordering techniques.
Sabelfeld et al. (2023) [66]	Random vector estimator	Cluster, 2 × Intel Xeon E5-2697A v4 (32 cores, 64 threads per node), 128 GB RAM.	MPI and OpenMP	Dense matrices of size ${10}^4$ and ${10}^5$.	The "RAM" implementation is faster and preferable for large linear systems if the matrix fits in the node’s RAM.	The implementations developed are restricted in problem size by the node’s limited memory.
Catalán et al. (2022) [67]	QR and SVD factorization	Servers, Intel Xeon Gold 6138 (20 cores), 96 GB RAM; AMD EPYC 7742 (64 cores), 512 GB RAM.	OpenMP	Square matrices of dimensions 1000 to 16,000.	Outperforms Intel’s MKL and the AMD AOCL routine. It is highly competitive with PLASMA and outperforms its counterparts.	Manufacturers’ effort in tuning the performance of linear algebra libraries is rarely shared with the scientific community.
Rivera et al. (2022) [68]	Barrett reduction for Wiedemann	Multicore CPU servers, Supercomputer ABACUS, NVIDIA TITAN.	OpenMP and CUDA	Quadratic, cubic, and quartic matrices of dimensions 55,000 to 266,000.	GPU is faster than the CPU for the cubic and quartic families. CPU outperforms GPU for the quadratic matrix.	The large size of this matrix causes a costly divergence between the thread computations.
Li and Han (2022) [69]	Gauss–Newton method	PC, Intel i5-6400 2.7 GHz Quad Core processor, 16 GB RAM.	MATLAB	Unbalanced IEEE 33 and 123-bus systems.	The algorithm is computationally efficient and requires fewer iterations.	Each iteration requires solving a large linear system.
Hwang et al. (2022) [70]	Gauss–Seidel method	Multiple input multiple output (MIMO) systems.	Rayleigh flat fading channel	Matrices with independent Gaussian random variables.	Up to a certain point, the performance of this model is better than the conventional Gauss–Seidel.	Performance with too much parallel computation is poorer than the Gauss–Seidel.
Catalán et al. (2021) [71]	Gauss–Jordan elimination	Server, Intel Xeon Gold 6138 (20 cores), 96 GB RAM.	OpenMP	Square matrices of dimension n up to 30,000.	Yields a high core occupation, and its parallel performance exceeds that of IntelMKL, BLAS and PLASMA.	Non-overlapping execution of the cores is likely to result in poor performance.
Marrakchi and Jemni (2021) [72]	Gaussian elimination	Cluster Econome, Intel Xeon E5-2660 (8 cores).	OpenMP	Square matrices of dimensions 1000 to 3500.	A higher degree of parallelism is achieved, and the approach is adjusted to theoretical values.	Efficiency decreases with each additional core.
Lu et al. (2021) [73]	LU and Cholesky factorizations	MLU270-S4 AI card (GDRAM and NRAM).	BANG C language	Square matrices of dimensions 128 to 8192.	A variety of optimizations demonstrated their effectiveness.	When the size of the matrix is larger, data transmission congestion occurs.
Lee and Achar (2021) [74]	LU factorization	8 × Intel Xeon i7-9700F, 16 GB RAM, NVIDIA Turing RTX2060 (1920 cores), 6 GB DRAM.	CUDA	Several matrices of dimensions 1879 to 1,585,478.	The proposed advancements provide superior performance compared to GLU 3.0 and KLU.	Because the GPU has limited global memory, it is necessary to limit the number of columns used at one time for parallel processing.
Zhang et al. (2021) [75]	LDL factorization	Xilinx Virtex-7 XC7VX690T FPGA.	Xilinx Vivado toolset	Square and triangular matrices of dimensions 32 to 128.	Square matrix inversion was achieved with different sizes in the FPGA chip.	Matrix inversion in the different FPGAs is not discussed.
Rubensson et al. (2021) [76]	Localized inverse factorization	Rackham cluster, Intel Xeon E5-2630 v4 (10 cores), 128 GB RAM.	MPI and OpenBLAS	Several matrices of dimensions up to 5,373,954.	Represents a dramatic improvement over the regular recursive inverse factorization.	Localized inverse factorization is completely dominated by the solutions to the subproblems.
Rodriguez et al. (2021) [77]	QR factorization	Xilinx VU7P FPGA and Xilinx VU9P FPGA.	LUT RAM	Square matrices of dimensions 4000 to 131,000.	This design outperforms highly optimized QR solvers running on CPUs and GPUs.	Overall performance is limited when the input matrix has few columns.
Duan and Dinavahi (2021) [78]	Linking-domain extraction (LDE)-based decomposition method	Xilinx VCU-118 board with the XCVU9P FPGA at 100 MHz frequency and NVIDIA Tesla V100 GPU with 5012 cores.	Not reported	Square matrices of dimensions 30 to 301.	LDE method can compute the matrix inversion directly and can also run faster compared to the Schur complement.	The connections between interface nodes are not dense, and there is no trans-conductance between the interface nodes and the other nodes.
Shäfer et al. (2021) [79]	Cholesky factorization	Server, Intel Skylake 2.10 GHz (32 threads), 192 GB RAM; PC, Intel Core i7-6400 4.00 GHz, 64 GB RAM.	IntelMKL	Square matrices of dimensions 10,000 to 1,000,000.	The optimal inverse Cholesky factor of a positive-definite matrix, subject to a sparsity pattern, can be computed in closed form.	More efficient squaring rules need to be implemented to compete with the state of the art in terms of wall clock times.
Boffi et al. (2021) [80]	Iterative incomplete LU (ILU) method	Laptop, Intel i7-6700HQ, 16 GB RAM.	MATLAB	Square matrices of dimensions 10,000 to 1,000,000.	The new preconditions have been successfully applied to linear systems and eigenvalue problems.	The proposed algorithms may become unstable and fail for some matrices.
Ahmadi et al. (2021) [81]	Jacobi-embedded Gauss–Seidel method	Server, 2 × Intel Xeon Gold 6148 (20 cores/CPU), 4 × NVIDIA Tesla V100-SXM2-16 GB.	MATLAB	Square matrices of dimensions 500 to 25,000.	Performance up to 7× faster on multicore CPUs and 87× on many-core GPUs.	Limitations with MATLAB linear algebra libraries for GPU implementation.
Liu et al. (2020) [82]	Blocked adaptive cross approximation (BACA) and SVD	Cori Haswell at NERSC (2388 dual-socket nodes), Intel Xeon E5-2698v3 (16 cores/each), 128 GB DDR4.	PBLAS and ScaLAPACK	Several matrices of dimensions 1000 to 21,788.	Robustness and favorable parallel performance compared to the baseline ACA algorithm.	The effects of block size variation merit further analysis.
Davis et al. (2020) [83]	LU factorization	Supercomputer (HPC2N), Intel Xeon E5-2690v4 (2×14 cores), 128 GB RAM.	OpenMP	Square matrices of dimensions 53,000 to 659,000.	Excellent performance for highly unsymmetrical matrices.	Sometimes produces factorizations with more fill-in.
Yang et al. (2020) [84]	Gauss–Seidel method	PC, Intel Core i5.	MATLAB (R2016a)	Matrices of dimensions 20 to 1000.	Numerical results show that the method is valid.	The dimensions of the matrices are not large enough.
Li and Zhang (2020) [85]	Gauss–Seidel method	Cluster, CPU IBM POWER, NVIDIA P100 and V100.	CUDA	Laplacian and general matrices with different dimensions.	Efficient algorithm compared to state-of-the-art software packages.	Performance deteriorates with the amount of fill-in in the ILU factorizations.
Singh et al. (2020) [86]	Gauss–Newton method	Blue Waters and Stampede2 Supercomputers of Texas Advanced Computing Center.	Intel compilers, MKL library for BLAS, and Cyclops	Square matrices with different dimensions.	Good scalability for the implementation of the Gauss–Newton method.	The method does not apply to triangular matrices.
Alyahya et al. (2020) [87]	Jacobi method	Aziz Supercomputer of King Abdulaziz University, Jeddah.	Intel MIC and OpenMP	Sparse matrices with 28M rows and 640M non-zero elements.	Speedup to 27.75× compared to the sequential method.	A method is needed for larger sparse SLEs of various application domains.
Huang et al. (2020) [88]	Jacobi, SOR, and other iterative methods	Server, 2 × Intel Xeon E5-2640 v3 2.60 GHz (16 cores).	OpenMP	Three-dimensional sphere DDA (SDDA). 10,000 spheres and 200,000 calculation steps.	About 6× faster than serial computing.	Other approaches can be used to improve the efficiency of solving the equations in the DDA.

In matrix-operations-based methods and decomposition-based methods, using parallel architectures such as multicore CPUs and GPUs [89], combined with parallel tools such as OpenMP [90], OpenBLAS [91], LAPACK [92], MPI [93], IntelMKL [94], and CUDA [95], are efficient and feasible for speeding up the solution of linear systems [44]. The results show increased performance and acceleration in the matrix factorization process. Given the large use of these processes for the computation of the MPGI matrix, it is convenient to implement them in the ELM algorithm to accelerate the training process. Different authors have reported efficiency improvements in the speedup of the SLE solution using these tools on matrices reaching up to 30,000 rows or columns. In addition to the traditional technologies, the all-optical signal processor of Xilinx Virtex-7 FPGAs from Xilinx has been implemented in iterative methods. This architecture includes a design option that reduces the number of different voltages required [96]. OpenMP, MPI, and CUDA are the most common parallel tools. The performance improvements for the SLE solution reported in the reviewed literature are good alternatives to speed up the training of the ELM algorithm because the largest computational cost is found in the calculation of the MPGI matrix. Below, Table 3 presents a summary of the methods used to compute the output layer weights in the proposals of parallel and distributed ELM networks reported in the last five years.

Table 3. Summary of methods used to compute output layer weights in parallel and distributed ELM networks proposed in the last five years.

Reference	Network Type	MPGI	Orthogonal Projection	SVD	Cholesky	Iterative Methods	Not Reported
Wang et al. (2024) [97]	Regularized ELM					✓
Jagadeesa et al. (2023) [98]	SVM-Based ELM	✓
Wang et al. (2023) [99]	Regularized ELM					✓
Wang and Soo (2023) [100]	Ensemble ELM	✓	✓
Zhang et al. (2023) [101]	Regularized ELM					✓
Gelvez-Almeida et al. (2022–2023) [102,103]	Ensemble Online ELM	✓	✓
Polat and Kayhan (2022) [51]	Online ELM	✓
Chidambaram and Gowthul (2022) [104]	Improved ELM			✓
Hira and Bai (2022) [105]	Regularized ELM					✓
Rajpal et al. (2022) [106]	Standard ELM	✓
Zha et al. (2022) [107]	Robust ELM	✓	✓
Vidhya and Aji (2022) [108]	Online ELM	✓		✓
Zehai et al. (2021) [50]	Ensemble Online ELM	✓	✓
Wu et al. (2021) [55]	Kernel ELM	✓
Rath et al. (2021) [109]	Hierarchical ELM	✓
Ji et al. (2021) [110]	Online ELM	✓
Luo et al. (2021) [111]	Kernel ELM				✓
Tahir and Loo (2021) [112]	Kernel ELM					✓
Dong et al. (2021) [113]	Standard ELM	✓	✓
Ezemobi et al. (2021) [114]	Deterministic ELM	✓
Xu et al. (2020) [115]	Distributed						✓
Li et al. (2020) [116]	Online ELM	✓
Safaei et al. (2019) [48]	Online ELM	✓
Grim et al. (2019) [49]	Online ELM		✓
Liang et al. (2019) [117]	Voltage ELM	✓
Dokeroglu and Sevinc (2019) [118]	Evolutionary ELM						✓

The methods reported for training parallel and distributed ELM networks include the MPGI, orthogonal projection, SVD, Cholesky factorization, and iterative techniques. While there is a greater tendency to use the Moore–Penrose inverse, the exact procedure for calculating it is not precisely reported. Iterative methods are favored for training regularized models. Given the MPGI connection with SLE and the array of parallel and distributed proposals in the literature (see Table 2), researching the parallel training of ELM networks is a field deserving of further exploration.

5. Review of Distributed and Parallel Systems for Extreme Learning Machine

Parallel and distributed computing technologies have been implemented to reduce the training time of randomized feedforward neural networks without losing generalization capability. Despite advances, parallel and distributed computing in ELM is a field that is still open for improvement [25]. Given the continuous growth of data due to technological and Internet advances, the traditional ELM algorithms have become insufficient to process this large amount of data [28]. The dimensions of the output matrix $\mathbf{H}$ of the hidden layer of the neural network in (4) depend on the number of samples N and the number of neurons in the hidden layer L. The weights $\mathit{\beta }$ of the output layer are calculated analytically using the MPGI of the matrix $\mathbf{H}$. When the number of samples is large, the number of rows of matrix $\mathbf{H}$ is also high, thus significantly increasing the training time. In some cases, if the dimensions of the $\mathbf{H}$ matrix are large, the computational architecture may be insufficient to perform the training. For this reason, some ELM variants have emerged that implement data distribution for parallel processing. This section presents implemented tools and technologies for distributed and parallel computing in ELM networks during the last decade. In addition, we give an updated review of the ELM models employing these tools and technologies to address the limitations presented by traditional models in terms of training time and memory consumption.

5.1. MapReduce

MapReduce is a parallel and distributed programming model proposed by Google [119,120]. The model can process large amounts of data, which would otherwise have to be processed on hundreds or thousands of machines to have reasonable processing times. Figure 4 shows a diagram of the MapReduce programming model.

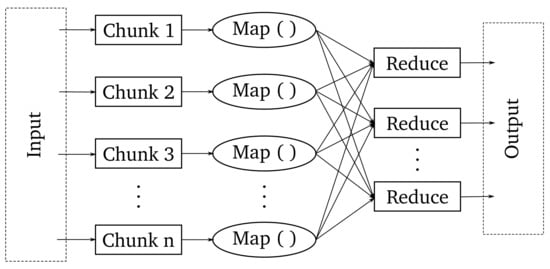
Figure 4. General scheme of the MapReduce programming model.

The proposed scheme takes a set of input key/value pairs and produces a set of output key/value pairs. The mapping operation takes a pair from the input, creating a set of intermediate key/value pairs. These pairs are grouped according to the intermediate key I and passed to the reduce function. The reduce function merges these values to create a possibly smaller set of values. Thus, it makes it possible to handle lists of values that are too large to fit in memory. Significant advances have been made in distributed ELM using the MapReduce model, allowing it to work with more data than traditional ELM models. Table 4 briefly summarizes ELM’s advances in addressing problems involving large data sets using the MapReduce model as a tool.

Table 4. Summary of advances in distributed ELM using the MapReduce model.

Reference	Application	Architecture	Data	Size (GB) *	Limitations
Chidambaram and Gowthul (2022) [104]	Classification	PC, Intel Core i5 9th Gen, 8 GB RAM.	Rotten Tomatoes movie and critic review data set (DS-I) and dermatology data set (DS-II).	0.004	A basic architecture was used during the experiments.
Hira and Bai (2022) [105]	Classification	Different cluster managers.	GSE13159, SRBCT, acute leukaemia, leukaemia 2, and colon cancer.	Information not provided	MapReduce is not suitable for applications that share data in more than one step.
Gayathri et al. (2021) [121]	Classification	Hadoop clusters.	PIMA Indians diabetes and activity recognition data set.	0.00005; 0.005	Feature selection and dimensionality reduction techniques have not been considered.
Rath et al. (2021) [109]	Regression	Not reported.	NASDAQ (ten years of historical data).	Information not provided	It must wait for all the parallel work tasks to be completed before moving on to the next step.
Yao and Ge (2019) [122]	Regression	Cluster (4 PCs), Intel Core i5-4590 3.30 GHz, 4 GB RAM.	DCS (110,000 samples × 20 processes).	Information not provided.	The files must have the same size.
Ku and Zheng (2017) [123]	Classification	Not reported.	AVIRIS Indian Pines (10,366 samples), ROSIS Pavia University (46,697 samples).	Information not provided	A second computer is needed when training data overcome some limitations when calculating the $\mathbf{H}$ matrix and pseudo-inverse.
Pang et al. (2017) [124]	Classification	Cluster (31 PCs), 2 × 3.1 GHz CPUs, 8 GB RAM, 500 GB hard disk.	DBLP (1,817 AI y 1,817 CV); Synthetic (500,000 pos. and 500,000 neg.; 4,997,537 total).	Information not provided	The proposed algorithm is time-consuming because the algorithm consists of several MapReduce jobs.
Inaba et al. (2016) [125]	Classification	PC, Intel Core i7 3.6 GHz, 8 GB RAM.	Various. DNA (3186 × 180); Satimage (6435 × 36).	0.004; 0.002	Training time for DGR-ELM can be improved by using GPU-based linear algebra packages.
Huang et al. (2016) [126]	Classification	Cluster (5 PCs), 2 × Intel Xeon E5-2620 (6 cores), 32 GB RAM.	Various. KDDcup99 (5,190,731 × 41); Synthetic (5,120,000 × 512).	0.67; 19.53	More scheduling and ensemble methods need to be integrated to make the algorithm more suitable for heterogeneous environments.
Wang et al. (2015) [127]	Classification	Cluster (9 PCs), Intel Quad core Q8400 2.66 GHz, 4 GB RAM.	Various. Covtype (580,000 × 54); Synthetic (1,280,000 × 128).	0.23; 1.22	The block size of the algorithm influences the learning performance.
Bi et al. (2015) [128]	Classification	Cluster (9 PCs), Intel Quad Core 2.66 GHz, 4 GB RAM.	Various. Synthetic (25,000 × 5000).	0.93	Some matrix operations cannot be implemented on MapReduce directly.
Han et al. (2015) [129]	Classification	Cluster (8 PCs), Intel core 2 Quad Q8400 2.66 GHz, 4 GB RAM.	Various. Iris (6,000,000 × 4); Spambase (18,400,000 × 57).	0.18; 7.81	When the block size is larger, the amount of computation increases, and the concurrency of the algorithm decreases.
Xiang et al. (2014) [130]	Classification	PC, 2 × CPU 2.53 GHz (4 cores/CPU), 32 GB RAM.	KDDcup99 (1 to 3 million samples).	Information not provided	A distributed approach is needed to solve a linear system to enable the use of larger network architectures.
Xin et al. (2014) [131]	Regression	Cluster (9 PCs), Intel Quad Core 2.66 GHz, 4 GB RAM.	Synthetic (3 to 7 million samples).	1.4 to 3.27	Training time increases with an increasing number of training lengths.
He et al. (2013) [132]	Regression	Cluster (10 PCs), 4 × 2.8 GHz cores, 4 GB RAM.	Stock (950 × 12).	0.000085	It is necessary to make better use of IT resources.

* An approximation of the size is made according to the information from the databases reported by the authors.

In this regard, He et al. [132] proposed a parallel ELM model for regression based on MapReduce, addressing problems involving large data sets and achieving better performance in general. Similarly, Xin et al. [131] introduced a new distributed ELM that can compute the matrix multiplication required by the MPGI in parallel with MapReduce to compute the output layer weights. The authors demonstrate that the proposed model can learn with large amounts of training data and emphasize that the strategy can improve applications with large-scale data. Xiang et al. [130] proposed the use of ELM to detect network intrusion attempts. The authors demonstrate that their variant can process data sets that traditional ELM cannot, and it tends to have a high performance in speedup and accuracy. Han et al. [129] introduced distributed ELM (DELM) and distributed ELM-based weighted set classifier (WE-DELM) as a way to optimize large-scale matrix operations. In DELM, the ${\left({\mathbf{H}}^T\mathbf{H}\right)}^{-1}$ and ${\mathbf{H}}^T\mathbf{T}$ operations are used to compute the weights $\mathit{\beta }$ of the output layer. The matrices are divided into blocks consisting of several rows and columns to be multiplied independently by a reduced work node. WE-DELM divides the database into several smaller blocks to independently train several DELM-based classifiers. The pre-trained classifiers classify the new samples. Finally, the classification error of each classifier is calculated to predict the final results. Experimental results showed that WE-DELM improves learning efficiency, accuracy, and speedup. In addition, a kernelized distributed ELM (DK-ELM) that implements kernel-based ELM in MapReduce was proposed in Bi et al. [128]. Experimental results show that this proposal has good scalability for massive learning applications. In the same year, Wang et al. [127] introduced a parallel online sequential ELM (POS-ELM) based on MapReduce, which was evaluated on real and synthetic data. Their results prove that POS-ELM has good accuracy and comparable performance to OS-ELM and ELM. The work in Huang et al. [126] presented a parallel assembly of OS-ELM (PEOS-ELM), and like the previous case, it was evaluated on real and synthetic data. The accuracy of the algorithm is quite similar to OS-ELM, achieving up to 40 speedups with a maximum of 80 cores.

Furthermore, Pang et al. [124] proposed a parallel algorithm to tackle the problem of classifying multiple graphs in massive data sets, obtaining effective and efficient results for real and synthetic data. In Ku and Zheng [123], the authors developed a distributed kernel-based ELM using the MapReduce framework (DK-ELMM). According to their results, DK-ELMM improves the results of equivalent ELM and SVD-based classifiers for classifying remotely sensed hyperspectral images. Yao et al. [122] designed two distributed and parallel models for ELM (DP-ELM) and hierarchical ELM (DP-HELM). The feasibility and efficiency of the algorithms are evaluated by building an industrial-quality prediction model with big data processing. The proposal by Rath et al. [109] processes historical large-scale data sets by developing a MapReduce-based ELM (ELM-MapReduce). In the same year, a wavelet kernel ELM (WKELM) model based on the activity recognition and diabetes data sets was implemented in Gayathri et al. [121]. The authors use the MapReduce model to deal with the large-scale data set, where the presented model outperforms the compared methods with a maximum accuracy of 98%. Chidambaram and Gowthul Alam [104] proposed a novel MapReduce framework based on the improved Archerfish hunter spotted hyena optimization-based ELM (AHSHO-IELM) classifier for big data classification. Finally, a novel MapReduce based on parallel feature selection and ELM method was proposed in Hira and Bai [105] for classifying microarray cancer data. The authors show that the proposed method achieves a perfect classification accuracy of 99.58%.

5.2. Spark

Spark is a framework proposed to address problems that are not possible with MapReduce while preserving scalability and fault tolerance [133]. Spark introduces resilient distributed data sets (RDDs) as a read-only collection from partitioned objects on a set of machines, which is rebuilt if a partition is lost. The process involves reduce (to combine elements of the data set) and collect (to send all elements to the driver program) and a foreach passes each element through a function provided by the username. Figure 5 represents a schematic of the main components of Apache Spark.

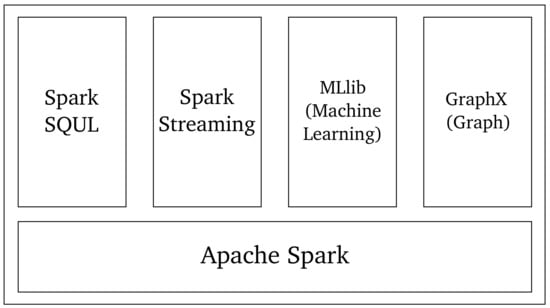
Figure 5. Apache Spark main components.

The framework is composed of five main parts: Spark Core, which is the base or set libraries supporting the other modules; Spark SQL, for structured or semi-structured data processing; Spark Streaming, for real-time data processing; Spark MLlib, which is a library for machine learning; and Spark Graph, for graph processing. Considering the aforementioned features, Spark has been used in distributed ELM algorithms. Table 5 presents a summary of ELM’s advances in processing large data sets using the Spark framework.

Table 5. Summary of advances in distributed ELM using the Spark framework.

Reference	Application	Architecture	Data	Size (GB) *	Limitations
Jagadeesan et al. (2023) [98]	Classification	Cluster (3 nodes), Intel Core i5 3470 3.2 GHz (8 cores, 16 threads), 16 GB RAM.	Over 11,000 tweets relevant to disasters are included, along with tweets from news agencies and disaster relief organizations on Twitter.	Information not provided	Reliance on random operators for implementation, which can slightly affect output results when applied in different domains.
Jaya et al. (2022) [134]	Classification	Cluster (8 nodes), 4 × 2.4 GHz processors, 200 GB hard disk, 16 GB RAM.	Various from UCI data repository.	Information not provided	Limited use of classifiers available in the distributed Spark environment.
Ji et al. (2021) [110]	Classification	Cluster (5-node OMNISKY), 2 × Intel Xeon E5-2603V4 1.70 GHz, 2 × NVIDIA Quadro M4000, 16 TB hard disk, 64 GB RAM.	Synthetic data set.	0.1	The combination of distributed computing and GPU acceleration has not been used with a real data set.
Luo et al. (2021) [111]	Classification	Single-server and multi-node in Spark cluster, 4-core 2 GHz CPU, 8 GB RAM.	Various from Mulan and extreme repository data sets.	Information not provided	The analysis of the relationship between the labels should be strengthened.
Xu et al. (2020) [115]	Regression	Different nodes on the clusters of the Apache Spark platform.	Three real wind speed data sets and a group of analog wind speed big data (1000 to 600,000 samples).	Information not provided	The Spark platform needs time to start the framework and distribute tasks.
Kozik et al. 2018 [135]	Classification	HPC cluster.	Real-world attacks data set.	Information not provided	The computation time increases as the number of training samples increases.
Kozik (2018) [136]	Classification	Computing cluster.	CTU data set.	5.2 to 60	Other algorithms perform better in terms of accuracy and error rates.
Oneto et al. (2017–2018) [137,138]	Regression	PC, 4 × Intel Xeon E5-4620 2.20 GHz, 128 GB RAM, 500 GB SSD disk; 4 × n1-standard-16 of the Google Compute Engine, 60 GB RAM, 16 cores, 500 GB SSD disk.	Real data of Rete Ferroviaria Italiana (RFI) and the Italian infrastructure manager (IM).	Information not provided	It does not take into account information available from external sources.
Duan et al. (2017) [139]	Classification	Cluster (10–35 servers), 2.5 GHz Core, 16 GB RAM, 2 TB disk.	Various. Hypertension (38 M × 8); heart disease (10 M × 35).	4.65; 5.08	There is a high probability that one or more nodes will not be able to function.
Liu et al. (2016) [140]	Classification	Local Cluster, VMare workstation 9.0.2 for Windows Ubuntu system.	Various. Forest types prediction (581,012 × 54).	2.34	As the number of hidden layer nodes increases, the learning and training time will gradually increase.

* An approximation of the size is made according to the information from the databases reported by the authors.

To increase the analysis speed of the traditional ELM algorithm, Liu et al. [140] presented a parallel ELM algorithm on the Spark platform. In Duan et al. [139], an efficient Spark-based ELM (SELM) is proposed by partitioning the data set appropriately and improving the performance in matrix computation of the output layer values. The model proposed by the authors achieves speedups of 8.71×, 13.19×, 18.74×, 23.79×, and 33.81× in clusters with 10, 15, 20, 25, and 30 nodes, respectively. Oneto et al. [137,138] developed a dynamic prediction system that leverages historical data on train movements and weather data provided by meteorological services. Their experimental results showed that the proposal improved the real systems of the Italian rail network. Moreover, a cost-sensitive distributed ELM training algorithm for network security was presented by Kozik [136]. The author implemented the proposed algorithm using the Apache Spark framework, a NetFlow data structure, and the MapReduce programming model. Their results indicated that the proposed ELM-based NetFlow analysis was valuable for network incident detection. In the same year, Kozik et al. [135] designed a model based on ELM to transfer computationally expensive operations to the cloud to improve attack detection, successfully decoupling and moving the training process to the cloud. Meanwhile, in Xi et al. [115], distributed computing is applied for time speed prediction using an improved ELM predictor with a data decomposition and reconstruction component result in Spark.

Later, a multi-label algorithm based on a kernel extreme learning machine (ML-KELM) was proposed by Luo et al. [111]. The proposed method provides an efficient solution to multi-label classification with large-scale data sets. In the same year, an efficient stream-based distributed framework for ELM and OS-ELM was proposed by Ji et al. [110]. The proposed model achieves better performance concerning offline and online training in different data arrival modes and user needs. Meanwhile, in Jaya et al. [134], a health status prediction system was proposed to detect cardiovascular diseases through patients’ tweets. The performance of the proposed framework with ELM outperforms other classifiers in both accuracy and time. Finally, Jagadeesan et al. [98] introduced a novel approach for predicting disaster events in big data, utilizing a model based on the ensemble support vector machine (ESVM-ELM) optimized by the city councils evolution (CCE) algorithm. The model enhances accuracy, precision, recall, and F-measure compared to baselines. Additionally, it improves prediction accuracy, speed, and scalability for big data classification.

5.3. Graphics Processing Unit

GPU programming has been a useful tool in speeding up the execution times of programs that process large volumes of data in different applications, and randomized feedforward neural networks are no exception. The GPU programming model is organized by three hierarchical levels corresponding to threads, blocks, and grids [141]. The implementation of parallel algorithms using tools such as CUDA [95] allows applications to be accelerated and performance scales according to the characteristics of the GPU; the higher the power, the greater the scalability. The advantages of GPU programming have been used in ELM to accelerate the training process, enabling large-scale data processing. Table 6 presents a summary of the reported ELM-based approaches to address large-scale problems on GPU platforms.

Table 6. Summary of advances in parallel ELM-based approaches using GPU computing.

Reference	Application	Architecture	Parallel Tool	Data	Size (GB) *	Limitations
Wang et al. (2023) [99]	Classification	PCs, Intel Core i7-10700 (8 cores) 2.9 GHz; Intel Core i7-4790 (4 cores) 3.60 GHz; Intel Core i7-8700 (6 cores) 3.2 GHz; NVIDIA GeForce GT 730	MATLAB toolbox (gpuArray function).	Various. Gissete (7000 samples).	0.26	Requires a large amount of storage and computation.
Polat and Kayhan (2022) [51]	Classification	PC, Intel Core i7-6700K, 32 GB RAM, NVIDIA GeForce GTX 1070, 1920 CUDA cores.	C++ and CUDA Toolkit 10.2.	Various. Landsat Satellite (6435 × 36); MNIST (70,000 × 784).	0.002; 0.409	Computationally, it is very time-consuming to apply cross-validation for each different hyper-parameter for online learning.
Tahir and Loo (2021) [112]	Classification	Server, 16 GB GPU, 64 GB RAM.	Python Django framework.	Various. Food101 (101 images); VireoFood-172 (110,241 images).	0.041; 7.22	Various image quality distortions affect the robustness of the features.
Hou et al. (2021) [142]	Classification	PC, Intel Core i7-8700K 3.7 GHz, NVIDIA GeForce RTX-2080Ti, 64 GB RAM.	MATLAB 2017.	Various. NORB (74,300 images); MNIST (70,000 × 784).	3.34; 0.35	Parameter selection and efficiency are not explored when memory is limited.
El Zini et al. (2021) [143]	Regression	PCs, Intel core-i7 and Core-i5, NVIDIA Tesla K20m (2688 CUDA cores), NVIDIA Quadro K2000, 16 GB RAM.	CUDA.	Various. Electric Motor Temperature data set (998,000 instances).	Up to 0.12	Portability and scalability of the proposed algorithm need to be further studied.
Rajpal et al. (2021) [106]	Classification	NVIDIA Tesla K80 (Google Collaboratory).	Python.	Chest X-ray images (CXRs).	Information not provided	It is necessary to explore the segmentation of the pulmonary region.
Grim et al. (2019) [49]	Regression	Virtual machine, 6 vCPUs Xeon E5-2690 2.60 GHz, 1 Tesla K80 823.5 MHz and 11.5 GB, 56 GB RAM.	OpenBLAS, IntelMKL and MAGMA.	Environmental data set with samples of particulate matter concentrations.	Information not provided	For a small set of samples, the number of function calls is higher and this time overhead becomes considerable.
Li et al. (2017) [144]	Classification	PC, Intel E5-2650 2.0 GHz, 512 GB RAM, NVIDIA Tesla K20c (2496 CUDA cores).	CUDA (MAGMA), OpenBLAS (MPICH).	Various. COIL-100 (70,000 × 2500); MNIST (6,000,000 × 784).	1.30; 0.35	The performance of the heterogeneous CPU–GPU blocked algorithm is slightly better.
Chen et al. (2017) [145]	Classification	Flink cluster, Intel Core i5-4590 3.30 GHz, 12 GB RAM, 2 × NVIDIA GeForce GTX 750 (512 CUDA cores).	Flink and CUDA.	Various. MNIST (6,000,000 × 784).	0.35	Performance on some GPUs is almost the same.
Lam and Wunsch (2016) [146]	Classification	PC, Intel Xeon E5645 2.4 GHz, 12 GB RAM, NVIDIA Tesla M2075 (448 cores clocked) 1.5 GHz, 6 GB RAM.	CUDA.	CIFAR-10 (60,000 × 3072); MNIST (70,000 × 784).	1.37; 0.41	Each thread has a limited number of fast registers to store local variables.

* An approximation of the size is made according to the information from the databases reported by the authors.

In this regard, Van Heeswijk et al. [147] presented GPU-accelerated ELM models to perform regression on large data sets. The work focuses on accelerating the training by implementing parallel computations on the GPU and combining processes in GPUs and CPUs, with the goal of building multiple models simultaneously. The results obtained show that the use of GPUs achieves significant acceleration compared to using a single CPU. Similarly, the work of Jezowicz et al. [148] demonstrated that the ELM learning algorithm is significantly accelerated on GPU platforms. In addition, Li et al. [149] proposed an ELM-based coordinated memory-to-GPU power-saving approach based on ELM that proved effective and could provide a maximum power saving of 10.63% and an average power saving of 2.68% compared to traditional dynamic voltage and frequency scaling. Krawczyk [150] proposed using the online version of ELM to address the class imbalance problem and use GPU scheduling to speed up the classifier. Their results enabled faster classification of the data stream with high accuracy. In the same year, a method to improve both the speed and accuracy performance of an ELM model based on radial basis function (ELM-RBF) by exploiting the parallel computing attributes of modern GPUs was presented in Lam and Wunsch [146]. The results showed that the precision is maintained compared to other algorithms, while the acceleration is up to 20× times with optimized linear algebra packages. Also, a parallel H-ELM algorithm based on Flink, which is one of the most popular in-memory and GPU cluster computing platforms, was introduced by Chen et al. [145]. The authors confirmed that the proposed model processes large amounts of data with accuracy, scalability, and speedup in training time.

Li et al. [144] developed three approaches to improve ELM based on local receptive fields (ELM-LRF) as follows: (1) a new blocked LU decomposition algorithm, (2) an efficient blocked Cholesky decomposition algorithm, and (3) a locked heterogeneous CPU–GPU parallel algorithm to maximize the resources on a GPU node. The authors believe that the proposed algorithms can also be adapted to other ELM variants and easily applied to a distributed system. Parallel implementations for OS-ELM applied to particle prediction are discussed by Grim et al. [49]. They show that the implementation of parallel versions of the algorithm in the C language with the OpenBLAS, Intel MKL, and MAGMA libraries is more advantageous compared to the reference version of MATLAB. Afterward, Rajpal et al. [106] addressed the problem of ELM-based COVID-19 classification (COV-ELM) into three classes: (1) COVID-19, (2) normal, and (3) pneumonia. The results showed that COV-ELM outperforms new-generation machine learning algorithms. In El Zini et al. [143], an ELM-based recurrent neural network training algorithm was presented that takes advantage of GPU-shared memory and parallel QR factorization algorithms to reach optimal solutions efficiently. The proposed algorithm reaches up to 461 times the speedup of its sequential counterpart. In the same year, an alternating direction multiplier method (ADMM) for regularized ELM (RELM) was developed by Hou et al. [142]. The results show GPU speedup, which demonstrates the high parallelism of the proposed RELM. Meanwhile, a progressive kernel ELM (PKELM) for food categorization and ingredient recognition was introduced by Tahir and Loo [112]. During online learning, the novelty detection mechanism of PKELM detects label noise and assigns labels to those unlabeled training instances, performing better than other online variants of ELM.

In recent work by Polakt and Kayhan [51], they proposed a version of ELM accelerated by a GPU to shorten training time. This version processes relevant parts in parallel using custom kernels, outperforming OS-ELM in training speed and testing accuracy. Finally, Wang et al. [99] proposed an adaptive method to automatically tune algorithm parameters during training for the regularized extreme learning machine (ELM), improving computation efficiency for large-scale convex optimization problems. Their results suggest that the algorithm can enhance convergence speed due to its simpler solution process.

5.4. Other Tools and Technologies for Distributed and Parallel Computing

In addition to MapReduce, Spark, and GPU, other distributed and parallel computing tools and technologies have been used in ELM to improve training times. Table 7 summarizes ELM-based work using other tools and technologies for distributed and parallel computing on large-scale data sets.

Table 7. Summary of advances in ELM using other tools and technologies for distributed and parallel computing.

Reference	Application	Architecture	Parallel Tool	Data	Size (GB) *	Limitations
Wang et al. (2024) [97]	Classification	PC, Intel Core i7-10700 (8 core), 16 GB RAM.	MATLAB (2019).	Various. Gissete (7000 samples).	0.26	The algorithm computes and stores the matrix in each iteration, resulting in high computational cost and slow convergence.
Wang and Soo (2023) [100]	Classification	PC, Intel(R) Xeon(R) Silver 4114 2.20 GHz, 16.0 GB RAM.	Python 3.8.	Various. Adults (44,222 samples).	0.0046	Optimal ELM number undefined, lacks online version, and adaptation to changing environments not developed.
Zhang et al. (2023) [101]	Classification and regression	PC, AMD Ryzen 2600 3.40 GHz (6 cores), 16 GB RAM.	MATLAB (2021a).	Various. Mushroom (8124 samples).	0.0013	Further enhancements are needed, particularly in exploring additional regularization terms.
Gelvez-Almeida et al. (2022–2023) [102,103]	Classification	Server, 2 × Intel(R) Xeon(R) Gold 2.20 GHz, 128 GB RAM.	OpenMP.	Synthetic fingerprint data set (2,000,000 samples).	3.01	It is necessary to compare with other ensemble models for validation and benchmarking.
Zha et al. (2022) [107]	Regression	PC, Intel Core i5-9400F 2.9 GHz, 16 GB RAM.	MATLAB R2018b.	Various. SinC (5000 data).	8.8 × 10−5	The proposed model makes the model training time longer.
Vidhya and Aji (2022) [108]	Classification	PC, Intel Core i5 2.90 GHz (6 core), 32 GB RAM.	Not reported	Various. RCV1 data set.	Up to 42.22	The process of updating knowledge is not explored.
Dong et al. (2021) [113]	Regression	PC, Intel Core i7-6700-K 3.4 GHz.	MATLAB and PSpice software platforms.	Various high-resolution images with 512 × 512 pixels.	0.0003	The passive-resistive network limits the size of the array and its use in memory design.
Dwivedi et al. (2021) [151]	Classification	PC, Intel Core i7, 16 GB RAM.	MATLAB R2016.	NSL-KDD; AWID-ATK-R; NGIDS-DS data sets.	0.052; 2.92; 5.04	Only the basic architecture was used during the experiments.
Zehai et al. (2021) [50]	Regression	Not reported.	Not reported.	Sinc and Mackey–Glass time-series data set.	Up to 0.002	There are still many problems and challenges in other modular systems.
Ezemobi et al. (2021) [114]	Regression	Texas F28379D microcontroller unit (MCU) board.	MATLAB.	2 Ah capacity lithium-ion (does not report the number of samples).	Information not provided	The performance of the model is influenced by the choice of the discrete point-invariance interval of the input characteristics.
Wu et al. (2021) [55]	Regression	PC, Intel Core i7-4700, 16 GB RAM.	R program.	Real data set (1966–2000 training and 2001–2015 testing).	Information not provided	The selection of the appropriate number of classifications remains a problem.
Li et al. (2020) [116]	Regression	PC, 2.5 GHz CPU, 4 GB RAM.	MATLAB 2012a.	Various. Bank domains (8190 × 8); Elevator (8752 × 18); CBM (11,934 × 15).	0.00024; 0.00058; 0.00066	Decreasing learning is not considered in the model.
Liang et al. (2019) [117]	Classification	Not reported.	Not reported.	It is obtained by the calibration experiment.	Information not provided	Excessive numbers of neurons will increase training time and may result in overfitting.
Dokeroglu and Sevinc et al. (2019) [118]	Classification	Server, 64-bit CPU (8 cores), 256 GB RAM, 1.5 TB disk.	MPI.	Various. CHESS (3196 × 36); SPAM (4601 × 57).	0.00043; 0.00097	Future work proposes the use of hybrid metaheuristic algorithms supported by the GPU.
Safaei et al. (2019) [48]	Classification	Xilinx Zynq platform.	System-on-a-chip (SoC) FPGA-based.	Housing (500 samples), Hollywood 3D and HON4D.	Information not provided	Floating-point is not used in this work.
Li et al. (2018) [152]	Classification	PC, AMD Athlon TM X2 250 3.00 GHz, 2 GB RAM.	MATLAB 7.11.0	Various. DNA (data with 180 features); Wine (data with 178 features).	Information not provided	Real-world applications should consider an online version of parallel ELM.
Ming et al. (2018) [153]	Classification and regression	Supercomputer (2048 PCs), 2 × Intel Xeon X5670 2.93 GHz (6 cores), 48 GB RAM.	MPI and MKL (BLAS, PBLAS, ScaLAPACK, BLACS, among others.).	Various. YearPredictionMSD (515,345 × 90); MNIST8M (8.1M × 784).	0.17; 23.65	The method cannot support a large number of hidden neuron nodes, and the communication overhead is large.
Henríquez and Ruz (2017) [154]	Classification and regression	PC, Intel Core i5 2.6 GHz, 8 GB RAM.	fOptions, RSNNS, MASS, and car.	Various. Skin (245,057 × 4); PPPT (45,730 × 9).	0.0073; 0.003	The performance of the proposed algorithm and ELM with some data sets is similar.
Luo et al. (2017) [155]	Classification and regression	Server, 8 × 2.8 GHz, 8 GB RAM.	Not reported.	Various. Banknote (1372 × 4); Stock (950 × 12).	0.000085; 0.00004	More iterations with a larger number of processors are required to converge the objective function.
Wang et al. (2016) [156]	Classification	Cluster (6 nodes), 2 × Intel Xeon E5-2640 2.5 GHz (12 cores), 64 GB RAM.	Armadillo, LAPACK, OpenBLAS, and MPICH.	Various. NORB (97,200 × 9216).	3.34	On the same data set, the upscaling is slightly reduced in the presence of more computational nodes.

* An approximation of the size is made according to the information from the databases reported by the authors.

From this perspective, two variants of parallel ELM were proposed by Wang et al. [156] and Ming et al. [153], named data-parallel regularized ELM (DPR-ELM) and model parallel regularized ELM (MPR-ELM), respectively. Both approaches together are referred to as parallel regularized ELM (PR-ELM) and aim to improve large-scale learning. The authors used a multi-node platform using the message passing interface (MPI) [93]. Experiments show that the proposed models have better performance and scalability than other distributed approaches. Similarly, in Luo et al. [155], a distributed ELM (DELM) was evaluated on a multicore computer with eight 2.8 GHz cores. For their part, Henríquez and Ruz [154] developed a model based on a parallel nonlinear layer with a deterministic assignment in the hidden layer weights and bias, using low discrepancy sequences (LDSs). In Li et al. [152], a parallel ELM model of a kernel-based class was introduced to address the unbalanced classification problem. The model consists of separating the data according to the number of classes, k, and then, using the kernel-based one-class ELM to train each subset of data separately. Finally, conditional and prior probabilities are estimated for each class, and they are used to obtain the final classification results. The training of the subsets separated by class is performed in parallel because each training is independent. Experimental results show that P-ELM can significantly improve classification performance compared to various class imbalance learning approaches. In Safaei et al. [48], an ELM and OS-ELM were implemented using a system-on-a-chip field-programmable gate array (SoC FPGA) architecture, including parallel extraction and efficient shared memory communication in the process. Dokeroglu and Sevinc [118] proposed an island parallel evolutionary ELM (IPE-ELM) classification algorithm that combines evolutionary genetic algorithms, ELM, parallel computation, and parameter tuning. In the same year, Liang et al. [117] presented a parallel voltage ELM-based nonlinear decoupling method (PV-ELM) that outperforms linear decoupling algorithms for six-axis F/M sensors.

Furthermore, in Li et al. [116] a parallel least squares ELM and a kernel-based ELM model combining Kmeans-FFA-KELM were proposed for regression problems, and both models were applied for estimating baseline evapotranspiration (${\mathrm{ET}}_0$), which is an important process for determining water requirements, designing an irrigation schedule, and managing agricultural water resources. In Ezemobi et al. [114], the parallel layer ELM (PL-ELM) model is analyzed to estimate battery health status; the results show the model is suitable for online applications. Multiple enhanced parallel ELMs were proposed by Zehai et al. [50] for remaining-useful-life prediction of integrated modular avionics. The prediction results demonstrate that the proposed method is suited for the online prediction of a real-time system. In Dwivedi et al. [151], an ELM model with a grasshopper multi-parallel adaptive optimization technique was used to detect anonymous attacks in wireless networks. The proposed intrusion detection technique outperforms other detection techniques concerning classification performance. A new hardware implementation of memristor-based ELM with a suitable training method was presented by Dong et al. [113]. The proposed method can produce more details on the final images. A distributed ELM version of batch processing was proposed by Vidhya and Aji [108]. This method outperformed the other methods in terms of performance metrics. A new approach based on an improved M-estimation-optimized double-parallel ELM was proposed by Zha et al. [107]. The proposed method is applied to a real operational condition of a power plant with efficient processing of the influence of outliers and noise with strong anti-interference ability.

More recently, Gelvez Almeida et al. [102,103] introduced a parallel training approach with multiple OS-ELM running on separate CPU cores to reduce ELM’s training time. Initial findings indicate that increasing the thread count reduces training time with minimal impact on test accuracy. Zang et al. [101] introduced the regularized functional extreme learning machine (RF-ELM), which uses a regularization functional instead of a preset parameter to adaptively select regularization parameters. The authors also created a parallel version of RF-ELM for handling big data tasks. Experimental results show the effectiveness and competitiveness of these models. Wang and Soo [100] introduced a novel biological ensemble approach for ELMs, emphasizing the advantage of parallelizing multiple ELM base learners without explicit aggregation, simplifying the learning process. Experimental results demonstrated its superior generalization performance compared to traditional ELMs and other state-of-the-art ensemble ELMs. Finally, Wang et al. [97] introduced a computationally efficient alternating direction method of multipliers (ADMM) with approximate curvature information for solving the update in ADMM inexactly. This algorithm, when applied to the RELM model, decomposes the model fitting problem into parallelizable subproblems, enhancing classification efficiency. Results in machine learning tasks indicate that this method is competitive, offering improved computational efficiency and accuracy compared to similar approaches.

6. Discussion

This section presents a discussion of the results of this review. To draw conclusions, we analyzed current trends in distributed and parallel methods for solving both SLE and ELM models. Turning to the related topic of solving SLE with parallel and distributed methods, we reviewed three groups of methods for solving this type of system. The first group included approaches based on operations such as Gaussian elimination and its variants (Gauss–Jordan and Gauss–Huard). Within this group, research has considered matrices with dimensions ranging from 64 to 30,000 rows and columns. The second group is related to the factorization-based methods and, within this group, the literature reports algorithms such as Cholesky decomposition, singular value decomposition, and QR factorization. In factorization methods, researchers have worked on matrices ranging from 1000 to 115,000 rows and columns. The most common iterative methods reported in the third group are Gauss–Seidel, Gauss–Newton, SOR techniques, and Jacobi methods based on both the original version and its variants.

In terms of parallel tools, one of the most popular is CUDA programming, which takes advantage of the different features of the GPU architecture. In this regard, the most widely used GPUs are the NVIDIA GeForce GTX, TITAN, and TESLA series, while there is extensive research on using CPU-based architectures such as IntelMCI and tools like MPI, IntelMKL, LAPACK, and Plasma. Thus, in the iteration-based SLE solution, several authors have processed matrices of up to 28 million rows and columns using the IntelMIC architecture. According to this scenario, we can establish that the use of both CPUs combined with IntelMKL and GPU architecture considering CUDA, MPI, and OpenMP improves the performance quality of computer systems compared to traditional methods. In this sense, the aforementioned methods for SLE resolution show that parallel versions with these tools and architectures are significantly more efficient in execution time, scalability, and overall performance.

In ELM models, GPU programming via CUDA is widely used to address regression and classification problems with ELM models and databases containing a lot of data. In several papers reviewed, the computers were equipped with NVIDIA GeForce GTX, GeForce GT, and TESLA and processed databases ranging from 96.46 KB to 1.79 GB. In addition, other distributed ELM models have been proposed with tools such as MPI, Intel MKL, SoC-FPGAs through the Xilinx Zynq platform, and other machine learning toolboxes. The ELM variants proposed by many authors are presented in Section 5.3. In this case, the size of databases ranges from approximately 89 KB to 3.34 GB. Moreover, MapReduce has emerged as a dynamic tool for data distribution, so it has been widely accepted in the ELM model and its variants. The proposed ELM implementations using MapReduce were described in Section 5.1. The architecture typically used by the authors is mainly clusters composed of several computers without GPU. Using MapReduce, the size of the databases varies between approximately 180 MB and 19.53 GB. Another tool that has been widely accepted in ELM-based models is Apache Spark. Proposed ELM variants that have used Apache Spark were reviewed in Section 5.3.

Like MapReduce, multi-computer clustering is the architecture reported by different authors working on databases ranging in size from approximately 2.34 GB to 60 GB. Among all the works analyzed, the largest database used was 60 GB under the Spark architecture. In addition, it remains a challenge to process information that greatly exceeds the size reported in this review. In practical applications, the ELM models have increased the amount of data to be processed. However, their variants are still being developed to handle information close to the scope of big data. Similarly, parallel architectures and programming tools are evolving rapidly, offering great opportunities for the ELM model and its variants to process larger amounts of data than currently reported. Finally, in the presented review, it is possible to identify parallel architectures that have not yet been used with ELM models, such as multi-GPU, multi-FPGA, multi-node/multi-FPGA, or multi-node/multi-GPU. Therefore, addressing these problems can be considered as an open field of research.

7. Conclusions

For this paper, we have performed an updated review of distributed and parallel ELM models to address regression and classification problems with large databases. Mainly, we focus on the data dimension and the parallel architectures reported in the literature. Moreover, this paper presents a review of current trends in solving SLE using distributed and parallel approaches, which are useful for improving the computation of the MPGI matrix required in ELM models. In addition, as the data’s dimensions has been a relevant aspect in this review, we estimated the size of databases considering their characteristics.

ELM models with distributed and parallel computing have advanced significantly in the last decade. However, we can conclude that distributed and parallel ELMs are still in an early stage of development. Different authors have reported significant improvements in accuracy and training time using both distributed and parallel computing compared with traditional methods. In addition, that fact has allowed a more complete and optimal use of the available architectures. In fact, parallel and distributed computing is used for large-scale data sets, while the cost of time is replaced by the cost of hardware. In the context of ELM models, the most used architectures are GPU and multi-node programming considering tools such as CUDA, MPI, IntelMKL, MapReduce, and Spark. There are also works developed on IntelMCI architectures and programmable chips such as the Xilinx Zynq platform.

The need to process ever-increasing data volumes and the constant advancement of parallel architectures constitute a broad scenario of opportunities for both the ELM models and the scientific community. In this sense, distributed and parallel computing can be considered a constantly advancing framework for tackling problems involving more and more data. In particular, our review shows that in solving SLE, distributed and parallel approaches have achieved speedups of up to 27.75× compared to sequential methods; in addition GPUs can offer speedups of 46× compared to CPUs.

Regarding the size of the databases, we can state that it is a challenging feature both in the solution of an SLE and in parallel and distributed ELM models. In the first case, the literature reports processes with matrices of up to 28 million rows and columns. In the second, the authors have evaluated different approaches with databases sizing up to 60 GB. The parallel SLE solution is in direct relation to the MPGI matrix and has undergone constant improvements. This type of solution can generate a positive impact on ELM models and their variants because it can reduce the high computational cost associated with the training process.

Moreover, the ELM models based on distributed and parallel programming belong to a scientific field in permanent development. Thus, thanks to the advance of the Internet and the constant generation of big data, these models have generated remarkable high-level improvements. Despite all the work performed in the international context, it is still a challenge to work with databases of the order of terabytes. The following aspects can be considered as strengths in this review article:

• Researchers who wish to use distributed and parallel computing in ELM, its variants, and other randomized feedforward neural network models can use this work as a reference to identify the technologies and tools that have been implemented so far.
• According to the large amount of time involved in computing the MPGI matrix, we have presented an updated review of the most widely used methods and their implementation with distributed and parallel architectures and tools.
• The review on distributed and parallel methods for computing the MPGI matrix is relevant to accelerate the training of ELM, its variants, and other randomized feedforward neural network models.

Some weaknesses have been detected during the development of this review. First, little recognition has been given to older randomized feedforward neural network models that have inspired the ELM model and its variants. Second, many reviewed works have been developed with synthetic or traditional public databases without implementing the results to real-world applications. In future work, we invite researchers to recognize the older randomized feedforward neural network models and conduct research on distributed and parallel ELM models to address problems with more realistic database sizes that can be used in real-world applications.