Model-Based Assessment of Elastic Material Parameters in Rheumatic Heart Disease Patients and Healthy Subjects
Abstract
:1. Introduction
2. Methods
2.1. Study Population
2.2. CMR Image Analysis
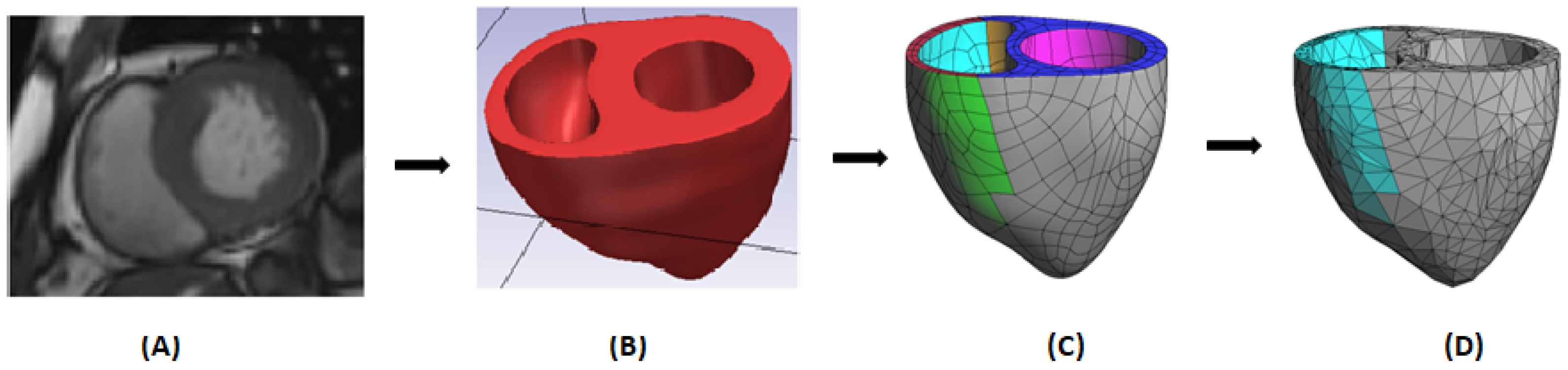
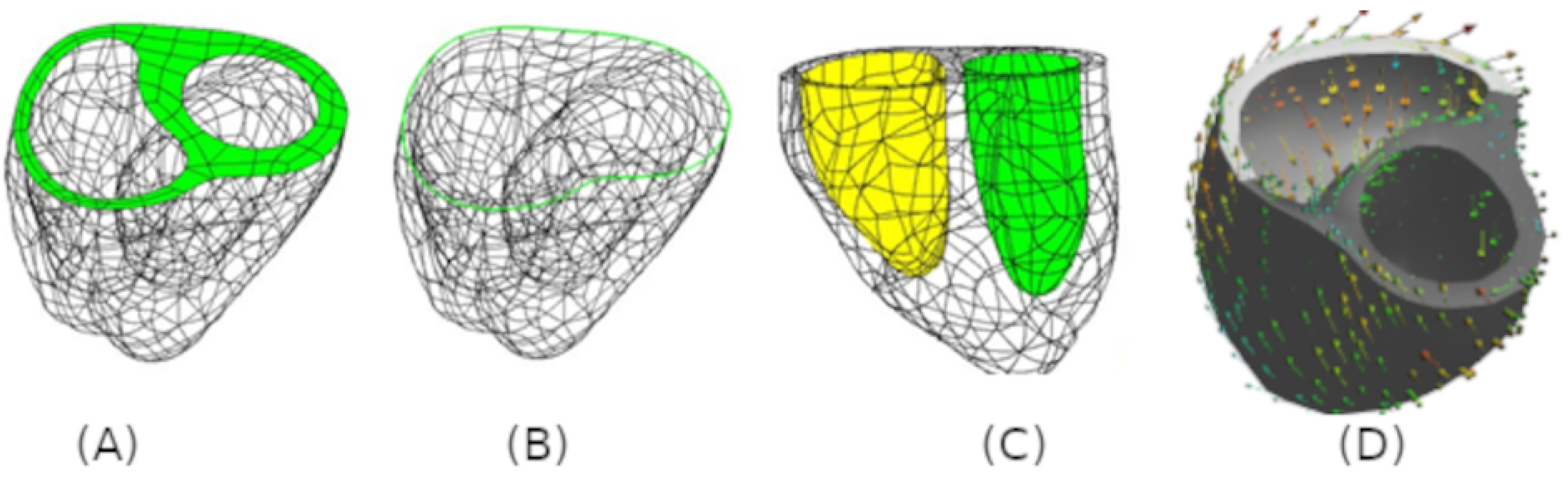
2.3. Geometric Segmentation and Finite Element Model Creation of The Biventricle
2.4. Constitutive Model for Elastic Myocardium
2.5. Boundary Conditions
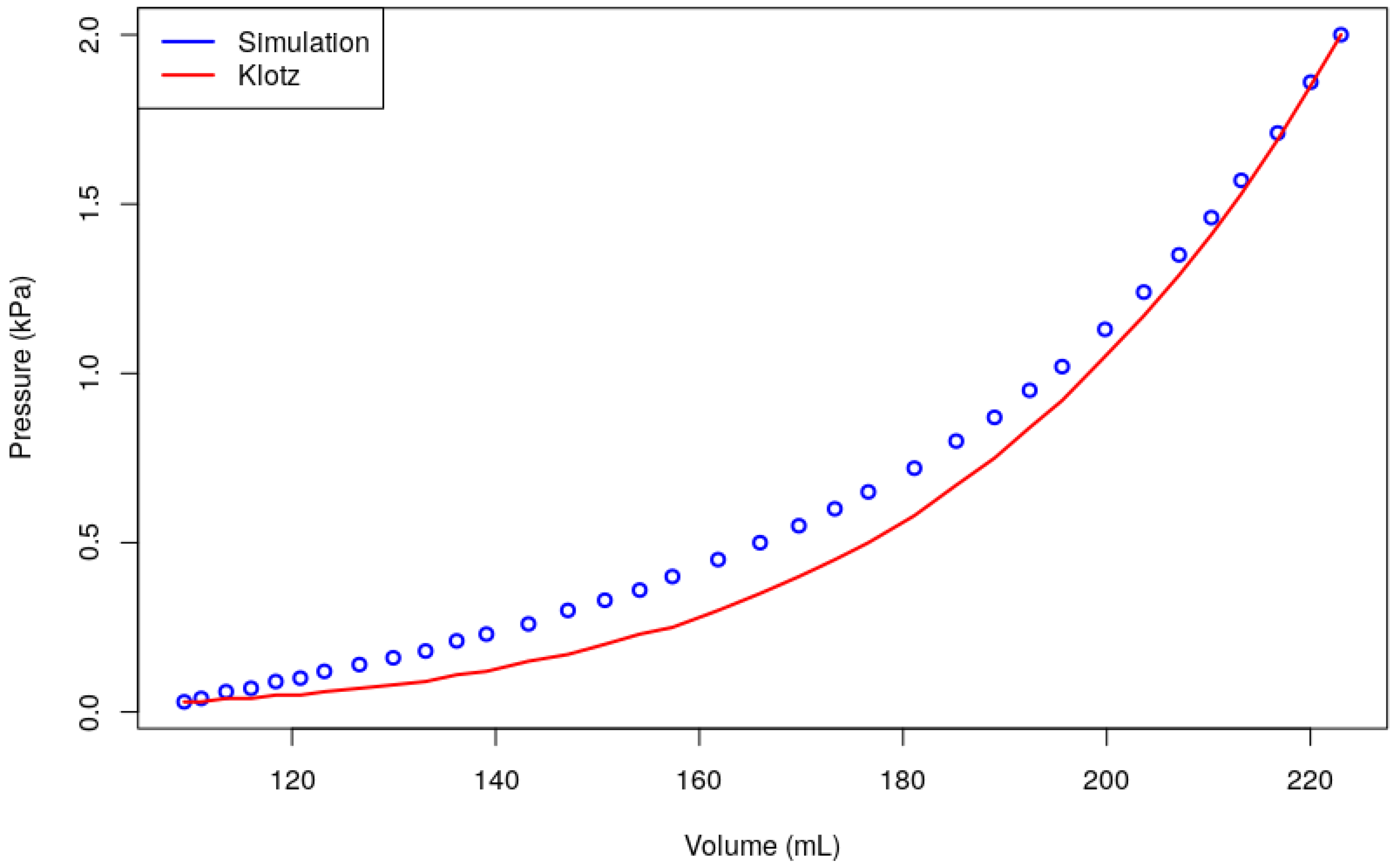
2.6. Parameter Optimization Procedure
3. Results
3.1. Geometric Segmentation
3.2. Statistical Analysis
3.3. Baseline Characteristics and CMR Global Function
3.4. Estimation of Elastic Material Parameters
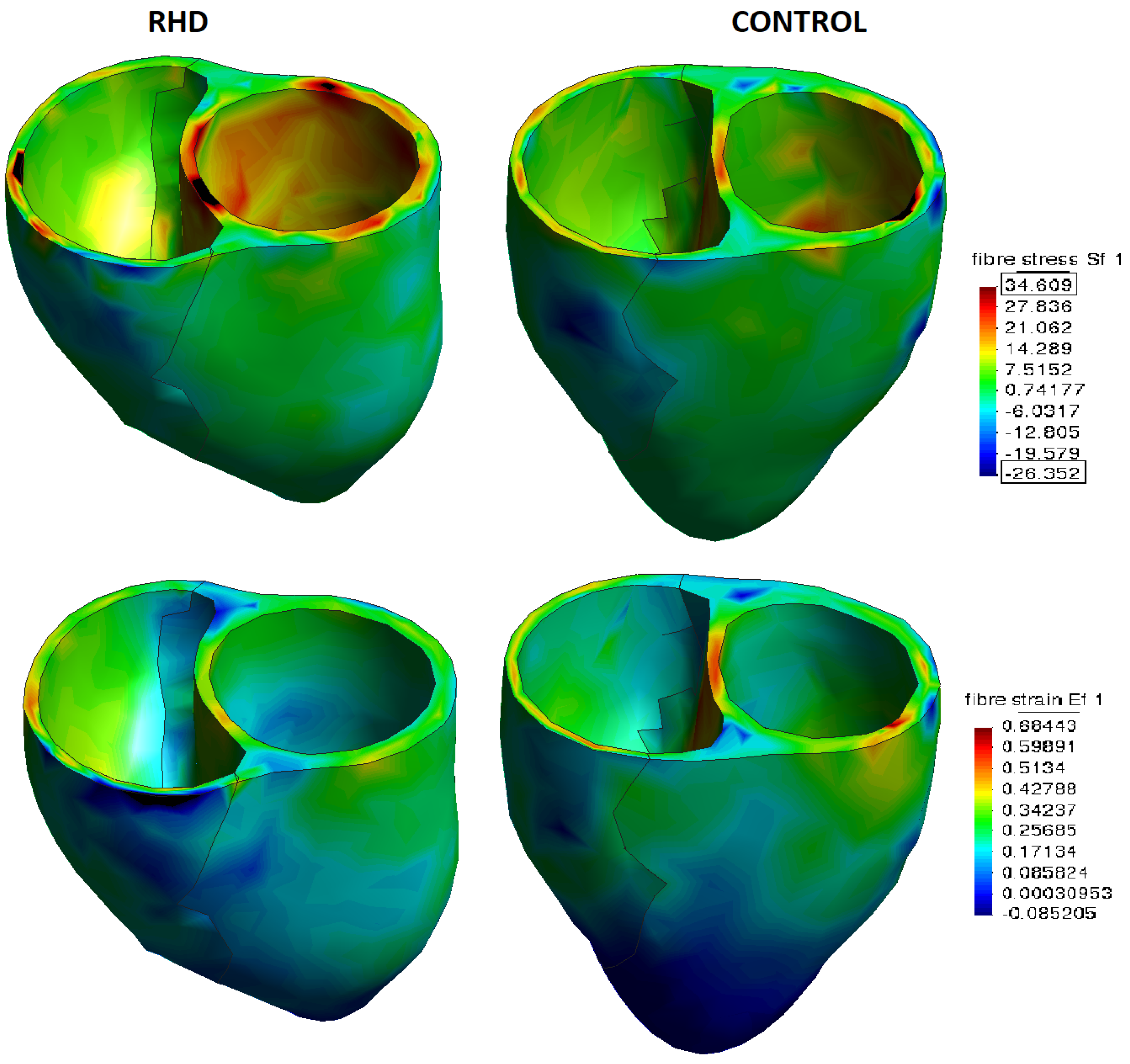
3.5. Global Strain And Stress
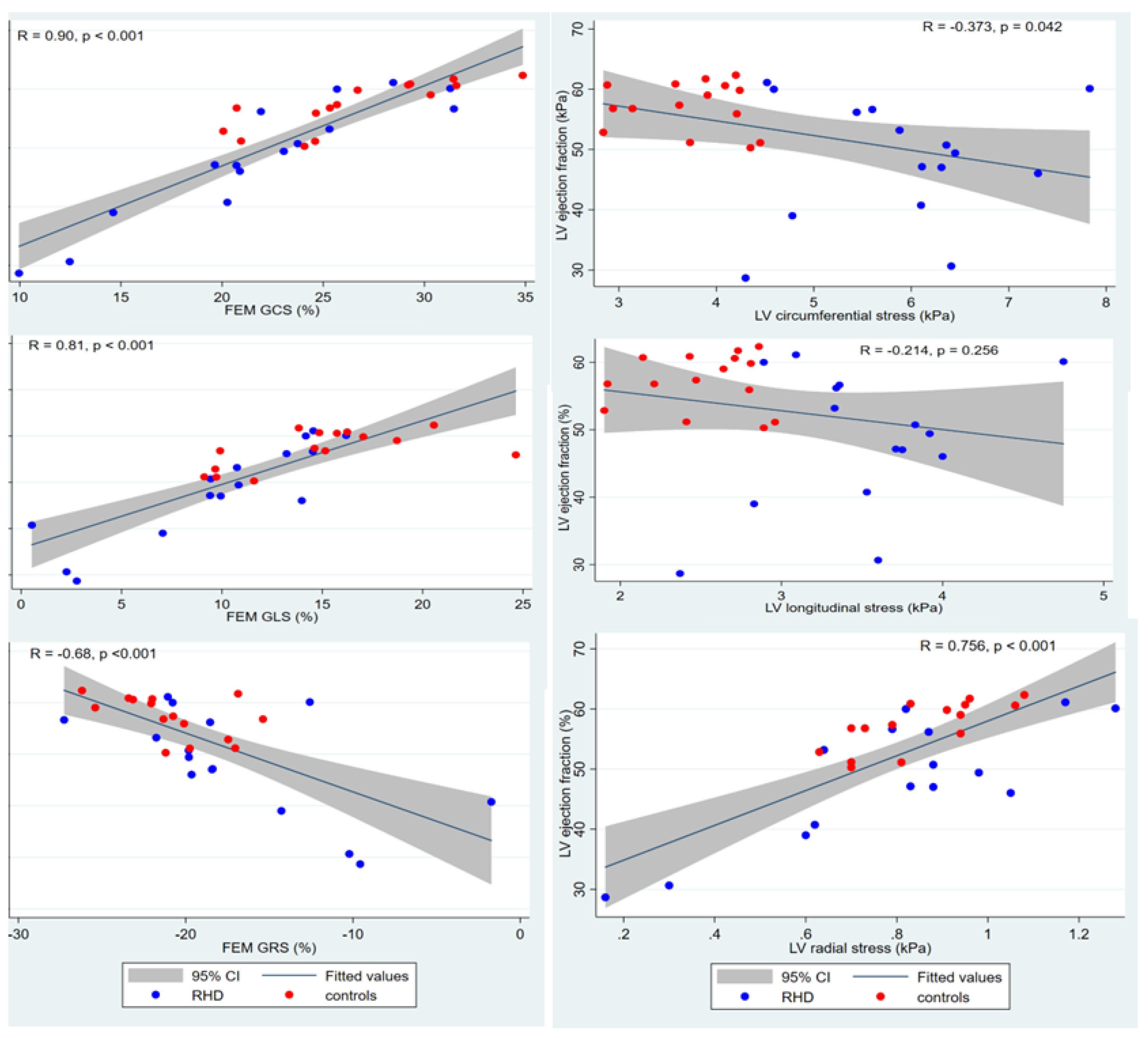
3.6. Association between CMR and Simulated Parameters
3.7. Sensitivity Analysis
4. Discussion
Model Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Watkins, D.A.; Johnson, C.O.; Colquhoun, S.M.; Karthikeyan, G.; Beaton, A.; Bukhman, G.; Forouzanfar, M.H.; Longenecker, C.T.; Mayosi, B.M.; Mensah, G.A.; et al. Global, regional, and national burden of rheumatic heart disease, 1990–2015. N. Engl. J. Med. 2017, 377, 713–722. [Google Scholar] [CrossRef] [PubMed]
- Zühlke, L.J.; Engel, M.E.; Watkins, D.; Mayosi, B.M. Incidence, prevalence and outcome of rheumatic heart disease in South Africa: A systematic review of contemporary studies. Int. J. Cardiol. 2015, 199, 375–383. [Google Scholar] [CrossRef] [PubMed]
- Yutzey, K.E.; Demer, L.L.; Body, S.C.; Huggins, G.S.; Towler, D.A.; Giachelli, C.M.; Hofmann-Bowman, M.A.; Mortlock, D.P.; Rogers, M.B.; Sadeghi, M.M.; et al. Calcific aortic valve disease: A consensus summary from the Alliance of Investigators on Calcific Aortic Valve Disease. Arterioscler. Thromb. Vasc. Biol. 2014, 34, 2387–2393. [Google Scholar] [CrossRef] [PubMed]
- Nikou, A.; Dorsey, S.M.; McGarvey, J.R.; Gorman, J.H.; Burdick, J.A.; Pilla, J.J.; Gorman, R.C.; Wenk, J.F. Computational modeling of healthy myocardium in diastole. Ann. Biomed. Eng. 2016, 44, 980–992. [Google Scholar] [CrossRef]
- Lee, L.C.; Ge, L.; Zhang, Z.; Pease, M.; Nikolic, S.D.; Mishra, R.; Ratcliffe, M.B.; Guccione, J.M. Patient-specific finite element modeling of the Cardiokinetix Parachute® device: Effects on left ventricular wall stress and function. Med. Biol. Eng. Comput. 2014, 52, 557–566. [Google Scholar] [CrossRef]
- Sack, K.L.; Davies, N.H.; Guccione, J.M.; Franz, T. Personalised computational cardiology: Patient-specific modelling in cardiac mechanics and biomaterial injection therapies for myocardial infarction. Heart Fail. Rev. 2016, 21, 815–826. [Google Scholar] [CrossRef]
- Göktepe, S.; Acharya, S.; Wong, J.; Kuhl, E. Computational modeling of passive myocardium. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 1–12. [Google Scholar] [CrossRef]
- Genet, M.; Lee, L.C.; Nguyen, R.; Haraldsson, H.; Acevedo-Bolton, G.; Zhang, Z.; Ge, L.; Ordovas, K.; Kozerke, S.; Guccione, J.M. Distribution of normal human left ventricular myofiber stress at end diastole and end systole: A target for in silico design of heart failure treatments. J. Appl. Physiol. 2014, 117, 142–152. [Google Scholar] [CrossRef]
- Walker, J.C.; Ratcliffe, M.B.; Zhang, P.; Wallace, A.W.; Hsu, E.W.; Saloner, D.A.; Guccione, J.M. Magnetic resonance imaging-based finite element stress analysis after linear repair of left ventricular aneurysm. J. Thorac. Cardiovasc. Surg. 2008, 135, 1094–1102. [Google Scholar] [CrossRef]
- Xi, J.; Lamata, P.; Niederer, S.; Land, S.; Shi, W.; Zhuang, X.; Ourselin, S.; Duckett, S.G.; Shetty, A.K.; Rinaldi, C.A.; et al. The estimation of patient-specific cardiac diastolic functions from clinical measurements. Med. Image Anal. 2013, 17, 133–146. [Google Scholar] [CrossRef]
- Hadjicharalambous, M.; Asner, L.; Chabiniok, R.; Sammut, E.; Wong, J.; Peressutti, D.; Kerfoot, E.; King, A.; Lee, J.; Razavi, R.; et al. Non-invasive model-based assessment of passive left-ventricular myocardial stiffness in healthy subjects and in patients with non-ischemic dilated cardiomyopathy. Ann. Biomed. Eng. 2017, 45, 605–618. [Google Scholar] [CrossRef] [PubMed]
- Winslow, R.L.; Trayanova, N.; Geman, D.; Miller, M.I. Computational medicine: Translating models to clinical care. Sci. Transl. Med. 2012, 4, 158rv11. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, J.; Strumpf, R.; Yin, F. Determination of a constitutive relation for passive myocardium: I. A new functional form. J. Biomech. Eng. 1990, 112, 333–339. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, J.; Yin, F. On constitutive relations and finite deformations of passive cardiac tissue: I. A pseudostrain-energy function. J. Biomech. Eng. 1987, 112, 333–339. [Google Scholar] [CrossRef]
- Kerckhoffs, R.; Bovendeerd, P.; Kotte, J.; Prinzen, F.; Smits, K.; Arts, T. Homogeneity of cardiac contraction despite physiological asynchrony of depolarization: A model study. Ann. Biomed. Eng. 2003, 31, 536–547. [Google Scholar] [CrossRef]
- Costa, K.D.; Holmes, J.W.; McCulloch, A.D. Modelling cardiac mechanical properties in three dimensions. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 359, 1233–1250. [Google Scholar] [CrossRef]
- Sack, K.; Skatulla, S.; Sansour, C. Biological tissue mechanics with fibers modelled as one-dimensional Cosserat continua. Applications to cardiac tissue. Int. J. Solids Struct. 2016, 81, 84–94. [Google Scholar] [CrossRef]
- Dokos, S.; Smaill, B.H.; Young, A.A.; LeGrice, I.J. Shear properties of passive ventricular myocardium. Am. J. Physiol.-Heart Circ. Physiol. 2002, 283, H2650–H2659. [Google Scholar] [CrossRef]
- Sommer, G.; Schriefl, A.J.; Andrä, M.; Sacherer, M.; Viertler, C.; Wolinski, H.; Holzapfel, G.A. Biomechanical properties and microstructure of human ventricular myocardium. Acta Biomater. 2015, 24, 172–192. [Google Scholar] [CrossRef]
- Hunter, P.J. Computational electromechanics of the heart. In Computational Biology of the Heart; John Wiley & Sons: Hoboken, NJ, USA, 1997; pp. 345–407. [Google Scholar]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of passive myocardium: A structurally based framework for material characterization. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 3445–3475. [Google Scholar] [CrossRef]
- Schmid, H.; Nash, M.; Young, A.; Hunter, P. Myocardial material parameter estimation—A comparative study for simple shear. J. Biomech. Eng. 2006, 128, 742–750. [Google Scholar] [CrossRef] [PubMed]
- Usyk, T.; Mazhari, R.; McCulloch, A. Effect of laminar orthotropic myofiber architecture on regional stress and strain in the canine left ventricle. J. Elast. Phys. Sci. Solids 2000, 61, 143–164. [Google Scholar]
- Mojsejenko, D.; McGarvey, J.R.; Dorsey, S.M.; Gorman, J.H.; Burdick, J.A.; Pilla, J.J.; Gorman, R.C.; Wenk, J.F. Estimating passive mechanical properties in a myocardial infarction using MRI and finite element simulations. Biomech. Model. Mechanobiol. 2015, 14, 633–647. [Google Scholar] [CrossRef] [PubMed]
- Skatulla, S.; Sansour, C. On a path-following method for nonlinear solid mechanics with applications to structural and cardiac mechanics subject to arbitrary loading scenarios. Int. J. Solids Struct. 2016, 96, 181–191. [Google Scholar] [CrossRef]
- Legner, D.; Skatulla, S.; MBewu, J.; Rama, R.; Reddy, B.; Sansour, C.; Davies, N.; Franz, T. Studying the influence of hydrogel injections into the infarcted left ventricle using the element-free Galerkin method. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 416–429. [Google Scholar] [CrossRef]
- Rama, R.R.; Skatulla, S. Real-time nonlinear solid mechanics computations for fast inverse material parameter optimization in cardiac mechanics. J. Eng. Mech. 2019, 145, 04019020. [Google Scholar] [CrossRef]
- Skatulla, S.; Sansour, C.; Familusi, M.; Hussan, J.; Ntusi, N. Non-invasive in silico determination of ventricular wall pre-straining and characteristic cavity pressures. arXiv 2023, arXiv:2308.00461. http://arxiv.org/abs/2308.00461. [Google Scholar]
- Lee, L.C.; Wenk, J.F.; Zhong, L.; Klepach, D.; Zhang, Z.; Ge, L.; Ratcliffe, M.B.; Zohdi, T.I.; Hsu, E.; Navia, J.L.; et al. Analysis of patient-specific surgical ventricular restoration: Importance of an ellipsoidal left ventricular geometry for diastolic and systolic function. J. Appl. Physiol. 2013, 115, 136–144. [Google Scholar] [CrossRef]
- Wang, H.; Gao, H.; Luo, X.; Berry, C.; Griffith, B.; Ogden, R.; Wang, T. Structure-based finite strain modelling of the human left ventricle in diastole. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 83–103. [Google Scholar] [CrossRef]
- Palit, A.; Bhudia, S.K.; Arvanitis, T.N.; Turley, G.A.; Williams, M.A. Computational modelling of left-ventricular diastolic mechanics: Effect of fiber orientation and right-ventricle topology. J. Biomech. 2015, 48, 604–612. [Google Scholar] [CrossRef]
- Wong, J.; Kuhl, E. Generating fiber orientation maps in human heart models using Poisson interpolation. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1217–1226. [Google Scholar] [CrossRef] [PubMed]
- Rama, R.R.; Skatulla, S.; Sansour, C. Real-time modelling of diastolic filling of the heart using the proper orthogonal decomposition with interpolation. Int. J. Solids Struct. 2016, 96, 409–422. [Google Scholar] [CrossRef]
- Guyon, F.; Le Riche, R. Least Squares Parameter Estimation and the Levenberg–Marquardt Algorithm: Deterministic Analysis, Sensitivities and Numerical Experiments; Technical Report 041/99; Institut National des Sciences Appliquées: Paris, France, 2000. [Google Scholar]
- Gee, M.W.; Förster, C.; Wall, W. A computational strategy for prestressing patient-specific biomechanical problems under finite deformation. Int. J. Numer. Methods Biomed. Eng. 2010, 26, 52–72. [Google Scholar] [CrossRef]
- Klotz, S.; Hay, I.; Dickstein, M.L.; Yi, G.H.; Wang, J.; Maurer, M.S.; Kass, D.A.; Burkhoff, D. Single-beat estimation of end-diastolic pressure-volume relationship: A novel method with potential for noninvasive application. Am. J. Physiol.-Heart Circ. Physiol. 2006, 291, H403–H412. [Google Scholar] [CrossRef] [PubMed]
- Krishnamurthy, A.; Villongco, C.T.; Chuang, J.; Frank, L.R.; Nigam, V.; Belezzuoli, E.; Stark, P.; Krummen, D.E.; Narayan, S.; Omens, J.H.; et al. Patient-specific models of cardiac biomechanics. J. Comput. Phys. 2013, 244, 4–21. [Google Scholar] [CrossRef] [PubMed]
- Rama, R.R.; Skatulla, S. Towards real-time cardiac mechanics modelling with patient-specific heart anatomies. Comput. Methods Appl. Mech. Eng. 2018, 328, 47–74. [Google Scholar] [CrossRef]
- Rama, R.; Skatulla, S. Towards real-time modelling of passive and active behavior of the human heart using PODI-based model reduction. Comput. Struct. 2020, 232, 105897. [Google Scholar] [CrossRef]
- McHugh, M.L. The chi-square test of independence. Biochem. Medica 2013, 23, 143–149. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- McKnight, P.E.; Najab, J. Mann-Whitney U Test. Corsini Encycl. Psychol. 2010, 1. [Google Scholar] [CrossRef]
- Sedgwick, P. Pearson’s correlation coefficient. BMJ 2012, 345, e4483. [Google Scholar] [CrossRef]
- StataCorp, L. Stata statistical software: Release 15 College Station, TX, 2017. Erişim Adres. Erişim Tarihi 2017, 28, 2022. Available online: www.stata.com/features/documentation/ (accessed on 1 March 2018).
- Ferreira, V.M.; Piechnik, S.K.; Robson, M.D.; Neubauer, S.; Karamitsos, T.D. Myocardial tissue characterization by magnetic resonance imaging: Novel applications of T1 and T2 mapping. J. Thorac. Imaging 2014, 29, 147. [Google Scholar] [CrossRef] [PubMed]
- Ntusi, N.A.; Francis, J.M.; Sever, E.; Liu, A.; Piechnik, S.K.; Ferreira, V.M.; Matthews, P.M.; Robson, M.D.; Wordsworth, P.B.; Neubauer, S.; et al. Anti-TNF modulation reduces myocardial inflammation and improves cardiovascular function in systemic rheumatic diseases. Int. J. Cardiol. 2018, 270, 253–259. [Google Scholar] [CrossRef]
- Kellman, P.; Hansen, M.S. T1-mapping in the heart: Accuracy and precision. J. Cardiovasc. Magn. Reson. 2014, 16, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Ajmone Marsan, N.; Delgado, V.; Shah, D.J.; Pellikka, P.; Bax, J.J.; Treibel, T.; Cavalcante, J.L. Valvular heart disease: Shifting the focus to the myocardium. Eur. Heart J. 2023, 44, 28–40. [Google Scholar] [CrossRef]
- Marx, L.; Niestrawska, J.A.; Gsell, M.A.; Caforio, F.; Plank, G.; Augustin, C.M. Robust and efficient fixed-point algorithm for the inverse elastostatic problem to identify myocardial passive material parameters and the unloaded reference configuration. J. Comput. Phys. 2022, 463, 111266. [Google Scholar] [CrossRef]
- Zhou, X.; Lei, M.; Zhou, D.; Li, G.; Duan, Z.; Zhou, S.; Jin, Y. Clinical factors affecting left ventricular end-diastolic pressure in patients with acute ST-segment elevation myocardial infarction. Ann. Palliat. Med. 2020, 9, 1834–1840. [Google Scholar] [CrossRef]
- Mielniczuk, L.M.; Lamas, G.A.; Flaker, G.C.; Mitchell, G.; Smith, S.C.; Gersh, B.J.; Solomon, S.D.; Moyé, L.A.; Rouleau, J.L.; Rutherford, J.D.; et al. Left ventricular end-diastolic pressure and risk of subsequent heart failure in patients following an acute myocardial infarction. Congest. Heart Fail. 2007, 13, 209–214. [Google Scholar] [CrossRef]
- Alter, P.; Rupp, H.; Rominger, M.; Klose, K.; Maisch, B. A new methodological approach to assess cardiac work by pressure–volume and stress–length relations in patients with aortic valve stenosis and dilated cardiomyopathy. Pflügers Arch.-Eur. J. Physiol. 2008, 455, 627–636. [Google Scholar] [CrossRef]
- Young, A.A.; Dokos, S.; Powell, K.A.; Sturm, B.; McCulloch, A.D.; Starling, R.C.; McCarthy, P.M.; White, R.D. Regional heterogeneity of function in nonischemic dilated cardiomyopathy. Cardiovasc. Res. 2001, 49, 308–318. [Google Scholar] [CrossRef]
- Münch, J.; Abdelilah-Seyfried, S. Sensing and responding of cardiomyocytes to changes of tissue stiffness in the diseased heart. Front. Cell Dev. Biol. 2021, 9, 403. [Google Scholar] [CrossRef]
- Wang, V.Y.; Lam, H.; Ennis, D.B.; Cowan, B.R.; Young, A.A.; Nash, M.P. Modelling passive diastolic mechanics with quantitative MRI of cardiac structure and function. Med. Image Anal. 2009, 13, 773–784. [Google Scholar] [CrossRef]
- Brower, G.L.; Gardner, J.D.; Forman, M.F.; Murray, D.B.; Voloshenyuk, T.; Levick, S.P.; Janicki, J.S. The relationship between myocardial extracellular matrix remodeling and ventricular function. Eur. J. Cardio-Thorac. Surg. 2006, 30, 604–610. [Google Scholar] [CrossRef]
- Izawa, H.; Murohara, T.; Nagata, K.; Isobe, S.; Asano, H.; Amano, T.; Ichihara, S.; Kato, T.; Ohshima, S.; Murase, Y.; et al. Mineralocorticoid receptor antagonism ameliorates left ventricular diastolic dysfunction and myocardial fibrosis in mildly symptomatic patients with idiopathic dilated cardiomyopathy: A pilot study. Circulation 2005, 112, 2940–2945. [Google Scholar] [CrossRef]
- Bortone, A.S.; Hess, O.M.; Chiddo, A.; Gaglione, A.; Locuratolo, N.; Caruso, G.; Rizzon, P. Functional and structural abnormalities in patients with dilated cardiomyopathy. J. Am. Coll. Cardiol. 1989, 14, 613–623. [Google Scholar] [CrossRef]
- Weber, K.; Janicki, J.; Shroff, S.; Pick, R.; Chen, R.; Bashey, R. Collagen remodeling of the pressure-overloaded, hypertrophied nonhuman primate myocardium. Circ. Res. 1988, 62, 757–765. [Google Scholar] [CrossRef]
- Beltrami, C.A.; Finato, N.; Rocco, M.; Feruglio, G.A.; Puricelli, C.; Cigola, E.; Quaini, F.; Sonnenblick, E.H.; Olivetti, G.; Anversa, P. Structural basis of end-stage failure in ischemic cardiomyopathy in humans. Circulation 1994, 89, 151–163. [Google Scholar] [CrossRef]
- Ling, L.h.; Kistler, P.M.; Ellims, A.H.; Iles, L.M.; Lee, G.; Hughes, G.L.; Kalman, J.M.; Kaye, D.M.; Taylor, A.J. Diffuse ventricular fibrosis in atrial fibrillation: Noninvasive evaluation and relationships with aging and systolic dysfunction. J. Am. Coll. Cardiol. 2012, 60, 2402–2408. [Google Scholar] [CrossRef]
- Cheng-Baron, J.; Chow, K.; Pagano, J.J.; Punithakumar, K.; Paterson, D.I.; Oudit, G.Y.; Thompson, R.B. Quantification of circumferential, longitudinal, and radial global fractional shortening using steady-state free precession cines: A comparison with tissue-tracking strain and application in Fabry disease. Magn. Reson. Med. 2015, 73, 586–596. [Google Scholar] [CrossRef]
- Parisi, A.; Moynihan, P.; Feldman, C.; Folland, E. Approaches to determination of left ventricular volume and ejection fraction by real-time two-dimensional echocardiography. Clin. Cardiol. 1979, 2, 257–263. [Google Scholar] [CrossRef]
- Piersanti, R.; Regazzoni, F.; Salvador, M.; Corno, A.F.; Vergara, C.; Quarteroni, A. 3D–0D closed-loop model for the simulation of cardiac biventricular electromechanics. Comput. Methods Appl. Mech. Eng. 2022, 391, 114607. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, J.; Rezavand, M.; Wu, D.; Hu, X. An integrative smoothed particle hydrodynamics method for modeling cardiac function. Comput. Methods Appl. Mech. Eng. 2021, 381, 113847. [Google Scholar] [CrossRef]
- Sack, K.L.; Aliotta, E.; Ennis, D.B.; Choy, J.S.; Kassab, G.S.; Guccione, J.M.; Franz, T. Construction and validation of subject-specific biventricular finite-element models of healthy and failing swine hearts from high-resolution DT-MRI. Front. Physiol. 2018, 9, 539. [Google Scholar] [CrossRef]
- Ochs, A.; Riffel, J.; Ochs, M.M.; Arenja, N.; Fritz, T.; Galuschky, C.; Schuster, A.; Bruder, O.; Mahrholdt, H.; Giannitsis, E.; et al. Myocardial mechanics in dilated cardiomyopathy: Prognostic value of left ventricular torsion and strain. J. Cardiovasc. Magn. Reson. 2021, 23, 1–13. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, S.; Tang, X.; Ren, H.; Li, S.; Zou, Q.; Xiong, F.; Zheng, T.; Gong, L. Evaluation of left ventricular strain in patients with dilated cardiomyopathy. J. Int. Med Res. 2017, 45, 2092–2100. [Google Scholar] [CrossRef]
- Vietheer, J.; Lehmann, L.; Unbehaun, C.; Fischer-Rasokat, U.; Wolter, J.S.; Kriechbaum, S.; Weferling, M.; von Jeinsen, B.; Hain, A.; Liebetrau, C.; et al. CMR-derived myocardial strain analysis differentiates ischemic and dilated cardiomyopathy—A propensity score-matched study. Int. J. Cardiovasc. Imaging 2022, 38, 863–872. [Google Scholar] [CrossRef]
- Pfeffer, M.A.; Braunwald, E. Ventricular remodeling after myocardial infarction: Experimental observations and clinical implications. Circulation 1990, 81, 1161–1172. [Google Scholar]
- MG, S. Sharpe N. Left ventricular remodeling after myocardial infarction: Pathophysiology and therapy. Circulation 2000, 101, 2981–2988. [Google Scholar]
- Matiwala, S.; Margulies, K.B. Mechanical approaches to alter remodeling. Curr. Heart Fail. Rep. 2004, 1, 14–18. [Google Scholar] [CrossRef]
- Lee, L.C.; Wall, S.T.; Klepach, D.; Ge, L.; Zhang, Z.; Lee, R.J.; Hinson, A.; Gorman III, J.H.; Gorman, R.C.; Guccione, J.M. Algisyl-LVR™ with coronary artery bypass grafting reduces left ventricular wall stress and improves function in the failing human heart. Int. J. Cardiol. 2013, 168, 2022–2028. [Google Scholar] [CrossRef]
- Westermann, D.; Kasner, M.; Steendijk, P.; Spillmann, F.; Riad, A.; Weitmann, K.; Hoffmann, W.; Poller, W.; Pauschinger, M.; Schultheiss, H.P.; et al. Role of left ventricular stiffness in heart failure with normal ejection fraction. Circulation 2008, 117, 2051–2060. [Google Scholar] [CrossRef]


| Left Ventricle | Right Ventricle | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ESV | EDV | ESV | EDV | |||||||||||
| FEM | CMR | FEM | Error | CMR | FEM | Error | FEM | CMR | FEM | Error | CMR | FEM | Error | |
| 1 | 35.0 | 37.0 | 35.1 | 5.2 | 90.0 | 90.0 | 0.0026 | 50.7 | 78.0 | 77.0 | 1.3 | 121.0 | 121.0 | 0.0002 |
| 2 | 53.0 | 51.0 | 53.5 | 4.9 | 135.0 | 135.0 | 0.0031 | 77.9 | 82.0 | 82.5 | 0.6 | 165.0 | 165.0 | 0.0018 |
| 3 | 108.9 | 111.0 | 110.2 | 0.7 | 235.0 | 235.0 | 0.0001 | 35.5 | 75.0 | 71.2 | 5.1 | 101.0 | 101.0 | 0.0003 |
| 4 | 75.5 | 77.0 | 78.5 | 1.9 | 178.0 | 178.0 | 0.0002 | 61.3 | 61.0 | 61.2 | 0.3 | 136.0 | 136.0 | 0.0020 |
| 5 | 110.6 | 109.0 | 111.5 | 2.3 | 256.0 | 256.0 | 0.0045 | 97.6 | 104.0 | 103.5 | 0.5 | 185.0 | 185.0 | 0.0140 |
| 6 | 135.9 | 144.0 | 143.7 | 0.2 | 243.0 | 243.0 | 0.0014 | 50.4 | 72.0 | 70.5 | 2.0 | 109.0 | 109.0 | 0.0007 |
| 7 | 83.1 | 90.0 | 88.7 | 1.4 | 168.0 | 168.0 | 0.0002 | 45.2 | 61.0 | 63.4 | 3.9 | 96.0 | 96.0 | 0.0021 |
| 8 | 94.9 | 101.0 | 101.9 | 0.9 | 189.0 | 189.0 | 0.0001 | 36.9 | 69.0 | 68.2 | 1.1 | 92.0 | 92.0 | 0.0003 |
| 9 | 82.3 | 86.0 | 86.0 | 0.0 | 170.0 | 170.0 | 0.0015 | 56.9 | 67.0 | 65.8 | 1.9 | 118.0 | 118.0 | 0.0005 |
| 10 | 137.8 | 141.0 | 143.9 | 2.0 | 292.0 | 292.0 | 0.0025 | 104.4 | 130.0 | 129.9 | 0.1 | 226.0 | 226.0 | 0.0006 |
| 11 | 118.8 | 119.0 | 120.1 | 0.9 | 301.0 | 301.0 | 0.0043 | 73.9 | 81.0 | 81.1 | 0.1 | 155.0 | 155.0 | 0.0011 |
| 12 | 129.8 | 146.0 | 145.6 | 0.3 | 210.0 | 210.0 | 0.0007 | 66.9 | 179.0 | 179.2 | 0.1 | 227.0 | 227.0 | 0.0010 |
| 13 | 76.0 | 97.0 | 97.2 | 0.2 | 136.0 | 136.0 | 0.0031 | 57.5 | 63.0 | 67.4 | 7.0 | 109.0 | 109.0 | 0.0012 |
| 14 | 68.4 | 80.0 | 79.2 | 1.0 | 132.0 | 132.0 | 0.0108 | 73.1 | 75.0 | 77.9 | 3.8 | 152.0 | 152.1 | 0.0448 |
| 15 | 77.5 | 82.0 | 83.1 | 1.3 | 157.0 | 157.0 | 0.0001 | 74.7 | 78.0 | 80.5 | 3.2 | 160.0 | 160.0 | 0.0010 |
| Left Ventricle | Right Ventricle | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ESV | EDV | ESV | EDV | |||||||||||
| FEM | CMR | FEM | Error | CMR | FEM | Error | FEM | CMR | FEM | Error | CMR | FEM | Error | |
| 1 | 79.0 | 78.0 | 79.8 | 2.3 | 203.0 | 203.0 | 0.0007 | 76.7 | 78.0 | 78.0 | 0.0 | 186.0 | 186.0 | 0.0001 |
| 2 | 53.4 | 54.0 | 54.3 | 0.5 | 125.0 | 125.0 | 0.0008 | 66.2 | 74.0 | 71.0 | 4.1 | 137.0 | 137.0 | 0.0008 |
| 3 | 56.2 | 54.0 | 57.6 | 6.7 | 123.0 | 123.0 | 0.0052 | 64.0 | 72.0 | 71.7 | 0.4 | 134.0 | 134.0 | 0.0007 |
| 4 | 57.5 | 57.0 | 58.0 | 1.7 | 154.0 | 154.0 | 0.0002 | 66.9 | 67.0 | 68.0 | 1.6 | 169.0 | 169.0 | 0.0001 |
| 5 | 68.5 | 71.0 | 69.7 | 1.9 | 162.0 | 162.0 | 0.0001 | 84.7 | 106.0 | 105.7 | 0.3 | 189.0 | 189.0 | 0.0006 |
| 6 | 49.5 | 50.0 | 50.1 | 0.3 | 122.0 | 122.0 | 0.0035 | 57.4 | 61.0 | 60.1 | 1.4 | 130.0 | 130.0 | 0.0017 |
| 7 | 60.4 | 63.0 | 63.3 | 0.5 | 129.0 | 129.0 | 0.0015 | 57.7 | 66.0 | 61.7 | 6.5 | 124.0 | 124.0 | 0.0011 |
| 8 | 46.4 | 49.0 | 47.0 | 4.0 | 117.0 | 117.0 | 0.0031 | 46.2 | 45.0 | 47.2 | 5.0 | 111.0 | 111.0 | 0.0003 |
| 9 | 80.0 | 85.0 | 81.6 | 4.0 | 186.0 | 186.0 | 0.0011 | 86.5 | 95.0 | 90.6 | 4.7 | 185.0 | 185.0 | 0.0006 |
| 10 | 106.3 | 106.0 | 109.4 | 3.2 | 223.0 | 223.0 | 0.0044 | 106.8 | 118.0 | 116.3 | 1.5 | 203.0 | 203.0 | 0.0062 |
| 11 | 57.3 | 57.0 | 58.5 | 2.6 | 136.0 | 136.0 | 0.0006 | 54.3 | 59.0 | 55.8 | 5.4 | 124.0 | 124.0 | 0.0024 |
| 12 | 44.4 | 50.0 | 44.9 | 10.1 | 115.0 | 115.0 | 0.0016 | 55.9 | 58.0 | 58.3 | 0.6 | 126.0 | 126.0 | 0.0000 |
| 13 | 77.1 | 79.0 | 80.5 | 2.0 | 162.0 | 162.0 | 0.0024 | 79.7 | 95.0 | 95.2 | 0.2 | 179.0 | 179.0 | 0.0016 |
| 14 | 56.2 | 57.0 | 56.6 | 0.7 | 144.0 | 144.0 | 0.0014 | 79.2 | 81.0 | 83.2 | 2.7 | 169.0 | 169.0 | 0.0013 |
| 15 | 50.1 | 55.0 | 50.5 | 8.1 | 132.0 | 132.0 | 0.0039 | 71.3 | 72.0 | 74.1 | 3.0 | 164.0 | 164.0 | 0.0006 |
| Characteristics | RHD (n = 15) | Controls (n = 15) | p-Value |
|---|---|---|---|
| Median (IQR) | Median (IQR) | ||
| Sex | |||
| Male n(%) | 6 (40) | 9 (60) | |
| Female n(%) | 9 (60) | 6 (40) | 0.237 |
| Age (years) | 38 (26–48) | 43 (36–54) | 0.309 |
| Height (cm) | 169 (158–175) | 172 (163–178) | 0.191 |
| Weight (kg) | 73 (64–95) | 83 (73–97) | 0.130 |
| BMI (kg/m) | 20 (23–32) | 29 (26–33) | 0.534 |
| LVEDV (mL) | 178 (136–243) | 136 (123–162) | 0.038 * |
| LVESV (mL) | 97 (77–119) | 57 (54–78) | 0.005 * |
| LVEF (%) | 51 (46–60) | 57 (53–61) | 0.036 * |
| RVEDV (mL) | 136 (109–185) | 164 (126–185) | 0.245 |
| RVESV (mL) | 78 (67–104) | 72 (61–95) | 0.309 |
| RVEF (%) | 42 (26–48) | 52 (46–56) | 0.001 * |
| Native T1 (ms) | 1290 (1248–1341) | 1213 (1194–1239) | 0.001 * |
| ECV (%) | 34 (30–39) | 28 (27–29) | 0.001 * |
| Right Ventricle | Left Ventricle | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Subjects | A (kPa) | B (-) | A (kPa) | (-) | (-) | (-) | (-) | (-) | (-) |
| 1 | 0.10 | 1.64 | 0.09 | −6.04 | −5.43 | 10.22 | 15.31 | 13.37 | −6.58 |
| 2 | 0.11 | 1.35 | 0.10 | −6.11 | −5.39 | 10.26 | 15.55 | 14.32 | −6.40 |
| 3 | 0.10 | 1.07 | 0.11 | −6.48 | −6.10 | 14.32 | 20.41 | 17.53 | −6.32 |
| 4 | 0.07 | 1.02 | 0.14 | −6.55 | −5.74 | 12.55 | 16.79 | 15.53 | −6.19 |
| 5 | 0.34 | 1.29 | 0.31 | −6.06 | −5.19 | 9.65 | 13.64 | 12.94 | −6.16 |
| 6 | 0.35 | 1.67 | 0.32 | −6.88 | −6.49 | 16.87 | 25.80 | 20.27 | −7.30 |
| 7 | 0.10 | 1.33 | 0.11 | −6.48 | −6.54 | 17.02 | 24.65 | 19.88 | −6.50 |
| 8 | 0.10 | 1.17 | 0.11 | −6.62 | −6.70 | 17.73 | 26.12 | 20.32 | −6.70 |
| 9 | 0.11 | 1.70 | 0.11 | −6.43 | −6.23 | 15.33 | 22.57 | 19.35 | −6.39 |
| 10 | 0.11 | 1.56 | 0.10 | −6.46 | −6.24 | 15.14 | 22.59 | 19.00 | −6.58 |
| 11 | 0.11 | 1.40 | 0.10 | −6.20 | −5.52 | 11.27 | 16.50 | 14.71 | −6.38 |
| 12 | 0.73 | 1.30 | 0.66 | −6.71 | −6.80 | 19.10 | 28.03 | 22.85 | −6.42 |
| 13 | 0.24 | 1.56 | 0.22 | −6.89 | −7.07 | 18.69 | 27.53 | 22.24 | −6.63 |
| 14 | 0.12 | 1.52 | 0.11 | −6.57 | −6.80 | 17.77 | 26.62 | 22.34 | −6.50 |
| 15 | 0.10 | 1.12 | 0.11 | −6.57 | −6.47 | 16.30 | 23.65 | 19.84 | −6.48 |
| Right Ventricle | Left Ventricle | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Subjects | A (kPa) | B (-) | A (kPa) | (-) | (-) | (-) | (-) | (-) | (-) |
| 1 | 0.10 | 0.90 | 0.10 | −6.09 | −5.12 | 9.71 | 12.75 | 12.54 | −5.97 |
| 2 | 0.12 | 1.75 | 0.11 | −6.26 | −5.50 | 9.97 | 15.78 | 15.43 | −6.55 |
| 3 | 0.11 | 1.66 | 0.10 | −6.15 | −5.59 | 10.76 | 17.20 | 15.64 | −6.63 |
| 4 | 0.10 | 1.02 | 0.10 | −6.00 | −5.00 | 8.99 | 12.02 | 12.03 | −6.01 |
| 5 | 0.13 | 1.98 | 0.10 | −6.48 | −5.43 | 10.69 | 13.94 | 14.73 | −6.11 |
| 6 | 0.12 | 1.63 | 0.10 | −6.13 | −5.26 | 9.53 | 14.06 | 13.92 | −6.23 |
| 7 | 0.11 | 1.45 | 0.11 | −6.55 | −5.86 | 12.91 | 18.32 | 16.71 | −6.34 |
| 8 | 0.10 | 0.96 | 0.10 | −6.17 | −5.27 | 10.30 | 13.77 | 13.21 | −6.09 |
| 9 | 0.11 | 1.22 | 0.10 | −6.25 | −5.47 | 10.74 | 15.34 | 14.15 | −6.36 |
| 10 | 0.38 | 1.57 | 0.31 | −6.26 | −5.47 | 10.56 | 15.26 | 14.24 | −6.22 |
| 11 | 0.10 | 1.07 | 0.10 | −6.20 | −5.35 | 10.57 | 14.54 | 13.77 | −6.15 |
| 12 | 0.11 | 1.36 | 0.10 | −6.06 | −5.12 | 9.05 | 12.82 | 12.72 | −6.12 |
| 13 | 0.12 | 1.85 | 0.10 | −6.33 | −5.90 | 12.18 | 19.54 | 17.39 | −6.70 |
| 14 | 0.12 | 1.57 | 0.10 | −6.20 | −5.31 | 8.91 | 13.84 | 13.37 | −6.47 |
| 15 | 0.13 | 1.65 | 0.10 | −6.31 | −5.13 | 8.91 | 12.21 | 13.37 | −6.04 |
| Characteristics | RHD (n = 15) | Controls (n = 15) | p-Value |
|---|---|---|---|
| Median (IQR) | Median (IQR) | ||
| Right ventricle | |||
| A (kPa) | 0.11 (0.10–0.24) | 0.12 (0.10–0.12) | 0.633 |
| B | 1.35 (1.17–1.56) | 1.57 (1.57–1.66) | 0.468 |
| Left ventricle | |||
| A (kPa) | 0.11 (0.11–0.22) | 0.10 (0.10–0.10) | 0.003 * |
| (-) | −6.48 (−6.62–(−6.20)) | −6.20 (−6.31–(−6.13)) | 0.021 * |
| (-) | −6.24 (−6.70–(−5.52)) | −5.35 (−5.50–(−5.13)) | 0.001 * |
| (-) | 15.33 (11.27–17.73) | 10.30 (9.05–10.74) | 0.001 * |
| (-) | 22.59 (16.50–26.12) | 14.06 (12.82–15.78) | <0.001 * |
| (-) | 19.35 (14.71–20.32) | 13.92 (13.21–15.43) | 0.001 * |
| (-) | −6.48 (−6.58–(−6.38)) | −6.22 (−6.47–(−6.09)) | 0.015 * |
| (o) | 69.63 (67.08–72.42) | 72.07 (71.30–74.45) | 0.006 * |
| (o) | −58.45 (−59.8–(−57.1)) | −58.04 (−58.8–−56.9) | 0.395 |
| Characteristics | RHD (n = 15) | Controls (n = 15) | p-Value |
|---|---|---|---|
| Median (IQR) | Median (IQR) | ||
| 1.26 (1.12–1.36) | 0.96 (0.89–1.05) | <0.001 * | |
| 1.78 (1.73–2.10) | 2.07 (1.81–2.41) | 0.033 * | |
| 1.44 (1.27–1.88) | 2.10 (1.98–2.62) | <0.001 * | |
| 3.38 (3.23–3.75) | 3.68 (3.49–3.85) | 0.027 * | |
| 2.59 (2.43–3.08) | 3.51 (3.26–3.73) | <0.001 * | |
| 1.28 (1.22–1.34) | 1.07 (1.02–1.15) | <0.001 * |
| RHD (n = 15) | Controls (n = 15) | |||
|---|---|---|---|---|
| CMR | FEM | CMR | FEM | |
| GLS (%) | 18.8 | 9.1 | 23.8 | 11.4 |
| GCS (%) | 22.2 | 24.2 | 28.1 | 27.4 |
| GRS (%) | −14.7 | −18.7 | −17.4 | −20.5 |
| RHD (n = 15) | Controls (n = 15) | |
|---|---|---|
| Median (IQR) | Median (IQR) | |
| Longitudinal | 3.57 (3.16–3.80) | 2.58 (2.28–2.75) |
| Circumferential | 6.02 (5.09–6.30) | 3.90 (3.33–4.15) |
| Radial | 0.83 (0.77–0.93) | 0.82 (0.74–0.90) |
| LVEF | GCS | GLS | GRS | |
|---|---|---|---|---|
| R (p-Value) | R (p-Value) | R (p-Value) | R (p-Value) | |
| A (kPa) | −0.584 (0.001 *) | −0.433 (0.017 *) | −0.400 (0.029 *) | 0.473 (0.008 *) |
| (-) | −0.913 (<0.001 *) | −0.795 (<0.001 *) | −0.732 (<0.001 *) | 0.809 (<0.001 *) |
| (-) | −0.925 (<0.001 *) | −0.781 (<0.001 *) | −0.729 (<0.001 *) | 0.797 (<0.001 *) |
| (-) | −0.905 (<0.001 *) | −0.734 (<0.001 *) | −0.720 (<0.001 *) | 0.763 (<0.001 *) |
| (-) | −0.924 (<0.001 *) | −0.788 (<0.001 *) | −0.735 (<0.001 *) | 0.804 (<0.001 *) |
| (-) | −0.919 (<0.001 *) | −0.788 (<0.001 *) | −0.733 (<0.001 *) | 0.805 (<0.001 *) |
| (-) | −0.927 (<0.001 *) | −0.774 (<0.001 *) | −0.731 (<0.001 *) | 0.794 (<0.001 *) |
| Right Ventricle | Left Ventricle | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| LVEDP (kPa) | A (kPa) | B | A (kPa) | (o) | (o) | ||||||
| 1.5 | 0.11 | 1.91 | 0.10 | −6.37 | −5.85 | 11.44 | 18.53 | 16.77 | −6.92 | 75.27 | −57.9 |
| 2.0 | 0.11 | 1.73 | 0.10 | −6.39 | −5.99 | 12.95 | 20.31 | 17.72 | −6.81 | 72.23 | −58.4 |
| 2.5 | 0.11 | 1.62 | 0.10 | −6.49 | −6.18 | 14.28 | 21.61 | 18.59 | −6.79 | 71.06 | −58.4 |
| 3.0 | 0.11 | 1.56 | 0.10 | −6.46 | −6.24 | 15.14 | 22.59 | 19.00 | −6.58 | 70.41 | −58.3 |
| Characteristics | RHD (n = 15) | Controls (n = 15) | p-Value |
|---|---|---|---|
| Median (IQR) | Median (IQR) | ||
| Right ventricle | |||
| A (kPa) | 0.11 (0.10–0.24) | 0.11 (0.10–0.11) | 0.310 |
| B | 1.35 (1.17–1.56) | 1.33 (0.94–1.52) | 0.351 |
| Left ventricle | |||
| A (kPa) | 0.11 (0.11–0.22) | 0.10 (0.10–0.11) | 0.013 * |
| (-) | −6.48 (−6.62–(−6.20)) | −6.31 (−6.39–(−6.26)) | 0.141 |
| (-) | −6.24 (−6.70–(−5.52)) | −5.59 (−5.86–(−5.38)) | 0.021 * |
| (-) | 15.33 (11.27–17.73) | 11.83 (10.59–13.17) | 0.027 * |
| (-) | 22.59 (16.50–26.12) | 16.14 (14.57–19.66) | 0.008 * |
| (-) | 19.35 (14.71–20.32) | 15.20 (13.84–17.23) | 0.021 * |
| (-) | −6.48 (−6.58–(−6.38)) | −6.21 (−6.52–(−6.13)) | 0.029 * |
| (o) | 69.63 (67.08–72.42) | 70.91 (70.51–72.37) | 0.093 |
| (o) | −58.45 (−59.8–(−57.1)) | −57.49 (−57.8–(−56.4)) | 0.085 |
| Right Ventricle | Left Ventricle | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (kPa) | A (kPa) | B (-) | A (kPa) | (-) | (-) | (-) | (-) | (-) | (-) | (o) | (o) |
| 50 | 0.11 | 1.74 | 0.11 | −6.60 | −6.39 | 15.90 | 23.14 | 19.91 | −6.42 | 71.44 | −58.9 |
| 100 | 0.11 | 1.70 | 0.11 | −6.57 | −6.37 | 15.68 | 23.08 | 19.78 | −6.54 | 71.57 | −59.5 |
| 300 | 0.11 | 1.42 | 0.11 | −6.82 | −6.45 | 15.22 | 22.33 | 18.96 | −6.87 | 71.26 | −59.3 |
| 500 | 0.11 | 1.20 | 0.11 | −7.16 | −6.56 | 14.59 | 21.23 | 18.47 | −7.12 | 71.19 | −58.1 |
| Left Ventricle | |||||||
|---|---|---|---|---|---|---|---|
| (kPa) | (kJoule) | ||||||
| 50 | 1.22 | 1.74 | 1.43 | 2.57 | 3.19 | 1.24 | 3.94e05 |
| 100 | 1.23 | 1.81 | 1.47 | 2.59 | 3.24 | 1.25 | 4.06e05 |
| 300 | 1.24 | 1.86 | 1.50 | 2.67 | 3.42 | 1.28 | 4.24e05 |
| 500 | 1.18 | 1.88 | 1.59 | 2.81 | 3.50 | 1.24 | 4.30e05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Familusi, M.A.; Skatulla, S.; Hussan, J.R.; Aremu, O.O.; Mutithu, D.; Lumngwena, E.N.; Gumedze, F.N.; Ntusi, N.A.B. Model-Based Assessment of Elastic Material Parameters in Rheumatic Heart Disease Patients and Healthy Subjects. Math. Comput. Appl. 2023, 28, 106. https://doi.org/10.3390/mca28060106
Familusi MA, Skatulla S, Hussan JR, Aremu OO, Mutithu D, Lumngwena EN, Gumedze FN, Ntusi NAB. Model-Based Assessment of Elastic Material Parameters in Rheumatic Heart Disease Patients and Healthy Subjects. Mathematical and Computational Applications. 2023; 28(6):106. https://doi.org/10.3390/mca28060106
Chicago/Turabian StyleFamilusi, Mary A., Sebastian Skatulla, Jagir R. Hussan, Olukayode O. Aremu, Daniel Mutithu, Evelyn N. Lumngwena, Freedom N. Gumedze, and Ntobeko A. B. Ntusi. 2023. "Model-Based Assessment of Elastic Material Parameters in Rheumatic Heart Disease Patients and Healthy Subjects" Mathematical and Computational Applications 28, no. 6: 106. https://doi.org/10.3390/mca28060106
APA StyleFamilusi, M. A., Skatulla, S., Hussan, J. R., Aremu, O. O., Mutithu, D., Lumngwena, E. N., Gumedze, F. N., & Ntusi, N. A. B. (2023). Model-Based Assessment of Elastic Material Parameters in Rheumatic Heart Disease Patients and Healthy Subjects. Mathematical and Computational Applications, 28(6), 106. https://doi.org/10.3390/mca28060106









