Buckling of Cracked Euler–Bernoulli Columns Embedded in a Winkler Elastic Medium
Abstract
1. Introduction
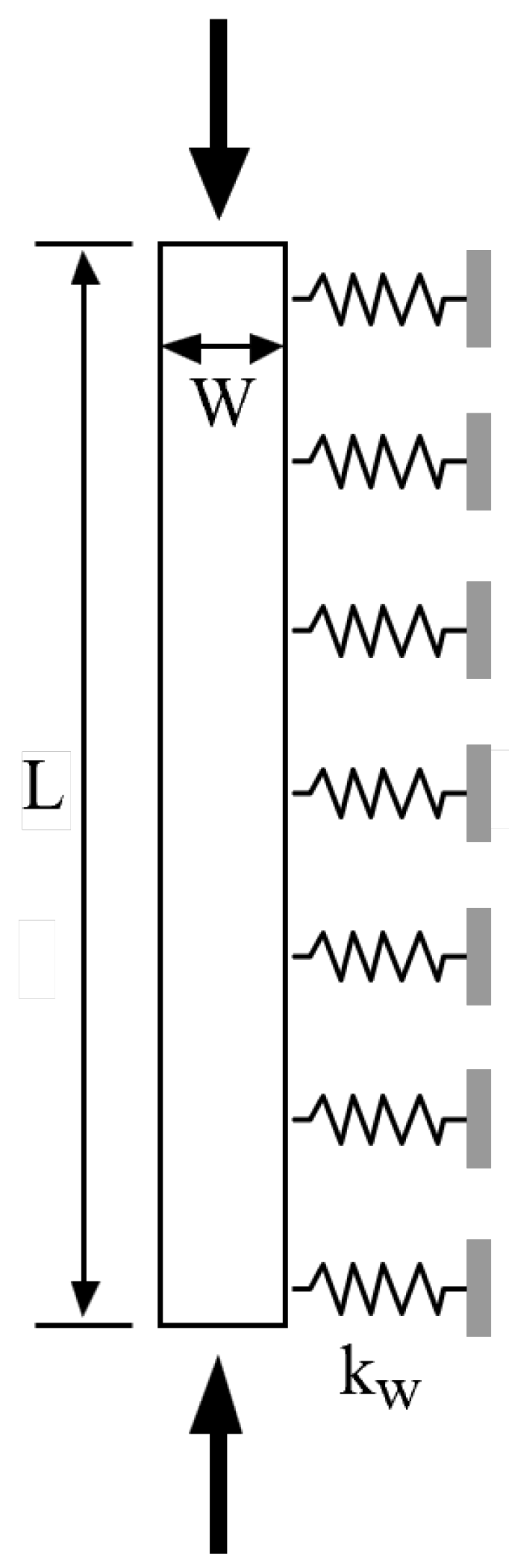
2. Euler–Benoulli Column Model in an Elastic Medium
2.1. Theoretical Formulation of an Intact Column
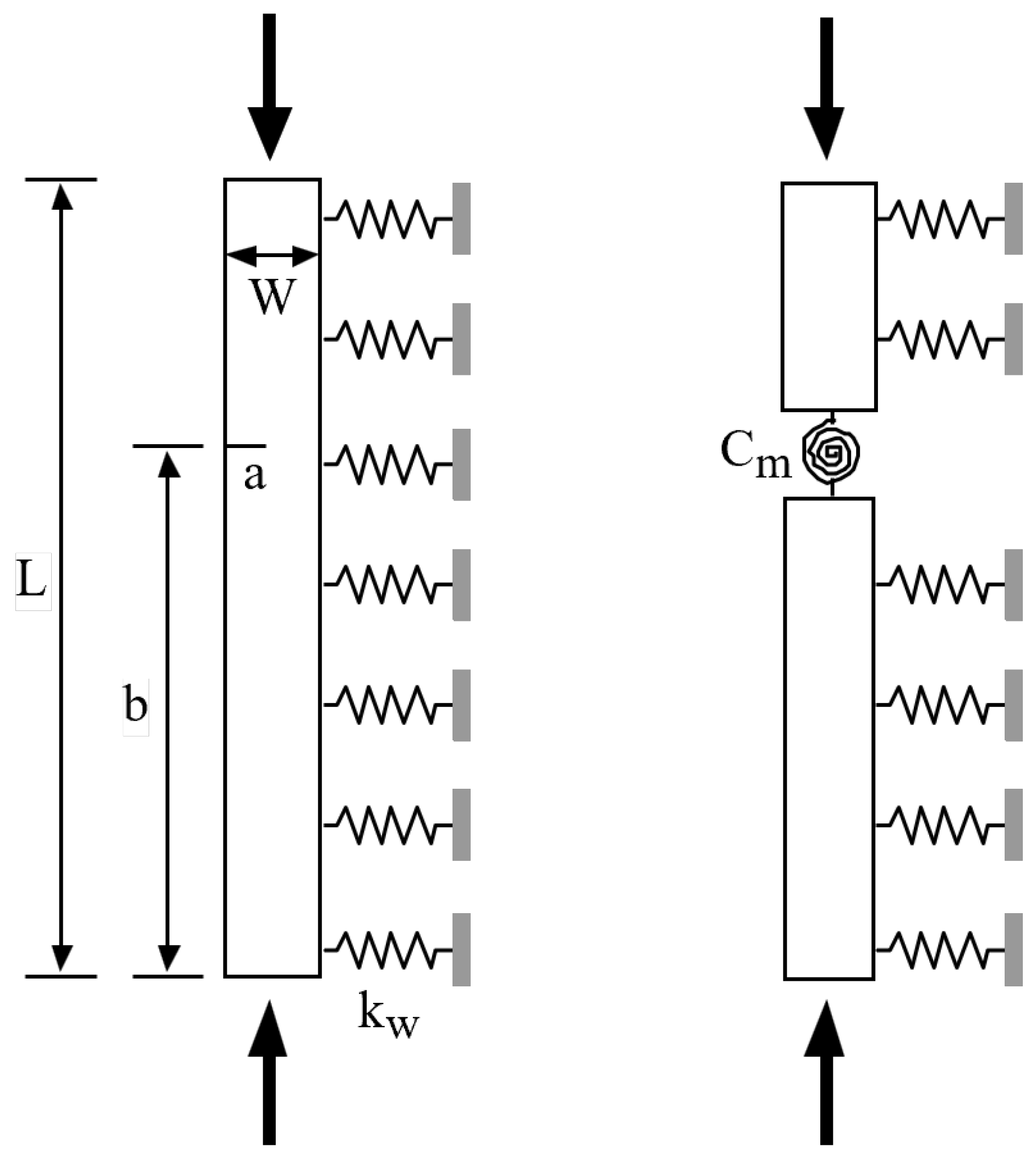
2.2. Problem Formulation in Cracked Columns
- Continuity in deflection:
- Continuity in bending moment:
- Continuity in shear force:
- Jump in the slope deflection:
3. Direct Solution
4. Numerical Results
4.1. Influence of the Crack on the Buckling Load
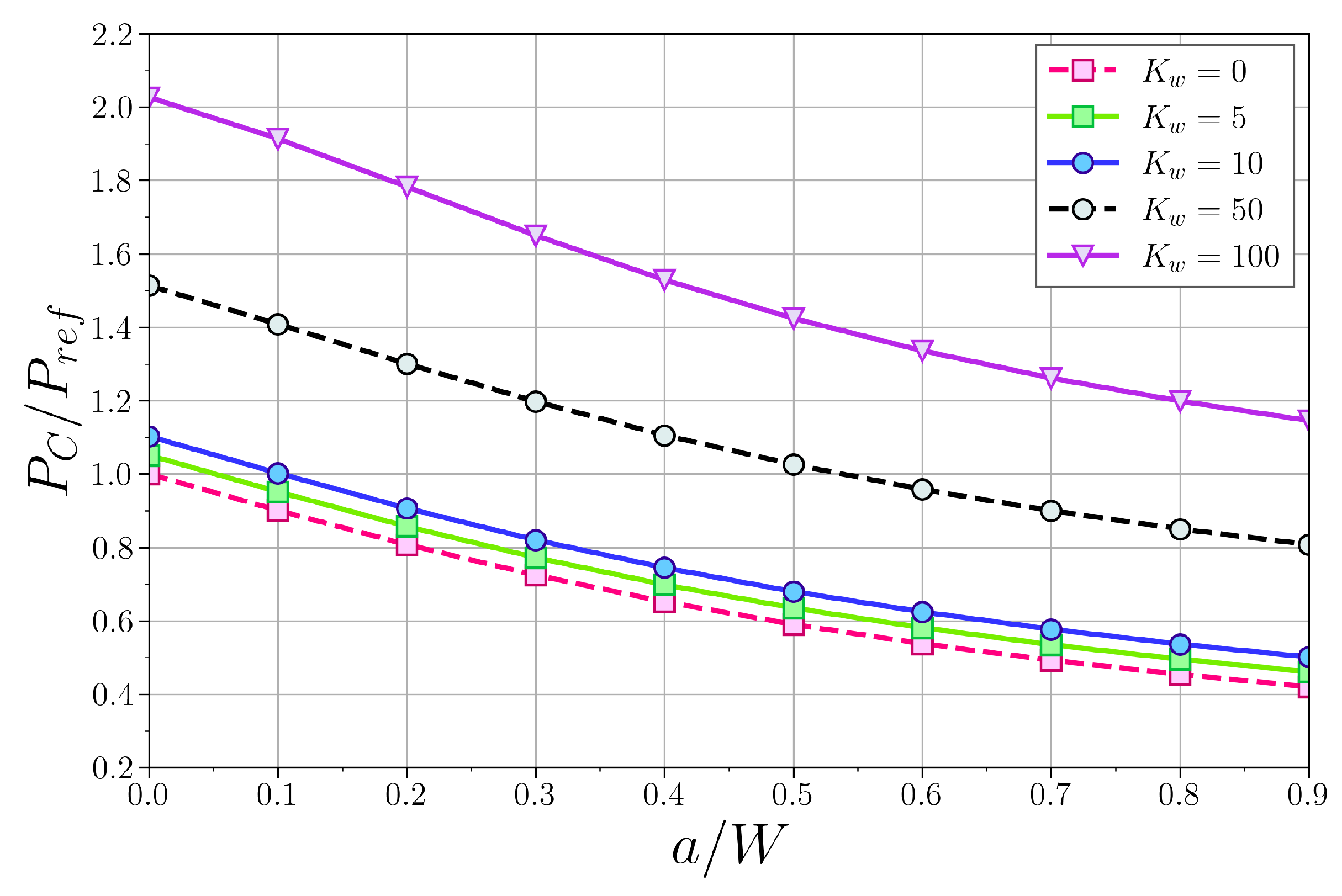
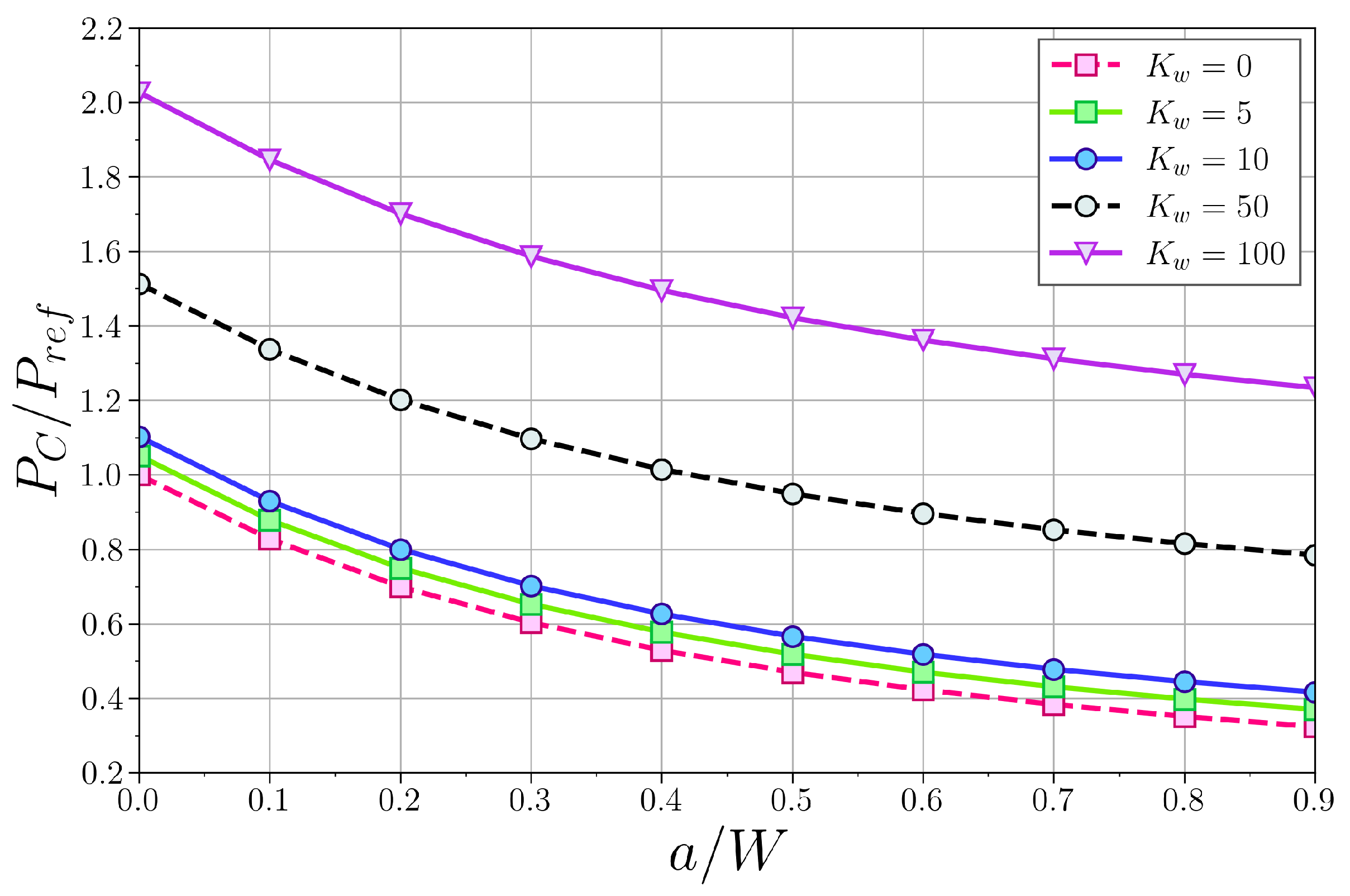
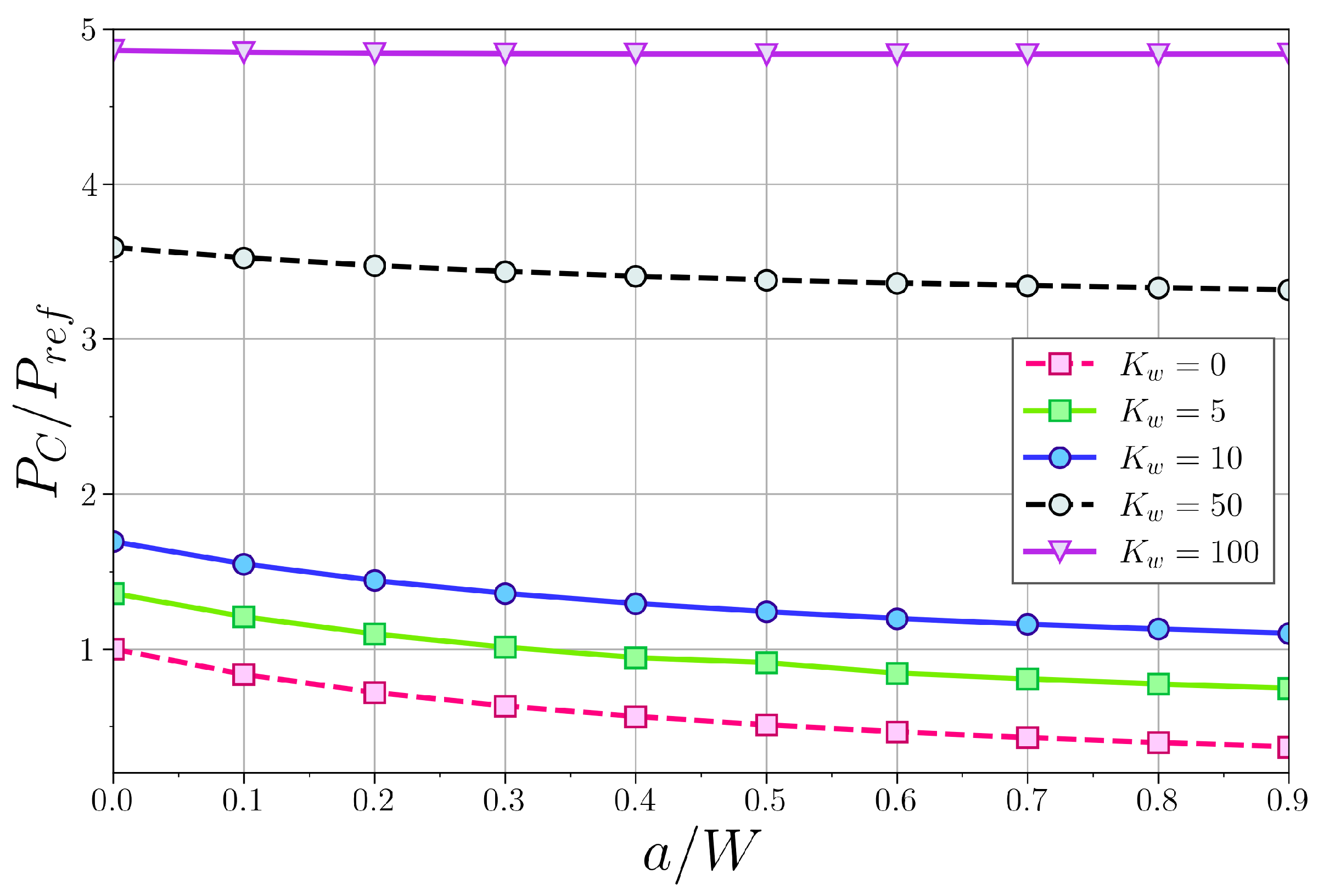
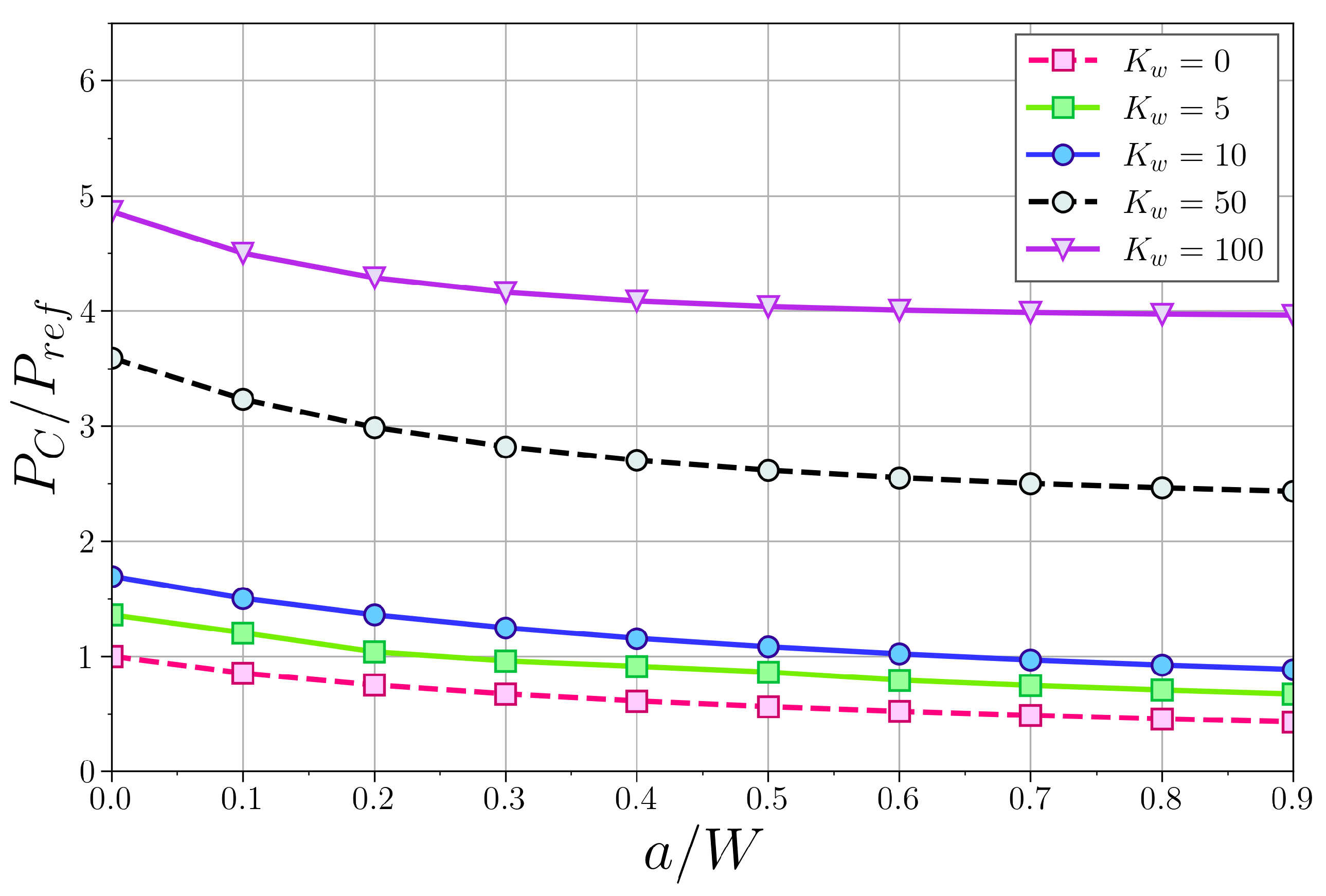
4.2. Influence of the Crack and Elastic Medium on the Buckling Load
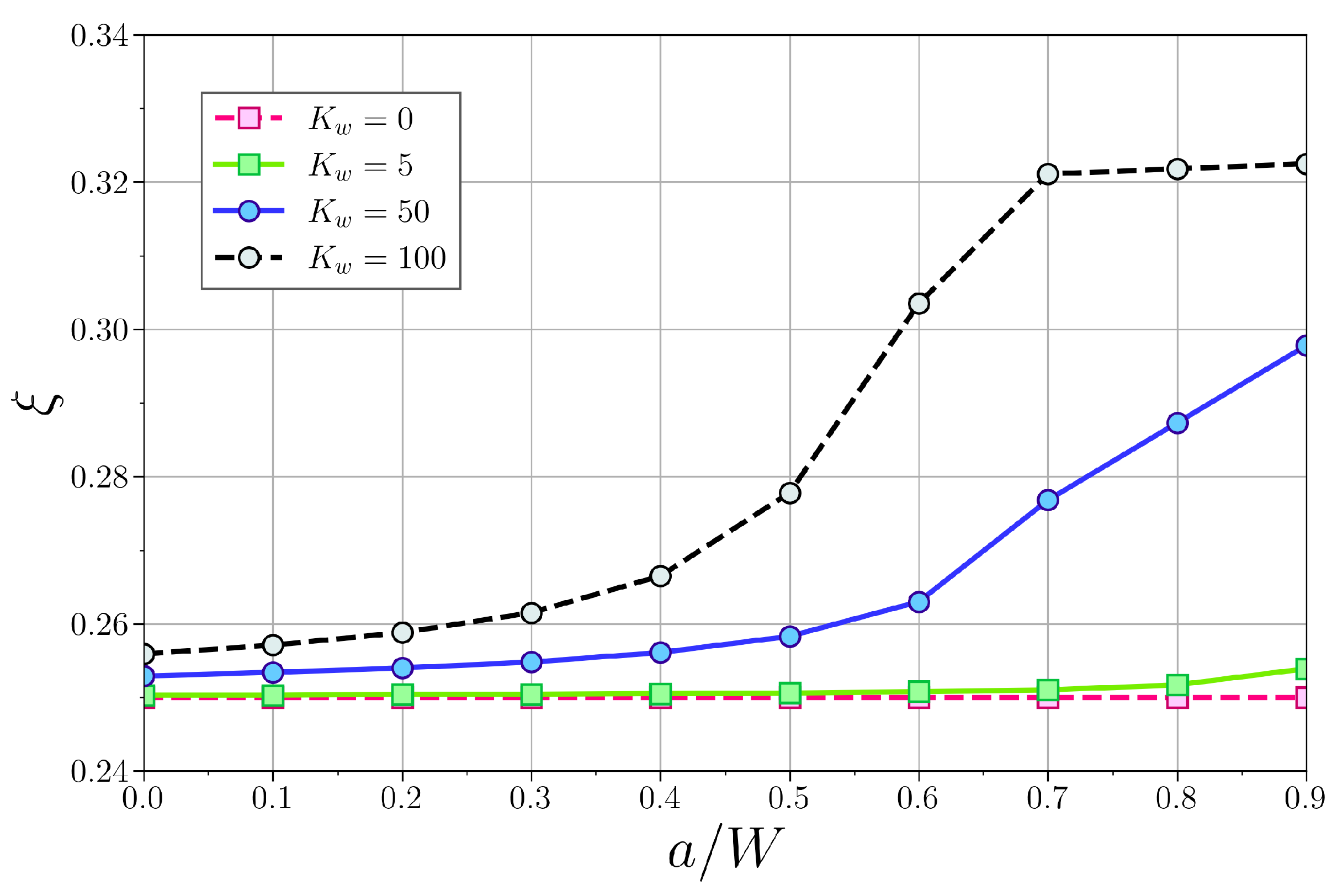
4.3. Combined Influence of the Crack and the Elastic Medium on the Buckling Load
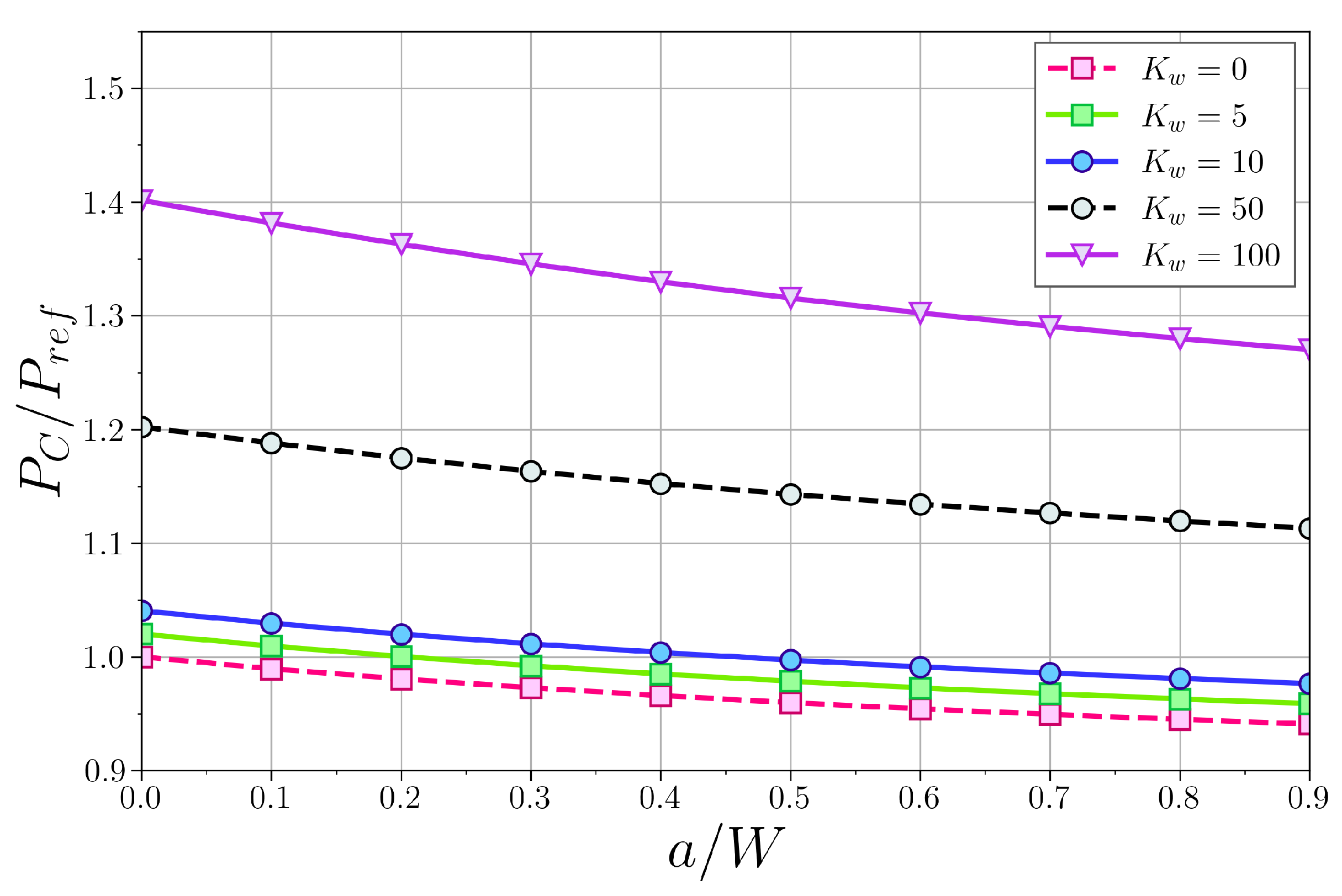
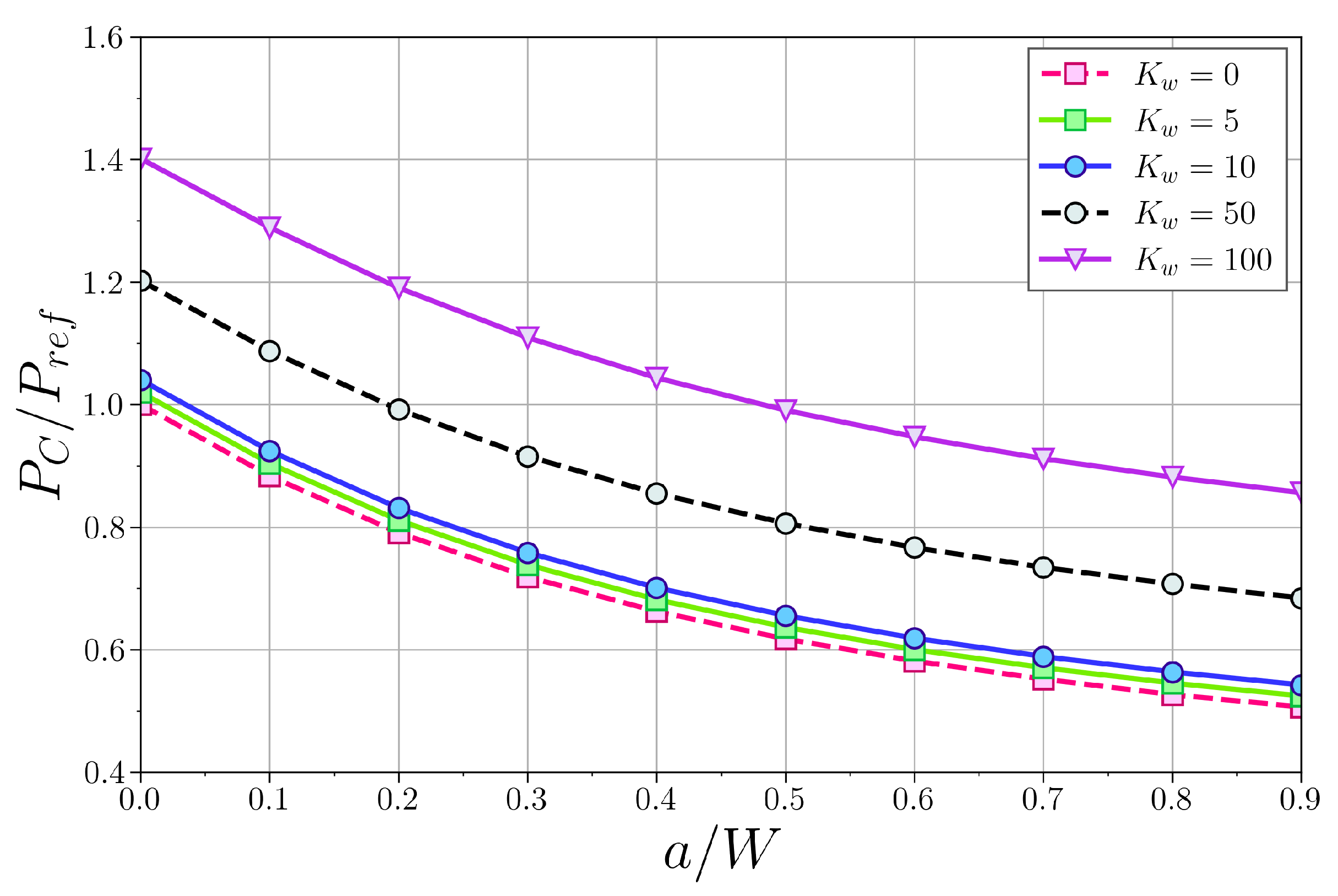
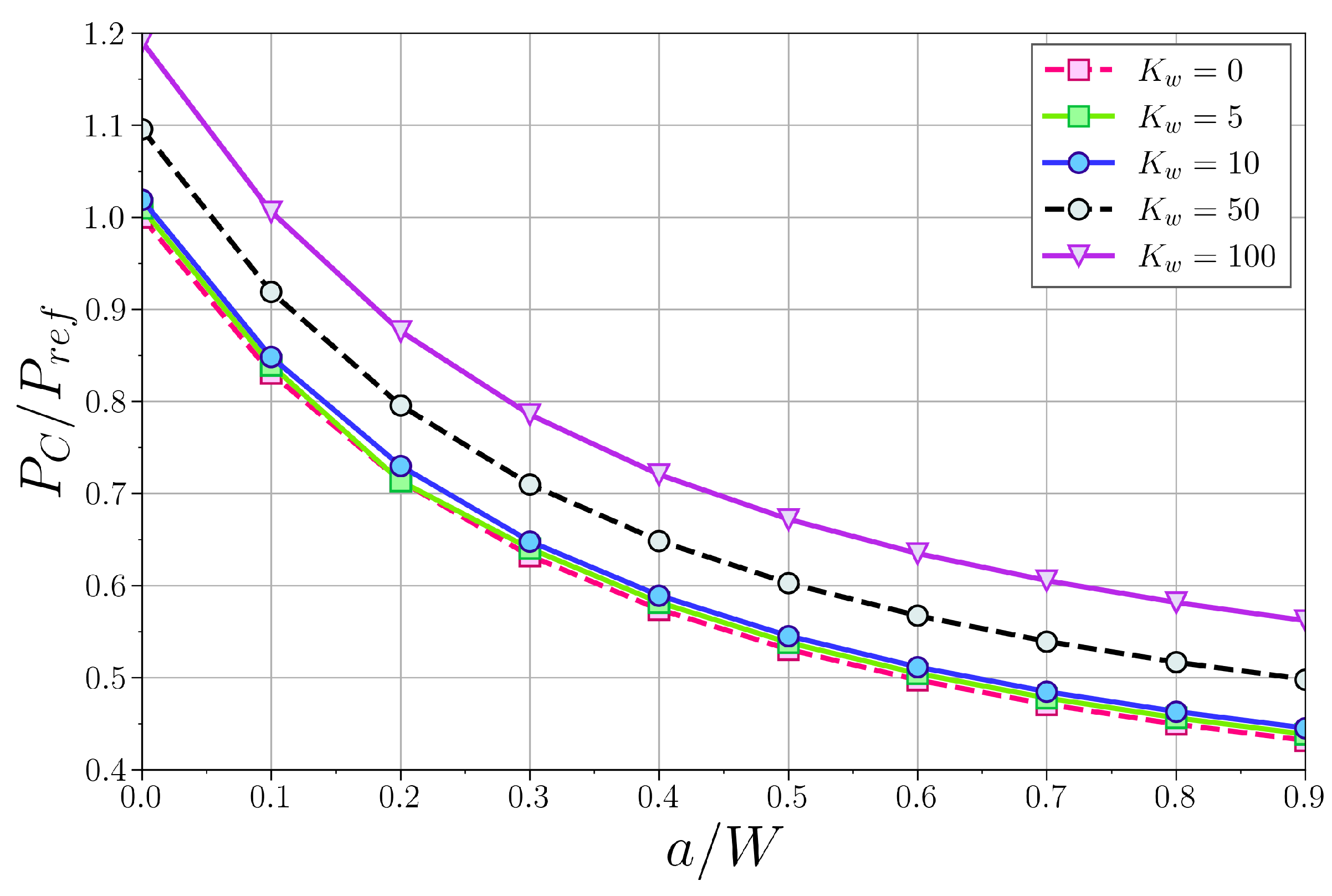
4.3.1. Simply Supported Column
4.3.2. Clamped–Supported Column
4.3.3. Clamped–Clamped Column
4.3.4. Cantilever Column
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Eisenberger, M.; Clastornik, J. Vibrations and buckling of a beam on Winkler elastic foundation. J. Sound Vib. 1987, 2, 233–241. [Google Scholar] [CrossRef]
- Stojanovic, V.; Kozic, P.; Janevski, G. Buckling instabilities of elastically connected Timoshenko beams on an elastic layer subjected to axial forces. J. Mech. Mat. Struc. 2012, 7, 363–374. [Google Scholar] [CrossRef][Green Version]
- Aristizabal-Ochoa, J.D. Stability of slender columns on an elastic foundation with generalised end conditions. Ing. Investig. 2013, 33, 34–40. [Google Scholar] [CrossRef]
- Hassan, M.H.; Hadima, S.A. Analysis of nonuniform beams on elastic foundations using recursive differentiation method. Eng. Mech. 2015, 22, 83–94. [Google Scholar]
- Anghel, V.; Mares, C. Integral formulation for stability and vibration analysis of beams on elastic foundation. Proc. Rom. Acad. Ser. A 2019, 20, 285–293. [Google Scholar]
- Ike, C.C. Stodola-Vianello method for the buckling load analysis of Euler–Bernoulli beam on Winkler foundation. UNIZIK J. Eng. Appl. Sci. 2023, 23, 250–259. [Google Scholar]
- Soltani, M. Finite element modeling for buckling analysis of tapered axially functionally graded Timoshenko beam on elastic foundation. Mech. Adv. Compos. Struct. 2020, 7, 203–218. [Google Scholar]
- Mohammed, A.T.; Hareb, M.A.; Eqal, A.K. Investigation on the analysis of bending and buckling for FGM Euler–Bernoulli beam resting on Winkler-Pasternak elastic foundation. J. Phys. Conf. Ser. 2020, 1773, 012027. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Nguyen, T.N.; Nguyen, T.K.; Vo, T.P. A Legendre-Ritz solution for bending, buckling and free vibration behaviours of porous beams resting on the elastic foundation. Structures 2023, 50, 1934–1950. [Google Scholar] [CrossRef]
- Mellal, F.; Bennai, R.; Avcar, M.; Nebab, M.; Atmane, H.A. On the vibration and buckling behaviors of porous FG beams resting on variable elastic foundation utilizing higher-order shear deformation theory. Acta Mech. 2023, 234, 3955–3977. [Google Scholar] [CrossRef]
- Xu, C.; Li, Y.; Dai, Z. Investigation on buckling of Timoshenko nanobeams resting on Winkler–Pasternak foundations in a non-uniform thermal environment via stress-driven nonlocal elasticity and nonlocal heat conduction. J. Therm. Stress 2023, 46, 317–332. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wang, C.M.; Aung, T.M. Buckling of a weakened column. J. Eng. Mech. 2004, 130, 1373–1376. [Google Scholar] [CrossRef]
- Biondi, B.; Cademi, S. Closed form solutions of Euler–Bernoulli beams with singularities. Int. J. Solids Struct. 2005, 42, 3027–3044. [Google Scholar] [CrossRef]
- Biondi, B.; Cademi, S. Euler–Bernoulli beams with multiple singularities in the flexural stiffness. Eur. J. Mech. A/Solids 2007, 26, 789–809. [Google Scholar] [CrossRef]
- Caddemi, S.; Caliò, I. Exact solution of the multi-cracked Euler–Bernoulli column. Int. J. Solids Struct. 2008, 45, 1332–1351. [Google Scholar] [CrossRef]
- Loya, J.A.; Vadillo, G.; Fernández-Sáez, J. First-order solutions for the buckling loads of Euler–Bernoulli weakened columns. J. Eng. Mech. 2010, 136, 674–679. [Google Scholar] [CrossRef]
- Saimi, A.; Bensaid, I.; Fellah, A. Effect of crack presence on the dynamic and buckling responses of bidirectional functionally graded beams based on quasi-3D beam model and differential quadrature finite element method. Arch. Appl. Mech. 2023, 93, 3131–3151. [Google Scholar] [CrossRef]
- Darban, H.; Luciano, R.; Darban, R. Buckling of cracked micro- and nanocantilevers. Acta Mech. 2023, 234, 693–704. [Google Scholar] [CrossRef]
- Loya, J.A.; Aranda-Ruiz, J.; Zaera, R. Natural frequencies of vibration in cracked Timoshenko beams within an elastic medium. Theor. Appl. Frac. Mech. 2022, 118, 103257. [Google Scholar] [CrossRef]
- Karnovsky, I.A.; Lebed, O. Advanced Methods of Structural Analysis; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Freund, L.B.; Herrmann, G. Dynamic fracture of a beam or plate in plane bending. Trans. ASME J. Appl. Mech. 1976, 43, 112–116. [Google Scholar] [CrossRef]
- Adams, R.; Cawley, P.; Pye, C.; Stone, B. A vibration technique for non-destructive assessing the integrity of structures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1978, 20, 93–100. [Google Scholar]
- Morassi, A. Crack-induced changes in eigenfrequencies of beam structures. J. Eng. Mech. 1993, 119, 1798–1803. [Google Scholar] [CrossRef]
- Narkis, Y. Identification of crack location in vibrating simply supported beams. J. Sound Vib. 1994, 172, 549–558. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Rubio, L.; Navarro, C. Approximate calculation of the fundamental frequency for bending vibrations of cracked beams. J. Sound Vib. 1999, 225, 345–352. [Google Scholar] [CrossRef]
- Krawczuk, M.; Palacz, M.; Ostachowicz, W. The dynamic analysis of cracked Timoshenko beams by spectral element. J. Sound Vib. 2003, 264, 1139–1153. [Google Scholar] [CrossRef]
- Loya, J.A.; Rubio, L.; Fernández-Sáez, J. Natural frequencies for bending vibrations of Timoshenko cracked beams. J. Sound Vib. 2006, 290, 640–653. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.; Irwin, G. The Stress Analysis of Cracks Handbook; Paris Productions: St. Louis, MI, USA, 1985. [Google Scholar]
- Jančo, R. Numerical and Exact Solution of Buckling Load For Beam on Elastic Foundation. Trans. VŠB Tech. Univ. Ostrav. Mech. Ser. 2013, 59, 21–26. [Google Scholar] [CrossRef] [PubMed]




| Type of Support | Restrictions |
|---|---|
| Simple support | |
| Fixed support | |
| Free end |
| [N] | |||||
|---|---|---|---|---|---|
| 0 | 5 | 10 | 50 | 100 | |
| Theoretical [29] | 1644.94 | 1729.36 | 1814.82 | 2489.28 | 3334.65 |
| Proposed | 1644.94 | 1729.44 | 1813.94 | 2489.95 | 3334.97 |
| Error [%] | 0 | 0 | 0.01 | 0.03 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loya, J.A.; Santiuste, C.; Aranda-Ruiz, J.; Zaera, R. Buckling of Cracked Euler–Bernoulli Columns Embedded in a Winkler Elastic Medium. Math. Comput. Appl. 2023, 28, 87. https://doi.org/10.3390/mca28040087
Loya JA, Santiuste C, Aranda-Ruiz J, Zaera R. Buckling of Cracked Euler–Bernoulli Columns Embedded in a Winkler Elastic Medium. Mathematical and Computational Applications. 2023; 28(4):87. https://doi.org/10.3390/mca28040087
Chicago/Turabian StyleLoya, José Antonio, Carlos Santiuste, Josué Aranda-Ruiz, and Ramón Zaera. 2023. "Buckling of Cracked Euler–Bernoulli Columns Embedded in a Winkler Elastic Medium" Mathematical and Computational Applications 28, no. 4: 87. https://doi.org/10.3390/mca28040087
APA StyleLoya, J. A., Santiuste, C., Aranda-Ruiz, J., & Zaera, R. (2023). Buckling of Cracked Euler–Bernoulli Columns Embedded in a Winkler Elastic Medium. Mathematical and Computational Applications, 28(4), 87. https://doi.org/10.3390/mca28040087







