A Quantile Functions-Based Investigation on the Characteristics of Southern African Solar Irradiation Data
Abstract
1. Introduction
1.1. Rationale of the Study
1.2. Contribution of the Study
1.3. Review of Literature
2. Materials and Methods
2.1. Quantile Functions
- the uniform transformation rule applies and
- ordered Ur leads to the corresponding ordered Xr such that
- If X has a quantile distribution, R(p), on the positive axis, 0 ≤ x < 1, then the distribution −R(1 − p) is the quantile distribution that is its reflection in the axis at x = 0, called the reflected distribution on −1 < x ≤ 0.
- The reciprocal 1/X has the reciprocal distribution 1/R(1 − p) also on 0 ≤ x < 1.
2.2. Method of Percentiles
2.3. Parameter Estimation
2.4. Model Validation
2.4.1. Graphical Analysis
2.4.2. Chi-Square Goodness of Fit Test
3. Results and Discussions
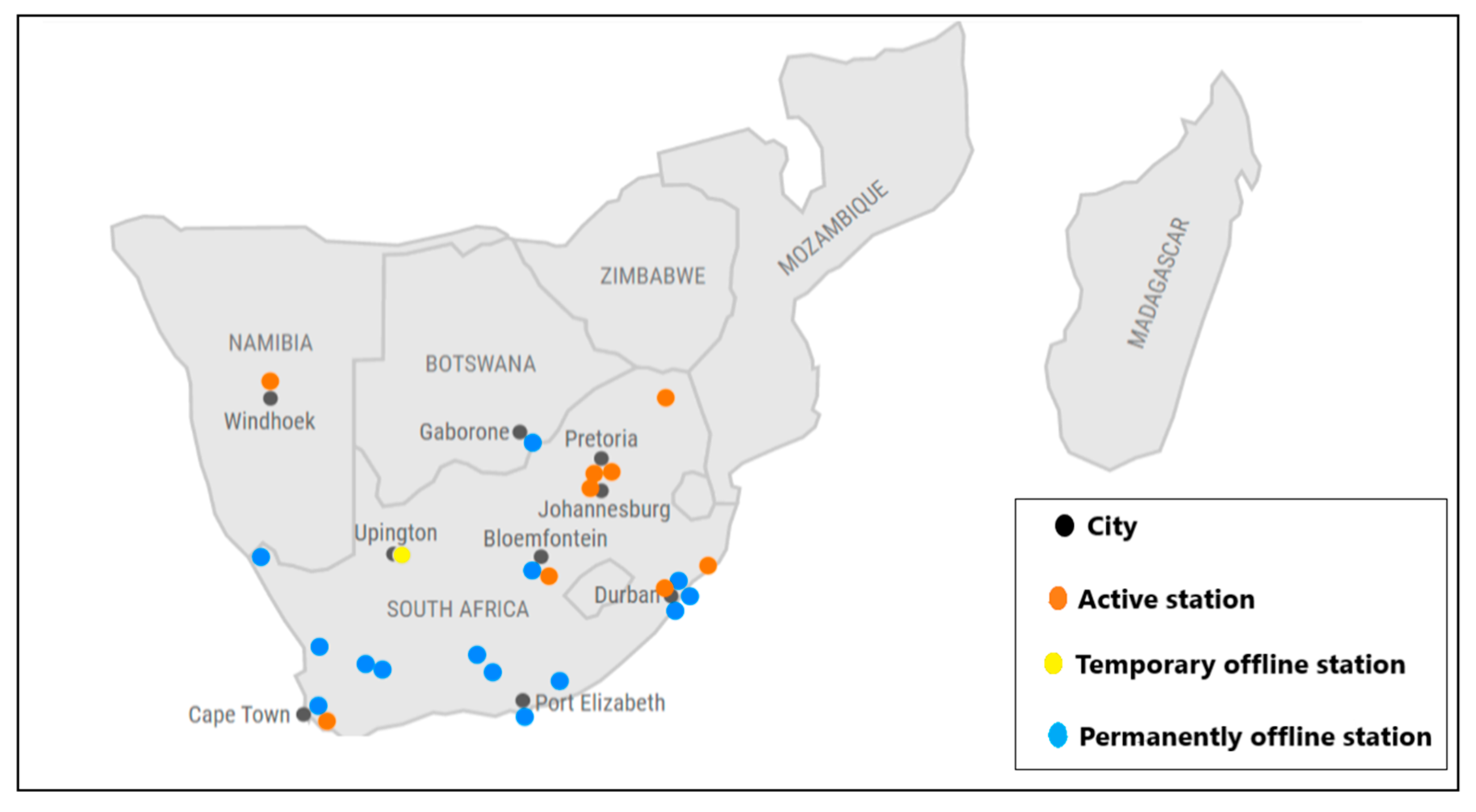
3.1. Ground-Based Data
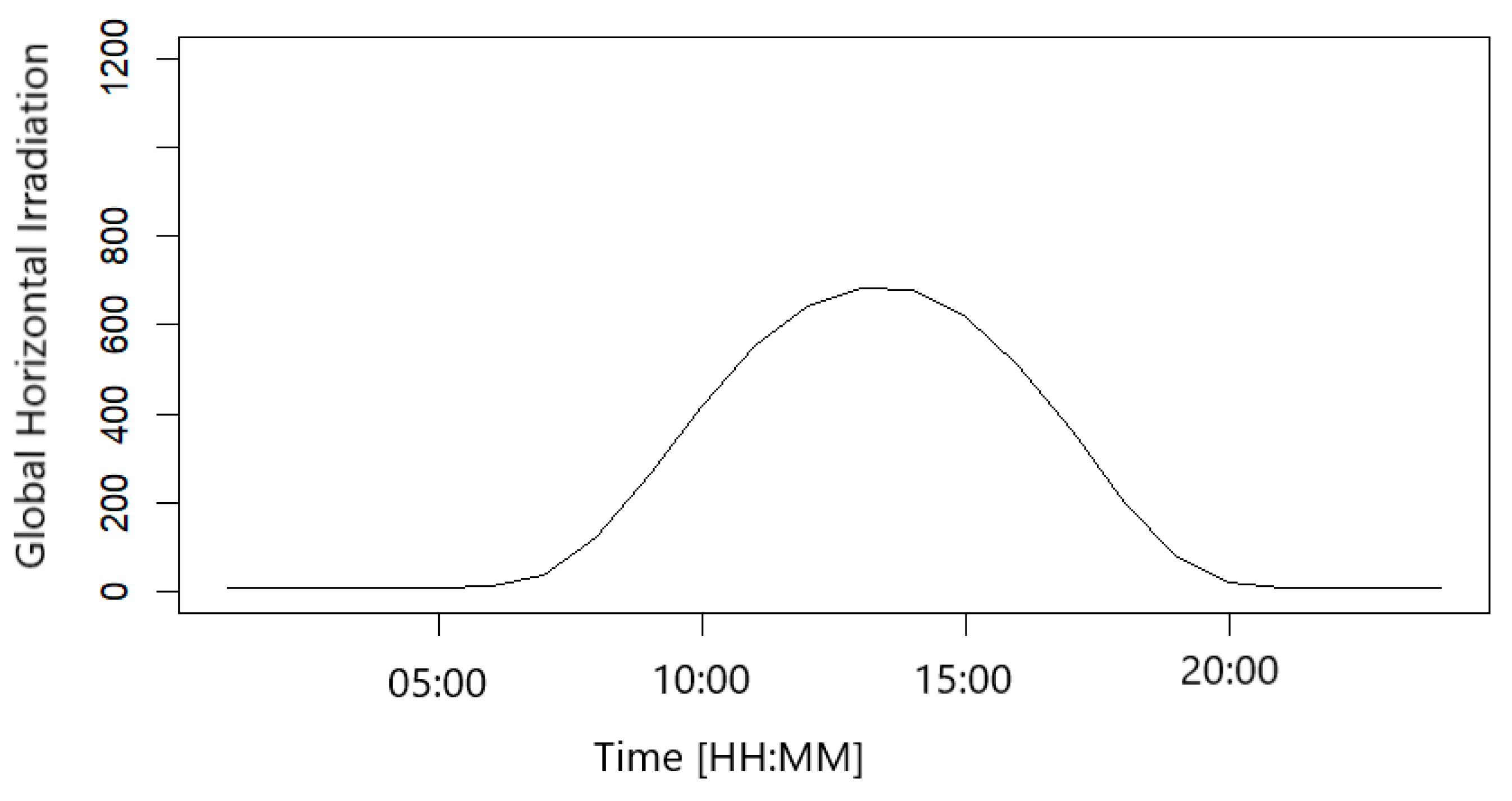
3.2. Hourly Solar Irradiance Distributional Modelling
- ysunrise = ysunset = 0.
- ysunrise−1hr = ysunset+1hr = 0.
3.2.1. Venda and Gaborone Hourly Quantile Profiles
3.2.2. Durban, Pretoria, Cape Town and Windhoek Hourly Quantile Profiles
3.2.3. Hourly Population Means
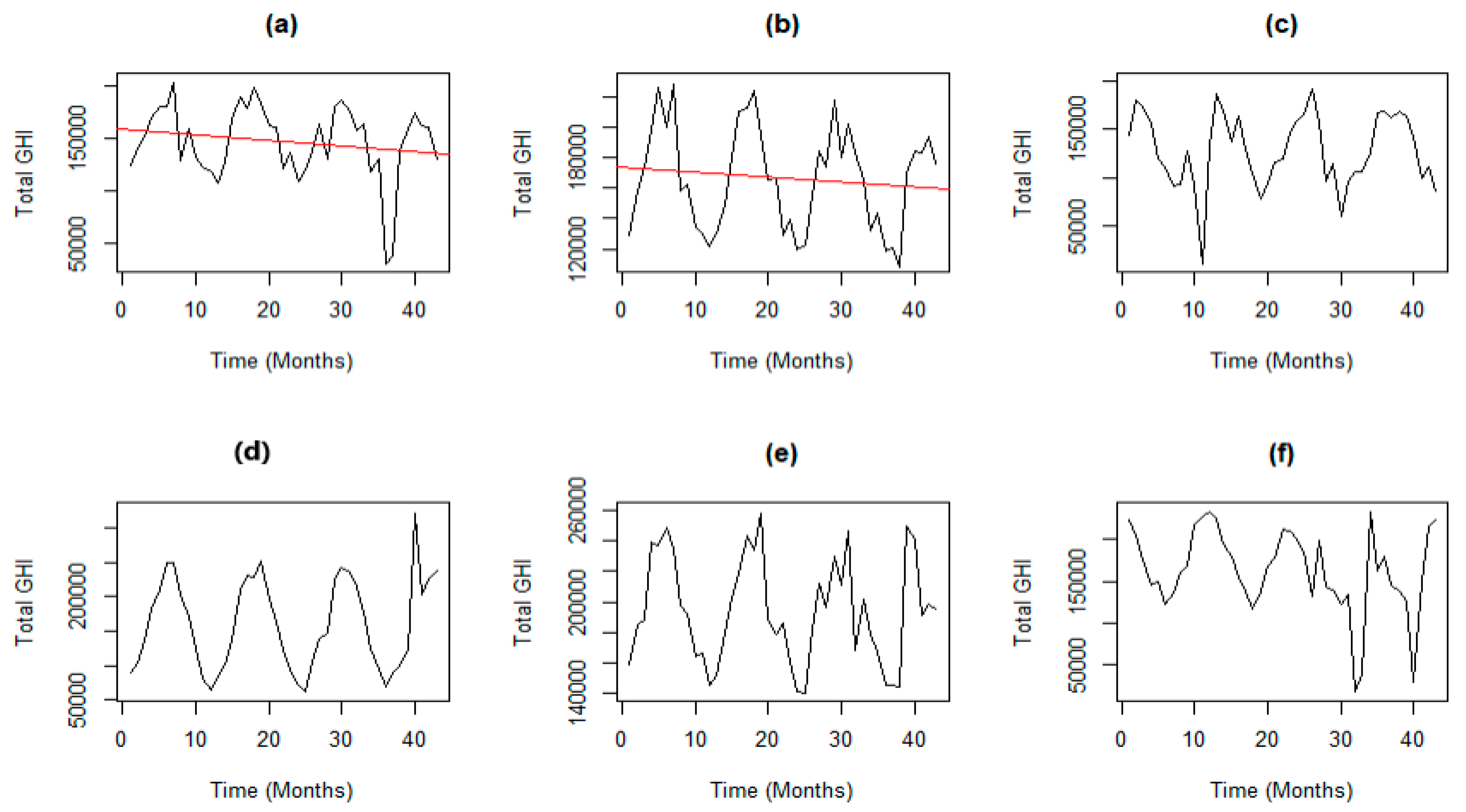
3.3. Daily Total SI Distributional Modelling
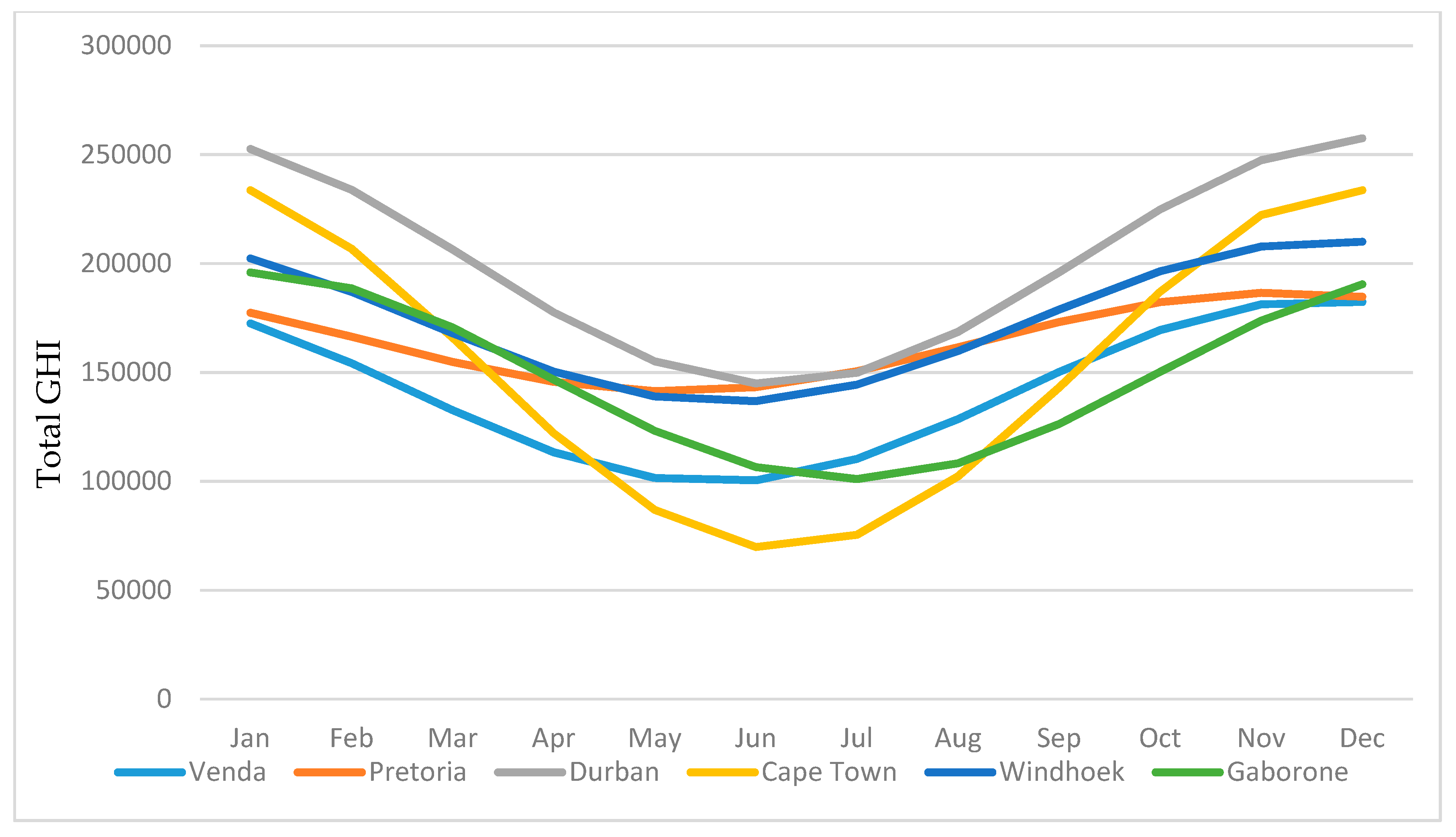
3.4. Monthly Total SI Distribution Modelling
3.5. Model Validations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Fitted Probability Distributions on Modelling Residuals from Trigonometric Regression of the Hourly Profiles

Appendix A.2. Hourly Profile QDFM Validation Plots

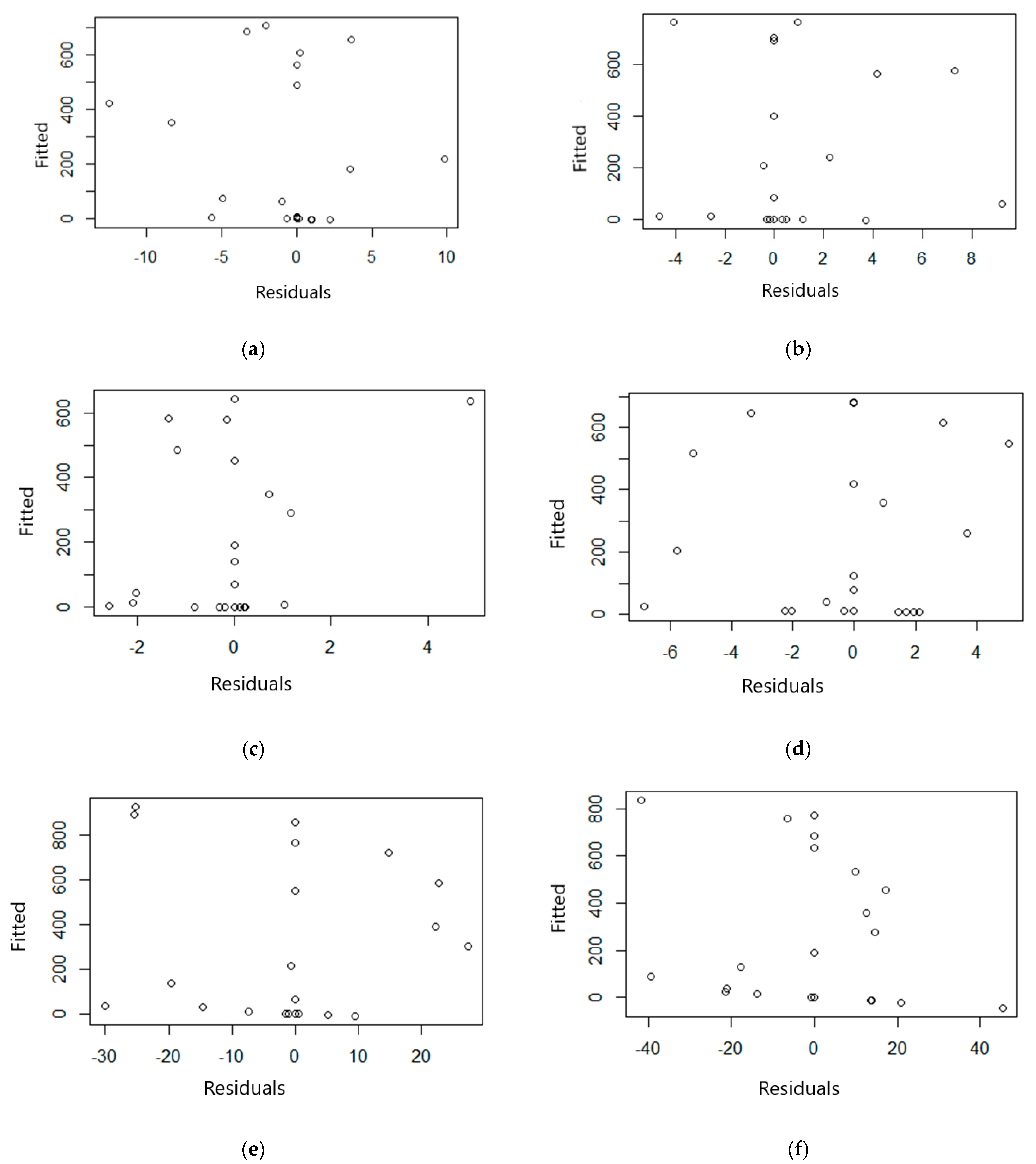
Appendix B
Appendix B.1. Fitted Probability Distributions on Modelling Residuals from Trigonometric Regression of Monthly Totals
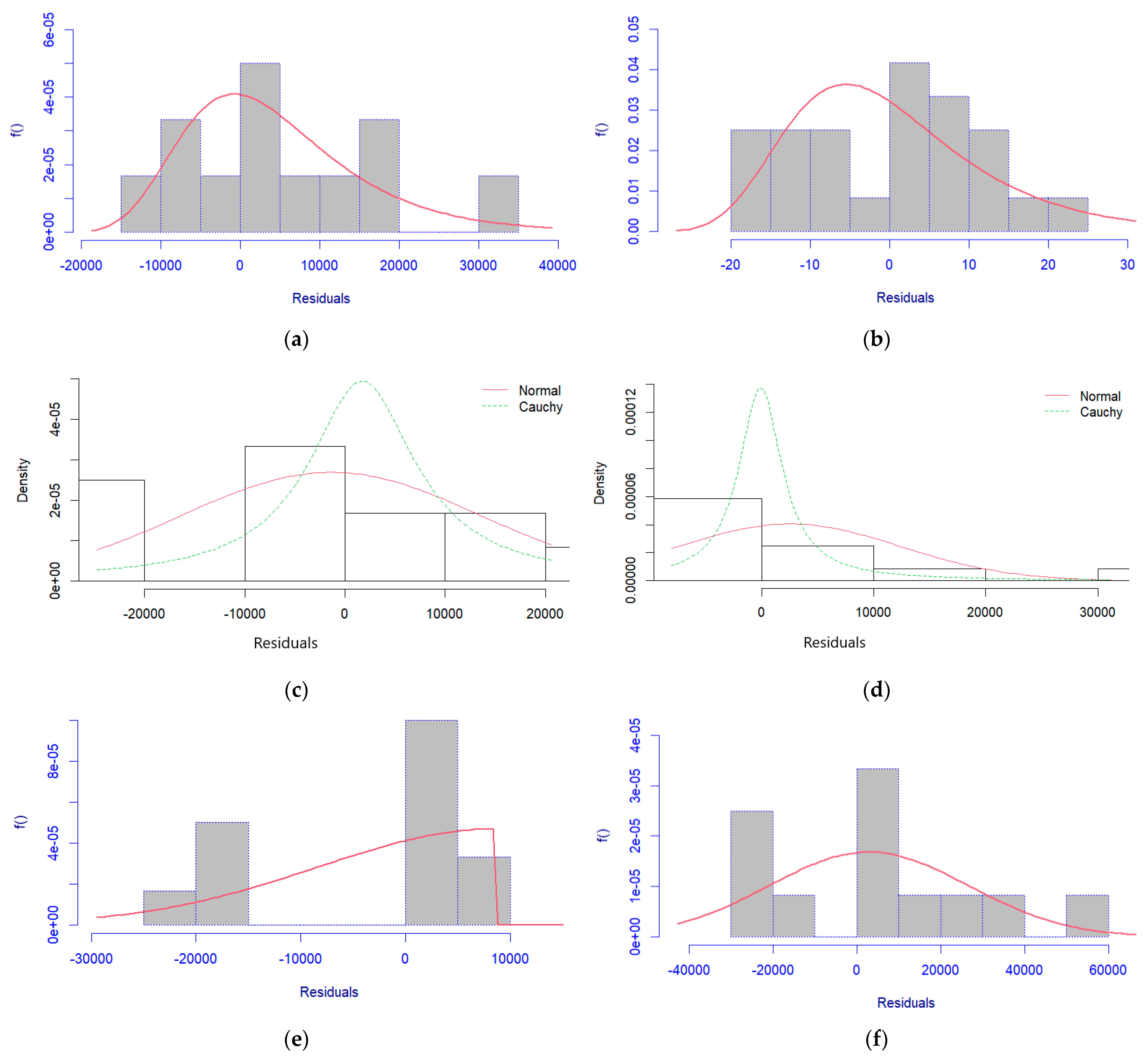
Appendix B.2. Monthly Total Profile QDFMS Validation Plots

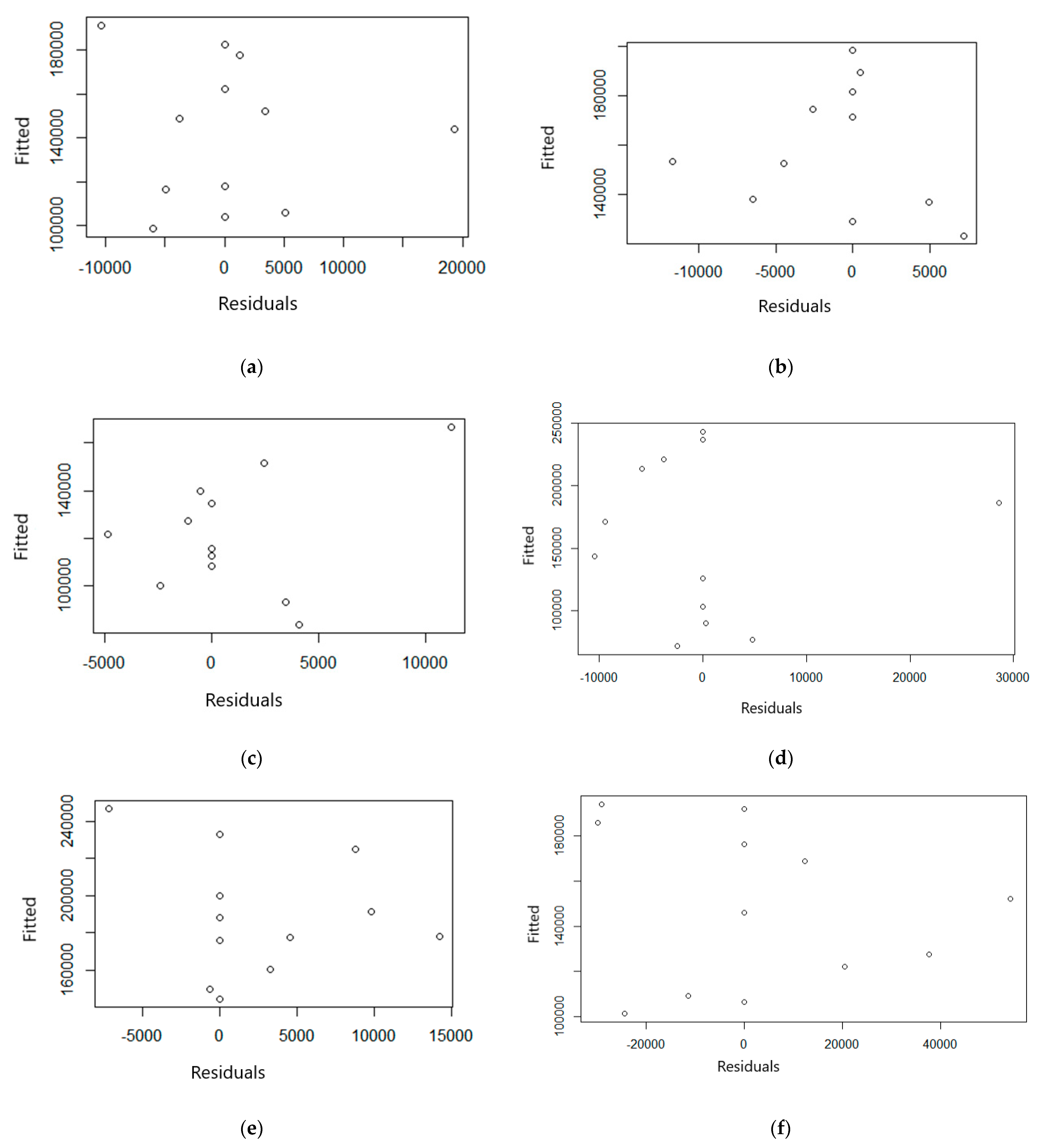
References
- Parzen, E. Quantile probability and statistical modelling. Stat. Sci. 2004, 19, 652–662. [Google Scholar] [CrossRef]
- Gilchrist, W.G. Regression Revisited. Int. Stat. Rev. 2008, 76, 401–439. [Google Scholar] [CrossRef]
- Yang, D. A universal benchmarking method for probabilistic solar irradiance forecasting. Sol. Energy 2019, 184, 410–416. [Google Scholar] [CrossRef]
- Jain, P.K.; Lungu, E.M.; Prakash, J. Stochastic characteristics of solar irradiation—Extremum temperatures processes. In Proceedings of the World Renewable Energy Congress VII (WREC 2002), Cologne, Germany, 29 June–5 July 2002. [Google Scholar]
- Jain, P.K.; Prakash, J.; Lungu, E.M. Correlation between temperature and solar irradiation in Botswana: Bivariate model. In Proceedings of the 2nd IASTED Africa Conference Modelling and Simulation (Africa MS 2008), Gaborone, Botswana, 8–10 September 2008. [Google Scholar]
- Salima, G.; Chavuka, G.M.S. Determining Angstrom constants for estimating solar radiation in Malawi. Int. J. Geosci. 2012, 3, 391–397. [Google Scholar] [CrossRef]
- Sivhugwana, K.S.; Ranganai, E. Intelligent techniques, harmonically coupled and SARIMA models in forecasting solar radiation data: A hybridisation approach. J. Energy South. Afr. 2020, 31, 14–37. [Google Scholar] [CrossRef]
- Mutavhatsindi, T.; Sigauke, C.; Mbuvha, R. Forecasting Hourly Global Horizontal Solar Irradiance in South Africa. IEEE Access 2020, 8, 19887. [Google Scholar] [CrossRef]
- Jain, P.K.; Lungu, E.M. Stochastic models for sunshine duration and solar irradiation. Renew. Energy 2002, 27, 197–209. [Google Scholar] [CrossRef]
- Jain, P.K.; Prakash, J.; Lungu, E.M. Climate characteristics of Botswana. In Proceedings of the Sixth IASTED International Conference, Gaborone, Botswana, 11–13 September 2006. [Google Scholar]
- Madhlopa, A. Study of diurnal production of distilled water by using solar irradiation distribution about solar noon. In Proceedings of the EuroSun 2006 Conference, Glasgow, Scotland, 27–30 June 2006. [Google Scholar]
- Madhlopa, A. Solar radiation climate in Malawi. Sol. Energy 2006, 80, 1055–1057. [Google Scholar] [CrossRef]
- Jain, P.K.; Lungu, E.M.; Prakash, J. Bivariate models: Relationships between solar irradiation and either sunshine or extremum temperatures. Renew. Energy 2003, 28, 1211–1223. [Google Scholar] [CrossRef]
- Govender, P.; Brooks, M.J.; Mathews, A.P. Cluster analysis for classification and forecasting of solar irradiance in Durban, South Africa. J. Energy South. Afr. 2018, 29, 1–6. [Google Scholar] [CrossRef]
- Bessafi, M.; Delage, O.; Jeanty, P.; Heintz, A.; Cazal, J.-D.; Delsaut, M.; Gangat, Y.; Partal, L.; Lan-Sun-Luk, J.-D.; Chabriat, J.-P.; et al. Research collaboration in solar radiometry between the University of Reunion Island and the University of Kwazulu-Natal. In Proceedings of the Third Southern African Solar Energy Conference, Mpumalanga, South Africa, 11–13 May 2015. [Google Scholar]
- Mpfumali, P.; Sigauke, C.; Bere, A.; Mlaudzi, S. Day Ahead Hourly Global Horizontal Irradiance Forecasting-Application to South African Data. Energies 2019, 12, 3569. [Google Scholar] [CrossRef]
- Ranganai, E.; Sigauke, C. Capturing Long-Range Dependence and Harmonic Phenomena in 24-Hour Solar Irradiance Forecasting. IEEE Access 2020, 8, 172204–172218. [Google Scholar] [CrossRef]
- Ratshilengo, M.; Sigauke, C.; Bere, A. Short-Term Solar Power Forecasting Using Genetic Algorithms: An Application Using South African Data. Appl. Sci. 2021, 11, 4214. [Google Scholar] [CrossRef]
- Chandiwana, E.; Sigauke, C.; Bere, A. Twenty-four-hour ahead probabilistic global horizontal irradiation forecasting using Gaussian process regression. Algorithms 2021, 14, 177. [Google Scholar] [CrossRef]
- Conde-Amboage, M.; Gonzalez-Manteiga, W.; Sanchez-Sellero, C. Quantile regression: Estimation and lack-of-fit tests. Bol. De Estad. E Investig. Oper. 2018, 34, 97–116. [Google Scholar]
- Gilchrist, W.G. Statistical Modelling with Quantile Functions; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Karian, Z.A.; Dudewicz, E.J. Handbook of Fitting Statistical Distributions with R.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Boland, J. Time series modelling of solar radiation. In Modelling Solar Radiation at the Earth’s Surface: Recent Advances; Badescu, V., Ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2008; Chapter 11; pp. 283–312. [Google Scholar]
- Delignette-Muller, M.-L.; Dutang, C.; Pouillot, R.; Denis, J.-B.; Siberchicot, A. Package ‘fitdistrplus’. J. Stat. Softw. 2015, 24, 1–14. [Google Scholar]
- Stasinopoulos, D.M.; Rigby, A. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 2007, 23, 507–554. [Google Scholar] [CrossRef]
- Richards, W.A.; Antoine, R.; Sahai, A.; Acharya, M.R. An Efficient Polynomial Approximation to the Normal Distribution Function and Its Inverse Function. J. Math. Res. 2010, 2, 47–51. [Google Scholar] [CrossRef]
- Aludaat, K.M.; Alodat, M.T. A note on approximating the normal distribution function. Appl. Math. Sci. 2008, 2, 425–429. [Google Scholar]
- Soranzo, A.; Epure, E. Very Simply Explicitly Invertible Approximations of Normal Cumulative and Normal Quantile Function. Appl. Math. Sci. 2014, 8, 4323–4341. [Google Scholar] [CrossRef]
- Lipoth, J.; Tereda, Y.; Papalexiou, S.N.; Spiteri, R.J. A new very simply explicitly invertible approximation for the standard normal cumulative distribution function. AIMS Math. 2022, 7, 11635–11646. [Google Scholar] [CrossRef]
- Yan, K.; Shen, H.; Wang, L.; Zhou, H.; Xu, M.; Mo, Y. Short-Term Solar Irradiance Forecasting Based on a Hybrid Deep Learning Methodology. Information 2020, 11, 32. [Google Scholar] [CrossRef]
- Crowley, T.J. Causes of Climate Change Over the Past 1000 Years. Science 2000, 289, 270–277. [Google Scholar] [CrossRef]
- Argueso, D.; Evans, J.P.; Fita, L.; Kathryn, J. Temperature response to future urbanization and climate change. Clim. Dyn. 2014, 42, 2183–2199. [Google Scholar] [CrossRef]
- Chapman, S.; Watson, J.E.M.; Salazar, A.; Thatcher, M.; McAlpine, C.A. The impact of urbanization and climate change on urban temperatures: A systematic review. Landsc. Ecol. 2017, 32, 1921–1935. [Google Scholar] [CrossRef]
- Paulescu, M.; Tulcan-Paulescu, E.; Sudhansu, S.S. A temperature-based model for global solar irradiance and its application to estimate daily irradiation values. Int. J. Energy Res. 2011, 35, 520–529. [Google Scholar] [CrossRef]
- Mohanty, S.; Patra, P.K.; Sahoo, S.S. Prediction of global solar radiation using nonlinear autoregressive network with exogenous inputs (narx). In Proceedings of the 2015 39th National Systems Conference (NSC), IEEE, Greater Noida, India, 14–16 December 2015. [Google Scholar]
- Grantham, A.; Gel, Y.R.; Boland, J. Nonparametric short-term probabilistic forecasting for solar radiation. Sol. Energy 2016, 133, 465–475. [Google Scholar] [CrossRef]
- Boland, J. Characterising seasonality of solar radiation and solar farm output. Energies 2020, 13, 471. [Google Scholar] [CrossRef]
| Name of Plot | y | Against | Comment |
|---|---|---|---|
| Fit observation | x(r) | Q’(pr) | Points to exhibit an approximately linear pattern |
| Distributional plots | fr = x(r) − Q’(pr) | Q’(pr) | Points to be randomly distributed |
| Station | Latitude | Longitude | Location | Period |
|---|---|---|---|---|
| University of Venda (UV) | −23.13100052 | 30.42399979 | Venda | April 2015–April 2022 |
| University of Pretoria (UP) | −25.75308037 | 28.22859001 | Pretoria | July 2017–June 2021 |
| University of KwaZulu-Natal Howard College (UKZNH) | −29.87097931 | 30.97694969 | Durban | December 2015–September 2022 |
| Stellenbosch University (SUN) | −33.92810059 | 18.86540031 | Cape Town | July 2017–June 2021 |
| Namibian University of Science and Technology (NUST) | −22.56500053 | 17.07500076 | Windhoek | July 2017–June 2021 |
| University of Gaborone (UG) | −24.6609993 | 25.93400002 | Gaborone | January 2015–November 2020 |
| Location | Shape | Scale | Skewness |
|---|---|---|---|
| Venda | 22.676906 | −2.308079 | −5.612271 |
| Gaborone | 23.233404 | 2.127659 | −1.204687 |
| Location | ||||||||
|---|---|---|---|---|---|---|---|---|
| Venda | 143.24 | −327.52 | −55.60 | 148.90 | 57.37 | −17.33 | 18.81 | 2.02 |
| Gaborone | 422.36 | −372.09 | −92.34 | 163.73 | 71.42 | −16.13 | −6.71 | −8.17 |
| Location | Metric | Normal | Cauchy |
|---|---|---|---|
| Durban | AIC | 187.4920 | 199.3287 |
| BIC | 189.8481 | 201.6848 | |
| Cape Town | AIC | 196.7216 | 211.7815 |
| BIC | 199.077 | 214.1376 | |
| Windhoek | AIC | 218.9350 | 222.8473 |
| BIC | 221.2911 | 225.2034 |
| Location | ||||||||
|---|---|---|---|---|---|---|---|---|
| Durban | 186.88 | −300.05 | −27.46 | 145.53 | 28.01 | −26.56 | −11.13 | 1.089 |
| Cape Town | 220.88 | −309.44 | −111.00 | 110.03 | 91.52 | −6.93 | −11.83 | 1.034 |
| Windhoek | 267.82 | −400.60 | −137.34 | 159.85 | 114.20 | −27.07 | −29.39 | 3676.63 |
| Pretoria | 247.62 | −362.25 | −54.47 | 163.33 | 51.28 | −23.25 | −10.66 | −312.92 |
| Location | 12:00 | 13:00 | 14:00 |
|---|---|---|---|
| Venda | 704.5501 | 724.3324 | 664.2824 |
| Pretoria | 792.3848 | 798.1858 | 720.3530 |
| Durban | 653.7334 | 646.0031 | 566.3265 |
| Cape Town | 647.2710 | 702.8115 | 690.4624 |
| Windhoek | 856.5969 | 927.0284 | 892.8881 |
| Gaborone | 789.5647 | 814.5785 | 756.4473 |
| Probability Distribution | Quantile Function |
|---|---|
| Normal | |
| Lognormal | Exp |
| Skewed Lambda | |
| Weibull | |
| Gumbel | |
| Reverse Gumbel | |
| Logistic | |
| Cauchy | |
| Weibull Type 3 |
| Month | Venda | Pretoria | Durban | Cape Town | Windhoek | Gaborone |
|---|---|---|---|---|---|---|
| January | 5808.48 | 6570.46 | 7419.84 | 8350.78 * | 7966.67 | 7045.33 |
| February | 5118.63 | 5796.38 | 5569.62 | 7339.92 * | 6655.05 | 6741.43 |
| March | 5328.46 | 5549.78 | 5727.71 | 5478.89 | 6969.69 * | 5847.43 |
| April | 4218.16 | 4563.87 | 3869.33 | 4241.18 | 5855.68 * | 5143.91 |
| May | 4189.18 | 4626.59 | 2832.39 | 3321.19 | 5183.17 * | 4593.42 |
| June | 4207.39 | 4002.05 | 3543.30 | 2380.00 | 4946.30 * | 4292.30 |
| July | 4463.09 | 4554.78 | 3146.75 | 3077.00 | 5109.11 * | 4522.42 |
| August | 4338.57 | 5237.01 | 4393.84 | 3331.33 | 10,342.86 * | 3966.38 |
| September | 5820.81 | 6381.69 | 4684.33 | 4937.00 | 10,678.41 * | 6310.75 |
| October | 5441.11 | 6508.65 | 5773.34 | 7396.06 * | 7342.81 | 6881.60 |
| November | 5992.28 | 7045.96 | 5197.02 | 7909.29 | 8022.61 * | 7370.91 |
| December | 5786.87 | 7165.13 | 7118.95 | 8392.25 | 8799.95 * | 6856.38 |
| Maximum | 5992.28 | 7165.13 | 7419.84 | 8350.78 | 10,678.41 | 7370.91 |
| Minimum | 4189.79 | 4002.05 | 2832.39 | 2379.96 | 4946.30 | 4292.30 |
| Location | With | Without |
|---|---|---|
| Venda | 266.7684 | 265.613 |
| Pretoria | 256.3586 | 255.4424 |
| Location | Metric | Normal | Cauchy |
|---|---|---|---|
| Cape Town | AIC | 187.4920 | 199.3287 |
| BIC | 189.8481 | 201.6848 | |
| Durban | AIC | 268.5895 | 271.3327 |
| BIC | 269.5593 | 272.3025 |
| Location | Probability Distribution | ||||||
|---|---|---|---|---|---|---|---|
| Venda | R. Gumbel | 1,678,882.00 | −8767.19 | 40,937.26 | 2013.06 | −768.98 | 9.11 |
| Pretoria | R. Gumbel | 3,692,969.00 | −9175.68 | 20,756.98 | 4163.51 | −852.62 | 8.72 |
| Windhoek | SN2 | −24,798,121 | −5434.35 | 36,610.50 | 2870.26 | 8700.05 | −0.69 |
| Location | Probability Distribution | ||||||
| Cape Town | Normal | 155,245.11 | 12,380.08 | 82,328.01 | −39.04 | −2.31 × 10−16 | 11.06526 |
| Durban | Normal | 197,409.84 | 3445.95 | 37,525.34 | 2536.12 | 2488.44 | 9834.54 |
| Gaborone | Normal | 148,521.33 | 22,150.61 | 41,991.97 | 2372.42 | 2863 | 23,670.46 |
| Location | Hourly QDFM | Monthly QDFM | ||
|---|---|---|---|---|
| HL | Runs test | HL | Runs test | |
| Venda | 1 | 0.09498 | 1 | 0.0154 |
| Pretoria | 1 | 1 | 1 | 0.2259 |
| Durban | 1 | 0.4038 | 1 | 0.5431 |
| Cape Town | 1 | 0.4038 | 1 | 0.2154 |
| Windhoek | 1 | 0.4038 | 1 | 0.2259 |
| Gaborone | 1 | 0.2105 | 1 | 0.0154 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maposa, D.; Masache, A.; Mdlongwa, P. A Quantile Functions-Based Investigation on the Characteristics of Southern African Solar Irradiation Data. Math. Comput. Appl. 2023, 28, 86. https://doi.org/10.3390/mca28040086
Maposa D, Masache A, Mdlongwa P. A Quantile Functions-Based Investigation on the Characteristics of Southern African Solar Irradiation Data. Mathematical and Computational Applications. 2023; 28(4):86. https://doi.org/10.3390/mca28040086
Chicago/Turabian StyleMaposa, Daniel, Amon Masache, and Precious Mdlongwa. 2023. "A Quantile Functions-Based Investigation on the Characteristics of Southern African Solar Irradiation Data" Mathematical and Computational Applications 28, no. 4: 86. https://doi.org/10.3390/mca28040086
APA StyleMaposa, D., Masache, A., & Mdlongwa, P. (2023). A Quantile Functions-Based Investigation on the Characteristics of Southern African Solar Irradiation Data. Mathematical and Computational Applications, 28(4), 86. https://doi.org/10.3390/mca28040086






