An Analysis of Numerical Homogenisation Methods Applied on Corrugated Paperboard
Abstract
1. Introduction
2. Materials and Methods
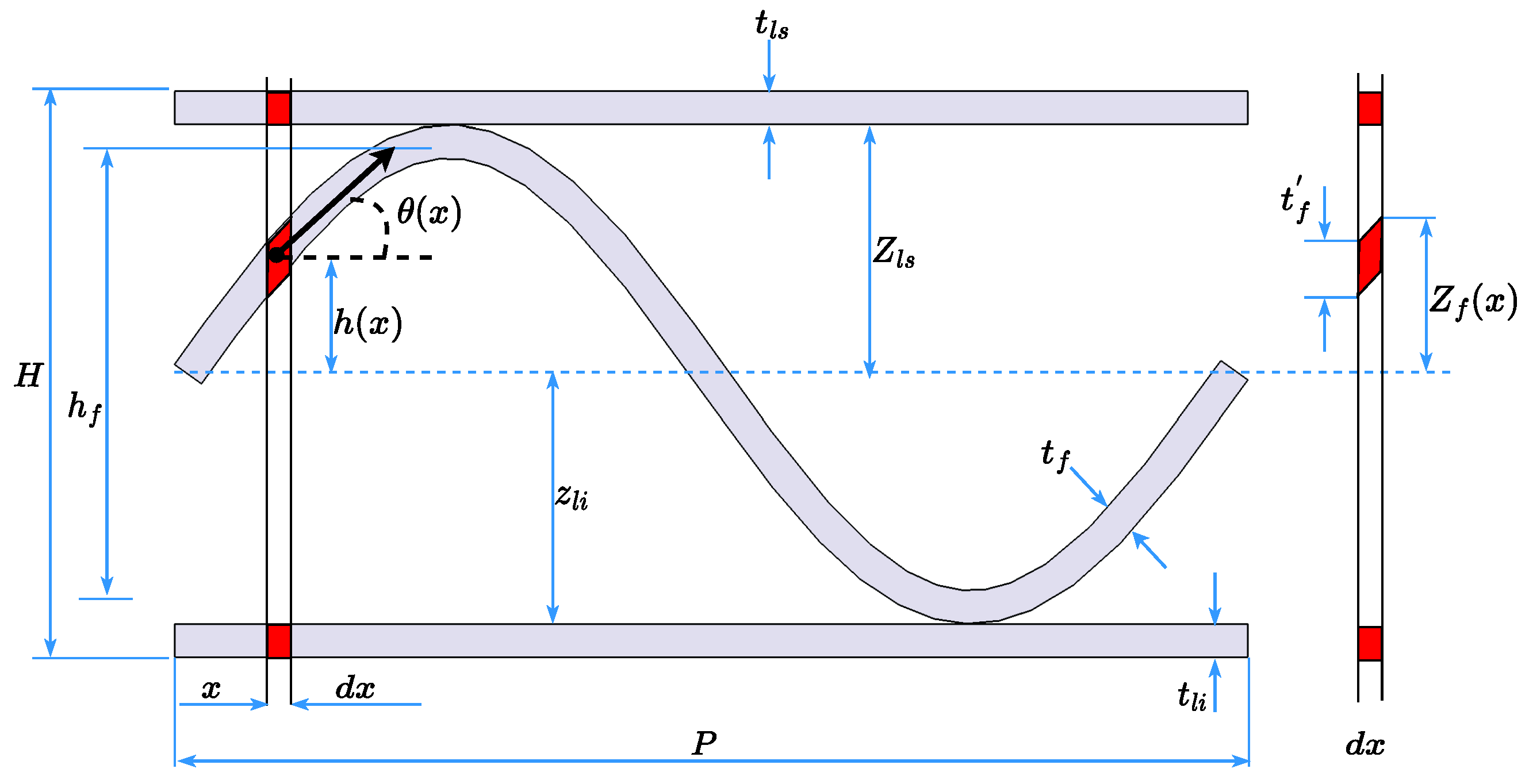
2.1. Homogenisation of Corrugated Paperboard
2.1.1. Classical Laminate Plate Theory
2.1.2. First-Order Shear Deformation Theory
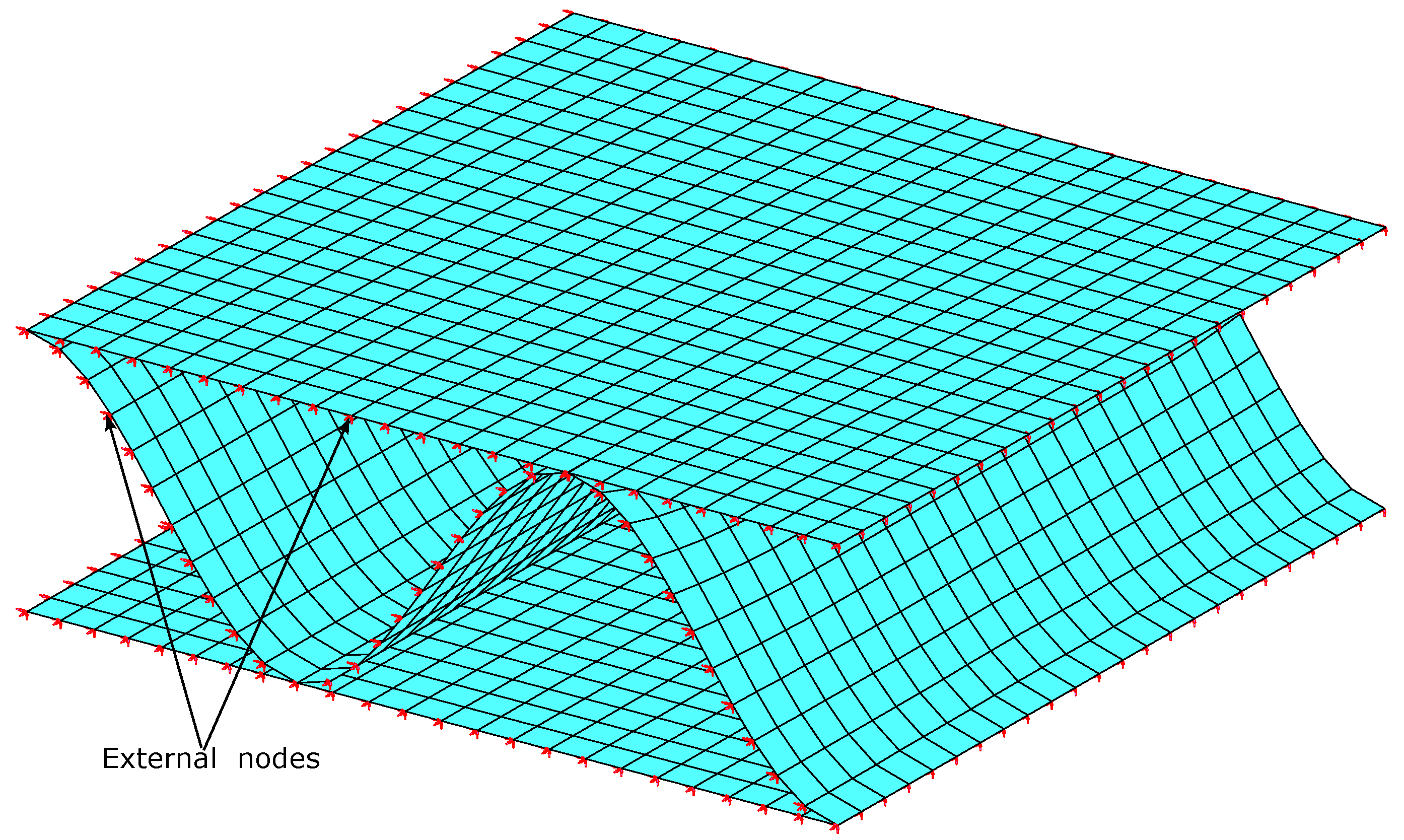
2.1.3. Deformation Energy-Equivalence Method
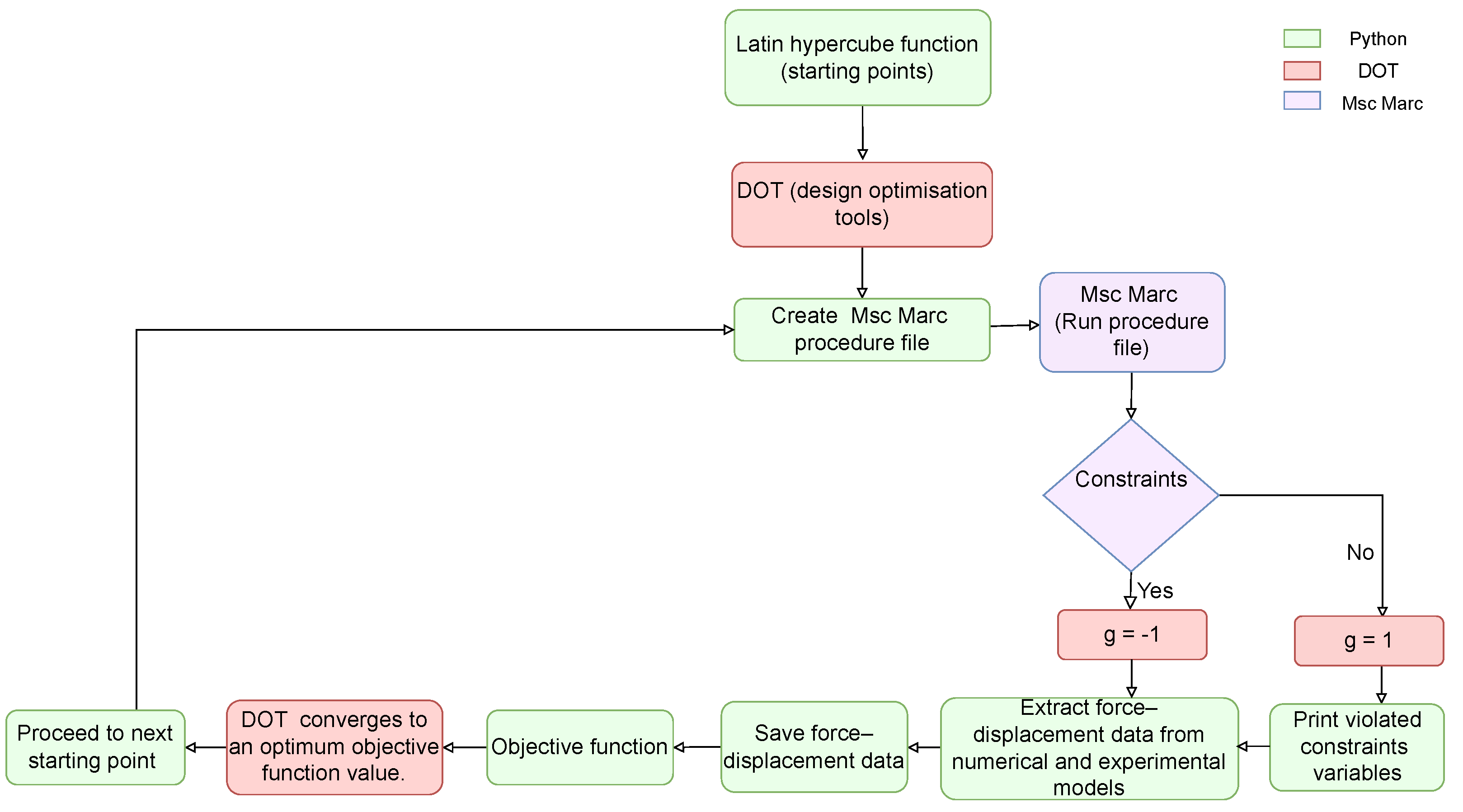
2.2. Inverse Analysis
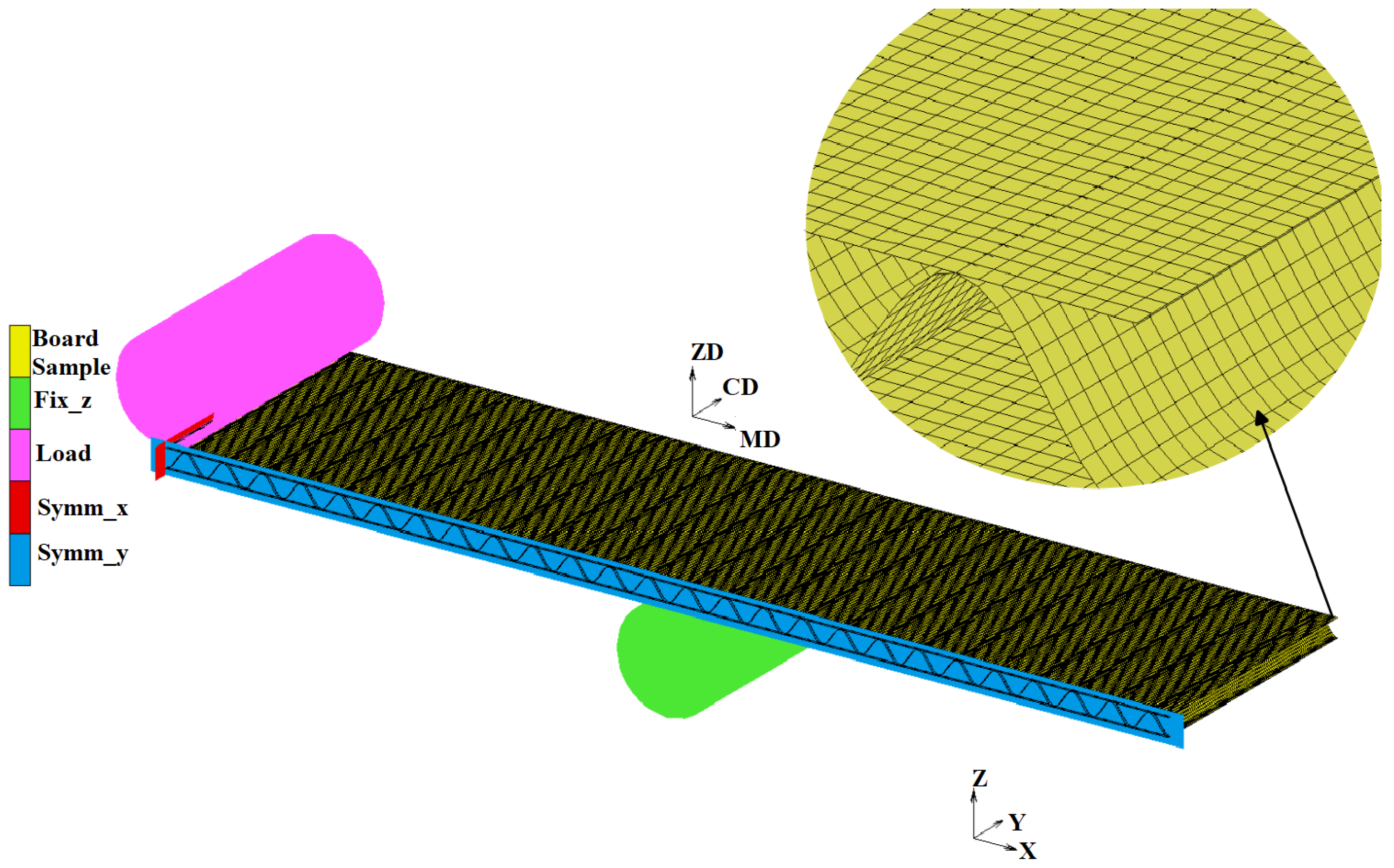
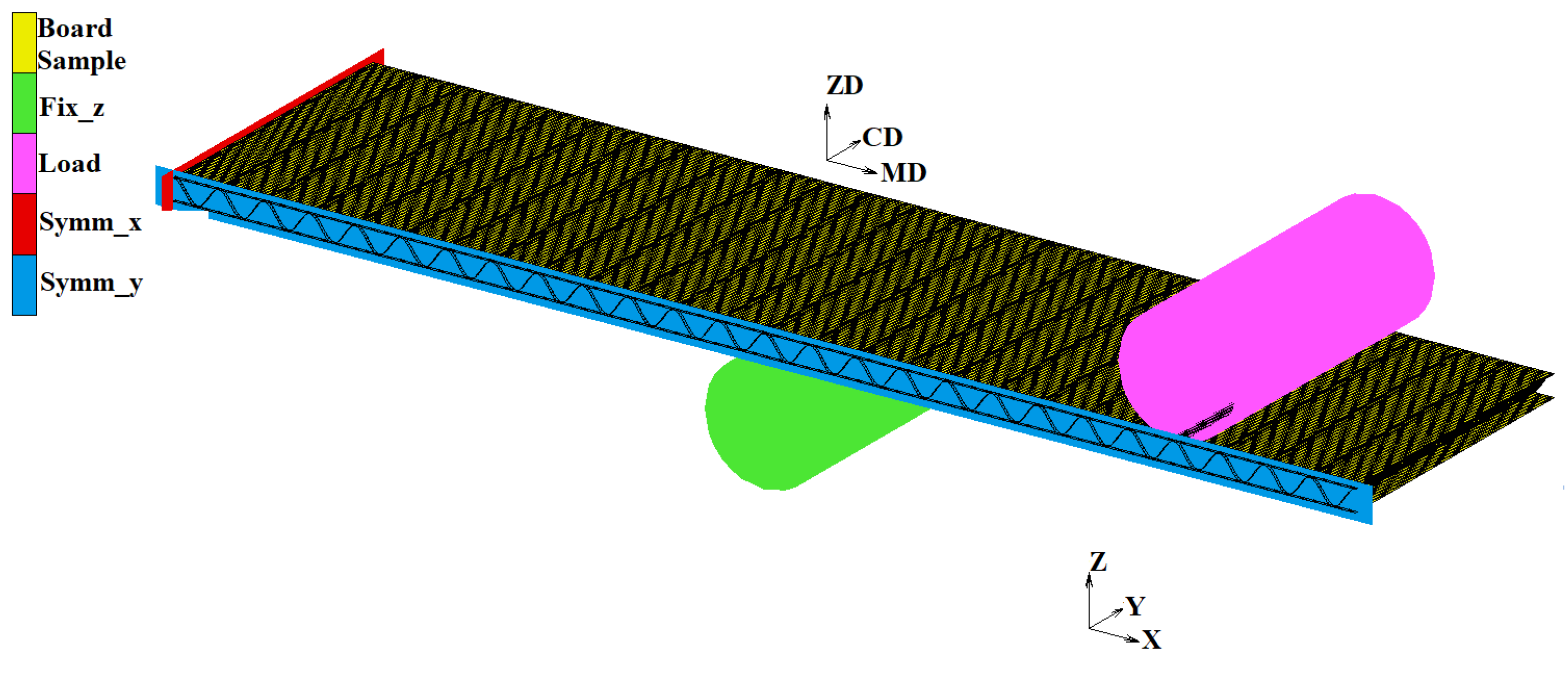
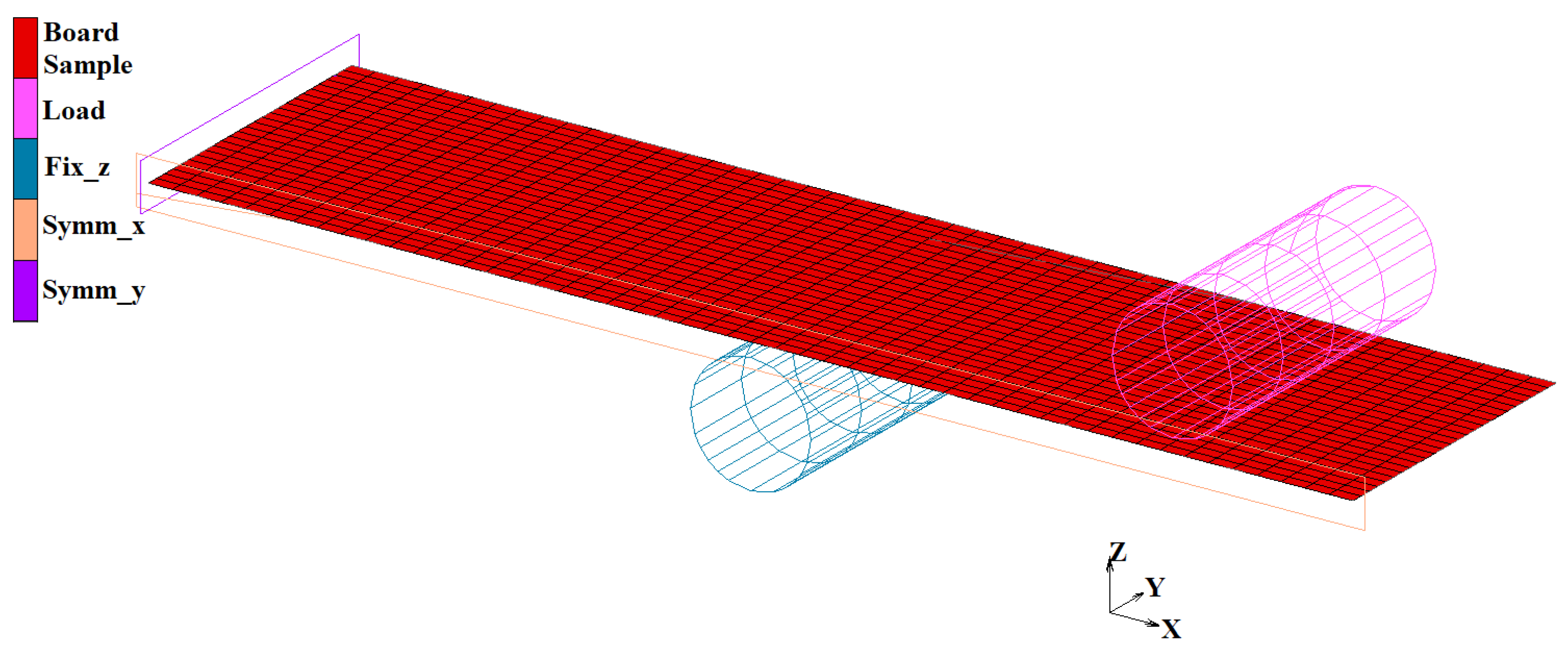
2.3. Four Point Bending Experiment and FE Modelling
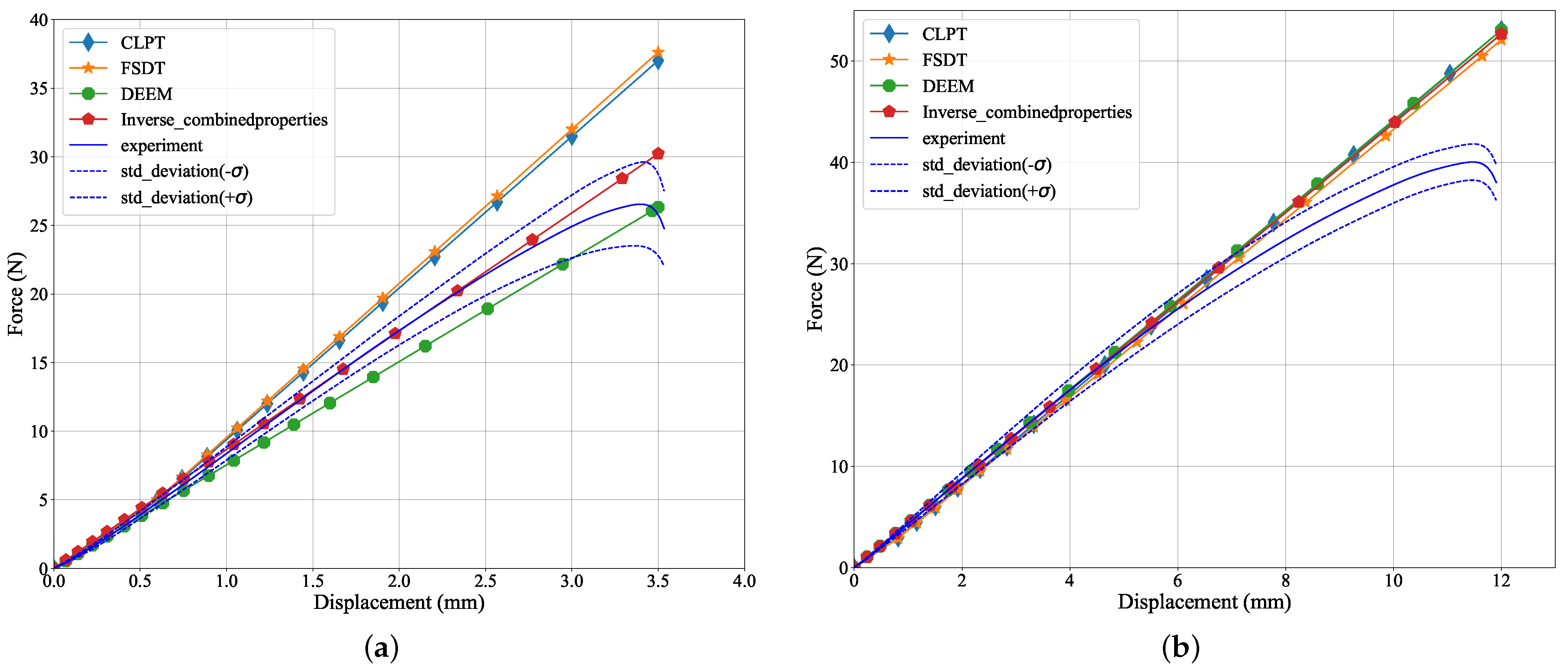
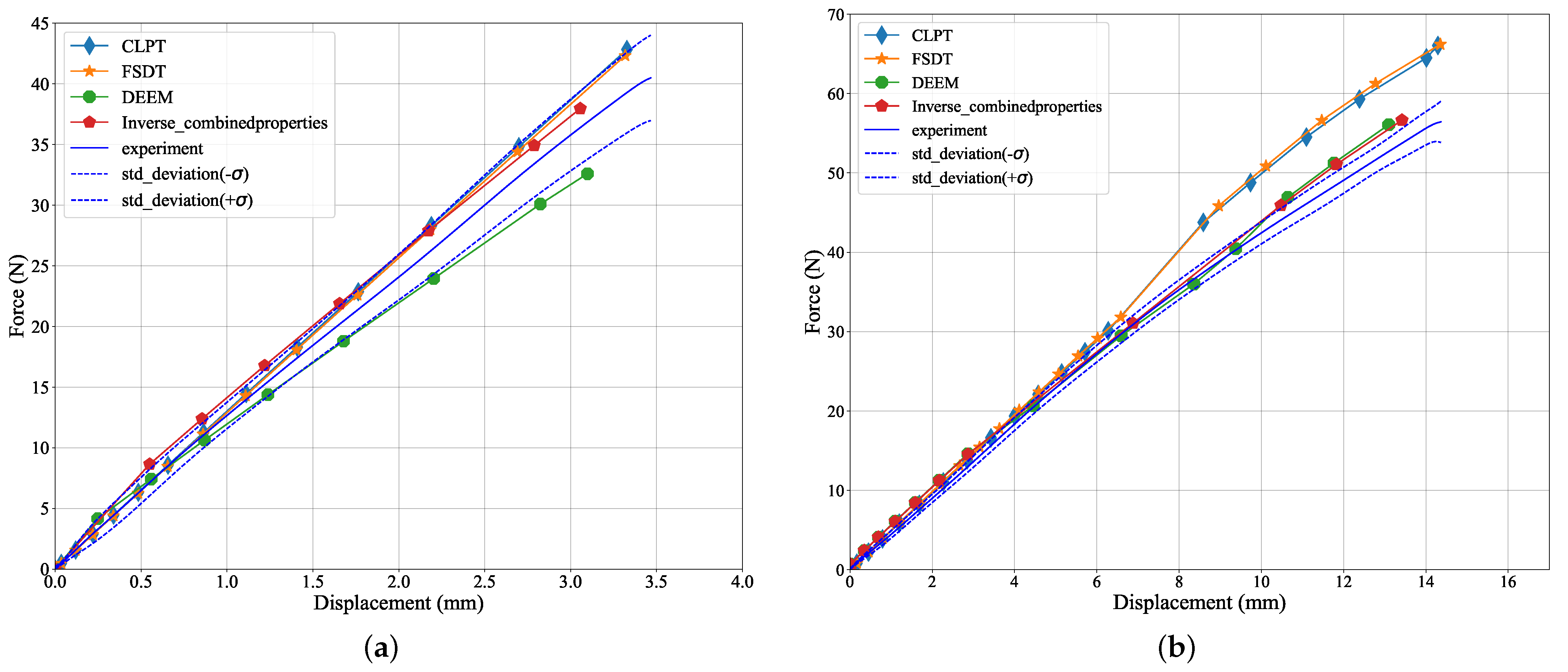
3. Results and Discussion
3.1. Homogenised Material Properties
3.2. Bending Tests
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Stiffness Matrices Obtained from Homogenisation
| A & B | B & D | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1 | 1.18 | 0 | 0 | 0 | 0 | ||
| A & B | 2 | 2.43 | 0 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 9.12 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0.34 | 0.07 | 0 | |
| B & D | 2 | 0 | 0 | 0 | 0.07 | 1.49 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0.20 | |
| A & B | B & D | H | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| A & B | 2 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 1.01 | 0.23 | 0 | 0 | 0 | |
| B & D | 2 | 0 | 0 | 0 | 0.07 | 1.48 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0.07 | 0 | 0 | |
| H | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A & B | B & D | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1 | |||||||
| A & B | 2 | ||||||
| 3 | |||||||
| 1 | |||||||
| B & D | 2 | ||||||
| 3 | |||||||
Appendix B. Material Properties Obtained from Inverse Analysis
| MD | CD | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | Optimal RMSE | (MPa) | (MPa) | (MPa) | Optimal RMSE | ||
| Reference properties (DEEM) | 797 | 442 | 182 | - | 797 | 442 | 182 | - | |
| 1 | 939.72 | 494.76 | 210.48 | 0.03 | 747.33 | 438.77 | 163.18 | 0.03 | |
| 2 | 939.58 | 499.11 | 215.53 | 0.03 | 885.18 | 441.56 | 172.86 | 0.03 | |
| 3 | 938.62 | 527.98 | 217.79 | 0.03 | 735.99 | 438.10 | 212.10 | 0.03 | |
| 4 | 941.20 | 477.57 | 157.01 | 0.03 | 800.63 | 440.25 | 178.58 | 0.03 | |
| Starting Points | 5 | 939.50 | 520.24 | 197.78 | 0.03 | 827.54 | 440.67 | 185.60 | 0.02 |
| 6 | 940.36 | 497.52 | 176.98 | 0.03 | 869.99 | 441.09 | 203.21 | 0.03 | |
| 7 | 941.95 | 429.07 | 182.52 | 0.03 | 850.88 | 441.27 | 157.75 | 0.03 | |
| 8 | 941.75 | 433.85 | 207.28 | 0.03 | 754.78 | 438.75 | 198.07 | 0.03 | |
| 9 | 940.73 | 499.01 | 160.38 | 0.03 | 750.76 | 438.28 | 206.69 | 0.03 | |
| 10 | 938.97 | 523.90 | 205.21 | 0.03 | 745.12 | 438.81 | 154.29 | 0.03 | |
| Average | 940.24 | 490.30 | 193.10 | 796.83 | 439.76 | 183.23 | |||
| Standard Deviation | 1.15 | 34.59 | 22.43 | 57.49 | 1.34 | 21.15 | |||
| Combined MD and CD | |||||
|---|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | Optimal RMSE | ||
| Reference Properties (DEEM) | 797 | 442 | 182 | - | |
| 1 | 940.54 | 441.88 | 193.06 | 0.05 | |
| 2 | 913.60 | 441.55 | 201.67 | 0.13 | |
| 3 | 940.88 | 442.15 | 173.63 | 0.05 | |
| 4 | 941.44 | 442.06 | 179.17 | 0.05 | |
| Starting Points | 5 | 940.44 | 442.07 | 210.35 | 0.05 |
| 6 | 941.47 | 442.24 | 158.87 | 0.05 | |
| 7 | 940.66 | 441.89 | 213.76 | 0.05 | |
| 8 | 941.46 | 442.15 | 166.30 | 0.05 | |
| 9 | 941.53 | 442.24 | 153.32 | 0.05 | |
| 10 | 940.88 | 441.90 | 184.79 | 0.05 | |
| Average | 938.29 | 442.01 | 183.49 | ||
| Standard Deviation | 8.68 | 0.21 | 21.05 | ||
References
- Hagman, A. Investigations of In-Plane Properties of Paperboard. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2013. [Google Scholar]
- Fadiji, T.S. Numerical and Experimental Performance Evaluation of Ventilated Packages. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2019. [Google Scholar]
- Latka, J.F. Paper in architecture: Research by design, engineering and prototyping. A+ BE—Archit. Built Environ. 2017, 19, 1–532. [Google Scholar]
- Luong, V.D.; Abbès, F.; Abbès, B.; Duong, P.; Nolot, J.-B.; Erre, D.; Guo, Y.-Q. Finite element simulation of the strength of corrugated board boxes under impact dynamics. In Proceedings of the International Conference on Advances in Computational Mechanics, Phu Quoc Island, Vietnam, 2–7 August 2017; pp. 369–380. [Google Scholar]
- Harrysson, A.; Ristinmaa, M. Large strain elasto-plastic model of paper and corrugated board. Int. J. Solids Struct. 2008, 45, 3334–3352. [Google Scholar] [CrossRef]
- Talbi, N.; Batti, A.; Ayad, R.; Guo, Y. An analytical homogenization model for finite element modelling of corrugated cardboard. Compos. Struct. 2009, 88, 280–289. [Google Scholar] [CrossRef]
- Starke, M.M. Material and Structural Modelling of Corrugated Paperboard Packaging for Horticultural Produce. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2020. [Google Scholar]
- Pathare, P.B.; Berry, T.M.; Opara, U.L. Changes in moisture content and compression strength during storage of ventilated corrugated packaging used for handling apples. Packag. Res. 2016, 1, 1–6. [Google Scholar] [CrossRef]
- Fadiji, T.; Ambaw, A.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Application of finite element analysis to predict the mechanical strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar] [CrossRef]
- Beldie, L.; Sandberg, G.; Sandberg, L. Paperboard packages exposed to static loads– finite element modelling and experiments. Packag. Technol. Sci. Int. 2001, 14, 171–178. [Google Scholar] [CrossRef]
- Biancolini, M.; Brutti, C. Numerical and experimental investigation of the strength of corrugated board packages. Packag. Technol. Sci. Int. J. 2003, 16, 47–60. [Google Scholar] [CrossRef]
- Biancolini, M. Evaluation of equivalent stiffness properties of corrugated board. Compos. Struct. 2005, 69, 322–328. [Google Scholar] [CrossRef]
- Aboura, Z.; Talbi, N.; Allaoui, S.; Benzeggagh, M. Elastic behavior of corrugated cardboard: Experiments and modeling. Compos. Struct. 2004, 63, 53–62. [Google Scholar] [CrossRef]
- Gilchrist, A.; Suhling, J.; Urbanik, T. Nonlinear finite element modeling of corrugated board. In Proceedings of the the ASME Joint Applied Mechanicals and Materials Division Meeting, Blacksburg, VA, USA, 27–30 June 1999. [Google Scholar]
- Nordstrand, T. Parametric study of the post-buckling strength of structural core sandwich panels. Compos. Struct. 1995, 30, 441–451. [Google Scholar] [CrossRef]
- Allansson, A.; Svard, B. Stability and Collapse of Corrugated Board: Numerical and Experimental Analysis. Available online: https://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=3566619&fileOId=3957829 (accessed on 12 February 2023).
- Garbowski, T.; Jarmuszczak, M. Homogenization of corrugated paperboard. Part 1. Anal. Homog. 2014, 70, 345–349. (In Polish) [Google Scholar]
- Buannic, N.; Cartraud, P.; Quesnel, T. Homogenization of corrugated core sandwich panels. Compos. Struct. 2003, 59, 299–312. [Google Scholar] [CrossRef]
- Duong, P.T.M. Analysis and simulation for the double corrugated cardboard plates under bending and in-plane shear force by homogenization method. Int. J. Mech. 2017, 11, 176–181. [Google Scholar]
- Jekel, C.F.; Venter, G.; Venter, M.P. Obtaining a hyperelastic non-linear orthotropic material model via inverse bubble inflation analysis. Struct. Multidiscip. Optim. 2016, 4, 927–935. [Google Scholar] [CrossRef]
- Gajewski, T.; Garbowski, T. Calibration of concrete parameters based on digital image correlation and inverse analysis. Arch. Civ. Mech. Eng. 2014, 14, 170–180. [Google Scholar] [CrossRef]
- Gajewski, T.; Garbowski, T. Mixed experimental/numerical methods applied for concrete parameters estimation. In Proceedings of the 20th International Conference on Computer Methods in Mechanics, Poznan, Poland, 27–31 August 2013; pp. 293–302. [Google Scholar]
- Mann, R.W.; Baum, G.A.; Habeger, C.C., Jr. Determination of All Nine Orthotropic Elastic Constants for Machine-Made Paper. Available online: https://smartech.gatech.edu/bitstream/handle/1853/3101/tps-084.pdf (accessed on 12 February 2023).
- Baum, G. Orthotropic elastic constants of paper. Tappi J. 1981, 64, 97–101. [Google Scholar]
- Marek, A.; Garbowski, T. Homogenization of sandwich panels. Comput. Assist. Eng. Sci. 2017, 22, 39–50. [Google Scholar]
- Suarez, B.; Muneta, M.L.M.; Sanz-Bobi, J.D.; Romero, G. Application of homogenization approaches to the numerical analysis of seating made of multi-wall corrugated cardboard. Compos. Struct. 2021, 262, 113642. [Google Scholar] [CrossRef]
- Berthelot, J.-M.; Ling, F.F. Composite Materials: Mechanical Behavior and Structural Analysis; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Barbero, E.J. Introduction to Composite Materials Design; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Miehe, C.; Koch, A. Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch. Appl. Mech. 2002, 72, 142–149. [Google Scholar] [CrossRef]
- Vanderplaats Research & Development Inc. DOT Users Manual, 5th ed.; Vanderplaats Research & Development Inc.: Colorado Springs, CO, USA, 2001. [Google Scholar]
- McKee, R.; Gander, J.; Wachuta, J. Compression strength formula for corrugated boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
- Garbowski, T.; Jarmuszczak, M. Homogenization of corrugated paperboard. Part 2. Pol. Pap. Rev. 2014, 70, 345–349. (In Polish) [Google Scholar]

| Paper Type | Thickness (mm) | (MPa) | (MPa) | |
|---|---|---|---|---|
| 150SC | 0.25 | 4709 | 2918 | 0.39 |
| 250KL | 0.35 | 6695 | 2310 | 0.50 |
| Technique | Effective Thickness (mm) | (MPa) | (MPa) | (MPa) | |
|---|---|---|---|---|---|
| CLPT | 4.4 | 26.66 | 235.03 | 0.02 | 20.64 |
| FSDT | 4.6 | 73.13 | 218.47 | 0.07 | 15.72 |
| DEEM | 6.0 | 797.19 | 442.51 | 0.41 | 182.15 |
| Technique | (MPa) | Standard Deviation | (MPa) | Standard Deviation | (MPa) | Standard Deviation |
|---|---|---|---|---|---|---|
| MD | 940.24 | 1.15 | 490.30 | 34.59 | 193.10 | 22.43 |
| CD | 796.83 | 57.49 | 439.76 | 1.34 | 183.23 | 21.15 |
| Combined MD & CD | 938.29 | 8.68 | 442.01 | 0.21 | 183.49 | 21.05 |
| Type | Experiment | CLT | FSDT | DEEM | Inverse Analysis |
|---|---|---|---|---|---|
| MD | 20.44 | 22.52 | 22.32 | 18.40 | 21.73 |
| Error (%) | - | 10 | 9 | 10 | 6 |
| - | 0.90 | 0.90 | 0.99 | 0.99 | |
| CD | 7.22 | 8.08 | 8.07 | 7.49 | 7.72 |
| Error (%) | - | 12 | 12 | 4 | 7 |
| - | 0.98 | 0.97 | 0.97 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aduke, R.N.; Venter, M.P.; Coetzee, C.J. An Analysis of Numerical Homogenisation Methods Applied on Corrugated Paperboard. Math. Comput. Appl. 2023, 28, 46. https://doi.org/10.3390/mca28020046
Aduke RN, Venter MP, Coetzee CJ. An Analysis of Numerical Homogenisation Methods Applied on Corrugated Paperboard. Mathematical and Computational Applications. 2023; 28(2):46. https://doi.org/10.3390/mca28020046
Chicago/Turabian StyleAduke, Rhoda Ngira, Martin P. Venter, and Corné J. Coetzee. 2023. "An Analysis of Numerical Homogenisation Methods Applied on Corrugated Paperboard" Mathematical and Computational Applications 28, no. 2: 46. https://doi.org/10.3390/mca28020046
APA StyleAduke, R. N., Venter, M. P., & Coetzee, C. J. (2023). An Analysis of Numerical Homogenisation Methods Applied on Corrugated Paperboard. Mathematical and Computational Applications, 28(2), 46. https://doi.org/10.3390/mca28020046








