Numerical Computation of Ag/Al2O3 Nanofluid over a Riga Plate with Heat Sink/Source and Non-Fourier Heat Flux Model
Abstract
:1. Introduction
- Modify the current mathematical model to include nanofluids based on -water, Cattaneo–Christov heat flux, non-linear thermal radiation, and heat source/sink.
- In what ways does it affect Darcy–Forchheimer flow on a Riga plate?
- Exactly how do the Cattaneo–Christov heat flux phenomenon and non-linear thermal radiation influence heat transfer?
- When convective heating conditions are applied, how does the heat transfer gradient respond?
2. Mathematical Formulation
3. Numerical Solution
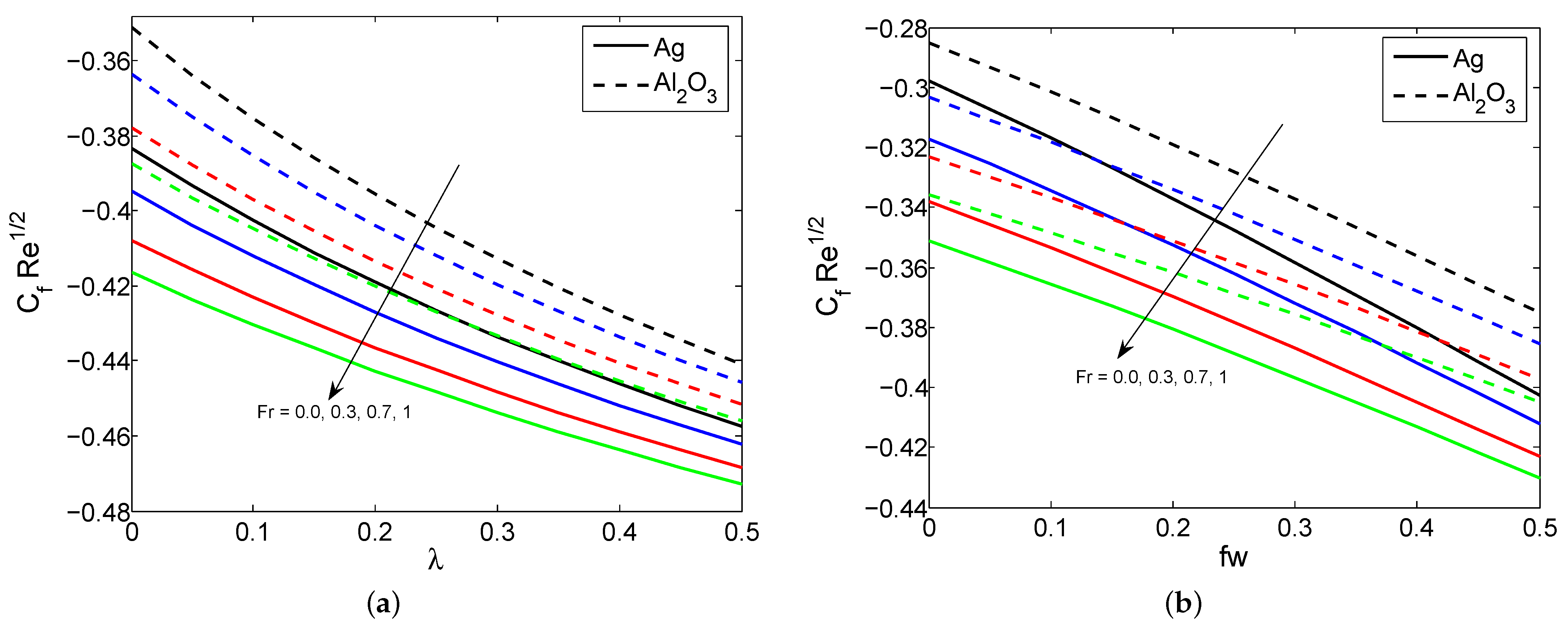
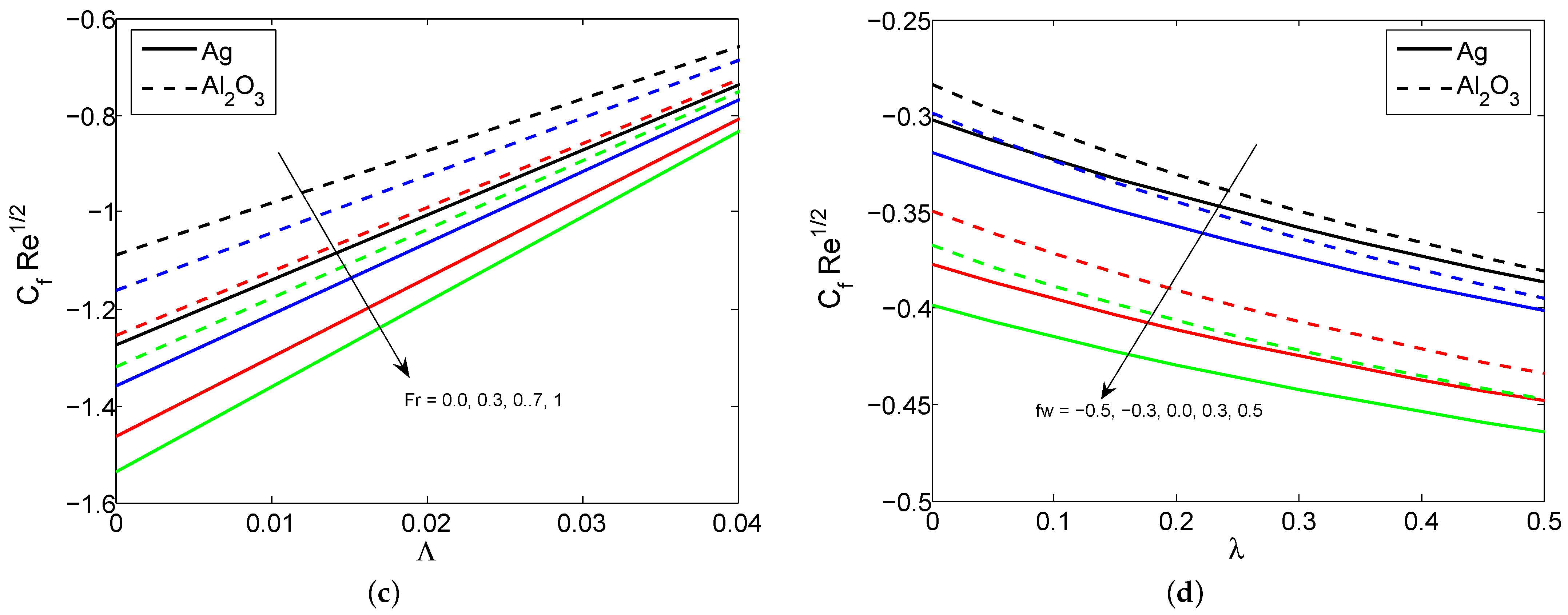
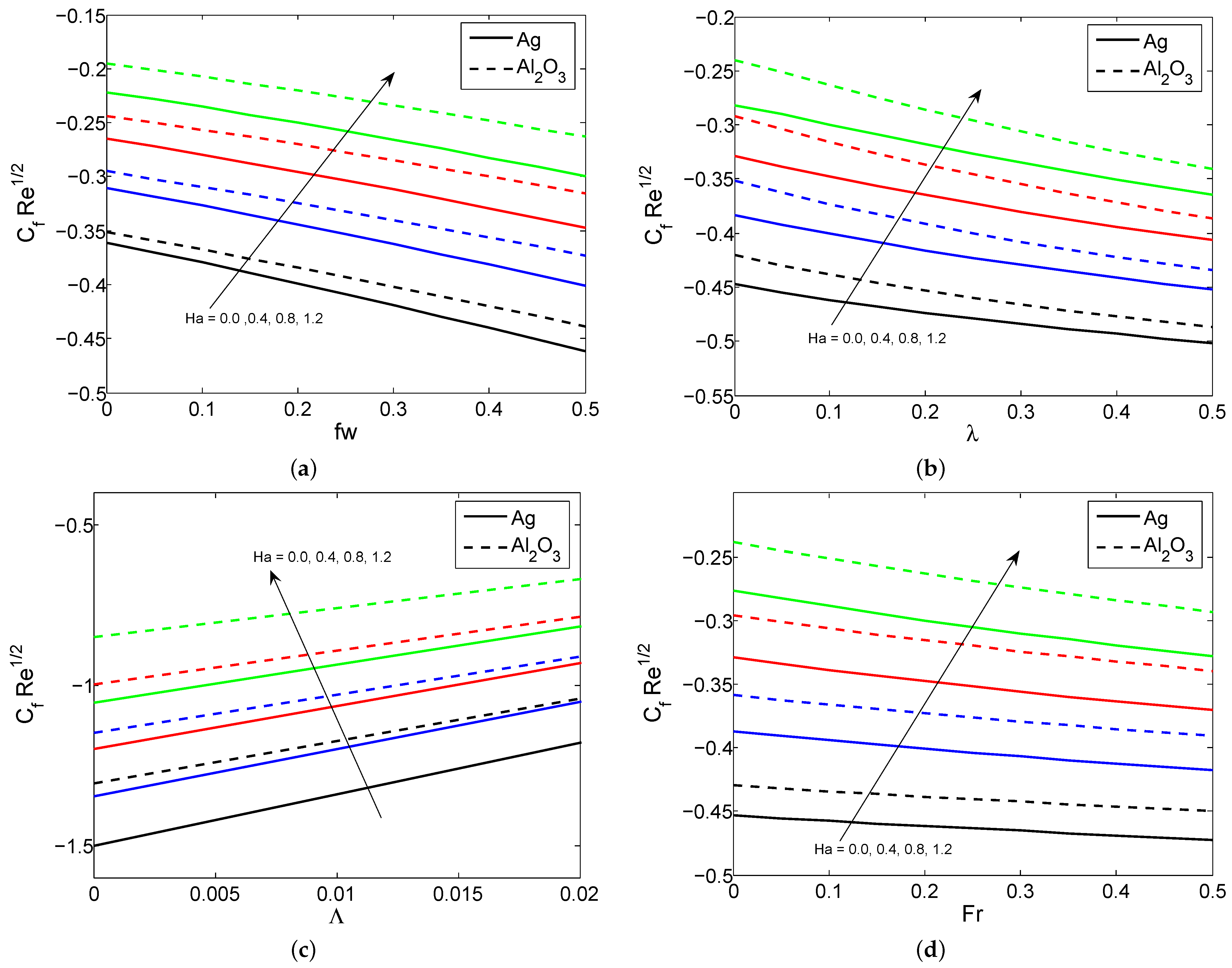
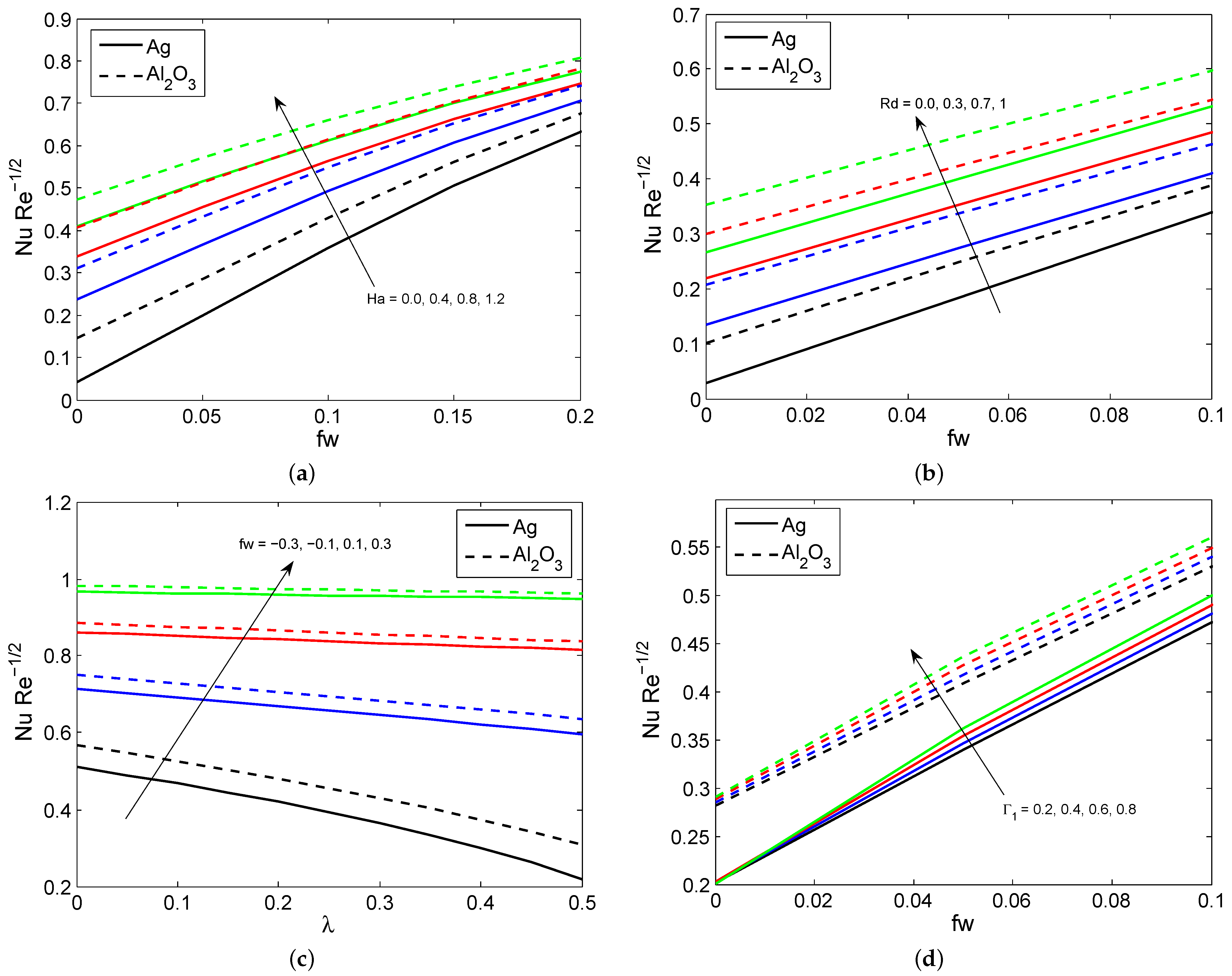
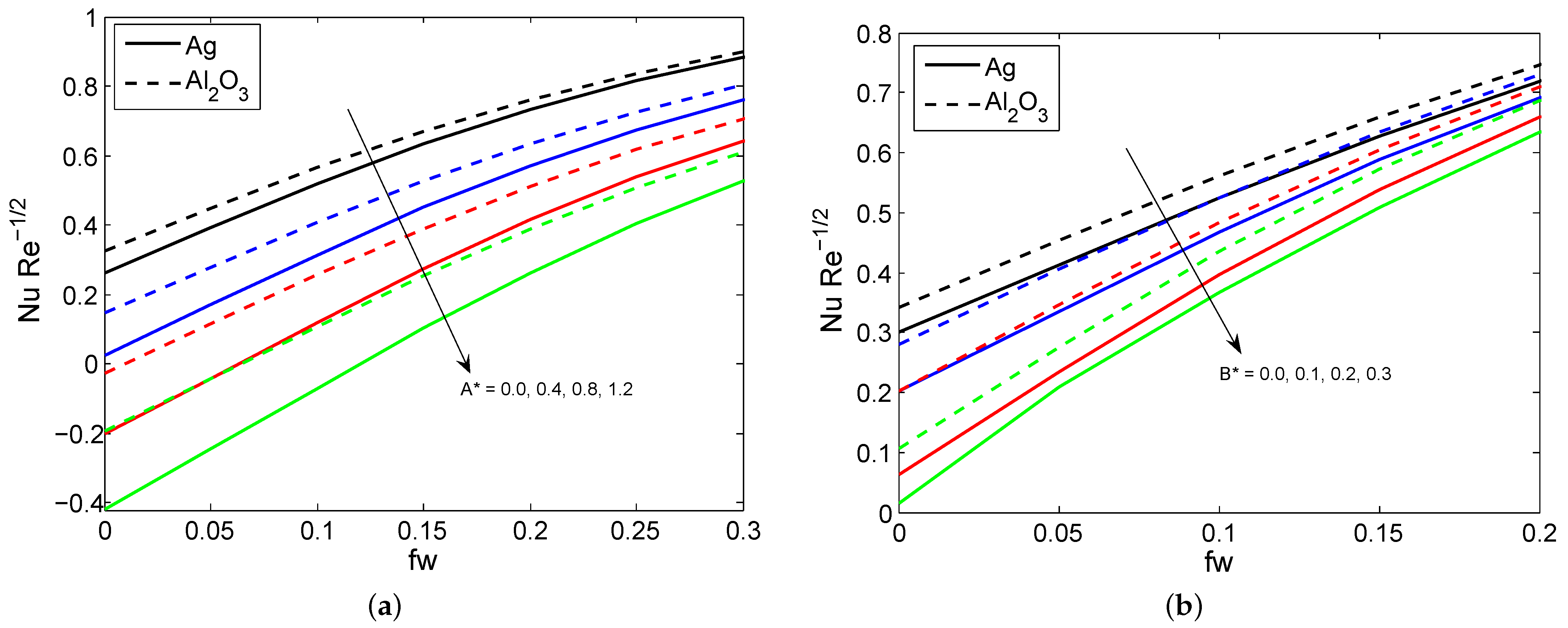
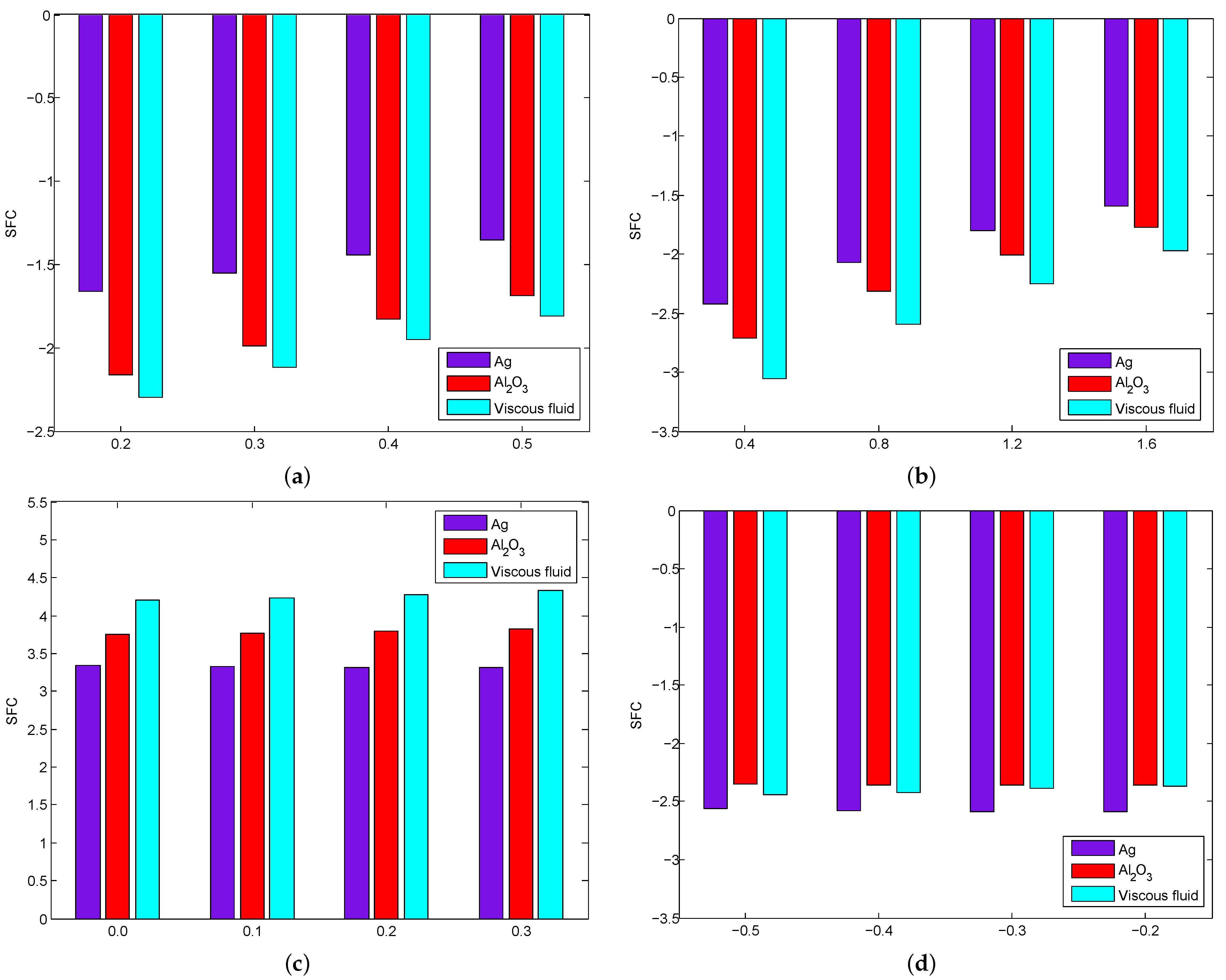
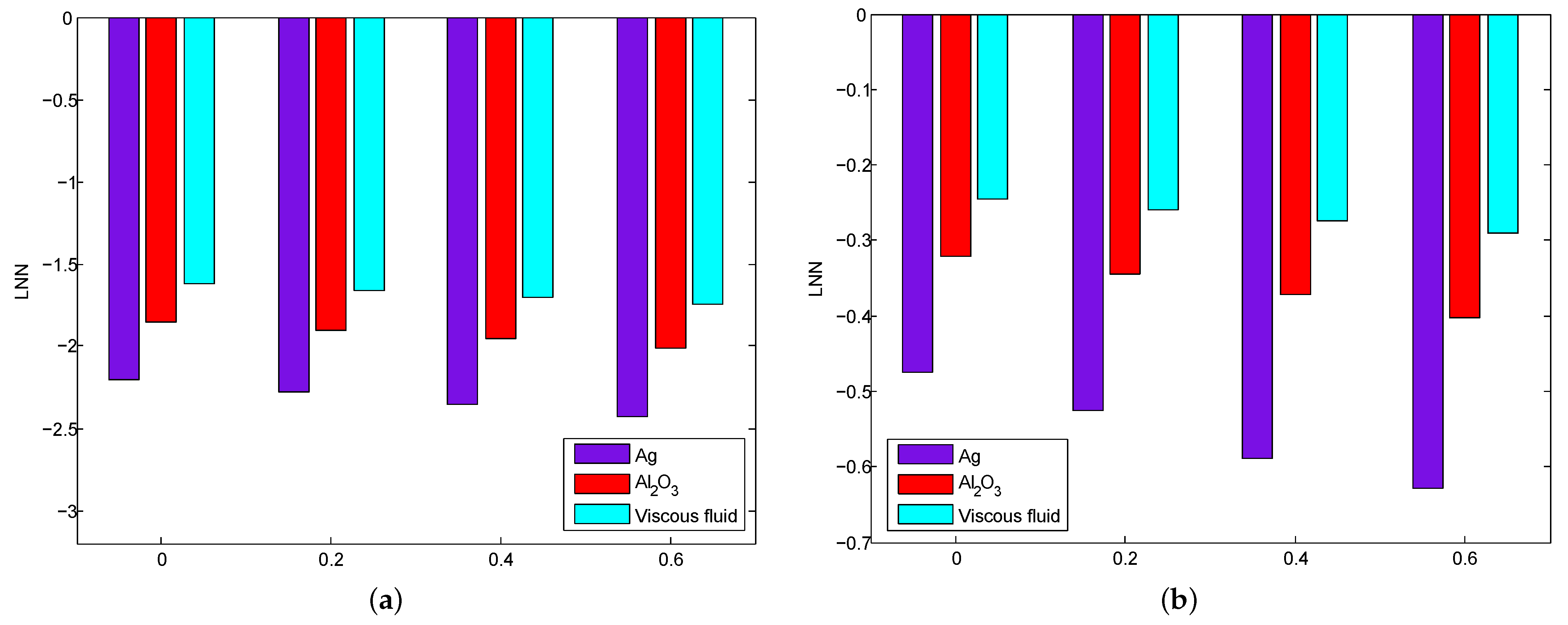
4. Results and Discussion
5. Conclusions
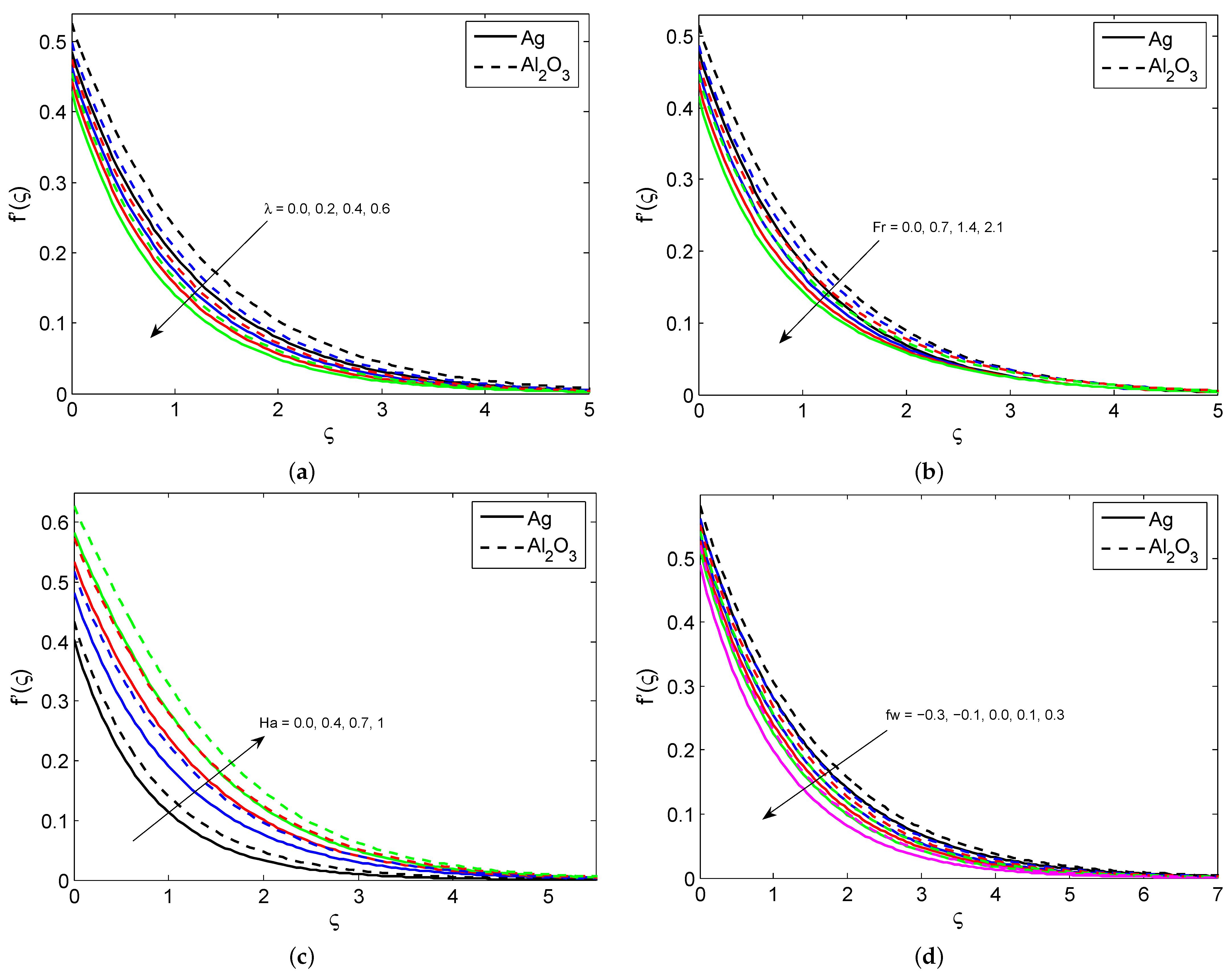
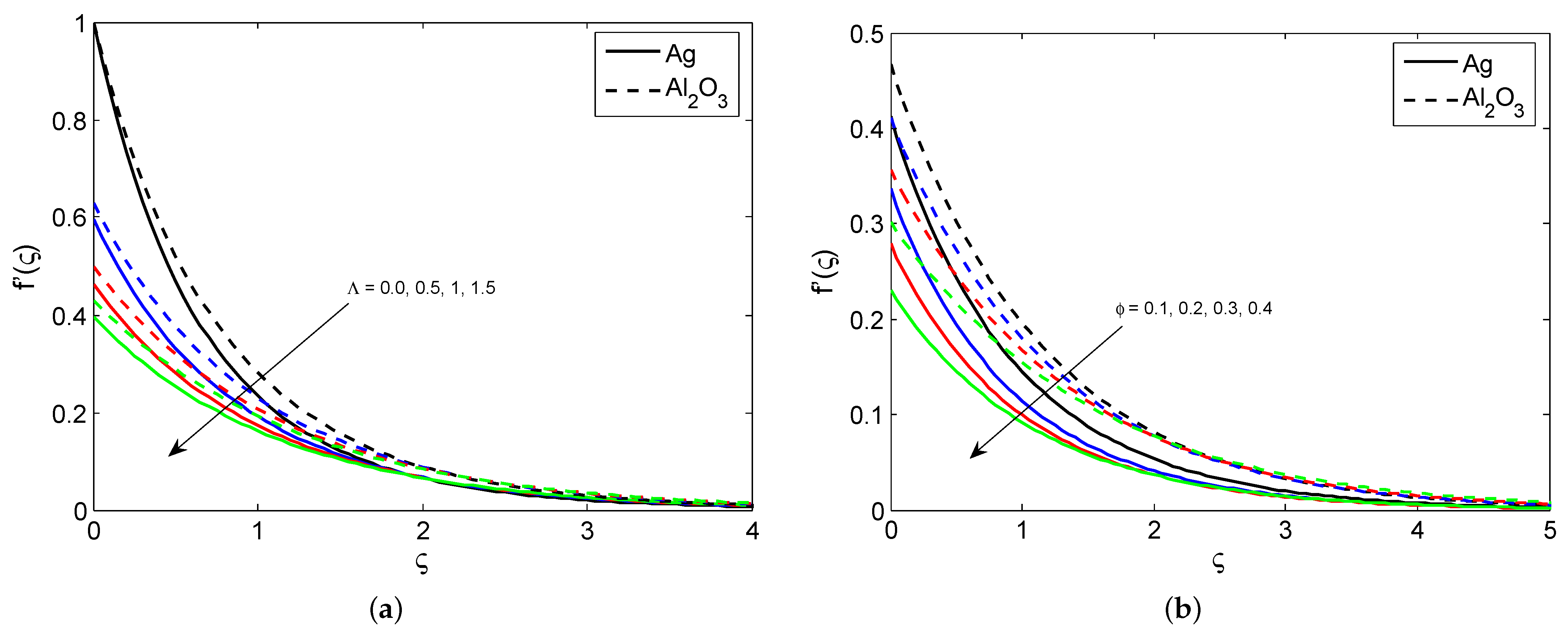
- The nanofluid velocity profile reduces for higher values of porosity, the Forchheimer number, the suction/injection parameter, and the slip parameter.
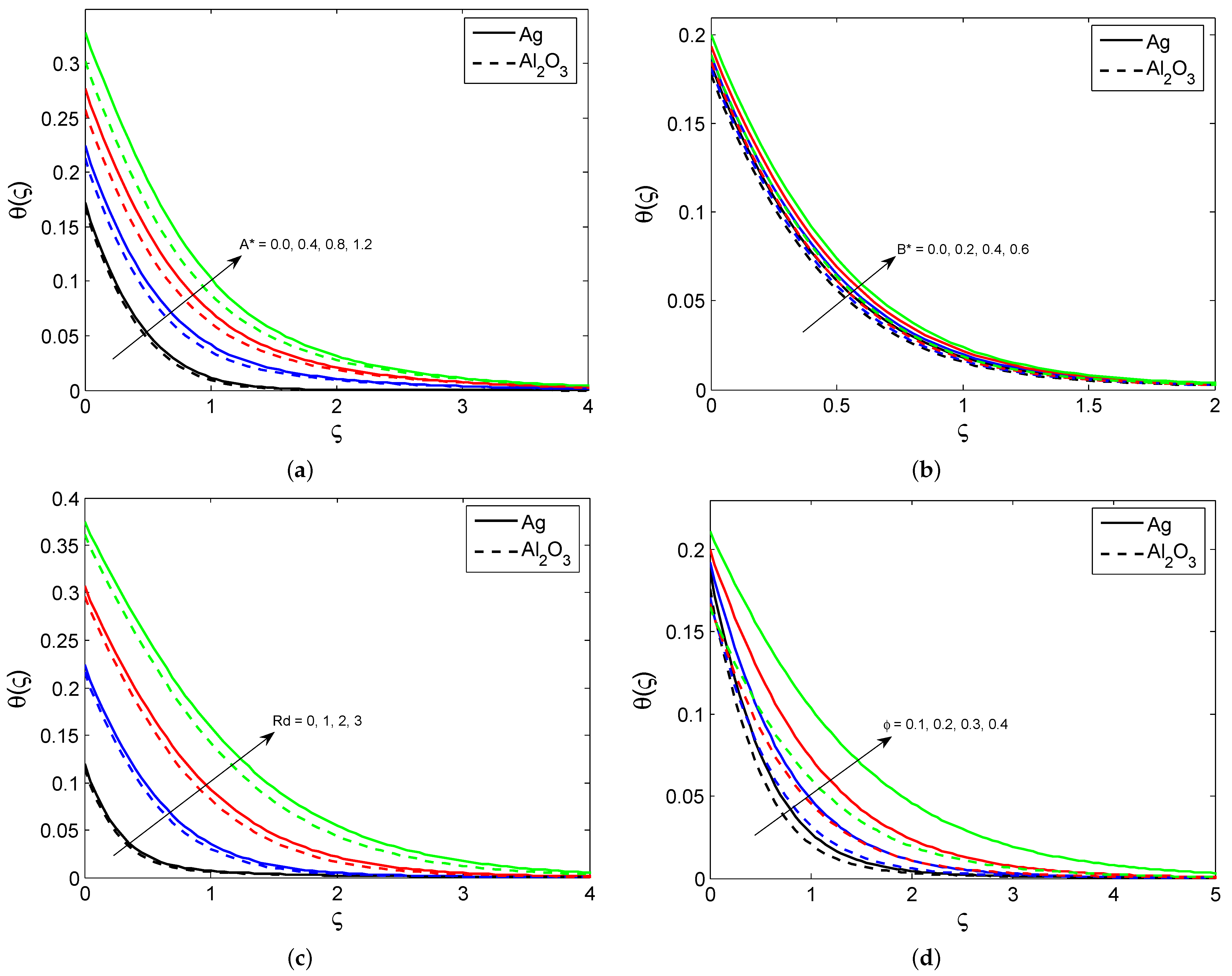
- The greater the thermal radiation, nanoparticle volume fraction, space and temperature dependent heat source parameter, the greater the nanofluid temperature profile.
- The nanofluid temperature declines for larger values of convection cooling, injection/suction and the thermal relaxation time parameter.
- The skin friction coefficient declines for increasing values of the Forchheimer number and suction/injection parameter, and increases when the modified Hartmann number increases.
- The heat transfer gradient increases with increasing values for the Hartmann number, radiation, suction/injection and the thermal relaxation time parameter, whereas it declines when the space and temperature dependent heat source parameter is increased.
- In future, we will expand this flow model by including hybrid and ternary hybrid nanofluids with different shape factors.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| f | |
| M | |
| T | |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. (No. ANL/MSD/CP-84938; CONF-951135-29); Argonne National Lab. (ANL): Argonne, IL, USA, 1995.
- Martin, E.; Sastre, F.; Velazquez, A.; Bairi, A. Heat transfer enhancement around a finned vertical antenna by means of porous media saturated with Water-Copper nanofluid. Case Stud. Therm. Eng. 2021, 28, 101555. [Google Scholar] [CrossRef]
- Uddin, M.J.; Al-Balushi, J.; Mahatabuddin, S.; Rahman, M.M. Convective heat transport for copper oxide-water nanofluid in an isosceles triangular cavity with a rippled base wall in the presence of magnetic field. Int. J. Thermofluid 2022, 16, 100195. [Google Scholar] [CrossRef]
- Nayak, M.K.; Shaw, S.; Khan, M.I.; Pandey, V.S.; Nazeer, M. Flow and thermal analysis on Darcy–Forchheimer flow of copper-water nanofluid due to a rotating disk: A static and dynamic approach. J. Mater. Res. Technol. 2020, 9, 7387–7408. [Google Scholar] [CrossRef]
- Adem, G.A.; Kishan, N. Slip effects in a flow and heat transfer of a nanofluid over a nonlinearly stretching sheet using optimal homotopy asymptotic method. Int. J. Eng. Manuf. Sci. 2018, 8, 25–46. [Google Scholar]
- Uddin, M.J.; Rasel, S.K.; Adewole, J.K.; Al Kalbani, K.S. Finite element simulation on the convective double diffusive water-based copper oxide nanofluid flow in a square cavity having vertical wavy surfaces in presence of hydro-magnetic field. Results Eng. 2022, 13, 100364. [Google Scholar] [CrossRef]
- Verma, A.K.; Rajput, S.; Bhattacharyya, K.; Chamkha, A.J. Nanoparticle’s radius effect on unsteady mixed convective copper-water nanofluid flow over an expanding sheet in porous medium with boundary slip. J. Adv. Chem. Eng. 2022, 12, 100366. [Google Scholar] [CrossRef]
- Yousef, N.S.; Megahed, A.M.; Ghoneim, N.I.; Elsafi, M.; Fares, E. Chemical reaction impact on MHD dissipative Casson-Williamson nanofluid flow over a slippery stretching sheet through porous medium. Alex. Eng. J. 2022, 61, 10161–10170. [Google Scholar] [CrossRef]
- Mohamed, M.K.A.; Ong, H.R.; Alkasasbeh, H.T.; Salleh, M.Z. Heat Transfer of Ag-Al2O3/Water Hybrid Nanofluid on a Stagnation Point Flow over a Stretching Sheet with Newtonian Heating. J. Phys. Conf. Ser. 2020, 1529, 042085. [Google Scholar] [CrossRef]
- Shahzad, A.; Liaqat, F.; Ellahi, Z.; Sohail, M.; Ayub, M.; Ali, M.R. Thin film flow and heat transfer of Cu-nanofluids with slip and convective boundary condition over a stretching sheet. Sci. Rep. 2022, 12, 14254. [Google Scholar] [CrossRef]
- Gailitis, A.; Lielausis, O. On a possibility to reduce the hydrodynamic resistance of a plate in an electrolyte. Appl. Magnetohydrodyn. 1961, 12, 143–146. [Google Scholar]
- Vaidya, H.; Prasad, K.V.; Tlili, I.; Makinde, O.D.; Rajashekhar, C.; Khan, S.U.; Kumar, R.; Mahendra, D.L. Mixed convective nanofluid flow over a non linearly stretched Riga plate. Case Stud. Therm. Eng. 2021, 24, 100828. [Google Scholar] [CrossRef]
- Shah, S.; Hussain, S.; Sagheer, M. Impacts of variable thermal conductivity on stagnation point boundary layer flow past a Riga plate with variable thickness using generalized Fourier’s law. Results Phys. 2018, 9, 303–312. [Google Scholar] [CrossRef]
- Rizwana, R.; Nadeem, S. Series solution of unsteady MHD oblique stagnation point flow of copper-water nanofluid flow towards Riga plate. Heliyon 2020, 6, e04689. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Roopa, G.S.; Gireesha, B.J.; Shehzad, S.A.; Abbasi, F.M. An electro-magneto-hydrodynamic flow Maxwell nanoliquid past a Riga plate: A numerical study. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4547–4554. [Google Scholar] [CrossRef]
- Abbas, T.; Ayub, M.; Bhatti, M.M.; Rashidi, M.M.; Ali, M.E.S. Entropy generation on nanofluid flow through a horizontal Riga plate. Entropy 2016, 18, 223. [Google Scholar] [CrossRef]
- Waqas, H.; Kafait, A.; Muhammad, T.; Farooq, U. Numerical study for bio-convection flow of tangent hyperbolic nanofluid over a Riga plate with activation energy. Alex. Eng. J. 2022, 61, 1803–1814. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Alessa, N.; Sangeethavaanee, M.; Namgyel, N. Numerical and Analytical Investigation for Darcy–Forchheimer Flow of a Williamson Fluid over a Riga Plate with Double Stratification and Cattaneo–Christov Dual Flux. Adv. Math. Phys. 2021, 2021, 1867824. [Google Scholar] [CrossRef]
- Faizan, M.; Ali, F.; Loganathan, K.; Zaib, A.; Reddy, C.A.; Abdelsalam, S.I. Entropy Analysis of Sutterby Nanofluid Flow over a Riga Sheet with Gyrotactic Microorganisms and Cattaneo–Christov Double Diffusion. Mathematics 2022, 10, 3157. [Google Scholar] [CrossRef]
- Karthik, T.S.; Loganathan, K.; Shankar, A.N.; Carmichael, M.J.; Mohan, A.; Kaabar, M.K.; Kayikci, S. Zero and nonzero mass flux effects of bioconvective viscoelastic nanofluid over a 3D Riga surface with the swimming of gyrotactic microorganisms. Adv. Math. Phys. 2021, 2021, 9914134. [Google Scholar] [CrossRef]
- Parvine, M.; Alam, M.M. Nano fluid flow along the Riga plate with electromagnetic field in a rotating system. AIP Conf. Proc. 2019, 2121, 070003. [Google Scholar]
- Rafique, K.; Alotaibi, H.; Ibrar, N.; Khan, I. Stratified Flow of Micropolar Nanofluid over Riga Plate: Numerical Analysis. Energies 2022, 15, 316. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Ramesh, G.K.; Aly, E.H.; Chamkha, A.J. Dynamics of water conveying SWCNT nanoparticles and swimming microorganisms over a Riga plate subject to heat source/sink. Alex. Eng. J. 2022, 61, 2418–2429. [Google Scholar] [CrossRef]
- Oke, A.S.; Animasaun, I.L.; Mutuku, W.N.; Kimathi, M.; Shah, N.A.; Saleem, S. Significance of Coriolis force, volume fraction, and heat source/sink on the dynamics of water conveying 47 nm alumina nanoparticles over a uniform surface. Chin. J. Phys. 2021, 71, 716–727. [Google Scholar] [CrossRef]
- Qasim, M. Heat and mass transfer in a Jeffrey fluid over a stretching sheet with heat source/sink. Alex. Eng. J. 2013, 52, 571–575. [Google Scholar] [CrossRef]
- Sharma, B.K.; Gandhi, R. Combined effects of Joule heating and non-uniform heat source/sink on unsteady MHD mixed convective flow over a vertical stretching surface embedded in a Darcy–Forchheimer porous medium. Propuls. Power Res. 2022, 11, 276–292. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Shah, N.A.; Yook, S.J. Unsteady natural convection flow due to fractional thermal transport and symmetric heat source/sink. Alex. Eng. J. 2022, 64, 761–770. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. Momentum and heat transfer behaviour of Jeffrey, Maxwell and Oldroyd-B nanofluids past a stretching surface with non-uniform heat source/sink. Ain Shams Eng. J. 2018, 9, 517–524. [Google Scholar] [CrossRef]
- Jena, S.; Dash, G.C.; Mishra, S.R. Chemical reaction effect on MHD viscoelastic fluid flow over a vertical stretching sheet with heat source/sink. Ain Shams Eng. J. 2018, 9, 1205–1213. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink. Eng. Sci. Technol. Int. J. 2015, 18, 738–745. [Google Scholar] [CrossRef]
- Reddy, P.S.; Rao, K.S. MHD natural convection heat and mass transfer of Al2O3-water and Ag-water nanofluids over a vertical cone with chemical reaction. Procedia Eng. 2015, 127, 476–484. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Alotaibi, A.M.; Eldin, S.M.; Akkurt, N.; Waini, I.; Madhukesh, J.K. Stability Analysis of Buoyancy Magneto Flow of Hybrid Nanofluid through a Stretchable/Shrinkable Vertical Sheet Induced by a Micropolar Fluid Subject to Nonlinear Heat Sink/Source. Magnetochemistry 2022, 8, 188. [Google Scholar] [CrossRef]
- Yu, Y.; Khan, U.; Zaib, A.; Ishak, A.; Waini, I.; Raizah, Z.; Galal, A.M. Exploration of 3D stagnation-point flow induced by nanofluid through a horizontal plane surface saturated in a porous medium with generalized slip effects. Ain Shams Eng. J. 2023, 14, 101873. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ganesh, N.V.; Hakeem, A.A.; Ganga, B. Buoyancy effect on MHD flow of nanofluid over a stretching sheet in the presence of thermal radiation. J. Mol. Liq. 2014, 198, 234–238. [Google Scholar] [CrossRef]
- Kameswaran, P.K.; Sibanda, P.; Murti, A.S.N. Nanofluid flow over a permeable surface with convective boundary conditions and radiative heat transfer. Math. Probl. Eng. 2013, 2013, 201219. [Google Scholar] [CrossRef]
- Maleki, H.; Alsarraf, J.; Moghanizadeh, A.; Hajabdollahi, H.; Safaei, M.R. Heat transfer and nanofluid flow over a porous plate with radiation and slip boundary conditions. J. Cent. South Univ. 2019, 26, 1099–1115. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Loganathan, K.; Jain, R.; Gyeltshen, S. Darcy–Forchheimer 3D Flow of Glycerin-Based Carbon Nanotubes on a Riga Plate with Nonlinear Thermal Radiation and Cattaneo–Christov Heat Flux. J. Nanomater. 2022, 2022, 5286921. [Google Scholar] [CrossRef]
- Mahat, R.; Saqib, M.; Khan, I.; Shafie, S.; Noor, N.A.M. Thermal radiation effect on Viscoelastic Walters’-B nanofluid flow through a circular cylinder in convective and constant heat flux. Case Stud. Therm. Eng. 2022, 39, 102394. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; Animasaun, I.L. Exploration of non-linear thermal radiation and suspended nanoparticles effects on mixed convection boundary layer flow of nanoliquids on a melting vertical surface. J. Nanofluids 2018, 7, 833–843. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Al-Khaled, K.; Khan, S.U.; Chammam, W.; Awais, M. Darcy–Forchheimer higher-order slip flow of Eyring–Powell nanofluid with nonlinear thermal radiation and bioconvection phenomenon. J. Dispers. Sci. Technol. 2021, 1–11. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Thamaraiselvi, S.; Loganathan, K. Exploration of Darcy–Forchheimer Flows of Non-Newtonian Casson and Williamson Conveying Tiny Particles Experiencing Binary Chemical Reaction and Thermal Radiation: Comparative Analysis. Math. Comput. Appl. 2022, 27, 52. [Google Scholar] [CrossRef]
- Mahanta, G.; Das, M.; Nayak, M.K.; Shaw, S. Irreversibility analysis of 3D magnetohydrodynamic Casson nanofluid flow past through two bi-directional stretching surfaces with nonlinear radiation. J. Nanofluids 2021, 10, 316–326. [Google Scholar] [CrossRef]
- Waqas, M.; Khan, U.; Zaib, A.; Ishak, A.; Albaqami, M.D.; Waini, I.; Alotabi, R.G.; Pop, I. Radiation effect on MHD three-dimensional stagnation-point flow comprising water-based graphene oxide nanofluid induced by a nonuniform heat source/sink over a horizontal plane surface. Int. J. Mod. Phys. B 2022, 2022, 2350146. [Google Scholar] [CrossRef]
- Jha, B.K.; Samaila, G. The role of thermal radiation on the boundary layer past a stationary flat plate with constant surface boundary condition. J. Nat. 2022, 2, 7–11. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Divya, S.; Faisal, M.; Namgyel, N. Entropy and heat transfer analysis for MHD flow of-water-based nanofluid on a heated 3D plate with nonlinear radiation. Math. Probl. Eng. 2022, 2022, 7319988. [Google Scholar] [CrossRef]
- Alzahrani, H.A.; Alsaiari, A.; Madhukesh, J.K.; Naveen Kumar, R.; Prasanna, B.M. Effect of thermal radiation on heat transfer in plane wall jet flow of Casson nanofluid with suction subject to a slip boundary condition. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Aldabesh, A.; Khan, S.U.; Habib, D.; Waqas, H.; Tlili, I.; Khan, M.I.; Khan, W.A. Unsteady transient slip flow of Williamson nanofluid containing gyrotactic microorganism and activation energy. Alex. Eng. J. 2020, 59, 4315–4328. [Google Scholar] [CrossRef]
- Mahmood, A.; Jamshed, W.; Aziz, A. Entropy and heat transfer analysis using Cattaneo–Christov heat flux model for a boundary layer flow of Casson nanoliquid. Results Phys. 2018, 10, 640–649. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Khan, T.A.; Khan, M.I.; Ahmad, S.; Alsaedi, A. Entropy generation in Darcy–Forchheimer bidirectional flow of water-based carbon nanotubes with convective boundary condition. J. Mol. Liq. 2018, 265, 629–638. [Google Scholar] [CrossRef]
- Afify, A.A. The influence of slip boundary condition on Casson nanofluid flow over a stretching sheet in the presence of viscous dissipation and chemical reaction. Math. Probl. Eng. 2017, 2017, 3804751. [Google Scholar] [CrossRef]
- Asshaari, I.; Jedi, A.; Abdullah, S. Brownian Motion and Thermophoresis Effects in co-Flowing Carbon Nanotubes towards a Moving Plate. Results Phys. 2022, 44, 106165. [Google Scholar] [CrossRef]
- Shampine, L.F.; Kierzenka, J.; Reichelt, M.W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. World J. Mech. 2013, 3, 1–27. [Google Scholar]
- Shampine, L.F.; Gladwell, I.; Thompson, I. Solving ODEs with MATLAB, 1st ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Prabakaran, R.; Eswaramoorthi, S.; Loganathan, K.; Gyeltshen, S. Thermal Radiation and Viscous Dissipation Impacts of Water and Kerosene-Based Carbon Nanotubes over a Heated Riga Sheet. J. Nanomater. 2022, 2022, 1865763. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Roja, A.; Gireesha, B.J. Impact of Hall and Ion effects on MHD couple stress nanofluid flow through an inclined channel subjected to convective, hydraulic slip, heat generation, and thermal radiation. Heat Transf. 2020, 49, 3314–3333. [Google Scholar] [CrossRef]
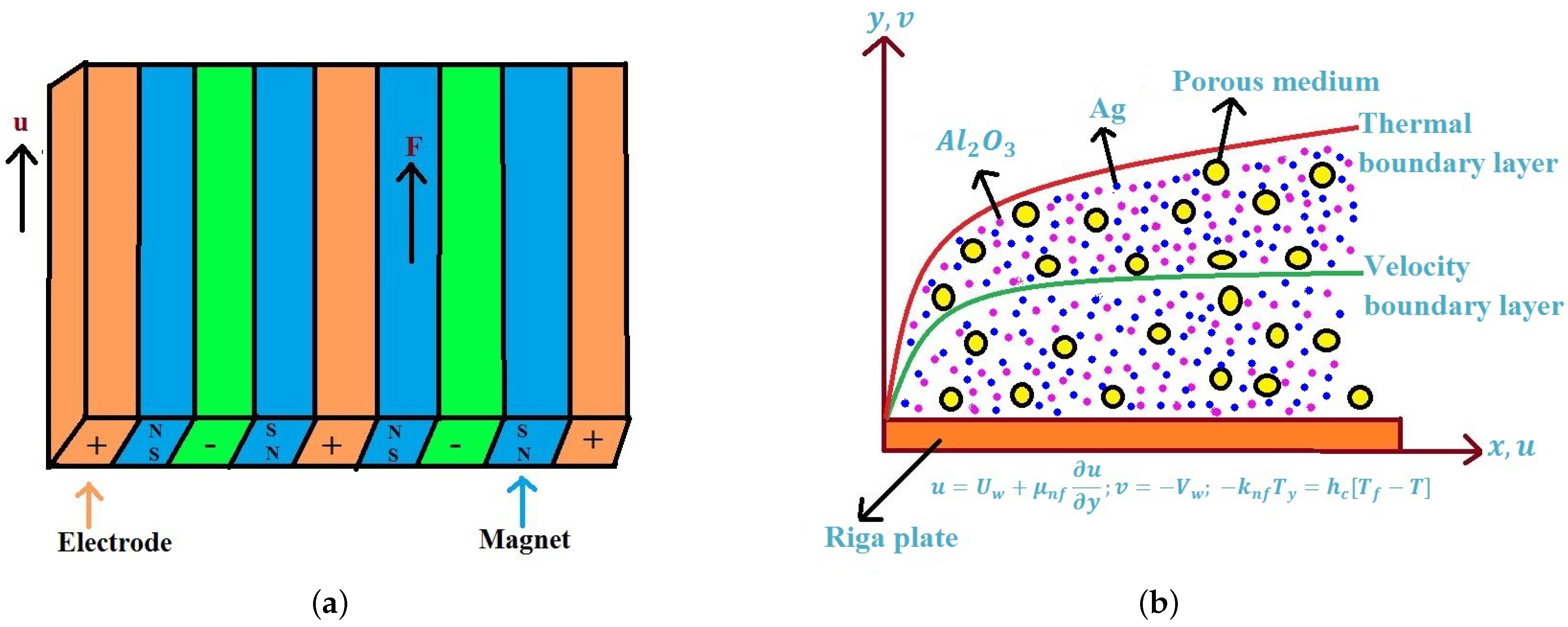

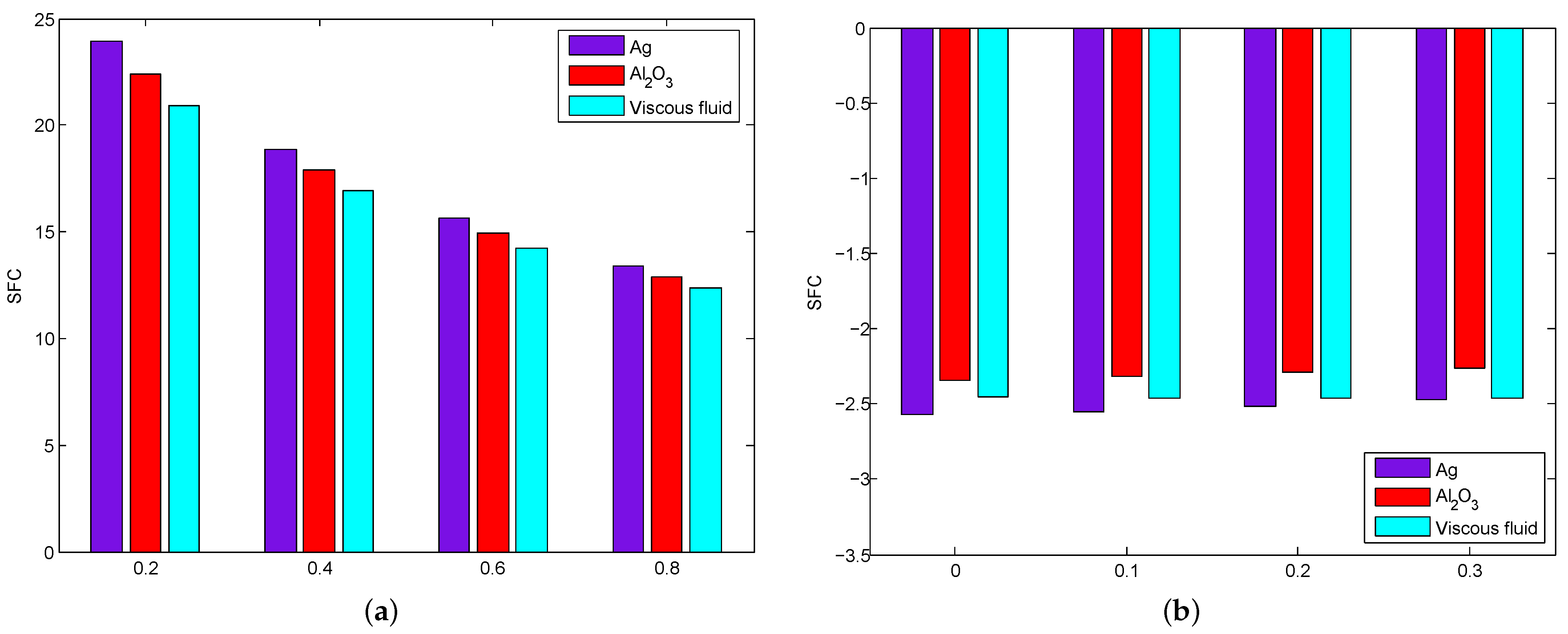

| Physical Properties | Silver (Ag) | Aluminium Oxide (AlO) | Water (HO) |
|---|---|---|---|
| 3970 | |||
| 235 | 765 | 4179 | |
| 429 | 40 |
| Ref. [54] | Ref. [55] | ||
|---|---|---|---|
| 0 | |||
| Ag | |||||||
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 1 | |||||||
| 2 | |||||||
| 0 | 1 | ||||||
| 1 | |||||||
| 0 | |||||||
| 1 | |||||||
| 1 | 0 | ||||||
| Al2O3 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 1 | |||||||
| 2 | |||||||
| 0 | 1 | ||||||
| 1 | |||||||
| 0 | |||||||
| 1 | |||||||
| 1 | 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Divya, S.; Eswaramoorthi, S.; Loganathan, K. Numerical Computation of Ag/Al2O3 Nanofluid over a Riga Plate with Heat Sink/Source and Non-Fourier Heat Flux Model. Math. Comput. Appl. 2023, 28, 20. https://doi.org/10.3390/mca28010020
Divya S, Eswaramoorthi S, Loganathan K. Numerical Computation of Ag/Al2O3 Nanofluid over a Riga Plate with Heat Sink/Source and Non-Fourier Heat Flux Model. Mathematical and Computational Applications. 2023; 28(1):20. https://doi.org/10.3390/mca28010020
Chicago/Turabian StyleDivya, S., S. Eswaramoorthi, and Karuppusamy Loganathan. 2023. "Numerical Computation of Ag/Al2O3 Nanofluid over a Riga Plate with Heat Sink/Source and Non-Fourier Heat Flux Model" Mathematical and Computational Applications 28, no. 1: 20. https://doi.org/10.3390/mca28010020
APA StyleDivya, S., Eswaramoorthi, S., & Loganathan, K. (2023). Numerical Computation of Ag/Al2O3 Nanofluid over a Riga Plate with Heat Sink/Source and Non-Fourier Heat Flux Model. Mathematical and Computational Applications, 28(1), 20. https://doi.org/10.3390/mca28010020








