Abstract
Association rule mining plays a crucial role in the medical area in discovering interesting relationships among the attributes of a data set. Traditional association rule mining algorithms such as Apriori, FP growth, or Eclat require considerable computational resources and generate large volumes of rules. Moreover, these techniques depend on user-defined thresholds which can inadvertently cause the algorithm to omit some interesting rules. In order to solve such challenges, we propose an evolutionary multi-objective algorithm based on NSGA-II to guide the mining process in a data set composed of 15.5 million records with official data describing the COVID-19 pandemic in Mexico. We tested different scenarios optimizing classical and causal estimation measures in four waves, defined as the periods of time where the number of people with COVID-19 increased. The proposed contributions generate, recombine, and evaluate patterns, focusing on recovering promising high-quality rules with actionable cause–effect relationships among the attributes to identify which groups are more susceptible to disease or what combinations of conditions are necessary to receive certain types of medical care.
1. Introduction
The coronavirus (COVID-19) pandemic has affected societies around the world for more than two years now since 11 March 2020, when the World Health Organization recognized the pandemic []. However, unlike similar phenomena experienced several times in human history, this pandemic has been meticulously documented, with millions of records about almost any conceivable aspect of the phenomenon’s mechanics, including hospital occupation, infection and death rates, medical care protocols, and medication availability. Even government reactions, safety measures taken, social responsibility, and economic consequences have also been recorded []. The availability of this enormous amount of data poses an opportunity to test traditional data mining and knowledge discovery techniques and algorithms, as well as design and test new ones. Association rule mining is the most widely used technique when the goal is to reveal behavioral patterns in phenomena.
As is always the case, both private institutions and government agencies focus their attention only on mined information that is considered useful, namely behavioral patterns that can suggest some course of action to take. In that sense, traditional association rule mining is not enough, and causal rules are needed. Instead of discovering associations that have only strong statistical presence in the data set, causal rule mining aims to discover causality relations that hold in the studied phenomenon, particularly relations that can bring some degree of certainty about the future effects to indicate the rule evaluation measures and regulations established to cope with a situation.
From the computational viewpoint, data sets consisting of thousands of millions of records are not the ideal scenario for performing data mining. Exhaustive search techniques are evidently not an option. More efficient ways to traverse the data and analyze huge search spaces must be selected, but huge search spaces are the specialty of bio-inspired meta-heuristics, which in part explains why some recent papers have used diverse meta-heuristics as the guiding tool to perform data mining []. In this paper, we present a new evolutionary algorithm specifically designed to serve both traditional and causal association rule mining. This model allows a more focused data search and offers the user a set of parameters for increased flexibility over the intended mining process. We tested our model with the official COVID-19 pandemic database from the Mexican government [].
The authors of this article state that the application of artificial evolution processes in this work only partially falls under the field of medicine since no diagnosis, prescription, or treatment decisions are involved. Our mining process only analyzes data from previously treated patients, and an evolutionary algorithm is used as a dynamic model of the studied phenomenon. Moreover, neither the identification nor the interpretation of any rule mined from the database can modify the results of the real phenomenon.
The remainder of this paper is organized as follows. First, we state the conceptual and theoretical basis of the research in Section 2 (Background and Basic Concepts). These include basic concepts about association rule mining, causality relations described by mined rules, and some of the evaluation functions traditionally used to assess the nature and strength of identified causality relations. Then, in Section 3 (Related Previous Works), we briefly review some of the most relevant publications relating to association rule mining and evolutionary algorithms, both as a prediction tool and as a guide for the mining process. Section 4 (Proposal) describes the architecture, mathematical foundations, and implementation details of the proposed causal mining algorithm. This section dives into the artificial evolution process, recombination, and mutation operators, as well as the nuances of the mining process. Section 5 (Experiments and Results) shows the designs of different experimentation scenarios, the conditions of each experiment, the obtained results, and their interpretation. Finally, we draw some relevant conclusions in Section 6.
2. Background and Basic Concepts
2.1. Association Rule Mining
Association rule mining is a set of data analysis techniques aiming to discover the interesting but implicit relational patterns present in a data set. Usually, the data set is expressed in an attribute-value language, and the relations found are expressed as association rules. An association rule is a logical expression with the following structure:
In traditional association rule mining, a rule is considered interesting if it reveals an association between its antecedent and its consequent with a strong statistical presence (in the source or mine). Since interesting associations can occur in several different ways, evaluation functions are defined for each rule so that the evaluation obtained precisely measures the strength of the association described by the rule. Consequently, there are several measures for assessing the rules discovered during a mining process, such as the classical functions of , , and lift defined by Equations (1)–(3), respectively []. Traditional association rule mining algorithms seek to find all rules that exceed certain user-defined thresholds for one or more of these functions:
Here, the support (supp) function defined in the above equations computes the quotient of the number of records containing both the A and C item sets and the total number of records (U).
A different scenario is found in causal association rule mining. Causal association rules can be read as “The simultaneous occurrence of and and … and , causes (is the cause for) the occurrence of and and … and ”. In causal association rule mining, a rule is considered interesting when it reveals a cause–effect relation between its antecedent and its consequent. Additionally, a causal rule must offer a degree of actionability; that is, it should be possible to modify the situation modeled by the antecedent in order to obtain some specific and predictable effect on the situation modeled by the consequent. Therefore, a causal rule is interesting when it describes a strong causality relation and it has high actionability. However, evaluating those properties is not a trivial task, and that is why the causality relationship has always been elusive to modeling.
Causality has historically been studied from several different perspectives. Within the computational view, actionability is the most important property of a causal model []. From the artificial intelligence perspective, Judea Pearl [] pointed out that an autonomous intelligent system trying to build a model of its environment cannot rely exclusively on preprogrammed causal knowledge. It must have the ability to transform perceptual observations into cause–effect relations. By describing causal relations among the variables considered, a causal model allows estimating new environment states as a result of specific modifications on the causal conditions. In this work, we apply the following causal models to help in the identification and magnitude estimation of the causal effects as well as preview possible actions that could modify the consequent by changing the antecedent.
2.1.1. Absolute Risk (AR)
In a control case study to verify the hypothesis that “A causes C”, it must first be clear that both the presence and the absence of A have measurable effects on C. A balanced sample with two data groups is created: the first one, the experimental group with the causal conditions being studied (antecedent A), models the rule , and the second one, the control group without the antecedent, models the rule . The sample must be balanced. For each observation within the experimental group, there must be another observation within the control group (i.e., both groups must have the same support). Once the control case sample is constructed, the occurrence of the consequent C is computed within both groups, and the confidence of is used as the Experimental Event Rate (), while the confidence of is used as the Control Event Rate (). Both event rates must then be compared. When the comparison is measured as , the result is labeled the Absolute Risk [] (see Equation (4)). Its range is . A value greater than zero indicates that the antecedent has a causal effect on the consequent:
2.1.2. Probability of Sufficiency (PS)
2.1.3. Population Attributable Fraction (PAF)
The population attributable fraction (PAF) or population impact is an evaluation measure used to study the impact of exposure to a specific variable in the population []. In data mining, the population refers to the total number of records that show the consequent C, the effect being studied. The formula to calculate the impact on the population, proposed by Miettinen [], is given in Equation (7). The measure involves the support of C and the relative risk. The population impact measure has a causal interpretation which indicates the estimated fraction of all observations of the consequent that did not occur when the antecedent also did not occur:
2.2. Discrete Multi-Objective Optimization Problems
Consider a discrete multi-objective optimization problem (DMOP) with m objective functions (, ) and n decision variables (, ). The goal of multi-objective optimization is to minimize all objectives simultaneously. Mathematically, it can be described as follows:
where is the feasible search space and is the vector of the decision variables. Each , is an objective function. Let us assume that we have two vectors . Then, we say that dominates (denoted by ) if for every , and for at least one index . We say that a decision variable vector is Pareto optimal if no other such that exists.
The Pareto Optimal Set (POS) is defined by . The vector corresponds to the non-dominated solutions. The Pareto Optimal Front (POF) is defined by . We thus wish to determine the POS from the set of all the decision variable vectors that satisfy Equation (9). The dominance phenomenon occurs in the decision variable (POS) and the objective function (POF) spaces. From here on, each time we mention Pareto dominance, we are referring to the same concept in both spaces.
3. Related Previous Works
This Section shows a review of some related previous works focused on association rule mining in COVID-19 data sets. Two groups were defined: (1) works related to traditional assessment measures (support, confidence, and lift) optimized by classical algorithms such as Apriori, FP growth, and Eclat and (2) works that simultaneously optimize more than one association measure function with evolutionary algorithms.
Recently, the work of Cortes et al. in [] provided an extensive review of the state-of-the-art machine learning techniques and data mining algorithms for predicting the COVID-19 pandemic. Their paper analyzed the role of diverse data mining techniques in classification, regression, text analysis, clustering, and association. Another comprehensive study is the work of Flora et al. [] with a review of machine learning modeling. There, association rule mining was used as a knowledge discovery tool in the analysis of vaccines and the identification of potential risk factors.
The work of Zicheng Shan and Wei Miao [] proposed a data mining algorithm based on association rules for the diagnosis and treatment of COVID-19 patients. During the study, some disadvantages of the proposed algorithm were found because of the delicate data preprocessing required in order to improve the efficiency of the Apriori algorithm. Moreover, the authors reported notably low values in some association-measure functions such as support and confidence.
Wasiq et al. [] proposed a framework for identifying patterns and class associations between demographic attributes and COVID-19 death rates across different regions of the world. Their approach suggested a workflow (pipeline) that includes data preprocessing, class association learning, clustering, and data analysis to discover significant association patterns.
In [], Tandan et al. showed a comparative study of association rule mining works using the Apriori, FP growth, and Eclat algorithms to discover symptom patterns by age, gender, chronic condition, and mortality status among COVID-19 patients. Their study optimized the support, confidence, and lift measures one by one, in order to determine a ranking of symptoms and chronic conditions of COVID-19 patients.
In [,,], a multi-objective genetic association rule mining algorithm based on NSGA-II was proposed. These pioneering works introduced new concepts such as comprehensibility, surprise, interestingness, and confidence as useful measures for extracting interesting rules. However, these studies were only tested on small data sets with categorical or numerical attributes and never with mixed attribute values.
The work of Luna et al. [] introduced the first grammar-guided genetic programming approach for mining association rules from relational databases. The performance of this algorithm was checked using both synthetic relational data and a real-world database, but this work focused only on support and confidence measures.
In this paper, we propose a causal association rule mining process guided by an evolutionary algorithm with non-standard recombination and mutation operators. The proposed algorithm was designed precisely to be used on a COVID-19 official database in order to learn the behavior of the contagion and hospitalization phenomena during the pandemic. The causality nature of the mined rules ensures a certain degree of actionability that decision makers can leverage while combating the COVID-19 pandemic.
4. Proposal
In this section, we describe the mining methodology proposed to extract association rules in a COVID-19 data set. Figure 1 shows the principal steps for our proposal, while the following subsections describe the details for each one.
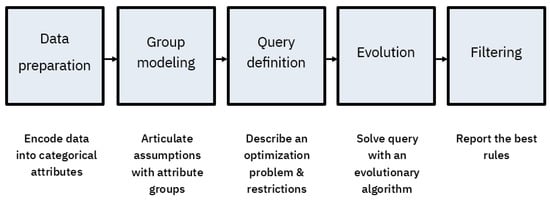
Figure 1.
The rule mining process.
4.1. Data Preparation
Experimentation was performed with an official pandemic database generated by the Mexican government []. At the moment of performing these experiments, the database was composed of records from 1 January 2020 to 1 April 2022. The total number of records within this period was 15,578,792 with 37 attributes.
Numerical data were discretized using the quintile-based technique [] in order to provide the following properties in the information:
- Uniform support: Each selector had approximately the same support, which was 20%.
- Reduced impact of outliers: Quantile-based discretization accumulates outliers in two ranges, assigning very low values to the first quintile and very high values to the last quintile.
- Pareto principle, or the 80-20 rule: This empirical principle states that 80% of the incidence of a factor is attributable to 20% of the observations [].
4.2. Group Modeling
The set of all attributes initially used to describe the data is manually clustered in order to define smaller groups of attributes with related semantics. The user can select any two attribute groups to be related as the antecedent and consequent, starting a causal mining process. This selection helps to narrow the mining process to causal rules with a specific kind of actionability. Table 1 shows the sets of attributes manually selected that define a semantic group. Here, the term comorbidities refers to the previous illnesses that a person has suffered, such as diabetes or hypertension.

Table 1.
Sets of attributes for each semantic group.
Table 2 summarizes the number of attributes in each group, the number of possible selectors, and the total number of possible combinations or rules to estimate the search space size for each scenario. In Table 3, we consider three scenarios, with each one defined by a pair of related attribute groups and a target optimization function (used as fitness criteria). The search space contains all possible association rules according to the number of attributes and selectors. Moreover, we considered four periods of time called waves, with each one representing the increase in the number of people with COVID-19. Finally, we applied the process of association rule mining in the following intervals (see Table 4).

Table 2.
Description of the number of attributes and selectors in COVID-19 data set.

Table 3.
Experimentation scenarios with search space size.

Table 4.
Periods of time in which the number of people with COVID-19 increased.
4.3. Query Definition by Optimization Problem
We defined three discrete multi-objective optimization problems (DMOPs). In all three cases, the association-measure functions showed a conflict when optimizing them simultaneously. Additionally, we included three constraints to obtain correct and complete association rules:
- Support greater than zero: The association rule must be true for at least one record. In the formal definition of optimization problems, this is stated as .
- Absolute positive effect: An association rule with an absolute positive effect and with a value greater than zero indicates that observing the antecedent increases the probability of observing the consequent, thus rejecting rules in which the antecedent inhibits the consequent. Formally, in optimization problems, this is stated as .
- Statistical significance: The odds ratio must be statistically significant; that is, the lower bound of its 95% confidence interval must be greater than or equal to one. Formally, in problems of optimization, this is stated as .
DMOP-1. Classic association rule mining aims to obtain rules with the highest possible support, confidence, and lift. However, simultaneously optimizing these measures is impossible because a sustained increase or decrease in one does not guarantee behavior in the same direction in the other two. The formal definition of the optimization problem for this query is described by Equation (10):
DMOP-2. From a logical perspective, a biconditional expression can be interpreted as “A if and only C” or “A is a necessary and sufficient condition for C”. Its truth value is equivalent to the expression . The sufficiency condition falls to the association rule , interpreted as “A is a sufficient condition for C”. The sufficiency condition is considered to be satisfied if the causal effect of is large enough. On the other hand, to satisfy the necessary condition of the biconditional expression, the causal effect of must be considered as well (see Equation (11)):
DMOP-3. In this problem, we seek to find the rules that maximize susceptibility, a measure that quantifies the capacity of the antecedent to produce the consequent, and the population attributable fraction, a measure that indicates the proportion of observations of the consequences that were caused by the antecedent (see Equation (12)):
4.4. Evolution Proposal and Heuristically Guided Mining
Since direct exhaustive search strategies are not an option for mining a large data set, a heuristically guided mining mode is used. When in this mode, previous knowledge about the structure of the data is fed to a meta-heuristic optimization which evolves a set of specific patterns with the adequate structure to be Pareto front elements in the process of optimizing a selected objective function (i.e., absolute risk, relative risk, or any other).
The evolutionary algorithm proposed herein performs artificial evolution based on NSGA-II []. Some arguments for using NSGA-II include its mechanisms for solving combinatorial optimization problems with two and three objective functions [], particularly the following:
- The non-dominated sorting of solutions based on the Pareto dominance concept assigns a ranking to the non-dominated members of the population.
- A crowding distance strategy for assessing the density of individuals surrounding a particular solution allows for preserving a better population diversity.
Our proposal controls the selector structure of each pattern, allowing the system to answer specific user questions to discover association rules with particular semantics. In addition, the regulation of the search space exploration/exploitation process allows the generation of a wide range of causal rule complexities, from very simple rules with only one selector in the antecedent and consequent to more elaborate rules with the antecedent and consequent formed by several selectors. Once these patterns are known to have optimal structures and values, the mining system can directly search for these patterns in the actual data set. This has the effect of speeding up the mining process.
In order to guarantee the statistical significance of causal rules, two criteria are proposed. First, a diversity preservation criterion will be used as an essential evolution guide in the algorithm. Second, a statistical significance test on the set of causal rules mined is used.
Rule Evolution
The proposed algorithm evolves a population of selector lists as any other artificial evolution process would. Each list represents a possible association rule in the data set. The structure of those lists is straightforward, as is the structure of association rules. Each list has two main sections representing the antecedent and consequent of the rule, and then each section may have one or more subsections in correspondence with the selectors that conform it. The label and domain of all attributes are considered background knowledge, so the proper validation restrictions can be applied every time a new selector enters the expression.
During successive generations, the algorithm selects individuals from its population based on their fitness and applies recombination and mutation operators to generate new individuals, which are also evaluated by their aptitude. As the population size is fixed to N individuals, each new generation is selected from the best fit rules among previously known and newly generated rules:
- The stop criterion for the evolution process is triggered after 100 generations without improvement in the fitness value of the fittest rule.
- Recombination: This generates new individuals (new rules) from a pair of previously known rules and , referred to as the ancestor rules. Four new individuals are created using the following recombination modalities:
- Interchange: The antecedent and consequent from the ancestor rules are interchanged. Two new individuals are created: and .
- Set operations: The union (∪), intersection (∩), and symmetric difference (∆) operators are applied to the sets of selectors in the antecedent and consequent of the ancestor rules. For each one of those set operators, the antecedent of new rules results from applying the operator on sets and , and the consequent results from applying the same operator on sets and . Selectors with repeated attributes are pruned, as well as all cases that result in an empty antecedent or consequent. At most, three new individuals are created with this recombination process.
- Mutation: Each new rule generated by any recombination method is subjected to either an extension or a contraction transformation to introduce variability into the population. The extension randomly adds a new selector not previously present in the rule, while the contraction randomly prunes a selector from the rule.
- Elitism: The non-dominated sorting and crowding distance methods used by NSGA-II [] are adopted to select the fittest rule and preserve the diversity of the population.
5. Experiments and Results
We designed two main experiments. The first one explored the association rules in the complete data set (15,578,792 records). Here, our data mining methodology described in the previous section was applied while considering the three scenarios (A, B, and C) illustrated in Table 3. In this experiment, we intended to solve a single-objective optimization problem to find the best (maximum) values for each association measure function (equations described in Section 2.1) and validate the convergence of our proposed algorithm. Table 5 shows each case’s fitness mean (and standard deviation). The best values are shown in boldface. We considered 10 executions with different seeds for random generation. We established this number of executions for two reasons: the data mining process is computationally expensive, and we corroborated that after 10 executions, there was no variation in the results for the majority of the scenarios (standard deviation equals zero). In the classical measures, the best association rules reached a support function value that was low in each case’s fitness means (rather than 0.6), and the lift function was variable in these three scenarios. In the causal association measures, the functions of the probability of sufficiency and attributable fraction reported low values in scenarios A and C, respectively. In general, scenario B reported the maximum values for the association measures.

Table 5.
The maximum mean values found by an evolutionary algorithm for each objective function.
The second experiment had two purposes: (1) solve the DMOP described in Section 4.3 in order to compare the classic and causal association rule models as adequate and feasible tools for analyzing the COVID-19 pandemic phenomenon and (2) find association rules along four different and well-defined time periods (labeled as waves) to clearly characterize the behavior and tendencies of each contagion wave. Then, we applied our genetic algorithm in the three scenarios and the four waves for each DMOP. Then, we filtered the experimental results using criteria that selected non-dominated rules.
Table 6 reports the mean and standard deviation (in parenthesis) of the number of non-dominated rules found after 10 executions for each case. We can note that scenarios A and B, related to the comorbidities, age, gender, medical care, and outcome, were very consistent in the non-dominated rules. In contrast, scenario C (location and comorbidities) showed more variation in the association rules found.

Table 6.
The mean of the non-dominated rules found for each DMOP in all scenarios.
Figure 2, Figure 3 and Figure 4 show the obtained Pareto front with the levels of the maximum values reached by interesting rules according to causal measures. For Scenario B, DMOP-1, and DMOP-2, the mined rules were very similar. We appreciated some differences in scenarios B and C, where the absolute risk function, reciprocal absolute risk, population attributable fraction, and probability of sufficiency reported low values in the last period, called wave 4. Here, we can understand these results as a positive effect of the vaccine on the population.
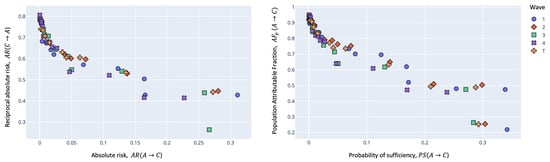
Figure 2.
Obtained Pareto fronts of DMOP-2 (absolute risk and reciprocal absolute risk) and DMOP-3 (probability of sufficiency and population attributable fraction) for all waves in Scenario A. The antecedent group is age and gender, and the consequent group is comorbidities.
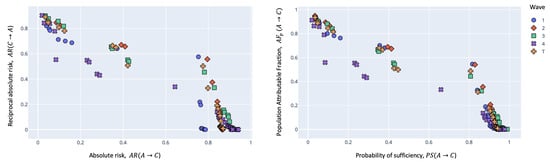
Figure 3.
Obtained Pareto fronts of DMOP-2 (absolute risk and reciprocal absolute risk) and DMOP-3 (probability of sufficiency and population attributable fraction) for all waves in Scenario B. The antecedent group is comorbidities, and the consequent group is medical care.
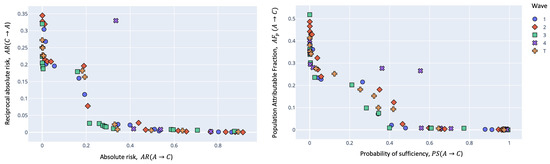
Figure 4.
Obtained Pareto fronts of DMOP-2 (absolute risk and reciprocal absolute risk) and DMOP-3 (probability of sufficiency and population attributable fraction) for all waves in Scenario C. The antecedent group is location, and the consequent group is comorbidities.
Table 7 reports the same non-dominated association rules discovered for the classic and causal measures in scenarios A and B. Both logical models for the data mining process found the same patterns demonstrating that causal measures can find interesting rules as a classical model. According to the results, the diseases with the greatest influence on the association rules found for the time periods called waves were diabetes, hypertension, pneumonia, and COPD. The ages of the patients were directly related to the diseases. Therefore, the majority of the population older than 53 had the highest comorbidity statistics as the most vulnerable sector. From the viewpoint of the association measures, we observed that the numerical values for the causal measures were more evident. Unlike these, the support and confidence numerical values were very small.

Table 7.
The best association rules were obtained in scenarios A (age and gender → comorbidities) and B (comorbidities and medical care). The evolutionary algorithm found these rules in the last population generated.
All supplementary material for this research can be found in https://github.com/sinisterra/mscgp (accessed on 1 November 2022). There, we provide the Python code used to generate all experiments.
6. Conclusions
In this research, we used NSGA-II mechanisms for guiding an association rule mining process to learn the behavior of the COVID-19 contagion phenomenon at a country-wide scale from an official government database in Mexico. Our mining algorithm includes non-classical crossover and mutation operators that have shown certain reliability for optimizing both classical and causal rule evaluation measures. Using artificial evolution as a guide to the mining process, we designed three experimentation scenarios as multi-objective optimization problems and considered the four officially identified waves of contagion.
Each experiment correctly found the rules with the maximum values for support, confidence, lift, absolute risk, and probability of sufficiency in a DMOP context. Since all those values were obtained under the constraint of having a confidence interval greater than or equal to one, they all had a strong correspondence with the concept of interesting rules expressed at the end of the Introduction section. Therefore, all mined rules identified the strongest associations between the antecedent and consequent in the database. The rules mined in DMOP-1 experiment were interesting in the classic mining sense, while the rules mined in the DMOP-2 and DMOP-3 experiments were interesting in the causal mining sense. The set of all rules mined during each experiment constituted the learned behavioral model of the studied phenomenon and brought forth interesting information about the phenomenon’s behavior.
The main contributions made by this work are the following:
- Design and testing of a new evolutionary algorithm for association rule mining with enough flexibility to integrate domain knowledge in order to solve single-objective and multi-objective association rule mining problems;
- The inclusion of a causal model to restate the semantics of the search process by providing a measure of the actionability of mined rules;
- The inclusion of a set of proposed crossover and mutation operators into the mining process.
Some of the next steps considered in this research include the following:
- Extending the evolution process with logical expressions;
- Incorporating a target group discovery algorithm;
- Considering the opposite optimization criteria to generate interesting rules;
- Including the proposed algorithm in other case studies.
Supplementary Materials
The supporting information is shared and available online by visiting https://github.com/sinisterra/mscgp.
Author Contributions
S.S.-S., S.G.-C. and M.P.-R. have contributed equally in conceptualization, methodology, and formal analysis; software and validation S.S.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Secretaría de Investigación y Posgrado (SIP-IPN) through projects/grants SIP-20230252 and SIP-20230105.
Acknowledgments
The authors wish to acknowledge and gratefully thank Consejo Nacional de Ciencia y Tecnología (CONACyT) and Instituto Politécnico Nacional (IPN).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sohrabi, C.; Alsafi, Z.; O’Neill, N.; Khan, M.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, R. World Health Organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19). Int. J. Surg. 2020, 76, 71–76. [Google Scholar] [CrossRef] [PubMed]
- López, L.; Rodó, X. The end of social confinement and COVID-19 re-emergence risk. Nat. Hum. Behav. 2020, 4, 746–755. [Google Scholar] [CrossRef] [PubMed]
- Telikani, A.; Gandomi, A.H.; Shahbahrami, A. A survey of evolutionary computation for association rule mining. Inf. Sci. 2020, 524, 318–352. [Google Scholar] [CrossRef]
- De Salud, S. COVID-19 Pandemic Data Set from Mexico. 2022. Available online: https://datos.gob.mx/busca/dataset/informacion-referente-a-casos-covid-19-en-mexico (accessed on 7 December 2022).
- Fürnkranz, J.; Gamberger, D.; Lavrač, N. Foundations of Rule Learning; Cognitive Technologies; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Pearl, J.; Mackenzie, D. The Book of Why: The New Science of Cause and Effect; Basic Books: New York, NY, USA, 2018. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning, and Inference; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2000. [Google Scholar]
- Hernán, M.A.; Robins, J.M. Causal Inference: What If; CRC Press: Boca Raton, FL, USA, 2020; p. 311. [Google Scholar]
- Mansournia, M.A.; Altman, D.G. Population attributable fraction. BMJ 2018, 360, k757. [Google Scholar] [CrossRef] [PubMed]
- Miettinen, O.S. Proportion of disease caused or prevented by a given exposure, trait or intervention. Am. J. Epidemiol. 1974, 99, 325–332. [Google Scholar] [CrossRef] [PubMed]
- Cortés-Martínez, K.V.; Estrada-Esquivel, H.; Martínez-Rebollar, A.; Hernández-Pérez, Y.; Ortiz-Hernández, J. The State of the Art of Data Mining Algorithms for Predicting the COVID-19 Pandemic. Axioms 2022, 11, 242. [Google Scholar] [CrossRef]
- Flora, J.; Khan, W.; Jin, J.; Jin, D.; Hussain, A.; Dajani, K.; Khan, B. Usefulness of Vaccine Adverse Event Reporting System for Machine-Learning Based Vaccine Research: A Case Study for COVID-19 Vaccines. Int. J. Mol. Sci. 2022, 23, 8235. [Google Scholar] [CrossRef] [PubMed]
- Shan, Z.; Miao, W. COVID-19 patient diagnosis and treatment data mining algorithm based on association rules. Expert Syst. 2021, e12814. [Google Scholar] [CrossRef] [PubMed]
- Wasiq, K.; Abir, H.; Ahmed, K.S.; Mohammed, A.J.; Raheel, N.; Panos, L. Analysing the impact of global demographic characteristics over the COVID-19 spread using class rule mining and pattern matching. R. Soc. 2021, 8, 201823. [Google Scholar]
- Tandan, M.; Acharya, Y.; Pokharel, S.; Timilsina, M. Discovering symptom patterns of COVID-19 patients using association rule mining. Comput. Biol. Med. 2021, 131, 104249. [Google Scholar] [CrossRef] [PubMed]
- Wakabi-Waiswa, P.P.; Baryamureeba, V. Extraction of interesting association rules using genetic algorithms. Adv. Syst. Model. ICT Appl. 2007. Available online: https://www.researchgate.net/publication/255610299_Extraction_of_interesting_association_rules_using_genetic_algorithms (accessed on 1 November 2022).
- Anand, R.; Vaid, A.; Singh, P.K. Association rule mining using multi-objective evolutionary algorithms: Strengths and challenges. In Proceedings of the 2009 World Congress on Nature and Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 385–390. [Google Scholar] [CrossRef]
- Martín, D.; Rosete, A.; Alcalá-Fdez, J.; Herrera, F. A multi-objective evolutionary algorithm for mining quantitative association rules. In Proceedings of the 2011 11th International Conference on Intelligent Systems Design and Applications, Cordoba, Spain, 22–24 November 2011; pp. 1397–1402. [Google Scholar]
- Luna, J.M.; Cano, A.; Ventura, S. Genetic Programming for Mining Association Rules in Relational Database Environments. In Handbook of Genetic Programming Applications; Springer International Publishing: Cham, Switzerland, 2015; pp. 431–450. [Google Scholar] [CrossRef]
- Elhilbawi, H.; Eldawlatly, S.; Mahdi, H. The Importance of Discretization Methods in Machine Learning Applications: A Case Study of Predicting ICU Mortality. In Advanced Machine Learning Technologies and Applications; Chang, K.C., Hassanien, A.E., Mincong, T., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 1339, pp. 214–224. [Google Scholar] [CrossRef]
- Tanabe, K. Pareto’s 80/20 rule and the Gaussian distribution. Phys. A Stat. Mech. Its Appl. 2018, 510, 635–640. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Shanu, V.; Millie, P.; Vaclav, S. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).