Spectral Analysis of the Finite Element Matrices Approximating 3D Linearly Elastic Structures and Multigrid Proposals

Abstract

The so-called material distribution methods for topology optimization cast the governing equation as an extended or fictitious domain problem, in which a coefficient field represents the design. In practice, the finite element method is typically used to approximate that kind of governing equations by using a large number of elements to discretize the design domain, and an element-wise constant function approximates the coefficient field in that domain. This paper presents a spectral analysis of the coefficient matrices associated with the linear systems stemming from the finite element discretization of a linearly elastic problem for an arbitrary coefficient field in three spatial dimensions. The given theoretical analysis is used for designing and studying an optimal multigrid method in the sense that the (arithmetic) cost for solving the problem, up to a fixed desired accuracy, is linear in the corresponding matrix size. Few selected numerical examples are presented and discussed in connection with the theoretical findings.

1. Introduction

In our previous paper [1], we applied the theory of generalized locally Toeplitz (GLT) sequences to compute and analyze the asymptotic spectral distribution of the sequence of stiffness matrices ${\left\{{\mathit{K}}_n\right\}}_n$, with ${\mathit{K}}_n$ being the finite element (FE) approximation of the considered one spatial dimension topology optimization problem, for a given fineness parameter associated to n. In a later contribution [2], we extended the analysis to the two-dimensional setting using so-called multilevel block GLT sequences. In this paper, we further expand the theory to cover the three-dimensional case.

Since the first material distribution method for topology design was introduced in the late 1980s [3], topology optimization [4,5], a well-known computational tool for finding the optimal distribution of material within a given design domain, has been studied extensively. The material distribution topology optimization has contributed to the development of several areas, such as electromagnetic [6,7,8], fluid–structure interaction [9,10], acoustics [11,12], additive manufacturing [13], and especially (non-)linear elasticity [14,15,16]. For problems in linear elasticity, which motivates the study in this paper, the most common method to solve this type of problem is the so-called density-based or material distribution approach. In this approach, a so-called material indicator function $\alpha \left(\mathit{x}\right)$—typically referred to as the density or the physical design—models the presence/absence of material; $\alpha =1$ where material is present, else $\alpha =0$. However, the binary design problem is computationally intractable. A standard approach to make the problem computationally feasible is employing a combination of relaxation, penalization, and filtering, in which the physical density is defined as $\rho \left(x\right)=\underline{\alpha }+(1-\underline{\alpha })g\left(\mathcal{F}\left(\alpha \right)\left(x\right)\right)$ by $\underline{\rho }\ge 0$, which is a constant, the penalization operator is g, and the filtering procedure is $\mathcal{F}$. In this approach, the finite element method (FEM) is the standard choice for generating numerical solutions of a linearly elastic boundary value problem. In practice, the physical design is typically represented as an element-wise constant function. Moreover, a combination of allowing intermediate values of the design, filtering, and penalization has been crucial for the success of these methods. In this paper, we limit our attention to studying the linear system that stems from the FE discretization of the governing equation and its solution. From a high performance computing perspective, this limitation is natural since the computational effort in solving topology optimization problems is dominated by the cost of solving the discretized governing equations—a fact that is particularly prominent when studying three-dimensional problems. Over the last decades, there has been significant work in improving the efficiency of topology optimization, aiming at solving large-scale design problems [17,18,19,20,21]. Although our study is directly motivated by the material-distribution or density-based approach to topology optimization, the work is relevant for other design descriptions, such as level sets [22,23] or moving morphable components [24,25,26,27], provided that the physics description uses the so-called ersatz material approach, which in some cases can be justified rigorously [4].

The theory of multilevel block GLT sequences [28,29] is a generalization of the GLT sequences theory [30,31] that is typically used for computing/analyzing the spectral distribution of matrix sequences arising from, for example, the numerical discretization, such as the FE approximation of partial differential equations (PDEs) with proper boundary conditions. In the considered matrix sequences, the size of the given linear systems $d_n$ increases with n, in which $d_n$ tends to infinity as $n\to \infty$. In this paper, the entire sequence of linear systems with increasing size arising from the three spatial dimension problems is the primary consideration. Under mild conditions, essentially relying on regularity assumptions on the meshes, we show that the sequence of discretization matrices has an asymptotic spectral distribution. By leveraging the theory of multilevel block GLT sequences, we now extend our previous works [1,2] further to perform a detailed spectral analysis of the linear systems associated with the FE discretization of the governing equation in the three-dimensional setting. Similar to our previous work [2], we also make use of the information obtained from the spectral symbol f to design a fast, multigrid solver in three dimensions for optimizing the (arithmetic) cost to solve the related linear systems up to a fixed desired accuracy, which is proportional to the matrix–vector cost, which is linear in the corresponding matrix size. This solver is also verified and comes up with very satisfying numerical results, in terms of the linear cost and number of iterations, which are bounded independently of the matrix size and mildly depending on the desired accuracy.

In the following sections, we will go into detail on the problem description, spectral analysis, multigrid method, and a brief conclusion. The description of the continuous problem and the resulting coefficient matrices arising from our FE approximation is delivered in Section 2 and Section 3 is devoted to the spectral analysis of the FE matrices from the perspective of the GLT theory. In Section 4, a brief account of multigrid methods with special attention to the block case encountered in the present context is given, and the spectral information is a core component in the development of the multigrid proposal for our specific 3D setting presented in Section 5. Eventually, the conclusions are reported in Section 6, and some relevant model information is explained in Appendix A and Appendix B.

2. Problem Description

We consider a linearly elastic structure that occupies (part of) the hyper-rectangular domain $\mathrm{\Omega }\subset {\mathbb{R}}^3$. In particular, we are interested in the setting used in material distribution based topology optimization, where a function, typically denoted as the physical density, $\rho :\mathrm{\Omega }\to [0,1]$, describes the layout of the unloaded structure. We assume that the structure is clamped along the boundary portion ${\mathrm{\Gamma }}_D\subset \partial \mathrm{\Omega }$. Moreover, we let $b\in L^2{\left(\mathrm{\Omega }\right)}^3$ be a given body load (a volume force) in $\mathrm{\Omega }$, $t\in L^2{\left({\mathrm{\Gamma }}_F\right)}^3$ be the surface traction acting on the non-clamped boundary ${\mathrm{\Gamma }}_F\subset \partial \mathrm{\Omega }$ of the solid, and u denote the resulting equilibrium displacement, which solves the following problem.

$$\mathrm{Find}u\in \mathcal{U}\mathrm{such}\mathrm{that}a(u,v;\rho )=\ell \left(v\right)\forall v\in \mathcal{U},$$

(1)

where the set of all kinematically admissible displacements of the structure is

$$\mathcal{U}=\left\{u\in H^1{\left(\mathrm{\Omega }\right)}^3{\mid u|}_{{\mathrm{\Gamma }}_D}\equiv 0\right\}.$$

The energy bilinear form a and the load linear form ℓ are defined as

$$\begin{array}{cc}\hfill a(u,v;\rho )& =\underset{\mathrm{\Omega }}{\int }\rho \left(E_cϵ\left(u\right)\right):ϵ\left(v\right),\hfill \\ \hfill \ell \left(v\right)& =\underset{{\mathrm{\Gamma }}_F}{\int }t·v+\underset{\mathrm{\Omega }}{\int }b·v,\hfill \end{array}$$

where $ϵ\left(\mathit{u}\right)=\left(\nabla u+\nabla u^T\right)/2$ is the strain tensor of u. The colon “:” denotes the full contraction between the two tensors; when using the standard basis, the full contraction of the two matrices is their Frobenius scalar product. $E_c$ is a constant fourth-order elasticity tensor. In this paper, we study an FE discretization of problem (1), in which the physical density is approximated by an element-wise constant function, which is typical in material distribution based topology optimization. The domain $\mathrm{\Omega }$ is discretized into n trilinear hexahedral elements and then applying FE approximation, the variational problem (1) is reduced to the linear system

$${\mathit{K}}_n\left(\rho \right)\mathit{u}=\mathit{f},$$

where $\mathit{u}$ and $\mathit{f}$ are the nodal displacement and load vector, respectively, and ${\mathit{K}}_n\left(\rho \right)$ is the stiffness matrix of element-wise constant physical density function $\rho$—the entries of the vector $\mathit{\rho }=[{\rho }_1,{\rho }_2,\cdots ,{\rho }_n]$ are the element values of $\rho$; that is, ${\rho }_i$ is the value of $\rho$ in the ith element in the FE mesh. The stiffness matrix ${\mathit{K}}_n$ is typically assembled by looping over each element so that

$${\mathit{K}}_n\left(\rho \right)=\sum _{i=1}^n{\rho }_i{\mathit{K}}_e^{\left(i\right)},$$

where ${\mathit{K}}_e^{\left(i\right)}$ is the element stiffness matrix. We emphasize that the formal expression of the relevant matrices is a key ingredient for applying the multilevel block GLT theory to produce a global spectral description of the matrix sequences under consideration. More precisely, the non-zero blocks of three-dimensional element stiffness matrix can be expressed as

$${\mathit{K}}_e=\frac{h}{2}\frac{E_0}{1+\nu }\left[\begin{array}{cccccccc}{K}_1& K_2& K_3& K_4& K_5& K_6& K_7& K_8\\ & K_9& K_{10}& K_{11}& K_{12}& K_{13}& K_{14}& K_7\\ & & K_{15}& K_{16}& K_{17}& K_{18}& K_{13}& K_6\\ & & & K_{19}& K_{20}& K_{17}& K_{12}& K_5\\ & & & & K_{19}& K_{16}& K_{11}& K_4\\ & & sym.& & & K_{15}& K_{10}& K_3\\ & & & & & & K_9& K_2\\ & & & & & & & K_1\end{array}\right]$$

(2)

where each $K_i$ block has size $3\times 3$ and is associated with one node on a so-called reference element, $E_0$ is Young’s modulus, and $\nu$ is Poisson’s ratio. More details are provided in Appendix A for the explicit expressions for the element stiffness matrix and in Appendix B for the stress–strain relation and various bounds. With regard to Equation (2), the lower part of the matrix is not explicitly given because the matrix is globally real symmetric and so is every block $K_l,l=1,\dots ,20$, whose expressions are reported in Appendix A, Equation (A1).

3. Spectral Analysis

The current section is devoted to the spectral analysis of the FE coefficient matrices derived in the previous section and is complemented by a selection of numerical tests that confirm the theoretical analysis (more numerical experiments have been performed but here we report only a selection for the sake of brevity). We limit our focus to isotropic materials; for more information about various bounds, see the discussion in Appendix B. From a mathematics perspective, this means that we limit our attention to when the Poisson’s ratio $\nu$ is in the range $[0,0.5)$. In particular, Section 3.1 contains the minimal set of preliminary concepts and tools, while Section 3.2 and Section 3.3 are focused on the specific study in 3D in the constant and variable coefficient cases, respectively.

3.1. Premises

The premises include the formal definition of the eigenvalue and singular value distribution, the notion of multi-indexing, the concepts of multilevel block Toeplitz matrices, multilevel block sampling matrices, and multilevel block GLT matrix sequences.

3.1.1. Singular Value/Eigenvalue Distributions

We first give the formal definitions, and then we briefly discuss their informal and practical meaning.

Definition 1.

Let$r,t$ be two positive integers. Let ${\left\{A_n\right\}}_n$ be a sequence of matrices, with $A_n$ of size $d_n$ with eigenvalues ${\lambda }_1\left(A_n\right),\dots ,{\lambda }_{d_n}\left(A_n\right)$ and singular values ${\sigma }_1\left(A_n\right),\dots ,{\sigma }_{d_n}\left(A_n\right)$. Furthermore, let $f:D\subset {\mathbb{R}}^t\to {\mathbb{C}}^{r\times r}$ be a measurable function defined on a set D with $0<{\mu }_t\left(D\right)<\infty$, and with ${\mu }_t(·)$ denoting the Lebesgue measure on ${\mathbb{C}}^t$.

• We say that ${\left\{A_n\right\}}_n$ has a (asymptotic) singular value distribution described by f, and we write ${\left\{A_n\right\}}_n{\sim }_{\sigma }f$, if

  $$\underset{n\to \infty }{lim}\frac{1}{d_n}\sum _{i=1}^{d_n}F\left({\sigma }_i\left(A_n\right)\right)=\frac{1}{{\mu }_t\left(D\right)}{\int }_D\frac{{\sum }_{i=1}^{r}F\left({\sigma }_i\left(f\left(\mathbf{x}\right)\right)\right)}{r}\mathrm{d}\mathbf{x},\forall F\in C_c\left(\mathbb{R}\right),$$

  (3)

  with ${\sigma }_1\left(f\right),\dots ,{\sigma }_r\left(f\right)$ being the singular values of f, each of them being a measurable function non-negative almost everywhere.
• We say that ${\left\{A_n\right\}}_n$ has a (asymptotic) spectral (or eigenvalue) distribution described by f, and we write ${\left\{A_n\right\}}_n{\sim }_{\lambda }f$, if

  $$\underset{n\to \infty }{lim}\frac{1}{d_n}\sum _{i=1}^{d_n}F\left({\lambda }_i\left(A_n\right)\right)=\frac{1}{{\mu }_t\left(D\right)}{\int }_D\frac{{\sum }_{i=1}^{r}F\left({\lambda }_i\left(f\left(\mathbf{x}\right)\right)\right)}{r}\mathrm{d}\mathbf{x},\forall F\in C_c\left(\mathbb{C}\right),$$

  (4)

  with ${\lambda }_1\left(f\right),\dots ,{\lambda }_r\left(f\right)$ being the eigenvalues of f, each of them being a complex-valued measurable function.

If ${\left\{A_n\right\}}_n$ has both a singular value and an eigenvalue distribution described by f, we write ${\left\{A_n\right\}}_n{\sim }_{\sigma ,\lambda }f$. (In practice, in the Toeplitz setting and often in the GLT setting, the parameter r can be read at a matrix level as the size of the elementary blocks which form the global matrix $A_n$, as it will be clear both in our stiffness matrices in Section 3.2 and Section 3.3, and in the block Toeplitz/block diagonal sampling structures in Section 3.1.2.)

The symbol f contains spectral/singular value information briefly described informally as follows. With reference to relation (4), the eigenvalues of ${\mathit{K}}_n$ are partitioned into r subsets of the same cardinality, except possibly for a small number of outliers, such that the ith subset is approximately formed by the samples of ${\lambda }_i\left(f\right)$ over a uniform grid in D, $i=1,\dots ,r$. Thus, provided that n is large enough, the symbol f provides a ’compact’ and quite accurate description of the spectrum of the matrices ${\mathit{K}}_n$. Similarly, relation (3) has the same meaning when talking of the singular values of ${\mathit{K}}_n$ and by replacing ${\lambda }_i\left(f\right)$ with ${\sigma }_i\left(f\right)$, $i=1,\dots ,r$.

3.1.2. Multilevel Block Toeplitz Matrices, Multilevel Block Diagonal Sampling Matrices, and Multilevel Block GLT Sequences

The present section is specifically devoted to matrix-theoretic notations and definitions, which are essential when dealing with multi-dimensional problems and with the related sequences of matrices.

Definition 2.

A multi-index $\mathit{i}\in {\mathbb{Z}}^d$, also called a d-index, is a (row) vector in ${\mathbb{Z}}^d$, whose components are denoted by $i_1,\dots ,i_d$.

• $\mathbf{0},{1},\mathbf{2},\dots$ are the vectors of all zeros, all ones, all twos, … (their size will be clear from the context).
• For any d-index $\mathit{m}\in {\mathbb{N}}_{+}^d$, we set $N\left(\mathit{m}\right)={\prod }_{j=1}^d{m}_j$ and we write $\mathit{m}\to \infty$ to indicate that $min\left(\mathit{m}\right)\to \infty$.
• If $\mathit{h},\mathit{k}$ are d-indices, $\mathit{h}\le \mathit{k}$ means that $h_r\le k_r$ for all $r=1,\dots ,d$.
• If $\mathit{h},\mathit{k}$ are d-indices such that $\mathit{h}\le \mathit{k}$, the multi-index range $[\mathit{h},\dots ,\mathit{k}]$ is the set $\{\mathit{j}\in {\mathbb{Z}}^d:\mathit{h}\le \mathit{j}\le \mathit{k}\}$. The standard lexicographic ordering is assumed uniformly

  $${\left[\dots {\left[{\left[(j_1,\dots ,j_d)\right]}_{j_d=h_d,\dots ,k_d}\right]}_{j_{d-1}=h_{d-1},\dots ,k_{d-1}}\dots \right]}_{j_1=h_1,\dots ,k_1}.$$

With regard to the previous definition, in the case $d=2$, the lexicographic ordering is the following: $(h_1,h_2)$, $(h_1,h_2+1)$, $\dots ,$$(h_1,k_2)$, $(h_1+1,h_2)$,$(h_1+1,h_2+1),\dots (h_1+1,k_2)$, $\dots (k_1,h_1)$, $(k_1,h_1+1)$, $\dots ,$$(k_1,k_2)$. Notice that, in general, a multi-index range $[\mathit{h},\dots ,\mathit{k}]$, $\mathit{h}\le \mathit{k}$ is used with $\mathit{h}=\mathbf{0}$ or with $\mathit{h}=\mathbf{1}$.

Definition 3. (Multilevel) Block Toeplitz Matrices).

Given $\mathbf{n}\in {\mathbb{N}}^d$, a matrix of the form

$${\left[A_{\mathbf{i}-\mathbf{j}}\right]}_{\mathbf{i},\mathbf{j}=\mathbf{e}}^{\mathbf{n}}\in {\mathbb{C}}^{N\left(\mathbf{n}\right)r\times N\left(\mathbf{n}\right)r}$$

with $\mathbf{e}$ vector of all ones, with blocks $A_{\mathbf{k}}\in {\mathbb{C}}^{r\times r}$, $\mathbf{k}=-(\mathbf{n}-\mathbf{e}),\dots ,\mathbf{n}-\mathbf{e}$, is called a multilevel block Toeplitz matrix, or, more precisely, a d-level r-block Toeplitz matrix. Let $\varphi :{[-\pi ,\pi ]}^d\to {\mathbb{C}}^{r\times r}$ be a matrix-valued function in which each entry belongs to $L^1\left({[-\pi ,\pi ]}^d\right)$. We denote the Fourier coefficients of the generating function ϕ as

$${\widehat{f}}_{\mathbf{k}}=\frac{1}{{\left(2\pi \right)}^d}{\int }_{{[-\pi ,\pi ]}^d}\varphi \left(\theta \right)e^{-\widehat{l}(\mathbf{k},\mathit{\theta })}d\mathit{\theta }\in {\mathbb{C}}^{r\times r},\mathbf{k}\in {\mathbb{Z}}^d,$$

where the integrals are computed componentwise, ${\widehat{l}}^2=-1$, and $(\mathbf{k},\mathit{\theta })=k_1{\theta }_1+\dots +k_d{\theta }_d$. For every $\mathbf{n}\in {\mathbb{N}}^d$, the $\mathbf{n}$th Toeplitz matrix associated with ϕ is defined as

$$T_{\mathbf{n}}\left(\varphi \right):={\left[{\widehat{f}}_{\mathbf{i}-\mathbf{j}}\right]}_{\mathbf{i},\mathbf{j}=\mathbf{e}}^{\mathbf{n}}$$

or, equivalently, as

$$T_{\mathbf{n}}\left(\varphi \right)=\sum _{|j_1|<n_1}\dots \sum _{|j_d|<n_d}[J_{n_1}^{\left(j_1\right)}\otimes \dots J_{n_d}^{\left(j_d\right)}]\otimes {\widehat{f}}_{(j_1,\dots ,j_d)},$$

where ⊗ denotes the (Kronecker) tensor product of matrices, while $J_m^{\left(l\right)}$ is the matrix of order m whose $(i,j)$ entry equals 1 if $i-j=l$ and zero otherwise. We call ${\left\{T_{\mathbf{n}}\left(\varphi \right)\right\}}_{\mathbf{n}\in {\mathbb{N}}^d}$ the family of (multilevel block) Toeplitz matrices associated with ϕ, which, in turn, is called the generating function of ${\left\{T_{\mathbf{n}}\left(\varphi \right)\right\}}_{\mathbf{n}\in {\mathbb{N}}^d}$.

Definition 4. (Multilevel) Block Diagonal Sampling Matrices).

For $n\in \mathbb{N}$ and $a:[0,1]\to {\mathbb{C}}^{r\times r}$, we define the block diagonal sampling matrix $D_n\left(a\right)$ as the diagonal matrix

$$D_n\left(a\right)=\underset{i=1,\dots ,n}{\mathrm{diag}}a\left(\frac{i}{n}\right)=\left[\begin{array}{cccc}a\left(\frac{1}{n}\right)& & & \\ & a\left(\frac{2}{n}\right)& & \\ & & \ddots & \\ & & & a\left(1\right)\end{array}\right]\in {\mathbb{C}}^{rn\times rn}.$$

For $\mathit{n}\in {\mathbb{N}}^d$ and $a:{[0,1]}^d\to {\mathbb{C}}^{r\times r}$, we define the multilevel block diagonal sampling matrix $D_{\mathit{n}}\left(a\right)$ as the block diagonal matrix

$$D_{\mathit{n}}\left(a\right)=\underset{\mathit{i}=\mathbf{1},\dots ,\mathit{n}}{\mathrm{diag}}a\left(\frac{\mathit{i}}{\mathit{n}}\right)\in {\mathbb{C}}^{rN\left(\mathit{n}\right)\times rN\left(\mathit{n}\right)},$$

with the lexicographical ordering discussed at the beginning of Section 3.1.2.

Definition 5. (Zero-Distributed Sequences of Matrices).

According to Definition 1, a sequence of matrices ${\left\{Z_n\right\}}_n$ such that

$${\left\{Z_n\right\}}_n{\sim }_{\sigma }0$$

is referred to as a zero-distributed sequence. Note that, for any $r\ge 1$, ${\left\{Z_n\right\}}_n{\sim }_{\sigma }0$ is equivalent to ${\left\{Z_n\right\}}_n{\sim }_{\sigma }{O}_r$ (notice that $O_m$ and $I_m$ denote the $m\times m$ zero matrix and the $m\times m$ identity matrix, respectively).

Proposition 1 provides an important characterization of zero-distributed sequences together with a useful sufficient condition for detecting such sequences. Throughout this paper, we use the natural convention $1/\infty =0$.

Proposition 1.

[30] Let ${\left\{Z_n\right\}}_n$ be a sequence of matrices, with $Z_n$ of size $d_n$, and let $\parallel ·\parallel$ be the standard spectral matrix norm (the one induced by the Euclidean vector norm).

• ${\left\{Z_n\right\}}_n$ is zero distributed if and only if $Z_n=R_n+N_n$ with $\mathrm{rank}\left(R_n\right)/d_n\to 0$ and $\parallel N_n\parallel \to 0$ as $n\to \infty$.
• ${\left\{Z_n\right\}}_n$ is zero distributed if there exists a $p\in [1,\infty ]$ such that $\parallel Z_n{\parallel }_p/{\left(d_n\right)}^{1/p}\to 0$ as $n\to \infty$.

(Multilevel) Block GLT Matrix Sequences. Now, we give a very concise and operational description of the multilevel block GLT sequences, from which it will be clear that the multilevel block Toeplitz structures, the zero-distributed matrix sequences, and the multilevel block diagonal sampling matrices represent the basic building components. All the material is taken from the books [30,31] and from the papers [28,32].

Let $d,r\ge 1$ be fixed positive integers. A multilevel r-block GLT sequence (or simply a GLT sequence if $d,r$ can be inferred from the context or we do not need/want to specify them) is a special r-block matrix sequence ${\left\{A_n\right\}}_n$ equipped with a measurable function $\kappa :{[0,1]}^d\times {[-\pi ,\pi ]}^d\to {\mathbb{C}}^{r\times r}$, the so-called symbol. We use the notation ${\left\{A_n\right\}}_n{\sim }_{\mathrm{GLT}}\kappa$ to indicate that ${\left\{A_n\right\}}_n$ is a GLT sequence with symbol $\kappa$. The symbol of a GLT sequence is unique in the sense that if ${\left\{A_n\right\}}_n{\sim }_{\mathrm{GLT}}\kappa$ and ${\left\{A_n\right\}}_n{\sim }_{\mathrm{GLT}}\varsigma$ then $\kappa =\varsigma$ a.e. in ${[0,1]}^d\times {[-\pi ,\pi ]}^d$. The main properties of r-block GLT sequences proved in [28] are listed below. If A is a matrix, we denote by $A^{†}$ the Moore–Penrose pseudoinverse of A (recall that $A^{†}=A^{-1}$ whenever A is invertible).

GLT 1

If ${\left\{A_n\right\}}_n{\sim }_{\mathrm{GLT}}\kappa$ then ${\left\{A_n\right\}}_n{\sim }_{\sigma }\kappa$. If moreover each $A_n$ is Hermitian, then ${\left\{A_n\right\}}_n{\sim }_{\lambda }\kappa$.

GLT 2

We have the following:

• ${\left\{T_n\left(\varphi \right)\right\}}_n{\sim }_{\mathrm{GLT}}\kappa (\mathbf{x},\mathit{\theta })=\varphi \left(\mathit{\theta }\right)$ if $\varphi :{[-\pi ,\pi ]}^d\to {\mathbb{C}}^{r\times r}$ is in $L^1\left({[-\pi ,\pi ]}^d\right)$;
• ${\left\{D_n\left(a\right)\right\}}_n{\sim }_{\mathrm{GLT}}\kappa (\mathbf{x},\mathit{\theta })=a\left(\mathbf{x}\right)$ if $a:{[0,1]}^d\to {\mathbb{C}}^{r\times r}$ is Riemann integrable;
• ${\left\{Z_n\right\}}_n{\sim }_{\mathrm{GLT}}\kappa (\mathbf{x},\mathit{\theta })=O_r$ if and only if ${\left\{Z_n\right\}}_n{\sim }_{\sigma }0$ (zero-distributed sequences coincide exactly with the GLT sequences having GLT symbol equal to $O_r$ a.e.).

GLT 3

If ${\left\{A_n\right\}}_n{\sim }_{\mathrm{GLT}}\kappa$ and ${\left\{B_n\right\}}_n{\sim }_{\mathrm{GLT}}\varsigma$, then

• ${\left\{A_n^{\ast }\right\}}_n{\sim }_{\mathrm{GLT}}{\kappa }^{\ast }$;
• ${\{\alpha A_n+\beta B_n\}}_n{\sim }_{\mathrm{GLT}}\alpha \kappa +\beta \varsigma$ for all $\alpha ,\beta \in \mathbb{C}$;
• ${\left\{A_n{B}_n\right\}}_n{\sim }_{\mathrm{GLT}}\kappa \varsigma$;
• ${\left\{A_n^{†}\right\}}_n{\sim }_{\mathrm{GLT}}{\kappa }^{-1}$ provided that $\kappa$ is invertible a.e.

3.2. Constant Coefficient Case $\rho \equiv 1$

In the current section, we report the derivation and the formal expression of the symbol for the matrix sequences in the constant coefficient setting $\rho \equiv 1$, according to the standard notion of generating function in the Toeplitz theory (see Section 3.1.2 and the paper by Garoni et al. [29] for more details) and according to the notion of symbol reported in Definition 1.

3.2.1. Symbol Definition

Recall that the computational domain $\mathrm{\Omega }$ is a hyper-rectangular domain in 3D, and the boundary of $\mathrm{\Omega }$ comprises six sides. Let $A_n(1,{\mathtt{DN}}^5)$ be the stiffness matrix obtained with a ${\mathbb{Q}}_1$ FE approximation with proper boundary conditions, Dirichlet ‘D’ on one of $\mathrm{\Omega }$’s sides and Neumann ‘N’ in the other five sides of $\mathrm{\Omega }$ (and hence the formal notation $A_n(1,{\mathtt{DN}}^5)$), where we have chosen a uniform meshing with n intervals in the $x_1$ direction, n intervals in the $x_2$ direction, and n intervals in the $x_3$ direction. According to the previously considered ordering of the nodes, the matrix $A_n(1,{\mathtt{DN}}^5)$ is a three-level block tridiagonal structure of size n with two-level tridiagonal blocks of size $n+1$, with tridiagonal blocks of size $n+1$, whose elements are small matrices of size 3. We notice that the size is dictated by all the meshpoints, including those in the boundaries when considering Neumann boundary conditions, while only the internal meshpoints are involved when the Dirichlet boundary conditions are enforced.

In accordance with the 2D case [2], if all the boundary conditions are of the Dirichlet type, then we obtain a matrix $A_n(1,{\mathtt{D}}^6)$, which is a three-level block Toeplitz structure with elementary blocks of size 3, having global dimension $3{(n-1)}^3$, since all the nodes on the boundaries are not unknowns. More precisely, we obtain

$$A_n(1,{\mathtt{D}}^6)=\left[\begin{array}{ccc}{a}_0& a_{-1}& \\ a_1& a_0& a_{-1}& \\ & \ddots & \ddots & \ddots & \\ & & a_1& a_0& a_{-1}\\ & & & a_1& a_0\end{array}\right]=\mathrm{tridiag}{\left(a_i\right)}_{i=-1,0,1},$$

and, for $i=-1,0,1$, we have

$$a_i=\left[\begin{array}{ccc}{a}_{i0}& a_{i-1}& \\ a_{i1}& a_{i0}& a_{i-1}& \\ & \ddots & \ddots & \ddots & \\ & & a_{i1}& a_{i0}& a_{i-1}\\ & & & a_{i1}& a_{i0}\end{array}\right]=\mathrm{tridiag}{\left(a_{ij}\right)}_{j=-1,0,1},$$

while, for $i,j=-1,0,1$, the following block tridiagonal matrices are defined:

$$a_{ij}=\left[\begin{array}{ccc}{a}_{ij0}& a_{ij-1}& \\ a_{ij1}& a_{ij0}& a_{ij-1}& \\ & \ddots & \ddots & \ddots & \\ & & a_{ij1}& a_{ij0}& a_{ij-1}\\ & & & a_{ij1}& a_{ij0}\end{array}\right]=\mathrm{tridiag}{\left(a_{ijk}\right)}_{k=-1,0,1}.$$

By reading the entries of $A_n(1,{\mathtt{D}}^6)$, analogously to the process in the 2D setting as in [2], we can compute explicitly the related generating function, following the rules given in Definition 3:

$$\begin{array}{cc}\hfill & f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)=f_{a_0}({\theta }_1,{\theta }_2)+f_{a_{-1}}({\theta }_1,{\theta }_2)e^{-\widehat{l}{\theta }_3}+f_{a_1}({\theta }_1,{\theta }_2)e^{\widehat{l}{\theta }_3}\hfill \\ & =\left(f_{a_{00}}\left({\theta }_1\right)+f_{a_{0-1}}\left({\theta }_1\right)e^{-\widehat{l}{\theta }_2}+f_{a_{01}}\left({\theta }_1\right)e^{\widehat{l}{\theta }_2}\right)\hfill \\ & +\left(f_{a_{-10}}\left({\theta }_1\right)+f_{a_{-1-1}}\left({\theta }_1\right)e^{-\widehat{l}{\theta }_2}+f_{a_{-11}}\left({\theta }_1\right)e^{\widehat{l}{\theta }_2}\right)e^{-\widehat{l}{\theta }_3}\hfill \\ & +\left(f_{a_{10}}\left({\theta }_1\right)+f_{a_{1-1}}\left({\theta }_1\right)e^{-\widehat{l}{\theta }_2}+f_{a_{11}}\left({\theta }_1\right)e^{\widehat{l}{\theta }_2}\right)e^{\widehat{l}{\theta }_3}\hfill \\ & =\left(a_{000}+a_{00-1}{e}^{-\widehat{l}{\theta }_1}+a_{001}{e}^{\widehat{l}{\theta }_1}\right)+\left(a_{0-10}+a_{0-1-1}{e}^{-\widehat{l}{\theta }_1}+a_{0-11}{e}^{\widehat{l}{\theta }_1}\right)e^{-\widehat{l}{\theta }_2}\hfill \\ & +\left(a_{010}+a_{01-1}{e}^{-\widehat{l}{\theta }_1}+a_{011}{e}^{\widehat{l}{\theta }_1}\right)e^{\widehat{l}{\theta }_2}\hfill \\ & +[\left(a_{-100}+a_{-10-1}{e}^{-\widehat{l}{\theta }_1}+a_{-101}{e}^{\widehat{l}{\theta }_1}\right)\hfill \\ & +\left(a_{-1-10}+a_{-1-1-1}{e}^{-\widehat{l}{\theta }_1}+a_{-1-11}{e}^{\widehat{l}{\theta }_1}\right)e^{-\widehat{l}{\theta }_2}\hfill \\ & +\left(a_{-110}+a_{-11-1}{e}^{-\widehat{l}{\theta }_1}+a_{-111}{e}^{\widehat{l}{\theta }_1}\right)e^{\widehat{l}{\theta }_2}]e^{-\widehat{l}{\theta }_3}\hfill \\ & +[\left(a_{100}+a_{10-1}{e}^{-\widehat{l}{\theta }_1}+a_{101}{e}^{\widehat{l}{\theta }_1}\right)+\left(a_{1-10}+a_{1-1-1}{e}^{-\widehat{l}{\theta }_1}+a_{1-11}{e}^{\widehat{l}{\theta }_1}\right)e^{-\widehat{l}{\theta }_2}\hfill \\ & +\left(a_{110}+a_{11-1}{e}^{-\widehat{l}{\theta }_1}+a_{111}{e}^{\widehat{l}{\theta }_1}\right)e^{\widehat{l}{\theta }_2}]e^{\widehat{l}{\theta }_3},\hfill \end{array}$$

where every $a_{rst}$, $r,s,t\in \{-1,0,1\}$ is a $3\times 3$ matrix because three degrees of freedom are associated to each node of the mesh. Each $a_{rst}$ is a sum of the building blocks of the elementary matrix (2). More precisely, in terms of the block matrices $K_i$, cf. definition (A1) in Appendix A, we can write

$$\begin{array}{ccccc}\hfill a_{000}& =2\left(K_1+K_9+K_{15}+K_{19}\right),\hfill & \hfill a_{001}& =a_{00-1}=2\left(K_2+K_{16}\right),\hfill & \\ \hfill a_{010}& =a_{0-10}=2\left(K_3+K_{11}\right),\hfill & \hfill a_{011}& =a_{0-1-1}=2K_4,\hfill & \\ \hfill a_{01-1}& =a_{0-11}=2K_{10},\hfill & \hfill a_{100}& =a_{-100}=2\left(K_5+2K_{13}\right),\hfill & \\ \hfill a_{101}& =a_{-10-1}=2K_6,\hfill & \hfill a_{10-1}& =a_{-101}=2K_{12},\hfill & \\ \hfill a_{110}& =a_{-1-10}=2K_7,\hfill & \hfill a_{1-10}& =a_{-110}=2K_{17},\hfill & \\ \hfill a_{111}& =a_{-1-1-1}=K_8,\hfill & \hfill a_{11-1}& =a_{-1-11}=K_{14},\hfill & \\ \hfill a_{1-11}& =a_{-11-1}=K_{18},\hfill & \hfill a_{-111}& =a_{1-1-1}=K_{20}.\hfill & \end{array}$$

Thus, we have

$$f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)=\left[\begin{array}{ccc}{f}_{11}({\theta }_1,{\theta }_2,{\theta }_3)& f_{12}({\theta }_1,{\theta }_2,{\theta }_3)& f_{13}({\theta }_1,{\theta }_2,{\theta }_3)\\ f_{12}({\theta }_1,{\theta }_2,{\theta }_3)& f_{22}({\theta }_1,{\theta }_2,{\theta }_3)& f_{23}({\theta }_1,{\theta }_2,{\theta }_3)\\ f_{13}({\theta }_1,{\theta }_2,{\theta }_3)& f_{23}({\theta }_1,{\theta }_2,{\theta }_3)& f_{33}({\theta }_1,{\theta }_2,{\theta }_3)\end{array}\right],$$

(5)

where

$$\begin{array}{cc}\hfill f_{11}({\theta }_1,{\theta }_2,{\theta }_3)& =8k_1+8k_{3}cos\left({\theta }_1\right)+2cos\left({\theta }_2\right)\left(4k_3+4k_{5}cos\left(x\right)\right)\hfill \\ & +2cos\left({\theta }_3\right)\left(4k_6+2cos\left({\theta }_2\right)\left(2k_7+2k_{9}cos\left({\theta }_1\right)\right)+4k_{7}cos\left({\theta }_1\right)\right),\hfill \\ \hfill f_{12}({\theta }_1,{\theta }_2,{\theta }_3)& =4k_2+4k_8+4cos\left({\theta }_1\right)(k_4+k_{10})\hfill \\ & +2e^{-i{\theta }_3}\left(e^{i{\theta }_2}\left(k_2+k_{4}cos\left({\theta }_1\right)\right)+e^{-i{\theta }_2}\left(k_8+k_{10}cos\left({\theta }_1\right)\right)\right)\hfill \\ & +2e^{i{\theta }_3}\left(e^{i{\theta }_2}\left(k_8+k_{10}cos\left({\theta }_1\right)\right)+e^{-i{\theta }_2}\left(k_2+k_{4}cos\left({\theta }_1\right)\right)\right),\hfill \\ \hfill f_{13}({\theta }_1,{\theta }_2,{\theta }_3)& =4k_2+4k_8+8k_{0}cos\left({\theta }_1\right)+4cos\left({\theta }_2\right)\left(k_4+k_{10}+2k_{0}cos\left({\theta }_1\right)\right)\hfill \\ & +2e^{-i{\theta }_3}\left(k_2{e}^{i{\theta }_1}+k_8{e}^{-i{\theta }_1}+\left(k_4{e}^{i{\theta }_1}+k_{10}{e}^{-i{\theta }_1}\right)cos\left({\theta }_2\right)\right)\hfill \\ & +2e^{i{\theta }_3}\left(k_2{e}^{-i{\theta }_1}+k_8{e}^{i{\theta }_1}+\left(k_4{e}^{-i{\theta }_1}+k_{10}{e}^{i{\theta }_1}\right)cos\left({\theta }_2\right)\right),\hfill \\ \hfill f_{22}({\theta }_1,{\theta }_2,{\theta }_3)& =8k_1+8k_{3}cos\left({\theta }_1\right)+8cos\left({\theta }_2\right)\left(k_6+k_{7}cos\left({\theta }_1\right)\right)\hfill \\ & +8cos\left({\theta }_3\right)\left(k_3+k_{5}cos\left({\theta }_1\right)+cos\left({\theta }_2\right)\left(k_7+k_{9}cos\left({\theta }_1\right)\right)\right),\hfill \\ \hfill f_{23}({\theta }_1,{\theta }_2,{\theta }_3)& =4k_2+4k_8+2e^{-i{\theta }_2}\left(k_2{e}^{i{\theta }_1}+k_8{e}^{-i{\theta }_1}\right)+2e^{i{\theta }_2}(k_2{e}^{-i{\theta }_1}+k_8{e}^{i{\theta }_1})\hfill \\ & +2cos\left({\theta }_3\right)(2k_4+2k_{10}+4k_{0}cos\left({\theta }_1\right)+4k_{0}cos\left({\theta }_2\right)\hfill \\ \hfill & +e^{-i{\theta }_2}\left(k_4{e}^{i{\theta }_1}+k_{10}{e}^{-i{\theta }_1}\right)+e^{i{\theta }_2}\left(k_4{e}^{-i{\theta }_1}+k_{10}{e}^{i{\theta }_1}\right)),\hfill \\ \hfill f_{33}({\theta }_1,{\theta }_2,{\theta }_3)& =8k_1+8k_{6}cos\left({\theta }_1\right)+8cos\left({\theta }_2\right)\left(k_3+k_{7}cos\left({\theta }_1\right)\right)\hfill \\ & +8cos\left({\theta }_3\right)\left(k_3+k_{7}cos\left({\theta }_1\right)+cos({\theta }_2\right)(k_5+k_{9}cos\left({\theta }_1\right)\left)\right).\hfill \end{array}$$

Finally, by expanding the $k_i$s according to expressions (A2), we deduce the formal expression of the generating functions

$$\begin{array}{cc}\hfill f_{11}({\theta }_1,{\theta }_2,{\theta }_3)& =2cos\left({\theta }_3\right)[cos\left({\theta }_2\right)\left(\frac{2\nu }{3(2\nu -1)}+2cos\left({\theta }_1\right)\left(\frac{\nu }{3(2\nu -1)}-\frac{1}{9}\right)-\frac{4}{9}\right)\hfill \\ & +cos\left({\theta }_1\right)\left(\frac{2\nu }{3(2\nu -1}-\frac{4}{9}\right)-\frac{8}{9}]\hfill \\ & +\frac{8}{9}cos\left({\theta }_1\right)-\frac{16\nu }{3(2\nu -1)}\hfill \\ & +cos\left({\theta }_2\right)\left(2cos\left({\theta }_1\right)\left(\frac{2\nu }{3(2\nu -1)}+\frac{2}{9}\right)+\frac{8}{9}\right)+\frac{16}{9},\hfill \\ \hfill f_{22}({\theta }_1,{\theta }_2,{\theta }_3)& =8cos\left({\theta }_3\right)[cos\left({\theta }_2\right)\left(\frac{\nu }{6(2\nu -1)}+cos\left({\theta }_1\right)\left(\frac{\nu }{6(2\nu -1)}-\frac{1}{18}\right)-\frac{1}{9}\right)\hfill \\ & +cos\left({\theta }_1\right)\left(\frac{\nu }{6(2\nu -1)}+\frac{1}{18}\right)+\frac{1}{9}]\hfill \\ & +\frac{8}{9}cos\left({\theta }_1\right)-\frac{16\nu }{3(2\nu -1)}\hfill \\ & +8cos\left({\theta }_2\right)\left(cos\left({\theta }_1\right)\left(\frac{\nu }{6(2\nu -1)}-\frac{1}{9}\right)-\frac{2}{9}\right)+\frac{16}{9},\hfill \\ \hfill f_{33}({\theta }_1,{\theta }_2,{\theta }_3)& =8cos\left({\theta }_3\right)[cos\left({\theta }_2\right)\left(\frac{\nu }{6(2\nu -1)}+cos\left({\theta }_1\right)\left(\frac{\nu }{6(2\nu -1)}-\frac{1}{18}\right)+\frac{1}{18}\right)\hfill \\ & +cos\left({\theta }_1\right)\left(\frac{\nu }{6(2\nu -1)}-\frac{1}{9}\right)+\frac{1}{9}]\hfill \\ & -\frac{16\nu }{3(2\nu -1)}-\frac{16}{9}cos\left({\theta }_1\right)+\frac{16}{9}\hfill \\ & +8cos\left({\theta }_2\right)\left(cos\left({\theta }_1\right)\left(\frac{\nu }{6(2\nu -1)}-\frac{1}{9}\right)+\frac{1}{9}\right),\hfill \\ \hfill f_{12}({\theta }_1,{\theta }_2,{\theta }_3)& =-\frac{4}{3(2\nu -1)}\left(\nu sin\left({\theta }_2\right)sin\left({\theta }_3\right)\left(cos({\theta }_1\right)+2)\right),\hfill \\ \hfill f_{13}({\theta }_1,{\theta }_2,{\theta }_3)& =-\frac{4}{3(2\nu -1)}\left(\nu sin\left({\theta }_1\right)sin\left({\theta }_3\right)\left(cos\left({\theta }_2\right)+2\right)\right),\hfill \\ \hfill f_{23}({\theta }_1,{\theta }_2,{\theta }_3)& =-\frac{4}{3(2\nu -1)}\left(\nu sin\left({\theta }_1\right)sin\left({\theta }_2\right)\left(cos\left({\theta }_3\right)+2\right)\right).\hfill \end{array}$$

The following proposition links in a precise way the involved Toeplitz structures and matrices $A_n(1,{\mathtt{D}}^6)$ and $A_n(1,{\mathtt{DN}}^5)$.

Proposition 2.

Let $f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)$ be the symbol defined in the previous lines; see (5). Let us consider a uniform meshing in all the three directions with n subintervals. Then we have the following relationships:

$$A_n(1,{\mathrm{D}}^6)=T_{\mathit{n}}(f_{{\mathbb{Q}}_1}),\mathit{n}=(n_1,n_2,n_3),n_1=n_2=n_3=n-1,$$

$$A_n(1,{\mathrm{DN}}^5)=T_{\mathit{n}}(f_{{\mathbb{Q}}_1})+R_{,}\mathit{n}=(n_1,n_2),n_1=n,n_2=n_3=n+1,$$

where R_n has rank of order $n^2=o(\mathrm{size}\left(R_{\mathit{n}}\right))$, with $\mathrm{size}\left(R_{\mathit{n}}\right)=\mathrm{size}\left(A_n(1,{\mathrm{DN}}^5)\right)=n_1{n}_2{n}_3$.

If the more general setting is considered with $n_1$ subintervals in the $x_1$ direction, $n_2$ subintervals in the $x_2$ direction, and $n_3$ intervals in the $x_3$ direction, then the analogous is true:

$$A_{\mathit{n}}(1,{\mathrm{D}}^6)=T_{\mathit{n}}(f_{{\mathbb{Q}}_1}),\mathit{n}=(n_1-1,n_2-1,n_3-1),$$

$$A_{\mathit{n}}(1,{\mathrm{DN}}^5)=T_{\mathit{n}}(f_{{\mathbb{Q}}_1})+R_{,}\mathit{n}=(n_1,n_2+1,n_3+1),$$

where R_n has a rank proportional to $n_1{n}_2+n_1{n}_3+n_2{n}_3=o(\mathrm{size}\left(R_{\mathit{n}}\right))$, with $\mathrm{size}\left(R_{\mathit{n}}\right)=\mathrm{size}\left(A_n(1,{\mathrm{DN}}^5)\right)=n_1{n}_2{n}_3$.

Proof. 

Since the grid points in a cube are $n_1{n}_2{n}_3$, if we consider Dirichlet boundary conditions in a facet orthogonal, for example, to the direction $x_1$, then the number of points and equations which are affected by the Neumann boundary conditions on the other 5 facets are $2l_3{n}_1{n}_2+2l_2{n}_1{n}_3+l_1{n}_2{n}_3$, where typically $l_3=l_2=l_1=2$ if the standard linear FEs are employed. Hence, the rank correction induced by the matrix R_n is proportional, as claimed to $n_1{n}_2+n_1{n}_3+n_2{n}_3=o(\mathrm{size}\left(R_{\mathit{n}}\right))$. □

In the following section, we prove that the function $f_{{\mathbb{Q}}_1}$ is the eigenvalue symbol, in the sense of Definition 1, of the matrix sequences ${\left\{A_n(1,{\mathtt{D}}^6)\right\}}_n$ and ${\left\{A_n(1,{\mathtt{DN}}^5)\right\}}_n$.

3.2.2. Symbol Spectral Analysis in 3D: Distribution, Extremal Eigenvalues, and Conditioning

We study the spectral distribution, extremal eigenvalues, and conditioning of our matrix sequences in 3D. All the results are based on the symbol and on its analytical features.

Proposition 3.

Let $f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)$ be the symbol defined in Section 3.2.1 According to the notation in Proposition 2, all the matrix sequences ${\left\{T_{\mathit{n}}\right(f_{{\mathbb{Q}}_1}\left)\right\}}_{\mathit{n}}$, ${\left\{A_n(1,{\mathrm{D}}^6)\right\}}_n$, ${\left\{A_{\mathit{n}}(1,{\mathrm{D}}^6)\right\}}_{\mathit{n}}$, ${\left\{A_n(1,{\mathrm{DN}}^5)\right\}}_n$, ${\left\{A_{\mathit{n}}(1,{\mathrm{DN}}^5)\right\}}_{\mathit{n}}$ are spectrally distributed as $f_{{\mathbb{Q}}_1}$ in the sense of Definition 1.

Proof. 

For the multilevel block Toeplitz sequences ${\left\{T_{\mathit{n}}\right(f_{{\mathbb{Q}}_1}\left)\right\}}_{\mathit{n}}$, ${\left\{A_n(1,{\mathtt{D}}^6)\right\}}_n$, and ${\left\{A_{\mathit{n}}(1,{\mathtt{D}}^6)\right\}}_{\mathit{n}}$ refer to Item GLT 2., part 1, and Item GLT 1., part 2 in Section 3.1.2. For the sequences ${\left\{A_n(1,{\mathtt{DN}}^5)\right\}}_n$, ${\left\{A_{\mathit{n}}(1,{\mathtt{DN}}^5)\right\}}_{\mathit{n}}$ first observe that the matrix sequence ${\left\{R_{\mathit{n}}\right\}}_{\mathit{n}}$ defined in Proposition 2 is zero distributed, thanks to Proposition 1 and Proposition 2 since rank $\left(R_{\mathit{n}}\right)/$size$\left(R_{\mathit{n}}\right)/$$\to 0$, as $\mathit{n}\to \infty$. Then the claim follows thanks to the *-algebra structure of the GLT sequences and more specifically thanks to Item GLT 3., part 2, Item GLT 2., part 1, and Item GLT 1., part 2. □

Now, we identify a few key analytical features of the spectral symbol which are shared by all the matrix sequences mentioned in Proposition 3. Theorem 1 is crucial for the study of the extremal eigenvalues and of the conditioning of the same matrix sequences and, in Section 5, it is the main ingredient for designing ad hoc multigrid solvers when dealing with the associated large linear systems.

Theorem 1.

Let $f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)$ be the symbol defined in (5). The following statements hold true:

• $f_{{\mathbb{Q}}_1}(0,0,0)\mathbf{e}=0$, $\mathbf{e}={[1,1,1]}^T$;
• All three eigenvalues of $f_{{\mathbb{Q}}_1}$ have a zero of order 2 at $(0,0,0)$.

Proof. 

Claim 1. The function $f_{{\mathbb{Q}}_1}$ evaluated at $(0,0,0)$ equals

$$f_{{\mathbb{Q}}_1}(0,0,0)=\left[\begin{array}{ccc}\alpha & \beta & \beta \\ \beta & \alpha & \beta \\ \beta & \beta & \alpha \end{array}\right]$$

with $\alpha =8(k_1+2k_3+k_5+k_6+2k_7+k_9)$ and $\beta =8(4k_0+k_2+k_4+k_8+k_{10})$, whose row-sum $\alpha +2\beta =0$ according to (A2).

Claim 2. It is just a direct check. Indeed, it is enough to check that the quantities

$$\mathrm{tr}\left(f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)\right)\mathrm{and}det\left(f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)\right)$$

have a zero of orders two and six, respectively, by considering the Taylor expansion centered at $(0,0,0)$. □

In accordance to what was proven in the 2D setting, the minimal eigenvalue of the symbol $f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)$ has a unique zero of order two at $({\theta }_1,{\theta }_2,{\theta }_3)=(0,0,0)$. In fact, the symbol $f_{{\mathbb{Q}}_1}$ is positive semi-definite, and all the eigenvalues of the symbol $f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)$ have a unique zero of order two at $({\theta }_1,{\theta }_2,{\theta }_3)=(0,0,0)$, that is, there exist positive constants $c\left(j\right),C\left(j\right)$, $j=1,2,3$ such that

$$c\left(j\right)\parallel {({\theta }_1,{\theta }_2,{\theta }_3)}^T{\parallel }^2\le {\lambda }_j\left(f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)\right)\le C\left(j\right){\parallel {({\theta }_1,{\theta }_2,{\theta }_3)}^T\parallel }^2$$

uniformly in a proper neighborhood of $(0,0,0)$.

Therefore, we can infer important information on the extremal eigenvalues and on the conditioning of the corresponding matrix sequences.

Proposition 4.

Let $f_{{\mathbb{Q}}_1}({\theta }_1,{\theta }_2,{\theta }_3)$ be the symbol defined in (5). Let us consider a uniform meshing in all the directions with n subintervals. Then we have the following relationships:

$$\begin{array}{cc}\hfill & {\lambda }_{min}\left(A_n(1,{\mathrm{D}}^6)\right)\sim n^{-2},\hfill \\ \hfill & max{f}_{{\mathbb{Q}}_1}-{\lambda }_{max}\left(A_n(1,{\mathrm{D}}^6)\right)\sim n^{-2},\hfill \\ \hfill & \mu \left(A_n(1,{\mathrm{D}}^6)\right)\sim n^2,\hfill \\ \hfill & A_n(1,{\mathrm{D}}^6)=T_{\mathit{n}}(f_{{\mathbb{Q}}_1}),\mathit{n}=(n_1,n_2,n_3),n_1=n_2=n_3=n-1\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\lambda }_{min}\left(A_n(1,{\mathrm{DN}}^5)\right)\sim n^{-2},\hfill \\ \hfill & max{f}_{{\mathbb{Q}}_1}-{\lambda }_{max}\left(A_n(1,{\mathrm{DN}}^5)\right)\sim n^{-2},\hfill \\ \hfill & \mu \left(A_n(1,{\mathrm{DN}}^5)\right)\sim n^2,\hfill \\ \hfill & A_n(1,{\mathrm{DN}}^5)=T_{\mathit{n}}(f_{{\mathbb{Q}}_1})+R_{\mathit{n}},\mathit{n}=(n_1,n_2,n_3),n_1=n,n_2=n_3=n+1,\hfill \end{array}$$

with R_n as in Proposition 2 and $\mu (·)$ denoting the condition number in spectral norm (the one induced by the Euclidean vector norm).

If the more general setting is considered with $n_1$ subintervals in the $x_1$ direction, $n_2$ subintervals in the $x_2$ direction, and $n_3$ subintervals in the $x_3$ direction, then analogous relations are true:

$$\begin{array}{cc}\hfill & {\lambda }_{min}(A_{(}1,{\mathrm{D}}^6))\sim {[min{n}_j]}^{-2},\hfill \\ \hfill & max{f}_{{\mathbb{Q}}_1}-{\lambda }_{max}(A_{(}1,{\mathrm{D}}^6))\sim {[min{n}_j]}^{-2},\hfill \\ \hfill & \mu (A_{(}1,{\mathrm{D}}^6))\sim n^2,\hfill \\ \hfill & A_{(}1,{\mathrm{D}}^6)=T_{\mathit{n}}(f_{{\mathbb{Q}}_1}),\mathit{n}=(n_1-1,n_2-1,n_3-1)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\lambda }_{min}(A_{(}1,{\mathrm{DN}}^5))\sim {[min{n}_j]}^{-2},\hfill \\ \hfill & max{f}_{{\mathbb{Q}}_1}-{\lambda }_{max}(A_{(}1,{\mathrm{DN}}^5))\sim {[min{n}_j]}^{-2},\hfill \\ \hfill & \mu (A_{(}1,{\mathrm{DN}}^5))\sim {[min{n}_j]}^2,\hfill \\ \hfill & A_{(}1,{\mathrm{DN}}^5)=T_{\mathit{n}}(f_{{\mathbb{Q}}_1})+R_{\mathit{n}},\mathit{n}=(n_1,n_2+1,n_3+1),\hfill \end{array}$$

with R_n as in Proposition 2.

3.3. Non-Constant Coefficient $\rho$ Case—3D

It should be observed that the natural extension of the previous analysis refers to the case of a non-constant coefficient $\rho$. According to a standard assembling procedure in FEs, given the triangulation $\mathcal{T}$ made by all the basic elements $\tau$, we write the stiffness matrix as

$$A_n\left(\rho \right)=\sum _{\tau \in \mathcal{T}}{\rho }_{\tau }{A}_{n,\tau }^{El},$$

(6)

where $A_{n,\tau }^{El}$ is the elementary matrix $K_n$ in (2) (possibly properly cut when nodes on the boundary are involved), but widened to size $N\left(\mathit{n}\right)$ according to the chosen global ordering of nodes. Here, $\mathit{n}=(n-1,n-1,n-1)$ in the case of the Dirichlet boundary conditions and n subintervals in all the directions such that $A_n\left(\rho \right)=A_n(\rho ,{\mathrm{D}}^6)$, while $\mathit{n}=(n,n+1,n+1)$ in the case of Dirichlet boundary conditions on one-side Neumann boundary conditions in the remaining ones with n subintervals in all the directions so that $A_n\left(\rho \right)=A_n(\rho ,{\mathrm{DN}}^5)$.

Clearly, the elementary matrix $K_e$ is positive semi-definite for $0\le \nu <1/2$. More precisely, the not zero eigenvalues are

$$\begin{array}{ccccccc}\hfill & 1\left(\mathrm{double}\right),\hfill & \hfill \frac{(1-\nu )}{3(1-2\nu )}\left(\mathrm{triple}\right),& \hfill & \hfill \frac{2\nu }{(1-2\nu )}\left(\mathrm{triple}\right),& \hfill & \hfill \frac{\nu }{3(1-2\nu )}\left(\mathrm{double}\right),\\ & \frac{4\nu }{3(1-2\nu )}\left(\mathrm{simple}\right),\hfill & \hfill \frac{(\nu +1)}{(1-2\nu )}\left(\mathrm{simple}\right),& \hfill & \hfill \frac{(\nu +1)}{3(1-2\nu )}\left(\mathrm{triple}\right),& \hfill & \hfill \frac{(\nu +1)}{9(1-2\nu )}\left(\mathrm{triple}\right).& \hfill \end{array}$$

In addition, every elementary matrix, which has been cut due to nodes on the boundary, is positive semi-definite as well since it is a principal submatrix of $K_e$ in (2).

Thus, on the basis of (6) and by applying the Courant–Fisher theorem, we can claim again

$$\begin{array}{cc}\hfill {\rho }_{min}{\lambda }_{min}\left(A_n\left(1\right)\right)\le {\lambda }_{min}\left(A_n\left(\rho \right)\right)& \le {\rho }_{max}{\lambda }_{min}\left(A_n\left(1\right)\right),\hfill \\ \hfill {\rho }_{min}{\lambda }_{max}\left(A_n\left(1\right)\right)\le {\lambda }_{max}\left(A_n\left(\rho \right)\right)& \le {\rho }_{max}{\lambda }_{max}\left(A_n\left(1\right)\right).\hfill \end{array}$$

with ${\rho }_{min}$ and ${\rho }_{max}$ minimum and maximum of $\rho$, respectively (see Figure 1 for an upperbound of the maximal eigenvalues of $A_n\left(1\right)$ as a function of $\nu$).

By combining the above inequalities and Proposition 4, we infer that the extremal eigenvalues and the conditioning have the same asymptotical behavior as in the constant coefficient setting.

The whole eigenvalues distribution is sketched below by referring to the basics of the GLT theory [29] reported in Section 3.1.2. Let $D_n\left(\rho \right)$ be a multilevel block diagonal sampling matrix according to the notions introduced in Section 3.1.2 and let $A_n\left(1\right)$ be the multilevel block Toeplitz matrix $T_{\mathit{n}}(f_{{\mathbb{Q}}_1})$ if the Dirichlet boundary conditions are used or $T_{\mathit{n}}(f_{{\mathbb{Q}}_1})+R_{\mathit{n}}$ in the other case. Then the following facts hold:

Fact 1

${\left\{D_n\left(\rho \right)\right\}}_n{\sim }_{\mathrm{GLT}}\rho$ according to Item GLT 2.

Fact 2

$\left\{R_{\mathit{n}}\right\}n{\sim }_{\mathrm{GLT}}0$ according to Proposition 2, Proposition 1, and Item GLT 2.

Fact 3

$\left\{T_{\mathit{n}}\right(f_{{\mathbb{Q}}_1}){\}}_n{\sim }_{\mathrm{GLT}}{f}_{{\mathbb{Q}}_1}$ according to Item GLT 2.

Fact 4

${\left\{A_n\left(1\right)\right\}}_n{\sim }_{\mathrm{GLT}}{f}_{{\mathbb{Q}}_1}$ according to Fact 2, Fact 3, and to the *-algebra structure of GLT sequences that is Item GLT 3.

Fact 5

given ${\Delta }_n=A_n\left(\rho \right)-D_n\left(\rho \right)A_n\left(1\right)$ a simple check shows that ${\left\{{\Delta }_n\right\}}_n{\sim }_{\mathrm{GLT}}0$, using Proposition 1.

Fact 6

${\left\{A_n\left(\rho \right)\right\}}_n{\sim }_{\mathrm{GLT}}\rho f_{{\mathbb{Q}}_1}$ as a consequence of Fact5, Fact 1, Fact 4, and of the *-algebra structure of GLT sequences that is Item GLT 3.; moreover since the matrix sequence ${\left\{A_n\left(\rho \right)\right\}}_n$ is made up by Hermitian matrices, by Item GLT 1. it follows that ${\left\{A_n\left(\rho \right)\right\}}_n{\sim }_{\sigma ,\lambda }\rho f_{{\mathbb{Q}}_1}$.

We stress that a unique notation has been employed for the sake of notational compactness. However, the main statement, Fact 6, holds for all the matrix sequences reported in Proposition 3 in the case of a variable $\rho$.

Finally, it is worth noticing that non-square domains can be treated as well, using the reduced GLT theory (see pages 398–399 in [33], Section 3.1.4 in [34], and the recent analysis [35]): here, we do not go in the details and this will be the subject of future investigations.

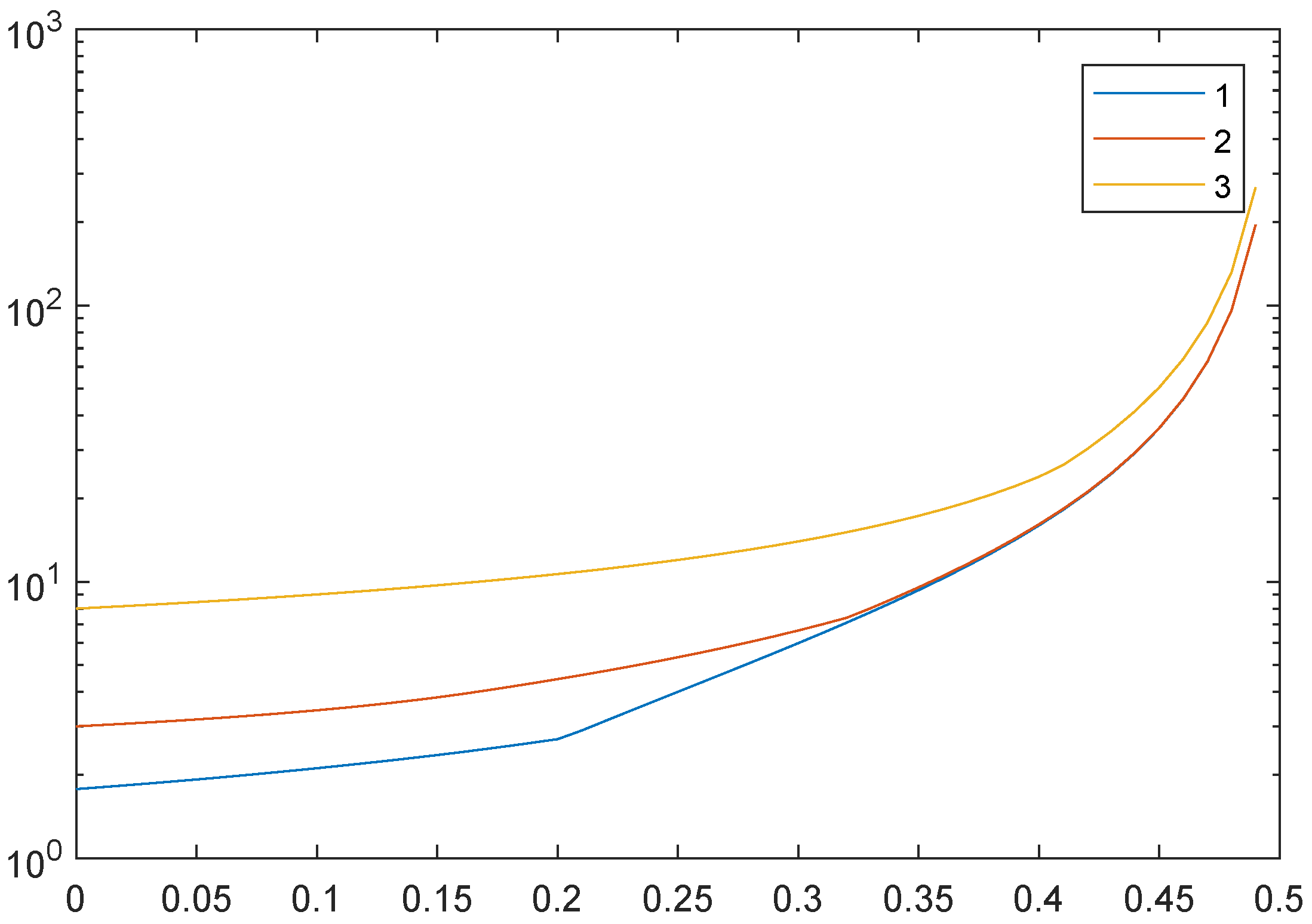
4. Two-Grid and Multigrid Methods

In this section, we concisely report few relevant results concerning the convergence theory of algebraic multigrid methods with special attention of the case of multilevel block Toeplitz structures generated by a matrix-valued symbol f.

We start by taking into consideration the generic linear system $A_m{x}_m=b_m$ with large dimension m, where $A_m\in {\mathbb{C}}^{m\times m}$ is a Hermitian positive definite matrix and $x_m,b_m\in {\mathbb{C}}^m$. Let $m_0=m>m_1>\dots >m_s>\dots >m_{s_{min}}$ and let $P_s^{s+1}\in {\mathbb{C}}^{m_{s+1}\times m_s}$ be a full-rank matrix for any s. At last, let us denote by ${\mathcal{V}}_s$ a class of stationary iterative methods for given linear systems of dimension $m_s$.

In accordance with [36], the algebraic two-grid method (TGM) can be easily seen as a stationary iterative method whose generic steps are reported below.

$x_s^{\mathrm{out}}=\mathrm{TGM}(s,x_s^{\mathrm{in}},b_s)$
$\boxed{x_s^{\mathrm{pre}}={\mathcal{V}}_{s,\mathrm{pre}}^{{\nu }_{\mathrm{pre}}}(x_s^{\mathrm{in}},b_s)}$	Pre-smoothing iterations
$\boxed{\begin{array}{l}{r}_s=A_s{x}_s^{\mathrm{pre}}-b_s\\ r_{s+1}=P_{m_s}^{m_{s+1}}{r}_s\\ A_{s+1}=P_{m_s}^{m_{s+1}}{A}_s{\left(P_{m_s}^{m_{s+1}}\right)}^H\\ \mathrm{Solve}{A}_{s+1}{y}_{s+1}=r_{s+1}\\ {\widehat{x}}_s=x_s^{\mathrm{pre}}-{\left(P_{m_s}^{m_{s+1}}\right)}^H{y}_{s+1}\end{array}}$	Exact coarse grid correction (CGC)
$\boxed{x_s^{\mathrm{out}}={\mathcal{V}}_{s,\mathrm{post}}^{{\nu }_{\mathrm{post}}}({\widehat{x}}_s,b_s)}$	Post-smoothing iterations

Here, we refer to the dimension $m_s$ by means of its subscript s.

In the first and last steps, a pre-smoothing iteration and a post-smoothing iteration are applied ${\nu }_{\mathrm{pre}}$ times and ${\nu }_{\mathrm{post}}$ times, respectively, taking into account the considered stationary iterative method in the class ${\mathcal{V}}_s$. Furthermore, the intermediate steps define the exact coarse grid correction operator, which is dependent on the considered projector operator $P_{s+1}^s$. The resulting iteration matrix of the TGM is then defined as

$$\begin{array}{cc}\hfill TG{M}_s& =V_{s,\mathrm{post}}^{{\nu }_{\mathrm{post}}}CG{C}_s{V}_{s,\mathrm{pre}}^{{\nu }_{\mathrm{pre}}},\hfill \\ \hfill CG{C}_s& =I^{\left(s\right)}-{\left(P_{m_s}^{m_{s+1}}\right)}^H{A}_{s+1}^{-1}{P}_{m_s}^{m_{s+1}}{A}_s\hfill \\ \hfill & A_{s+1}=P_{m_s}^{m_{s+1}}{A}_s{\left(P_{m_s}^{m_{s+1}}\right)}^H,\hfill \end{array}$$

where $V_{s,\mathrm{pre}}$ and $V_{s,\mathrm{post}}$ represent the pre-smoothing and post-smoothing iteration matrices, respectively, and $I^{\left(s\right)}$ is the identity matrix at the sth level.

By employing a recursive procedure, the TGM leads to a multigrid method (MGM). Indeed, the standard V-cycle can be expressed in the following way:

$x_s^{\mathrm{out}}=\mathrm{MGM}(s,x_s^{\mathrm{in}},b_s)$
if $s\le s_{min}$ then
$\boxed{\mathrm{Solve}{A}_s{x}_s^{\mathrm{out}}=b_s}$	Exact solution
else
$\boxed{x_s^{\mathrm{pre}}={\mathcal{V}}_{s,\mathrm{pre}}^{{\nu }_{\mathrm{pre}}}(x_s^{\mathrm{in}},b_s)}$	Pre-smoothing iterations
$\boxed{\begin{array}{l}{r}_s=A_s{x}_s^{\mathrm{pre}}-b_s\\ r_{s+1}=P_{m_s}^{m_{s+1}}{r}_s\\ y_{s+1}=\mathrm{MGM}(s+1,{\mathit{0}}_{s+1},r_{s+1})\\ {\widehat{x}}_s=x_s^{\mathrm{pre}}-{\left(P_{m_s}^{m_{s+1}}\right)}^H{y}_{s+1}\end{array}}$	Coarse grid correction
$\boxed{x_s^{\mathrm{out}}={\mathcal{V}}_{s,\mathrm{post}}^{{\nu }_{\mathrm{post}}}({\widehat{x}}_s,b_s)}$	Post-smoothing iterations

From a computational viewpoint, to reduce the related costs, it is more efficient that the matrices $A_{s+1}=P_s^{s+1}{A}_s{\left(P_s^{s+1}\right)}^H$ are computed in the so-called setup phase.

According to the previous setting, the global iteration matrix of the MGM is recursively defined as

$$\begin{array}{cc}\hfill & MG{M}_{s_{min}}=O\in {\mathbb{C}}^{s_{min}\times s_{min}},\hfill \\ \hfill & MG{M}_s=V_{s,\mathrm{post}}^{{\nu }_{\mathrm{post}}}\left[I^{\left(s\right)}-{\left(P_{m_s}^{m_{s+1}}\right)}^H\left(I^{(s+1)}-MG{M}_{s+1}\right)A_{s+1}^{-1}{P}_{m_s}^{m_{s+1}}{A}_s\right]V_{s,\mathrm{pre}}^{{\nu }_{\mathrm{pre}}},\hfill \\ & s=s_{min}-1,\dots ,0.\hfill \end{array}$$

Lastly, the W-cycle is just a variation of the previous V-cycle considering two recursive calls in the coarse grid correction as follows:

$x_s^{\mathrm{out}}=\mathrm{MGMW}(s,x_s^{\mathrm{in}},b_s)$
if $s\le s_{min}$ then
$\boxed{\mathrm{Solve}{A}_s{x}_s^{\mathrm{out}}=b_s}$	Exact solution
else
$\boxed{x_s^{\mathrm{pre}}={\mathcal{V}}_{s,\mathrm{pre}}^{{\nu }_{\mathrm{pre}}}(x_s^{\mathrm{in}},b_s)}$	Pre-smoothing iterations
$\boxed{\begin{array}{l}{r}_s=A_s{x}_s^{\mathrm{pre}}-b_s\\ r_{s+1}=P_{m_s}^{m_{s+1}}{r}_s\\ y_{s+1}^{\left(0\right)}={\mathit{0}}_{s+1}\\ \mathrm{for} \mu =1:2\\ y_{s+1}^{\left(\mu \right)}=\mathrm{MGMW}(s+1,y_{s+1}^{(\mu -1)},r_{s+1})\\ {\widehat{x}}_s=x_s^{\mathrm{pre}}-{\left(P_{m_s}^{m_{s+1}}\right)}^H{y}_{s+1}^{\left(2\right)}\end{array}}$	Coarse grid correction
$\boxed{x_s^{\mathrm{out}}={\mathcal{V}}_{s,\mathrm{post}}^{{\nu }_{\mathrm{post}}}({\widehat{x}}_s,b_s)}$	Post-smoothing iterations

In the following remark, we emphasize the relevant computational properties of the considered methods.

Remark 1.

The first part of the current remark concerns the computational cost. In the V-cycle, there is just one recursive call, while in the W-cycle, there are two recursive calls, which in principle, is more expensive. Let us analyze the related costs. Since our matrices are sparse and they remain sparse at the lower levels, the number of arithmetic operations in the V-cycle and W-cycle algorithms is of the type

$$C_V\left(m\right)\le C_V(m/q)+\alpha m,C_W\left(m\right)\le 2C_W(m/q)+\alpha m,$$

where $m=m_0$ and $m_{s+1}=m_s/q$. Now in the one-dimensional setting $q=2$ and $C_V\left(m\right)=O\left(m\right)$, while $C_W\left(m\right)=O(mlogm)$ and thus the W-cycle is asymptotically more expensive. Conversely, in a d-dimensional setting with $d\ge 2$, we have $q=2^d$ and, as a consequence of the recursive relations, both $C_V\left(m\right)$ and $C_W\left(m\right)$ are linear in the matrix-size m. To be precise, we have

$$C_V\left(m\right)\le \frac{2^d}{2^d-1}\alpha m,C_W\left(m\right)\le \frac{2^{d-1}}{2^{d-1}-1}\alpha m,$$

so that, in the current three-dimensional setting, the bounds of the V-cycle and W-cycle complexity are very close, i.e.,

$$C_V\left(m\right)\le \frac{8}{7}\alpha m,C_W\left(m\right)\le \frac{4}{3}\alpha m.$$

Another issue to be considered is the case where the discretization matrices appear in checkerboard fashion (see, for example, [37] and the references therein). We emphasize that our analysis, which is based on the Toeplitz generating function, is not directly applicable since we lose the Toeplitz character of the approximation matrices when a checkerboard (called also red–black) ordering is used. However, this is just a matter of a similarity transformation by a permutation matrix. Hence, with a careful work and without increasing the complexity analyzed in the previous lines, the algorithm discussed here and the related theoretical analysis can be adapted to the checkerboard context.

Remark 2.

In the relevant literature (see, for instance, [38]), the convergence analysis of the TGM splits into checking two separate conditions: the smoothing property and the approximation property. Regarding the latter and regarding scalar structured matrices [38,39], the TGM optimality is given in terms of choosing the proper conditions that the symbol p of a family of projection operators has to fulfill. Indeed, let $T_n\left(f\right)$ with $n=(2^t-1)$, where f is a non-negative trigonometric polynomial. Let ${\theta }^0$ be the unique zero of f. Then the TGM optimality applied to $T_n\left(f\right)$ is guaranteed if we choose the symbol p of the family of projection operators such that

$$\begin{array}{cc}\hfill \underset{\theta \to {\theta }^0}{limsup}\frac{{\left|p\left(\eta \right)\right|}^2}{f\left(\theta \right)}& <\infty ,\eta \in \mathcal{M}\left(\theta \right),\hfill \\ \hfill \sum _{\eta \in \mathrm{\Omega }\left(\theta \right)}{\left|p\left(\eta \right)\right|}^2& >0,\hfill \end{array}$$

(7)

where, for $d=1$, the sets $\mathrm{\Omega }\left(\theta \right)$ and $\mathcal{M}\left(\theta \right)$ are the following corner and mirror points

$$\mathrm{\Omega }\left(\theta \right)=\{\eta \in \{\theta ,\theta +\pi \left\}\right\},\mathcal{M}\left(\theta \right)=\mathrm{\Omega }\left(\theta \right)\setminus \left\{\theta \right\},$$

respectively. In the general case of $d>1$, we have

$$\mathrm{\Omega }\left(\mathit{\theta }\right)=\{\mathit{\eta }\in \{\mathit{\theta }+\pi \mathit{s}\},\mathit{s}=(s_1,\dots ,s_d),s_j\in \{0,1\},j=1,\dots ,d\}$$

with $\mathcal{M}\left(\mathit{\theta }\right)=\mathrm{\Omega }\left(\mathrm{\theta }\right)\setminus \left\{\mathrm{\theta }\right\}$, so that the cardinality of $\mathrm{\Omega }\left(\mathit{\theta }\right)$ and $\mathcal{M}\left(\mathit{\theta }\right)$ is $2^d$ and $2^d-1$, respectively.

Informally, for $d=1$, it means that the optimality of the two-grid method is obtained by choosing the family of projection operators associated to a symbol p such that ${\left|p\right|}^2\left(\vartheta \right)+{\left|p\right|}^2(\vartheta +\pi )$ does not have zeros and ${\left|p\right|}^2(\vartheta +\pi )/f\left(\vartheta \right)$ is bounded (if we require the optimality of the V-cycle, then the second condition is a bit stronger); see [38]. For approximation of an elliptic differential operator of order $2\alpha$ by local methods (e.g., finite differences, FEs, and isogeometric analysis), the previous conditions mean that p has a unique zero of order at least $\alpha$ at $\vartheta =\pi$ whenever f has a unique zero at ${\theta }^0=0$ of order $2\alpha$.

In our specific block setting, by interpreting the analysis given in [40], all the involved symbols are matrix valued, and the conditions which generalize (7) and are sufficient for the TGM convergence and optimality are the following:

(A) 

Zero of order 2 at all the mirror points of the eigenvalue functions of the symbol of the projector for our matrix sequences having common symbol $f_{{\mathbb{Q}}_1}$ (mirror point theory [38,39]);

(B) 

Positive definiteness of ${\sum }_{\eta \in \mathrm{\Omega }\left(\theta \right)}p{p}^H\left(\eta \right)$;

(C) 

Commutativity of all $p\left(\mathit{\eta }\right)$ for $\mathit{\eta }$ varying in the corner points.

Even if the theoretical extension to the V-cycle and W-cycle convergence and optimality is not given, in the subsequent section, we propose specific choices of the projection operators numerically showing how this leads to two-grid, V-cycle, and W-cycle procedures converging optimally or quasi-optimally with respect to all the relevant parameters (size, dimensionality, and polynomial degree k).

Our choices are in agreement with the mathematical conditions set in items (A), (B), and (C). We remark that the violation of condition (C) is discussed by Donatelli et al. [40], in their conclusion section.

5. Multigrid Proposals

Based on the theory in Section 4, we define the prolongation operator as

$$P_{2h}^h=P\otimes P\otimes P\otimes I_3/\sqrt{2}$$

in the case of matrices $A_n(1,{\mathtt{D}}^6)$, and

$$P_{2h}^h=P_c\otimes P_t\otimes P_t\otimes I_3/\sqrt{2}$$

in the case of matrices $A_n(1,{\mathtt{DN}}^5)$. In the expressions above,

$$P=\left[\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2}}& \hfill & \\ \hfill 1& \hfill & \\ \hfill {\displaystyle \frac{1}{2}}& \hfill {\displaystyle \frac{1}{2}}& \\ \hfill & \hfill 1& \\ \hfill & \hfill {\displaystyle \frac{1}{2}}& \hfill \ddots & \hfill {\displaystyle \frac{1}{2}}\\ \hfill & \hfill & & \hfill 1\\ \hfill & \hfill & & \hfill {\displaystyle \frac{1}{2}}\end{array}\right],P_t=\left[\begin{array}{cc}\hfill 1& \\ \hfill {\displaystyle \frac{1}{2}}& \hfill {\displaystyle \frac{1}{2}}& \hfill & \\ \hfill & \hfill 1& \hfill & \\ \hfill & \hfill {\displaystyle \frac{1}{2}}& \hfill {\displaystyle \frac{1}{2}}& \\ \hfill & \hfill & \hfill 1& \\ \hfill & \hfill & \hfill {\displaystyle \frac{1}{2}}& \hfill \ddots & \hfill {\displaystyle \frac{1}{2}}\\ \hfill & \hfill & & \hfill & \hfill 1\\ \hfill & \hfill & & \hfill & \hfill {\displaystyle \frac{1}{2}}& \hfill {\displaystyle \frac{1}{2}}\\ \hfill & \hfill & & \hfill & & \hfill 1\end{array}\right],\mathrm{and}{P}_c=\left[\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2}}& \hfill & \\ \hfill 1& \hfill & \\ \hfill {\displaystyle \frac{1}{2}}& \hfill {\displaystyle \frac{1}{2}}& \\ \hfill & \hfill 1& \\ \hfill & \hfill {\displaystyle \frac{1}{2}}& \hfill \ddots & \hfill {\displaystyle \frac{1}{2}}\\ \hfill & & \hfill & \hfill 1\\ \hfill & & \hfill & \hfill {\displaystyle \frac{1}{2}}& \hfill {\displaystyle \frac{1}{2}}\\ \hfill & & \hfill & & \hfill 1\end{array}\right],$$

Note that $A_{2h}=P^T{A}_{h}P$ equals the same FEM approximation on the coarse mesh in both cases, independently of the boundary conditions.

Independently of the boundary conditions, we observe that the symbol of the prolongation operator is a $3\times 3$ matrix-valued function as the symbol of the coefficient matrix sequence of the linear systems to be solved: more precisely we define

$$p({\theta }_1,{\theta }_2,{\theta }_3)=\sqrt{2^{-1}}(1+cos\left({\theta }_1\right)(1+cos\left({\theta }_2\right)(1+cos\left({\theta }_3\right)I_3.$$

Since the matrix-valued function $p({\theta }_1,{\theta }_2,{\theta }_3)$ is a scalar function times the identity, it automatically follows that the difficult condition (C) is satisfied. Moreover, taking into account Theorem 1, since the scalar function $1+cos\left(\theta \right)$ has a zero of order 2 at $\theta =\pi$, also condition (A) holds, while the positive definiteness of ${\sum }_{\mathit{\eta }\in \mathrm{\Omega }\left(\theta \right)}p{p}^H\left(\mathit{\eta }\right)$ is verified as well, so that also condition (B) is met.

Finally, we choose one iteration of Gauss–Seidel as the pre and post smoother. Given the analysis reported in the previous section, we expect that our multigrid method is convergent in an optimal way, that is, with a convergence speed independent of the matrix size. In

Table 1. Number of iteration for matrices $A_n(1,{\mathtt{D}}^6)$ and $A_n(1,{\mathtt{DN}}^5)$ of increasing dimension $N\left(n\right)$, with the numeric precision $\epsilon ={10}^{-4},{10}^{-6},{10}^{-8}$, respectively.

${\mathit{A}}_{\mathit{n}}(1,{\mathtt{D}}^6)$										${\mathit{A}}_{\mathit{n}}(1,{\mathtt{DN}}^5)$
	$\nu =0.1$
$N\left(n\right)$	Twogrid			Vcycle			Wcycle			$N\left(n\right)$	Twogrid			Vcycle			Wcycle
81	5	7	10	-	-	-	-	-	-	300	7	13	18	-	-	-	-	-	-
1029	7	10	15	7	10	15	7	10	15	1944	8	12	17	8	12	17	8	12	17
10125	8	13	18	8	13	18	8	13	18	13,872	8	13	18	9	14	19	8	13	18
	$\nu =0.2$
$N\left(n\right)$	Twogrid			Vcycle			Wcycle			$N\left(n\right)$	Twogrid			Vcycle			Wcycle
81	4	5	7	-	-	-	-	-	-	300	5	8	11	-	-	-	-	-	-
1029	5	7	9	5	7	9	5	7	9	1944	6	8	11	6	8	11	6	8	11
10125	6	8	11	6	8	11	6	8	11	13,872	8	10	12	8	10	12	8	10	12
	$\nu =0.4$
$N\left(n\right)$	Twogrid			Vcycle			Wcycle			$N\left(n\right)$	Twogrid			Vcycle			Wcycle
81	3	4	6	-	-	-	-	-	-	300	6	10	14	-	-	-	-	-	-
1029	4	7	9	4	7	9	4	7	9	1944	7	11	15	7	11	15	7	11	15
10125	4	7	11	5	8	12	4	7	11	13,872	6	11	15	8	14	19	7	11	15

, we find a plain confirmation of our theoretical expectations, which holds not only for a constant $\rho$, but also in the variable coefficient setting as long as $\rho$ remains positive.

6. Conclusions

We provided a quite complete spectral analysis of the (large) coefficient matrices associated with the linear systems stemming from the FE discretization of a linearly elastic problem for an arbitrary element-wise constant coefficient field. Our interest in this problem stems from the fact that in the material distribution method for topology optimization, such a problem is solved at each iteration. The solution for these linear systems typically dominates the computational effort required to solve the topology optimization problems. Based on the spectral information, we proposed a specialized multigrid method, which turned out to be optimal in the sense that the (arithmetic) cost for solving the related linear systems, up to a fixed desired accuracy, is proportional to the computational cost of matrix–vector products, which is linear in the corresponding matrix size and mildly depending on the given accuracy. The method was tested, and the preliminary numerical results are very satisfactory and promising, in terms of having a linear cost and a number of iterations that is bounded by a constant independent of the matrix size and only lightly influenced by the desired accuracy.

Finally, we mention future lines of research:

• The present analysis was performed also with variable coefficients, but with the restriction that the domain is Cartesian: this limitation can be easily overcome, but the computations are not trivial using the notion of reduced GLT sequences of matrices (see [35] for a recent very complete work and [33,34] for examples of applications and for the initial idea).
• The use of higher order FEs is another direction to explore: for more standard problems, we refer to [41,42] whose analysis can be the starting point for adapting the techniques to the present context.
• In the direction of more general approaches, we remind that the GLT machinery was used also in connection with finite differences, finite volumes, isogeometric analysis of high order and intermediate regularity (see [30,31] and references therein). Hence, we are convinced that such extensions can be formally obtained, also in the case of the current topology optimization problem.