The Generalized Odd Linear Exponential Family of Distributions with Applications to Reliability Theory
Abstract
:1. Introduction
2. The Generalized Odd Linear Exponential (GOLE-F) Family
3. Special Model of the GOLE-F Family
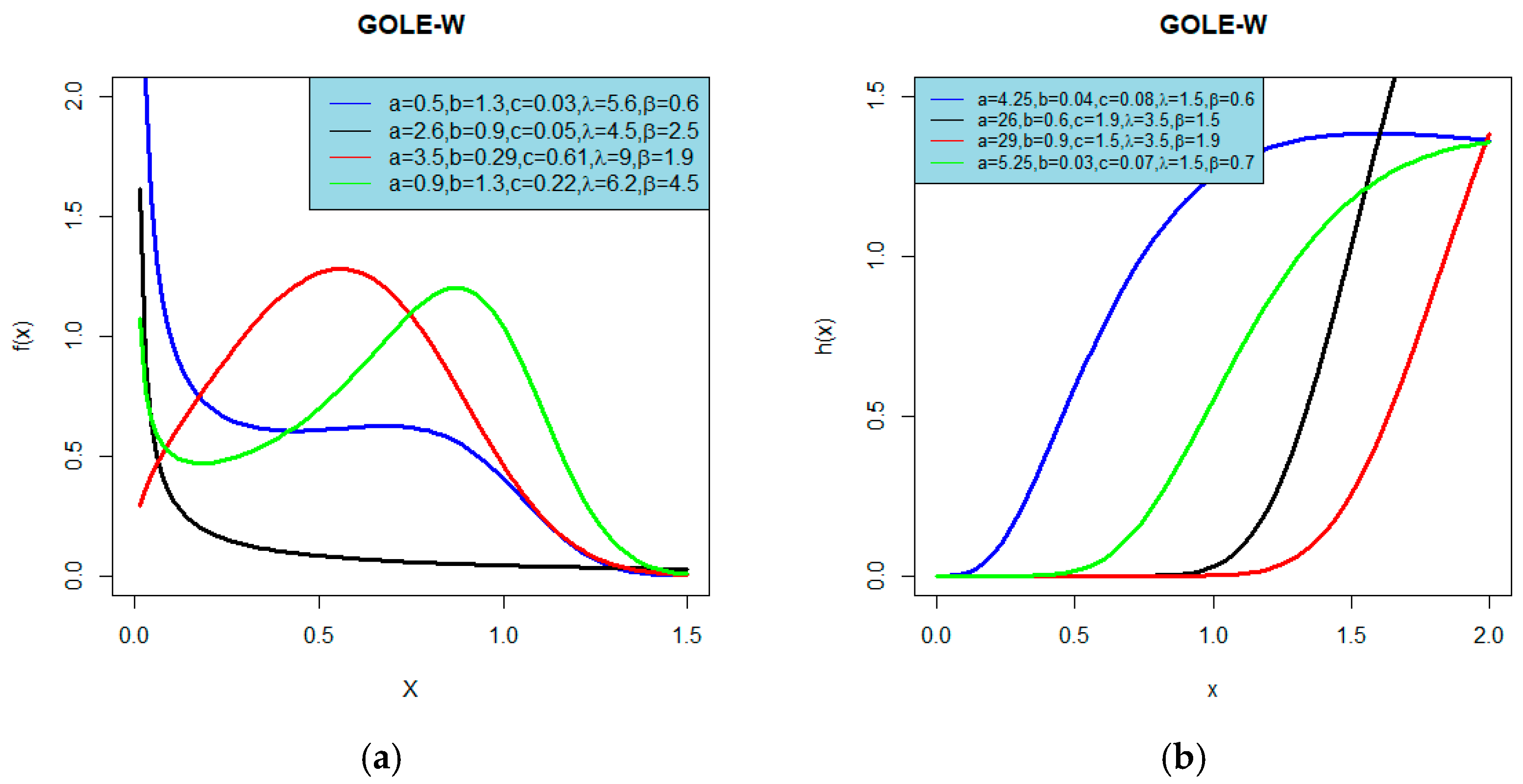
3.1. The Generalized Odd Linear Exponential-Weibull (GOLE-W) Distribution
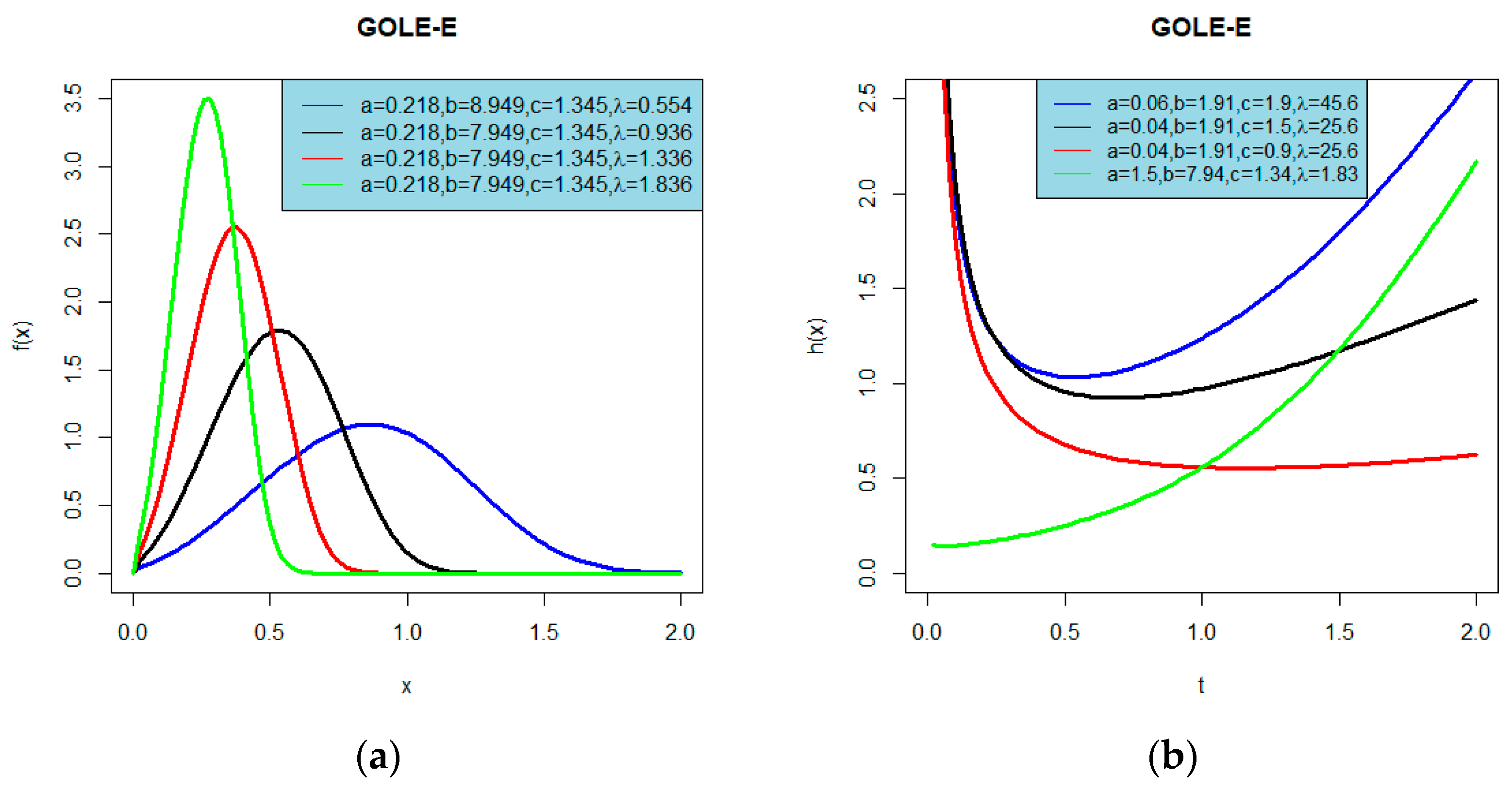
3.2. The Generalized Odd Linear Exponential-Exponential (GOLE-E) Distribution
4. Mathematical Properties of the GOLE-F Family
4.1. Asymptotic Behavior of GOLE-F Family
4.2. Useful Expansions for CDF and PDF of the New Family
4.3. Moments
4.4. Generating Function
4.5. Mean Deviations
4.6. Order Statistics
4.7. Stochastic Orderings
- usual stochastic order, denoted by , if , for all ;
- hazard rate order, denoted by , if , for all ;
- reversed hazard rate order, denoted by , if is decreases in ;
- mean residual life order, denoted by , if , for all ;
- likelihood ratio order, denoted by , if is decreases in .
4.8. Stress-Strength Model
5. Estimation and Simulation
5.1. Estimation of the Parameters
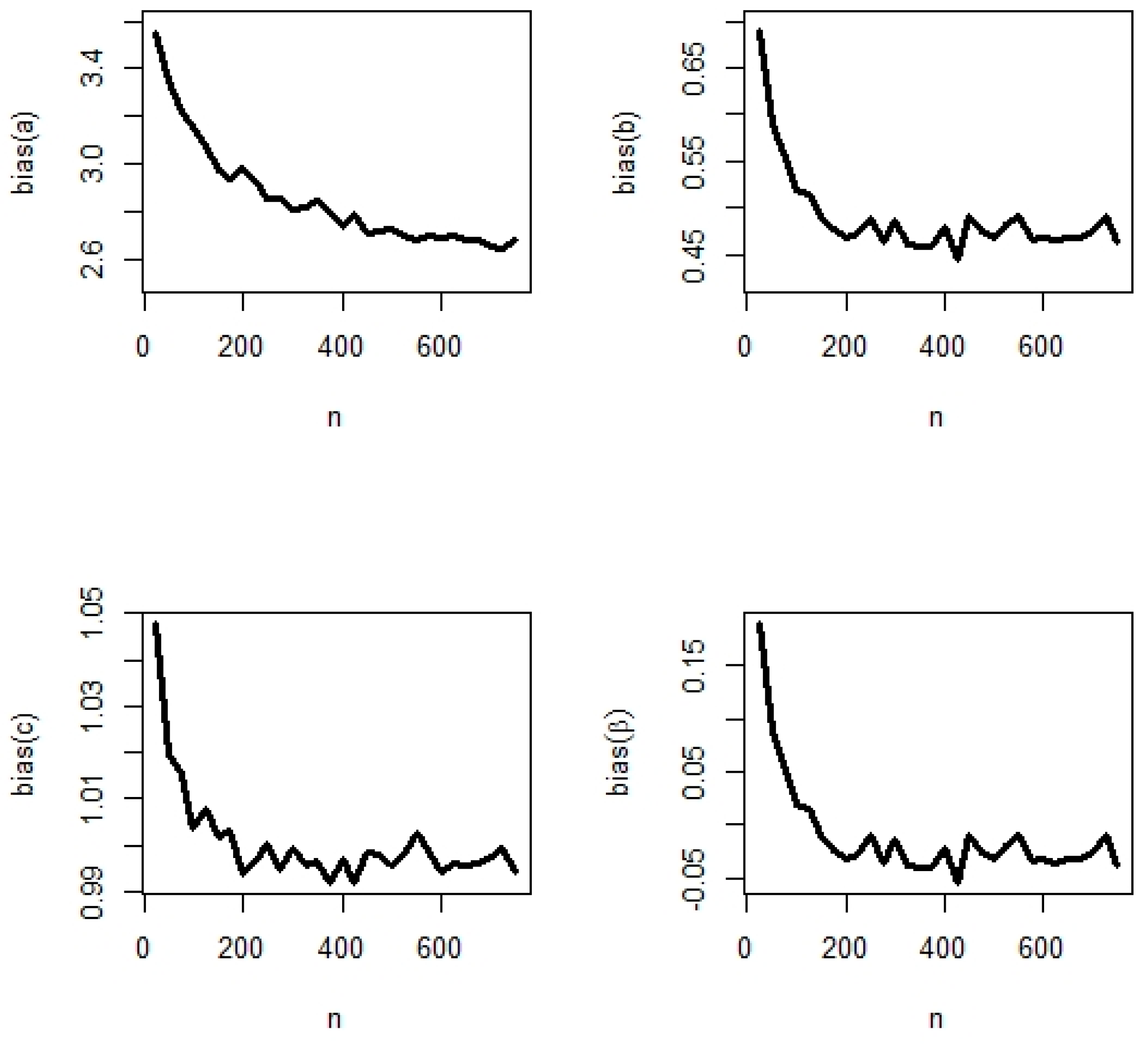
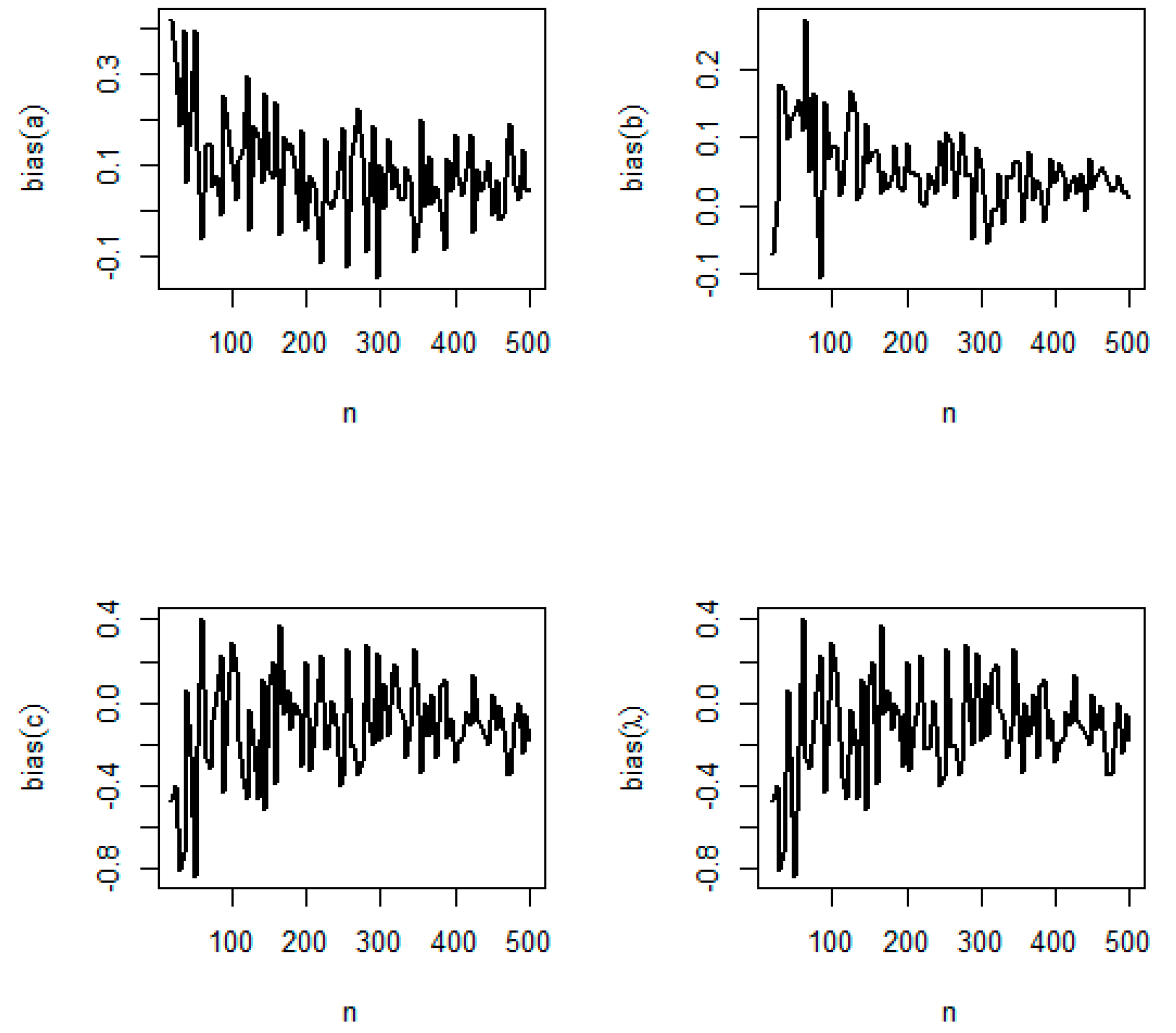
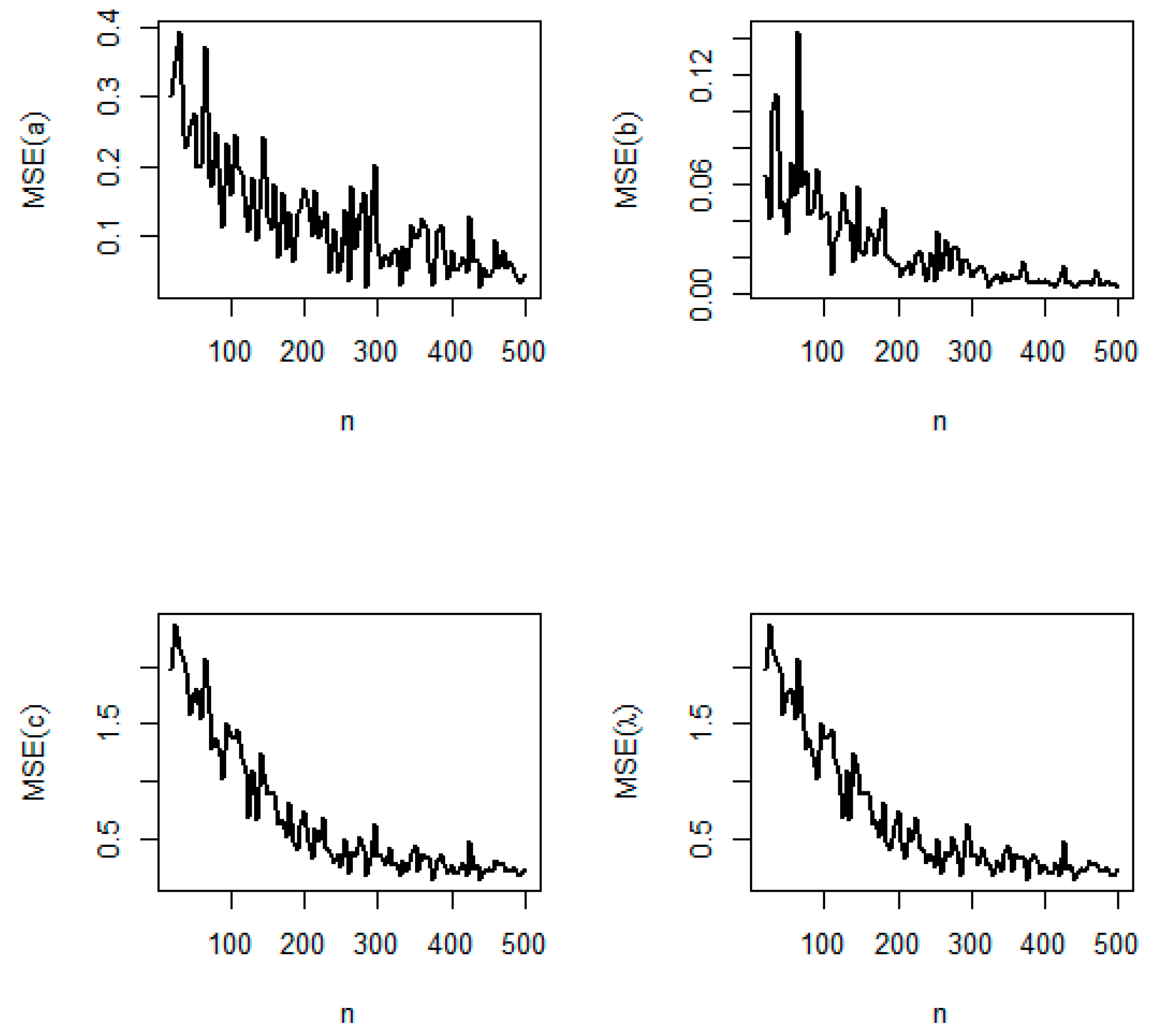
5.2. Simulation Study
6. Applications on Real-Life Data Sets
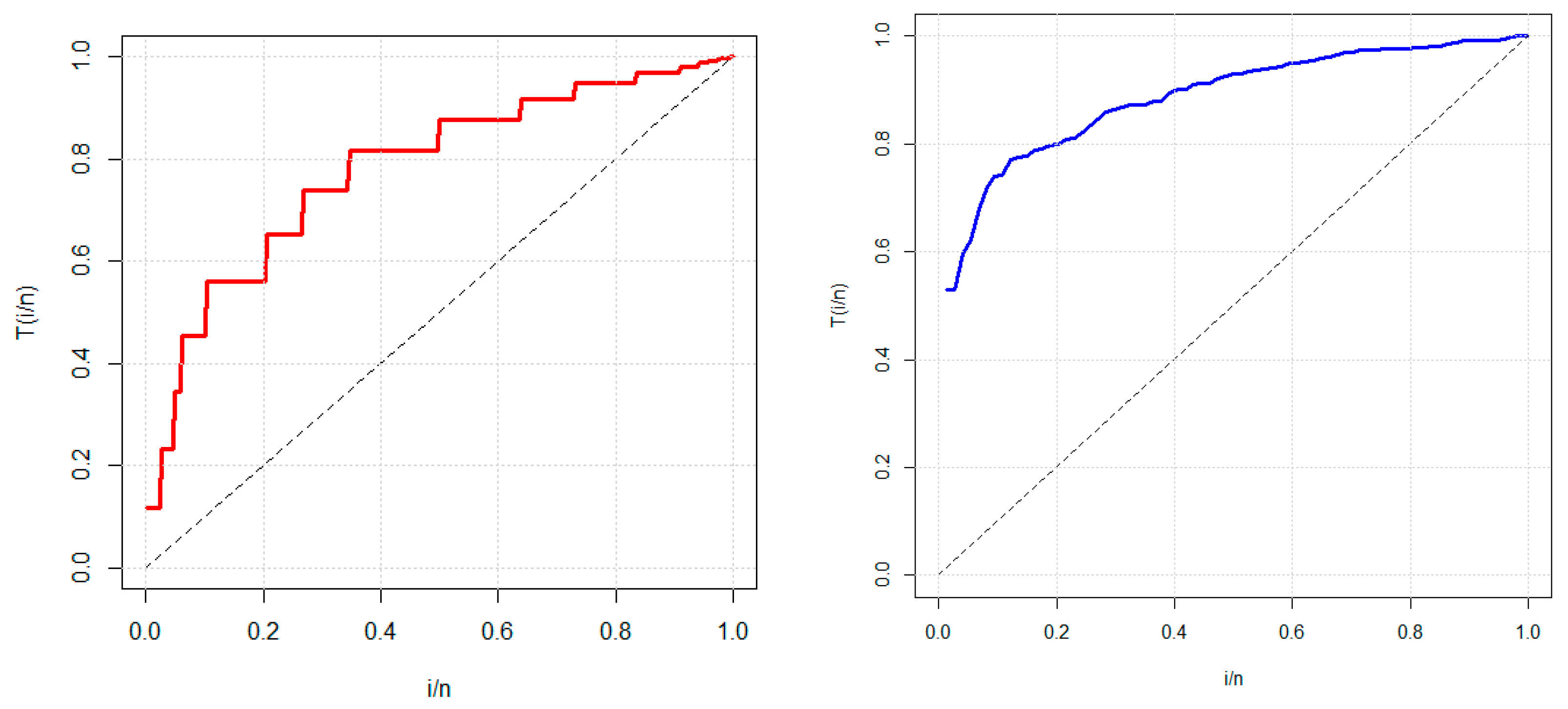
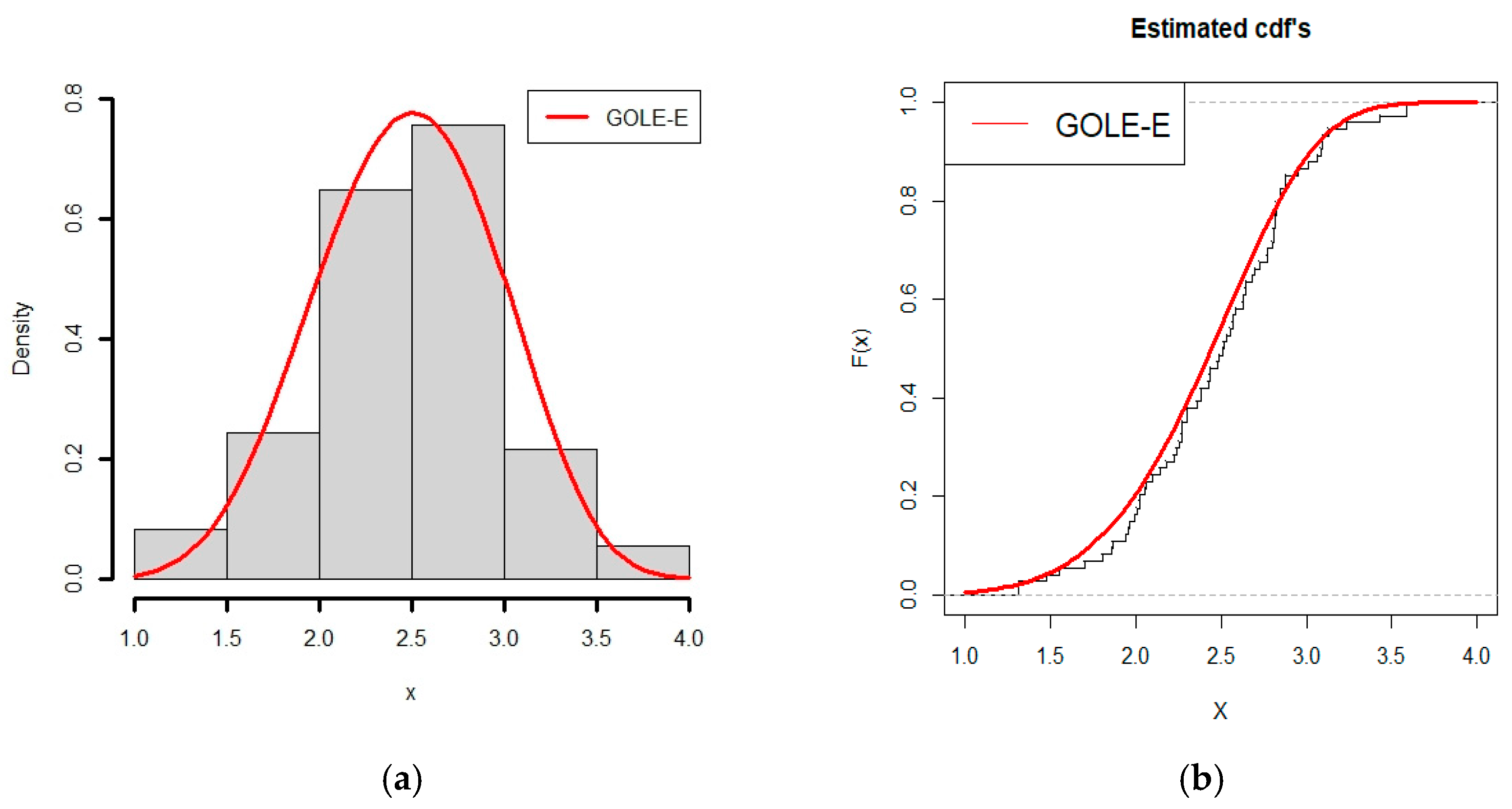
6.1. Application of GOLE-E
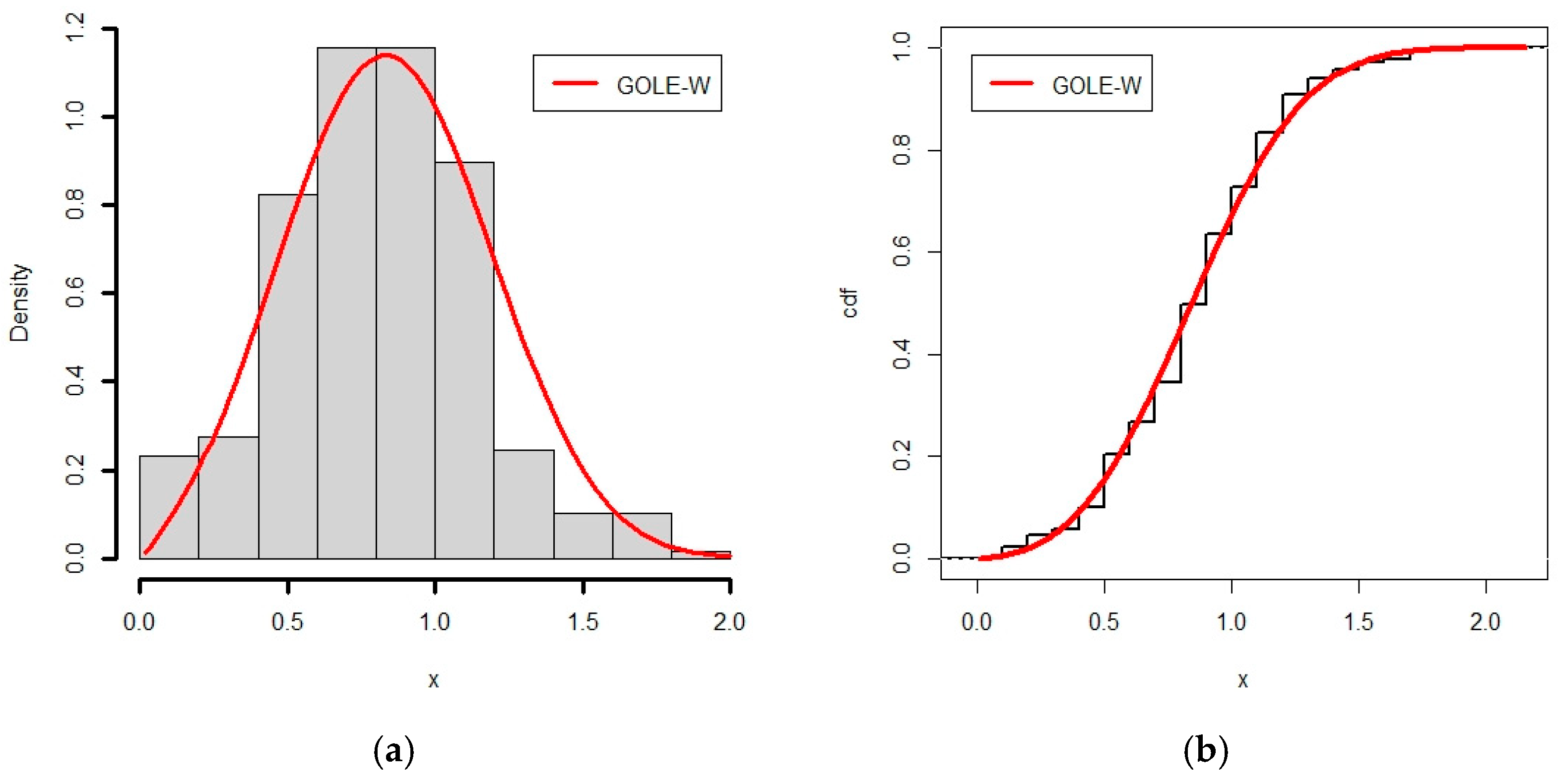
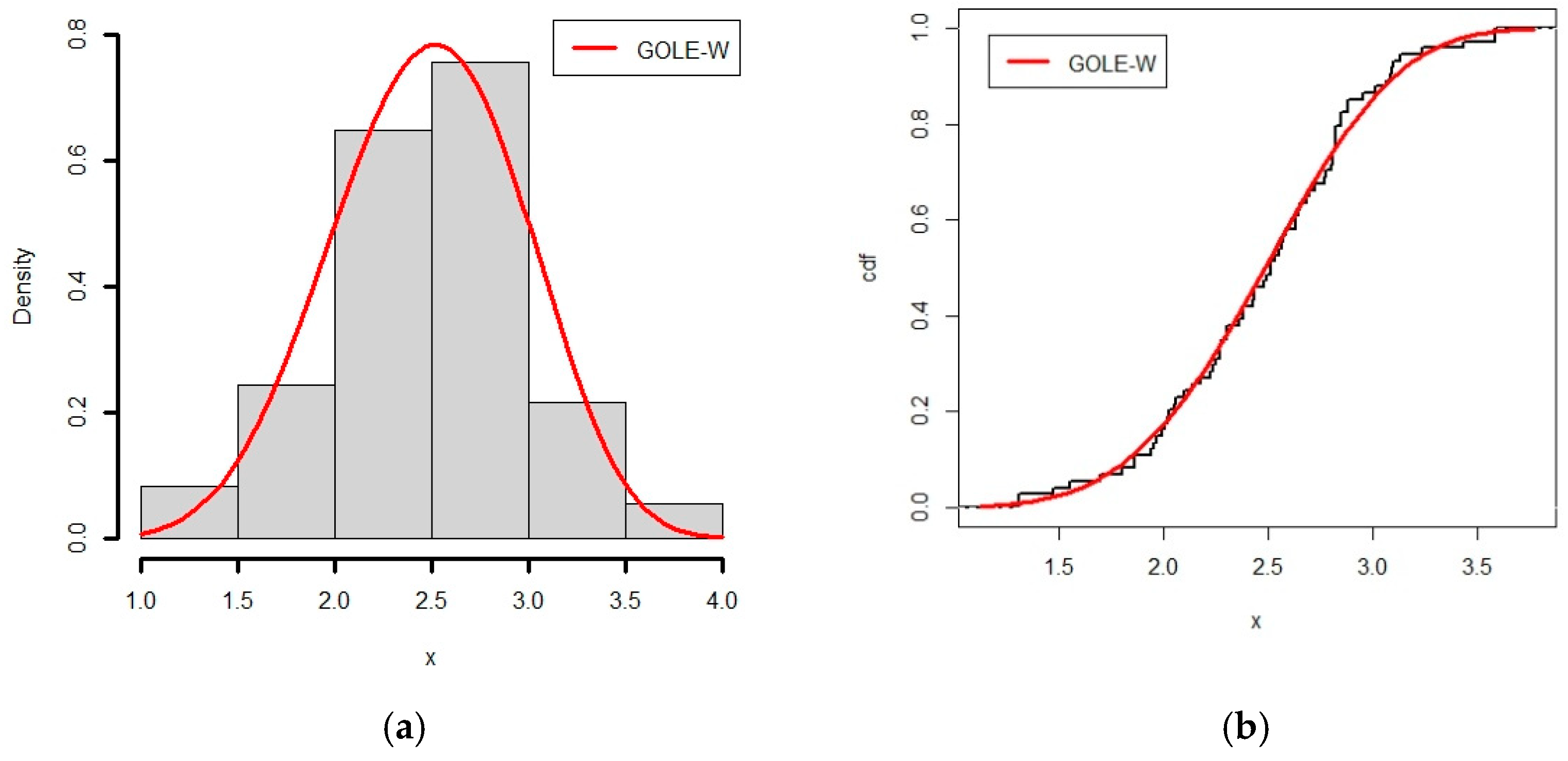
6.2. Application of GOLE-W
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Marshall, A.W. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling failure time data by Lehman alternatives. Commun. Stat.-Theory Methods 1998, 27, 887–904. [Google Scholar] [CrossRef]
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat. Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; De Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Alexander, C.; Cordeiro, G.M.; Ortega, E.M.; Sarabia, J.M. Generalized beta-generated distributions. Comput. Stat. Data Anal. 2012, 56, 1880–1897. Available online: https://EconPapers.repec.org/RePEc:eee:csdana:v:56:y:2012:i:6 (accessed on 19 May 2022). [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef] [Green Version]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G Family of Probability Distributions. J. Data Sci. 2014, 12, 53–68. Available online: http://www.jds-online.com/volume-12-number-1-january-2014 (accessed on 19 May 2022). [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Alizadeh, M.; Mansoor, M.; Zubair, M.; Hamedani, G.G. The odd generalized exponential family of distributions with applications. J. Stat. Distrib. Appl. 2015, 2, 1. [Google Scholar] [CrossRef] [Green Version]
- Cordeiro, G.M.; Alizadeh, M.; Ortega, E.M.; Serrano, L.H.V. The Zografos-Balakrishnan odd log-logistic family of distributions: Properties and Applications. Hacet. J. Math. Stat. 2015, 46, 11781–11803. Available online: https://dergipark.org.tr/hujms/issue/43489/524407 (accessed on 19 May 2022). [CrossRef]
- Gomes-Silva, F.; Percontini, A.; De Brito, E.; Ramos, M.W.; Venâncio, R.; Cordeiro, G.M. The Odd Lindley-G Family of Distributions. Austrian J. Stat. 2017, 46, 65–87. [Google Scholar] [CrossRef] [Green Version]
- Alizadeh, M.; Cordeiro, G.M.; Pinho, L.G.B.; Ghosh, I. The Gompertz-G family of distributions. J. Stat. Theory Pract. 2016, 11, 179–207. [Google Scholar] [CrossRef]
- Jamal, F.; Nasir, M.A.; Tahir, M.H.; Montazeri, N.H. The odd Burr-III family of distributions. J. Stat. Appl. Probab. 2017, 6, 105–122. Available online: http://www.naturalspublishing.com/files/published/4nk6g57u5e512l.pdf (accessed on 19 May 2022). [CrossRef]
- Khan, S.; Balogun, O.S.; Tahir, M.H.; Almutiry, W.; Alahmadi, A.A. An Alternate Generalized Odd Generalized Exponential Family with Applications to Premium Data. Symmetry 2021, 13, 2064. [Google Scholar] [CrossRef]
- Sen, A.; Bhattacharyya, G.K. Inference procedures for the linear failure rate model. J. Stat. Plan. Inference 1995, 46, 59–76. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders and Their Applications; Academic Press: San Diego, CA, USA, 2014. [Google Scholar] [CrossRef]
- Kotz, S.; Pensky, M. The Stress-Strength Model and Its Generalizations: Theory and Applications; World Scientific: Singapore, 2003. [Google Scholar] [CrossRef]
- Kundu, D.; Raqab, M.Z. Estimation of R = P (Y < X) for three-parameter Weibull distribution. Stat. Probab. Lett. 2009, 79, 1839–1846. [Google Scholar] [CrossRef]
- Aarset, M.V. How to Identify a Bathtub Hazard Rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
- Dara, S.T.; Ahmad, M. Recent Advances in Moment Distribution and Their Hazard Rates; Lap Lambert Academic Publishing: Chisinau, Republic of Moldova, 2012. [Google Scholar]
- Hasnain, S.A.; Iqbal, Z.; Ahmad, M. On exponentiated moment exponential distribution. Pak. J. Stat. 2015, 31, 267–280. Available online: https://www.statindex.org/journals/1313/31/2 (accessed on 19 May 2022).
- Gupta, R.D.; Kundu, D. Exponentiated Exponential Family: An Alternative to Gamma and Weibull Distributions. Biom. J. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. The beta exponential distribution. Reliab. Eng. Syst. Saf. 2006, 91, 689–697. [Google Scholar] [CrossRef]
- Mudholkar, G.; Srivastava, D. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Lai, C.D. Generalized Weibull Distributions. In Generalized Weibull Distributions; Springer Briefs in Statistics; Springer: Berlin/Heidelber, Germany, 2014. [Google Scholar] [CrossRef]
- Lee, C.; Famoye, F.; Olumolade, O. Beta-Weibull Distribution: Some Properties and Applications to Censored Data. J. Mod. Appl. Stat. Methods 2007, 6, 173–186. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]


| a | b | c | Mean | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| 0.5 | 0.5 | 1 | 0.6704 | 0.1330 | 1.2979 | 1.8368 |
| 2 | 1.1667 | 0.2186 | 1.1776 | 1.4755 | ||
| 5 | 1.9517 | 0.3004 | 1.0960 | 1.2512 | ||
| 10 | 2.5987 | 0.3351 | 1.0635 | 1.1656 | ||
| 20 | 3.2683 | 0.3541 | 1.0440 | 1.1146 | ||
| 50 | 4.1704 | 0.3660 | 1.0288 | 1.0753 | ||
| 100 | 4.8587 | 0.3701 | 1.0218 | 1.0571 | ||
| 1 | 1 | 1 | 0.4614 | 0.0824 | 1.3869 | 2.1392 |
| 2 | 0.8995 | 0.1587 | 1.2180 | 1.5987 | ||
| 5 | 1.6411 | 0.2408 | 1.1103 | 1.2923 | ||
| 10 | 2.2721 | 0.2776 | 1.0699 | 1.1839 | ||
| 20 | 2.9334 | 0.2982 | 1.0467 | 1.1226 | ||
| 50 | 3.8303 | 0.3114 | 1.0294 | 1.0774 | ||
| 100 | 4.5169 | 0.3159 | 1.0218 | 1.0574 | ||
| 2 | 1.5 | 1 | 0.3091 | 0.0488 | 1.5119 | 2.6112 |
| 2 | 0.6860 | 0.1130 | 1.2703 | 1.7688 | ||
| 5 | 1.3790 | 0.1919 | 1.1269 | 1.3424 | ||
| 10 | 1.9914 | 0.2297 | 1.0768 | 1.2044 | ||
| 20 | 2.6430 | 0.2514 | 1.0494 | 1.1308 | ||
| 50 | 3.5339 | 0.2654 | 1.0299 | 1.0793 | ||
| 100 | 4.2185 | 0.2702 | 1.0217 | 1.0574 |
| Data Sets | Min. | Mean | Median | S.D. | Skewness | Kurtosis | 1st Q. | 3rd Q. | Max. |
|---|---|---|---|---|---|---|---|---|---|
| I | 0.10 | 0.85 | 0.90 | 0.33 | 0.17 | 0.29 | 0.60 | 1.10 | 2.00 |
| II | 1.312 | 2.477 | 2.513 | 0.487 | −0.151 | −0.127 | 2.150 | 2.816 | 3.5 |
| Models | ||||
|---|---|---|---|---|
| 0.218 | 8.949 | 1.345 | 0.554 | |
| (0.315) | (3.246) | (0.237) | (0.083) | |
| [0, 0.84] | [2.58, 15.31] | [0.88, 1.81] | [0.39, 0.72] | |
| 3.020 | 105.575 | - | 0.252 | |
| (0.163) | (38.348) | (0.045) | ||
| [2.70, 3.34] | [30.41, 180.73] | [0.160.34] | ||
| 4.922 | 17.433 | - | 0.298 | |
| (0.364) | (8.216) | (0.128) | ||
| [4.21, 5.64] | [1.32, 33.54] | [0.05, 0.55] | ||
| - | 5.526 | - | 2.726 | |
| (0.514) | (0.128) | |||
| [4.52, 6.53] | [2.475, 2.98] | |||
| 2.574 | 0.284 | - | - | |
| (0.229) | (0.012) | |||
| [2.13, 3.02] | [0.26, 0.31] | |||
| - | 0.406 | - | - | |
| (0.016) | ||||
| [0.37, 0.44] | ||||
| - | - | - | 1.173 | |
| (0.063) | ||||
| [1.04, 1.29] |
| Models | AIC | BIC | CAIC | HQIC | A* | W* | KS (p-Value) |
|---|---|---|---|---|---|---|---|
| 232.14 | 247.54 | 232.28 | 238.30 | 2.67 | 0.47 | 0.25 (0.29) | |
| 236.92 | 248.46 | 236.99 | 241.51 | 3.37 | 0.58 | 0.12 (0.03) | |
| 276.04 | 287.59 | 276.11 | 280.66 | 6.48 | 1.09 | 0.24 (0.16) | |
| 302.44 | 310.14 | 302.47 | 305.52 | 9.42 | 1.59 | 0.22 (0.23) | |
| 290.62 | 298.32 | 290.65 | 293.70 | 8.48 | 1.46 | 0.24 (0.20) | |
| 388.70 | 392.55 | 388.71 | 390.24 | 6.49 | 1.09 | 0.23 (0.008) | |
| 583.66 | 587.51 | 583.67 | 585.20 | 6.54 | 1.11 | 0.34 (0.002) |
| Models | ||||
|---|---|---|---|---|
| 0.365 | 1.299 | 4.091 | 2.748 | |
| (0.160) | (0.657) | (1.248) | (0.531) | |
| [0.05, 0.68] | [0.01, 2.59] | [1.64, 6.54] | [1.71, 3.78] | |
| 12.473 | 24.773 | - | 0.559 | |
| (3.939) | (23.936) | (0.194) | ||
| [4.75, 20.19] | [0, 71.68] | [0.17, 0.93] | ||
| 26.259 | 14.354 | - | 0.421 | |
| (5.838) | (17.832) | (0.376) | ||
| [14.81, 37.70] | [0, 49.30] | [0, 1.16] | ||
| - | 89.394 | - | 2.018 | |
| (32.458) | (0.171) | |||
| [25.77, 153.01] | [1.68, 2.35] | |||
| 32.319 | 0.418 | - | - | |
| (10.705) | (0.032) | |||
| [11.33, 53.30] | [0.35, 0.48] | |||
| - | 1.238 | - | - | |
| (0.101) | ||||
| [1.04, 1.44] | ||||
| - | - | - | 0.403 | |
| (0.046) | ||||
| [0.31, 0.49] |
| Models | AIC | BIC | CAIC | HQIC | A* | W* | KS (p-Value) |
|---|---|---|---|---|---|---|---|
| 107.90 | 116.20 | 108.48 | 111.58 | 0.43 | 0.04 | 0.06 (0.83) | |
| 112.66 | 119.56 | 113.00 | 115.36 | 0.52 | 0.06 | 0.07 (0.79) | |
| 116.82 | 123.72 | 117.16 | 119.52 | 0.62 | 0.09 | 0.08 (0.71) | |
| 121.60 | 126.20 | 121.76 | 123.40 | 1.04 | 0.16 | 0.01 (0.44) | |
| 119.90 | 124.50 | 120.07 | 121.70 | 0.63 | 0.10 | 0.09 (0.52) | |
| 230.16 | 232.46 | 230.22 | 231.06 | 0.58 | 0.08 | 0.35 (0.002) | |
| 284.24 | 286.54 | 284.29 | 285.14 | 0.57 | 0.09 | 0.44 (0.01) |
| Models | |||||
|---|---|---|---|---|---|
| 2.3893 | 114.6653 | 4.8673 | - | 0.506777 | |
| (2.1340) | (50.1098) | (2.1515) | (0.1582) | ||
| [0, 6.57] | [16.45, 212.88] | [0.65, 9.08] | [0.20, 0.82] | ||
| 0.7103 | 0.2623 | - | 3.0464 | 3.8368 | |
| (0.0233) | (0.0263) | (0.0174) | |||
| [0.66, 0.76] | [0.23,0.29] | [2.99, 3.10] | [3.80, 3.87] | ||
| 0.7730 | 0.2276 | - | 3.0201 | 4.3742 | |
| (0.0673) | (0.0137) | (0.0042) | (0.0042) | ||
| [0.64, 0.90] | [0.20, 0.25] | [3.01, 3.02] | [4.37, 4.38] | ||
| - | 0.8090 | - | 3.068922 | 0.9440 | |
| (0.1515) | (0.3541) | (0.1732) | |||
| (4.52, 6.53) | (2.475, 2.98) | [0.60, 1.28] | |||
| 0.5597 | - | - | 2.7190 | 2.0240 | |
| (11.2701) | (0.1140) | (0.7523) | |||
| [0, 22.65] | [2.50, 2.94] | [0.55, 3.50] | |||
| - | 0.406 | - | - | - | |
| (0.016) | |||||
| [0.37, 0.44] | |||||
| - | - | - | 1.132926 | 2.71898 | |
| (0.0623) | (0.1140) | ||||
| [1.01, 1.26] | [2.50, 2.94] |
| Models | AIC | CAIC | BIC | HQIC | A* | W* | KS (p-Value) |
|---|---|---|---|---|---|---|---|
| 230.11 | 230.23 | 245.49 | 236.23 | 2.51 | 0.44 | 0.10 (0.17) | |
| 231.86 | 231.96 | 247.23 | 237.97 | 2.57 | 0.45 | 0.11 (0.03) | |
| 232.84 | 232.95 | 248.22 | 238.96 | 2.67 | 0.46 | 0.12 (0.01) | |
| 232.42 | 232.39 | 243.86 | 236.91 | 2.81 | 0.48 | 0.12 (0.000) | |
| 233.56 | 233.63 | 245.09 | 238.15 | 2.97 | 0.51 | 0.24 (0.000) | |
| 388.70 | 392.55 | 388.71 | 390.24 | 6.49 | 1.09 | 0.23 (0.008) | |
| 231.56 | 231.88 | 239.25 | 234.62 | 2.97 | 0.51 | 0.14 (0.000) |
| Models | |||||
|---|---|---|---|---|---|
| 6.9553 | 114.6653 | 20.1203 | - | 0.8448 | |
| (6.6794) | (50.1098) | (6.6638) | (0.31433) | ||
| [0,20.04] | [0, 27.65] | [7.06, 33.18] | [0.23, 1.46] | ||
| 1.6646 | 1.0950 | - | 4.3675 | 0.0187 | |
| (0.8438) | (0.5829) | (2.8871) | (0.0192) | ||
| [0.01, 3.32] | [0.23, 0.29] | [0, 10.0262] | [0, 0.0564] | ||
| 1.7401 | 0.9961 | - | 4.2987 | 0.0222 | |
| (1.3064) | (0.9249) | (2.0778) | (0.0253) | ||
| [0, 4.30] | [0, 2.81] | [0.23, 8.37] | [0, 0.07] | ||
| - | 1.7298 | - | 4.3083 | 0.9440 | |
| (0.7208) | (0.9066) | (0.1732) | |||
| [0.32, 3.14] | [2.53, 6.09] | [0, 0.07] | |||
| 1.5460 | - | - | 5.3816 | 0.0033 | |
| (0.9021) | (0.4906) | (0.0008) | |||
| [0, 3.3142] | [4.42, 6.34] | [0.002, 0.005] | |||
| - | 0.406 | - | - | - | |
| (0.016) | |||||
| [0.37, 0.44] | |||||
| - | - | - | 0.0036 | 5.7342 | |
| (0.0009) | (0.2428) | ||||
| [0.0002, 0.0053] | [5.26, 6.21] |
| Models | AIC | CAIC | BIC | HQIC | A* | W* | KS (p-Value) |
|---|---|---|---|---|---|---|---|
| 110.57 | 111.15 | 119.79 | 114.25 | 0.25 | 0.031 | 0.06 (0.93) | |
| 111.06 | 112.83 | 120.08 | 114.98 | 2.27 | 0.037 | 0.08 (0.91) | |
| 111.32 | 112.90 | 120.13 | 115.99 | 0.26 | 0.038 | 0.07 (0.92) | |
| 118.33 | 118.72 | 122.89 | 120.68 | 0.31 | 0.075 | 0.098 (0.89) | |
| 113.84 | 113.13 | 123.02 | 119.15 | 0.30 | 0.052 | 0.08 (0.88) | |
| 388.70 | 392.55 | 388.71 | 390.24 | 6.49 | 1.09 | 0.23 (0.008) | |
| 117.45 | 116.61 | 121.77 | 117.91 | 0.29 | 0.037 | 0.09 (0.87) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamal, F.; Handique, L.; Ahmed, A.H.N.; Khan, S.; Shafiq, S.; Marzouk, W. The Generalized Odd Linear Exponential Family of Distributions with Applications to Reliability Theory. Math. Comput. Appl. 2022, 27, 55. https://doi.org/10.3390/mca27040055
Jamal F, Handique L, Ahmed AHN, Khan S, Shafiq S, Marzouk W. The Generalized Odd Linear Exponential Family of Distributions with Applications to Reliability Theory. Mathematical and Computational Applications. 2022; 27(4):55. https://doi.org/10.3390/mca27040055
Chicago/Turabian StyleJamal, Farrukh, Laba Handique, Abdul Hadi N. Ahmed, Sadaf Khan, Shakaiba Shafiq, and Waleed Marzouk. 2022. "The Generalized Odd Linear Exponential Family of Distributions with Applications to Reliability Theory" Mathematical and Computational Applications 27, no. 4: 55. https://doi.org/10.3390/mca27040055
APA StyleJamal, F., Handique, L., Ahmed, A. H. N., Khan, S., Shafiq, S., & Marzouk, W. (2022). The Generalized Odd Linear Exponential Family of Distributions with Applications to Reliability Theory. Mathematical and Computational Applications, 27(4), 55. https://doi.org/10.3390/mca27040055







