Solution of a Complex Nonlinear Fractional Biochemical Reaction Model
Abstract
:1. Introduction
2. A Model of Complex Enzyme Inhibitor Reactions
3. Analytical Expressions for the Concentrations
3.1. Laplace Decomposition Approach
3.2. Differential Transformation Method
3.3. Padé Approximation
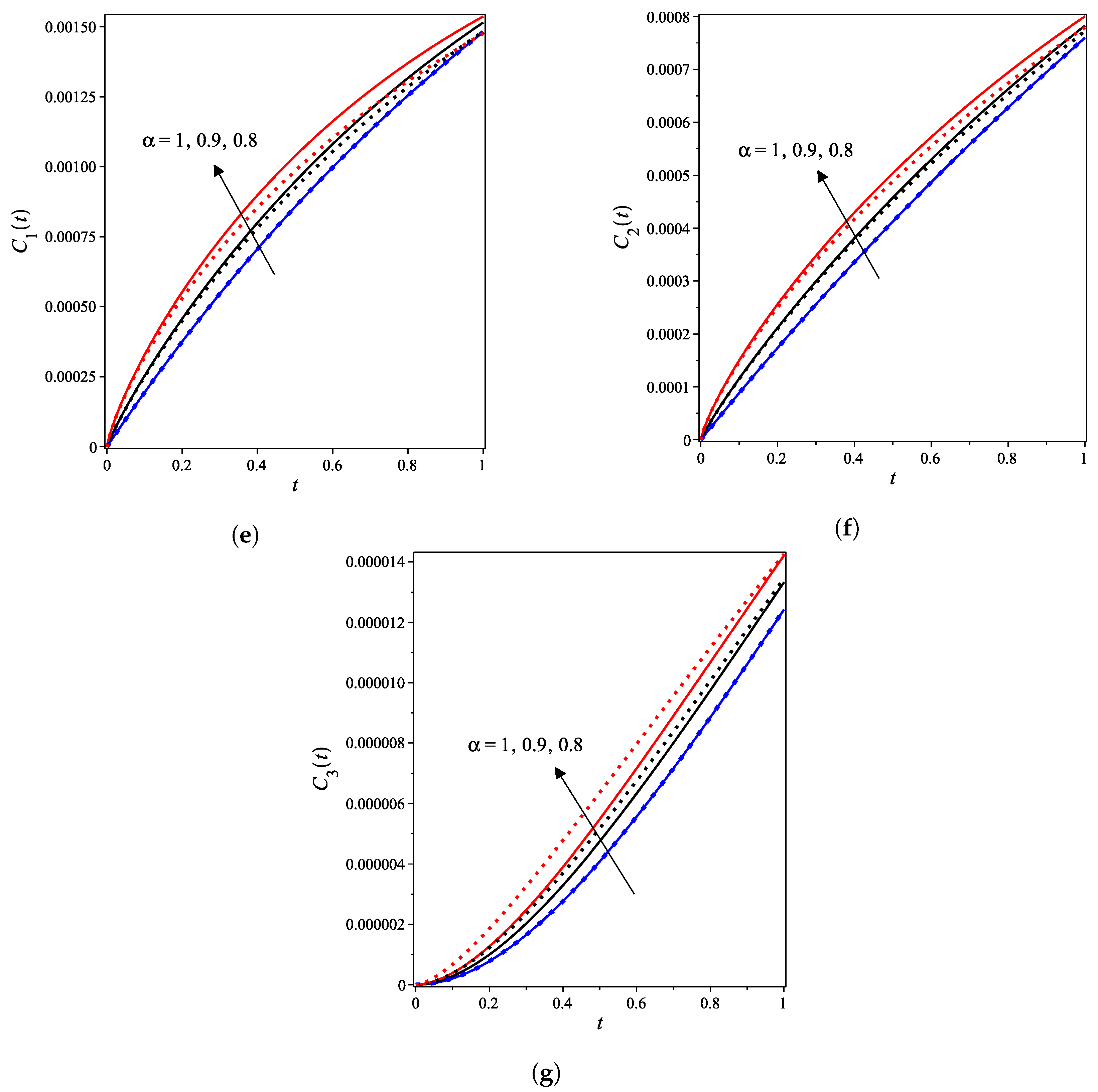
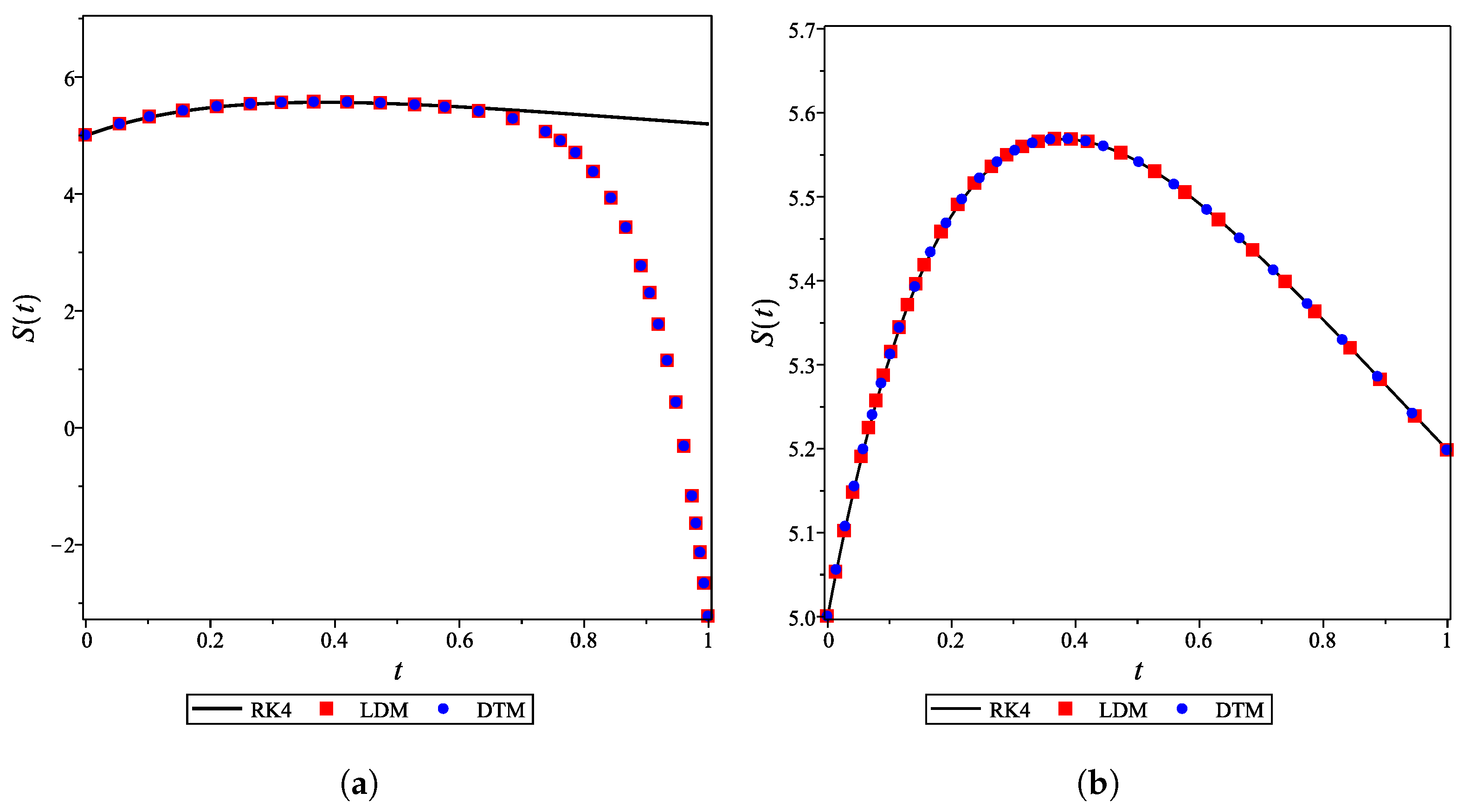
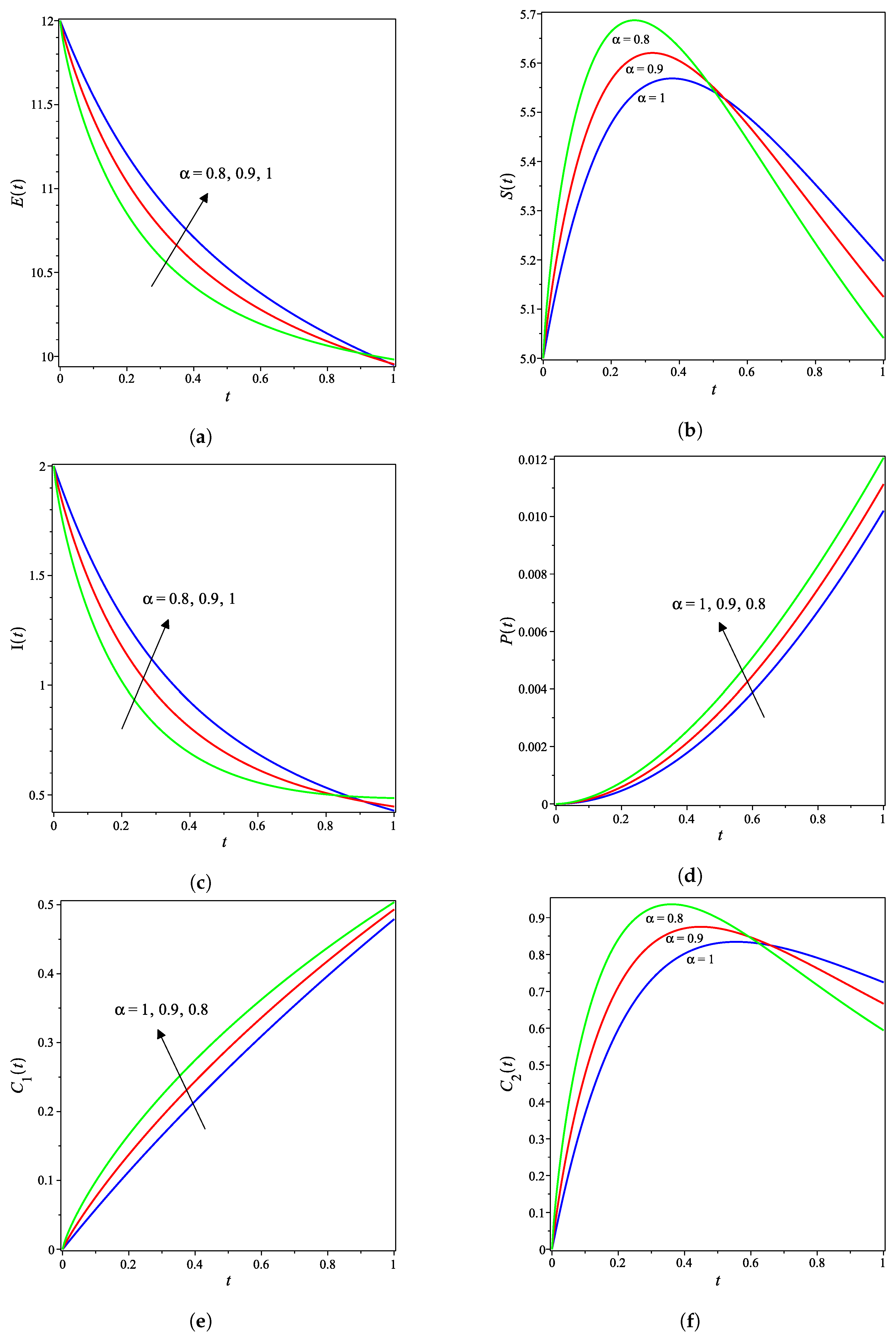
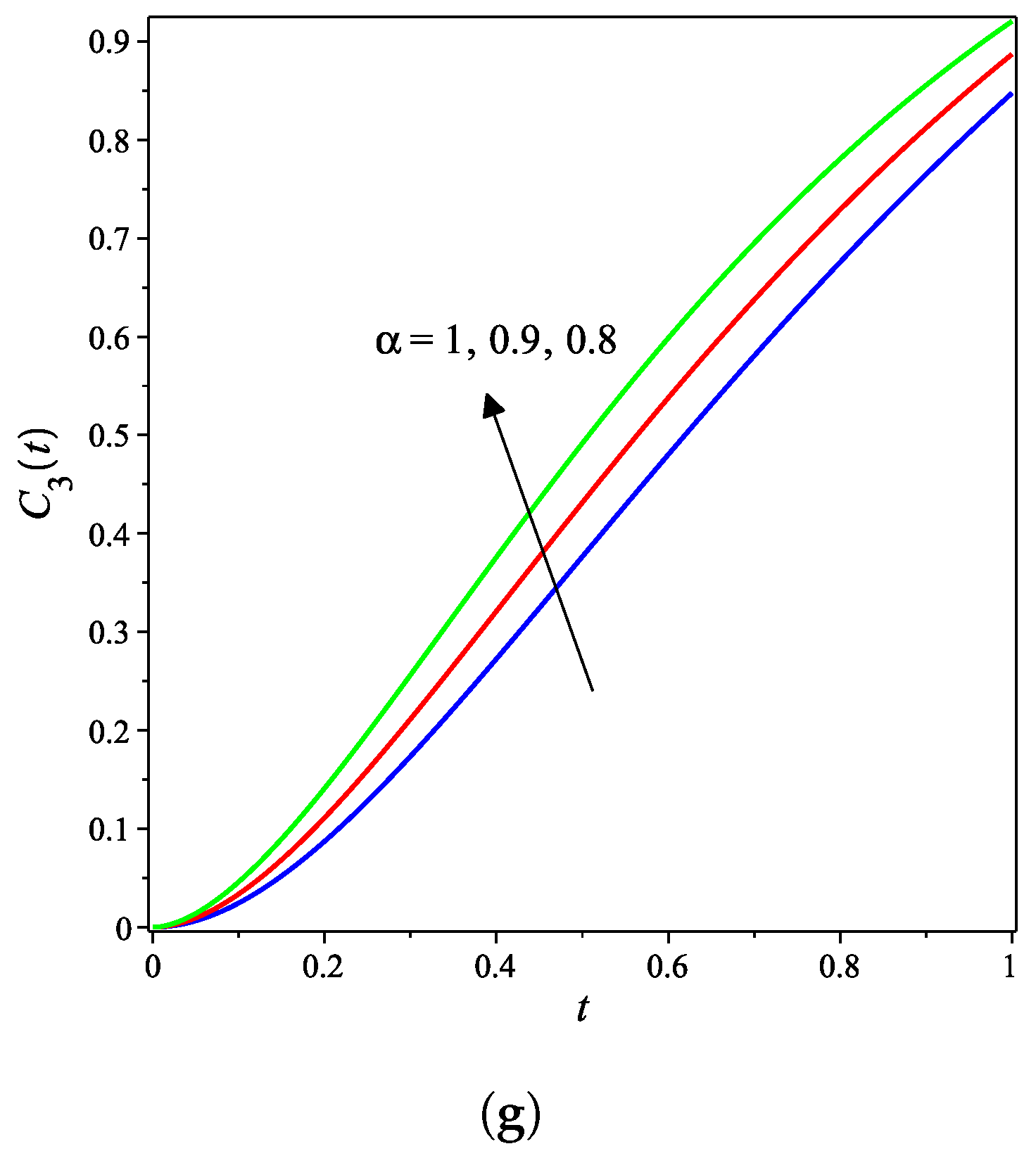
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Saravanakumar, R.; Pirabaharan, P.; Abukhaled, M.; Rajendran, L. Theoretical analysis of voltammetry at a rotating disk electrode in the absence of supporting electrolyte. J. Phys. Chem. B 2020, 124, 443–450. [Google Scholar] [CrossRef]
- Abukhaled, M.; Guessoum, N.; Alsaeed, N. Mathematical modeling of light curves of RHESSI and AGILE terrestrial gamma-ray flashes. Astrophys. Space Sci. 2019, 364, 120. [Google Scholar] [CrossRef]
- Saravanakumar, S.; Eswari, A.; Rajendran, L.; Abukhaled, M. A mathematical model of risk factors in HIV/AIDS transmission Dynamics: Observational study of female sexual network in India. Appl. Math. Inf. Sci. 2020, 14, 967–976. [Google Scholar]
- Devi, M.C.; Pirabaharan, P.; Abukhaled, M.; Rajendran, L. Analysis of the steady-state behavior of pseudo-first-order EC-catalytic mechanism at a rotating disk electrode. Electrochim. Acta 2020, 345, 136175. [Google Scholar] [CrossRef]
- Abukhaled, M.; Khuri, S. An efficient semi-analytical solution of a one-dimensional curvature equation that describes the human corneal shape. Math. Comput. Appl. 2019, 24, 8. [Google Scholar] [CrossRef] [Green Version]
- Selvi, M.S.M.; Rajendran, L.; Abukhaled, M. Estimation of Rolling Motion of Ship in Random Beam Seas by Efficient Analytical and Numerical Approaches. J. Mar. Sci. Appl. 2021, 20, 55–66. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef] [Green Version]
- Flores-Tlacuahuac, A.; Biegler, L. Optimization of Fractional Order Dynamic Chemical Processing Systems. Ind. Eng. Chem. Res. 2014, 53, 5110–5127. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.; Bates, J. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear. Sci. Numer. Simulat. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Rihan, F.A. Numerical modeling of fractional-order biological systems. Abstr. Appl. Anal. 2013, 2013, 816803. [Google Scholar] [CrossRef] [Green Version]
- Lazopoulos, K.A.; Lazopoulos, A.K. Fractional vector calculus and fluid mechanics. J. Mech. Behav. Biomed. Mater. 2017, 26, 43–54. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Cordova-Fraga, T.; Escalante-Martínez, J.E.; Calderon-Ram, C.; Escobar-Jimenez, R.F. Electrical circuits described by a fractional derivative with regular Kernel. Rev. Mex. De Fis. 2016, 62, 144–154. [Google Scholar]
- Meral, F.C.; Royston, T.J.; Magin, R. Fractional calculus in viscoelasticity: An experimental study. Ommun. Nonlinear. Sci. Numer. Simulat. 2010, 15, 939–945. [Google Scholar] [CrossRef]
- Matušů, R. Application of fractional order calculus to control theory. Math Model. Methods Appl. Sci. 2011, 5, 1162–1169. [Google Scholar]
- Srivastava, H.M. Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J. 2020, 60, 73–116. [Google Scholar]
- Dubey, V.P.; Kumar, R.; Kumar, D. Approximate analytical solution of fractional order biochemical reaction model and its stability analysis. Int. J. Biomath. 2019, 12, 1950059. [Google Scholar] [CrossRef]
- Dulf, E.-H.; Vodnar, D.C.; Danku, A.; Muresan, C.; Crisan, O. Fractional-Order Models for Biochemical Processes. Fractal Fract. 2020, 4, 12. [Google Scholar] [CrossRef] [Green Version]
- Iyiola, O.; Tasbozan, O.; Kurt, A.; Çenesiz, Y. On the analytical solutions of the system of conformable time-fractional Robertson equations with 1-D diffusion. Chaos Solitons Fractals 2017, 94, 1–7. [Google Scholar] [CrossRef]
- Arafa, A. Different approach for conformable fractional biochemical reaction diffusion models. Appl. Math. J. Chin. Univ. 2020, 35, 452. [Google Scholar] [CrossRef]
- Baeumer, B.; Kovacs, M.; Meerschaert, M. Numerical solutions for fractional reaction diffusion equations. Comput. Math. Appl. 2008, 55, 2212. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A. Modeling the Enzyme Kinetic Reaction. Acta Biotheor 2015, 63, 239. [Google Scholar] [CrossRef] [PubMed]
- Bhrawy, A.; Zaky, M. Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 2015, 80, 101–116. [Google Scholar] [CrossRef]
- Atangana, A.; Owolabi, K.M. New numerical approach for fractional differential equations. Math. Model. Nat. Phenom. 2018, 13, 3. [Google Scholar] [CrossRef] [Green Version]
- Milici, C.; Machado, J.T. Draganescu, G. Application of the Euler and Runge–Kutta Generalized Methods for FDE and Symbolic Packages in the Analysis of Some Fractional Attractors. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 159–170. [Google Scholar] [CrossRef]
- Jhinga, A.; Daftardar-Gejji, V. A new numerical method for solving fractional delay differential equations. Comput. Appl. Math. 2019, 38, 166. [Google Scholar] [CrossRef]
- Kumar, S.; Baleanu, D. A new numerical method for time fractional non-linear sharma-tasso-oliver equation and klein-gordon equation with exponential kernel law. Front. Phys. 2020, 8, 136. [Google Scholar] [CrossRef]
- Ali, U.; Khan, M.A.; Khater, M.M.A.; Mousa, A.A.; Attia, R.A.M. A new numerical approach for solving 1D fractional diffusion-wave equation. J. Funct. Spaces 2021, 2021, 1–7. [Google Scholar] [CrossRef]
- Toufik, M.; Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 2017, 132, 444. [Google Scholar] [CrossRef]
- Devi, M.C.; Pirabaharan, P.; Rajendran, L.; Abukhaled, M. An efficient method for finding analytical expressions of substrate concentrations for different particles in an immobilized enzyme system. Reac. Kinet. Mech. Cat. 2020, 130, 35–53. [Google Scholar] [CrossRef]
- Javeed, S.; Baleanu, D.; Waheed, A.; Shaukat, K.M.; Affan, H. Analysis of Homotopy Perturbation Method for Solving Fractional Order Differential Equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Zurigat, M.; Momani, S.; Odibat, Z.; Alawneh, A. The homotopy analysis method for handling systems of fractional differential equations. Appl. Math. Model. 2010, 34, 24–35. [Google Scholar] [CrossRef]
- Mohammed, O.; Salim, H. Computational methods based laplace decomposition for solving nonlinear system of fractional order differential equations. Alex. Eng. J. 2018, 57, 3549–3557. [Google Scholar] [CrossRef]
- He, C.-H.; Shen, Y.; Ji, F.-Y.; He, J.-H. Taylor series solution for fractal Bratu-type equation arising in electrospinning process. Fractals 2020, 28, 2050011. [Google Scholar] [CrossRef]
- Hadid, S.; Khuri, S.A.; Sayfy, A. A Green’s function iterative approach for the solution of a class of fractional BVPs arising in physical models. Int. J. Appl. Comput. Math. 2020, 6, 91. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gomez-Aguilar, J.F.; Saad, K.; Khan, M.; Agarwal, P. Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: A fractional calculus approach. Phys. A: Stat. Mech. Appl. 2019, 523, 48–65. [Google Scholar] [CrossRef]
- Abukhaled, M.; Khuri, S.; Rabah, F. Solution of a nonlinear fractional COVID-19 model. Int. J. Numer. Methods Heat Fluid Flow 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Ganjefar, S.; Rezaei, S. Modified homotopy perturbation method for optimal control problems using the Padé approximant. Appl. Math. Model. 2016, 40, 7062–7081. [Google Scholar] [CrossRef]
- Akgül, A.; Khoshnaw, S.H. Application of fractional derivative on non-linear biochemical reaction models. Int. J. Intell. Netw. 2020, 1, 52–58. [Google Scholar] [CrossRef]
- Alchikh, R.; Khuri, S.A. Numerical solution of a fractional differential equation arising in optics. Optik 2020, 208, 163911. [Google Scholar] [CrossRef]
- Zhou, J.K. Differential Transformation and Its Applications for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986. [Google Scholar]
- Arikoglu, A.; Ozkol, I. Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 2007, 34, 1473–1481. [Google Scholar] [CrossRef]
- Ertürk, V.S.; Momani, S. Solving systems of fractional differential equations using differential transform method. J. Comput. Appl. Math. 2008, 215, 142–151. [Google Scholar] [CrossRef] [Green Version]
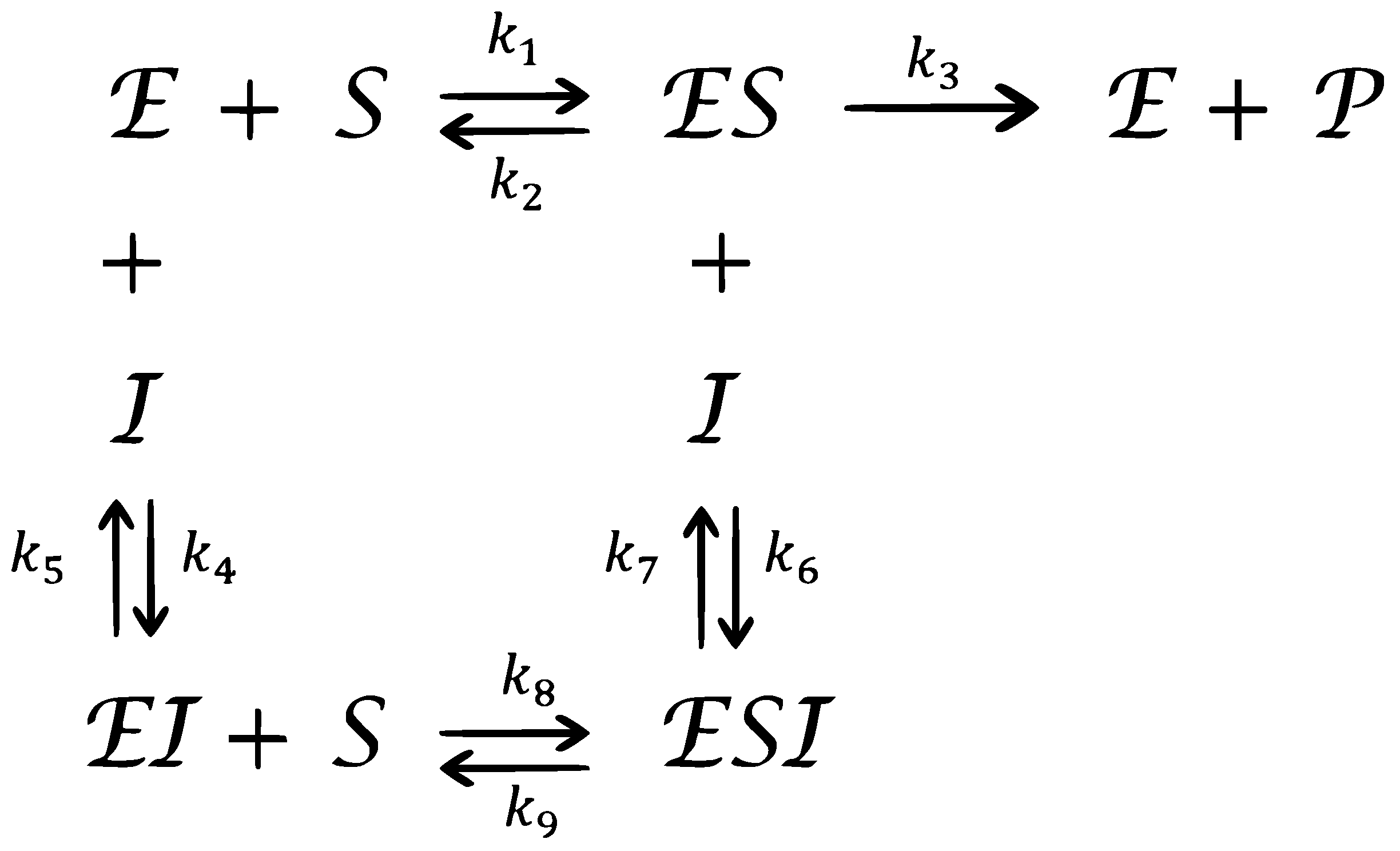
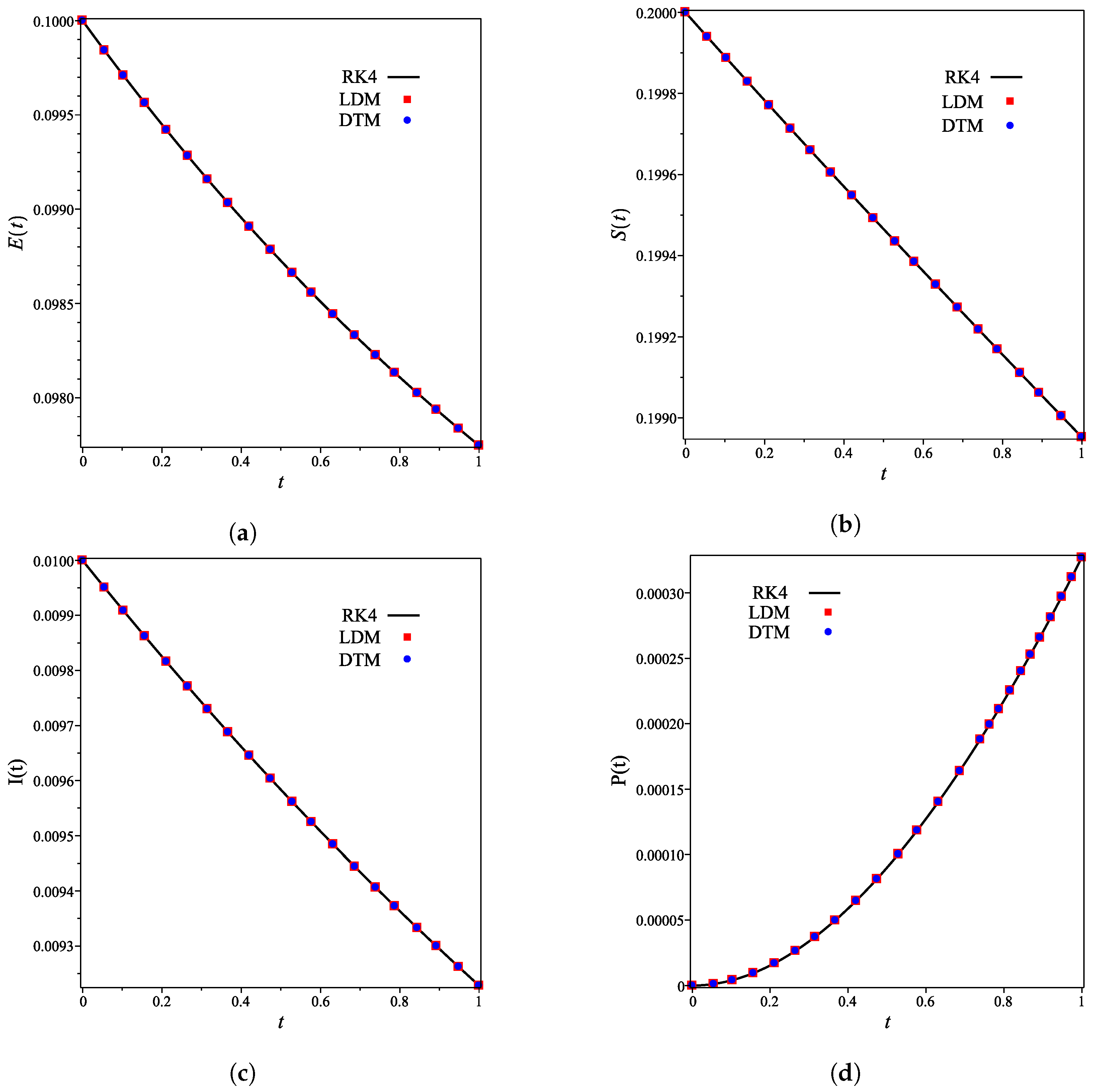
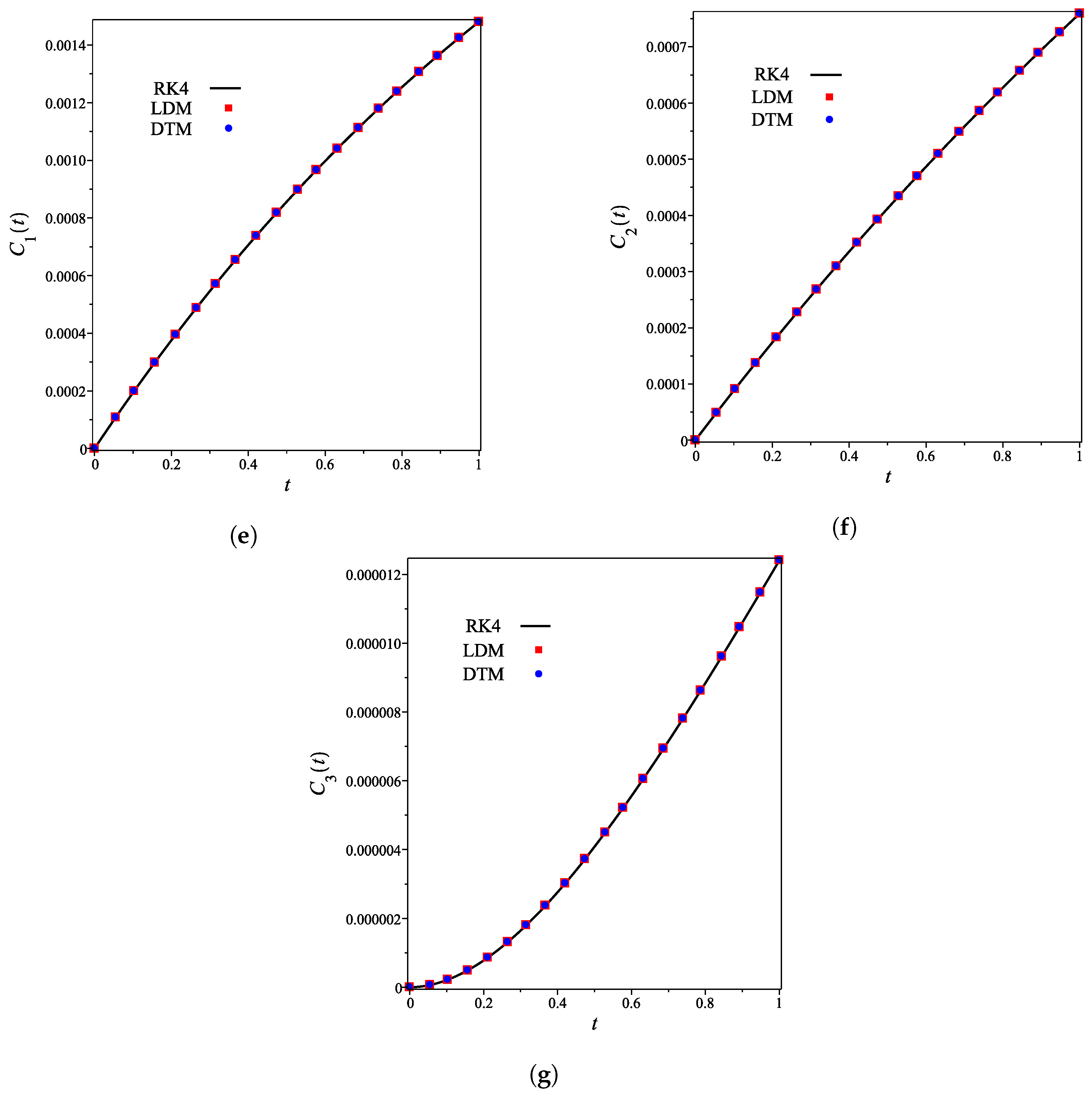
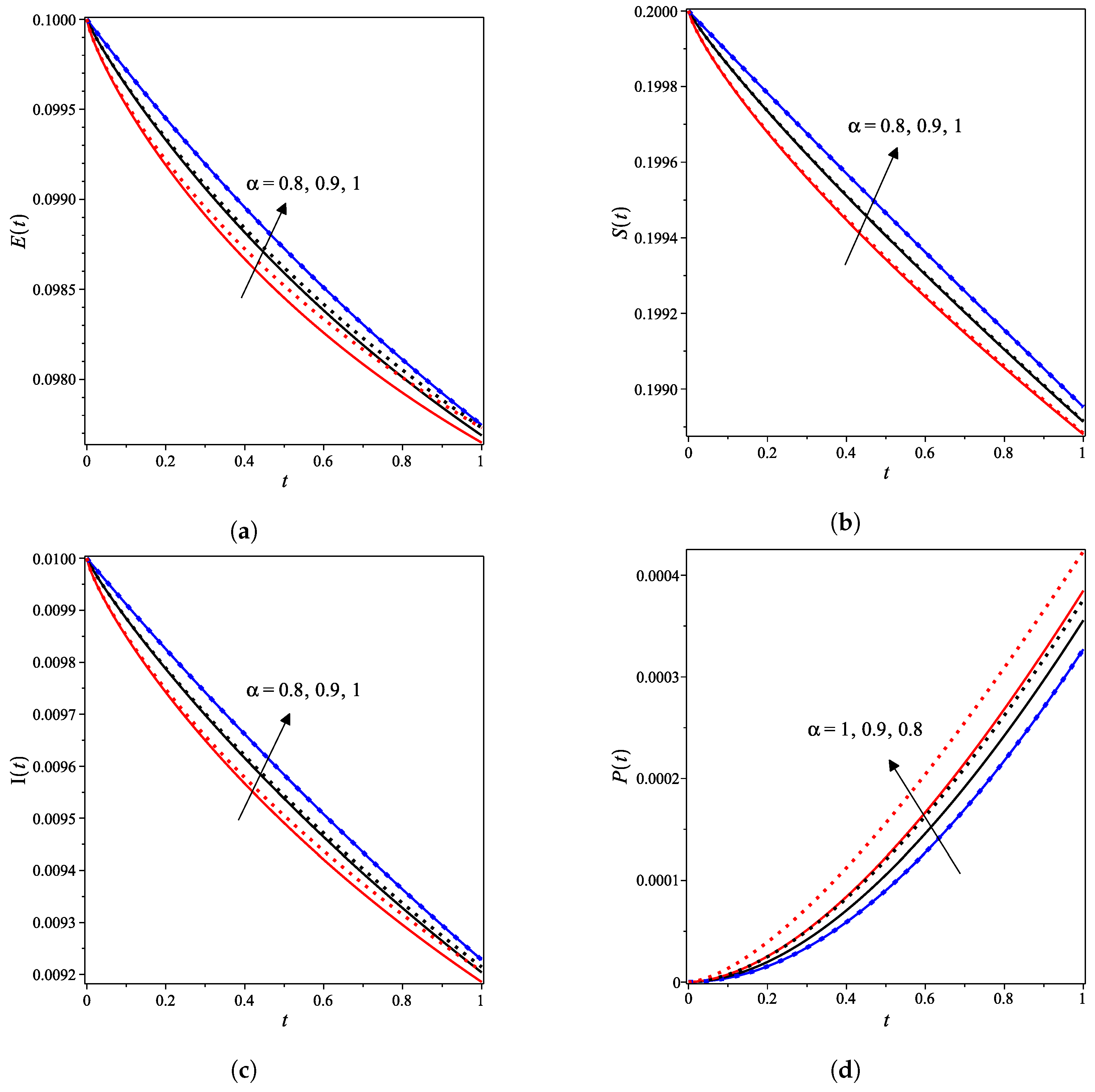

| Concentration | Maximum Difference | Occurred at x |
|---|---|---|
| Enzyme | 0.0000424 | 1.000 |
| Substrate | 0.0000024 | 0.007 |
| Inhibition | 0.0000103 | 1.000 |
| Production | 0.0000205 | 0.925 |
| Complex ES | 0.0000323 | 0.925 |
| Complex EI | 0.0000105 | 1.000 |
| Complex ESI | 0.0000004 | 0.525 |
| Concentration | Maximum Difference | Occurred at x |
|---|---|---|
| Enzyme | 0.0000843 | 0.850 |
| Substrate | 0.0000049 | 0.600 |
| Inhibition | 0.0000206 | 1.000 |
| Production | 0.0000408 | 0.825 |
| Complex ES | 0.0000643 | 0.825 |
| Complex EI | 0.0000208 | 1.950 |
| Complex ESI | 0.0000009 | 0.450 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabah, F.; Abukhaled, M.; Khuri, S.A. Solution of a Complex Nonlinear Fractional Biochemical Reaction Model. Math. Comput. Appl. 2022, 27, 45. https://doi.org/10.3390/mca27030045
Rabah F, Abukhaled M, Khuri SA. Solution of a Complex Nonlinear Fractional Biochemical Reaction Model. Mathematical and Computational Applications. 2022; 27(3):45. https://doi.org/10.3390/mca27030045
Chicago/Turabian StyleRabah, Fatima, Marwan Abukhaled, and Suheil A. Khuri. 2022. "Solution of a Complex Nonlinear Fractional Biochemical Reaction Model" Mathematical and Computational Applications 27, no. 3: 45. https://doi.org/10.3390/mca27030045
APA StyleRabah, F., Abukhaled, M., & Khuri, S. A. (2022). Solution of a Complex Nonlinear Fractional Biochemical Reaction Model. Mathematical and Computational Applications, 27(3), 45. https://doi.org/10.3390/mca27030045





