Alternative Initial Probability Tables for Elicitation of Bayesian Belief Networks
Abstract
1. Introduction
2. CPT Algorithms Using Limited Input
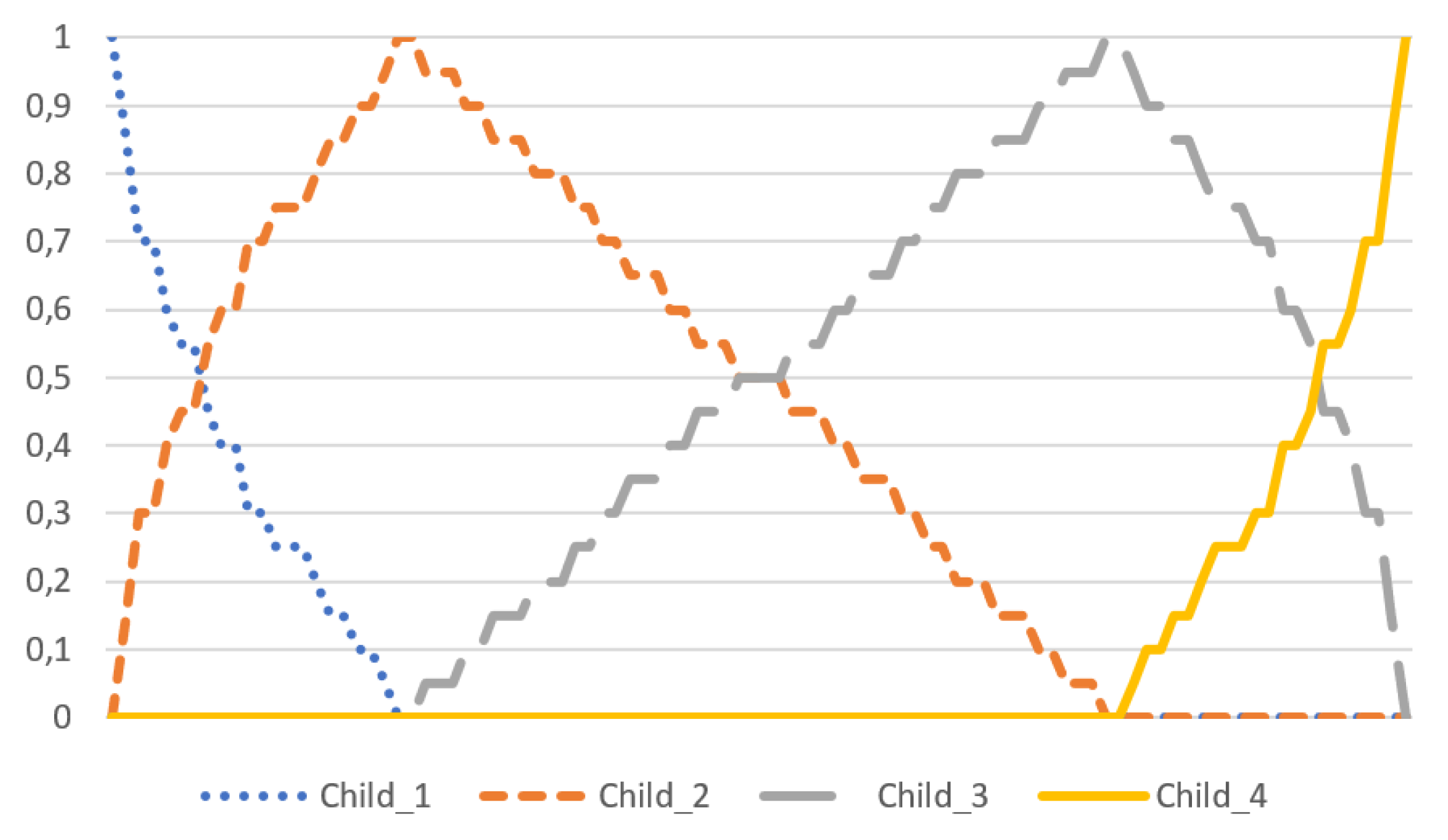
2.1. Hassall’s Algorithm
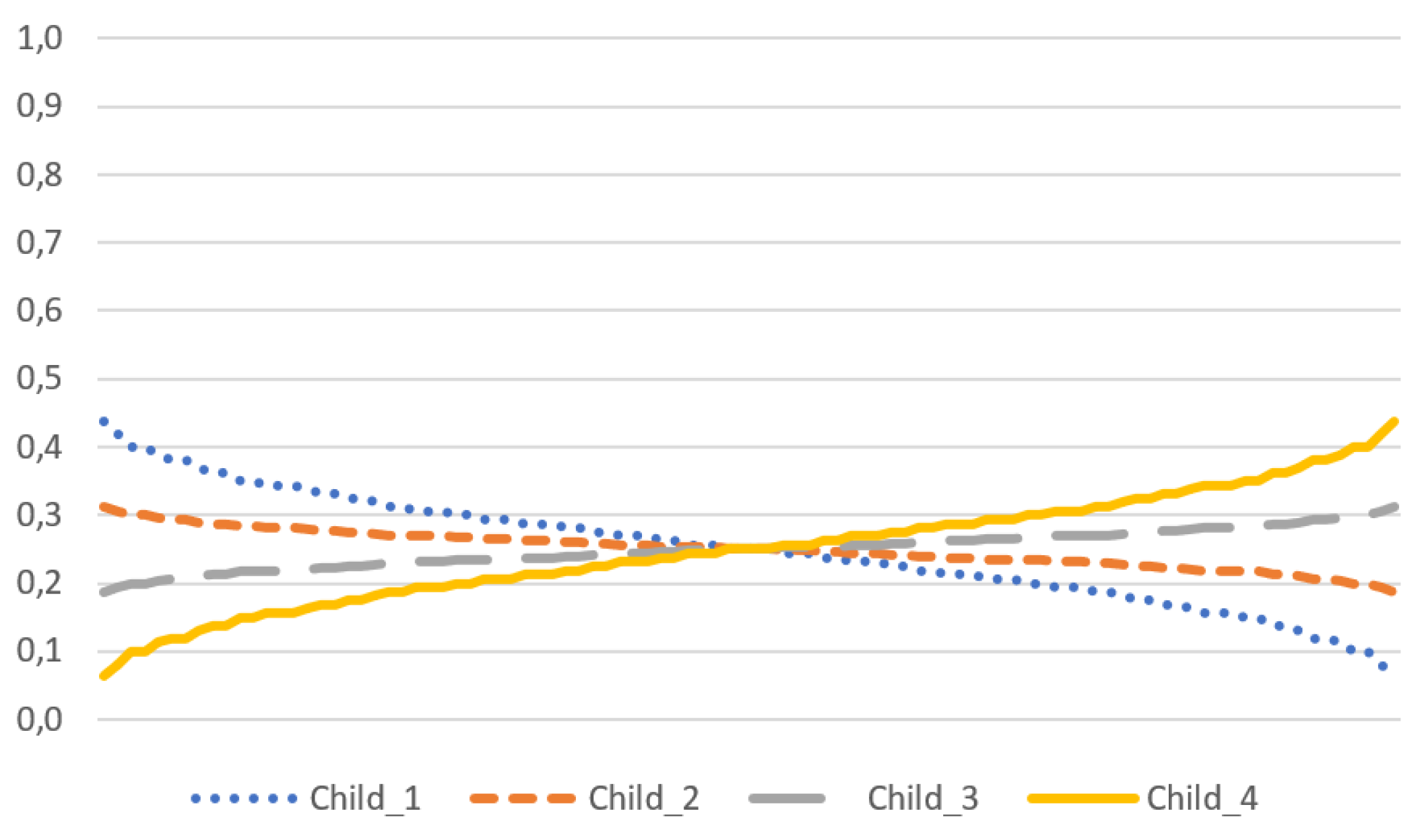
2.2. Weighted Diagonal
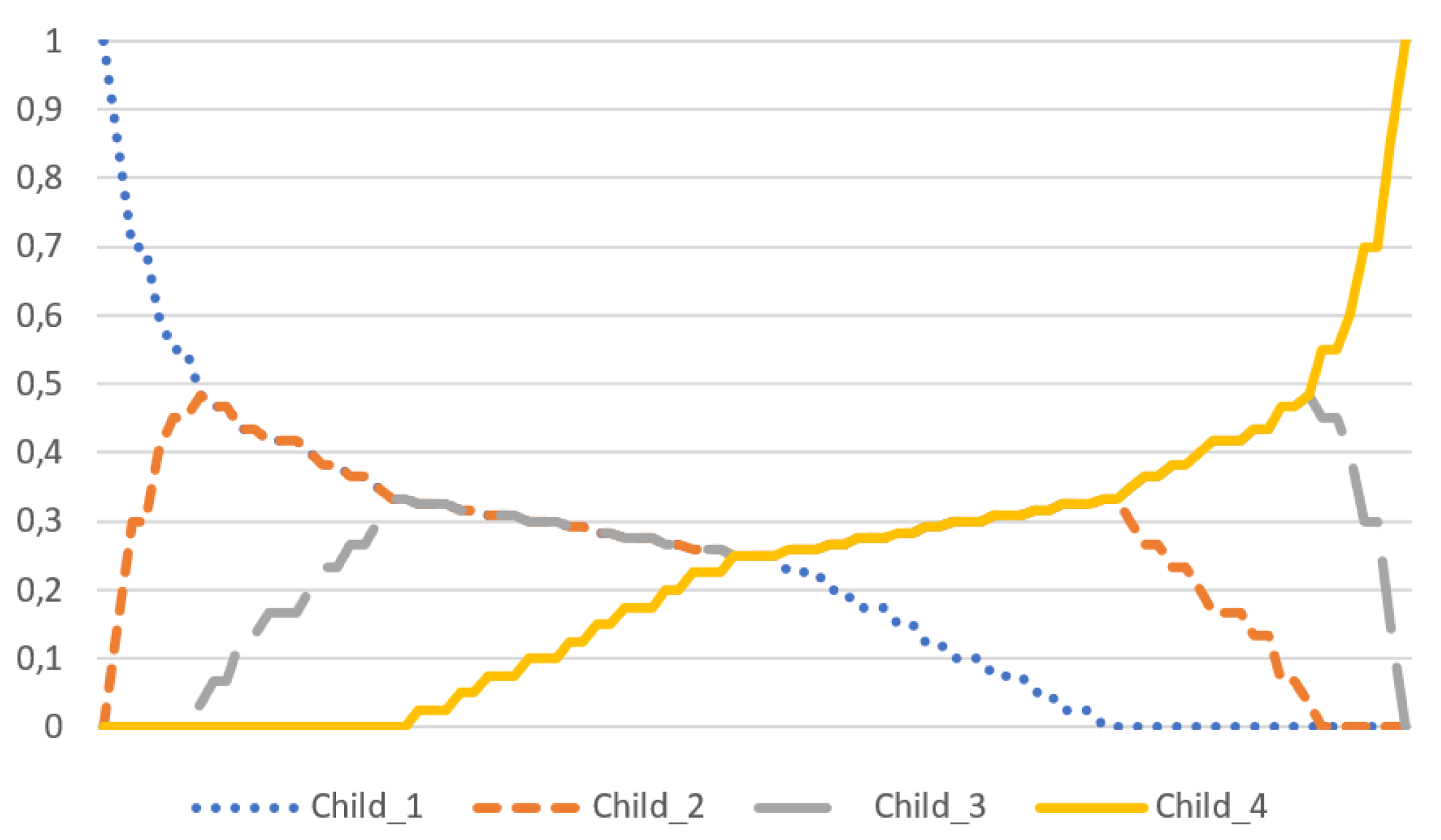
2.3. Weighted Diamond
2.4. Example
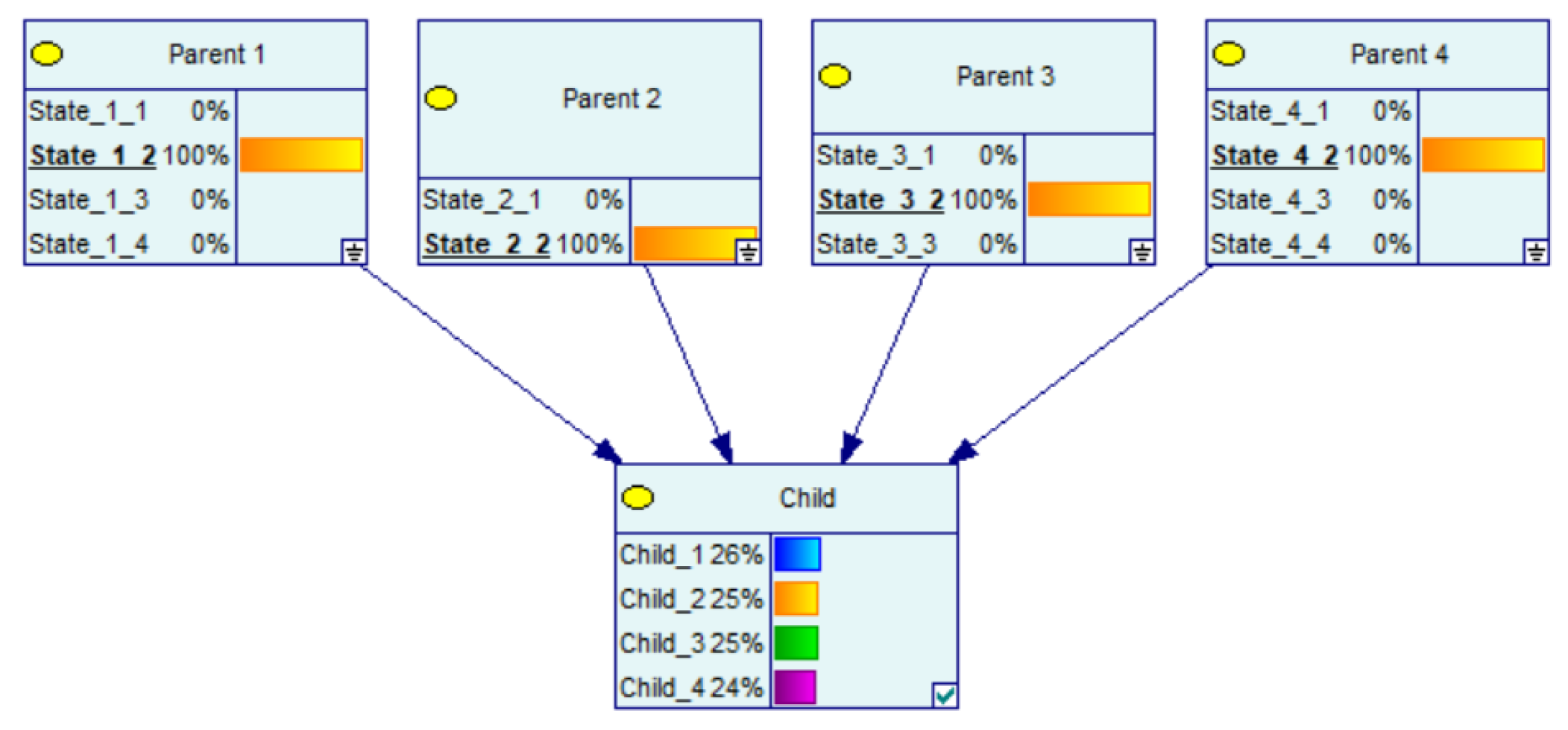
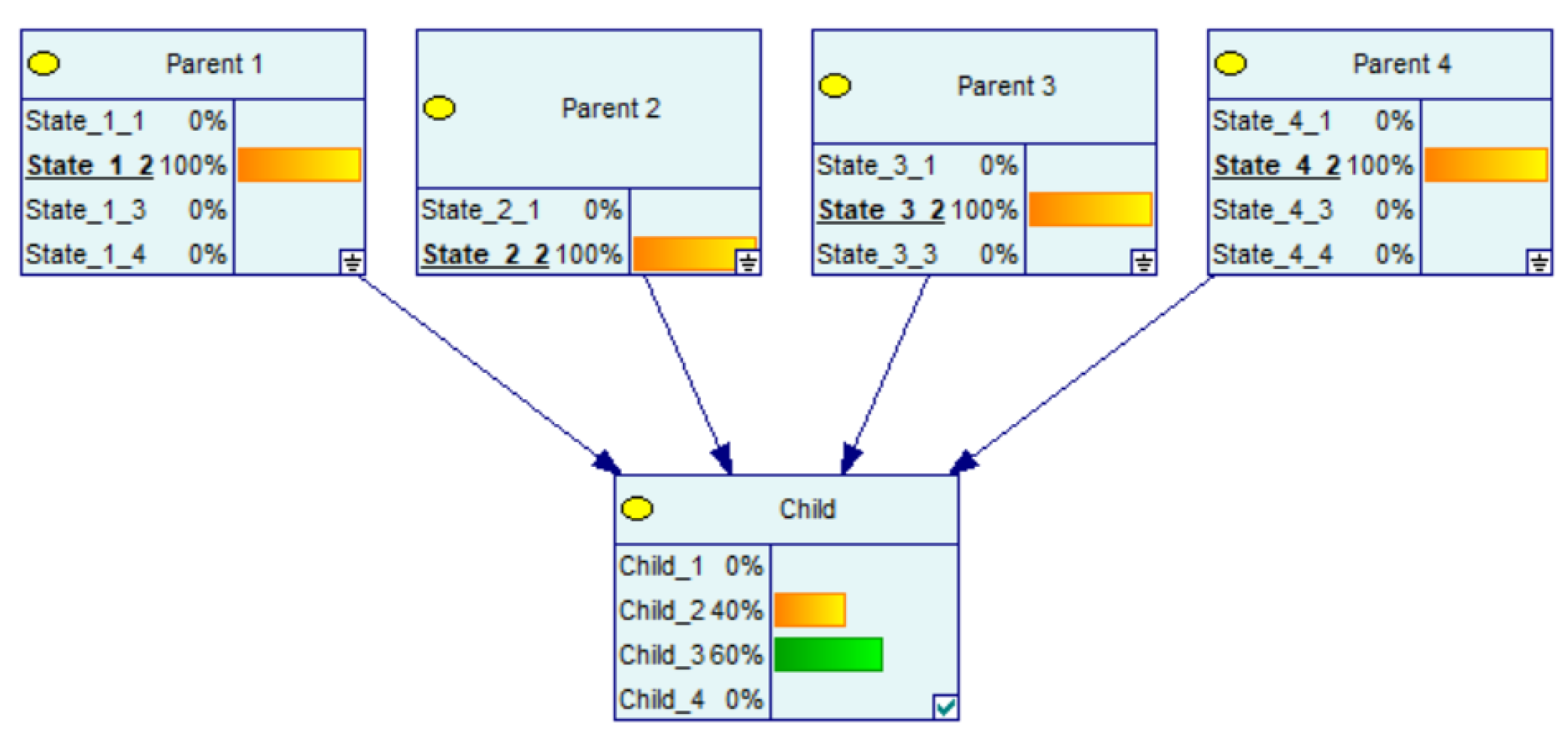
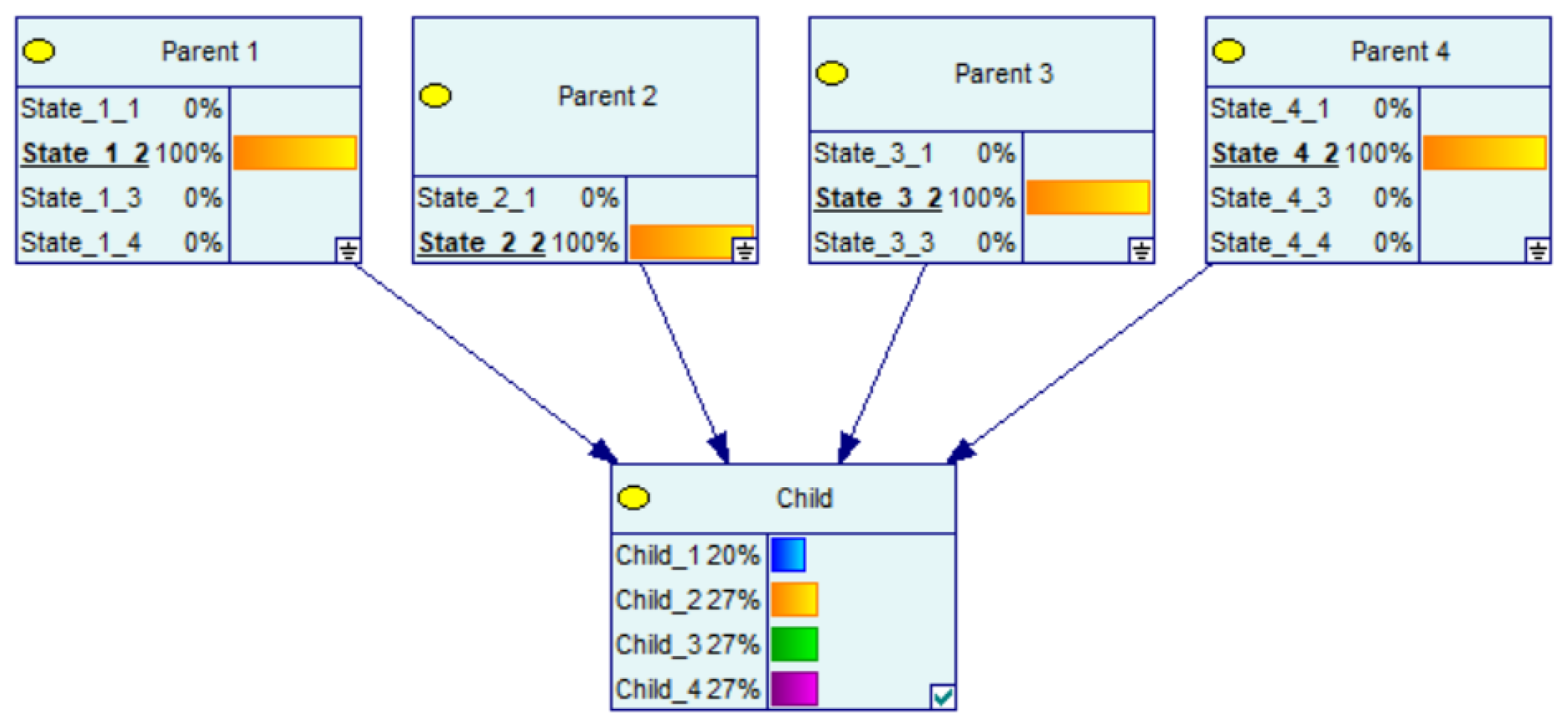
3. CPT Generation Using CPT per Parent
Example
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dang, K.B.; Windhorst, W.; Burkhard, B.; Müller, F. A Bayesian Belief Network-Based Approach to Link Ecosystem Functions with Rice Provisioning Ecosystem Services. Ecol. Indic. 2019, 100, 30–44. [Google Scholar] [CrossRef]
- Zeng, L.; Li, J. A Bayesian belief network approach for mapping water conservation ecosystem service optimization region. J. Geogr. Sci. 2019, 29, 1021–1038. [Google Scholar] [CrossRef]
- Delen, D.; Topuz, K.; Eryarsoy, E. Development of a Bayesian Belief Network-Based DSS for Predicting and Understanding Freshmen Student Attrition. Eur. J. Oper. Res. 2020, 281, 575–587. [Google Scholar] [CrossRef]
- Addae, J.H.; Sun, X.; Towey, D.; Radenkovic, M. Exploring user behavioral data for adaptive cybersecurity. User Model. User Adapt. Interact. 2019, 29, 701–750. [Google Scholar] [CrossRef]
- Sharma, V.K.; Sharma, S.K.; Singh, A.P. Risk enablers modelling for infrastructure projects using Bayesian belief network. Int. J. Constr. Manag. 2019, 1–18. [Google Scholar] [CrossRef]
- Tang, K.; Parsons, D.J.; Jude, S. Comparison of automatic and guided learning for Bayesian networks to analyse pipe failures in the water distribution system. Reliab. Eng. Syst. Saf. 2019, 186, 24–36. [Google Scholar] [CrossRef]
- Khakzad, N.; Khan, F.; Amyotte, P. Safety analysis in process facilities: Comparison of fault tree and Bayesian network approaches. Reliab. Eng. Syst. Saf. 2011, 96, 925–932. [Google Scholar] [CrossRef]
- Kammouh, O.; Gardoni, P.; Cimellaro, G.P. Probabilistic framework to evaluate the resilience of engineering systems using Bayesian and dynamic Bayesian networks. Reliab. Eng. Syst. Saf. 2020, 198, 106813. [Google Scholar] [CrossRef]
- Falzon, L. Using Bayesian network analysis to support centre of gravity analysis in military planning. Eur. J. Oper. Res. 2006, 170, 629–643. [Google Scholar] [CrossRef]
- Cao, T.; Coutts, A.; Lui, F. Combined Bayesian belief network analysis and systems architectural approach to analyse an amphibious C4ISR system. In Proceedings of the 22nd National Conference of the Australian Society for Operations Research, Adelaide, Australia, 1–6 December 2013; pp. 1–6. [Google Scholar]
- Phillipson, F.; Bastings, I.C.; Vink, N. Modelling the Effects of a CBRN Defence System Using a Bayesian Belief Model. In Proceedings of the 9th Symposium on CBRNE Threats—How does the Landscape Evolve? (NBC 2015), Helsinki, Finland, 18–21 May 2015. [Google Scholar]
- Potter, B.K.; Forsberg, J.A.; Silvius, E.; Wagner, M.; Khatri, V.; Schobel, S.A.; Belard, A.J.; Weintrob, A.C.; Tribble, D.R.; Elster, E.A. Combat-related invasive fungal infections: Development of a clinically applicable clinical decision support system for early risk stratification. Mil. Med. 2019, 184, e235–e242. [Google Scholar] [CrossRef] [PubMed]
- Arora, P.; Boyne, D.; Slater, J.J.; Gupta, A.; Brenner, D.R.; Druzdzel, M.J. Bayesian Networks for Risk Prediction Using Real-World Data: A Tool for Precision Medicine. Value Health 2019, 22, 439–445. [Google Scholar] [CrossRef] [PubMed]
- Phillipson, F.; Matthijssen, E.; Attema, T. Bayesian belief networks in business continuity. J. Bus. Contin. Emerg. Plan. 2014, 8, 20–30. [Google Scholar]
- Lee, H. Design of a BIA and Continuity Strategy in BCMS Using a Bayesian Belief Network for the Manufacturing Industry. J. Korean Soc. Hazard Mitig. 2019, 19, 135–141. [Google Scholar] [CrossRef][Green Version]
- Cooke, R. Experts in Uncertainty: Opinion and Subjective Probability in Science; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- O’Hagan, A.; Buck, C.E.; Daneshkhah, A.; Eiser, J.R.; Garthwaite, P.H.; Jenkinson, D.J.; Oakley, J.E.; Rakow, T. Uncertain Judgements: Eliciting Experts’ Probabilities; John Wiley & Sons: Chichester, UK, 2006. [Google Scholar]
- Hanea, A.; McBride, M.; Burgman, M.; Wintle, B.; Fidler, F.; Flander, L.; Twardy, C.; Manning, B.; Mascaro, S. Investigate Discuss Estimate Aggregate for Structured Expert Judgement. Int. J. Forecast. 2017, 33, 267–279. [Google Scholar] [CrossRef]
- Werner, C.; Bedford, T.; Cooke, R.M.; Hanea, A.M.; Morales-Napoles, O. Expert judgement for dependence in probabilistic modelling: A systematic literature review and future research directions. Eur. J. Oper. Res. 2017, 258, 801–819. [Google Scholar] [CrossRef]
- Wisse, B.W.; van Gosliga, S.P.; van Elst, N.P.; Barros, A.I. Relieving the Elicitation Burden of Bayesian Belief Networks. In Proceedings of the Sixth UAI Bayesian Modelling Applications Workshop (BMA), Helsinki, Finland, 9 July 2008. [Google Scholar]
- Hassall, K.L.; Dailey, G.; Zawadzka, J.; Milne, A.E.; Harris, J.A.; Corstanje, R.; Whitmore, A.P. Facilitating the Elicitation of Beliefs for Use in Bayesian Belief Modelling. Environ. Model. Softw. 2019, 122, 104539. [Google Scholar] [CrossRef]
- Dragos, V.; Ziegler, J.; de Villiers, J.P.; de Waal, A.; Jousselme, A.L.; Blasch, E. Entropy-Based Metrics for URREF Criteria to Assess Uncertainty in Bayesian Networks for Cyber Threat Detection. In Proceedings of the 2019 22th International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, 2–5 July 2019; pp. 1–8. [Google Scholar]
- Maung, I.; Paris, J.B. A note on the infeasibility of some inference processes. Int. J. Intell. Syst. 1990, 5, 595–603. [Google Scholar] [CrossRef]
- Holmes, D.E. Innovations in Bayesian Networks: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2008; Volume 156. [Google Scholar]
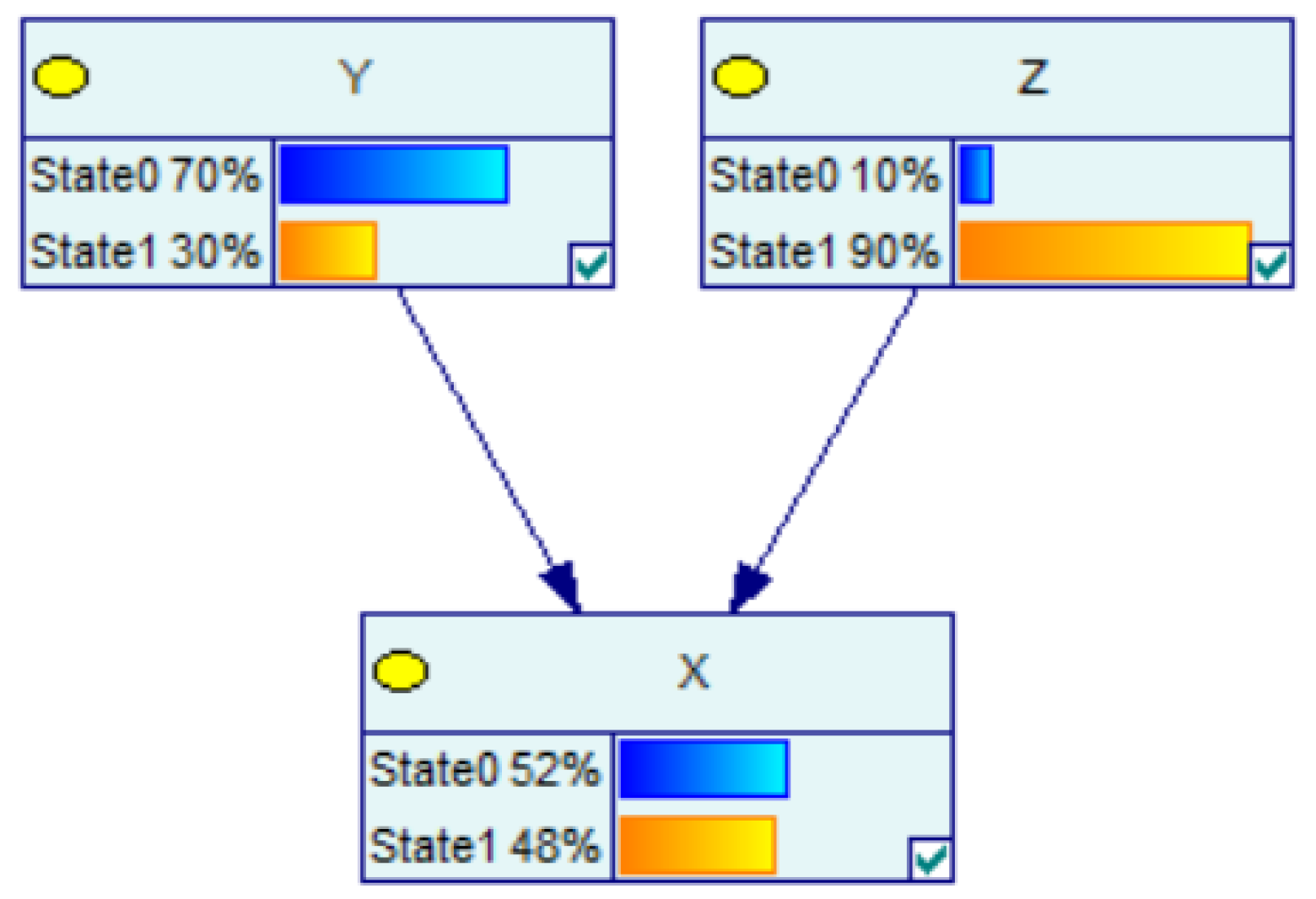



| Y | State 0 | State 1 | |||
|---|---|---|---|---|---|
| Z | State 0 | State 1 | State 0 | State 1 | |
| X-State 0 | 0.9 | 0.5 | 0.1 | 0.5 | |
| X-State 1 | 0.1 | 0.5 | 0.9 | 0.5 | |
| Node weight | 0.4 | 0.25 | 0.2 | 0.15 |
| weight | 2.0 | 2.0 | 2.0 | 2.0 |
| weight | 1.7 | 1.0 | 1.5 | 1.7 |
| weight | 1.3 | - | 1.0 | 1.3 |
| weight | 1.0 | - | - | 1.0 |
| Parent 1 | Parent 2 | Parent 3 | ||||
|---|---|---|---|---|---|---|
| State | SP11 | SP12 | SP21 | SP22 | SP31 | SP32 |
| Node weight | 4 | 4 | 4 | |||
| State 1 weight | 0.3 | 0.2 | 0.2 | 0.2 | 0.8 | 0.0 |
| State 2 weight | 0.2 | 0.6 | 0.2 | 0.5 | 0.2 | 0.5 |
| State 3 weight | 0.5 | 0.1 | 0.4 | 0.0 | 0.0 | 0.3 |
| ’NONE’ weight | 0.0 | 0.1 | 0.2 | 0.3 | 0.0 | 0.2 |
| SP11 | SP12 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SP21 | SP22 | SP21 | SP22 | ||||||||
| SP31 | SP32 | SP31 | SP32 | SP31 | SP32 | SP31 | SP32 | ||||
| State 1 | 0.46 | 0 | 0.48 | 0 | 0.44 | 0 | 0.46 | 0 | |||
| State 2 | 0.21 | 0.35 | 0.33 | 0.48 | 0.37 | 0.52 | 0.50 | 0.67 | |||
| State 3 | 0 | 0.46 | 0 | 0 | 0 | 0.32 | 0 | 0 | |||
| NONE | 0.32 | 0.19 | 0.19 | 0.52 | 0.19 | 0.16 | 0.04 | 0.33 | |||
| SP11 | SP12 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SP21 | SP22 | SP21 | SP22 | ||||||||
| SP31 | SP32 | SP31 | SP32 | SP31 | SP32 | SP31 | SP32 | ||||
| State 1 | 0.43 | 0.17 | 0.43 | 0.17 | 0.40 | 0.13 | 0.40 | 0.13 | |||
| State 2 | 0.20 | 0.30 | 0.30 | 0.40 | 0.33 | 0.43 | 0.43 | 0.53 | |||
| State 3 | 0.30 | 0.40 | 0.17 | 0.27 | 0.17 | 0.27 | 0.03 | 0.13 | |||
| NONE | 0.07 | 0.13 | 0.10 | 0.17 | 0.10 | 0.17 | 0.13 | 0.20 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phillipson, F.; Langenkamp, P.; Wolthuis, R. Alternative Initial Probability Tables for Elicitation of Bayesian Belief Networks. Math. Comput. Appl. 2021, 26, 54. https://doi.org/10.3390/mca26030054
Phillipson F, Langenkamp P, Wolthuis R. Alternative Initial Probability Tables for Elicitation of Bayesian Belief Networks. Mathematical and Computational Applications. 2021; 26(3):54. https://doi.org/10.3390/mca26030054
Chicago/Turabian StylePhillipson, Frank, Peter Langenkamp, and Reinder Wolthuis. 2021. "Alternative Initial Probability Tables for Elicitation of Bayesian Belief Networks" Mathematical and Computational Applications 26, no. 3: 54. https://doi.org/10.3390/mca26030054
APA StylePhillipson, F., Langenkamp, P., & Wolthuis, R. (2021). Alternative Initial Probability Tables for Elicitation of Bayesian Belief Networks. Mathematical and Computational Applications, 26(3), 54. https://doi.org/10.3390/mca26030054






