Abstract
This work presents a methodology to derive analytical functionals, with embedded linear constraints among the components of a vector (e.g., coordinates) that is a function a single variable (e.g., time). This work prepares the background necessary for the indirect solution of optimal control problems via the application of the Pontryagin Maximum Principle. The methodology presented is part of the univariate Theory of Functional Connections that has been developed to solve constrained optimization problems. To increase the clarity and practical aspects of the proposed method, the work is mostly presented via examples of applications rather than via rigorous mathematical definitions and proofs.
1. Introduction
The Theory of Functional Connections (TFC) is an analytical framework developed to perform functional interpolation, that is, to derive analytical functionals, called constrained expressions, describing all functions satisfying a set of assigned constraints. This framework has been developed for univariate and multivariate rectangular domains and for a wide class of constraints, including points and derivatives constraints, integral constraints, linear combination of constraints, and, partially, for component constraints. The TFC theory has been presented in detail in [1,2,3,4,5,6]. For instance, the extension to 2-dimensional space allows TFC to generate all surfaces connecting Dirichlet and Neumann boundary conditions. Recently, the domain mapping technique has been shown to be the first step toward extending TFC to any (non-rectangular) domain [7].
The first TFC application was to obtain least-squares solutions of linear and nonlinear ordinary (ODEs) and partial (PDEs) differential equations. Specifically, for ODEs the solutions have been obtained with the following features:
- solutions are approximate and analytical (this allows easier subsequent analysis and further manipulation);
- the approach solves initial, boundary, or multi-value problems by the same unified procedure;
- the approach is numerically robust (low condition number);
- solutions are usually provided at machine error accuracy;
- solutions are usually obtained at msec level (suitable for real-time applications); and
- constraint range is independent from the integration range (solution accuracy is maintained outside the constraints range).
The TFC application to ODEs and PDEs can be found in [6,8,9,10,11,12,13,14,15,16]. The successful applications of TFC to solutions of differential equations has generated subsequent applications in various fields, such as in optimization and optimal control [17,18,19,20,21,22,23,24], in astrodynamics [24,25,26,27,28,29,30], in transport theory [31,32], and in machine learning, with particular emphasis in physics-informed neural networks [33,34].
TFC applied to component constraints has been initially presented in [12] to solve first-order ODEs. However, the solution provided in [12] is restricted only to the cases presented. In this article, the general theory of univariate component constraints is presented. This theory can be further applied to solve more complex differential equations or optimization problems subject to component constraints, such as those generated in indirect optimal control problems. Applications on optimization, based on the theory presented in this work, will not be considered in this study and will be the subject of future works. However, a simple optimal control problem is included, as example.
This study considers a vector, , depending from a single independent variable, t (univariate case), whose components must satisfy a set of p constraints. Constraints can be absolute, relative, or any linear combination. The general multivariate case of a vector depending on m independent variables, , will be subject of future studies.
Before presenting the univariate Theory of Functional Connections for component constraints, a brief summary of univariate TFC and a summary of the initial (and incomplete) work on component constraints presented in [12] are provided in the next two sections
2. Summary of Univariate Theory of Functional Connections
The univariate Theory of Functional Connections derives analytical functionals, called constrained expressions, satisfying p distinct linear constraints. These constraints can be points and derivatives constraints (e.g., and ), integral constraints (e.g., ), and linear combination of constraints (e.g., ). These functionals can be analytically obtained using any of the following two equivalent formal expressions,
where is the free function; are p linearly independent support functions (e.g., monomials, Fourier, etc.); are functionals coefficients to be found by imposing the constraints (these are actually scalars in the univariate case and become functionals in the multivariate case); are switching functions satisfying if the k-th constraint is satisfied and if the i-th constraint, with , is satisfied; are projection functionals; and is a vector specifying where the p constraints are defined. This means that and are not continuous functions of t. A rigorous mathematical definition of and is given in [4].
Example
Consider to find the functional (constrained expression) always satisfying the constraints,
For constraints Equation (1) can be written as
By imposing the four constraints a system of four equations in the four unknowns
is obtained. By selecting the support functions as monomials, , , , and , the previous system becomes
whose solution
provides the functional (constrained expression) for the four specified constraints,
This functional represents all functions satisfying simultaneously all four constraints. Furthermore, this equation highlights the switching/projection formal expression given in Equation (1), where the corresponding switching functions and projection functionals are
3. Correct Functionals for the Component Constraints Previously Provided
The TFC functionals for component constraints provided in [12] were specifically obtained to be the most simple and specific functionals that can be used to solve first-order differential equations. However, while fitting the purpose of [12], the functionals provided cannot be adopted for the general case of component constraints. In this section, for completeness, we provide the correct expressions of these functionals by also highlighting the constraint requirements affecting the selected support functions. These correct expressions are derived using the general formalism provided in Section 4.
3.1. Two Absolute Constraints
The case of two absolute components constraints of a vector generates the single simple case
where
and the support functions are subject to and , respectively.
3.2. One Absolute and One Relative Constraints
The case of one absolute and one relative constraints generates two distinct cases:
- Case (1)
- wheresubject to and .
- Case (2)
- wheresubject to and .
3.3. Two Relative Constraints
The general case of two relative constraints generates three distinct cases:
- Case (1)
- wheresubject to and .
- Case (2)
- wheresubject to .
- Case (3)
- wheresubject to .
4. Univariate Theory of Functional Connections Subject to Component Constraints
Let us consider a set of p component constraints as linear combination of point, derivative, or integral of components defined at specific values (point and derivatives) or domain range (integral). To derive the constrained expression of each component the following rules apply.
- 1.
- The component appears in constraints whose indices are the elements of the vector of integers, . For instance, if the component appears in the constraint equations identified as “2”, “9”, and “19”, only, then and , which is the length of the vector.
- 2.
- The constrained expression of the component is made of a sum of the free function and a linear combination of functional coefficients, and linearly independent support functions, ,
Note that the total number of distinct functional coefficients, , is the total number of constraints to be satisfied. The coefficients are not continuous functions of t. They depend on the specific values of t where the constraints are defined. All these specific values are the elements of the vector . Each component, , has its own constrained expression and its own free function, . The following three examples help to clarify how to apply Equation (2).
Example 1.
Consider the constraints among the components of the vector ,
Note that, as the last component, , does not appear in any constraint equations, then , while the other vectors are
Therefore, for the two constraints given in Equation (3) the component constrained functionals are expressed as
because appears in the constraint Equation (1) while , appear in the constraint Equations (1) and (2), and .
The first constraint becomes
Collecting the terms we obtain
while the second constraint,
and collecting the terms we have
Therefore, the functional coefficients can be computed by matrix inversion, -4.6cm0cm
The support functions selected are consistent if the functional coefficients can be computed. In this case, the above matrix (which depend from the selected support functions, only) is nonsingular. The matrix is nonsingular if a linear combination of the selected support functions can be adopted to interpolate the constraints (this interpolation problem can be obtained by setting to zeros all free functions). This means that the consistency of the selected support functions is directly connected to an interpolation problem. By solving this interpolation problem the functional interpolation problem (also known as, its generalization) is also solved. The following simple equivalent example clarifies this interpolation issue.
Let us consider adopting the function
using and , to interpolate two known derivatives in two distinct points, and . This problem cannot be solved using the support functions selected. In this case, the selected support functions are inconsistent with the interpolation problem. The support functions become consistent with respect to the constraints by selecting, for instance, and .
Coming back to our example, by selecting , , the previous equation provides the expressions for the functional coefficients,
This equation also shows the connections between the functional coefficients, , and the projection functionals, , appearing in Equation (1) (see in [4] for the formal definition and properties of projection functionals). Therefore, the functional coefficients for this specific example can be written as
Example 2.
Consider the constraints among the components of the vector ,
For these constraints the vectors are
For the three constraints given in Equation (4) the component constrained expressions are
Selecting and , the constraints becomes
The functional coefficients can be then computed from
whose solution is
Example 3.
Consider the vector whose components are subject to the following four constraints,
For these constraints the vectors are
Therefore, for the constraints given in Equation (5) the component constrained expressions are
Selecting , , and , the constraints becomes
The functional coefficients can be computed from the linear system,
providing the solution
Application to a Simple Example of Optimal Control Problem
Consider the following one-dimensional optimal control problem. A unitary mass is in rectilinear motion subject to the one-dimensional control force, , in the direction of motion. Initial state conditions are set to be m and m/s, where . The goal is to find the optimal control, , to bring the point mass sufficiently close to the origin at the final time, s, with minimum control effort. Overall, the optimal control problem can be mathematically formulated as follows.
Find the optimal control and the trajectory and that minimize the following cost function
subject to the dynamic equations
and the boundary conditions
The necessary conditions are determined by applying the Pontryagin’s Maximum Principle (PMP) [35]. First, we compute the Hamiltonian
We find the optimal control by applying the optimality conditions, i.e.,
Therefore, the Hamiltonian becomes
State and costate dynamic equations are derived from the Hamiltonian as follows,
The constraints are the initial conditions,
while the boundary conditions can be determined as follows,
where
Here, and are the Lagrange multipliers associated with the initial states and , respectively. The optimal control and trajectory solution can be found by solving the set of ODEs (necessary conditions, i.e., two-point boundary value problem) provided by the Hamiltonian formulation, i.e.,
where and represent the costate components associated to x and v, respectively. This system of differential equations admits the following analytical solution,
Using the Theory of Functional Connections formulation for component constraints presented, the constraints given in Equation (16) can be embedded into the following functionals,
from which we immediately derive the expressions for and ,
while the expressions for and are computed from the constraint expressions,
providing the requirement for the support function selection,
Table 1 provides three examples of support functions selection and the requirements the constraints are subject to.

Table 1.
Examples of supports function selection.
For instance, using Selection 3 the expressions for and are
and, consequently, the constrained expressions are -4.6cm0cm
Using these expressions, the four free functions can be expanded as a linear combination of a set of basis functions with unknown coefficients,
and the system of differential equations given in Equation (16) can be written in a matrix form,
where the expression of the matrix is derived by applying the constrained expressions given in Equation (18) to the differential equation given in Equation (16). Discretizing the time from the initial value, , to the final value, , the overdetermined linear system
is obtained. Then, the four unknown coefficients vectors (, , , and ) can be computed by least-squares,
Particular attention should be given to vectors, like the state vectors in dynamical systems, where some components are derivatives of other components (e.g., position, velocity, and acceleration). For instance, it would be a mistake trying to merge the and constrained expressions given in Equation (17) by the following single constrained expression,
While this equation satisfies both initial constraints for and , it does not satisfy the dynamical equation obtained from the Hamiltonian formulation, given in Equation (16), where the control is embedded in the costate terms.
Figure 1 shows the numerical results obtained in this simple optimal control example. The left plots shows the errors with respect the true (analytical) solution of the numerical least-squares solution for , , , and , using basis functions (Chebyshev orthogonal polynomials of the first kind) and 16 collocation points. The top right plot show the control error, , while the bottom right plot shows the condition number of the matrix. The solution is obtained in 1.3 ms, using MATLAB® on a standard commercial laptop.
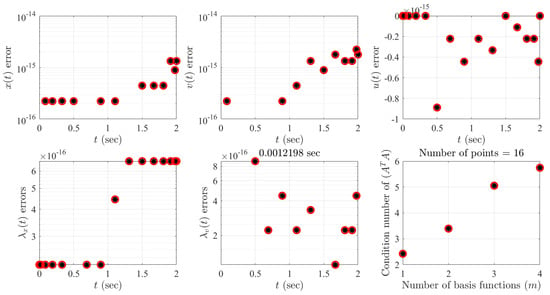
Figure 1.
Results of the optimal control example.
In this specific case, as the true solution is polynomial and the selected basis functions are also polynomial (Chebyshev orthogonal polynomials), the estimated solution fully captures the true solution with the corresponding minimum polynomial degree of the true solution (cubic). By increasing the number of basis functions, the solution does not changes and all the coefficients associated to polynomials with degree higher than are estimated as zero.
5. Conclusions
This paper provides a mathematical methodology to perform functional interpolation for vector’s components that are subject to a set of linear constraints. The methodology adopts the framework of the Theory of Functional Connections, a mathematical method to derive functionals that are always satisfying a set of linear constraints. These functional reduce the whole search space of functions to just the functions subspace satisfying the assigned constraints.
The main motivation of this study is to provide a numerical new method to solve indirect optimal control problems, where states and costates (components) are connected by constraints.
Several examples are provided showing how to derive the functionals fully satisfying the component constraints. This has been done for 2-dimensional time-varying vectors subject to three classic component constraints (two absolute, one absolute and one relative, and two relative) and three more complex examples involving constraints as linear combinations of points, derivatives, and integrals.
The study also includes a simple example of indirect optimal control problem that is solved using Pontryagin Maximum Principle and the proposed method. This example, whose solution is obtained by least-squares, has been numerically tested. The results validate the proposed approach in terms of speed and accuracy.
Author Contributions
Conceptualization, D.M. and R.F.; methodology, D.M. and R.F.; software, D.M.; validation, D.M.; formal analysis, D.M. and R.F.; investigation, D.M. and R.F.; resources, D.M.; data curation, D.M.; writing—original draft preparation, D.M.; writing—review and editing, D.M. and R.F.; visualization, D.M.; supervision, D.M. and R.F.; project administration, D.M. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mortari, D. The Theory of Connections: Connecting Points. Mathematics 2017, 5, 57. [Google Scholar] [CrossRef]
- Mortari, D. The Theory of Functional Connections: Connecting Functions. In Proceedings of the IAA-AAS-SciTech-072, Forum 2018, Peoples’ Friendship University of Russia, Moscow, Russia, 13–15 November 2018. [Google Scholar]
- Mortari, D.; Leake, C. The Multivariate Theory of Connections. Mathematics 2019, 7, 296. [Google Scholar] [CrossRef] [PubMed]
- Leake, C.; Johnston, H.; Mortari, D. The Multivariate Theory of Functional Connections: Theory, Proofs, and Application in Partial Differential Equations. Mathematics 2020, 8, 1303. [Google Scholar] [CrossRef]
- Leake, C.; Mortari, D. An Explanation and Implementation of the Multivariate Theory of Functional Connections via Examples. In Proceedings of the 2019 AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Johnston, H.; Leake, C.; Mortari, D. An Analysis of the Theory of Functional Connections Subject to Inequality Constraints. In Proceedings of the 2019 AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Mortari, D.; Arnas, D. Bijective Mapping Analysis to Extend the Theory of Functional Connections to Non-Rectangular 2-Dimensional Domains. Mathematics 2020, 8, 1593. [Google Scholar] [CrossRef] [PubMed]
- Mortari, D. Least-Squares Solution of Linear Differential Equations. Mathematics 2017, 5, 48. [Google Scholar] [CrossRef]
- Johnston, H.; Mortari, D. Linear Differential Equations Subject to Relative, Integral, and Infinite Constraints. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, 2018, 167, AAS 18-273, Snowbird, UT, USA, 19–23 August 2018; pp. 3107–3121. [Google Scholar]
- Mortari, D.; Johnston, H.; Smith, L. High accuracy least-squares solutions of nonlinear differential equations. J. Comput. Appl. Math. 2019, 352, 293–307. [Google Scholar] [CrossRef] [PubMed]
- Johnston, H.; Mortari, D. Weighted Least-Squares Solutions of Over-Constrained Differential Equations. In Proceedings of the IAA-AAS-SciTech-081, Forum 2018, Peoples’ Friendship University of Russia, Moscow, Russia, 13–15 November 2018. [Google Scholar]
- Mortari, D.; Furfaro, R. Theory of Connections Applied to First-Order System of Ordinary Differential Equations Subject to Component Constraints. In Proceedings of the 2018 AAS/AIAA Astrodynamics Specialist Conference, Snowbird, UT, USA, 19–23 August 2018. [Google Scholar]
- Schiassi, E.; Furfaro, R.; Leake, C.; De Florio, M.; Johnston, H.; Mortari, D. Extreme Theory of Functional Connections: A Fast Physics-Informed Neural Network Method for Solving Ordinary and Partial Differential Equations. Neurocomputing 2020. Submitted revised version. [Google Scholar]
- Leake, C.; Johnston, H.; Smith, L.; Mortari, D. Analytically Embedding Differential Equation Constraints into Least-Squares Support Vector Machines using the Theory of Functional Connections. Mach. Learn. Knowl. Extr. 2019, 1, 60. [Google Scholar] [CrossRef] [PubMed]
- Johnston, H.; Mortari, D. Least-squares Solutions of Boundary-value Problems in Hybrid Systems. arXiv 2019, arXiv:1911.04390v1. [Google Scholar]
- Leake, C.; Mortari, D. Deep Theory of Functional Connections: A New Method for Estimating the Solutions of Partial Differential Equations. Mach. Learn. Knowl. Extr. 2020, 2, 4. [Google Scholar] [CrossRef] [PubMed]
- Mai, T.; Mortari, D. Theory of Functional Connections Applied to Nonlinear Programming under Equality Constraints. In Proceedings of the 2019 AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Drozd, K.; Furfaro, R.; Mortari, D. Constrained Energy-Optimal Guidance in Relative Motion via Theory of Functional Connections and Rapidly-Explored Random Trees. In Proceedings of the 2019 Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Furfaro, R.; Mortari, D. Least-squares Solution of a Class of Optimal Guidance Problems via Theory of Connections. ACTA Astronaut. 2020, 168, 92–103. [Google Scholar] [CrossRef]
- Furfaro, R.; Drozd, K.; Mortari, D. Energy-Optimal Rendezvous Spacecraft Guidance via Theory of Functional Connections. In Proceedings of the 70th International Astronautical Congress 2019, IAF Astrodynamics Symposium, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Johnston, H.; Schiassi, E.; Furfaro, R.; Mortari, D. Fuel-Efficient Powered Descent Guidance on Large Planetary Bodies via Theory of Functional Connections. J. Astronaut. Sci. 2020, 67, 1521–1552. [Google Scholar] [CrossRef] [PubMed]
- Schiassi, E.; D’Ambrosio, A.; Johnston, H.; Furfaro, R.; Curti, F.; Mortari, D. Complete Energy Optimal Landing on Small and Large Planetary Bodies via Theory of Functional Connections. In Proceedings of the Astrodynamics Specialist Conference, AAS 20-557, Lake Tahoe, CA, USA, 9–13 August 2020. [Google Scholar]
- Furfaro, R.; Schiassi, E.; Drozd, K.; Mortari, D. Physics-Informed Neural Networks and Theory of Functional Connections for Optimal Space Guidance Applications. In Proceedings of the 71-st International Astronautical Congress (IAC 2020), Dubai, UAE, 12–16 October 2020. [Google Scholar]
- Schiassi, E.; D’Ambrosio, A.; Johnston, H.; De Florio, M.; Drozd, K.; Furfaro, R.; Curti, F.; Mortari, D. Physics-Informed Extreme Theory of Functional Connections Applied to Optimal Orbit Transfer. In Proceedings of the Astrodynamics Specialist Conference, Lake Tahoe, CA, USA, 9–13 August 2020. [Google Scholar]
- Johnston, H.; Mortari, D. The Theory of Connections Applied to Perturbed Lambert’s Problem. In Proceedings of the Astrodynamics Specialist Conference, Snowbird, UT, USA, 19–23 August 2018. [Google Scholar]
- Mortari, D. The Theory of Connections with Application. In Proceedings of the XVI Jornadas de Trabajo en Mecánica Celeste, Soria, Spain, 19–21 June 2017. [Google Scholar]
- Mortari, D. The Theory of Functional Connections: Current Status. In Proceedings of the XIX Colóquio Brasileiro de Dinâmica Orbital (CBDO-2018), Instituto Nacional de Pesquisas Espaciais, São José dos Campos, Brasil, 3–7 December 2018. [Google Scholar]
- Johnston, H.; Mortari, D. Orbit Propagation via the Theory of Functional Connections. In Proceedings of the Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- de Almeida, A.K., Jr.; Johnston, H.; Leake, C.; Mortari, D. Evaluation of Transfer Costs in the Earth-Moon System using the Theory of Functional Connections. In Proceedings of the Astrodynamics Specialist Conference, Lake Tahoe, CA, USA, 9–13 August 2020. [Google Scholar]
- Johnston, H.; Lo, M.; Mortari, D. Functional Interpolation Method to Compute Period Orbits in the Circular Restricted Three-Body Problem. In Proceedings of the Space Flight Mechanics Meeting, Virtual Conference, 1–4 February 2021. [Google Scholar]
- De Florio, M. Accurate Solutions of the Radiative Transfer Problem via Theory of Connections. Master’s Thesis, University of Bologna, Cesena, Italy, 2019. [Google Scholar]
- De Florio, M.; Schiassi, E.; Furfaro, R.; Ganapol, B.D.; Mostacci, D. Solutions of Chandrasekhar’s Basic Problem in Radiative Transfer via Theory of Functional Connections. J. Quant. Spectrosc. Radiat. Transf. 2021, 259, 107384. [Google Scholar] [CrossRef]
- Schiassi, E.; Leake, C.; De Florio, M.; Johnston, H.; Furfaro, R.; Mortari, D. Extreme Theory of Functional Connections: A Physics-Informed Neural Network Method for Solving Parametric Differential Equations. arXiv 2020, arXiv:2005.10632v1. [Google Scholar]
- Schiassi, E.; D’Ambrosio, A.; De Florio, M.; Furfaro, R.; Curti, F. Physics-Informed Extreme Theory of Functional Connections Applied to Data-Driven Parameters Discovery of Epidemiological Compartmental Models. arXiv 2020, arXiv:2008.05554v1. [Google Scholar]
- Hermes, H. Foundations of Optimal Control Theory; John Wiley: New York, NY, USA, 1968. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).