Investigation of Volumic Permanent-Magnet Eddy-Current Losses in Multi-Phase Synchronous Machines from Hybrid Multi-Layer Model
Abstract
1. Introduction
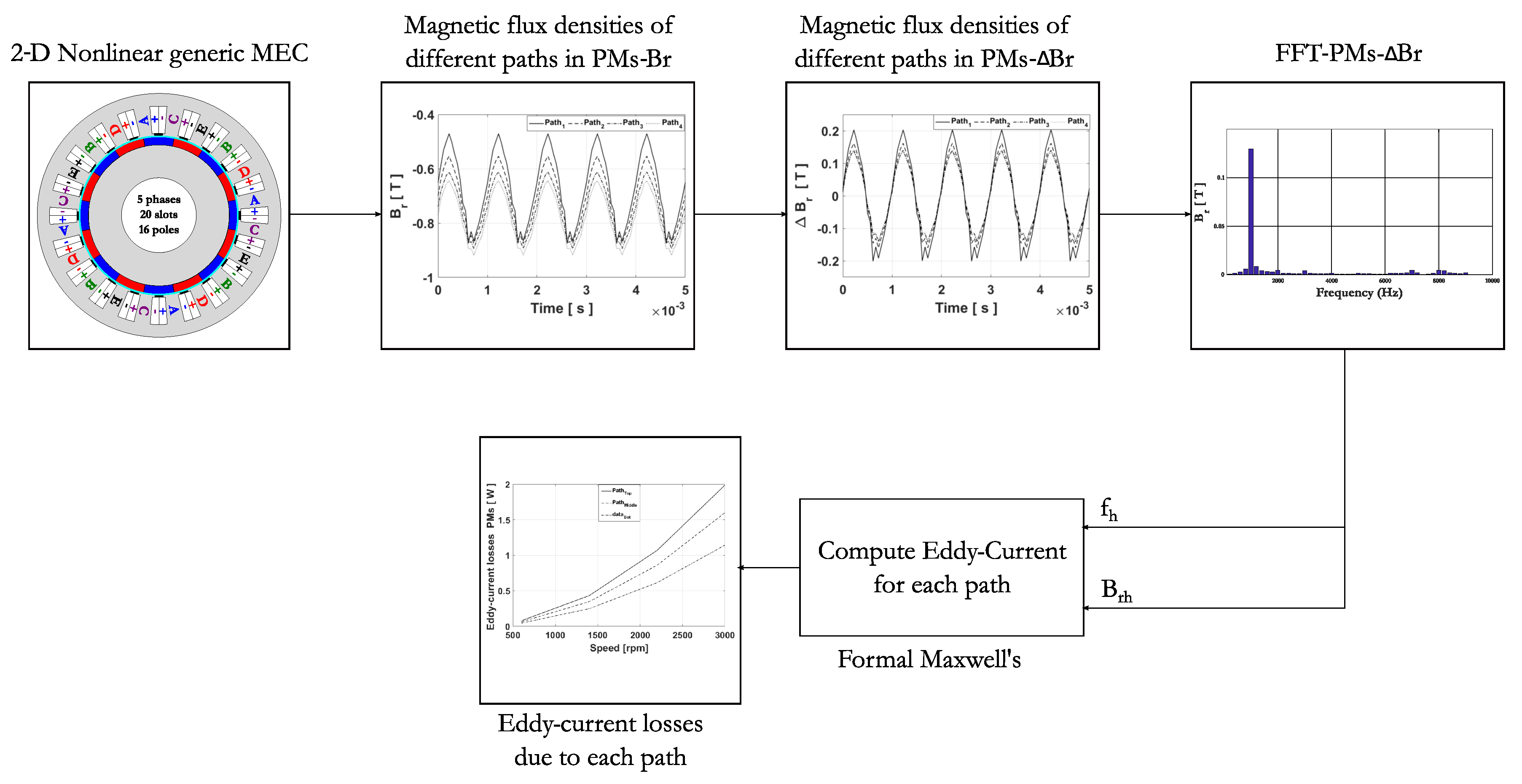
2. Hybrid Multi-Layer Model Description
2.1. Geometrical and Physical Parameters of PMSM
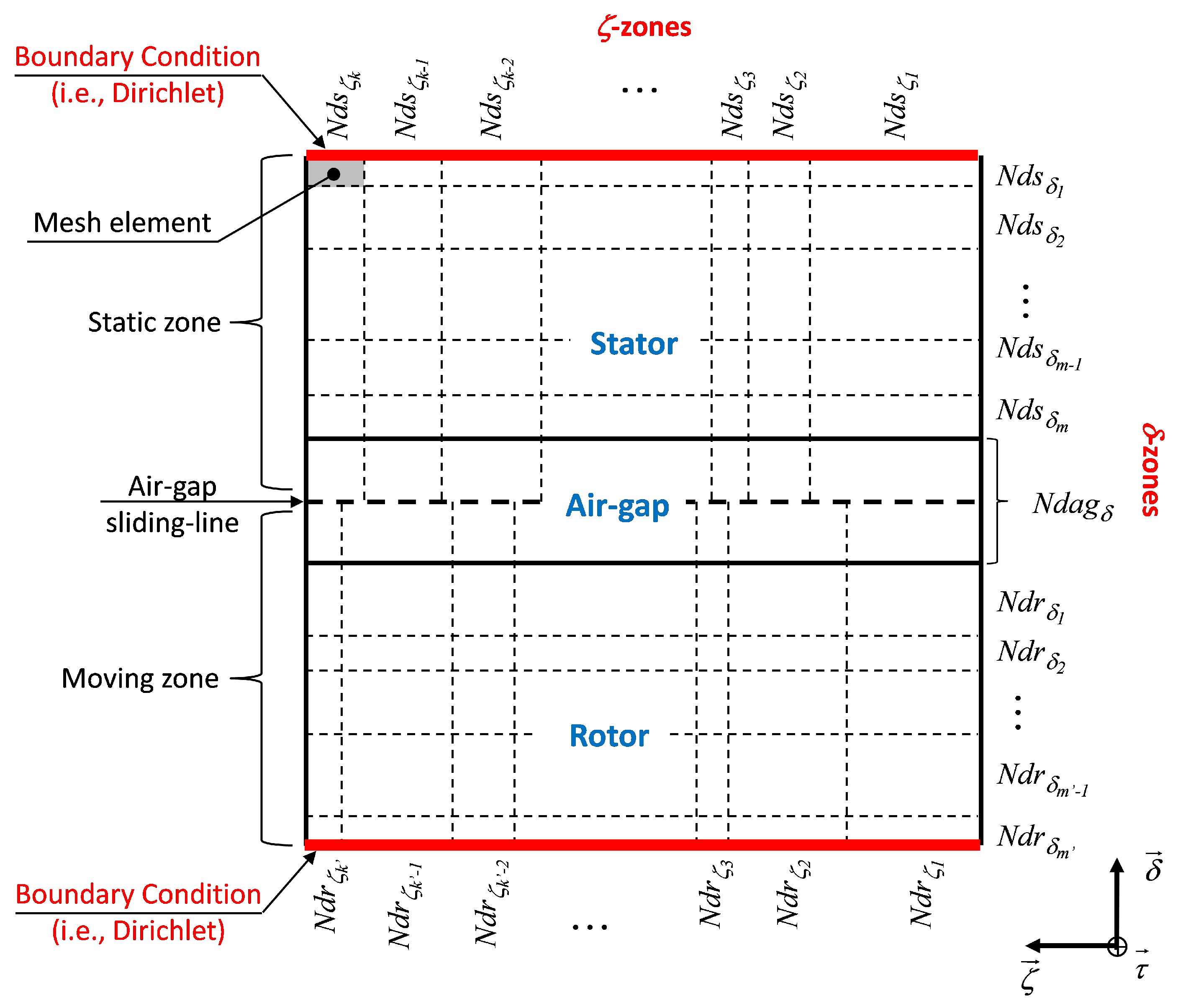
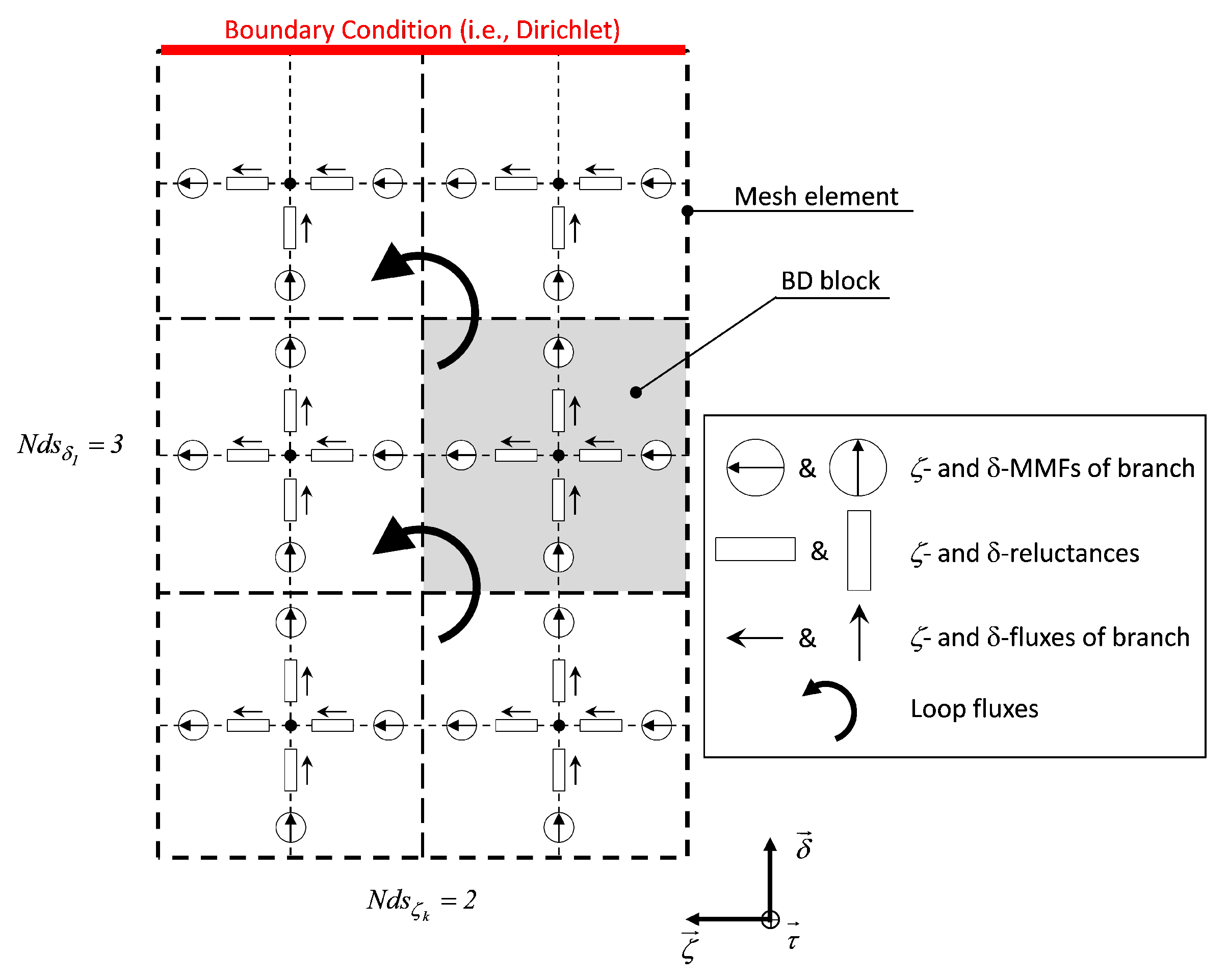
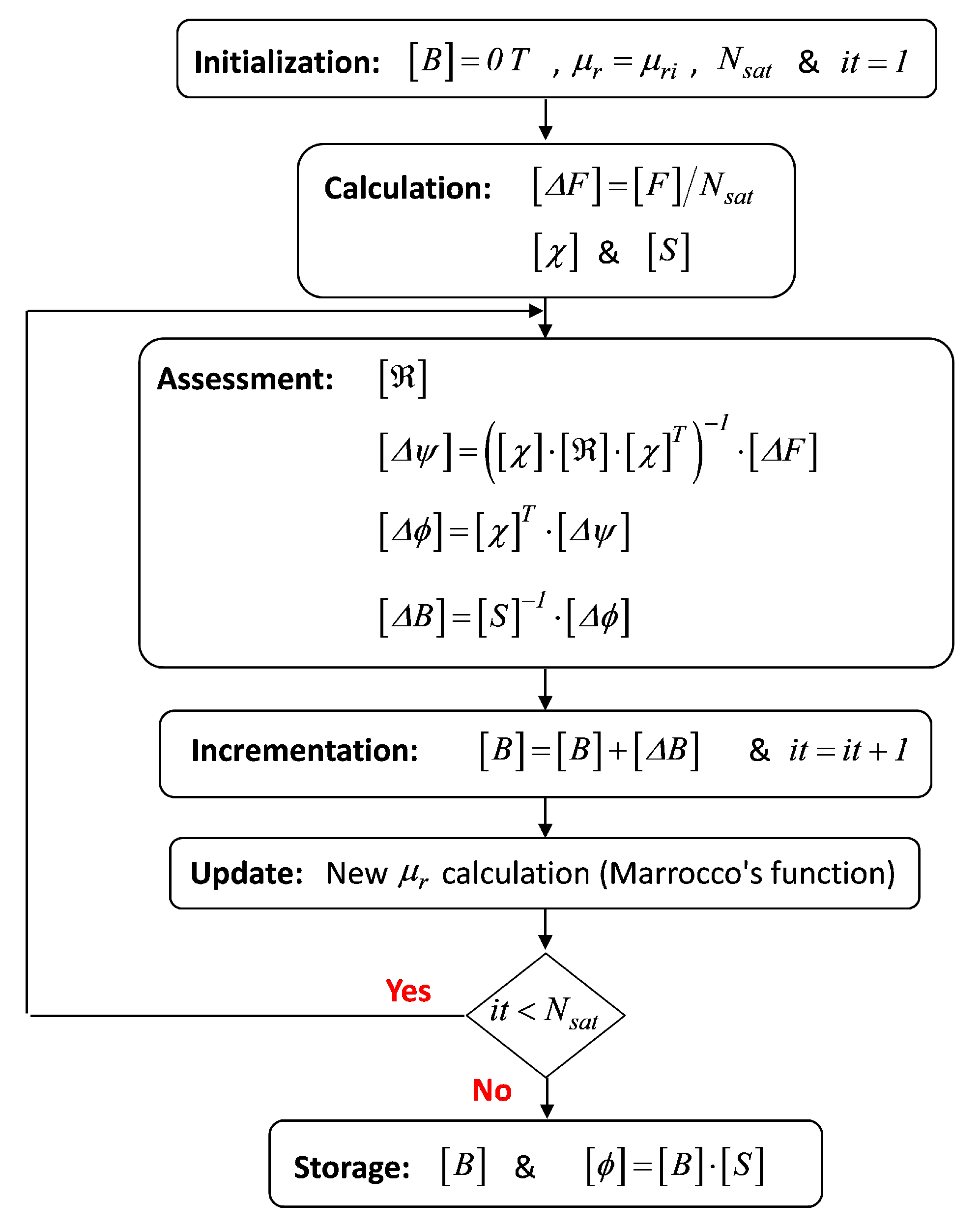
2.2. 2-D Generic MEC
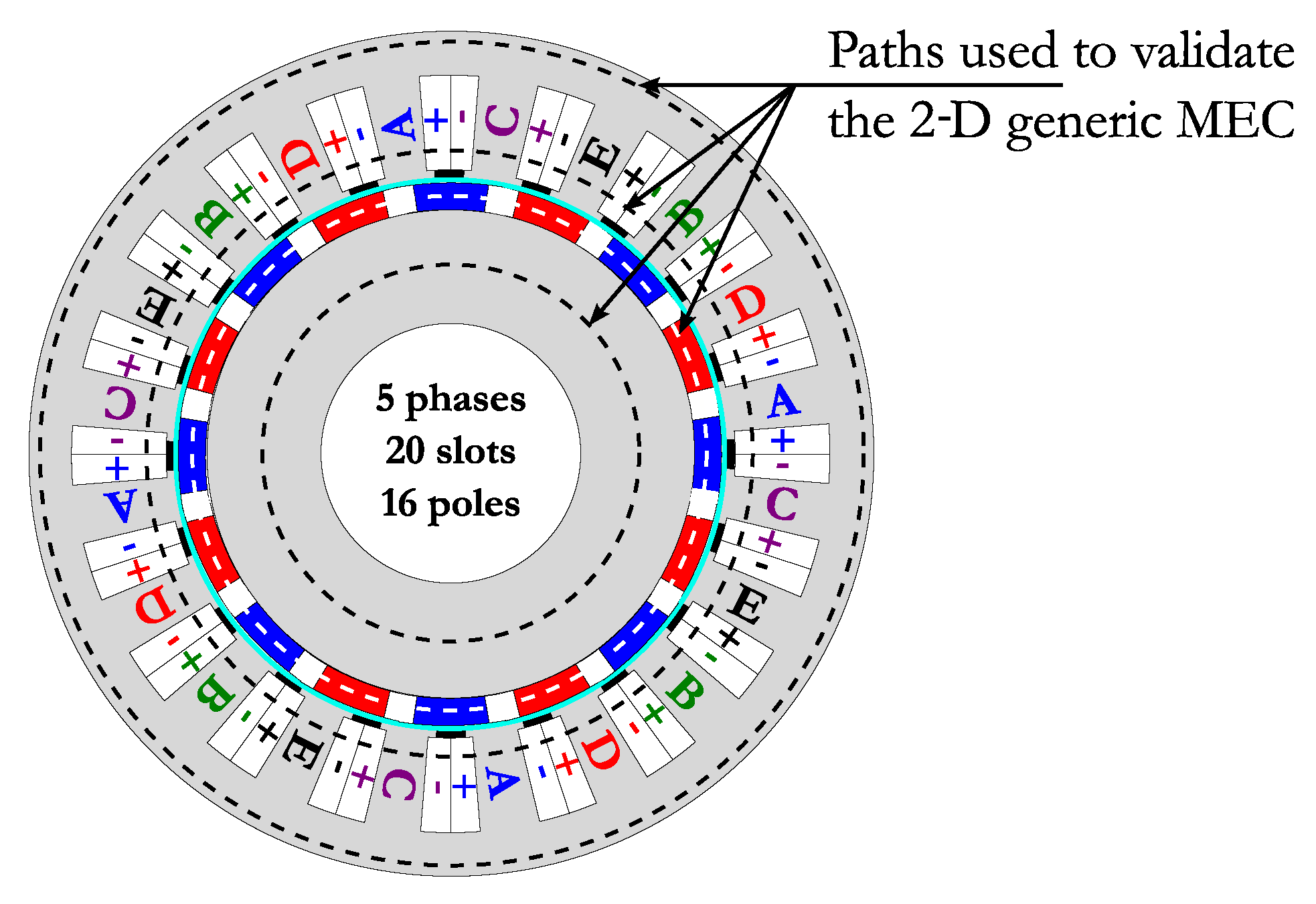
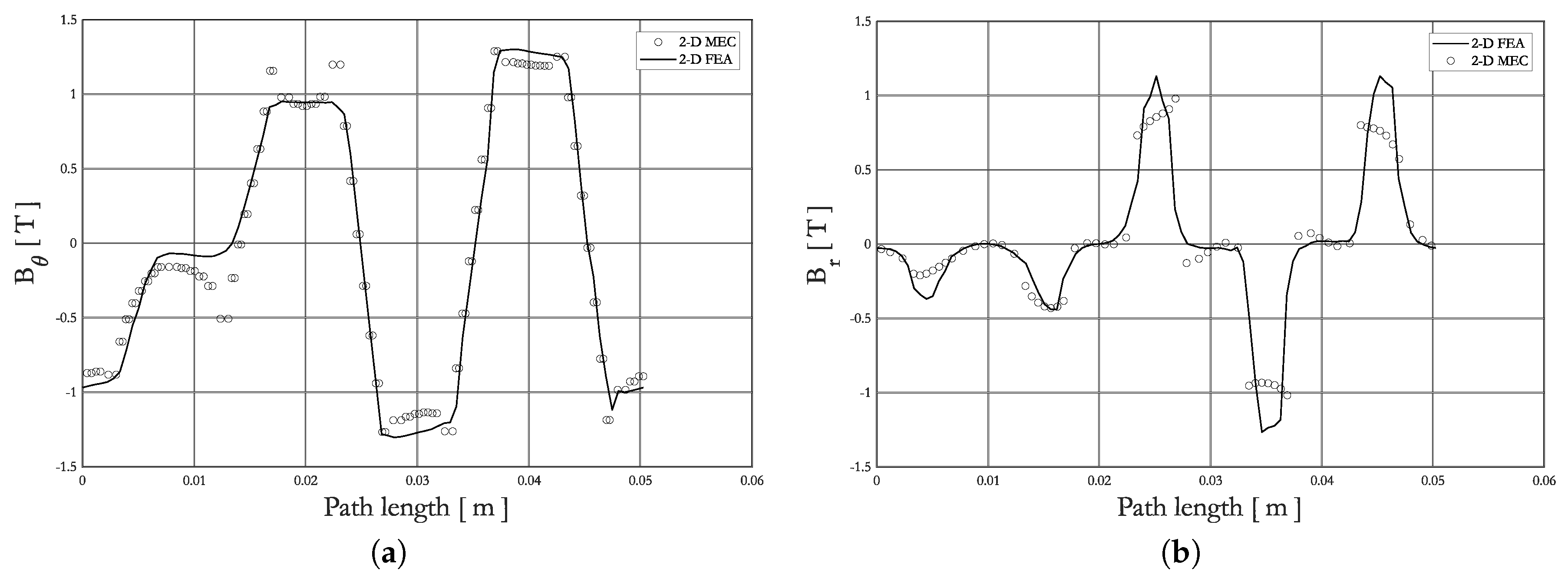
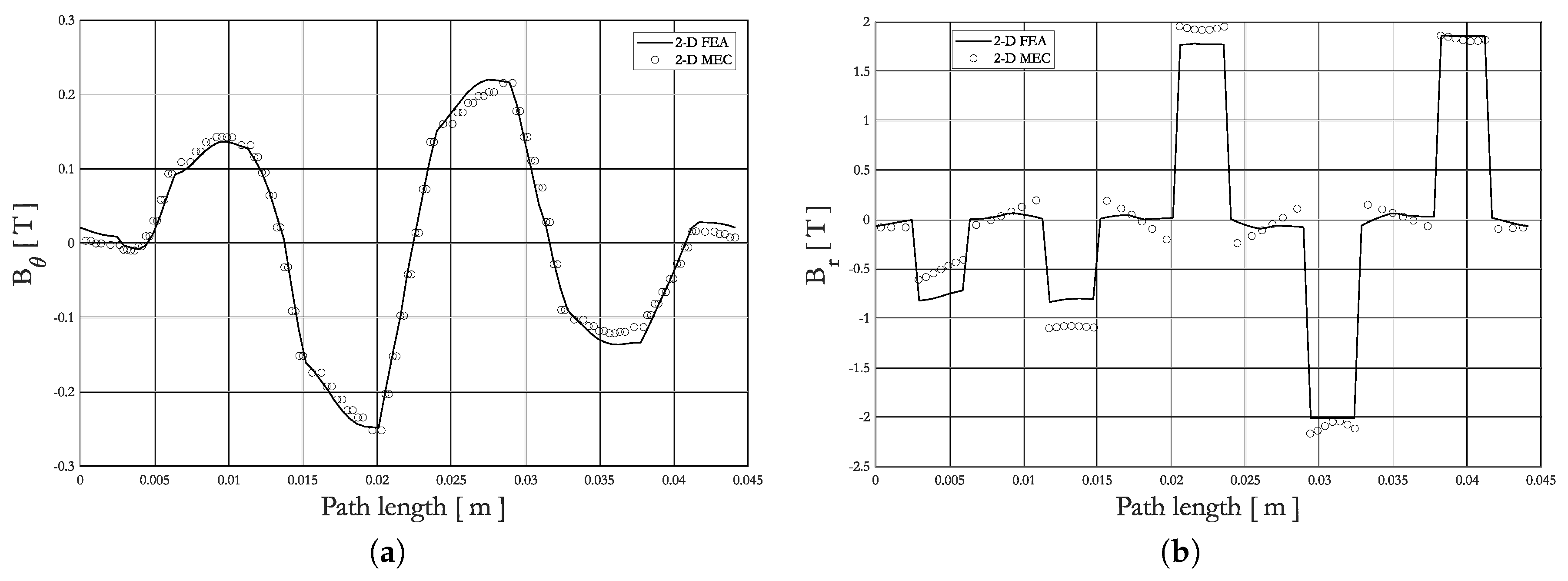
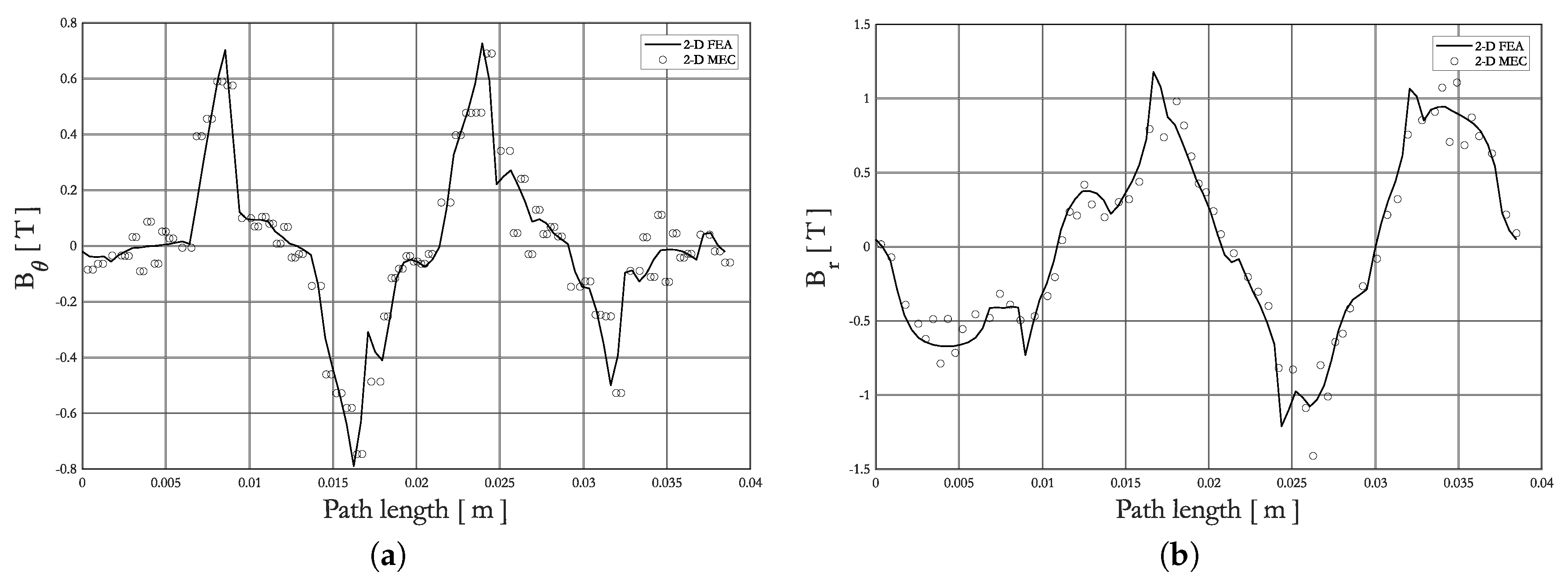
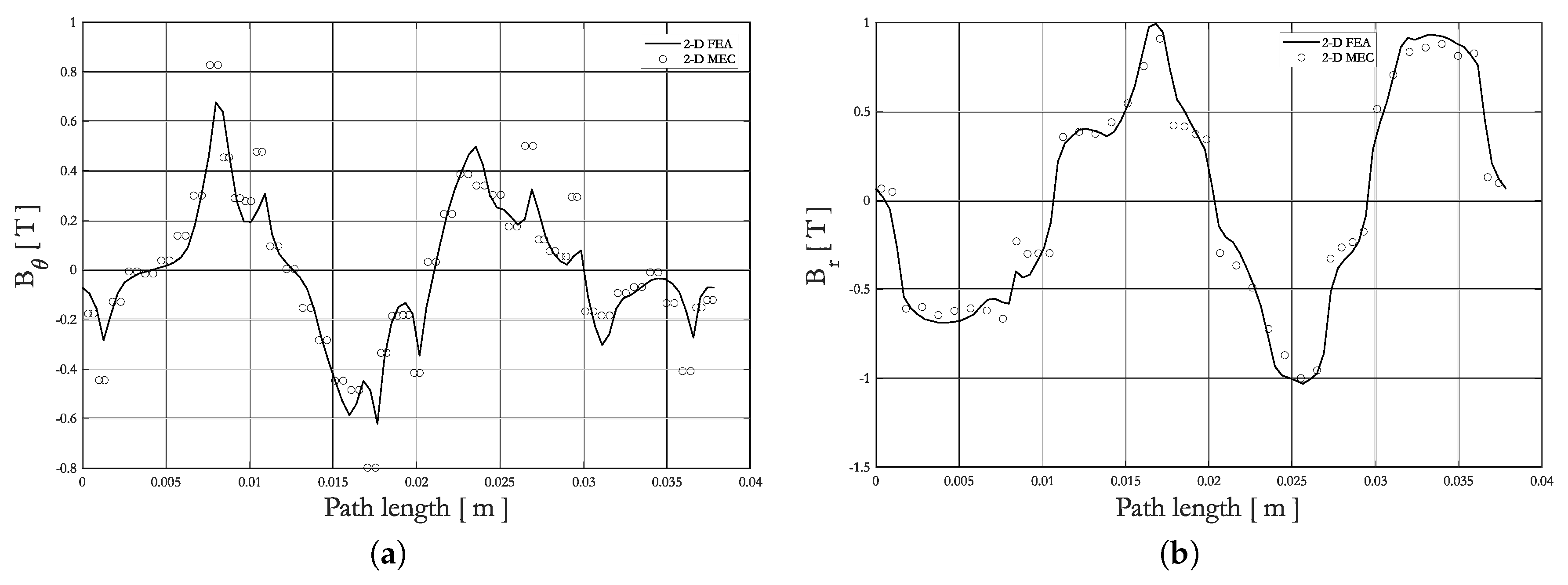
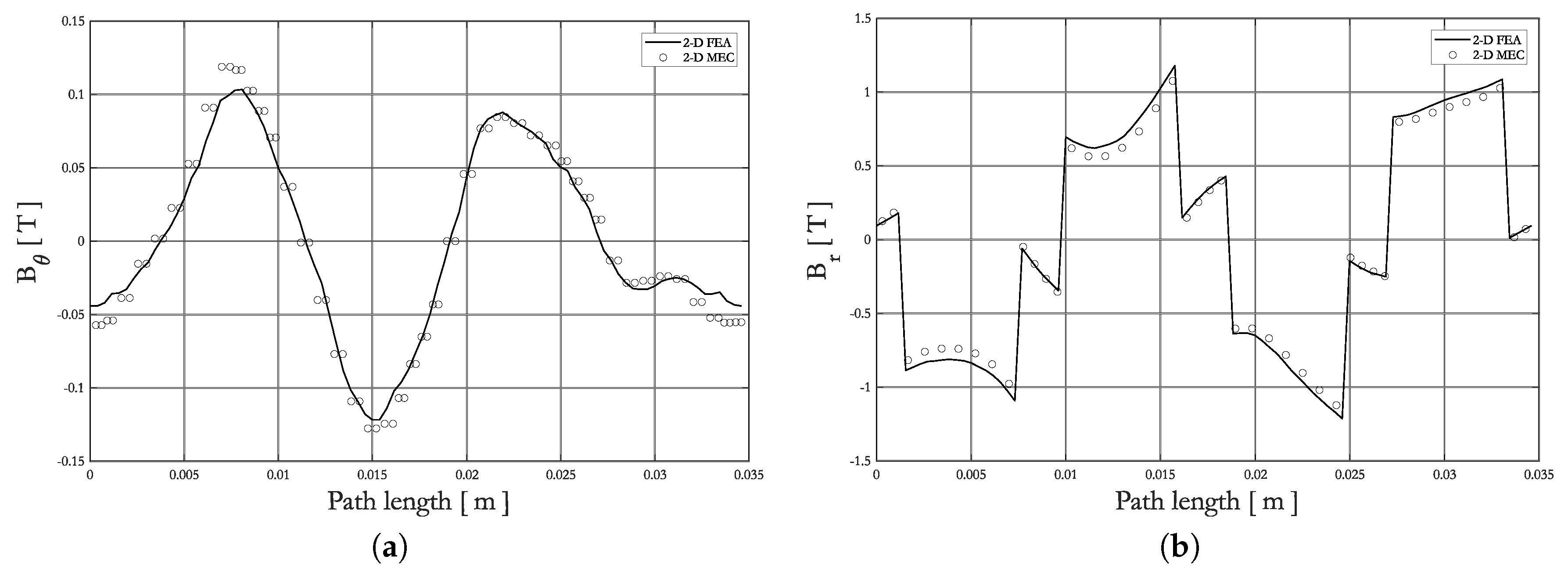
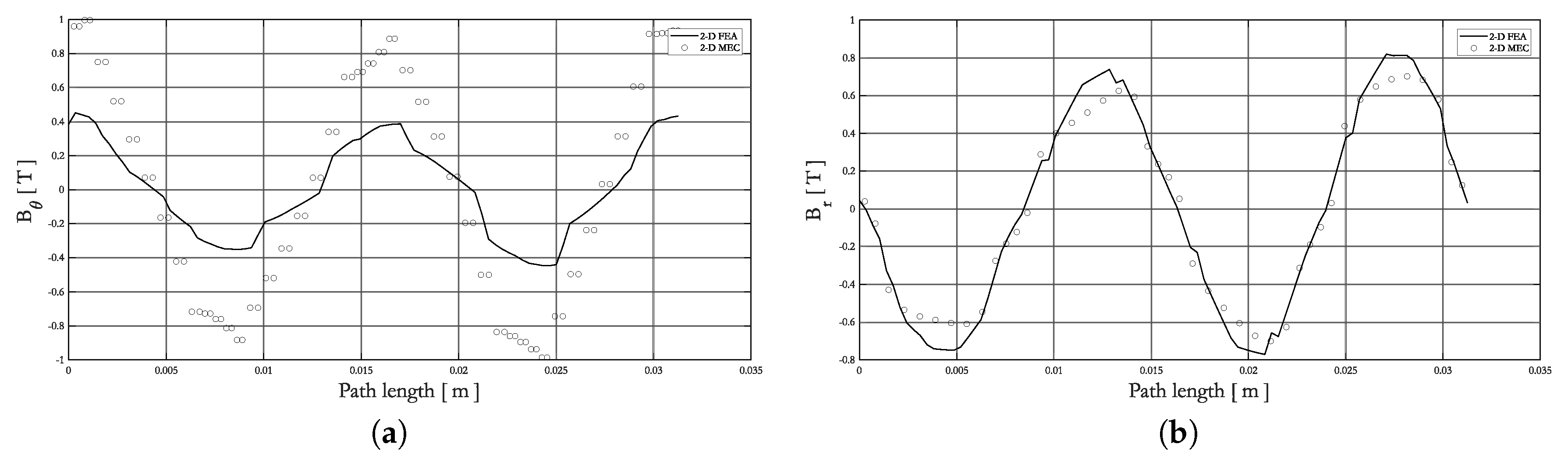
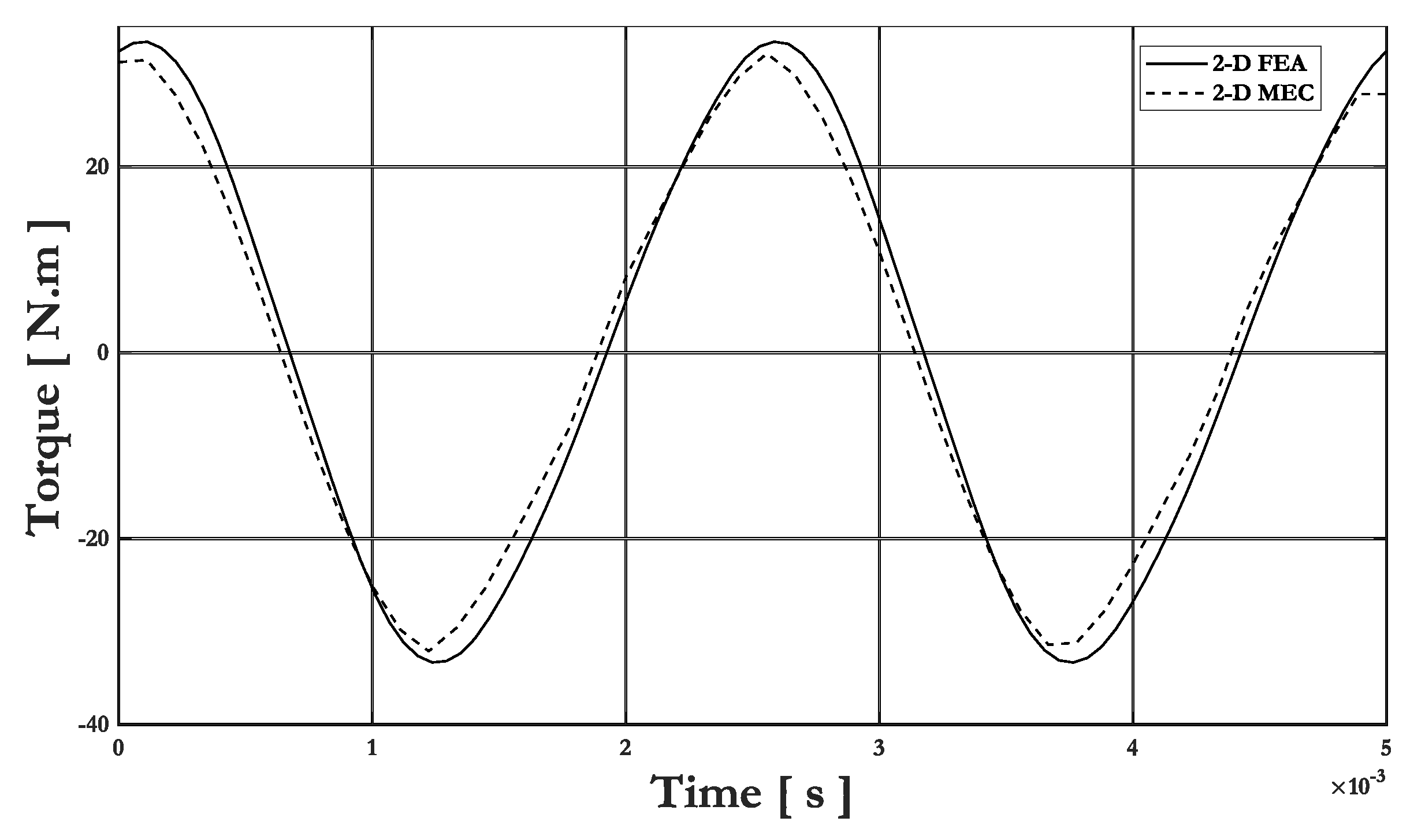
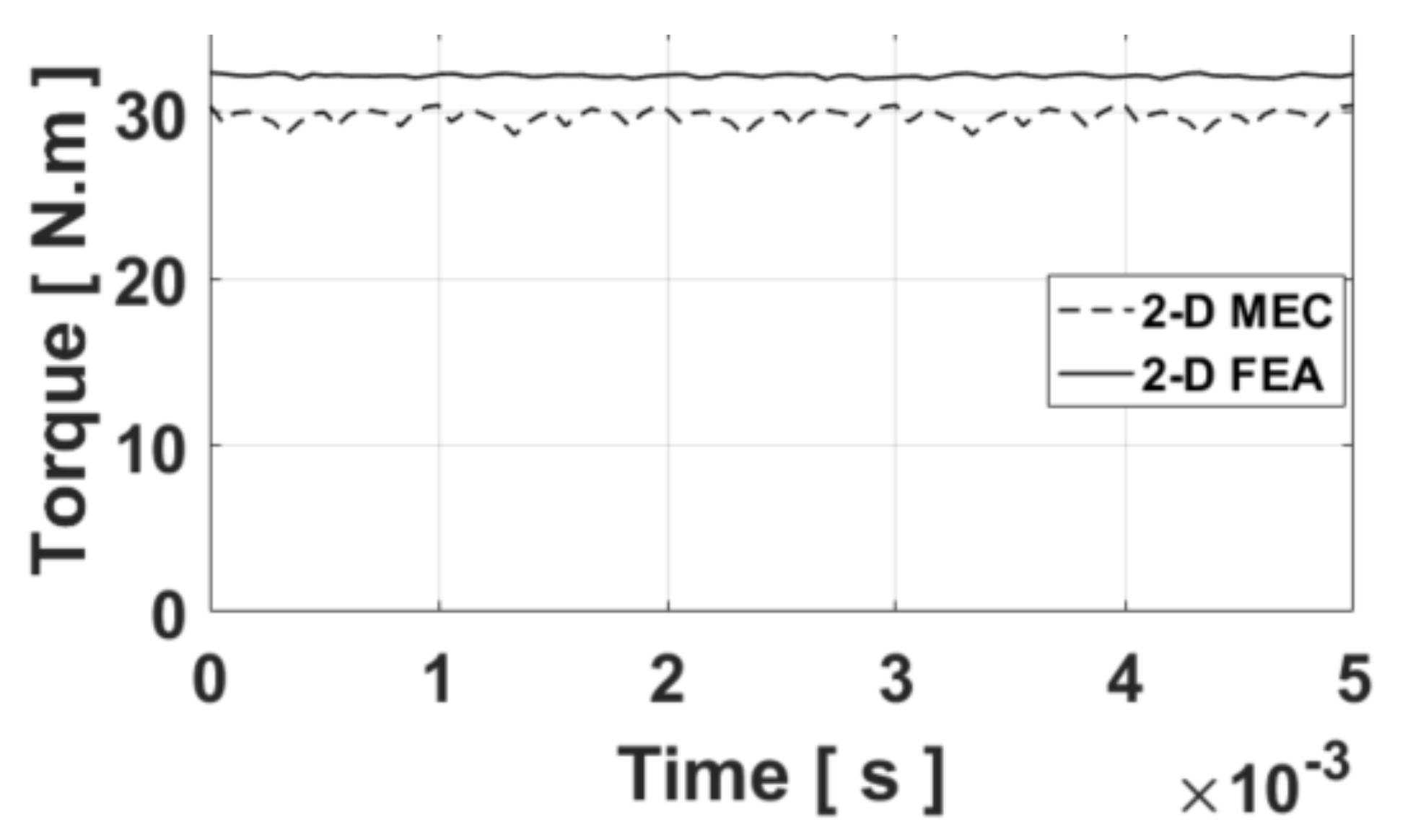
2.3. Validation of 2-D Generic MEC
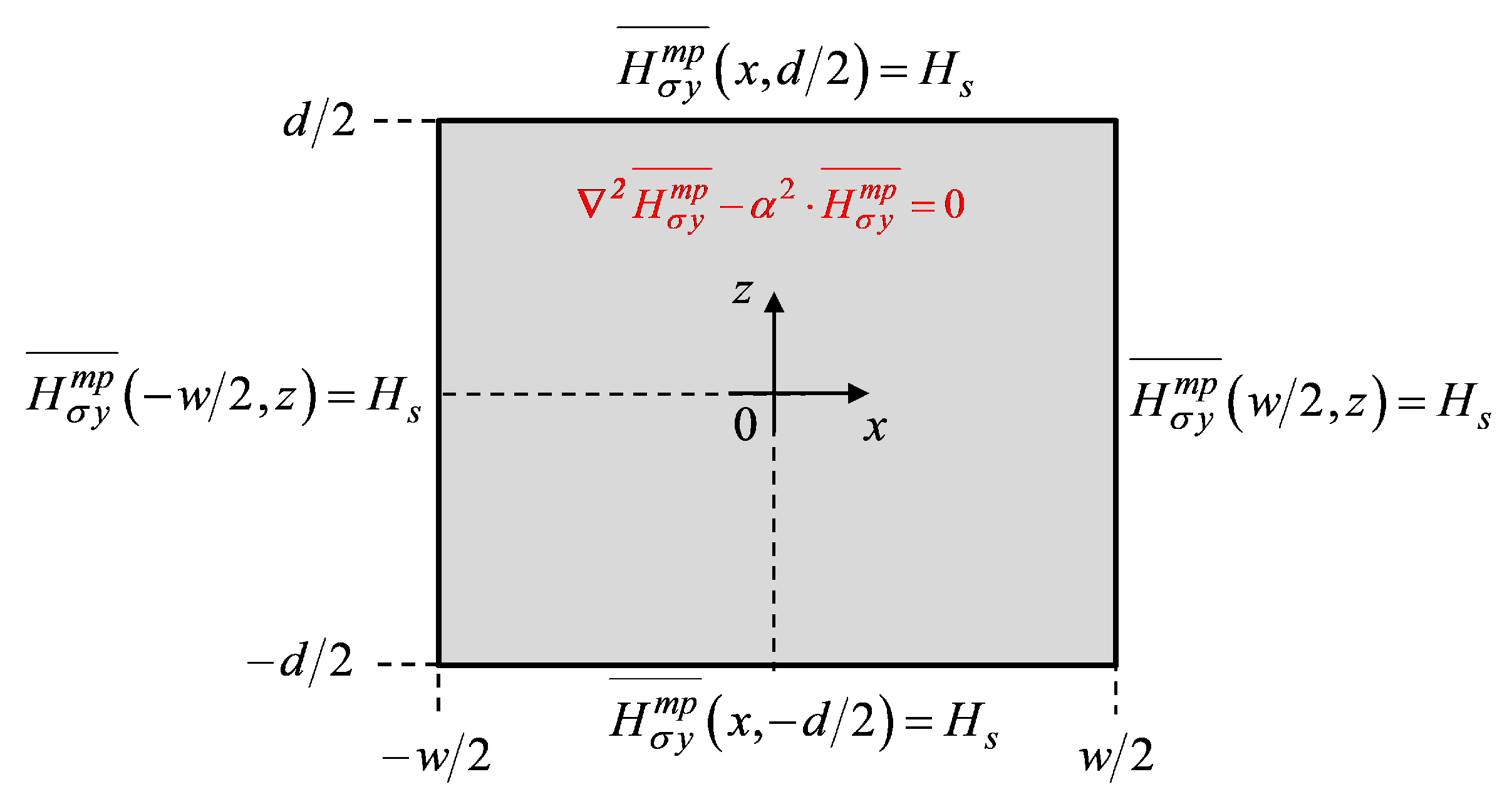
2.4. Formal Resolution of Maxwell’s Equations
2.4.1. General Solution of Magnetic Field with the Skin Effect
2.4.2. Eddy-Current Loss Formulation
3. Approach of PM Eddy-Current Loss Calculation
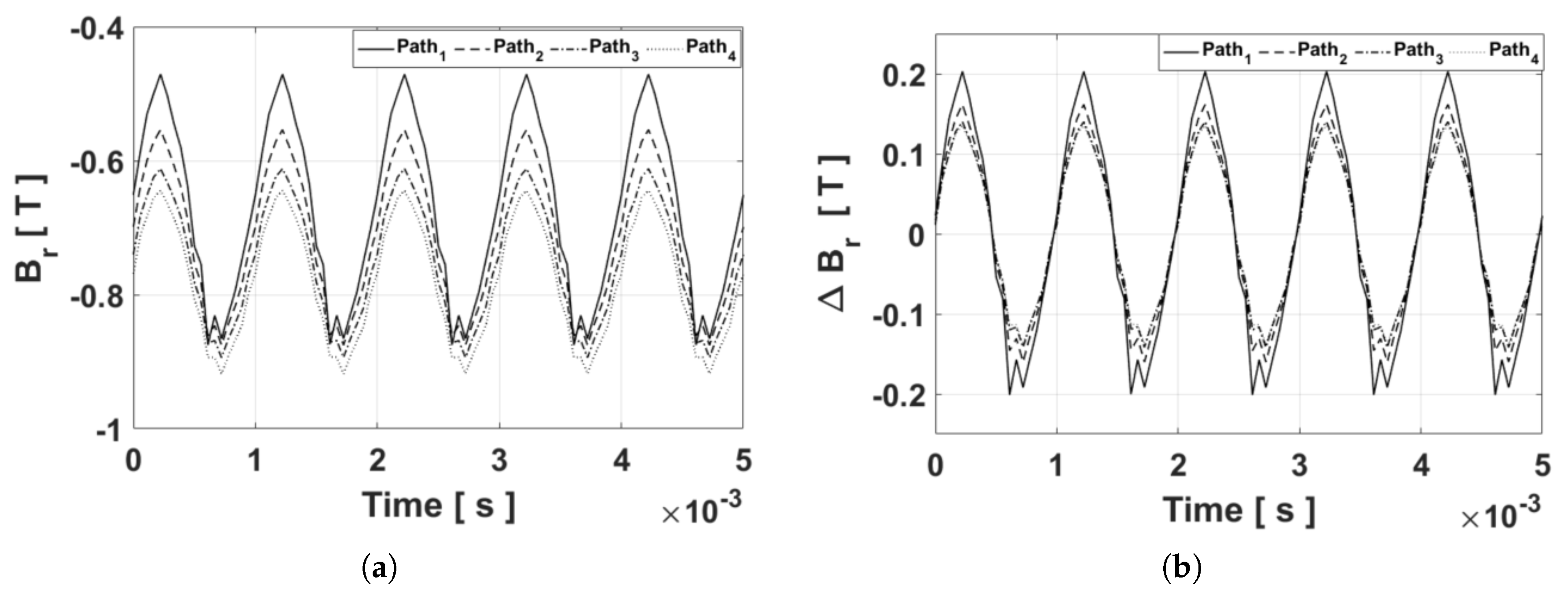
3.1. Magnetic Flux Density vs PM Thickness
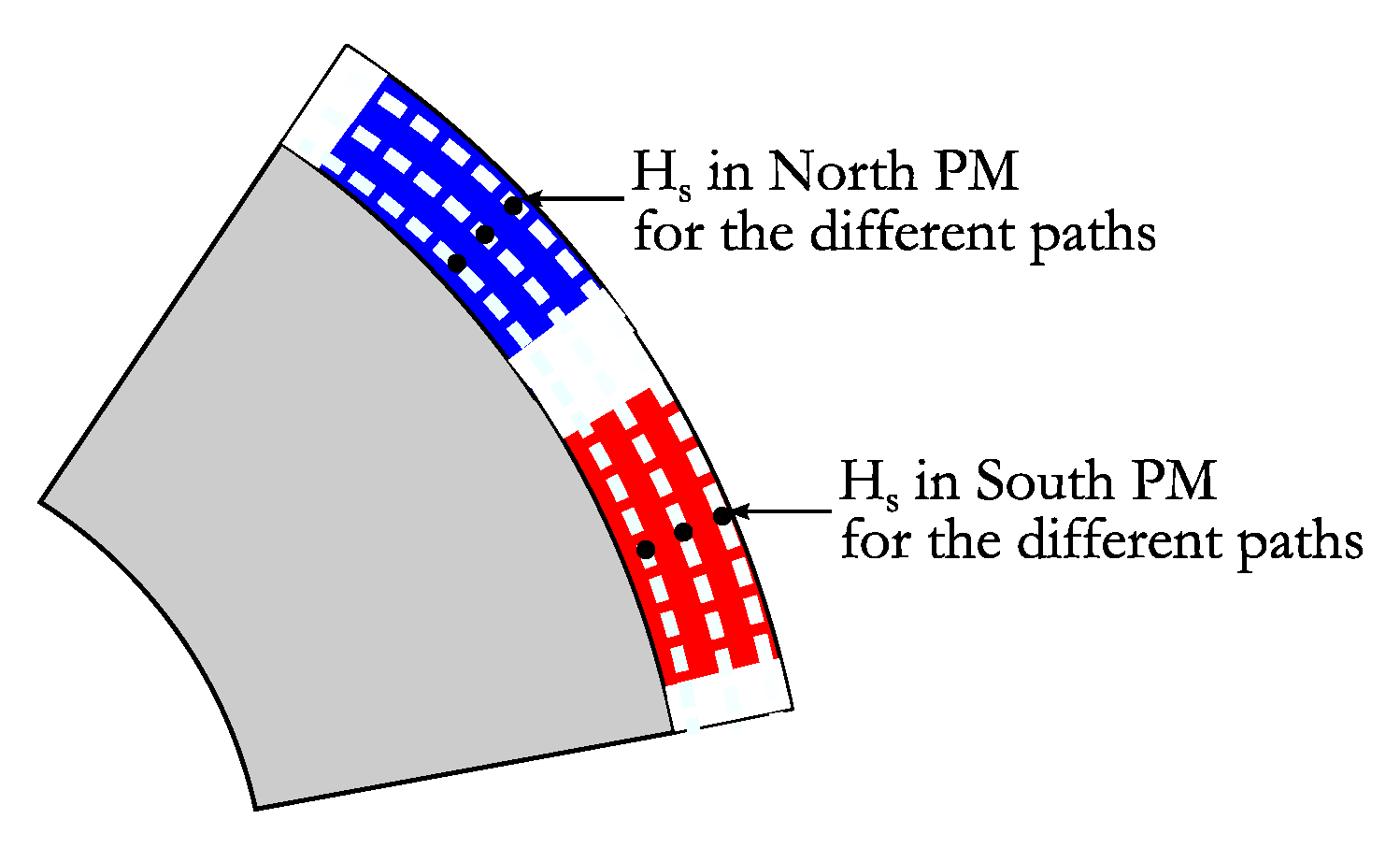
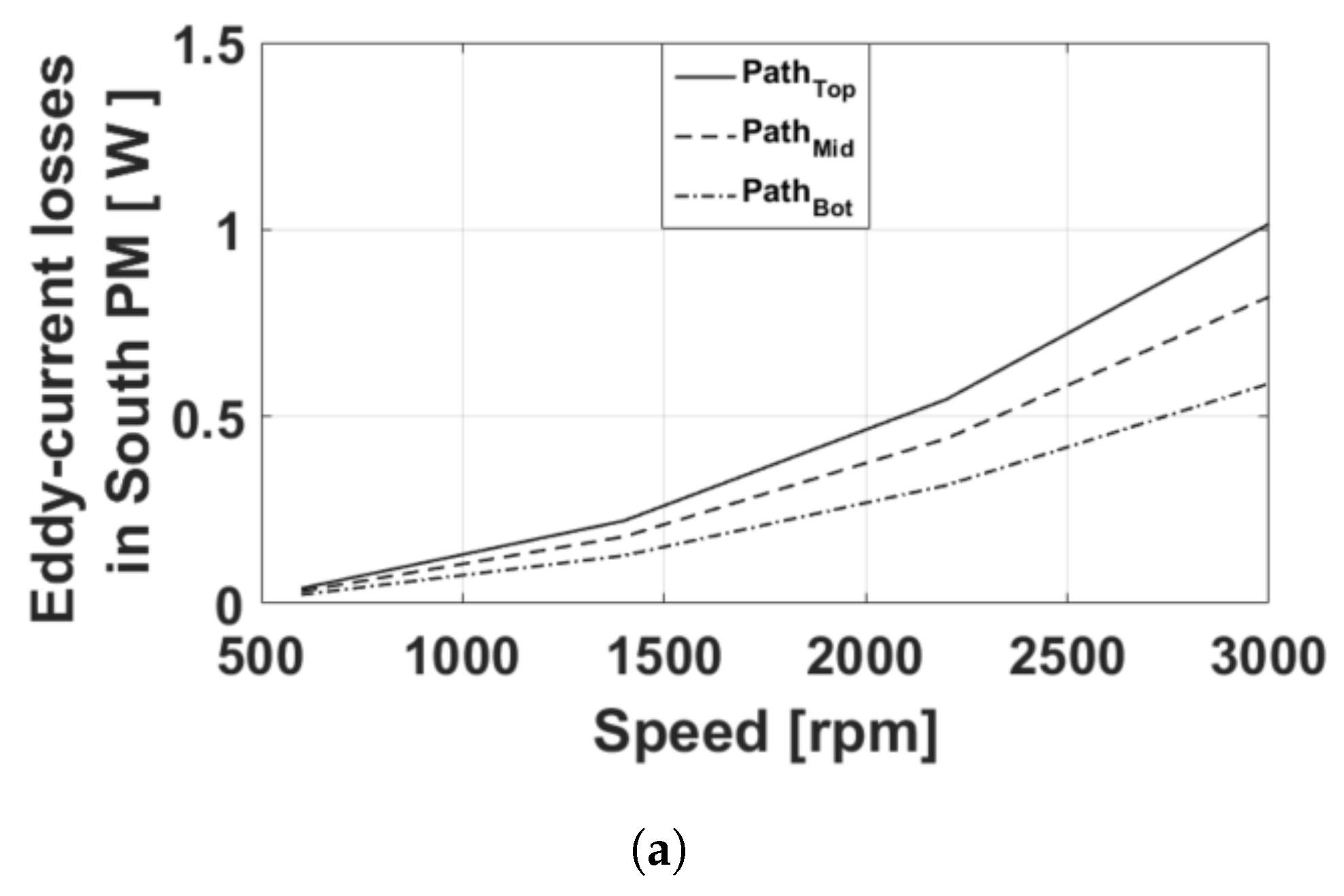
3.2. Eddy-Current Loss Evolution in Different Paths
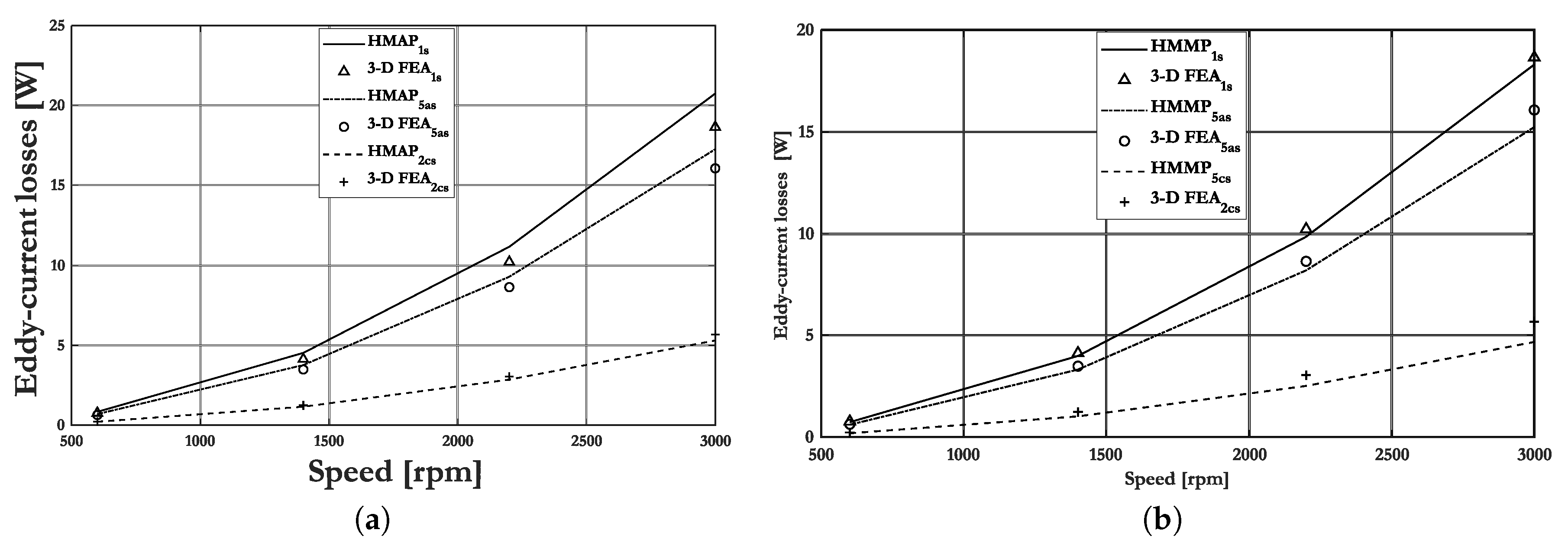
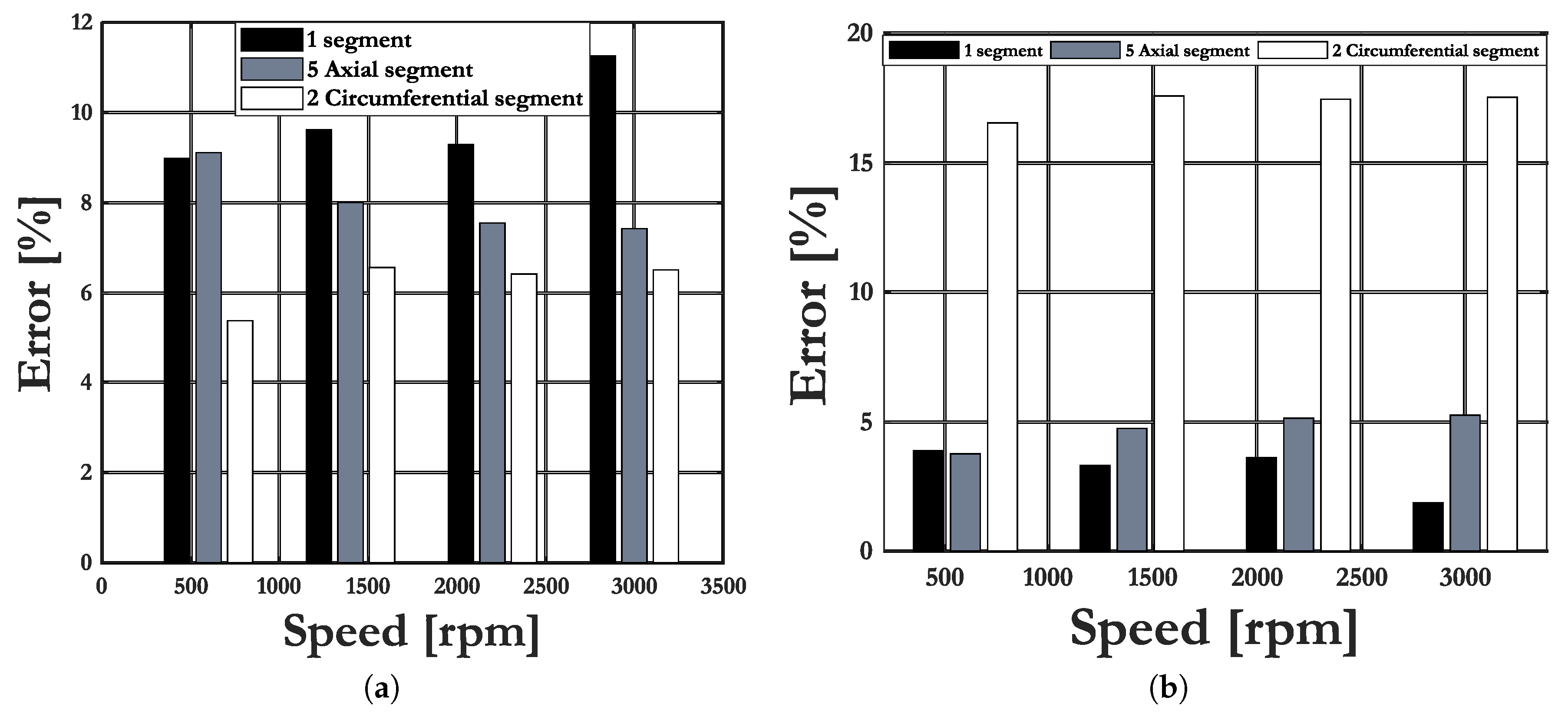
4. 3-D nonlinear FEA Validation With(out) PM Segmentation
- 1st approach: based on all paths;
- 2nd approach: based on the middle path of PMs.
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cassat, A.; Espanet, C.; Coleman, R.; Burdet, L.; Leleu, E.; Torregrossa, D.; M’Boua, J.; Miraoui, A. A practical solution to mitigate vibrations in industrial PM motors having concentric windings. IEEE Trans. Ind. Appl. 2012, 48, 1526–1538. [Google Scholar] [CrossRef]
- Levi, E. Multiphase Electric Machines for Variable-Speed Applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Scuiller, F.; Charpentier, J.F.; Semail, E.; Clenet, S. Comparison of two 5-phase permanent magnet machine winding configurations. Application on naval propulsion specifications. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; Volume 1, pp. 34–39. [Google Scholar] [CrossRef]
- de la Barriere, O.; Hlioui, S.; Ben Ahmed, H.; Gabsi, M. An Analytical Model for the Computation of No-Load Eddy-Current Losses in the Rotor of a Permanent Magnet Synchronous Machine. IEEE Trans. Magn. 2016, 52, 1–13. [Google Scholar] [CrossRef]
- Dubas, F.; Espanet, C. Semi-Analytical Solution of 2-D Rotor Eddy-Current Losses due to the Slotting Effect in SMPMM. In Proceedings of the 17th Conference on the Computation of Electromagnetic Fields COMPUMAG 2009, Florianopolis, Brasil, 22–26 November 2009; pp. 20–25. [Google Scholar]
- Markovic, M.; Perriard, Y. A simplified determination of the permanent magnet (PM) eddy current losses due to slotting in a PM rotating motor. In Proceedings of the 2008 International Conference on Electrical Machines and Systems (ICEMS), Wuhan, China, 17–20 October 2008; pp. 309–313. [Google Scholar]
- Dubas, F.; Espanet, C.; Miraoui, A. Field Diffusion Equation in High-Speed Surface-Mounted Permanent Magnet Motors, Parasitic Eddy-Current Losses. In Proceedings of the 6th International Symposium on Advanced Electromechanical Motion Systems, Lausanne, Switzerland, 27–29 September 2005; pp. 1–6. [Google Scholar]
- Deng, F.; Nehl, T. Analytical modeling of eddy-current losses caused by pulse-width-modulation switching in permanent-magnet brushless direct-current motors. IEEE Trans. Magn. 1998, 34, 3728–3736. [Google Scholar] [CrossRef]
- Nuscheler, R. Two-dimensional analytical model for eddy-current rotor loss calculation of PMS machines with concentrated stator windings and a conductive shield for the magnets. In Proceedings of the XIX International Conference on Electrical Machines (ICEM 2010), Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Mirzaei, M.; Binder, A.; Funieru, B.; Susic, M. Analytical Calculations of Induced Eddy Currents Losses in the Magnets of Surface Mounted PM Machines With Consideration of Circumferential and Axial Segmentation Effects. IEEE Trans. Magn. 2012, 48, 4831–4841. [Google Scholar] [CrossRef]
- Yoshida, K.; Hita, Y.; Kesamaru, K. Eddy-current loss analysis in PM of surface-mounted-PM SM for electric vehicles. IEEE Trans. Magn. 2000, 36, 1941–1944. [Google Scholar] [CrossRef]
- El-Hasan, T. Rotor eddy current determination using finite element analysis for High-Speed Permanent Magnet Machines. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 885–889. [Google Scholar] [CrossRef]
- Saban, D.M.; Lipo, T.A. Hybrid Approach for Determining Eddy-Current Losses in High-Speed PM Rotors. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; Volume 1, pp. 658–661. [Google Scholar] [CrossRef]
- Gerlach, T.; Rabenstein, L.; Dietz, A.; Kremser, A.; Gerling, D. Determination of eddy current losses in permanent magnets of SPMSM with concentrated windings: A hybrid loss calculation method and experimental verification. In Proceedings of the 2018 Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 April 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Dubas, F.; Rahideh, A. Two-Dimensional Analytical Permanent-Magnet Eddy-Current Loss Calculations in Slotless PMSM Equipped With Surface-Inset Magnets. IEEE Trans. Magn. 2014, 50, 54–73. [Google Scholar] [CrossRef]
- Ouamara, D.; Dubas, F. Permanent-Magnet Eddy-Current Losses: A Global Revision of Calculation and Analysis. Math. Comput. Appl. 2019, 24, 67. [Google Scholar] [CrossRef]
- Pfister, P.D.; Yin, X.; Fang, Y. Slotted Permanent-Magnet Machines: General Analytical Model of Magnetic Fields, Torque, Eddy Currents, and Permanent-Magnet Power Losses Including the Diffusion Effect. IEEE Trans. Magn. 2016, 52, 1–13. [Google Scholar] [CrossRef]
- Benlamine, R.; Dubas, F.; Randi, S.A.; Lhotellier, D.; Espanet, C. 3-D Numerical Hybrid Method for PM Eddy-Current Losses Calculation: Application to Axial-Flux PMSMs. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar] [CrossRef]
- Masmoudi, A.; Masmoudi, A. 3-D Analytical Model With the End Effect Dedicated to the Prediction of PM Eddy-Current Loss in FSPMMs. IEEE Trans. Magn. 2015, 51, 1–11. [Google Scholar] [CrossRef]
- Ouamara, D.; Dubas, F.; Randi, S.A.; Benallal, M.N.; Espanet, C. Optimal Design of Multi-phases Permanent-Magnet Synchronous Machines Using Genetic Algorithms. Mediterr. J. Model. Simul. 2018, 10, 29–44. [Google Scholar]
- Altair Flux. Electromagnetic, Electric, and Thermal Analysis. Available online: https://www.altair.com/flux/ (accessed on 4 March 2020).
- Dubas, F.; Benlamine, R.; Randi, S.A.; Lhotellier, D.; Espanet, C. 2-D or quasi 3-D nonlinear adaptative magnetic equivalent circuit, Part I: Generalized modeling with air-gap sliding-line technic. Appl. Energy. under review.
- Benlamine, R.; Dubas, F.; Randi, S.A.; Lhotellier, D.; Espanet, C. 2-D or quasi 3-D nonlinear adaptive magnetic equivalent circuit, Part II: Application to axial-flux interior permanent-magnet synchronous machines. Appl. Energy. under review.
- Benlamine, R.; Dubas, F.; Randi, S.A.; Lhotellier, D.; Espanet, C. Modeling of an axial-flux interior PMs machine for an automotive application using magnetic equivalent circuit. In Proceedings of the 2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; pp. 1266–1271. [Google Scholar] [CrossRef]
- Benlamine, R.; Hamiti, T.; Vangraefschepe, F.; Dubas, F.; Lhotellier, D. Modeling of a coaxial magnetic gear equipped with surface mounted PMs using nonlinear adaptive magnetic equivalent circuits. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1888–1894. [Google Scholar] [CrossRef]
- Benlamine, R.; Benmessaoud, Y.; Dubas, F.; Espanet, C. Nonlinear Adaptive Magnetic Equivalent Circuit of a Radial-Flux Interior Permanent-Magnet Machine Using Air-Gap Sliding-Line Technic. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017; Volume 24, pp. 1–6. [Google Scholar] [CrossRef]
- Utegenova, S.; Dubas, F.; Jamot, M.; Glises, R.; Truffart, B.; Mariotto, D.; Lagonotte, P.; Desevaux, P. An Investigation into the Coupling of Magnetic and Thermal Analysis for a Wound-Rotor Synchronous Machine. IEEE Trans. Ind. Electron. 2018, 65, 3406–3416. [Google Scholar] [CrossRef]
- Stoll, R.L. The Analysis of Eddy Currents; Clarendon Press: Oxford, UK, 1974. [Google Scholar]


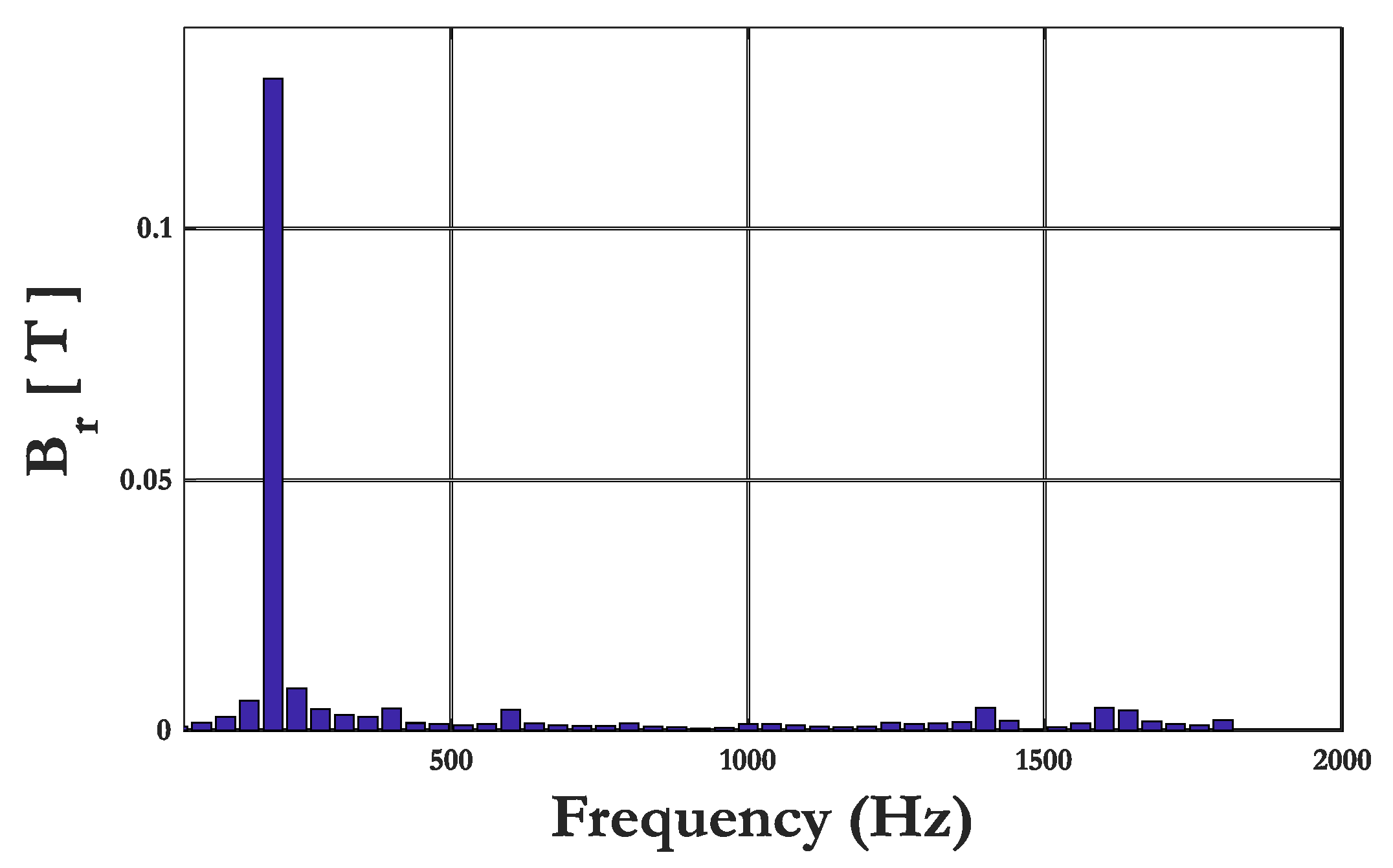
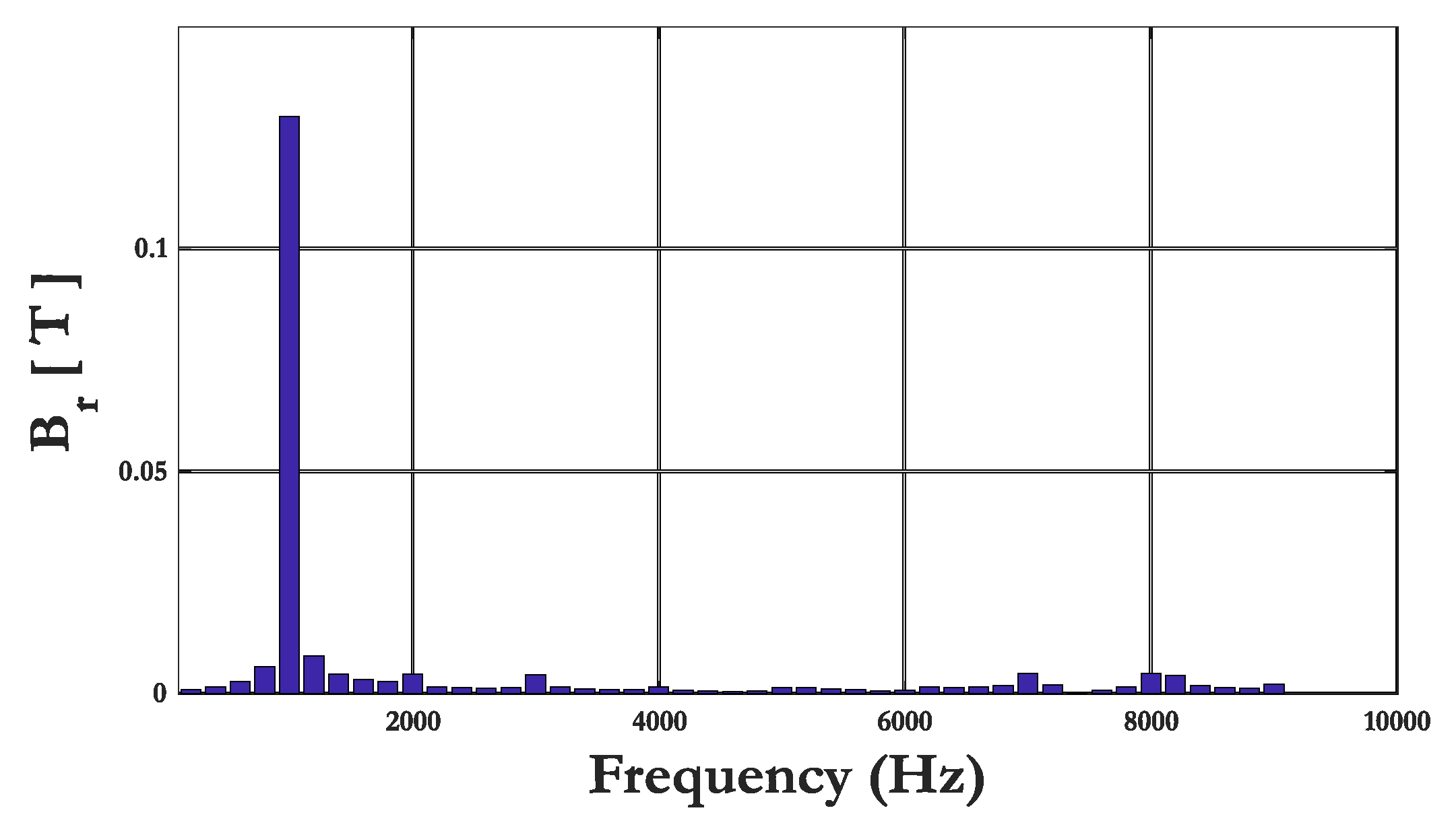

| Designation | Symbol | Value | Unit |
|---|---|---|---|
| Slots number | 20 | - | |
| Phases number | m | 5 | - |
| Poles number | 16 | - | |
| Slot-opening/tooth-pitch | 60 | % | |
| Isthmus-opening/slot | 53 | % | |
| PM pole-arc/pole-pitch | 72 | % | |
| Winding-opening/slot | 92 | % | |
| Stator bore diameter | mm | ||
| External diameter | mm | ||
| Internal diameter | mm | ||
| Stator yoke height | 3 | mm | |
| Rotor yoke height | 3 | mm | |
| PM height | mm | ||
| Tooth height | mm | ||
| Machine length | 100 | mm |
| Designation | Symbol | Value | Unit |
|---|---|---|---|
| Speed | N | 3000 | rpm |
| Electromagnetic torque | 30 | Nm | |
| Current | I | 30 | A |
| Discretization/Zones | Stator | Rotor |
|---|---|---|
| Tangential | ||
| Radial |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benmessaoud, Y.; Ouamara, D.; Dubas, F.; Hilairet, M. Investigation of Volumic Permanent-Magnet Eddy-Current Losses in Multi-Phase Synchronous Machines from Hybrid Multi-Layer Model. Math. Comput. Appl. 2020, 25, 14. https://doi.org/10.3390/mca25010014
Benmessaoud Y, Ouamara D, Dubas F, Hilairet M. Investigation of Volumic Permanent-Magnet Eddy-Current Losses in Multi-Phase Synchronous Machines from Hybrid Multi-Layer Model. Mathematical and Computational Applications. 2020; 25(1):14. https://doi.org/10.3390/mca25010014
Chicago/Turabian StyleBenmessaoud, Youcef, Daoud Ouamara, Frédéric Dubas, and Mickael Hilairet. 2020. "Investigation of Volumic Permanent-Magnet Eddy-Current Losses in Multi-Phase Synchronous Machines from Hybrid Multi-Layer Model" Mathematical and Computational Applications 25, no. 1: 14. https://doi.org/10.3390/mca25010014
APA StyleBenmessaoud, Y., Ouamara, D., Dubas, F., & Hilairet, M. (2020). Investigation of Volumic Permanent-Magnet Eddy-Current Losses in Multi-Phase Synchronous Machines from Hybrid Multi-Layer Model. Mathematical and Computational Applications, 25(1), 14. https://doi.org/10.3390/mca25010014








