Decision Making Approach under Pythagorean Dombi Fuzzy Graphs for Selection of Leading Textile Industry
Abstract
1. Introduction
2. Certain Pythagorean Dombi Fuzzy Graphs
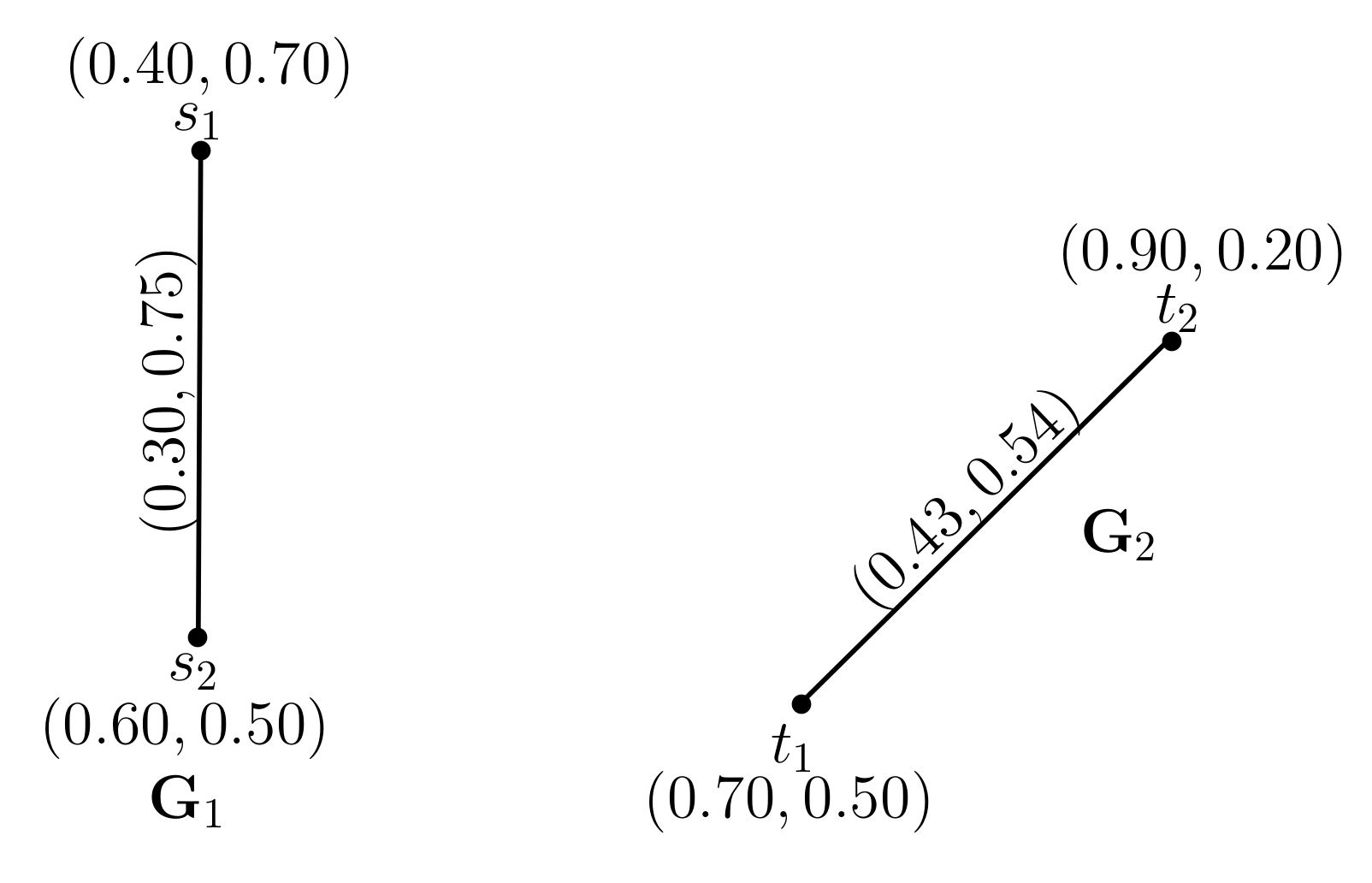
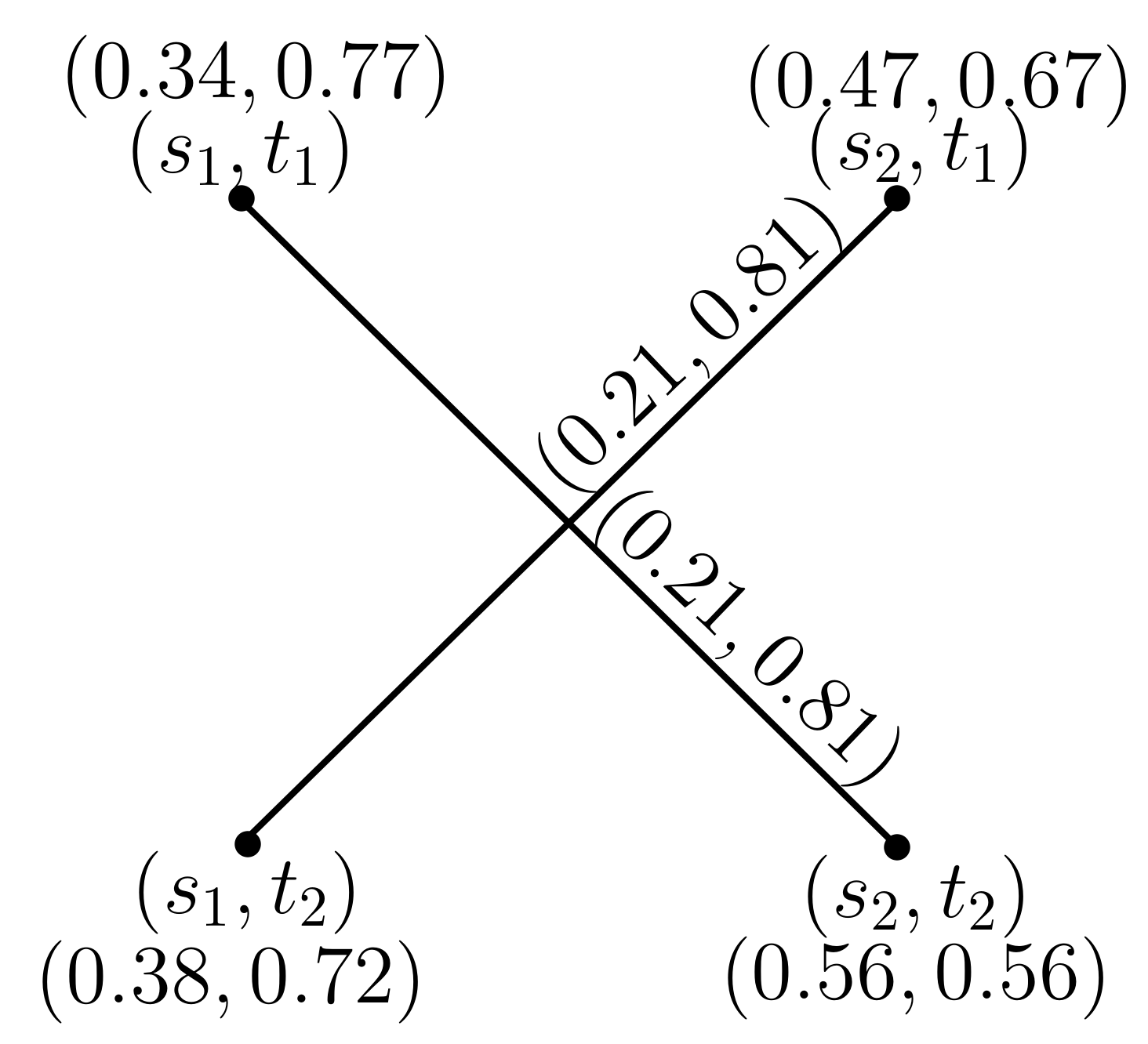
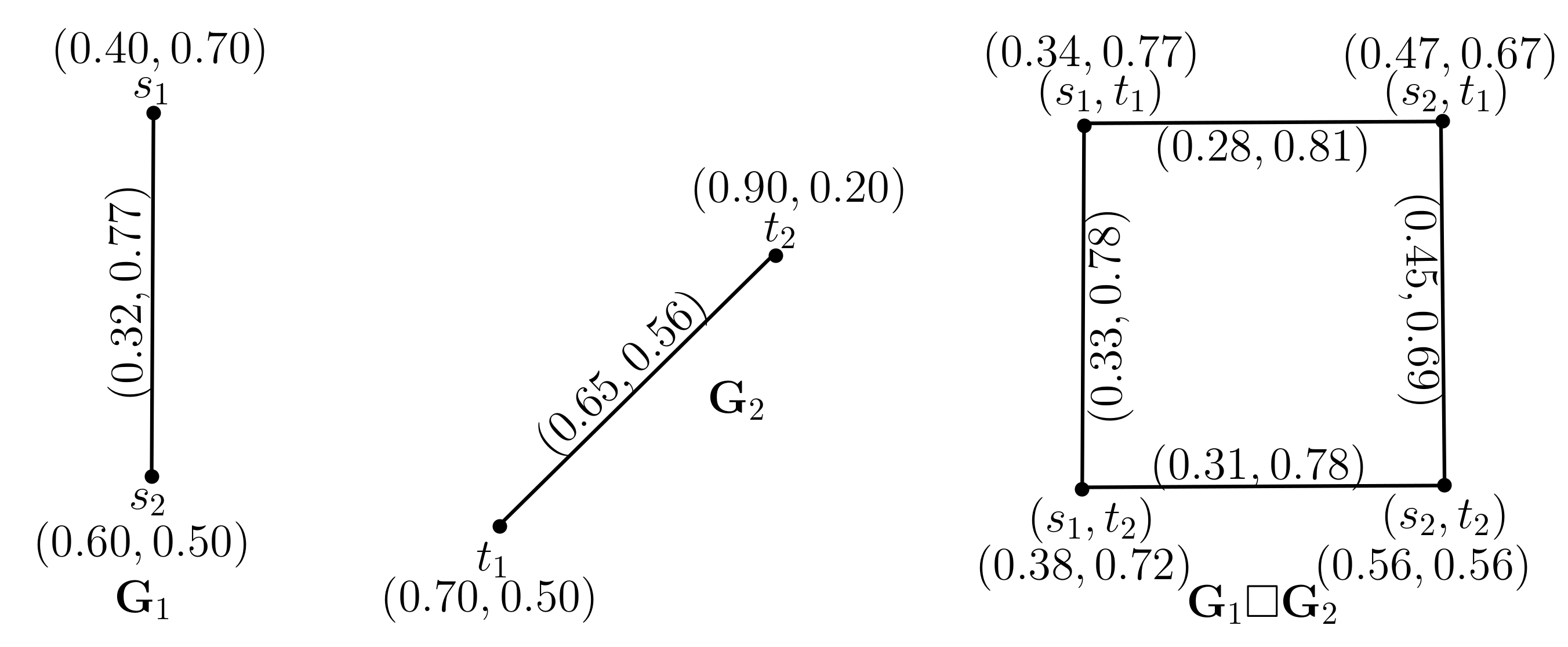
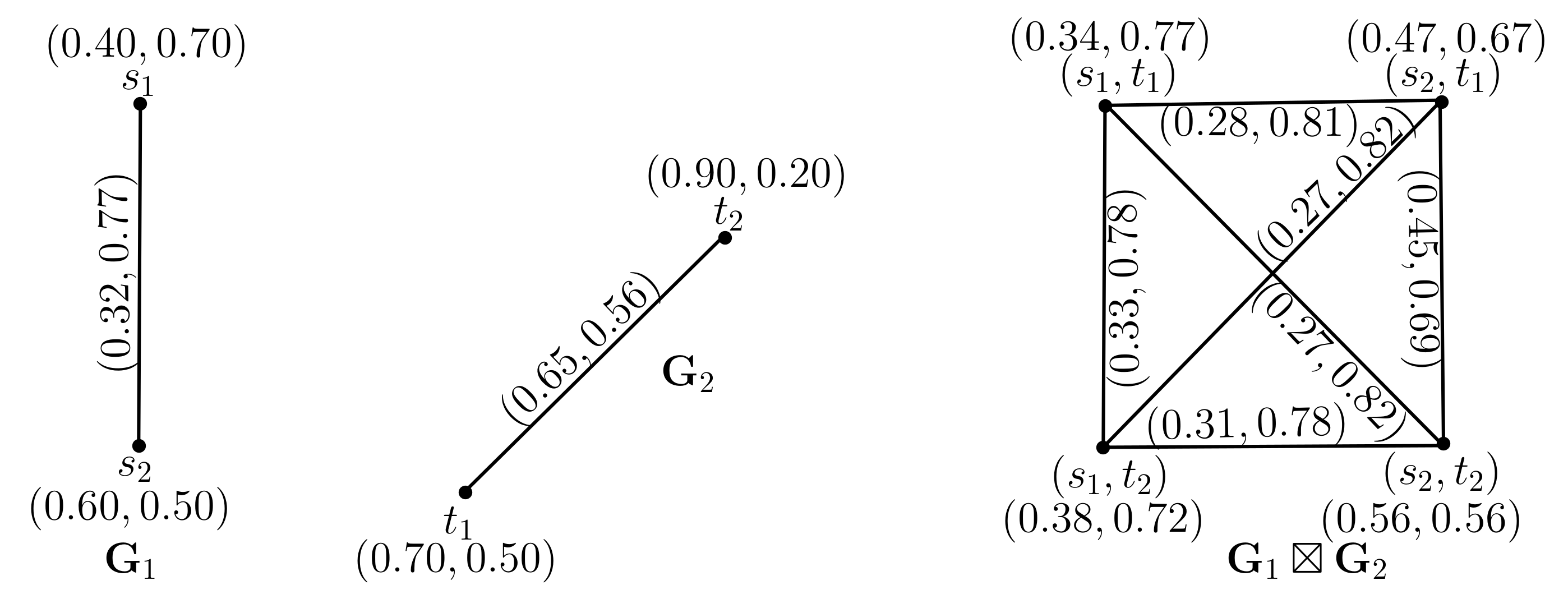
2.1. Direct Product of Pythagorean Dombi Fuzzy Graphs
- (i)
- for all
- (ii)
- for all and .
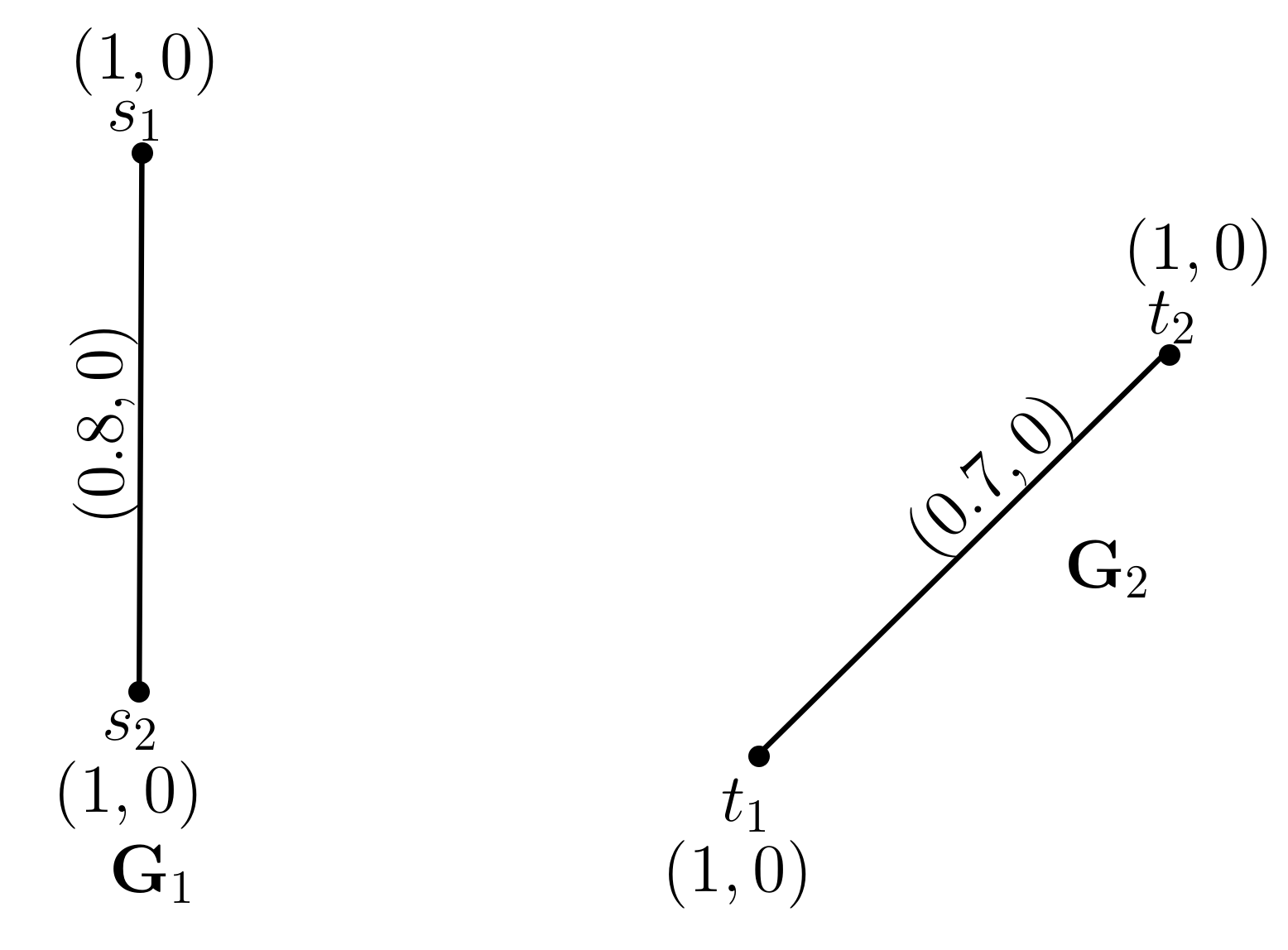
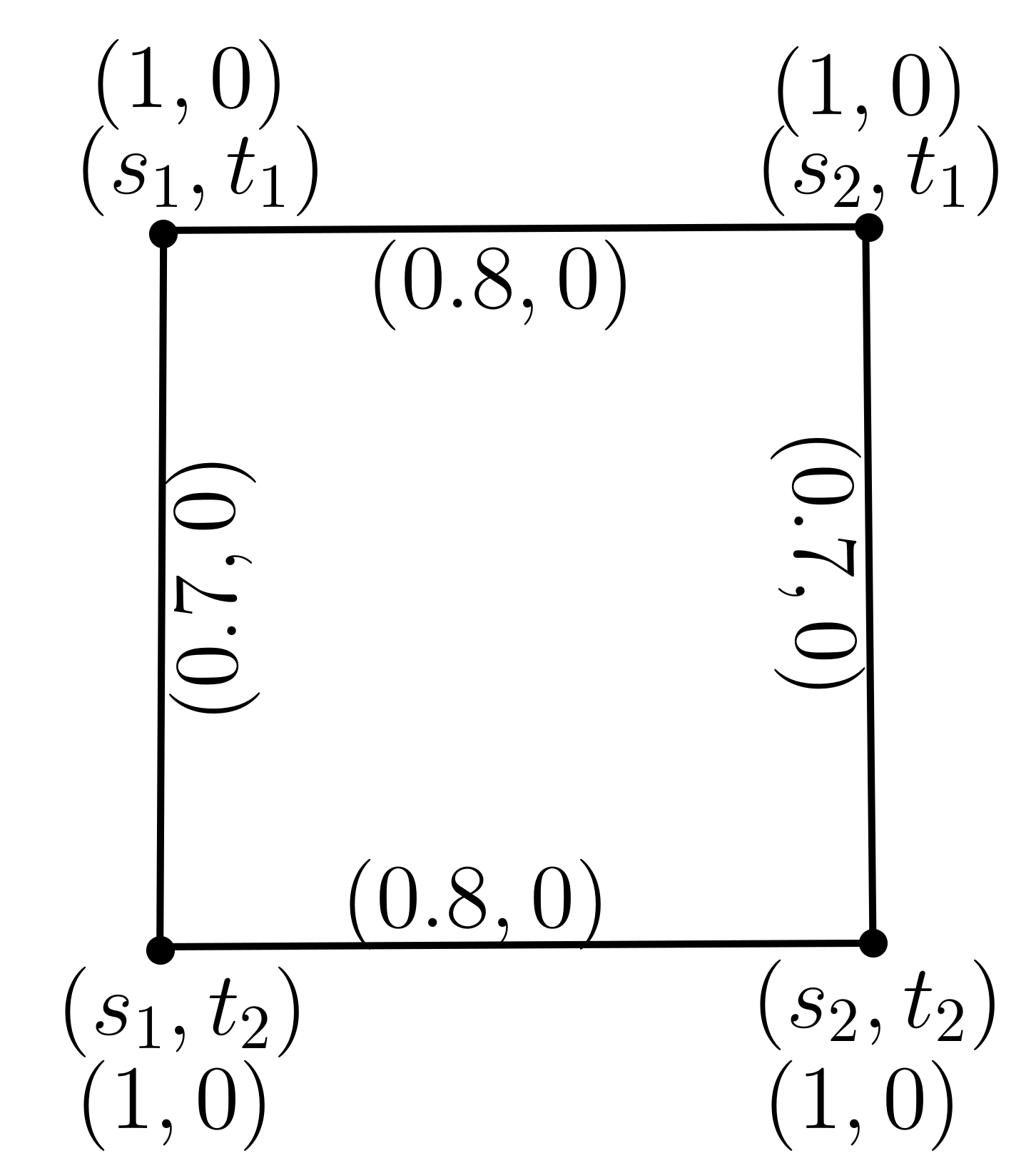
2.2. Cartesian Product of Pythagorean Dombi Fuzzy Graphs
- (i)
- for all
- (ii)
- for all and
- (iii)
- for all and
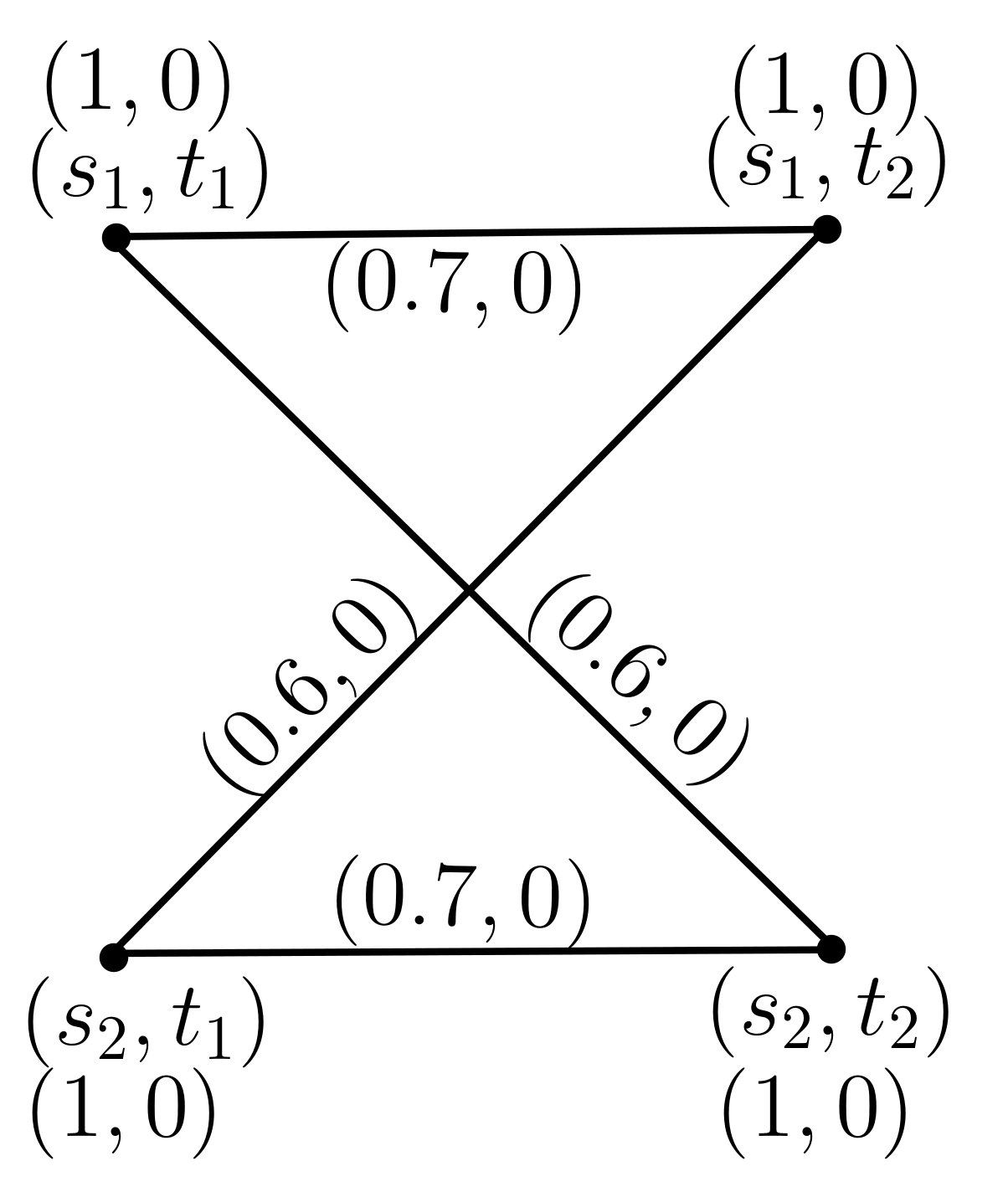
2.3. Semi-Strong Product of Pythagorean Dombi Fuzzy Graphs
- (i)
- for all
- (ii)
- for all and
- (iii)
- for all and .
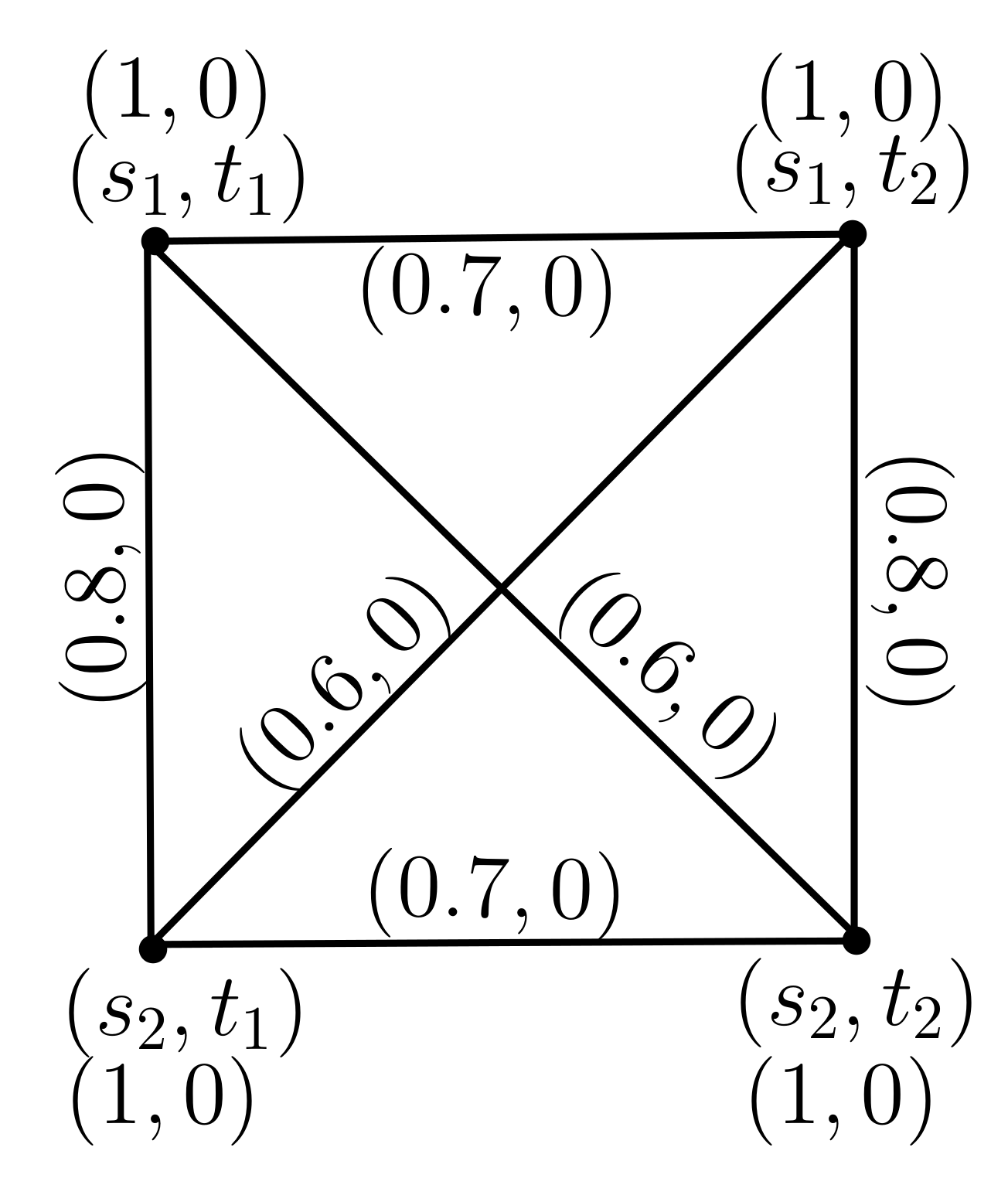
2.4. Strong Product of Pythagorean Dombi Fuzzy Graphs
- (i)
- for all
- (ii)
- for all and
- (iii)
- for all and
- (iv)
- for all and .
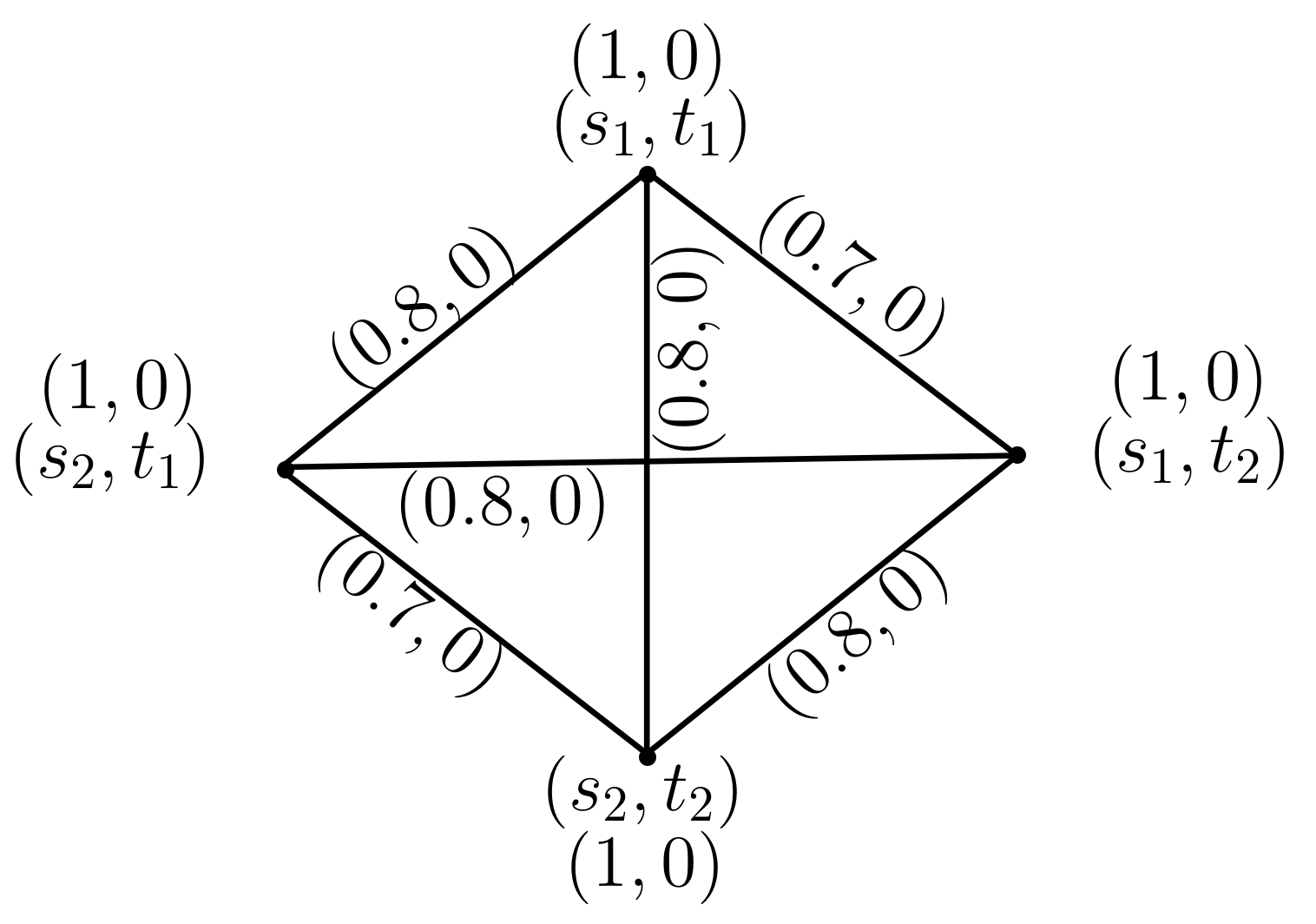
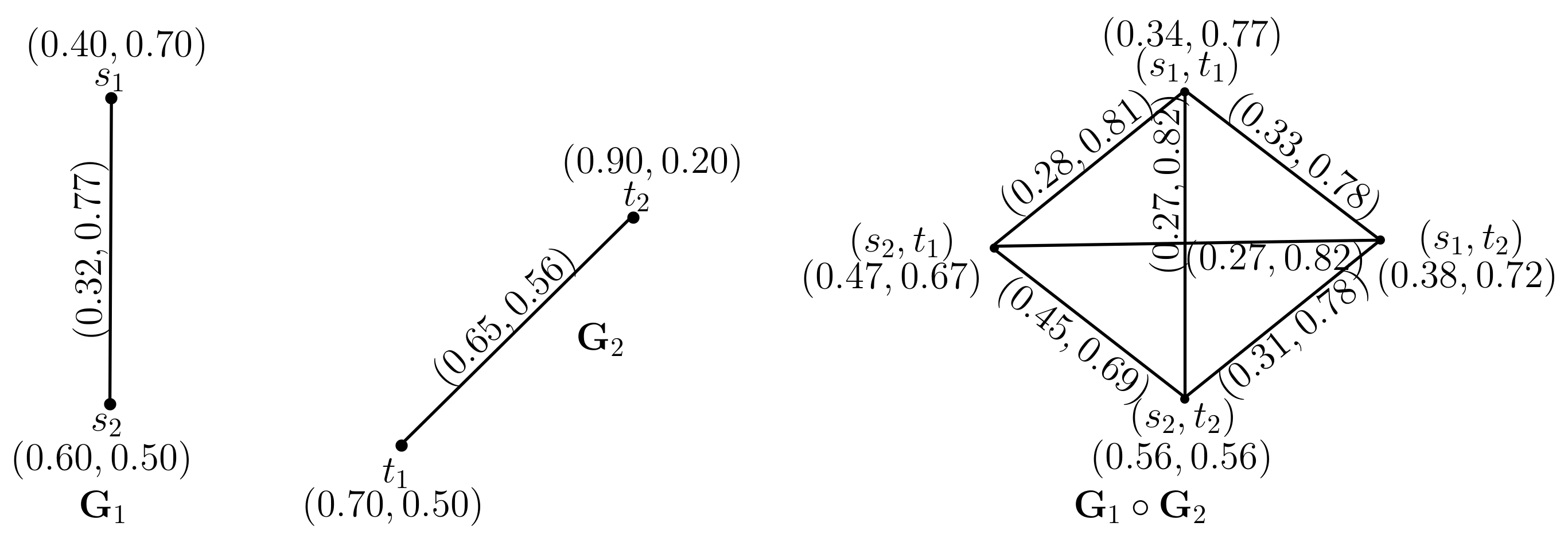
2.5. Composition of Pythagorean Dombi Fuzzy Graphs
- (i)
- for all
- (ii)
- for all and
- (iii)
- for all and
- (iv)
- for all and
3. Numerical Approach
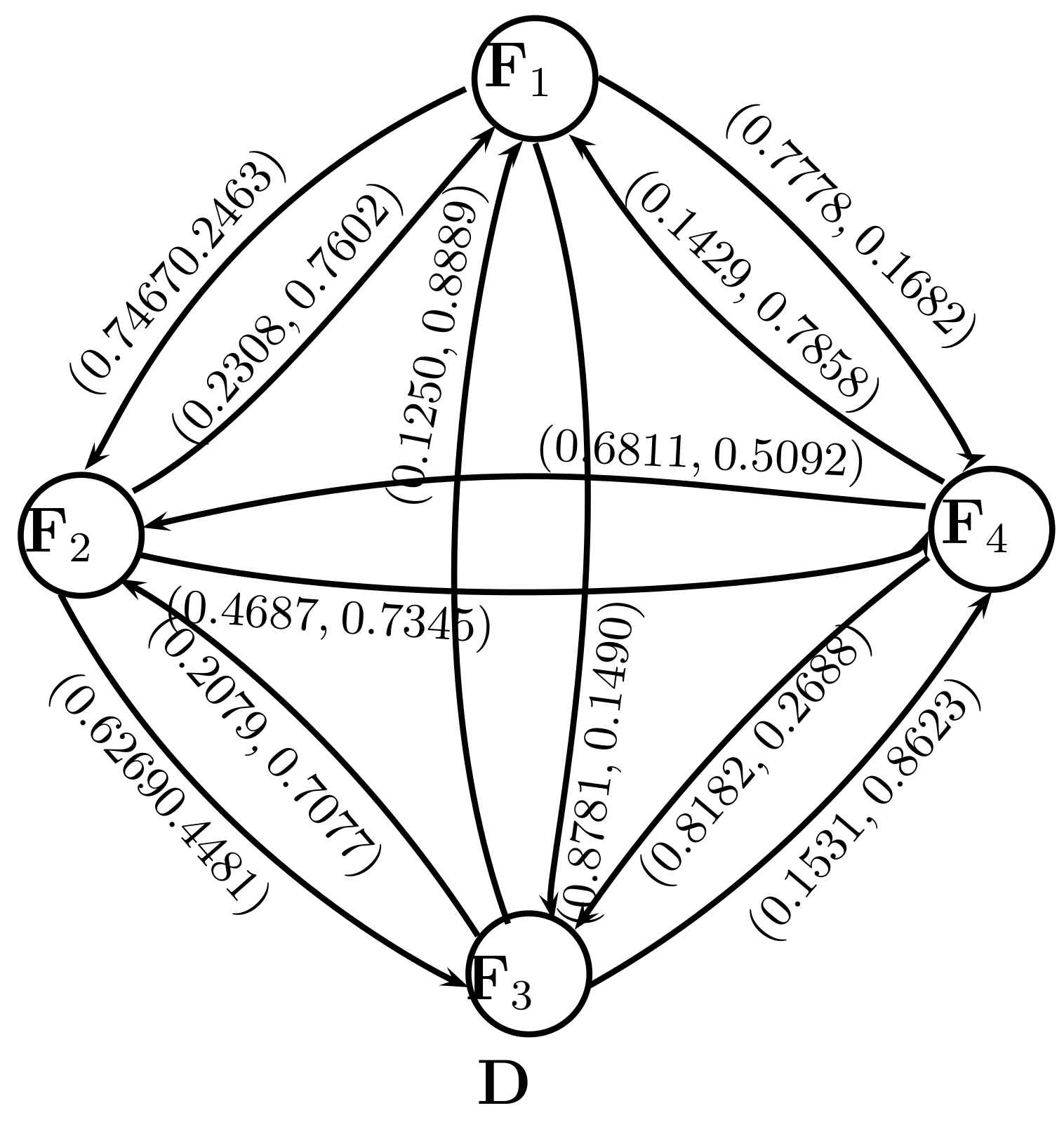
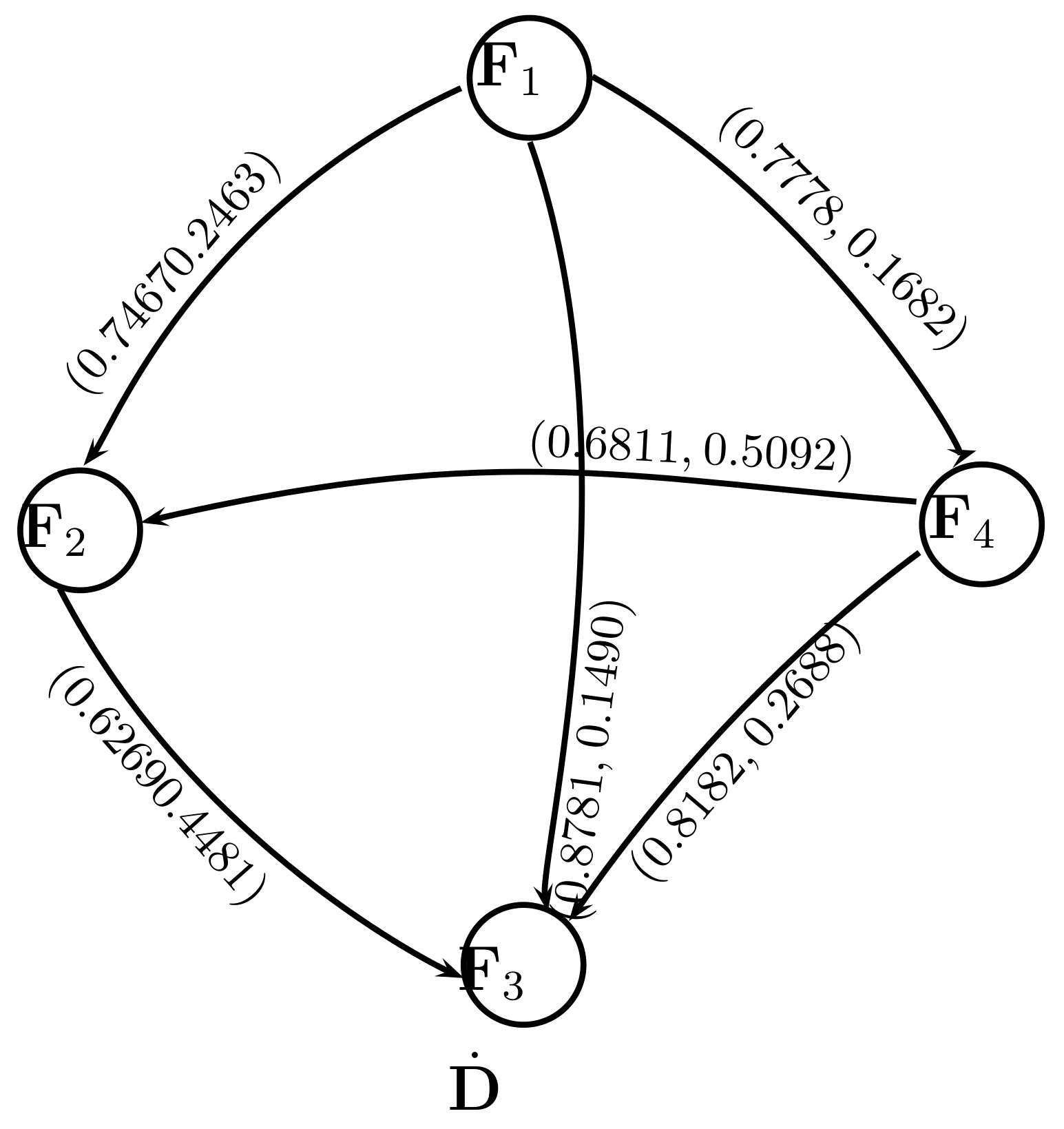
3.1. Selection of a Leading Textile Industry
- ;
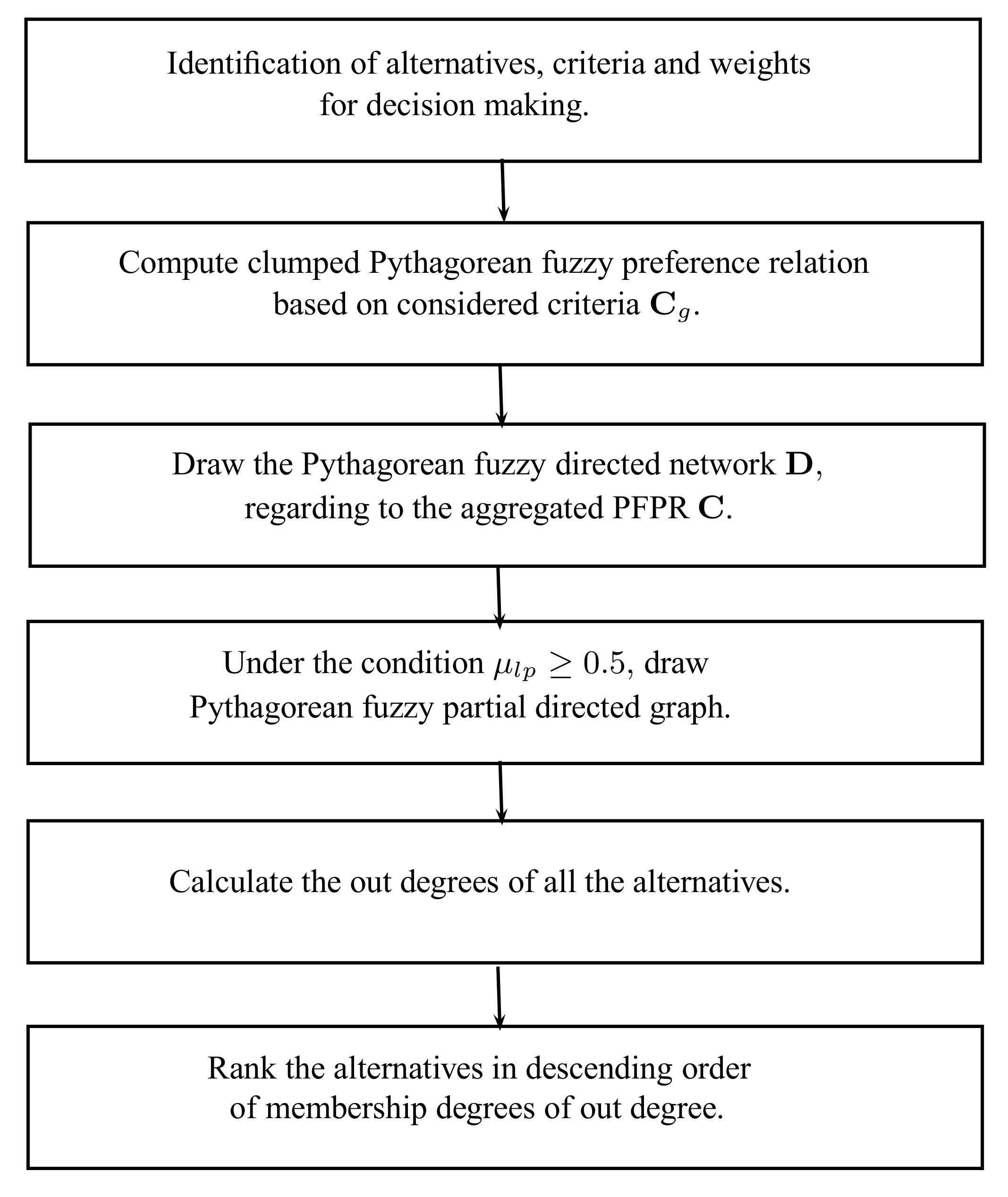
| Algorithm 1 The algorithm for the selection of a leading textile industry. |
| INPUT: A discrete set of feasible alternatives a set of conflicting criteria in order to achieve the target with weight vector , and construction of PFPR corresponding to each considered criteria. OUTPUT: The selection of the optimal alternative.
|
3.2. Comparative Analysis
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Hamacher, H. On Logical Aggregations of Non-Binar Explicit Decision Criteria; Rita, G., Ed.; Fischer Verlag: Frankfurt, Germany, 1978. [Google Scholar]
- Kuwagaki, A. Sur l’équation fonctionnelle f(x + y) = R{f(x), f(y)}. Mem. Coll. Sci. Univ. Kyoto Ser. A Math. 1950, 26, 139–144. Available online: https://projecteuclid.org/download/pdf_1/euclid.kjm/1250777986 (accessed on 13 December 2019). [CrossRef]
- Menger, K. Statistical metrics. J. Natl. Acad. Sci. 1942, 28, 535–537. [Google Scholar] [CrossRef] [PubMed]
- Schweizer, B.; Sklar, S. Probabilistic Metric Spaces; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Alsina, C.; Trillas, E.; Valverde, L. On some logical connectives for fuzzy sets theory. J. Math. Anal. Appl. 1983, 93, 15–26. [Google Scholar] [CrossRef]
- Klement, P.E.; Mesiar, R.; Pap, E. Triangular Norms; Kluwer Academic: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Hamacher, H. Logical combinations of fuzzy statements and their relative valuation functions. Cybern. Syst. Res. 1978, 3, 276–288. [Google Scholar]
- Dubois, D.; Ostasiewicz, W.; Prade, H. Fuzzy Sets: History and Basic Notions; Springer: Boston, MA, USA, 2000. [Google Scholar]
- Rosenfeld, A. Fuzzy graphs. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Zadeh, L.A., Fu, K.S., Shimura, M., Eds.; Academic Press: Cambridge, MA, USA, 1975; pp. 77–95. [Google Scholar]
- Mordeson, J.N.; Peng, C.S. Operations on fuzzy graphs. Inf. Sci. 1994, 79, 159–170. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Shannon, A.; Atanassov, K.T. A first step to a theory of intuitioistic fuzzy graphs. In Proceedings of the First Workshop on Fuzzy Based Expert Systems, Sofia, Bulgaria, 28–30 September 1994; pp. 59–61. [Google Scholar]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the Joint IFSA World Congress and NAFIPS Annual Meeting, Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multi-criteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z. Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Some results for Pythagorean fuzzy sets. Int. J. Intell. Syst. 2015, 30, 1133–1160. [Google Scholar] [CrossRef]
- Akram, M.; Dudek, W.A.; Ilyas, F. Group decision-making based on Pythagorean fuzzy TOPSIS method. Int. J. Intell. Syst. 2019. [Google Scholar] [CrossRef]
- Akram, M.; Ilyas, F.; Garg, H. Multi-criteria group decision making based on ELECTRIC I method in Pythagorean fuzzy information. Soft Comput. 2019. [Google Scholar] [CrossRef]
- Rangasamy, P.; Palaniappan, N. Some operations on intuitionistic fuzzy sets of second type. Notes Intuitionistic Fuzzy Sets 2003, 10, 1–19. [Google Scholar]
- Ren, P.; Xu, Z.; Gou, X. Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl. Soft Comput. 2016, 42, 246–259. [Google Scholar] [CrossRef]
- Peng, X.; Selvachandran, G. Pythagorean fuzzy set: State of the art and future directions. Artifical Intell. Rev. 2017. [Google Scholar] [CrossRef]
- Garg, H. A new exponential operational laws and their aggregation operators of interval-valued Pythagorean fuzzy information. Int. J. Intell. Syst. 2018, 33, 653–683. [Google Scholar] [CrossRef]
- Garg, H. Some methods for strategic decision-making problems with immediate probabilities in Pythagorean fuzzy environment. Int. J. Intell. Syst. 2018, 33, 687–712. [Google Scholar] [CrossRef]
- Garg, H. Linguistic Pythagorean fuzzy sets and its applications in multi attribute decision making process. Int. J. Intell. Syst. 2018, 33, 1234–1263. [Google Scholar] [CrossRef]
- Garg, H. Hesitant Pythagorean fuzzy sets and their aggregation operators in multiple-attribute decision-making. Int. J. Uncertain. Quantif. 2018, 8, 267–289. [Google Scholar] [CrossRef]
- Garg, H. A novel correlation coefficients between Pythagorean fuzzy sets and its applications to decision-making processes. Int. J. Intell. Syst. 2016, 31, 1234–1253. [Google Scholar] [CrossRef]
- Naz, S.; Ashraf, S.; Akram, M. A novel approach to decision-making with Pythagorean fuzzy information. Mathematics 2018, 6, 95. [Google Scholar] [CrossRef]
- Verma, R.; Merigo, J.M.; Sahni, M. Pythagorean fuzzy graphs: Some results. arXiv 2018, arXiv:1806.06721v1. [Google Scholar]
- Akram, M.; Naz, S. Energy of Pythagorean fuzzy graphs with applications. Mathematics 2018, 6, 136. [Google Scholar] [CrossRef]
- Akram, M.; Habib, A.; Ilyas, F.; Dar, J.M. Specific types of Pythagorean fyzzy graphs and application to decision-making. Math. Comput. Appl. 2018, 23, 42. [Google Scholar] [CrossRef]
- Akram, M.; Dar, J.M.; Naz, S. Certain graphs under Pythagorean fuzzy environment. Complex Intell. Syst. 2019, 5, 127–144. [Google Scholar] [CrossRef]
- Akram, M.; Dar, J.M.; Farooq, A. Planar graphs under Pythagorean fuzzy environment. Mathematics 2018, 6, 278. [Google Scholar] [CrossRef]
- Akram, M.; Ilyas, F.; Saeid, A.B. Certain notions of Pythagorean fuzzy graphs. J. Intell. Fuzzy Syst. 2019, 36, 5857–5874. [Google Scholar] [CrossRef]
- Naz, S.; Rashmanlou, H.; Malik, M.A. Operations on single-valued neutrosophic graphs with application. J. Intell. Fuzzy Syst. 2017, 32, 2137–2151. [Google Scholar] [CrossRef]
- Akram, M.; Habib, A. q-Rung picture fuzzy graphs: A creative view on regularity with applications. J. Appl. Math. Comput. 2019, 61, 235–280. [Google Scholar] [CrossRef]
- Habib, A.; Akram, M.; Farooq, A. q-Rung orthopair fuzzy competition graphs with application in the soil ecosystem. Mathematics 2019, 7, 91. [Google Scholar] [CrossRef]
- Akram, M.; Habib, A.; Koam, A.N. A novel description on edge-regular q-rung picture fuzzy graphs with application. Symmetry 2019, 11, 489. [Google Scholar] [CrossRef]
- Dombi, J. A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst. 1982, 8, 149–163. [Google Scholar] [CrossRef]
- Dombi, J. Towards a general class of operators for fuzzy systems. IEEE Trans. Fuzzy Syst. 2008, 16, 477–484. [Google Scholar] [CrossRef]
- Chen, J.; Ye, J. Some single-valued neutrosophic Dombi weighted aggregation operators for multiple attribute decision-making. Symmetry 2017, 9, 82. [Google Scholar] [CrossRef]
- Shi, L.; Ye, J. Dombi aggregation operators of neutrosophic cubic sets for multiple attribute decision-making. Algorithms 2018, 11, 29. [Google Scholar] [CrossRef]
- Jana, C.; Pal, M.; Wang, J. Bipolar fuzzy Dombi aggregation operators and its application in multiple-attribute decision-making process. J. Ambient Intell. Humaniz. Comput. 2018. [Google Scholar] [CrossRef]
- Liu, P.D.; Liu, J.L.; Chen, S.M. Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J. Oper. Res. Soc. 2018, 69, 1–24. [Google Scholar] [CrossRef]
- He, X. Typhoon disaster assessment based on Dombi hesitant fuzzy information aggregation operators. Nat. Hazards 2018, 90, 1153–1175. [Google Scholar] [CrossRef]
- Akram, M.; Dudek, W.A.; Dar, J.M. Pythagorean Dombi fuzzy aggregation operators with application in multi-criteria decision-making. Int. J. Intell. Syst. 2019. [Google Scholar] [CrossRef]
- Ashraf, S.; Naz, S.; Kerre, E.E. Dombi fuzzy graphs. Fuzzy Inf. Eng. 2018, 10, 58–79. [Google Scholar] [CrossRef]
- Akram, M.; Dar, J.M.; Naz, S. Pythagorean Dombi fuzzy graphs. Complex Intell. Syst. 2019, 1–26. [Google Scholar] [CrossRef]





| Q | ||||
|---|---|---|---|---|
| Q | ||||
|---|---|---|---|---|
| Techniques | Ranking of Alternatives | |
|---|---|---|
| Existing PFWA Technique [16] | ||
| Existing PFWG Technique [16] | ||
| Our Proposed PDFWAA Technique | ||
| Our Proposed PDFWGA Technique |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akram, M.; Mohsan Dar, J.; Shahzadi, S. Decision Making Approach under Pythagorean Dombi Fuzzy Graphs for Selection of Leading Textile Industry. Math. Comput. Appl. 2019, 24, 102. https://doi.org/10.3390/mca24040102
Akram M, Mohsan Dar J, Shahzadi S. Decision Making Approach under Pythagorean Dombi Fuzzy Graphs for Selection of Leading Textile Industry. Mathematical and Computational Applications. 2019; 24(4):102. https://doi.org/10.3390/mca24040102
Chicago/Turabian StyleAkram, Muhammad, Jawaria Mohsan Dar, and Sundas Shahzadi. 2019. "Decision Making Approach under Pythagorean Dombi Fuzzy Graphs for Selection of Leading Textile Industry" Mathematical and Computational Applications 24, no. 4: 102. https://doi.org/10.3390/mca24040102
APA StyleAkram, M., Mohsan Dar, J., & Shahzadi, S. (2019). Decision Making Approach under Pythagorean Dombi Fuzzy Graphs for Selection of Leading Textile Industry. Mathematical and Computational Applications, 24(4), 102. https://doi.org/10.3390/mca24040102





