Comparison of Splitting Methods for Deterministic/Stochastic Gross–Pitaevskii Equation
Abstract
:1. Introduction
- Transport part: a linear diffusion term, which smoothens and transports the soliton, see an example in Reference [3].
- Crank–Nicolson finite-difference (CNFD) scheme, where we deal with the benefit of the conservative finite-difference schemes (CFDS) but, based on the implicit parts, we need more computational time, see Reference [13].
- Time splitting sine pseudo spectral (TSSP) scheme, where we deal with the benefit of the fast computable pseudo spectral schemes but we do not have full energy conservation, see Reference [13].
- Time splitting finite-difference (TSFD) scheme, where we have a mixture (CFDS) and time-splitting schemes, which means that we have mass-conservation and fast numerical schemes, see Reference [13].
- For pure conservative finite difference schemes, which can be extended to stochastic schemes, we can also preserve the random potential, see Reference [12]. However, we have the drawback of more time-consuming numerical methods, while we deal with implicit parts.
- Pure splitting schemes, which decompose the different parts of the stochastic GPE into a deterministic and stochastic part, are simple to implement and very fast, such as with spectral methods, but they have energy conservation and stability problems, see Reference [11].
- Combinations of CFDS and splitting schemes are optimal to deal with both benefits, means fast computational results and at least mass-conservation and average energy conservation, see Section 4.
2. Mathematical Model
- , for , means that we are above the Bose–Einstein condensate temperature. Here, the bosons are normal, such that vanish, see Reference [4];
- , for , means that we are below the Bose–Einstein condensate temperature. Here, we obtain a corresponding definite phase of the BEC order parameter, see Reference [4];
2.1. Weakly Interacting Bosons
2.2. Weakly Interacting Bosons with Multiplicative White Noise
- We consider dilute gas, while we assume that the range of the interatomic forces is much more smaller than the distance between the atoms, which means , where n is the density of the atoms.
- For , we obtain small momenta, such that the scattering amplitude is independent of the energy. Therefore, one could replace it by a low-energy-value, which is determined by the solitary wave with scattering length a.
- We replace the potential with the effective soft potential , which has the same scattering properties and is defined as:where m is the atomic mass. We also replace .
- We transform , such that we skip the chemical potential, see Reference [4].
- The expectation value is given as .
- implies a repulsive interaction, where ,
- implies an attractive interaction, where .
3. Conservation Laws of the GPE for Multicomponents
- Mass conservation, which is given as the square of -norm of the solutionwith , while we define as a constant.
- Impulse conservation, which is given as the impulse functional of the solutionwith , where is the conjugate of u.
- Energy conservation, which is given as the energy functional of the solutionwith , where is the conjugate of .
3.1. Deterministic Case: Conservative Finite Difference Schemes (Multicomponents)
- Mass conservation, which is given as the square of -norm of the solutionwith .
- Impulse conservation, which is given as the impulse functional of the solutionwith , where is the conjugate of u.
- Energy conservation, which is given as the energy functional of the solutionwith .
3.2. Stochastic Case: Conservative Finite Difference Schemes (Multicomponents)
4. Numerical Methods
- Time-splitting spectral (TSSP) schemes, which are fast and numerical efficient schemes but failed in conservation properties, see Reference [14].
- Conservative finite difference schemes (CFDS), which are accurate in conservation of mass, momentum and energy via conservative finite difference schemes, see Reference [8].
- Improved splitting methods with finite difference schemes, such asABA-CN (ABA-Crank–Nicolson) splitting. We combine a time-splitting method for the nonlinear and deterministic/stochastic potential parts with conservation Crank–Nicolson scheme for the spatial parts. Here, we conserve with the ABA-splitting approach (see References [25,26]) the nonlinear and stochastic/deterministic potential parts with the spatial parts, see also Reference [14].
- Improved conservative finite difference schemes, such as ACFDS (asymptotic conservation finite difference scheme). We combine an iterative scheme with the CFDS, such that we gain a semi-implicit scheme and accelerate the solver process, see also Reference [14].
- Scalar case: GPE without multiplicative noise or with or with multiplicative noise is given as:with , and we have applied Dirichlet boundary conditions. Furthermore, we apply , which means the attractive interaction case.For an application of a single soliton, the exact solution is given aswhere , and are the speeds of the density profile and phase profile, see the derivation of the exact solutions in Reference [4].
- Vectorial case: coupled GPE without or with multiplicative noise is given as:where we assume , where we have the boundary conditions , see Reference [13].For simplified coupled GPEs, we also have exact solutions, see Reference [28].
4.1. Scalar Discretization Scheme
4.1.1. Conservative Finite Difference Schemes
4.1.2. Asymptotic Conservative Finite Difference Schemes
- where the starting condition at is .
- where the starting condition at is , we have . The solution is given as .If or , then we are done and go to step 3,else we go to the next iterative-step and we apply and go to step 1.
- If , then we are done,else go to the next time-step and we apply and go to step 1.
4.1.3. ABA(semiCN)
4.1.4. Standard Finite Difference Methods and Standard Splitting Approaches
Splitting Methods with Finite Difference Schemes
- Implicit Euler method:where, we start with .
- CN-method:where, we start with .
- AB splitting (implicit-explicit), where we deal with implicit for the diffusion and explicit time discretisation for the nonlinear term:where we start with .
- AB splitting (explicit-explicit), where we deal with explicit for the diffusion and explicit time discretisation for the nonlinear term:where we start with .
4.1.5. Standard Spectral Methods and Combinations with Splitting and Finite Difference Schemes
Time-Spitting Spectral Method
- Linear part:where we start to apply the Fourier transform for the input and obtain:We apply the Fourier transform to the linear term and obtain the result in the Fourier transformed space and the inverse Fourier transform. We then obtain the result:
- Nonlinear part plus potential and stochastic part:where we obtain an analytical solution, which is given as:where , we apply with W is based on a Wiener process with and is a Gaussian distributed random variable with and . We have .
AB Splitting Methods with Finite Difference and Spectral Schemes
- (1). TSSP Method: A and B are in the spectral version.
- (2). AB splitting: A operator is the nonlinear term with the spectral method for the reaction,B operator is the linear term and is in the FD scheme.
- (3). AB splitting: A operator is the nonlinear term with the FD scheme,B operator is the linear term in spectral method.
- (4). AB splitting: A operator is the nonlinear term with the FD scheme, B operator is the linear term is in FD scheme.
- (1). TSSP Method: A and B are in the spectral version.Algorithm 4.We apply the Time-splitting spectral method as follows:where and . Then, we start again with in step A.
- (2). AB splitting: A operator is the nonlinear term with the spectral method for the reaction,B operator is the linear term and is in the FD scheme.Algorithm 5.We apply the combined FD and spectral method as:whereThen, we start again with in step A.
- (3). AB splitting: A operator is the nonlinear term with the FD scheme, B operator is the linear term in spectral method.Algorithm 6.We apply the Time-splitting spectral method as follows:where and andwhere for with the spatial vector and M are the number of spatial points. Furthermore, is the vector at the grid points for .Then, we start again with in step A.
- (4). AB splitting: A operator is the nonlinear term with the FD scheme, B operator is the linear term is in FD scheme.Algorithm 7.We apply the splitting approach with the FD schemes as:wherewhere with spatial vector and M are the number of spatial points. Furthermore, is the vector at the grid points for .
- (5). ABA(CN) splitting: A operator is the linear term with the FD scheme B operator is the nonlinear term is in spectral methodAlgorithm 8.We apply the ABA-splitting approach with FD schemes and spectral schemes as:wherewhere with spatial vector and M are the number of spatial points. Furthermore, is the vector at the grid points for .
4.2. Vectorial Discretization Scheme
4.2.1. Vectorial Spectral Method
- A-step (collision-step with ):where .
- B-step (diffusion-step with ):whereand ,and .
- A-step (collision-step with ):where .
- Then, we apply , if , we start with and in step 1.), else we are done.
4.2.2. Vectorial ABA-CN Method
5. Numerical Experiments
- Single soliton with exact solution as corresponding solution.
- Collision of two solitons with numerically fine solution as corresponding solution.
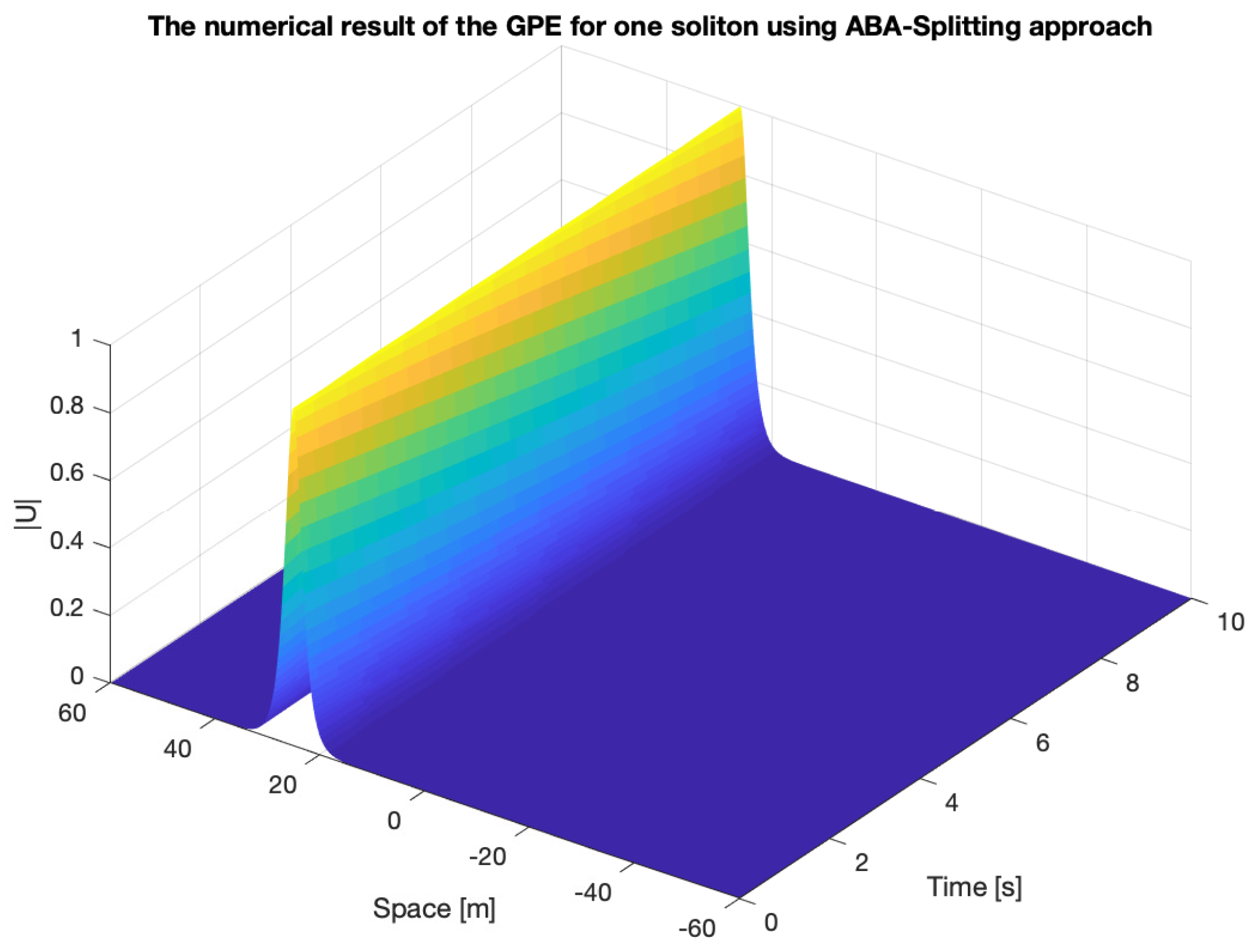
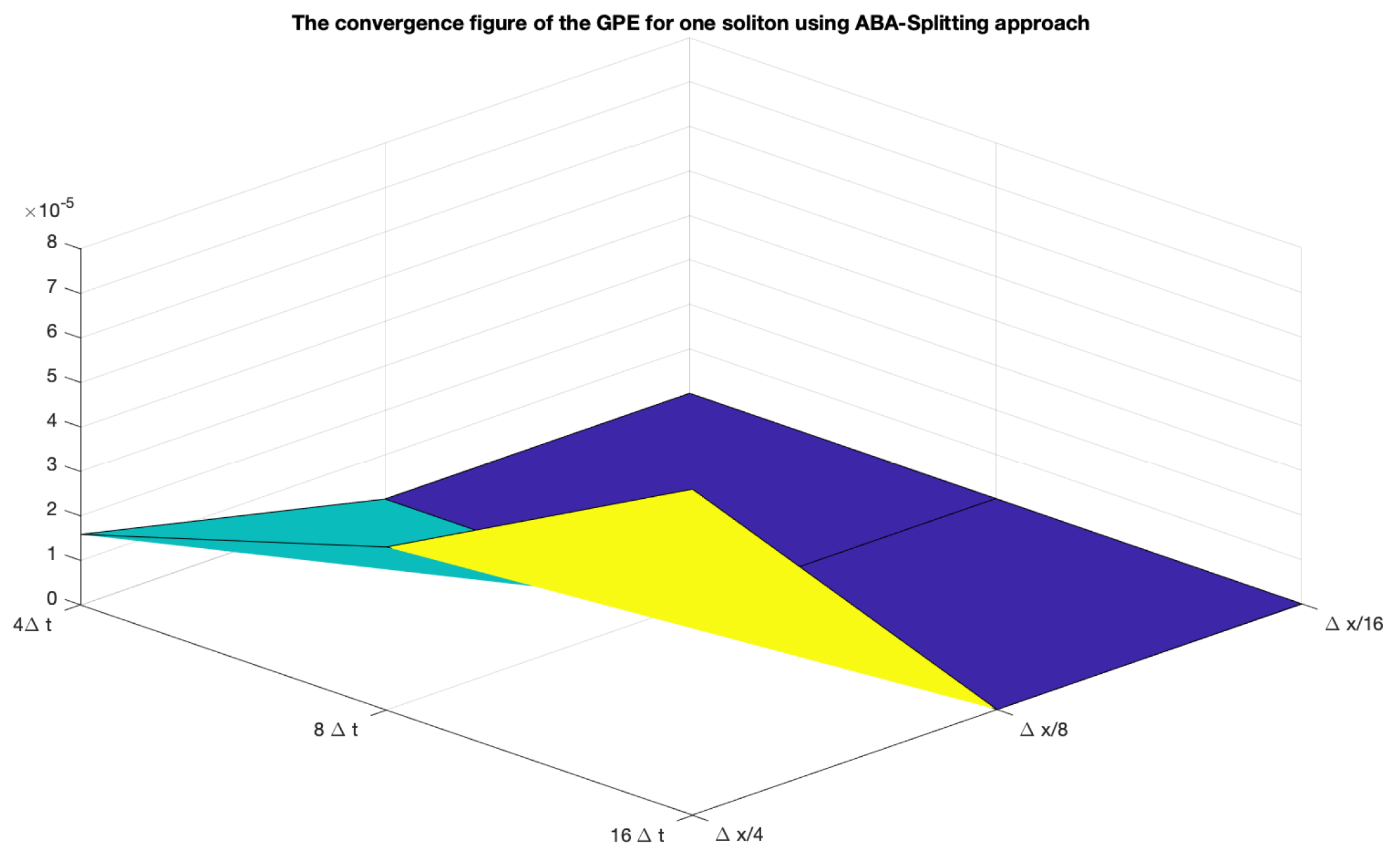
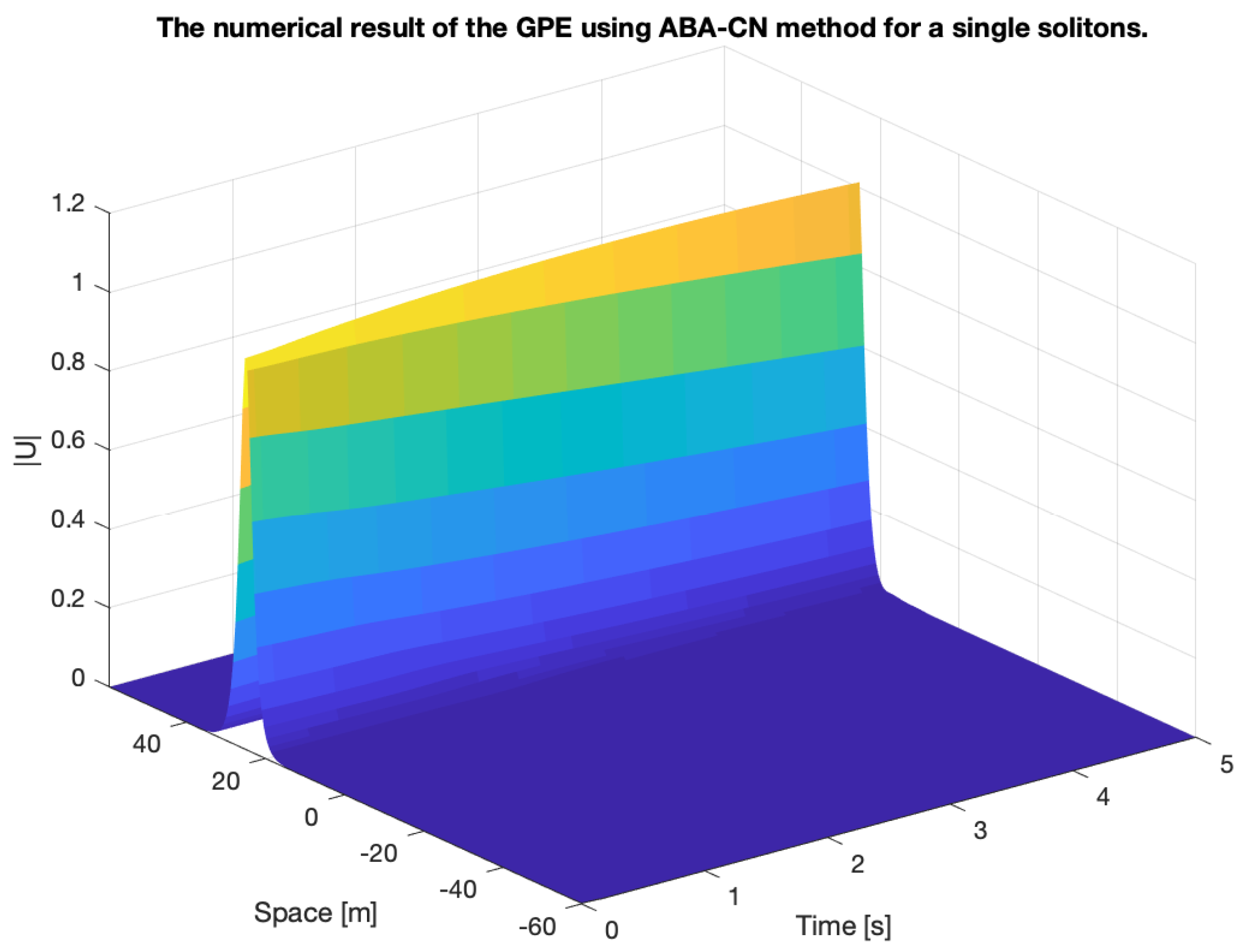
5.1. First Example: GPE with One Soliton
- Implicit Euler method (all operators are done with the implicit method),
- Crank–Nicolson scheme (all operators are done with the CN method),
- AB-splitting:
- -
- Linear operator is done with the Spectral method and nonlinear operator is done with the spectral method,
- -
- Linear operator is done with the FD method and nonlinear operator is done with the spectral method,
- -
- Linear operator is done with the Spectral method and nonlinear operator is done with the FD method,
- -
- Linear operator is done with the FD method and nonlinear operator is done with the FD method.
- ABA-splitting:
- -
- Linear operator is done with the Spectral method and nonlinear operator is done with the spectral method.
- ABA-CN and ABA-iCN:
- -
- Linear operator is done with the finite difference method, while the nonlinear operator is done with the spectral method.
- -
- For the iterative scheme, we apply different iterative steps.
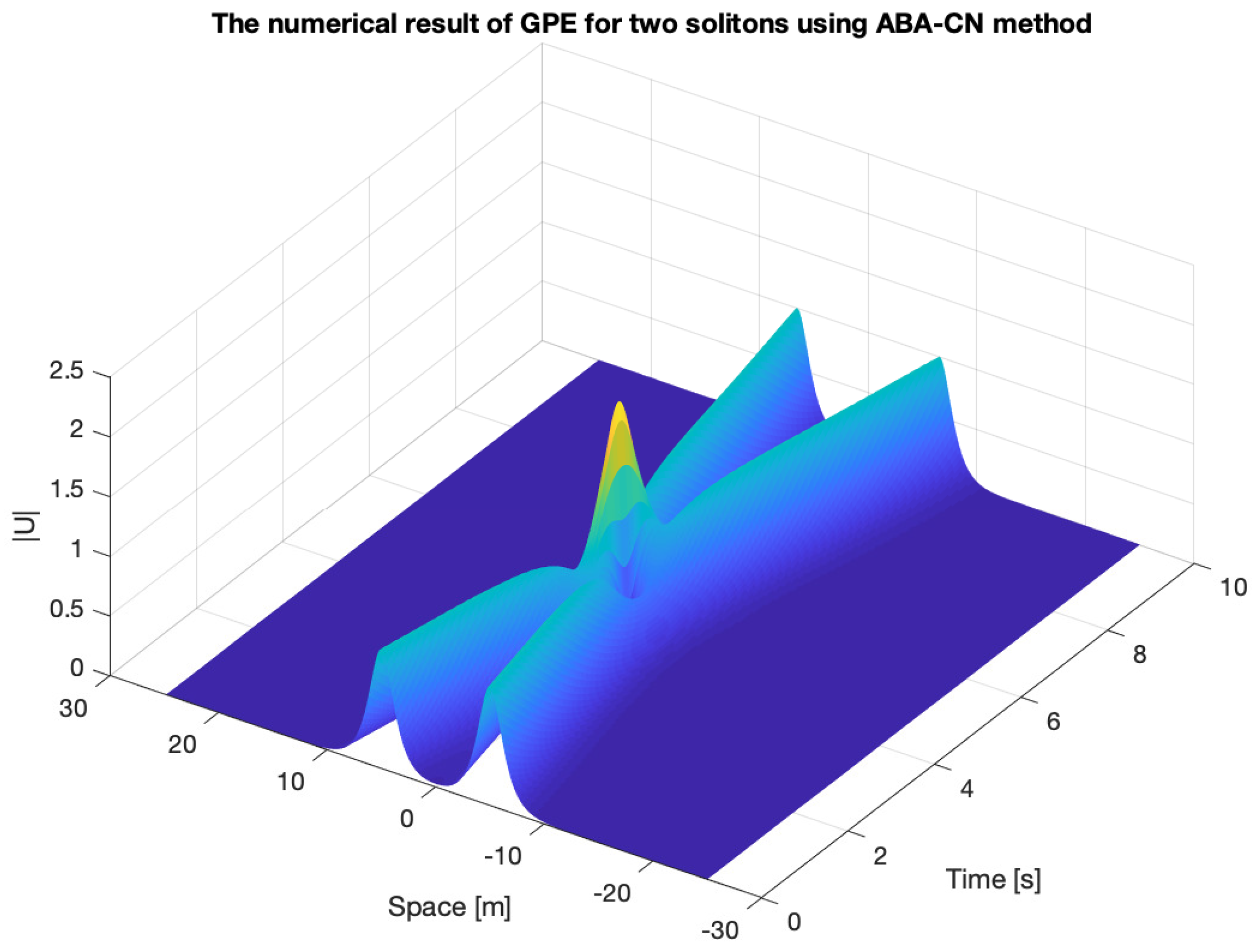
5.2. Second Example: Collision of Two Solitons
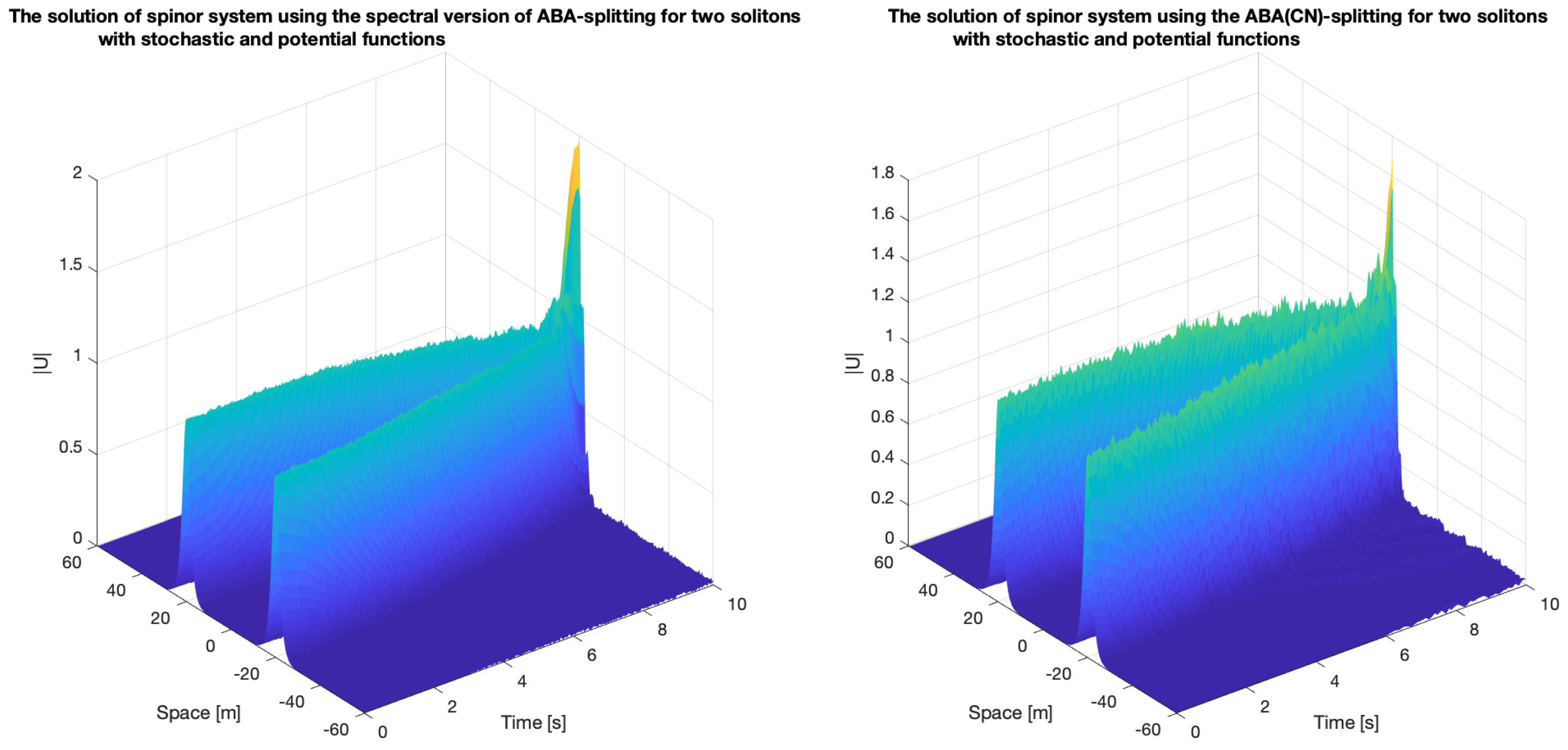
5.3. Spinor System (Coupled GPEs)
- Bright one-soliton:
- Bright two-soliton:
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proof for Continuous Mass-Conservation for the Deterministic Case
Appendix A.2. Proof for Discrete Mass-Conservation for the Deterministic Case
References
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose–Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463–512. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Gammal, A.; Kamchatnov, A.M.; Tomio, L. Dynamics of bright matter wave solitons in a Bose–Einstein condensate. Int. J. Mod. Phys. B 2005, 19, 3415–3473. [Google Scholar] [CrossRef]
- Dauxois, T.; Peyard, M. Physics of Solitons; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Balakrishnan, R.; Satija, I.I. Solitons in Bose–Einstein condensates. Pramana J. Phys. 2011, 77, 929–947. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-Gonzalez, R. Emergent Nonlinear Phenomena in Bose–Einstein Condensates Theory and Experiment; Springer Series on Atomic, Optical, and Plasma Physics; Springer: Heidelberg, Germany; New York, NY, USA, 2008. [Google Scholar]
- Shang, Y. Unveiling robustness and heterogeneity through percolation triggered by random-link breakdown. Phys. Rev. E 2014, 90, 032820. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y. Effect of link oriented self-healing on resilience of networks. J. Stat. Mech. Theory Exp. 2016, 8, 083403. [Google Scholar] [CrossRef]
- Trofimov, V.A.; Peskov, N.V. Comparison of finite difference schemes for the Gross–Pitaevskii equation. Math. Model. Anal. 2009, 14, 109–126. [Google Scholar] [CrossRef]
- Atre, R.; Panigrahi, P.K.; Agarwal, G.S. Class of solitary wave solutions of the one-dimensional Gross–Pitaevskii equation. Phys. Rev. E 2006, 73, 056611. [Google Scholar] [CrossRef] [PubMed]
- Bao, W.; Cai, Y. Mathematical models and numerical methods for spinor Bose–Einstein condensates. Commun. Comput. Phys. 2018, 24, 899–965. [Google Scholar] [CrossRef]
- Bao, W.; Zhang, Y. Dynamical laws of the coupled Gross–Pitaevskii equations for spin-1 Bose–Einstein condensates. Methods Appl. Anal. 2010, 17, 49–80. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, L.; Hong, J. Stochastic multi-symplectic integrator for stochastic nonlinear Schroedinger equation. Commun. Comput. Phys. 2013, 14, 393–411. [Google Scholar] [CrossRef]
- Antoine, X.; Bao, W.; Besse, C. Computational methods for the dynamics of the nonlinear Schrödinger and Gross–Pitaevskii equations. Comput. Phys. Commun. 2013, 184, 2621–2633. [Google Scholar] [CrossRef]
- Bao, W.; Cai, Y. Mathematical theory and numerical methods for Bose–Einstein condensation. Kinet. Relat. Mod. 2013, 6, 1–135. [Google Scholar] [CrossRef]
- Geiser, J. Iterative splitting method as almost asymptotic symplectic integrator for stochastic nonlinear Schrödinger equation. AIP Conf. Proc. 2017, 1863, 560005. [Google Scholar]
- Geiser, J. Multicomponent and Multiscale Systems: Theory, Methods, and Applications in Engineering; Springer: Cham, Switzerland; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2016. [Google Scholar]
- Geiser, J.; Nasari, A. Simulation of Multiscale Schroedinger Equation with Extrapolated Splitting Approaches. In Proceedings of the AIP Conference, ICNAAM 2018, Rhodes, Greece, 13–18 September 2018. [Google Scholar]
- Ho, T.-L. Spinor Bose condensates in optical traps. Phys. Rev. Lett. 1998, 81, 742–745. [Google Scholar] [CrossRef]
- Takhtajan, L.A. Quantum Mechanics for Mathematicians; Graduate Series in Mathematics; American Mathematical Society: Providence, RI, USA, 2008; Volume 95. [Google Scholar]
- Bao, W.; Tang, Q.; Xu, Z. Numerical methods and comparison for computing dark and bright solitons in the nonlinear Schrödinger equation. J. Comput. Phys. 2013, 235, 423–445. [Google Scholar] [CrossRef]
- Bao, W.; Jaksch, D.; Markowich, P.A. Numerical solution of the Gross–Pitaevskii equation for Bose–Einstein condensation. J. Comput. Phys. 2003, 187, 318–342. [Google Scholar] [CrossRef]
- Min, B.; Li, T.; Rosenkranz, M.; Bao, W. Subdiffusive spreading of a Bose–Einstein condensate in random potentials. Phys. Rev. A 2012, 86, 053612. [Google Scholar] [CrossRef]
- Bao, W.; Cai, Y. Ground states of two-component Bose–Einstein condensates with an internal atomic Josephson junction. East Asia J. Appl. Math. 2011, 1, 49–81. [Google Scholar] [CrossRef]
- Bao, W.; Cai, Y.; Wang, H. Efficient numerical methods for computing ground states and dynamics of dipolar Bose–Einstein condensates. J. Comput. Phys. 2010, 229, 7874–7892. [Google Scholar] [CrossRef]
- Strang, G. On the construction and comparison of differential schemes. SIAM J. Numer. Anal. 1968, 5, 506–517. [Google Scholar] [CrossRef]
- Geiser, J. Iterative Splitting Methods for Differential Equations; Numerical Analysis and Scientific Computing Series; Taylor & Francis Group: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2011. [Google Scholar]
- McLachlan, R.I.; Quispel, G.R.W. Splitting methods. Acta Numer. 2002, 11, 341–434. [Google Scholar] [CrossRef]
- Yan, Z.; Chow, K.W.; Malomed, B.A. Exact stationary wave patterns in three coupled nonlinear Schrödinger/Gross–Pitaevskii equations. Chaos Solitons Fract. 2009, 42, 3013–3019. [Google Scholar] [CrossRef]
- Brigham, E.O. The Fast Fourier Transform: An Introduction to Its Theory and Application; Prentice Hall: Upper Saddle River, NJ, USA, 1973. [Google Scholar]
| 1.593 | 4.216 | 2.211 | |
| 3.67 | 9.28 | 4.663 | |
| 7.34 | 1.855 | 9.326 |
| 1.312 | 3.3337 | 1.6673 | |
| 3.667 | 9.2733 | 4.6629 | |
| 7.334 | 1.8547 | 9.3258 |
| T = 2.5 | T = 5 | T = 7.5 | T = 10 | |
|---|---|---|---|---|
| Implicit Euler method | 0.8313 | 1.6785 | 2.1124 | 2.9281 |
| Crank–Nicolson scheme | 2.0496 | 3.8930 | 5.7764 | 7.1148 |
| AB-splitting: A and B operators are spectral | 0.0271 | 0.0486 | 0.0785 | 0.1007 |
| AB-splitting: A Spectral, B FD | 1.8159 | 3.2140 | 4.6932 | 5.7207 |
| AB-splitting: A FD, B Spectral | 0.0466 | 0.0551 | 0.0668 | 0.0962 |
| AB-splitting: A FD, B FD | 2.4798 | 3.8211 | 5.7146 | 7.0136 |
| ABA-splitting | 0.0352 | 0.0632 | 0.0940 | 0.1264 |
| BAB-splitting | 0.0343 | 0.0624 | 0.1003 | 0.1281 |
| ABA(CN)-splitting | 0.9762 | 1.9774 | 2.6190 | 3.2304 |
| ABA(semiCN)-splitting | 2.5906 | 4.5933 | 6.5765 | 8.5612 |
| T = 2.5 | T = 5 | T = 7.5 | T = 10 | |
|---|---|---|---|---|
| Implicit Euler method | 0.8977 | 1.9084 | 2.4616 | 2.6552 |
| Crank–Nicolson scheme | 0.9165 | 2.0208 | 2.7069 | 2.9975 |
| AB-splitting: A and B operators are spectral | 0.0330 | 0.0396 | 0.0420 | 0.0488 |
| AB-splitting: A Spectral, B FD | 0.9443 | 2.0468 | 2.7054 | 2.9648 |
| AB-splitting: A FD, B Spectral | 0.1333 | 0.3893 | 0.7650 | 1.2144 |
| AB-splitting: A FD, B FD | 0.9165 | 2.0208 | 2.7069 | 2.9975 |
| ABA-splitting | 0.0057 | 0.0080 | 0.0097 | 0.0111 |
| BAB-splitting | 0.0057 | 0.0080 | 0.0097 | 0.0111 |
| ABA(CN)-splitting | 0.9178 | 2.0201 | 2.6952 | 2.9630 |
| ABA(semiCN)-splitting | 0.9174 | 2.0208 | 2.7003 | 2.9740 |
| T = 2.5 | T = 5 | T = 7.5 | T = 10 | |
|---|---|---|---|---|
| Implicit Euler method | 2.4928 | 3.5601 | 4.9031 | 6.2648 |
| Crank–Nicolson scheme | 4.5648 | 8.8923 | 13.8926 | 15.9353 |
| AB-splitting: A and B operators are spectral | 0.0342 | 0.0632 | 0.1004 | 0.1429 |
| AB-splitting: A Spectral, B FD | 3.5292 | 6.7374 | 9.7683 | 12.9375 |
| AB-splitting: A FD, B Spectral | 0.0349 | 0.0678 | 0.0965 | 0.1380 |
| AB-splitting: A FD, B FD | 4.4182 | 8.5995 | 12.3086 | 16.4472 |
| ABA-splitting | 0.0445 | 0.0858 | 0.1408 | 0.1989 |
| BAB-splitting | 0.0425 | 0.0789 | 0.1524 | 0.1931 |
| ABA(CN)-splitting | 2.1821 | 4.4567 | 6.3876 | 7.7092 |
| ABA(semiCN)-splitting | 6.1543 | 10.5217 | 16.1007 | 19.6879 |
| T = 2.5 | T = 5 | T = 7.5 | T = 10 | |
|---|---|---|---|---|
| Implicit Euler method | 1.0605 | 4.6478 | 5.0486 | 5.1546 |
| Crank–Nicolson scheme | 1.0548 | 4.3745 | 9.1666 | 19.2207 |
| AB-splitting: A and B operators are spectral | 0.0866 | 0.1059 | 0.1501 | 0.1754 |
| AB-splitting: A Spectral, B FD | 0.7579 | 1.8421 | 2.4654 | 2.8003 |
| AB-splitting: A FD, B Spectral | 1.1001 | 6.0412 | 49.3173 | 114.0526 |
| AB-splitting: A FD, B FD | 1.0548 | 4.3745 | 9.1666 | 19.2207 |
| ABA-splitting | 0.0296 | 0.0320 | 0.0410 | 0.0453 |
| BAB-splitting | 0.0295 | 0.0314 | 0.0405 | 0.0447 |
| ABA(CN)-splitting | 0.7024 | 1.8489 | 2.4949 | 2.7952 |
| ABA(semiCN)-splitting | 0.8599 | 2.6645 | 2.7771 | 2.7894 |
| T = 2.5 | T = 5 | T = 7.5 | T = 10 | |
|---|---|---|---|---|
| ABA spectral method | 0.19117 | 0.38064 | 0.42071 | 0.54968 |
| ABA (CN) method | 5.4207 | 10.8046 | 15.4196 | 19.7318 |
| T = 2.5 | T = 5 | T = 7.5 | T = 10 | |
|---|---|---|---|---|
| ABA spectral method U1 | 93.1781 | 117.8641 | 131.5981 | 135.3722 |
| ABA spectral method U2 | 93.1308 | 117.9896 | 131.533 | 135.7863 |
| ABA spectral method U1 + U2 | 186.2656 | 235.8055 | 263.0822 | 271.0522 |
| ABA (CN) method U1 | 92.9585 | 118.1392 | 132.451 | 136.1172 |
| ABA (CN) method U2 | 93.0261 | 118.1044 | 132.4937 | 136.3657 |
| ABA (CN) method U1 + U2 | 185.8951 | 235.9406 | 264.3351 | 271.7702 |
| T = 2.5 | T = 5 | T = 7.5 | T = 10 | |
|---|---|---|---|---|
| ABA spectral method | 0.1878 | 0.37595 | 0.43802 | 0.53914 |
| ABA (CN) method | 5.3777 | 10.7832 | 15.582 | 19.9661 |
| T = 2.5 | T = 5 | T = 7.5 | T = 10 | |
|---|---|---|---|---|
| ABA spectral method U1 | 22.6749 | 68.1927 | 95.2834 | 113.0119 |
| ABA spectral method U2 | 22.8794 | 68.014 | 95.5527 | 113.0438 |
| ABA spectral method U1 + U2 | 32.2117 | 96.2128 | 134.6855 | 158.9924 |
| ABA (CN) method U1 | 22.6264 | 66.7965 | 93.5702 | 110.1788 |
| ABA (CN) method U2 | 22.1765 | 66.535 | 93.7642 | 110.2908 |
| ABA (CN) method U1 + U2 | 31.6815 | 94.2804 | 132.3647 | 155.4301 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geiser, J.; Nasari, A. Comparison of Splitting Methods for Deterministic/Stochastic Gross–Pitaevskii Equation. Math. Comput. Appl. 2019, 24, 76. https://doi.org/10.3390/mca24030076
Geiser J, Nasari A. Comparison of Splitting Methods for Deterministic/Stochastic Gross–Pitaevskii Equation. Mathematical and Computational Applications. 2019; 24(3):76. https://doi.org/10.3390/mca24030076
Chicago/Turabian StyleGeiser, Jürgen, and Amirbahador Nasari. 2019. "Comparison of Splitting Methods for Deterministic/Stochastic Gross–Pitaevskii Equation" Mathematical and Computational Applications 24, no. 3: 76. https://doi.org/10.3390/mca24030076
APA StyleGeiser, J., & Nasari, A. (2019). Comparison of Splitting Methods for Deterministic/Stochastic Gross–Pitaevskii Equation. Mathematical and Computational Applications, 24(3), 76. https://doi.org/10.3390/mca24030076






