Hedging Crop Yields Against Weather Uncertainties—A Weather Derivative Perspective
Abstract
:1. Introduction
2. Crop Yield–Weather Model and Feature Importance for Weather Derivatives
2.1. Machine Learning Ensemble Technique for Weather-Crop Yield Model
- If the long-term average crop yield is smaller than or equal to the present years crop yield , then there is an increase in crop yield; else:
- If the long-term average crop yield is greater than the present years crop yield , then there is a decrease or loss in crop yield.
2.2. Model Evaluation and Feature Importance
| Algorithm 1:Algorithm of Stacking Ensemble |
| Input: Output: An ensemble classifier H 1 Step 1. Learn base-level classifiers 2 for to N do 3 Learn a base classifier based on T, 4 end for 5 Step 2. Construct new data set from T, 6 for to n do 7 Construct a new data set that contains where 8 end for 9 Step 3. Learn a second-level classifier 10 Learn a new classifier based on the newly constructed data set. 11 Return ) |
3. Temperature-Based Weather Derivatives
3.1. Previous Temperature Dynamics Models
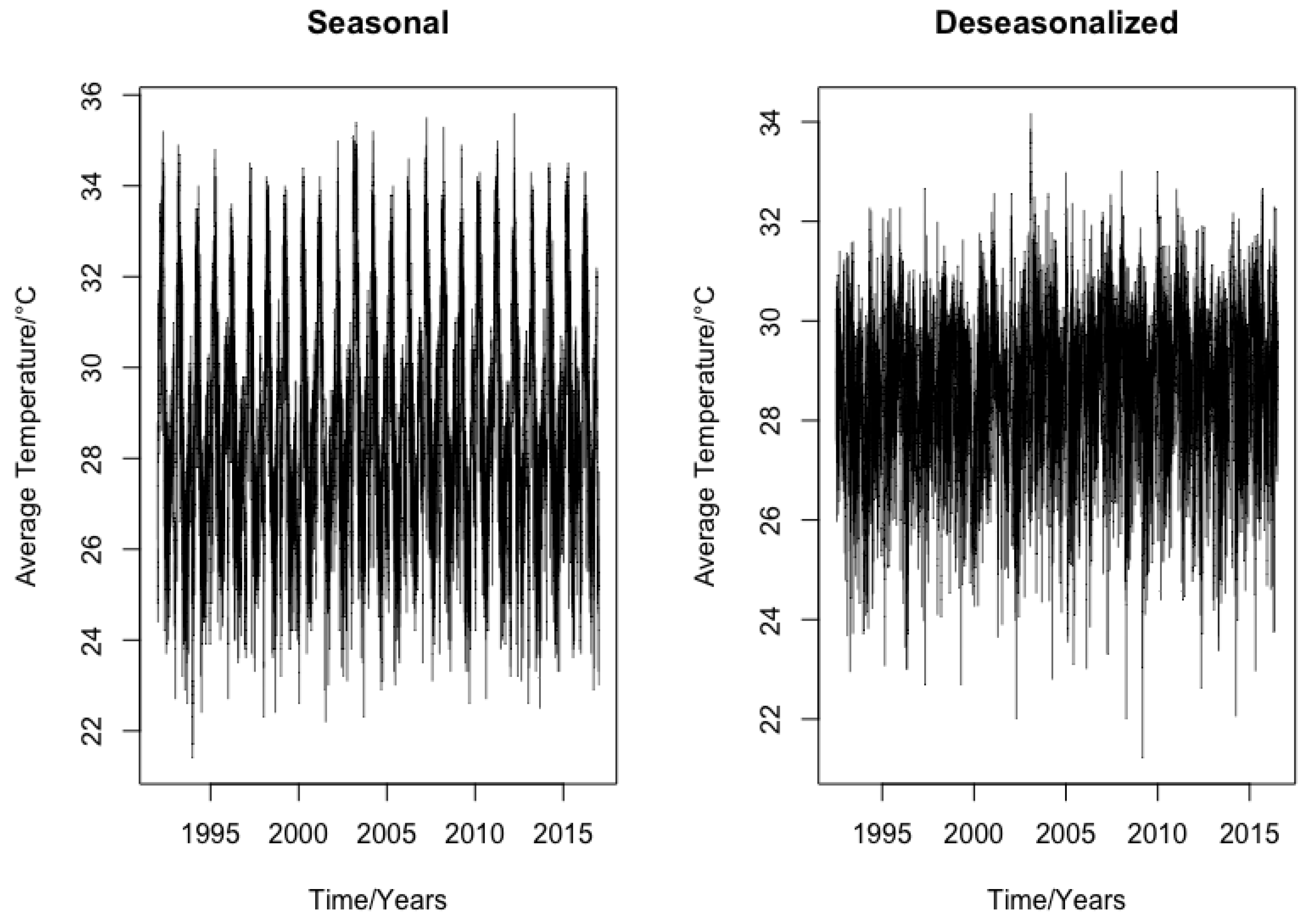
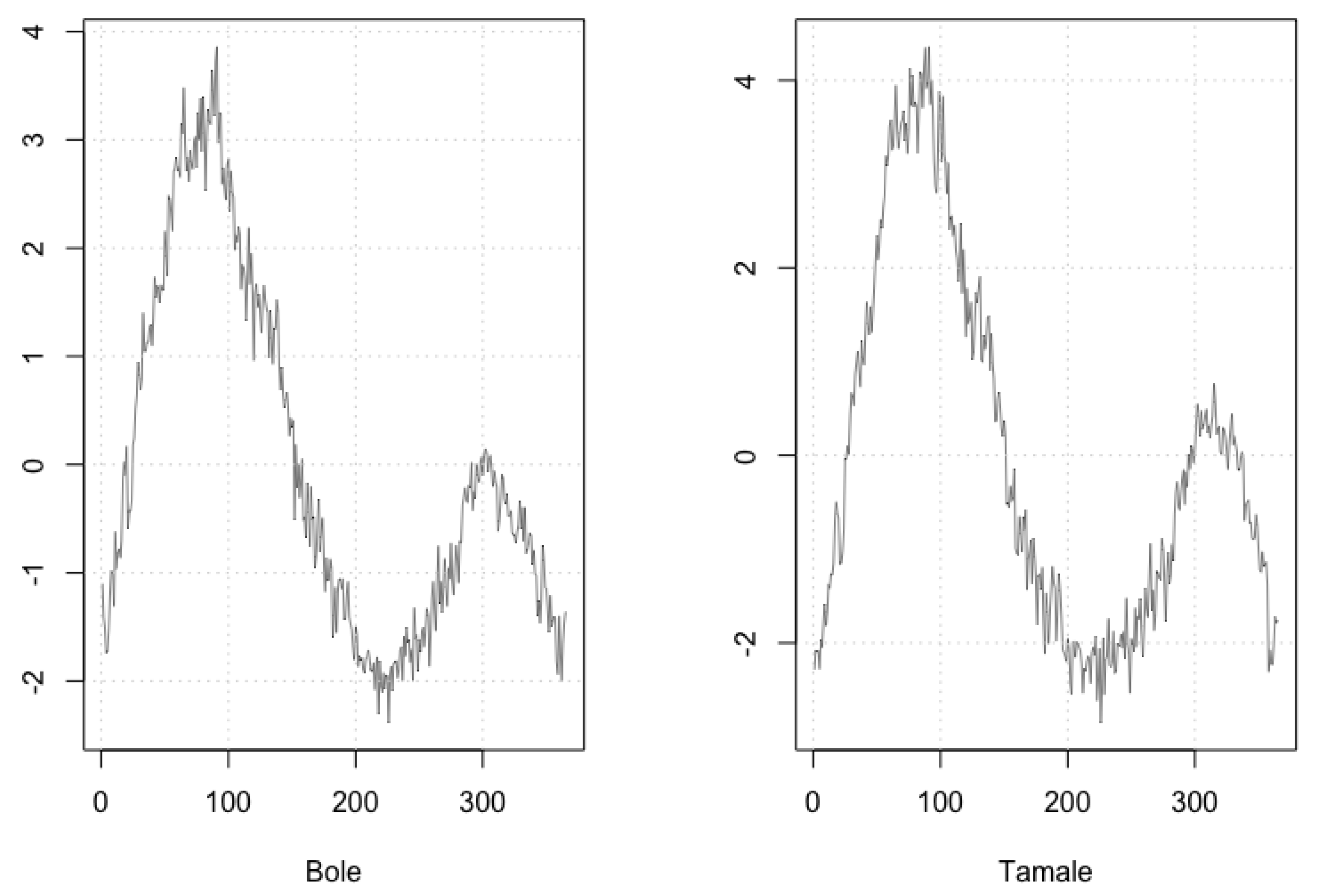
3.2. Daily Average Temperature Data
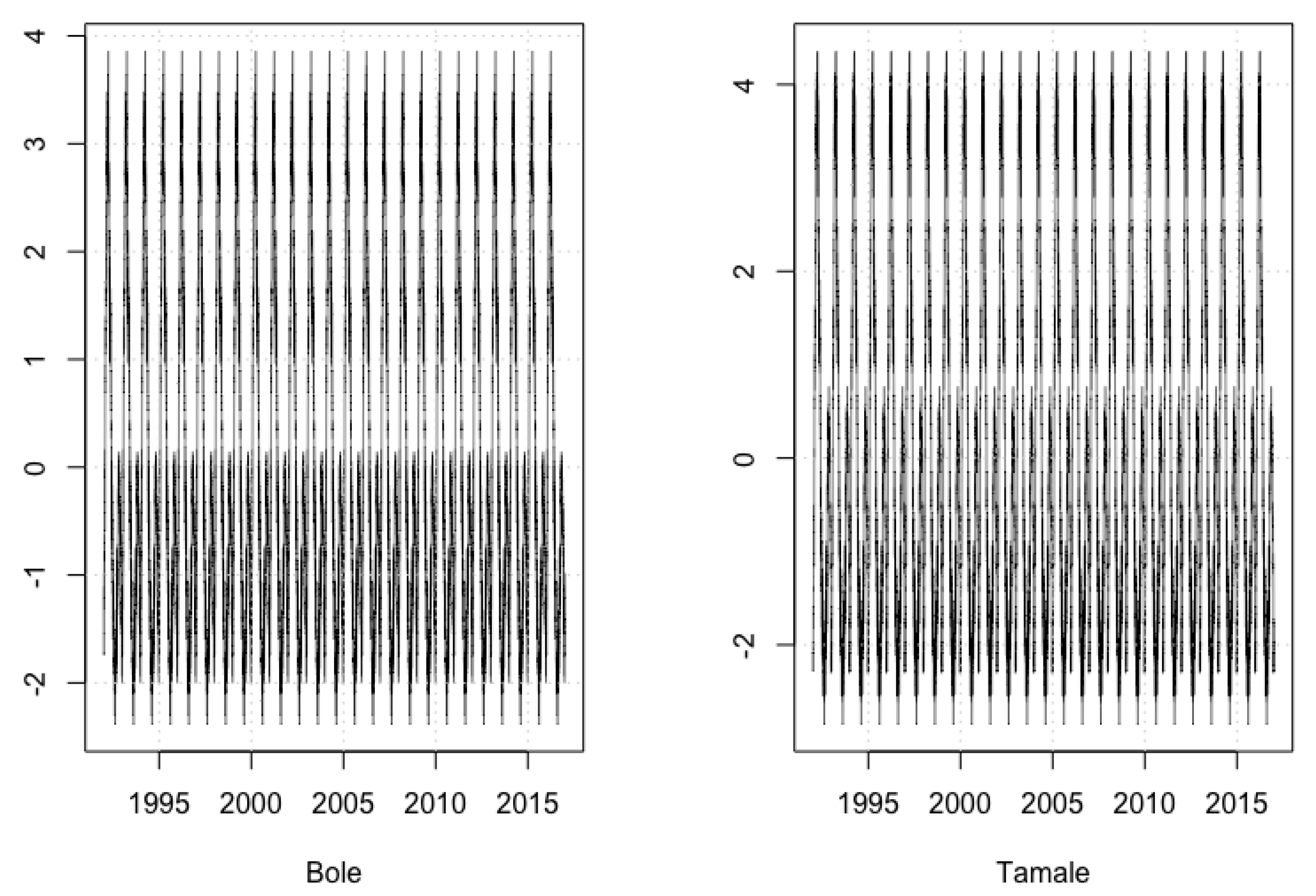
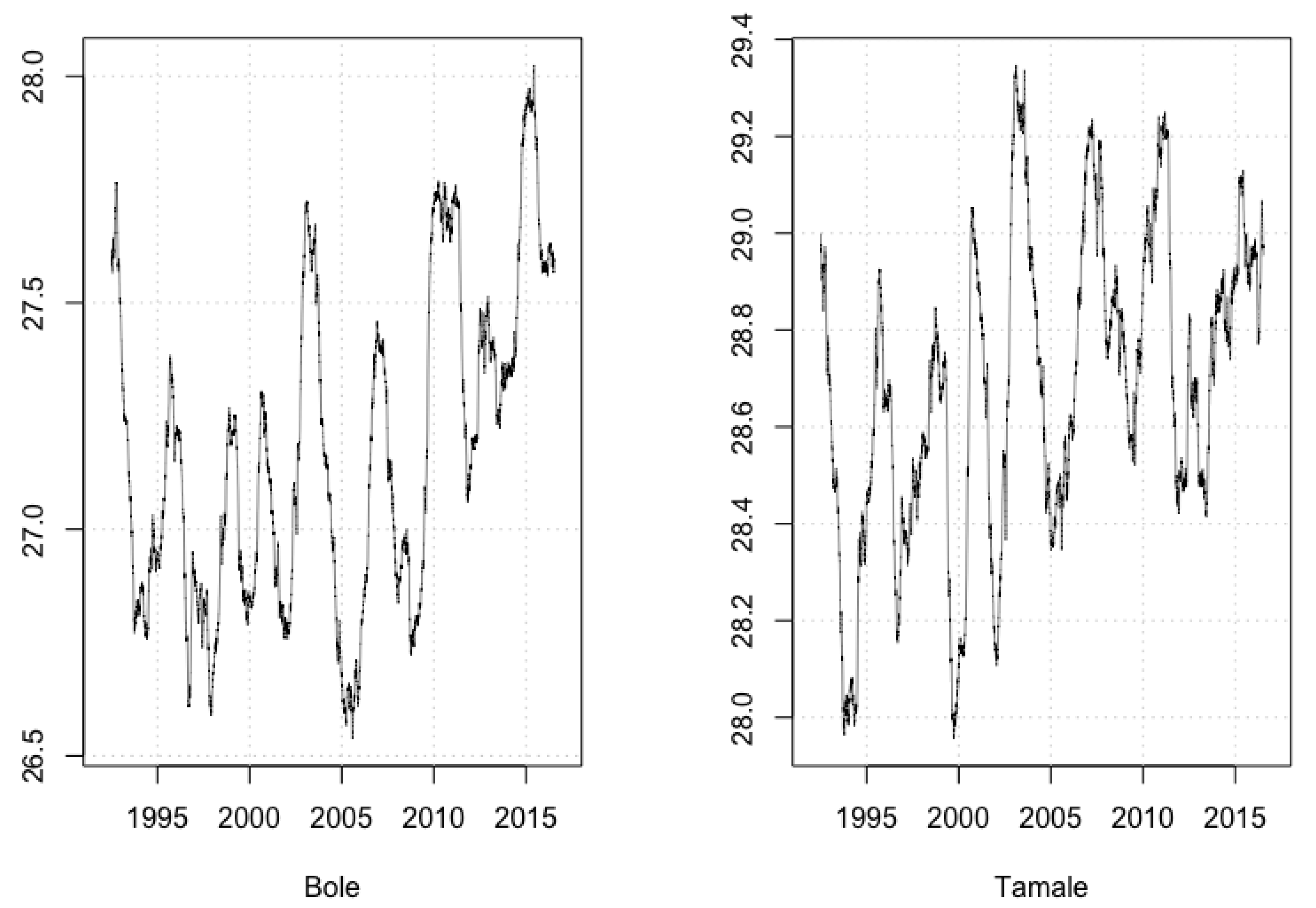
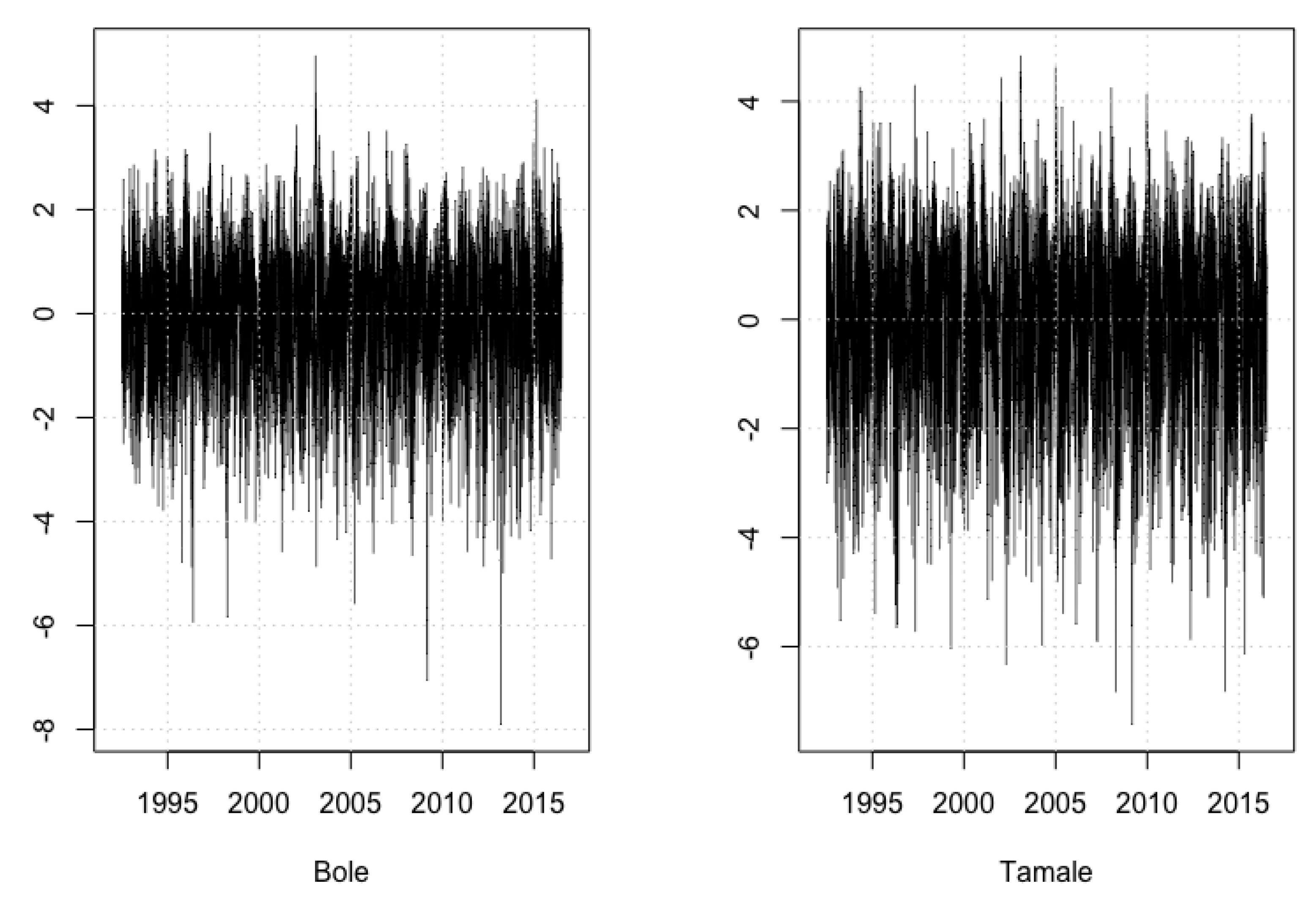
3.3. Stochastic Dynamics of Daily Average Temperature
3.4. Temperature-Based Weather Derivative Pricing
3.4.1. CAT Futures and Options on Futures
3.4.2. GDD Futures and Options on Futures
3.4.3. CAT and GDD Futures on Temperature Basket
3.4.4. Girsanov’s Theorem in
3.4.5. Pricing CAT and GDD Futures on Temperature Basket
4. Discussion and Conclusion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- UNECA. Challenges to agricultural development in Africa. In Economic Report on Africa 2009 Developing African Agriculture Through Regional Value Chains; UNECA: Addis Ababa, Ethiopia, 2009; Available online: https://www.uneca.org/sites/default/files/PublicationFiles/era2009_eng_full.pdf (accessed on 18 July 2019).
- Ibn Musah, A.A.; Du, J.; Bilaliib Udimal, T.; Abubakari Sadick, M. The nexus of weather extremes to agriculture production indexes and the future risk in Ghana. Climate 2018, 6, 86. [Google Scholar] [CrossRef]
- Turvey, C.G. Weather derivatives for specific event risks in agriculture. Rev. Agric. Econ. 2001, 23, 333–351. [Google Scholar] [CrossRef]
- Zong, L.; Ender, M. Spatially-aggregated temperature derivatives: Agricultural risk management in China. Int. J. Financial Stud. 2016, 4, 17. [Google Scholar] [CrossRef]
- Woodard, J.D.; Garcia, P. Basis risk and weather hedging effectiveness. Agric. Finance Rev. 2008, 68, 99–117. [Google Scholar] [CrossRef] [Green Version]
- Rohrer, M. The relevance of basis risk in the weather derivatives market. WIT Trans. Model. Simul. 2004, 38. [Google Scholar] [CrossRef]
- Ritter, M.; Musshoff, O.; Odening, M. Minimizing geographical basis risk of weather derivatives using a multi-site rainfall model. Comput. Econ. 2014, 44, 67–86. [Google Scholar] [CrossRef]
- Spicka, J.; Hnilica, J. A methodical approach to design and valuation of weather derivatives in agriculture. Adv. Meteorol. 2013, 2013, 146036. [Google Scholar] [CrossRef]
- Musshoff, O.; Odening, M.; Xu, W. Management of climate risks in agriculture—Will weather derivatives permeate? Appl. Econ. 2011, 43, 1067–1077. [Google Scholar] [CrossRef]
- Zariphopoulou, T. A solution approach to valuation with unhedgeable risks. Finance Stoch. 2001, 5, 61–82. [Google Scholar] [CrossRef]
- Henderson, V. Valuation of claims on nontraded assets using utility maximization. Math. Finance 2002, 12, 351–373. [Google Scholar] [CrossRef]
- Owen, M.P. Utility based optimal hedging in incomplete markets. Ann. Appl. Probab. 2002, 12, 691–709. [Google Scholar] [CrossRef]
- Davis, M. Pricing weather derivatives by marginal value. Quant. Finance 2001, 1, 305–308. [Google Scholar] [CrossRef]
- Brockett, P.L.; Goldens, L.L.; Wen, M.-M.; Yang, C.C. Pricing weather derivatives using the indifference pricing approach. N. Am. Actuar. J. 2009, 13, 303–315. [Google Scholar] [CrossRef]
- Barrieu, P.; Karoui, N.E. Optimal design of derivatives in illiquid markets*. Quant. Finance 2002, 2, 181–188. [Google Scholar] [CrossRef]
- Cao, M.; Wei, J. Equilibrium Valuation of Weather Derivatives; Queens University: Kingston, ON, Canada, 2000. [Google Scholar]
- Lucas, R.E., Jr. Asset prices in an exchange economy. Econom. J. Econom. Soc. 1978, 46, 1429–1445. [Google Scholar] [CrossRef]
- Alaton, P.; Djehiche, B.; Stillberger, D. On modelling and pricing weather derivatives. Appl. Math. Finance 2002, 9, 1–20. [Google Scholar] [CrossRef]
- Mraoua, M. Temperature stochastic modeling and weather derivatives pricing: Empirical study with Moroccan data. Afrika Statistika 2007, 2, 22–43. [Google Scholar] [CrossRef]
- Benth, F.E.; Benth, J.Š. Stochastic modelling of temperature variations with a view towards weather derivatives. Appl. Math. Finance 2005, 12, 53–85. [Google Scholar] [CrossRef]
- Benth, F.E.; Benth, J.Š. The volatility of temperature and pricing of weather derivatives. Quant. Finance 2007, 7, 553–561. [Google Scholar] [CrossRef]
- Hu, Q.; Buyanovsky, G. Climate effects on corn yield in Missouri. J. Appl. Meteorol. 2003, 42, 1626–1635. [Google Scholar] [CrossRef]
- Wood, T.N. Agricultural development in the Northern Savannah of Ghana. Ph.D. Thesis, University of Nebraska, Lincoln, NE, USA, 2013. [Google Scholar]
- Alexandridis, A.; Zapranis, A.D. Weather Derivatives: Modeling and Pricing Weather-Related Risk; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Jones, C.S. The dynamics of stochastic volatility: Evidence from underlying and options markets. J. Econom. 2003, 116, 181–224. [Google Scholar] [CrossRef]

| Bole | Tamale | Yendi | |
|---|---|---|---|
| Accuracy | 0.8319 | 0.8207 | 0.8895 |
| AUC | 0.8104 | 0.7991 | 0.8334 |
| Feature | Bole | Tamale | Yendi | |||
|---|---|---|---|---|---|---|
| Importance Value | Rank | Importance Value | Rank | Importance Value | Rank | |
| minT | 0.0908 | 4 | 0.2001 | 2 | 0.2452 | 4 |
| maxT | 0.2017 | 3 | 0.1402 | 4 | 0.2875 | 3 |
| aveT | 0.3042 | 1 | 0.2075 | 1 | 0.3006 | 2 |
| Rainfall | 0.2552 | 2 | 0.1905 | 3 | 0.3017 | 1 |
| Sunlight | 0.0646 | 5 | 0.0625 | 6 | 0.2501 | 5 |
| Humidity | 0.0579 | 6 | 0.0983 | 5 | 0.2466 | 6 |
| Bole | Tamale | Yendi | |
|---|---|---|---|
| Bole | 1 | 0.8733 | 0.8547 |
| Tamale | 0.8733 | 1 | 0.8998 |
| Yendi | 0.8547 | 0.8998 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gyamerah, S.A.; Ngare, P.; Ikpe, D. Hedging Crop Yields Against Weather Uncertainties—A Weather Derivative Perspective. Math. Comput. Appl. 2019, 24, 71. https://doi.org/10.3390/mca24030071
Gyamerah SA, Ngare P, Ikpe D. Hedging Crop Yields Against Weather Uncertainties—A Weather Derivative Perspective. Mathematical and Computational Applications. 2019; 24(3):71. https://doi.org/10.3390/mca24030071
Chicago/Turabian StyleGyamerah, Samuel Asante, Philip Ngare, and Dennis Ikpe. 2019. "Hedging Crop Yields Against Weather Uncertainties—A Weather Derivative Perspective" Mathematical and Computational Applications 24, no. 3: 71. https://doi.org/10.3390/mca24030071
APA StyleGyamerah, S. A., Ngare, P., & Ikpe, D. (2019). Hedging Crop Yields Against Weather Uncertainties—A Weather Derivative Perspective. Mathematical and Computational Applications, 24(3), 71. https://doi.org/10.3390/mca24030071





