1. Introduction
The problem of minimizing the ruin probability, when the insurance company is allowed to invest part of its surplus in the money and stock markets and to reduce its risk by entering into proportional reinsurance treaties, has been extensively studied in different forms since the ground-breaking work of Bachelier [
1]. Liang and Guo [
2] found that the minimal ruin probability maximizes the adjustment coefficient
under proportional reinsurance and that it satisfies the Lundberg inequality
. Wang [
3] considered the case of multiple risky assets in an optimal investment problem for an insurer whose surplus evolves according to a jump-diffusion process, while Liang and Guo [
4] considered the optimal reinsurance problem by combining quota-share and excess-of-loss reinsurance. The authors derived explicit expressions for the value function and the optimal strategies.
Kasozi et al. [
5] studied the problem of controlling ultimate ruin probability by quota-share reinsurance arrangements for an insurer that is allowed to invest part of the surplus in a risk-free and risky asset. They found that, for selected parameter values, the optimal quota-share retention lies in the interval
, i.e., the company should cede between 60% and
of its risks to a reinsurer. This study also found that the ruin probabilities increase when stock prices become more volatile. However, while [
5] assumed cheap reinsurance, in this paper we use noncheap reinsurance. Zhou et al. [
6] investigated the optimal proportional reinsurance and investment problem for a jump-diffusion surplus process in a constant elasticity of variance (CEV) stock market.
Liu and Yang [
7] revisited the model in Hipp and Plum [
8] by incorporating a risk-free interest rate. Since they could not obtain closed-form solutions in this case, they provided numerical results for optimal strategies for maximizing the survival probability under different claim-size distribution assumptions. Schmidli [
9] proved the existence and uniqueness of a solution of the ruin probability minimization problem in a model compounded by investment and dynamic proportional reinsurance for the case
and
, i.e., when there is no diffusion and when
F has a bounded density. But while [
9] uses proportional reinsurance in minimizing ruin probabilities in the Cramér–Lundberg model, this paper considers proportional reinsurance and investments of Black–Scholes type in the diffusion-perturbed model.
With the objective of determining the optimal investment and reinsurance strategies, Liang and Young [
10] studied the problem of minimizing the probability of ruin in the presence of per-loss reinsurance for an insurance company whose risk process follows a compound Poisson process or its diffusion approximation. Assuming that the financial market in which the company invests follows the Black–Scholes model, and under minimal assumptions regarding admissible reinsurance forms, ref. [
10] showed that the optimal per-loss reinsurance policy is excess-of-loss reinsurance. They found that for cheap reinsurance under both models, full reinsurance is never optimal, a result consistent with Mossin [
11]. While under the compound Poisson model it is optimal not to buy reinsurance when the surplus is sufficiently low, for the diffusion approximation model the insurer always buys some amount of reinsurance but the optimal retention is inversely proportional to the surplus. This is also true of the optimal investment level as it decreases with an increase in the surplus. However, ref. [
10] concerned itself with excess-of-loss reinsurance while this paper explores optimality of noncheap proportional reinsurance and employs different numerical methods from those of [
10].
Zhu et al. [
12] studied the optimal proportional reinsurance and investment problem in a general jump-diffusion financial market. With the objective of maximizing the expected exponential utility of terminal wealth, they added a general jump to the price of the risky asset, so that the financial market follows a general jump-diffusion model. They also incorporated a reasonable constraint on the proportional reinsurance strategy, thus making the model more reasonable and realistic, and derived closed-form expressions for the value function and optimal strategy. Glineur and Walhin [
13] revisited de Finetti’s retention problem for proportional reinsurance by applying the convex optimization method. The authors extended the result to variable quota-share and surplus reinsurance with table of lines and showed, by means of a numerical example, that neither variable quota share reinsurance nor surplus reinsurance with table of lines may be considered as optimal reinsurance structures. They were able to determine the optimal quota-share and surplus reinsurance strategies. However, the numerical example also led them to the conclusion that there exists no general rule asserting superiority of either quota-share-type or surplus-type reinsurance above the other.
An insurance company is said to have experienced ruin when its surplus becomes negative, thus making it impossible for the company to meet its financial obligations (e.g., claims). The time of ruin is the first time that the cedent’s surplus process enters and the associated probability is referred to as the ultimate ruin probability. Ruin is a technical term which does not necessarily mean that the company is bankrupt, but rather that bankruptcy is at hand and that the company should therefore be prompted to take action to improve its solvency status. Thus, insurance companies customarily take precautions to avoid ruin. These precautions are referred to as control variables and include investments, capital injections or refinancing, portfolio selection, volume control through the setting of premiums and reinsurance arrangements, to mention but a few. This study focuses on reinsurance as a risk control mechanism for a company that also invests part of its surplus in risk-free and risky assets.
According to Jang and Kim [
14], insurance companies generally face two sources of risk, viz., an insolvency risk that arises from unexpectedly large insurance claims, and a market risk that arises from risky investments in financial markets. Reinsurance can help mitigate the insolvency risk, while investing in some risk-free assets such as short-term bonds and money market funds could reduce the market risk. Reinsurance is the transfer of risk from a direct insurer (the cedent) to a second insurance carrier (the reinsurer). It serves the purpose of offering protection to cedents against very large individual claims or fluctuations in their aggregate portfolio of risks, as well as diversifying the financial losses caused by it. Reinsurance therefore allows the cedent to pass on some of its risk to the reinsurer but at the expense of a portion of the aggregate premiums receivable from the policyholders [
15].
Mikosch [
16] has pointed out that reinsurance treaties are of two types; random walk type reinsurance which includes proportional, excess-of-loss and stop-loss reinsurance, and extreme value type reinsurance which includes the largest claims and ECOMOR reinsurance (excédent du coût moyen relatif or ‘excess of the average cost’). Proportional, or pro rata, reinsurance is a common form of reinsurance for claims of ‘moderate’ size, and requires the reinsurer to cover a fraction of each claim equal to the fraction of total premiums ceded to the reinsurer. Proportional reinsurance treaties are traditionally subdivided into two forms; quota-share and surplus reinsurance. Quota-share reinsurance is a common type of proportional reinsurance in which the cedent and the reinsurer agree to share claims and premiums in the same proportion which remains constant throughout the portfolio [
17]. With surplus reinsurance the reinsurer agrees to accept an individual risk with sum insured in excess of the direct retention limit set by the cedent [
18].
It has been noted in [
19] that proportional reinsurance is the easiest way of covering an insurance portfolio. This paper focuses on quota-share (QS) proportional reinsurance due to its simplicity, but other forms of reinsurance could also be used. In addition, the reinsurer pays a ‘ceding commission’ to the cedent to compensate for the costs of underwriting the ceded business. This commission is ignored in this study. Thus, if a cedent enters into a quota-share reinsurance treaty with a reinsurer, then they will share claims and premiums according to a retention level
. For every claim
X that occurs at the time where the surplus prior to the claim payment is
u, the cedent pays
while the reinsurer pays
. Similarly, for every premium amount
c received by the insurer,
is paid to the reinsurer and
is retained by the cedent. Since the factor
represents the proportion of claims or premiums ceded to the reinsurer, it is called the cession level. It should be noted that for cheap reinsurance
.
It has been argued in the literature that the Cramér–Lundberg model is somewhat inadequate for modelling real-world insurance processes (see, e.g., [
20,
21]). The limitations of this model quickly led to its generalizations (e.g., in [
22,
23,
24]), even at the cost of tractability. The more complex the model gets, the more difficult its analysis and the drawing of conclusions becomes. In this paper, we make generalizations to the well known Cramér–Lundberg model by adding a diffusion term and also allowing the company to invest in the financial markets with returns of a Black–Scholes type. Thus, this paper focuses on ultimate ruin and considers proportional reinsurance coupled with investments as mechanisms for reducing the insurer’s ultimate ruin probability. Reinsurance can protect insurers against potentially large losses, while investment of insurance premiums enables insurers to achieve certain management objectives, some of the most common of which are the minimization of the ruin probability, maximization of expected utility and mean-variance criteria. Li et al. [
25] have pointed out that insurance companies commonly employ integrated reinsurance and investment strategies to increase their underwriting capacity, stabilize underwriting results, protect themselves against catastrophic losses, and achieve financial growth.
The models studied in this paper result in Volterra integral equations of the second kind (VIE-2s). As Press et al. [
26] have pointed out, there is general consensus that the block-by-block method, first proposed by Young [
27], is the best of the higher order methods for solving VIE-2s. The block-by-block methods are essentially extrapolation procedures which produce a block of values at a time. They are advantageous over linear multistep and step-by-step methods in that they can be of higher order and still be self-starting. Apart from not requiring special starting procedures or values, block-by-block methods have a simple structure, allow for easy switching of step-size and have the ability to compute several values of the unknown function at the same time [
28,
29]. In addition, the block-by-block method is chosen in this paper over such methods as saddlepoint approximation, importance sampling simulation, upper and lower bounds, Fast-Fourier Transform (FFT) and diagonally implicit multistep block [
30,
31,
32] because it is a fourth-order method while most of the other methods are of order less than four. In fact, some of the methods mentioned above are used for directly computing ruin probabilities and not for solving integrodifferential or integral equations.
Other methods have been used to solve integrodifferential equations arising in engineering such as the local Galerkin integral equation and thin plate spline collocation methods for solving second-order Volterra integrodifferential equations (VIDEs) with time-periodic coefficients [
33,
34]. Both of these methods are meshless and therefore do not require any background interpolation. As for the collocation method proposed by Cardone et al. [
35], although it has the advantages of variable step-size implementation, high order of convergence, strong stability and a high degree of flexibility, it suffers from the order-reduction phenomenon when applied to stiff problems since it does not have a uniform order of convergence.
In the literature, two-, three- and four-block block-by-block methods have been used to solve Volterra integral equations (e.g., [
36] for non-linear VIE-2s, [
37] for a system of linear VIE-2s). More recently, Kasozi and Paulsen [
38] used the two-block block-by-block method to study the flow of dividends under a constant interest force. They derived a linear VIE-2 and applied a fourth-order block by-block method of Paulsen et al. [
39] in conjunction with Simpson’s rule to solve the Volterra integral equation for the optimal dividend barrier. In another study, Kasozi and Paulsen [
40] applied a fourth-order block-by-block method to the numerical solution of the Volterra integral equation (VIE) for ultimate ruin in the Cramér–Lundberg model compounded by a constant force of interest. More pertinent literature on the block-by-block method is available, for example, in [
41,
42].
The remainder of the paper is organized as follows. In
Section 2, we present the models to be studied and the underlying assumptions. In
Section 3, we give the Hamilton–Jacobi–Bellman (HJB) equation and verification theorems for the ruin probabilities under proportional reinsurance, as well as the corresponding Volterra integrodifferential and integral equations.
Section 4 contains a presentation of numerical results and examples based on light- and heavy-tailed individual claim-size distributions. Finally, in
Section 5 we give some concluding remarks and possible extensions to this work.
2. The Models
To give a rigorous mathematical formulation of the problem, we assumed that all stochastic quantities are defined on a complete filtered probability space
satisfying the usual conditions, i.e., the filtration
, which represents the information available at time
t and forms the basis for all decision-making, is right-continuous and
-complete. Right-continuity is necessary for ensuring that the ruin time defined later in this section is a stopping time. The risk process considered in this paper is made up of two important processes; the insurance process and the investment-generating process. In the absence of reinsurance, the insurance process
is given by the diffusion-perturbed model
where the process
, defined as
is a compound Poisson process representing the aggregate claims made by policyholders. Here, the premiums are assumed to be calculated according to the expected value premium principle and to be collected continuously over time at a constant rate
, where
is the relative safety loading of the insurer.
is a one-dimensional standard Brownian motion independent of the compound Poisson process
,
is a homogeneous Poisson process with constant intensity
and the claim sizes
are a sequence of strictly positive i.i.d. random variables. We assumed that the processes
,
and
were mutually independent. We denoted by
F the distribution function of
, by
its first moment and by
its moment-generating function. We assumed that
and that at least one of
or
was non-zero.
The diffusion term
in the basic model (
1) has been interpreted in a two-fold manner in the literature. On the one hand,
could be understood as standing for the uncertainty or random fluctuations associated with the insurance process at time
t (the
U-
S case). This means that the aggregate claims up to time
t are given by the compound Poisson process
. This is the interpretation assumed in this paper. On the other hand,
could represent the additional small claims which account for uncertainty associated with the insurance market or the economic environment (the
A-
C case), so that the aggregate claims process is
(see, e.g., [
6]). It should be noted that, given an initial surplus
u, when there is no volatility in the surplus and claim amounts (i.e., when
), Equation (
1) becomes the well-known classical risk process (or the Cramér–Lundberg model).
Given that the insurer controls its insurance risk by taking QS proportional reinsurance at a retention level
, the insurance process in the presence of QS reinsurance is now
with dynamics
If
then there is full reinsurance, i.e., the entire portfolio of risks is ceded to the reinsurer, whereas if
then there is no reinsurance. The case
is precisely the model considered in [
39,
43]. In this study, we assumed noncheap reinsurance, meaning that the reinsurer used a higher safety loading than the insurer. Otherwise, the insurance company can take full reinsurance and receive a positive return without any risk, which is undesirable from the reinsurer’s standpoint, as was demonstrated in [
44]. Thus, if
is the reinsurance premium to be paid for the QS reinsurance, then the insurance premium rate is
, where
is the reinsurer’s safety loading. In order for the net profit condition (NPC) to be fulfilled, that is,
we need
otherwise ruin is certain for any initial capital
. Note that in noncheap reinsurance the fraction of the premiums diverted to the reinsurer is larger than that of each claim covered by the reinsurer. The classical risk process with noncheap reinsurance was also studied by, among others, Ma et al. [
45] who obtained the minimal probability of ruin as well as the optimal proportional reinsurance strategy using the dynamic programming approach, while cheap reinsurance (i.e.,
) was considered in Schmidli [
46] who allowed for investment in a risky asset and obtained, by means of an HJB equation, the optimal reinsurance and investment strategies for minimizing the ultimate ruin probability.
Suppose the insurer invests part of its surplus, into say, a risk-free asset (a bond) and a risky asset (stocks) as in [
7]. Let the return on investments process be:
where
r is the risk-free interest rate, so that
implies that one unit invested now will be worth
at time
t;
is another one-dimensional Brownian motion independent of the surplus-generating process
P and
is the volatility of the stock price, so that the diffusion term
accounts for random fluctuations in the investment returns. Equation (
5) is actually the famous Black–Scholes option pricing formula according to which the price of a stock is assumed to follow the stochastic differential equation
where
is the stock price at
The process
Y is a geometric Brownian motion. The solution to (
6) is the value of the stock at time
t and is given by
.
The risk process is therefore made up of a combination of the surplus-generating process compounded by proportional reinsurance (
2) and the investment-generating process (
5). Thus, the insurance portfolio is represented by the risk process
which has dynamics
A reinsurance strategy
k is said to be admissible if it is
-progressively measurable and takes values from the set
. Thus, given an admissible reinsurance strategy
, and assuming that the mutually independent processes
P and
R belong to the rather general class of semimartingales, then under some weak additional assumptions the risk process
is mathematically the solution of the linear stochastic differential equation (SDE)
where
is the initial surplus of the insurance company,
is the basic insurance (or surplus-generating) process in Equation (
2),
the investment-generating process in Equation (
5) and
denotes the insurer’s surplus (incorporating both proportional reinsurance and investments) just prior to time
t. Paulsen [
47], gave the solution of (
8) as
where
is the geometric Brownian motion so extensively used in mathematical finance and is the solution of the SDE
, with
.
Since both
P and
R have stationary independent increments,
is a homogeneous strong Markov process. We defined the value function of this optimization problem as
where
is the ultimate ruin probability under the reinsurance policy
k when the initial surplus is
u and
is the time of ruin, with
if
remains positive. Then the objective is to find the optimal value function, i.e., the minimal ruin probability
and the optimal policy
such that
, considered optimal if
minimizes the ruin probability. Since the ultimate survival probability
, we may alternatively find the value of
which maximizes
, so that the optimal value function becomes
3. HJB, Integrodifferential and Integral Equations
In this section, we derived the HJB equation for the problem and the corresponding integrodifferential and integral equations. By Itô’s formula, the infinitesimal generator of the process
in Equation (
8) is given by the integrodifferential operator
Since the investment-generating process
is governed by (
5), it follows that under weak assumptions the ruin probability
is twice continuously differentiable on
and is a solution to the equation (see [
48])
where
, with boundary conditions
and
if
(see Theorem 1 below). Sometimes it is more convenient, as we did in this paper, to work with the survival probability
, in which case (
13) becomes
The integrodifferential operator (
12) does not easily give rise to closed-form solutions, hence the need for the use of numerical methods. The following theorem is proved in [
48].
Theorem 1. Let be the ruin time, with if . Assume that the equation has a bounded, twice continuously differentiable solution (once continuously differentiable if ) that satisfies the boundary conditions Then is the survival probability.
We now present the HJB equation for this optimization problem.
Theorem 2. Assume that the survival probability defined by (11) is twice continuously differentiable on . Then, for , satisfies the HJB equationwhere is the infinitesimal generator (12) of the process . The function
will satisfy the HJB Equation (
15) only if it is strictly increasing, strictly concave, twice continuously differentiable and satisfies
for
[
8]. In the following, therefore,
will be assumed to be strictly increasing. This is consistent with the smoothness assumption and the intuition that the more wealth there is (through investment), the higher the probability of survival of the insurance company. It will also be assumed that
is concave. To ensure smoothness and concavity, the claim density function must be locally-bounded [
7].
The following verification theorem, whose proof is similar to that of Theorem 2 in Kasumo et al. [
44], is essential for solving the associated control problem as it leads to the integrodifferential equation for the problem.
Theorem 3. Suppose is an increasing strictly concave function satisfying the HJB Equation (15) subject to the boundary conditionsfor . Then the maximal survival probability given by (11) coincides with Φ. Furthermore, if satisfieswhen , where , then the policy is an optimal policy, that is, . The integrodifferential equation for the survival probability
, which follows immediately from Theorem 3, is of the form
(since, by Equation (
14),
for
), where
is the infinitesimal generator (
12) of the underlying risk process, that is,
for
. Equation (
17) is a second-order Volterra integrodifferential equation (VIDE) which is easily transformed, using successive integration by parts, into a linear Volterra integral equation of the second kind to be solved in this study. This leads to the following theorem which is our main result.
Theorem 4. The integrodifferential Equation (17) can be represented as a VIE-2with , where and are two known continuous functions, is the unknown function to be determined, and - 1.
For the case without diffusion (i.e., when ), the kernel and forcing function are given, respectively, bywith . - 2.
For the case with diffusion (i.e., when ), the kernel and forcing function are, respectively,with
Setting in both of the above cases gives the VIE-2 for the case without reinsurance, while setting leads to the VIE-2 for the case without investments.
Proof. We began by proving the diffusion case (Case 2) before dealing with the case without diffusion (Case 1). Integrating Equation (
17) by parts with respect to
u on
gives
Evaluating the third term in (
21) by integrating by parts yields
Integrating (22) by parts over
with respect to
z gives
The above is obtained by simplifying the double integrals in the last two terms by using integration by parts again and switching the order of integration using Fubini’s Theorem [
50]. Recall that
and
for
,
F being absolutely continuous with respect to Lebesgue measure. Thus, simplifying further and replacing
z with
x yields
where
. Equation (
23) can be written as
which is a VIE-2. Replacing
x with
gives the kernel and forcing function for the diffusion case (Equations (
18) and (
20)). The case without diffusion is really the Cramér–Lundberg model with a reinsurance retention and a constant force of interest, that is, the integrodifferential equation (IDE) is
It is known that
for
, and that
. Integrating (
25) by parts on
with respect to
u and replacing
x with
transforms the IDE into a VIE of the second kind with kernel and forcing function for the case without diffusion as given by Equations (
18) and (
19) above. ☐
4. Numerical Results
We now present some numerical results and study the impact of the volatility of stock prices on the ruin probability. To find the survival probabilities
, we took advantage of the fourth-order block-by-block method in conjunction with Simpson’s Rule of integration to solve the VIE (
18). This method, which produces solutions in blocks of two values, is fully developed in [
39] and appears in several papers, e.g., [
5,
38,
49]. Linz [
36] has shown that the block-by-block method always converges and has an order of convergence of four (see also [
51]). This method reduces the VIE-2 into a system of algebraic equations which are solved by matrix methods to obtain the blocks (for details, see [
49]).
Typical choices for light- and heavy-tailed claim-size distributions are the exponential and Pareto distributions, respectively. The merits of using these two distributions for modelling insurance claims are briefly well articulated in [
52]. Exp(
) refers to the exponential density
. The exponential distribution has distribution function
from which the tail distribution is
. Its mean excess function is
, so that
. The Pareto distribution is commonly used for modelling large claims. The probability density function of the Pareto distribution is
where
,
and the distribution function
. Hence the tail distribution is
. Also,
. Note also that the Pareto distribution has a mean excess function
(or
), meaning that
can alternatively be written as
.
A step-size of
was used throughout. All numerical simulations in this section were performed using a Samsung Series 3 PC with an Intel Celeron CPU 847 at 1.10 GHz and 6.0 GB internal memory. The block-by-block method was implemented using the FORTRAN programming language and taking advantage of its double precision feature to obtain satisfactory accuracy. Slower programs such as R, MATLAB, Maple or Mathematica could, of course, have been used but at the expense of considerably longer computing time. Although Theorem 4 deals with the survival probability
as the value function, the programs have been adjusted to output infinite ruin probabilities (since
). Since the block-by-block method does not require special starting procedures or values, it can be initiated using any value of
. The values stabilize at
which is used for scaling the probabilities. For
to be virtually equal to 1, the corresponding upper bound
should be sufficiently large. Without reinsurance, the results for ruin probabilities have been published widely (see, e.g., [
39] and the references therein). The graphs were constructed using MATLAB R2016a. Five cases will now be presented by way of illustration. Without loss of generality, we used the parameter values shown in
Table 1 in the numerical examples that follow.
From the net profit condition (
4), we must use QS retention values
k in the set
, where
. In addition, we took
as the parameter of the exponential distribution, and
as the parameters of the Pareto distribution.
4.1. Proportional Reinsurance in the Cramér–Lundberg Model
When
and
, then the SDE (
8) takes the form of the classical risk process compounded by proportional reinsurance
By Itô’s formula, the infinitesimal generator for the process
is given by
from which the VIDE corresponding to the survival probability
follows as
This VIDE reduces to an ordinary VIE of the second kind with kernel
, where
, and forcing function
. This is simply Equations (
18) and (
19) with
.
Example 1. Exponential distribution with .
Since the ruin probability is a function of the initial surpus
u, we observe from
Figure 1a that the ruin probability reduces as the initial surplus increases. We also noted that the higher the cession level
for QS reinsurance, the lower the ruin probability. From the results presented in
Figure 1, we see that the lowest value of
k that satisfies the NPC (
4) and at the same time gives the minimal ultimate ruin probability is
. Thus, the optimal retention for QS reinsurance is
. This means that the company should cede about
of its risks to a reinsurer.
Example 2. Pareto distribution with .
The ultimate ruin probabilities for large claims reduce more when QS reinsurance is applied to the portfolio of risks as shown in
Figure 1b. As for the small claim case, the optimal QS retention level in the large claim case is
. Thus, for large claims the insurer must cede about
of its risks to a reinsurer as well.
4.2. Proportional Reinsurance in the Cramér–Lundberg Model under Interest Force
Here we considered the case when
,
and
which lead to the Cramér–Lundberg Model (CLM) compounded by proportional reinsurance and a constant force of interest
The survival probability satisfies the VIDE
which reduces to a linear VIE of the second kind with kernel and forcing function given in (
19).
Example 3. Exponential distribution with .
The comments made under Example 1 apply here as well and the optimal QS reinsurance policy in this case is again
(see
Figure 2a). Though investing part of its surplus in a risk-free asset might provide the insurance company with the flexibility to operate with a lower optimal ruin probability, the company must still reinsure
of its business as ceding a higher percentage would violate the NPC (Equation (
4)).
Example 4. Pareto distribution with .
The comments made under Example 2 apply to this case also. Again, the optimal QS reinsurance policy is
as shown in
Figure 2b. For large claims in the CLM under a constant force of interest, the insurance company must again buy cover for
of its risks from a reinsurance company.
4.3. Proportional Reinsurance in the Diffusion-Perturbed Model
When
,
and
, then we had the diffusion-perturbed model (DPM) compounded by proportional reinsurance
In this case, the associated VIE has kernel and forcing function given, respectively, by
and
. This is simply (
20) with
.
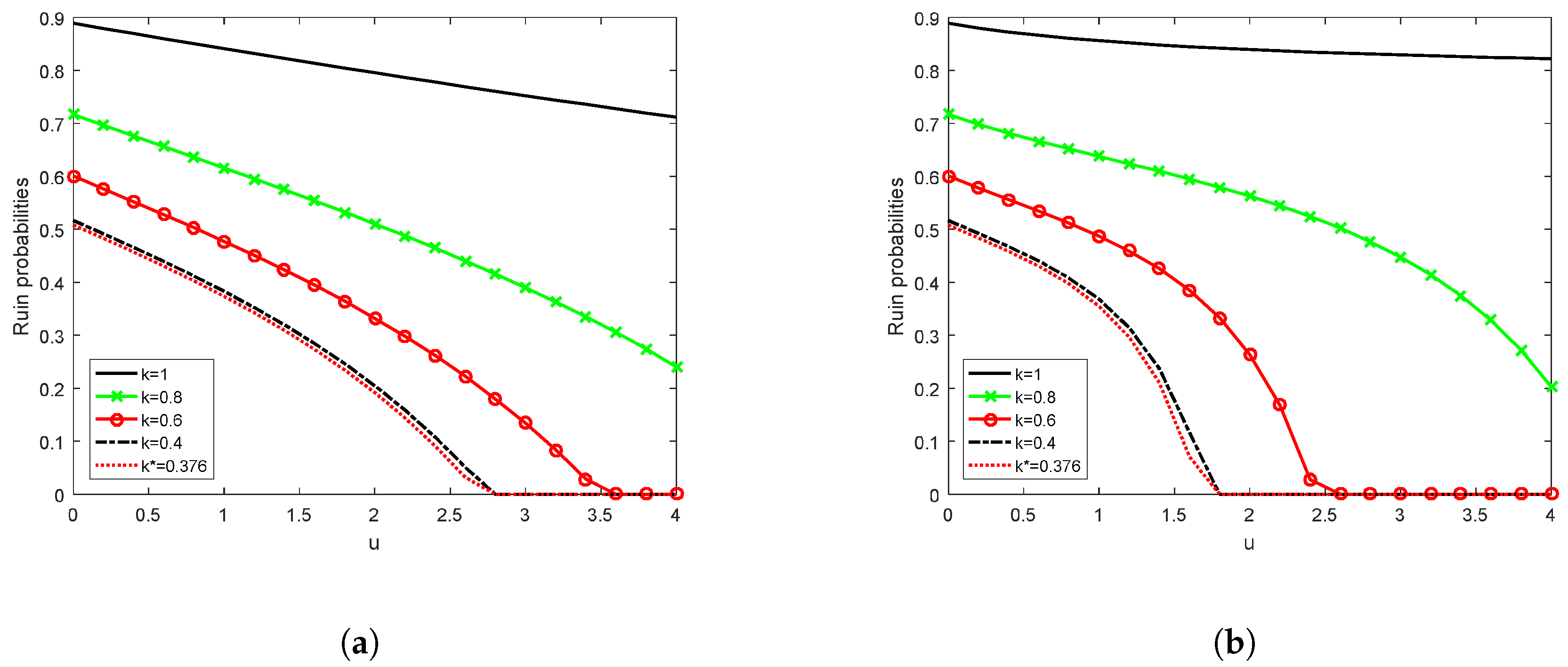
Example 5. Exponential distribution with , .
It can be seen from
Figure 3a that
for
and
for
. This means that in the DPM, the insurer should cede
of its risks if
and only
if
. In fact, going by the graph for
, it is expected that when
u is sufficiently large, it is optimal for the company not to reinsure, i.e.,
.
Example 6. Pareto distribution with .
For the large claim case in the DPM, the ruin probabilities increase instead of reducing with the application of proportional reinsurance, as can be seen from
Figure 3b. We can therefore conclude that it is optimal not to reinsure, i.e.,
.
4.4. Proportional Reinsurance in the Perturbed Model under Interest Force
This is the case when
,
,
and
, then we had the DPM compounded by proportional reinsurance and a constant force of interest
The corresponding VIE has kernel and forcing function given in (
20) with
.
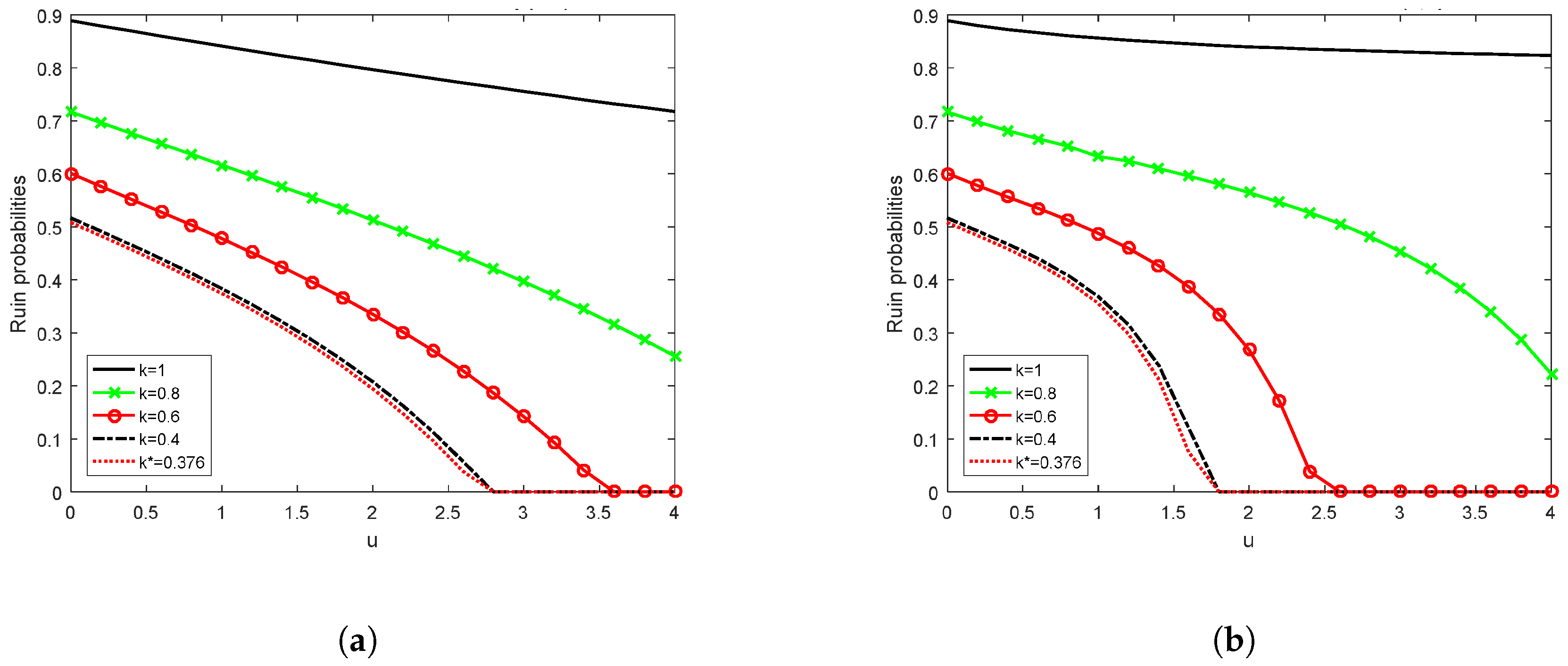
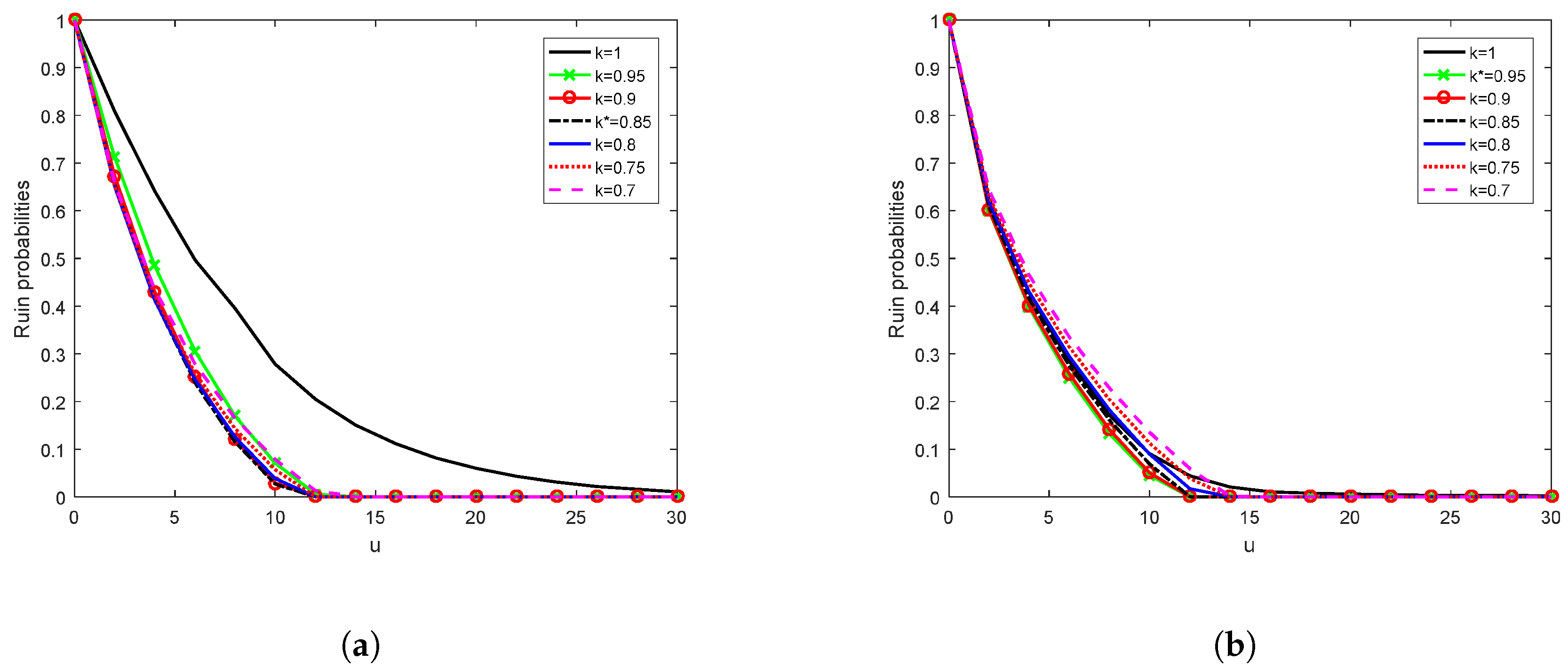
Example 7. Exponential distribution with .
For the DPM under interest force, it is evident from
Figure 4a that for exponentially distributed claim sizes the optimal QS reinsurance retention
since the graph for
is slightly higher for the first time than that for
. Thus, the optimal policy is to reinsure
of the risks, i.e.,
.
Example 8. Pareto distribution with .
For the large claim case in the DPM with interest force,
Figure 4b shows that the optimal QS retention
since the graph for
is higher for the first time than that for
. In this case, the company should cede only about
of its risks to a reinsurer since
.
4.5. Proportional Reinsurance with Investments of Black–Scholes Type
When we had stochastic return on investments, the model takes the form
Theorem 2, together with the integrodifferential operator (
12), gives the corresponding integrodifferential equation for the survival probability
as
for
, which is a second-order Volterra integrodifferential equation (VIDE). Repeated integration by parts transforms this into a VIE of the second kind with kernel and forcing function as given in (
20).
Example 9. Exponential distribution with .
This is the small claim case assuming that, in addition to purchasing noncheap proportional reinsurance, the insurance company invests part of its surplus in risk-free and risky assets according to the Black–Scholes options pricing formula. As shown in
Figure 5a, the optimal QS retention
. From the graph, we see that
, meaning that the company should reinsure about
of its risks.
Example 10. Pareto distribution with .
For the large claim case in the model involving investments of Black–Scholes type,
as shown in
Figure 5b. In fact,
, meaning that the company needs to transfer only
of its portfolio of risks to a reinsurer.
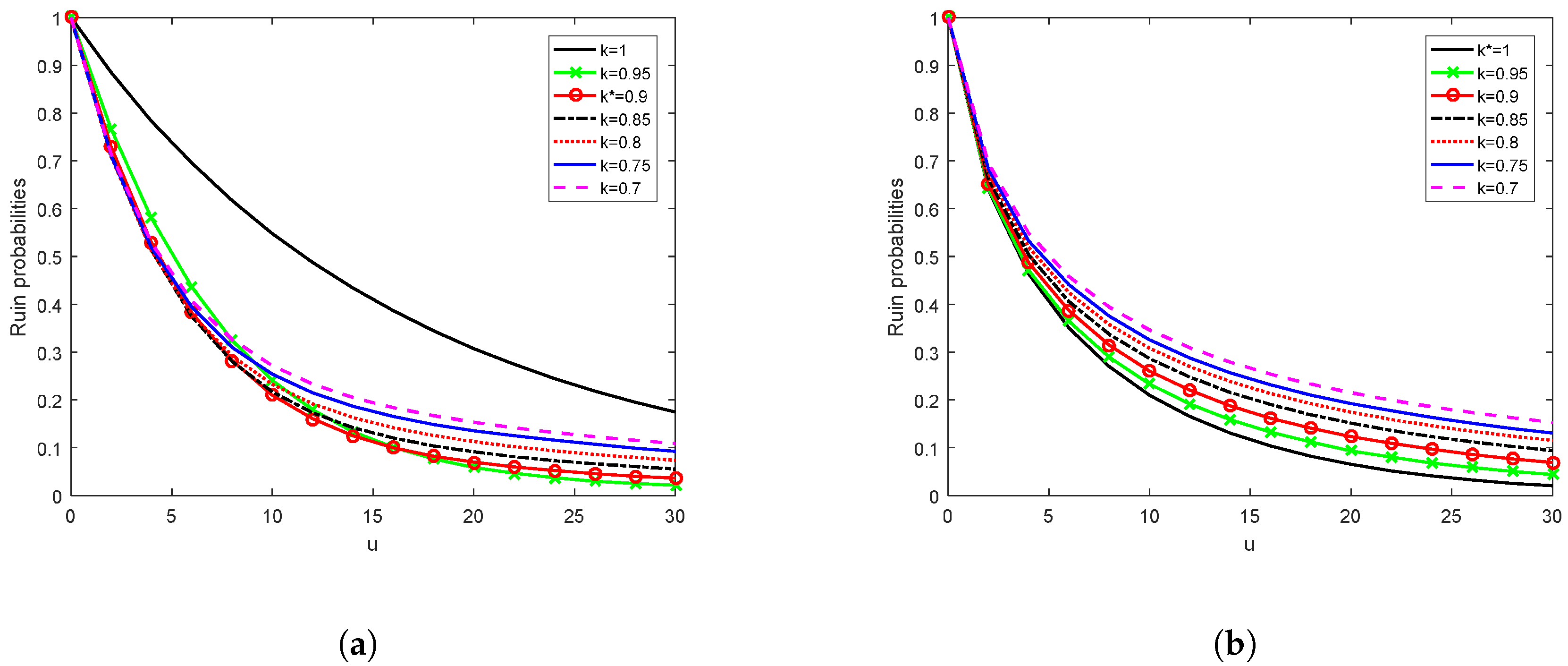
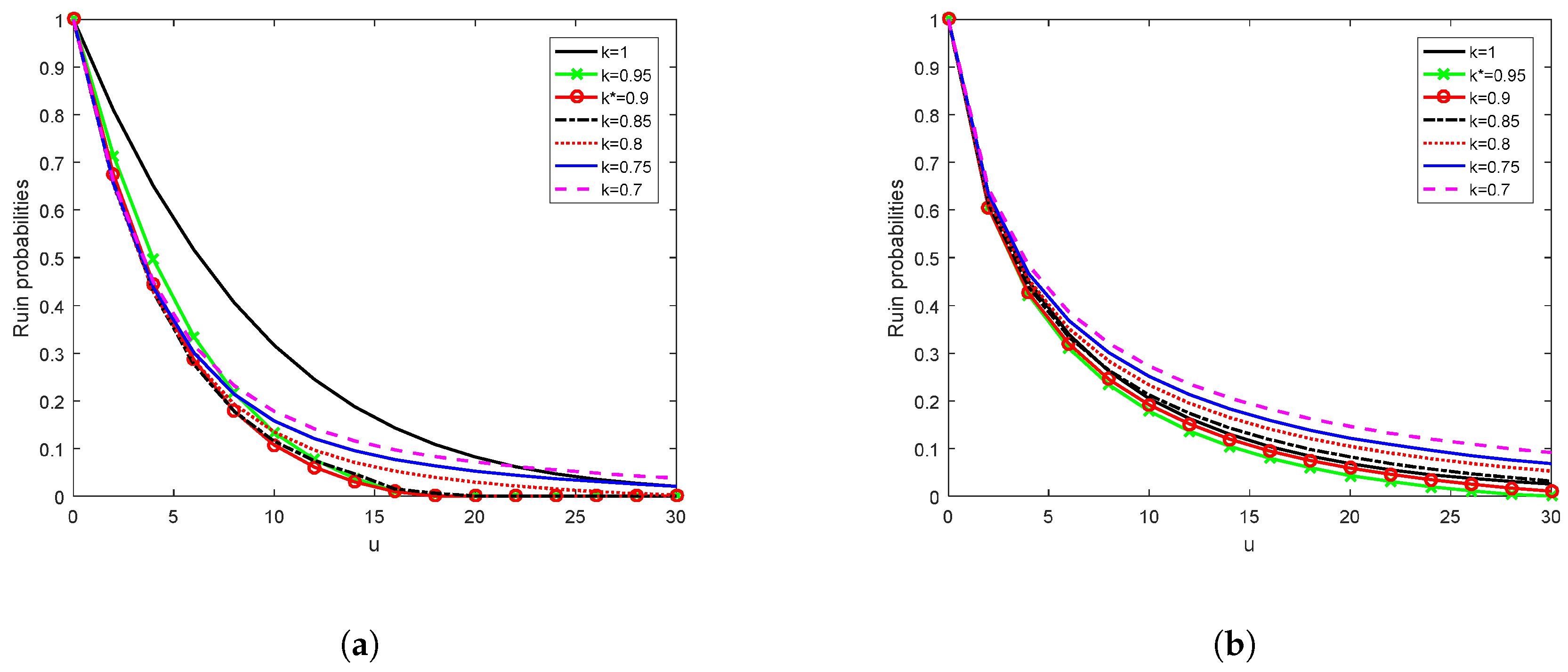
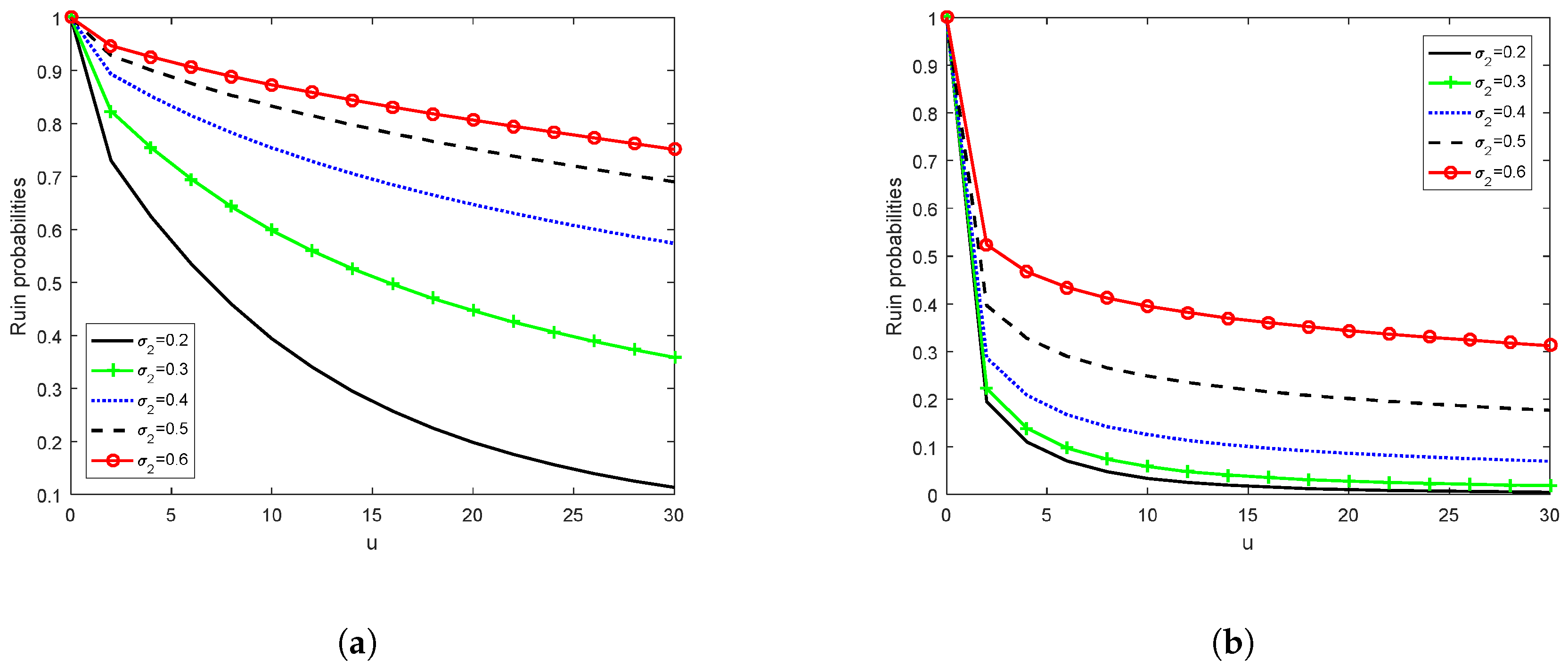
4.6. Sensitivity of Ruin Probability to Volatility of Stock Prices
Figure 6 shows the effect of volatility of stock prices on the ultimate ruin probability. Evidently, as stock prices become more volatile (that is, as
increases), the ruin probability also increases, and vice versa. Volatility is actually a measure of the riskiness of a stock. If the volatility of the stock price increases but the expected rate of return of the stock stays the same, then the insurer will find the reward for accepting the risk unattractive and would rather invest less in stocks and more in bonds. Conversely, a decrease in the volatility of the stock price enables the insurer to receive the same return but with a lower risk. For this reason, the company will find that it makes economic sense to invest in the stock. This applies to both the exponential and Pareto distributions as
Figure 6 shows.
However, we also observe from
Figure 6 that the ruin probabilities for large claims are much lower than those for small claims.