Modified Auxiliary Equation Method versus Three Nonlinear Fractional Biological Models in Present Explicit Wave Solutions
Abstract
:1. Introduction
2. Fundamental Steps of the New Technique
3. Applications
- Fractional biological population model:This model describes population dynamics. It also gives a simple example of how complex interactions and processes work. The model has the following form:where u impersonates the population density and constitutes the population changes because of deaths and births.
- Fractional equal width equation:This model is usually used to describe complex physical phenomena in various fields, and has the following formula:where are arbitrary constants.
- Fractional modified equal width equation:This model refers to the replica of one-dimensional wave propagation in nonlinear form with dispersion processes, and has the following formula:where are arbitrary constants.
3.1. Fractional Biological Population Model
3.2. Fractional Equal Width Model
3.3. Fractional Modified Equal Width Equation
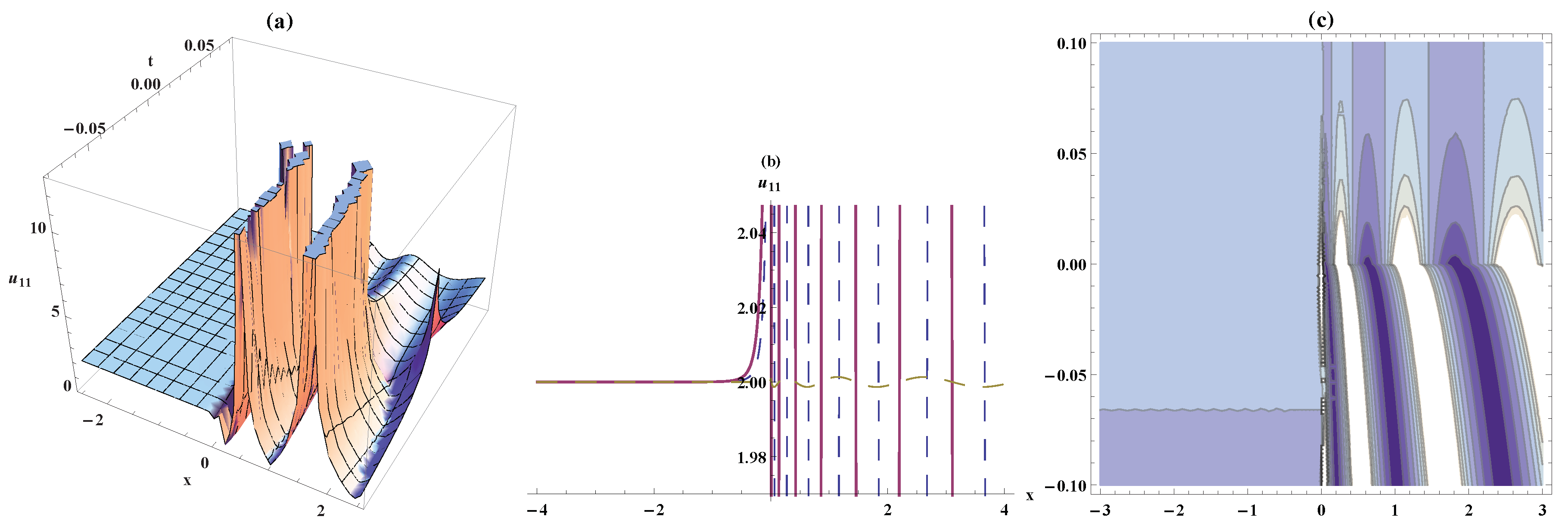
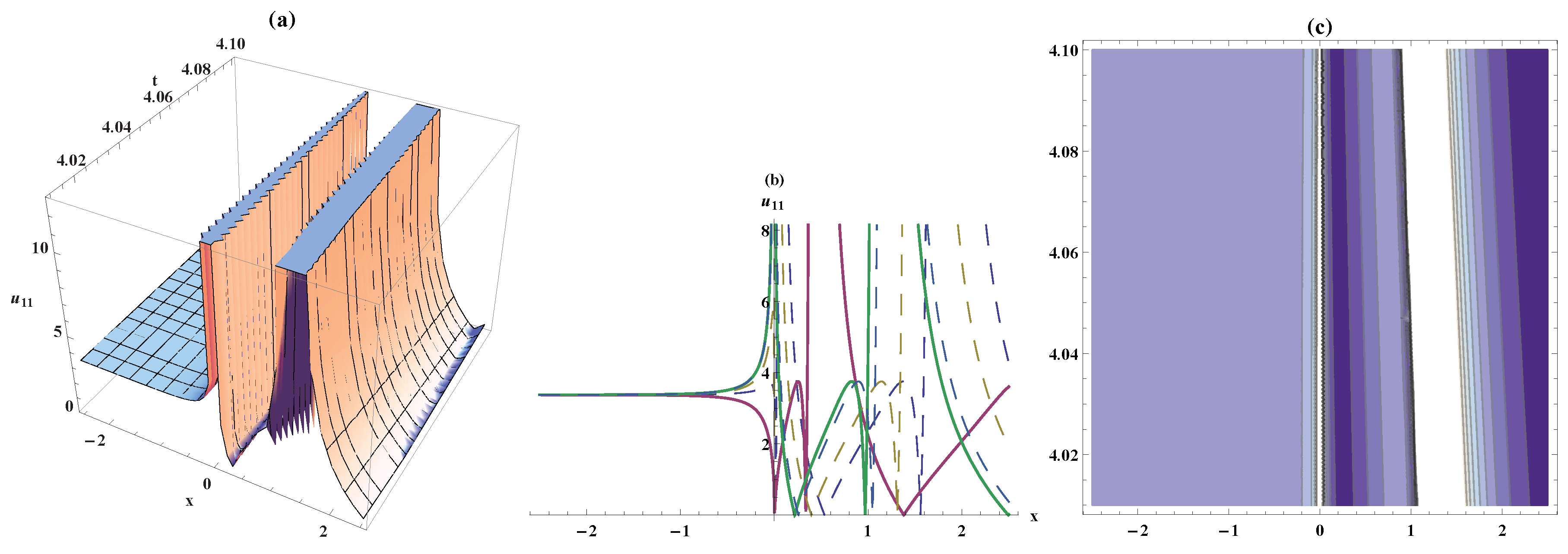
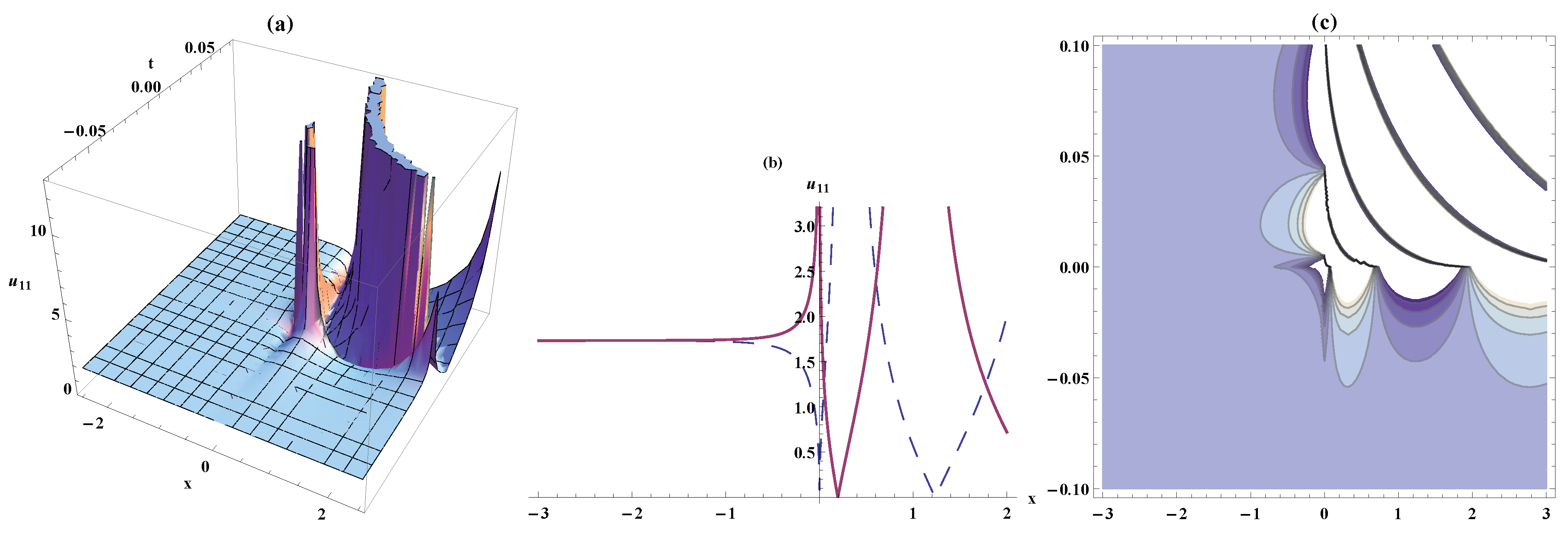
4. Results and Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Mei, F.X. Lie symmetries and conserved quantities of constrained mechanical systems. Acta Mech. 2000, 141, 135–148. [Google Scholar] [CrossRef]
- Berezinskii, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems having a continuous symmetry group I. Classical systems. Sov. Phys. JETP 1971, 32, 493–500. [Google Scholar]
- Wegner, F. The mobility edge problem: Continuous symmetry and a conjecture. Z. Phys. B Condens. Matter 1979, 35, 207–210. [Google Scholar] [CrossRef]
- Ibragimov, N.K.; Ibragimov, N.K. Elementary Lie Group Analysis and Ordinary Differential Equations; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Dorodnitsyn, V.A. Finite difference models entirely inheriting continuous symmetry of original differential equations. Int. J. Mod. Phys. C 1994, 5, 723–734. [Google Scholar] [CrossRef]
- Kegeles, A.; Oriti, D. Continuous point symmetries in group field theories. J. Phys. A Math. Theor. 2017, 50, 125402. [Google Scholar] [CrossRef]
- Lee, S.T.; Brockenbrough, J.R. A new approximate analytic solution for finite-conductivity vertical fractures. SPE Form. Eval. 1986, 1, 75–88. [Google Scholar] [CrossRef]
- Comrey, A.L. Factor-analytic methods of scale development in personality and clinical psychology. J. Consult. Clin. Psychol. 1988, 56, 754. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.J.; Chen, H.C. Finite analytic numerical method for unsteady two-dimensional Navier-Stokes equations. J. Comput. Phys. 1984, 53, 209–226. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Lu, D.; Zahran, E.H.M. Solitary wave solutions of the Benjamin-Bona-Mahoney-Burgers equation with dual power-law nonlinearity. Appl. Math. Inf. Sci. 2017, 11, 1–5. [Google Scholar] [CrossRef]
- Liao, S.J. On the analytic solution of magnetohydrodynamic flows of non-Newtonian fluids over a stretching sheet. J. Fluid Mech. 2003, 488, 189–212. [Google Scholar] [CrossRef]
- Alart, P.; Curnier, A. A mixed formulation for frictional contact problems prone to Newton like solution methods. Comput. Methods Appl. Mech. Eng. 1991, 92, 353–375. [Google Scholar] [CrossRef]
- Wertheim, M.S. Analytic solution of the Percus-Yevick equation. J. Math. Phys. 1964, 5, 643–651. [Google Scholar] [CrossRef]
- Liao, S.J. A uniformly valid analytic solution of two-dimensional viscous flow over a semi-infinite flat plate. J. Fluid Mech. 1999, 385, 101–128. [Google Scholar] [CrossRef]
- Liu, M.Z.; Li, D. Properties of analytic solution and numerical solution of multi-pantograph equation. Appl. Math. Comput. 2004, 155, 853–871. [Google Scholar] [CrossRef]
- Khater, M.M.; Kumar, D. New exact solutions for the time fractional coupled Boussinesq-Burger equation and approximate long water wave equation in shallow water. J. Ocean Eng. Sci. 2017, 2, 223–228. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Baleanu, D.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H. Laplace homotopy analysis method for solving linear partial differential equations using a fractional derivative with and without kernel singular. Adv. Differ. Equ. 2016, 2016, 164. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Torres-Jiménez, J.; Córdova-Fraga, T.; Escobar-Jiménez, R.F.; Olivares-Peregrino, V.H. Homotopy perturbation transform method for nonlinear differential equations involving to fractional operator with exponential kernel. Adv. Differ. Equ. 2017, 2017, 68. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Gómez-Aguilar, J.F.; Sosa, I.O.; Reyes, J.M.; Torres-Jiménez, J. The Feng’s first integral method applied to the nonlinear mKdV space-time fractional partial differential equation. Rev. Mex. Fís. 2016, 62, 310–316. [Google Scholar]
- Gómez-Aguilar, J.F.; Atangana, A. New insight in fractional differentiation: power, exponential decay and Mittag-Leffler laws and applications. Eur. Phys. J. Plus 2017, 132, 13. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Gómez-Aguilar, J.F.; Atangana, A. First integral method for non-linear differential equations with conformable derivative. Math. Model. Nat. Phenom. 2018, 13, 14. [Google Scholar] [CrossRef]
- Hammad, M.A.; Khalil, R. Abel’s formula and wronskian for conformable fractional differential equations. Int. J. Differ. Equ. Appl. 2014, 13. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Chung, W.S. Fractional Newton mechanics with conformable fractional derivative. J. Comput. Appl. Math. 2015, 290, 150–158. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 13, 889–898. [Google Scholar] [CrossRef]
- Çenesiz, Y.; Baleanu, D.; Kurt, A.; Tasbozan, O. New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Media 2017, 27, 103–116. [Google Scholar] [CrossRef]
- Hosseini, K.; Mayeli, P.; Ansari, R. Modified Kudryashov method for solving the conformable time-fractional Klein-Gordon equations with quadratic and cubic nonlinearities. Optik Int. J. Light Electron Opt. 2017, 130, 737–742. [Google Scholar] [CrossRef]
- Hosseini, K.; Bekir, A.; Ansari, R. New exact solutions of the conformable time-fractional Cahn-Allen and Cahn-Hilliard equations using the modified Kudryashov method. Optik Int. J. Light Electron Opt. 2017, 132, 203–209. [Google Scholar] [CrossRef]
- Latifizadeh, H. Application of homotopy analysis transform method to fractional biological population model. Rom. Rep. Phys. 2013, 65, 63–75. [Google Scholar]
- Srivastava, V.K.; Kumar, S.; Awasthi, M.K.; Singh, B.K. Two-dimensional time fractional-order biological population model and its analytical solution. Egypt. J. Basic Appl. Sci. 2014, 1, 71–76. [Google Scholar] [CrossRef]
- Baleanu, D.; Uǧurlu, Y.; Kilic, B. Improved (G′/G)-Expansion Method for the Time-Fractional Biological Population Model and Cahn-Hilliard Equation. J. Comput. Nonlinear Dyn. 2015, 10, 051016. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Kılıçman, A. Numerical solutions of nonlinear fractional partial differential equations arising in spatial diffusion of biological populations. Abstr. Appl. Anal. 2014, 2014, 535793. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Numerical solution of a biological population model using He’s variational iteration method. Comput. Math. Appl. 2007, 54, 1197–1209. [Google Scholar] [CrossRef]
- Morrison, P.J.; Meiss, J.D.; Cary, J.R. Scattering of regularized-long-wave solitary waves. Phys. D Nonlinear Phenom. 1984, 11, 324–336. [Google Scholar] [CrossRef]
- Yusufoglu, E.; Bekir, A. Numerical simulation of equal-width wave equation. Comput. Math. Appl. 2007, 54, 1147–1153. [Google Scholar] [CrossRef]
- Esen, A. A numerical solution of the equal width wave equation by a lumped Galerkin method. Appl. Math. Comput. 2005, 168, 270–282. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Ali, A. Dispersive traveling wave solutions of the Equal-Width and Modified Equal-Width equations via mathematical methods and its applications. Results Phys. 2018, 9, 313–320. [Google Scholar] [CrossRef]
- Korkmaz, A. Exact solutions of space-time fractional EW and modified EW equations. Chaos Solitons Fractals 2017, 96, 132–138. [Google Scholar] [CrossRef] [Green Version]
- Wazwaz, A.M. The tanh and the sine-cosine methods for a reliable treatment of the modified equal width equation and its variants. Commun. Nonlinear Sci. Numer. Simul. 2006, 11, 148–160. [Google Scholar] [CrossRef]
- Zaki, S.I. Solitary wave interactions for the modified equal width equation. Comput. Phys. Commun. 2000, 126, 219–231. [Google Scholar] [CrossRef]
- Khalique, C.M.; Adem, K.R. Exact solutions of the (2+1)-dimensional Zakharov-Kuznetsov modified equal width equation using Lie group analysis. Math. Comput. Model. 2011, 54, 184–189. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A. A novel method for nonlinear fractional differential equations using symbolic computation. Waves Random Complex Media 2017, 27, 163–170. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khater, M.M.A.; Attia, R.A.M.; Lu, D. Modified Auxiliary Equation Method versus Three Nonlinear Fractional Biological Models in Present Explicit Wave Solutions. Math. Comput. Appl. 2019, 24, 1. https://doi.org/10.3390/mca24010001
Khater MMA, Attia RAM, Lu D. Modified Auxiliary Equation Method versus Three Nonlinear Fractional Biological Models in Present Explicit Wave Solutions. Mathematical and Computational Applications. 2019; 24(1):1. https://doi.org/10.3390/mca24010001
Chicago/Turabian StyleKhater, Mostafa M. A., Raghda A. M. Attia, and Dianchen Lu. 2019. "Modified Auxiliary Equation Method versus Three Nonlinear Fractional Biological Models in Present Explicit Wave Solutions" Mathematical and Computational Applications 24, no. 1: 1. https://doi.org/10.3390/mca24010001
APA StyleKhater, M. M. A., Attia, R. A. M., & Lu, D. (2019). Modified Auxiliary Equation Method versus Three Nonlinear Fractional Biological Models in Present Explicit Wave Solutions. Mathematical and Computational Applications, 24(1), 1. https://doi.org/10.3390/mca24010001






