1. Introduction
In recent years, classical and non-classical algebra, as well as logical algebras have attracted the keen interest of researchers and have been widely considered as a strong tool for information systems and many other branches of computer sciences, including fuzzy information with rough and soft concepts. Many authors have studied graphs in classical structures, more precisely in commutative cases, e.g., commutative rings [
1], commutative semirings [
2], commutative semigroups [
3], nearrings [
4], Cayley vague graphs [
5], etc. Beck [
6] associated commutative rings and their zero divisor graphs
. Jun and Lee [
7] defined zero divisor graphs in BCK/BCI-algebras and showed related properties. Some properties of graphs related to BCH-algebras have been discussed by Hu and Li in [
8], whereas Zahiri and Borzooei [
9] defined a new graph of BCI-algebras
X and showed that the graphs defined by Jun and Lee [
7] and Zahiri and Borzooei [
9] are the same. They also proved that the
-divisor and
p-semisimple part of a BCI algebra
X is a quasi-ideal of
X. The fuzzy logic of most logical algebras has been the recent choice of numerous researchers, including Hajek [
10], who introduced the mathematics of fuzzy logic. Prabpayak and Leerawat [
11] introduced KU-ideals, which can be considered to be an interesting idea in logical algebras. Yaqoob et al. [
12] introduced cubic KU-ideals of KU-algebras. Roughness in KU-algebras was studied by Moin and Ali [
13], whereas rough set theory has been applied to UP-algebras by Moin et al. [
14]. Further, Mostafa et al. [
15] defined graphs of commutative KU-algebras.
Iampan introduced the concept of UP-algebras [
16], whereas Senapati et al. [
17] represented UP-algebras in an inter-valued intuitionistic fuzzy environment. Senapati et al. [
18] applied the cubic set structure in UP-algebras and proved the results based on them. Akram and Dudek [
19] showed interval-valued fuzzy graphs. Akram and Davvaz [
20] defined the concept of strong intuitionistic fuzzy graphs. Types of irregular bipolar fuzzy graphs and their applications were studied by Akram in [
21].
In this paper, we introduce a (undirected) UP-graph of commutative UP-algebras and denote it by , whose vertices are the elements of UP-algebra A with the condition that the vertices form an edge between them if and only if Further, it is shown that the graph of equivalence classes of A i.e., denoted by , and the graph folding of a commutative UP-algebra A are the same; more precisely, they form a complete bipartite graph.
2. Preliminaries
In this section, we shall consider concepts based on UP-algebras, UP-subalgebras, UP-ideals and other important terminologies with examples and some related results.
Definition 1. [16] By a UP-algebra, we mean an algebra of type with a single binary operation ∗
that satisfies the following identities: for any (UP1):
(UP2):
(UP3):
(UP4): implies
Example 1. [16] Let X be a universal set. Define a binary operation ∗
on the power set of X by putting = = for all . Then, is a UP-algebra, which is the power UP-algebra of Type 1. Example 2. [16] Let X be a universal set. Define a binary operation ∗
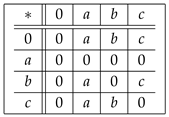
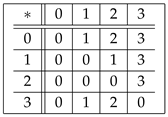
on the power set of X by putting = = ∀ . Then, is a UP-algebra, which is a power UP-algebra of Type 2. Example 3. Let be a set in which ∗ is defined by the following Cayley table:
It is easy to see that is a UP-algebra.
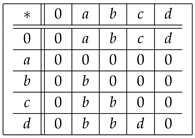
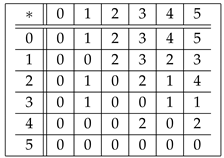
Example 4. Let be a set in which ∗ is defined by the following Cayley table:
Here, is a UP-algebra.
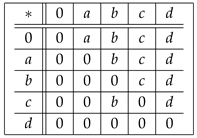
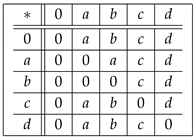
Example 5. Let be a set in which ∗ is defined by the following Cayley table:
Here, is a UP-algebra.
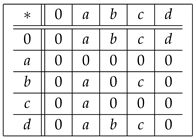
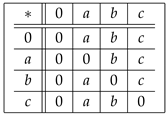
Example 6. Let be a set in which ∗ is defined by the following Cayley table:
Here, is a UP-algebra.
Proposition 1. In a UP-algebras A, the following properties hold for any
- (1)
,
- (2)
and
- (3)
- (4)
- (5)
- (6)
and
- (7)
We define a binary relation in a UP-algebras A as . We observe that this binary relation ≤ forms a POS, where zero is the smallest element of A. The following conditions are true for for all with
Proposition 2. Let be UP-algebras, then define a binary relation ≤ on A as follows: for all :
- (1)
,
- (2)
and
- (3)
and
- (4)
- (5)
- (6)
and
- (7)
Proposition 3. Let be UP-algebras, then define a binary relation ≤ on A as follows: for all :
(UP5):
(UP6):
(UP7):
(UP8):
Proposition 4. In a UP-algebra A, the given axioms are satisfied: for all :
- (1)
- (2)
Definition 2. Let be a UP-algebra. Then, a subset S of A is called the UP-subalgebras of A if the constant zero of A is in S and itself forms a UP-algebra. Clearly, A and are UP-algebras of A.
Definition 3. Let A be a UP-algebra. Then, a subset B of A is called a UP-ideal of A if it satisfies:
- (i)
The constant zero of A is in B and
- (ii)
for ant and
Clearly, A and are UP-ideals of A.
Example 7. Let be a set with operation *, which is defined in the table given in Example 5. We find that the subsets and are UP-ideals of A.
is a UP-algebra here. Further, and are UP-ideals of A.
Definition 4. Define then A is said to be the commutative UP-algebra if we get , i.e.,
Theorem 1. For a UP-algebra the following conditions are equivalent:
- (1)
A is commutative,
- (2)
- (3)
Proof. It is straightforward. ☐
Lemma 1. If A is a commutative UP-algebra, then
Proof. If A is a commutative UP-algebra, then we have, = (by (UP5))
Furthermore, (by (UP8))
Hence,
For its converse part, by using (UP5) and Proposition 4 (1), we have,
Hence, Therefore, ☐
From now on, by A, we mean commutative UP-algebra unless otherwise stated.
Definition 5. Let B be a subset of A. Then, the annihilator of B is defined by, This is known as the UP-annihilator of B. If it is written as ann
Lemma 2. Let B be a subset of A and ann be a UP-annihilator of then ann is an ideal of A.
Proof. Since so Further, let then Hence, by Lemma 1, which implies that Therefore, ann is an ideal of ☐
Lemma 3. If then we have the following.
- (1)
If then
- (2)
- (3)
Proof. (1) Suppose that so but hence That is, implies .
(2) Since and so by Part (1), and hence,
Conversely, if then and For any , and hence, we have implies
Therefore,
(3) We have , so from (1), and ☐
Lemma 4. If B is a non-empty subset of A, then
Proof. We have that
so by Lemma 3 (2):
☐
Definition 6. Define a relation ∼ on A as
From the above definition, we obtained the following straightforward result.
Lemma 5. The relation forms an equivalence relation on UP-algebra
3. Graphs of Commutative UP-Algebras
We shall introduce the graph and subgraph of UP-algebras A, as well as the graph and subgraph of equivalence classes of A. The set represents the graph of A, whereas the set represents the set of vertices of G and the set of edges. Graph G is said to be connected if there is a path between any two vertices, otherwise G is said to be disconnected. Further, G is said to be a complete graph if every two distinct vertices form exactly one edge. Graph G is said to be bipartite if its vertex set can be partitioned into disjoint subsets and such that every edge of G joins a vertex of with a vertex of A graph G is said to be a complete bipartite graph if every vertex in one bipartition subset is connected to every vertex in the other bipartition subset. The distance, represents the length of the shortest path from the vertices a to If there is no such path between a and b that forms the shortest path, then it is defined by The diameter of graph G is written as
We say that the diameter of G is zero if there is only one vertex in A connected graph with more than one vertex has a diameter of one if and only if each pair of distinct vertices forms an edge; such a graph is called a complete graph. The neighborhood of a vertex is the set of the vertices in G adjacent to In other words, }. Later, we will see that, if then
For terminologies related to graphs and various examples, one can refer to [
22,
23]. A graph
H is called a subgraph of
G if
and
Any two graphs
and
are said to be isomorphic if there is a bijective mapping
in such a way that
, then
; otherwise, graphs are called non-isomorphic. A fan graph
is a path
where
is an extra vertex connected to all vertices of the path
where
}.
Definition 7. We associate a graph corresponding to a commutative UP-algebra A, which is an undirected graph whose vertices are the elements of A and two distinct elements are adjacent if and only if A graph with this condition is said to be a UP-graph.
Theorem 2. The graph is a connected graph with diam
Proof. Let be any two distinct vertices of the graph Then, we have the following two cases.
Case I:
Case II: Then, there exists with If then will form a path of length two; and hence, If and then is a path of length three, and hence, In case then thus will be a path of length two, so In all these cases, diam From the above situations, there exists a path between any two distinct elements in A, and so, is connected. ☐
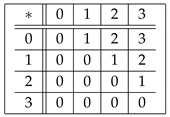
Example 8. Let be a set in which ∗ is defined by the following Cayley table:
By Algorithm 1, given later, it is easy to observe that
is a commutative UP-algebra. By considering vertices
the graph of
A is given below in
Figure 1:
| Algorithm 1: Algorithm for UP-algebras. |
![Mca 23 00061 i010 Mca 23 00061 i010]() |
4. Graph of Equivalence Classes of a Commutative UP-Algebra A
We can easily construct the graph of equivalence classes of A by using equivalence relation, as for any Therefore, if and , hence We define equivalence classes of a as
Lemma 6. Let be a set of equivalence classes of where Then,
Proof. We have that ann ann so Next, we claim that Let Then, ann Hence, we claim that ann If then i.e., Hence, That is, Then, ann Therefore, and Hence ☐
Definition 8. Graph formed by equivalence classes of A is called simple whose vertices are the elements of equivalence class , and two distinct classes are adjacent in:
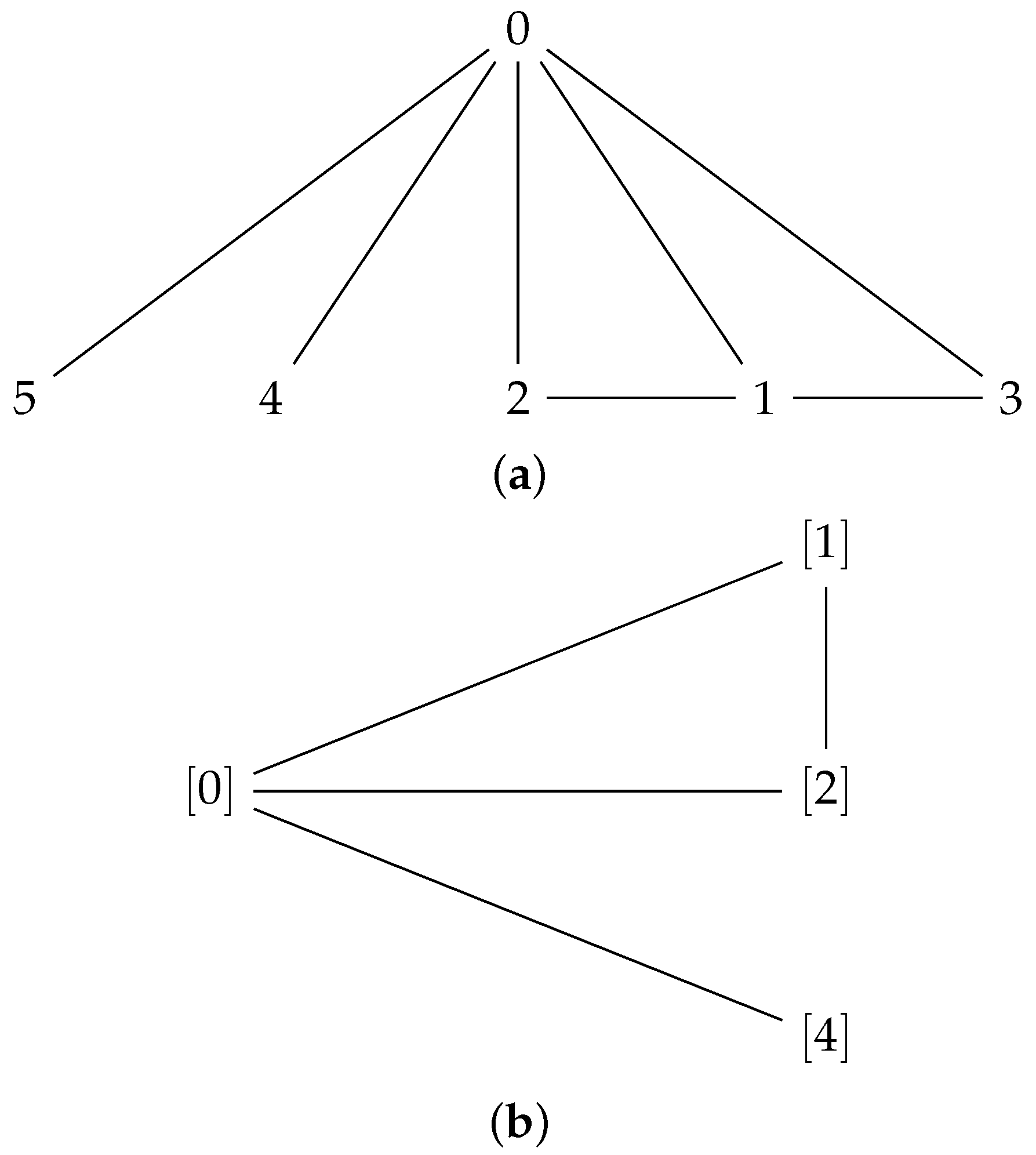
Example 9. Let be a set in which ∗ is defined by the following Cayley table:
We find by Algorithm 1 that is a commutative UP-algebra. Further, the graph of A whose set of vertices and edges are defined by and since ann ann ann ann then The given Figure 2 shows the graph of and Lemma 7. The following are true for in a UP-algebra
- (1)
is a subgraph of
- (2)
If then is a star graph.
Proof. It is straightforward. ☐
Theorem 3. Let be the graph of equivalence classes of Then, for any distinct vertices if and are connected by an edge, then ann and ann become distinct UP-annihilator ideals of
Proof. We consider ann = ann so Hence, = , which is a contradiction. That is, ann and ann are distinct UP-annihilator ideals of ☐
The converse of above Theorem 3 is not true. In the above Example 9, it is easy to find that vertices [
20,
21] are distinct UP-annihilators, but there is no edge between them.
Theorem 4. If is complete or fan graph, then
Proof. Consider
Here, if
is the complete graph, then every pair of vertices of
is adjacent. As a result, we get that:
and
for
Therefore, we get that
for all
⟹, every vertex of
is an equivalence class of
, and so, the vertices of
are distinct and equal to the same number of vertices of
thus, there exists an isomorphic map
such that
for each
and the mapping of edges
, which maps the edges
, which map the edge
in
to the edge
in
, which is a well-defined bijection, so
is complete. Therefore,
is isomorphic to
Next, to show that if
is a fan graph, then
is isomorphic to
, if we consider that
is a fan graph, then
consists of a path
and a vertex
such that
is connected to all vertices of the path
Clearly,
Therefore, for all Therefore, the vertices of are distinct, and there is the same number of vertices of Thus, finally, there exists an isomorphic map satisfying for each and the mapping of edge , which maps the edge in to the edge in , which is a well-defined bijection, hence showing that ☐
Theorem 5. If is complete bipartite graph, then is an edge.
Proof. We suppose that is complete bipartite, whose vertex set is As is complete bipartite, so we can split the vertices of into two parts, say and Therefore, we have
Therefore, and which implies that there are two distinct equivalence classes and in , which are adjacent. Hence, is an edge. ☐
Lemma 8. Let and be two graphs of commutative UP-algebra and For if then
Proof. It is straightforward. ☐
Theorem 6. If for corresponding to commutative UP-algebras A and then
Proof. Suppose that and such that there exists an isomorphism satisfying for each Therefore, by Lemma 8, for each i, so , and its edge mapping which maps the edge in to the edge in is a well-defined bijective map. Thus, ☐
The converse is not true, as is clear from the following example, where corresponding to two commutative UP-algebras A and B, but .
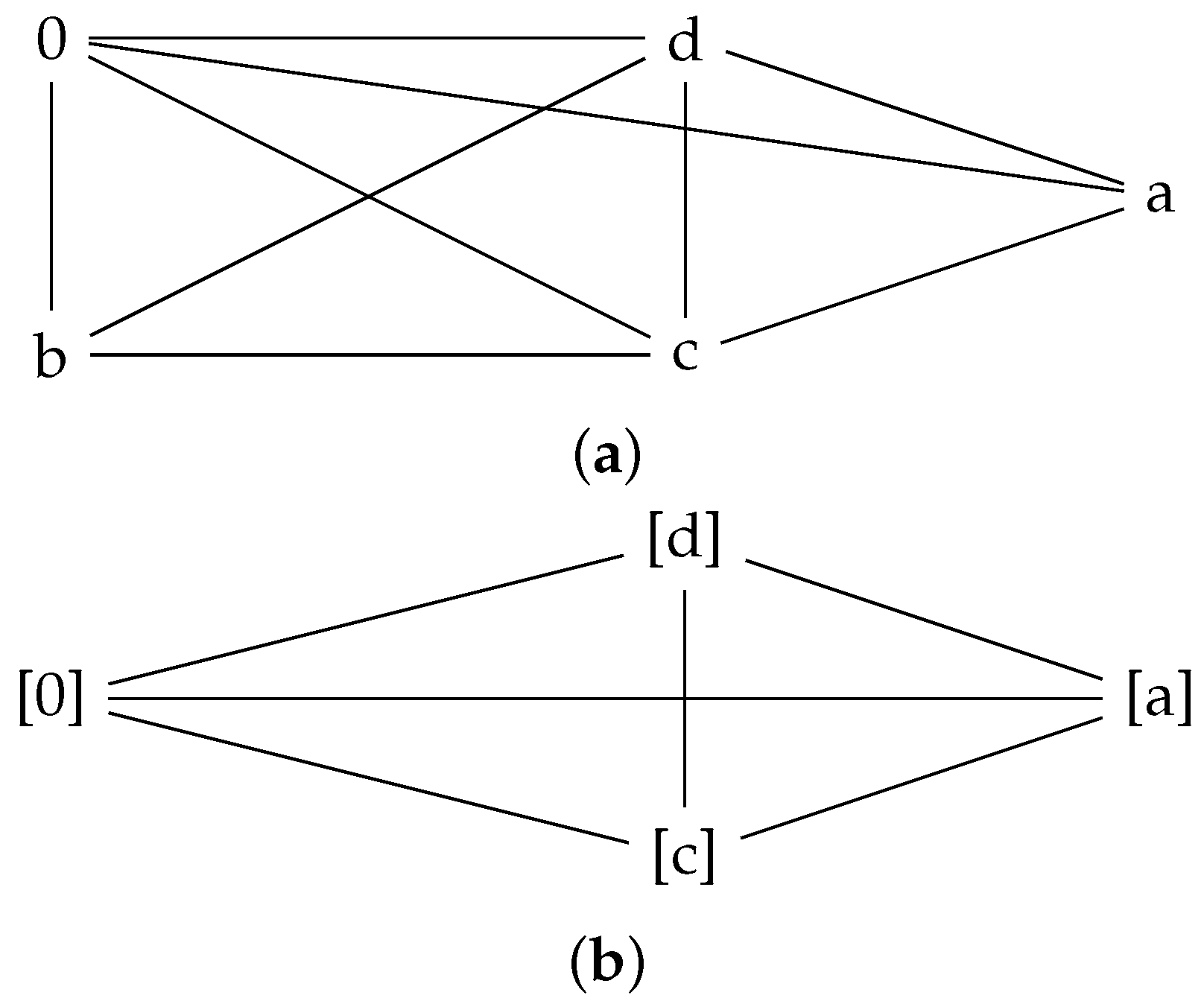
Example 10. (a) Let be a set in which ∗ is defined by the following Cayley table:
By Algorithm 1, it is clear that is a commutative UP-algebra. The corresponding graphs associated with A are given below in Figure 3a,b. (b). Let , then by Algorithm 1, it is clear that is a commutative UP-algebra under the given Cayley table:
The graphs and are shown below in Figure 4a,b: Clearly, the graphs , whereas
5. Graph Folding
In this section, we shall discuss the graph folding of a graph of a commutative UP-algebra.
Definition 9. [24] Let and be two graphs and be a continuous function. Then, F is called a graph map, if: - (1)
For each vertex is a vertex in
- (2)
For each edge dim
A graph map is called a graph folding if and only if F maps vertices to vertices and edges to edges. In other words, for , we have and for The graph folding is called non-trivial if and only if and Graph folding between two graphs and is denoted by , and for a simple graph , it is denoted by
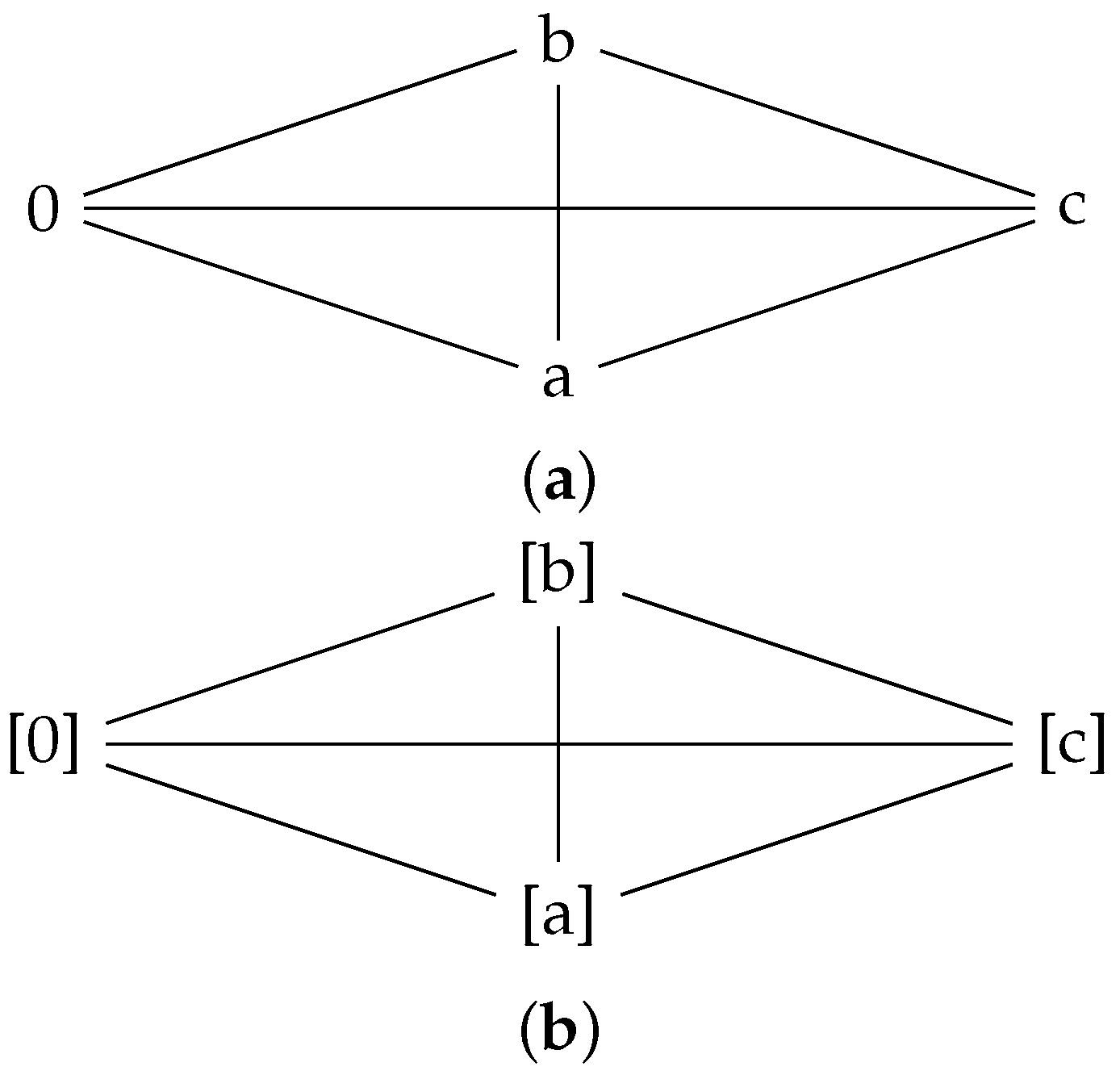
Example 11. Let with ∗ as an operation defined by the Cayley table:
We note here that
is a commutative UP-algebra by Algorithm 1. For a graph of
A, we have the set of vertices as
and the set of edges as,
The graph
is a complete bipartite and star graph. It is shown below in
Figure 5.
Define a graph map
by
and
Here,
F is a graph folding satisfying
The graph
is shown below in
Figure 6.
Here, a complete bipartite or a star graph can be folded onto an edge. We have a theorem based on the above statement.
Theorem 7. Any complete bipartite graph of A can be folded onto an edge.
Proof. Let
be a complete bipartite graph of a commutative UP-algebra
A with the vertex set as
Since
is a bipartite graph, we can split vertex set
into two sets.
, and
Since each vertex of
is adjacent to each vertex of
only by one edge, therefore
We define a graph folding map
as,
Clearly, is the edge ☐
The following corollary follows from Theorems 5 and 7.
Corollary 1. Let A be a commutative UP-algebra. If is the complete bipartite graph, then the graph and the graph folding of A are the same graphs.