1. Introduction
Many researchers and academics often need to solve optimal control problems that are frequently postulated in various engineering, social, and life sciences [
1,
2,
3]. An optimal control problem is concerned with finding control functions, (or policies), that achieve optimal trajectories for a set of controlled differential state variables. The optimal trajectories are determined by solving a constrained dynamical optimization problem, such that a cost index is minimized (or maximized), subject to constraints on state variables and control functions. Mathematically, an optimal control problem may be stated generally as follows (bold symbols indicate vector-valued functions):
Find control functions
and corresponding state variables
which minimize (or maximize) the cost index
subject to
with initial conditions
and end conditions and bounds
In the formulation (1)–(5), the generally nonlinear H, and G are scalar functions, whereas F, Q and S are vector valued functions. Typically, either H or Q are specified but not both in the same problem. Common forms of Q and S are end conditions on the state variables, , and bound constraints on the controls, respectively. More general forms of S considered in this paper include algebraic and integral constraints involving derivatives. The matrix M in (2) offers an optional coupling of states’ temporal derivatives by a mass matrix which may be singular. If M is singular, the equation system (2) is differential algebraic, or DAE. For uncoupled derivatives, M is the identity matrix which can be omitted. Furthermore, , which denotes the final time, may be fixed or free.
Numerical solution strategies for (1)–(5) can be classified into two approaches:
indirect and
direct methods. Indirect methods employ Pontryagin’s minimum principle to transform the problem into an augmented Hamiltonian system requiring the solution of a boundary value problem which may be hard to solve [
4,
5]. On the other hand, direct method approaches transform the original optimal control problem into a nonlinear programming problem which can be solved by various established NLP packages. The transformation is carried out via a discretization of the control and the state functions on a time grid using some form of a collocation method [
4,
6,
7]. Complete discretization of the state and control functions eliminate the need to iteratively solve the
inner initial value problem (IVP) (2) but at the expense of a large numbers of decision variables for the NLP solver. Other direct approaches rely only on a partial parametrization for the control functions using piecewise constant or higher order polynomial approximations [
8]. In this approach, the
inner IVP must be solved repeatedly by the
outer NLP algorithm while searching for the optimal parameter vector. Except for the most trivial cases, optimal control problems are inherently nontrivial to solve. They typically require a level of programming fluency, in addition to a good understanding of the general structure of the solution strategy, and the various solvers required to implement it [
9].
In [
10], the author introduced a practical spreadsheet method for solving a class of optimal control problems using basic spreadsheet skills. The method utilized two elementary calculus functions: an initial value problem solver and a discrete data integrator from an available Excel calculus Add-in [
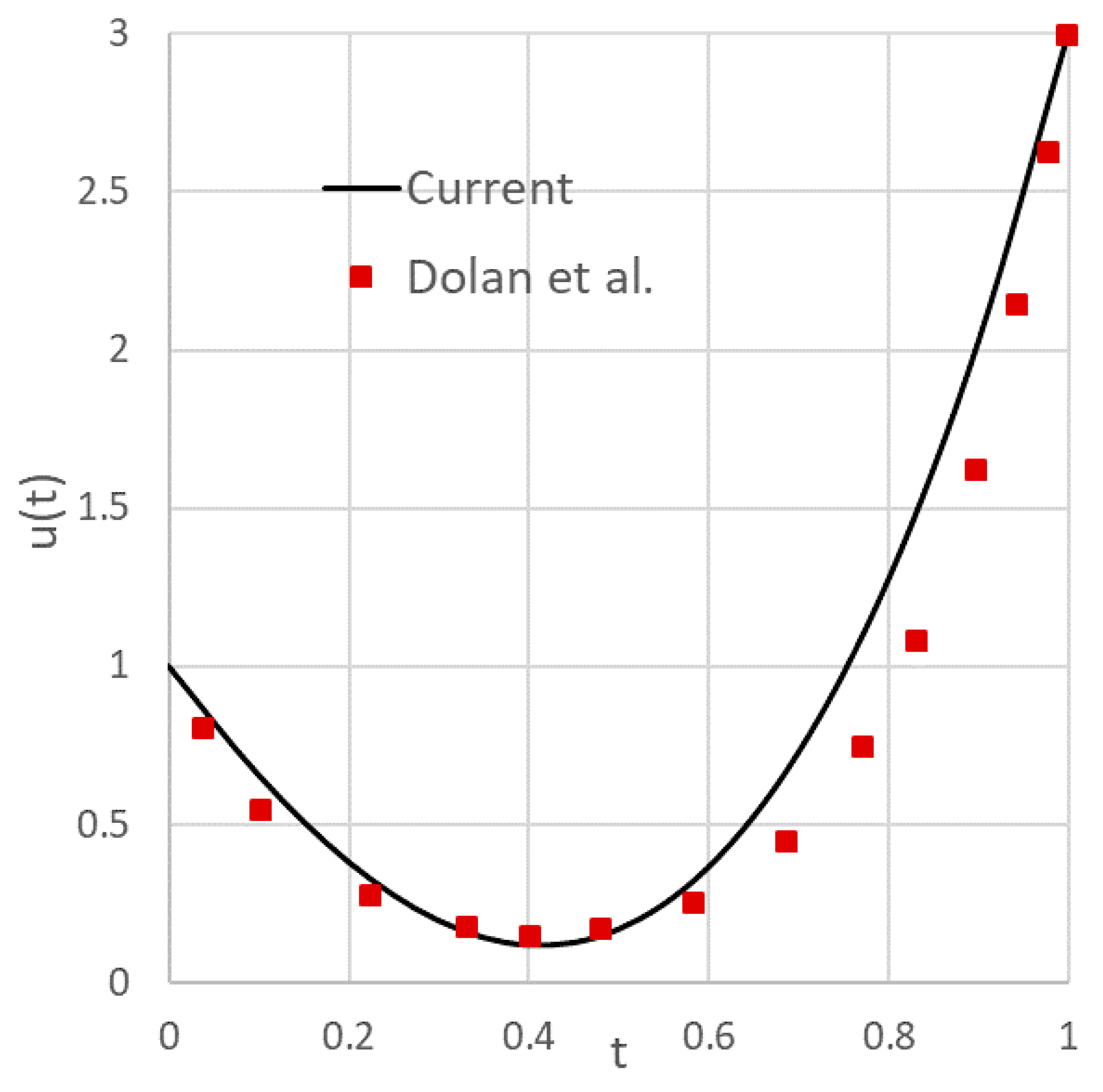
11] in conjunction with Excel intrinsic NLP solver to formulate a partial-parametrization direct solution strategy. With the aid of the calculus functions, a cost index was represented by an equivalent formula that fully encapsulated a control-parametrized inner IVP (2)–(3). Excel NLP solver was employed next for minimizing (or maximizing) the cost index formula, by varying a decision parameter vector, subject to bounds constraints on state and control variables. The method proved effective at solving several nonlinear optimal control problems reproduced from Elnagar and Kazemi [
6] who employed a full-parametrization direct method using pseudo-spectral approximation and NLPQL optimization software.
This research paper aims at generalizing the method introduced in [
10] for more general formulations of optimal control than previously considered. More specifically, this paper demonstrates a systematic solution strategy formulated by the aid of various elementary calculus functions, for optimal control problems involving one or more of the following conditions: dependence on higher order derivatives of state or control variables in the cost index and constraints; integral and algebraic dynamic constraints; as well as implicit inner IVP. In addition, this paper investigates convergence and error control of the method, and provides direct comparison of optimal trajectories with published solutions obtained by fundamentally different methods.
It should be noted that the solution strategy formulation pursued in this research, although founded on a common approach, follows closely the original mathematical problem statement, and thus implementation of the strategy varies according to the given problem. Therefore, the paper gives considerable emphasis on the application of the method using four representative problems selected from various applications. Results presented in
Section 3 are remarkable, in terms of convergence, agreement with published solutions, and notably, the minimal effort required to obtain them with basic spreadsheet formulas.
In view of traditional spreadsheet applications, the devised solution strategy represents a leap in the utilization of the spreadsheet for solving general optimal control problems. The strategy departs markedly from prior spreadsheet approaches [
12,
13] by shifting the effort from a low-level detailed algorithmic implementation to a high-level problem modeling. Prior approaches utilized the spreadsheet explicitly as the computational grid for the discretization and solution of the inner IVP. This effectively constrained the scope to rather simple problems that can be easily discretized with an explicit differencing scheme suitable for the spreadsheet. In contrast, we employ a set of pure calculus functions for computing integrals, derivatives and solving differential equations as the building blocks for a direct solution method. The calculus functions, described in
Appendix A, utilize adaptive algorithms which are independent of the spreadsheet grid and thus suitable for a general class for nonlinear stiff problems. The calculus functions are utilized in formulas just like intrinsic math functions based on a simple input/output model. In essence, the calculus functions represent a natural extension of the built-in spreadsheet math functions with the allowance that some of their input arguments are functions themselves and not just static values.
The reminder of this paper is organized as follows: In the next section, we present an outline of the general steps required to implement the direct spreadsheet solution strategy, and discuss sources of errors that impact convergence and accuracy of the solution as well as possible remedies. In
Section 3, we apply the method for solving four different optimal control problems selected to demonstrate the various conditions outlined earlier. Direct comparisons of optimal trajectories obtained by the method versus published solutions obtained by fundamentally different approaches are also provided. In addition, effects of parametrization order and error control are investigated in some problems.
Section 4 presents concluding remarks as well as directions for future research. Detailed descriptions of the various calculus functions utilized in this work are included in
Appendix A.
2. Mechanics of Spreadsheet Direct Method
The solution strategy is based on an adaptation of the control-parametrization direct approach [
4,
8] by an analogous spreadsheet functional formulation. The building blocks of the functional formulation are a set of calculus spreadsheet functions [
11,
14] which integrate with the spreadsheet, like intrinsic pure math functions, but also accept formulas as a new type of argument for solving problems in integral, algebraic, and differential calculus. For example, an integration function accepts a formula and limits as inputs, and it outputs an accurate integral value much like an intrinsic math function accepts a number and computes its square root. Specifically, we make use of the following functions from a calculus Add-in [
11]:
Initial value problem solver, IVSOLVE, using RADAU5 an implicit 5th-order Runge-Kutta algorithm with adaptive time step [
15].
Discrete data Integrator, QUADXY, using cubic splines [
16].
Discrete data differentiator, DERIVXY, using cubic splines [
16].
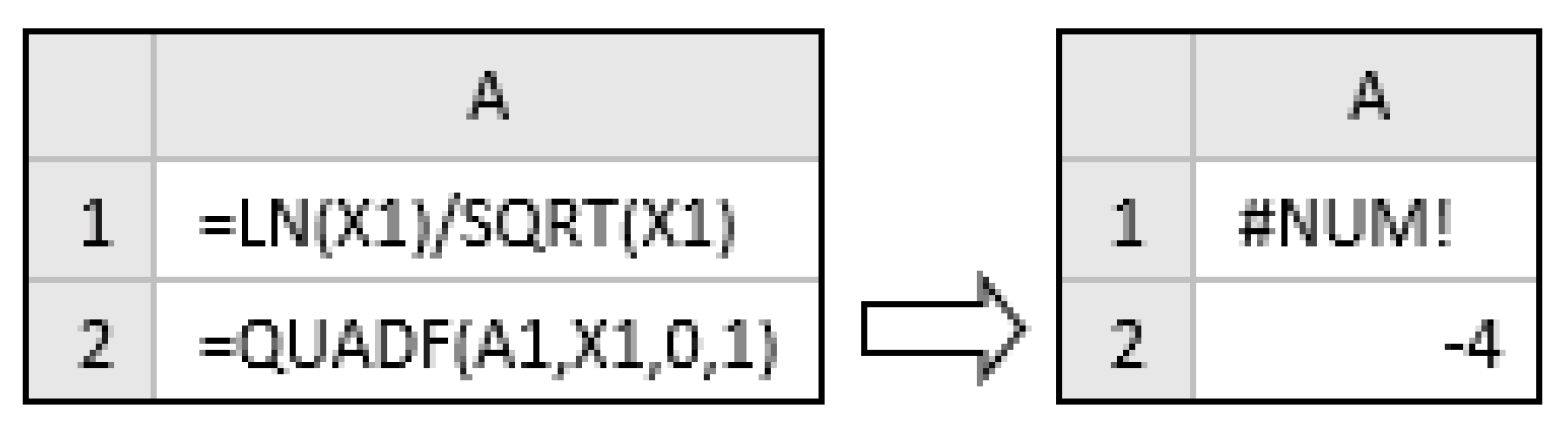
Formula integrator, QUADF, using Gauss quadrature with adaptive error control [
17].
The functions are utilized in combination with Excel NLP solver, which is based on the Generalized Reduced Gradient algorithm based on Lasdon and Waren [
18]. A detailed description of the calculus functions usage, and respective algorithms are given in
Appendix A. The critical characteristic of the calculus functions which permits their seamless utilization with the NLP solver in a functional paradigm, is the mathematical purity property. The calculus functions do not modify their inputs, and produce no side effects in the spreadsheet. They only compute and display a solution result in their allocated spreadsheet memory cells. The authority to modify the inputs to the calculus functions, via changes to the decision parameter vector, is confined to the outer NLP solver command.
Below, we describe the main elements of the solution strategy introduced originally in [
10] but generalized in this work for solving general optimal control problem (1)–(5) with the aim of supporting the various conditions outlined earlier.
2.1. Solution Strategy
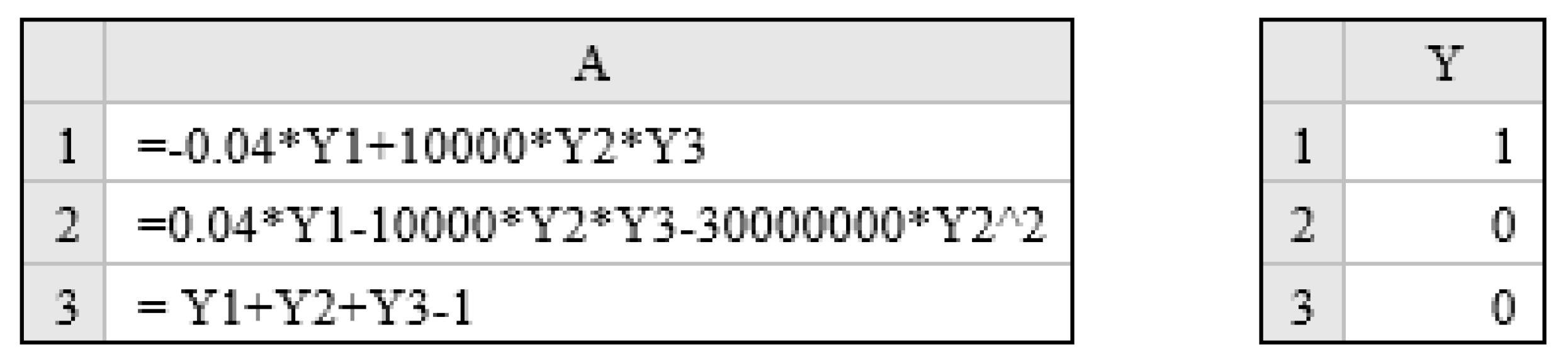
The strategy comprises three ordered steps which are implemented by the aid of calculus functions:
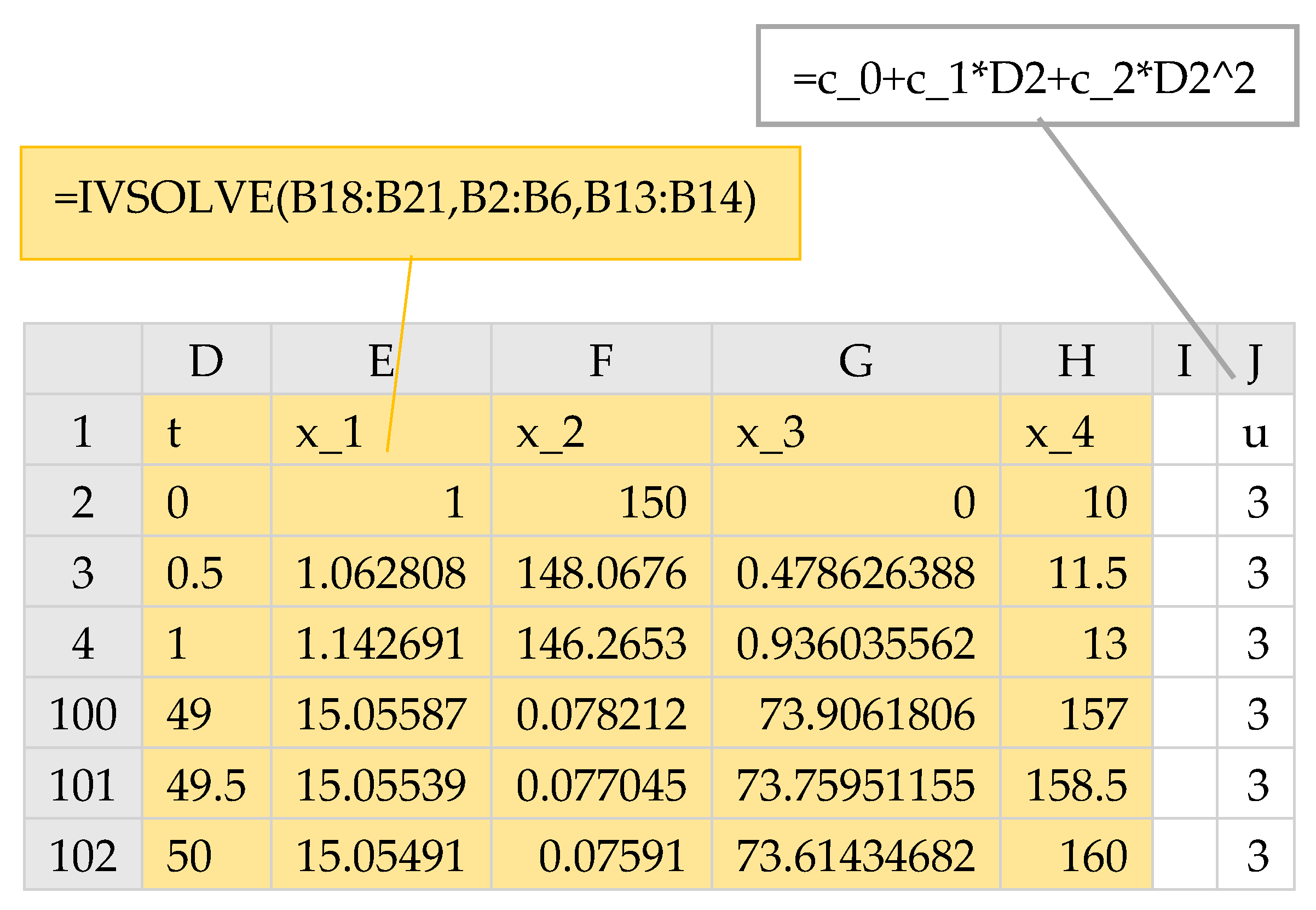
In the first step, we obtain an initial solution to the inner IVP (2)–(3), based on suitable parametrization for the control functions with initial guesses for the unknown parameters and a final time for free-time problems. The unknown parameters and the final time constitute the decision variables for the final optimization step by the outer NLP solver. Any prior information about the controls should be incorporated in the specified parametrization. Absent any information, a low-order polynomial is often an adequate choice. The initial IVP solution is obtained by the calculus function IVSOLVE which displays the state variables,
, in an allocated array of the spreadsheet at uniform output time points. It should be noted that output time grid is determined by the number of rows in the allocated output array but is, otherwise, unrelated to the accuracy of the computed solution. To display a finer output time grid, a larger output array should be allocated. However, the resolution of the output time grid affects the accuracy of the computed integrals for the cost index and any integral constraints which is discussed in
Section 2.2. Optional parameters to IVSOLVE could also be used to control or specify the output time points.
In the second step, we construct an analogous formula for the cost index (1) dependent on the initial solution outputted by IVSOLVE. The cost index may depend on
, the control values,
, as well as first and higher order derivatives of the state variables and controls. Values for
,
and higher derivatives are readily generated using the specified parametrized formula for a control
. The spreadsheet is particularly suited for such computations using its AutoFill feature. On the other hand, values for the state variables derivatives
and
are not readily available and must be approximated by differentiating
values obtained by IVSOLVE. We accomplish this task by the aid of a discrete data differentiator calculus function DERIVXY which computes derivatives using cubic splines to model the best function described by
. With all the necessary values obtained, we proceed to defining an analogous formula for the cost index, which is typically defined as a continuous time integral of an algebraic integrand. The devised method is to sample the integrand expression using the obtained values for the states, controls and their derivatives, followed by employing a discrete data integrator calculus function QUADXY to integrate a cubic-spline fit function through the sampled integrand. Depending on a particular problem formulation, it may be necessary to define additional formulas to represent constraints equations (5) that may be present. Such formulas can often be constructed in a similar way to the cost index formula using appropriate calculus functions. In particular, we shall demonstrate in
Section 3 using an additional formula integrator function QUADF to define an integral constraint formula.
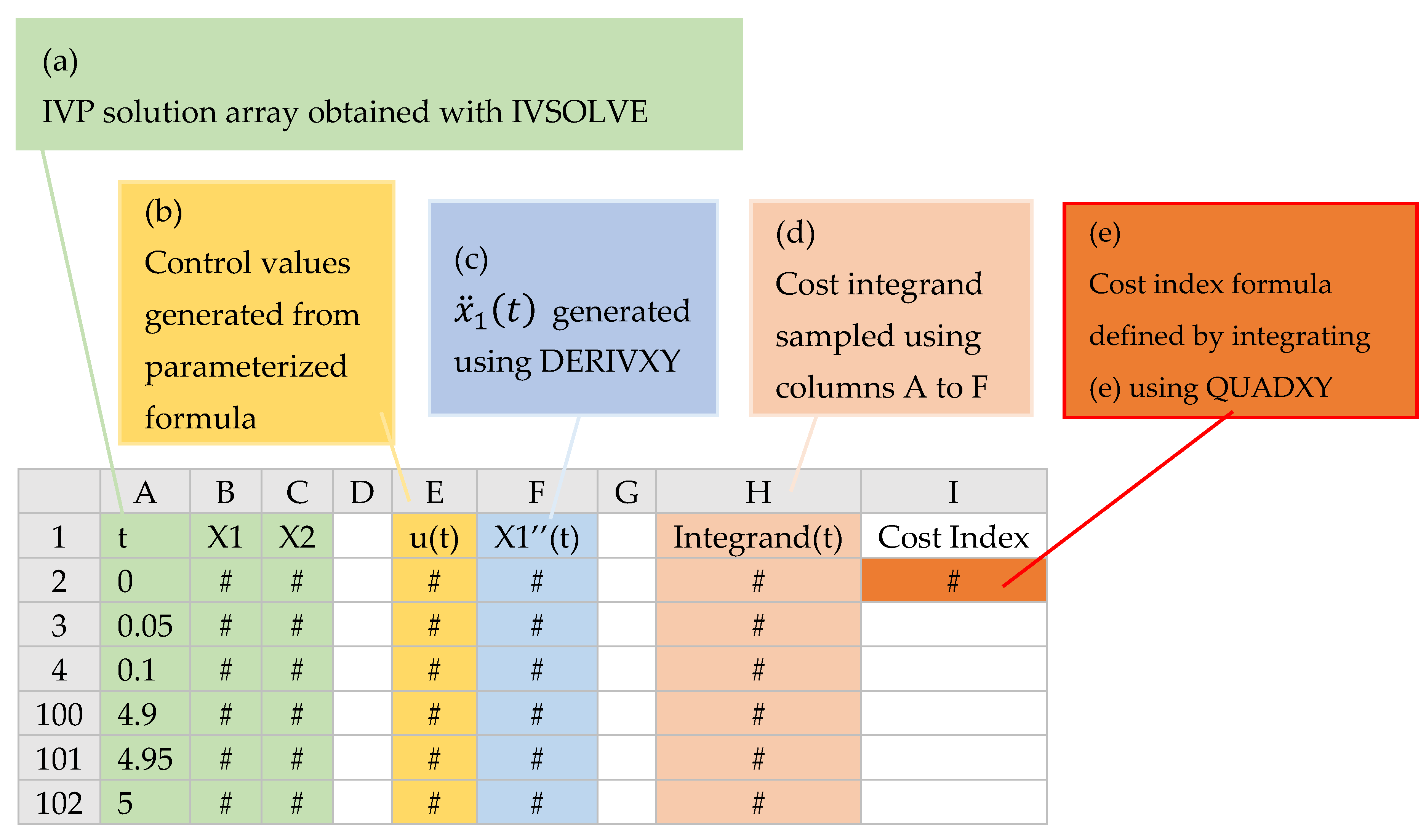
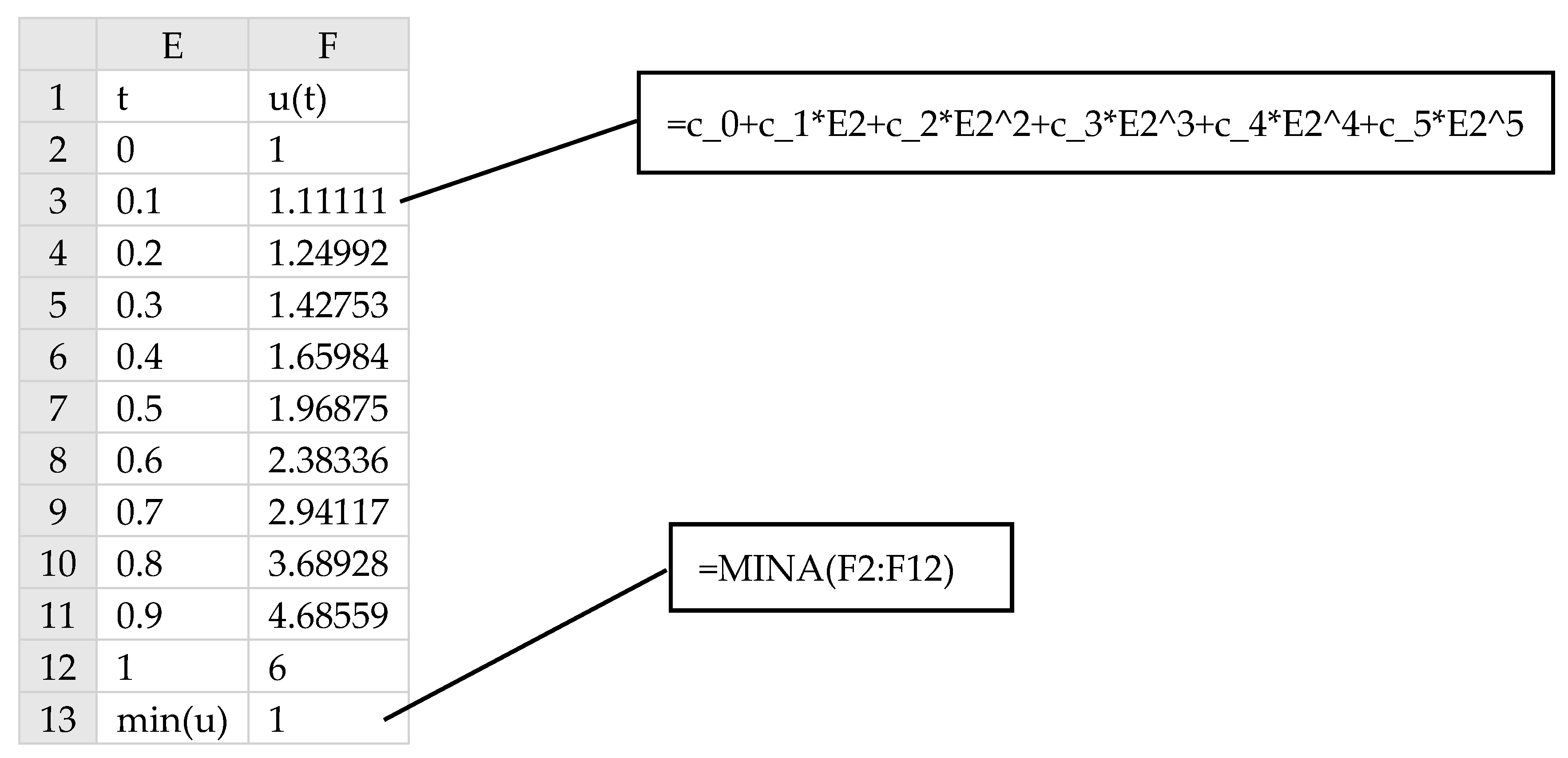
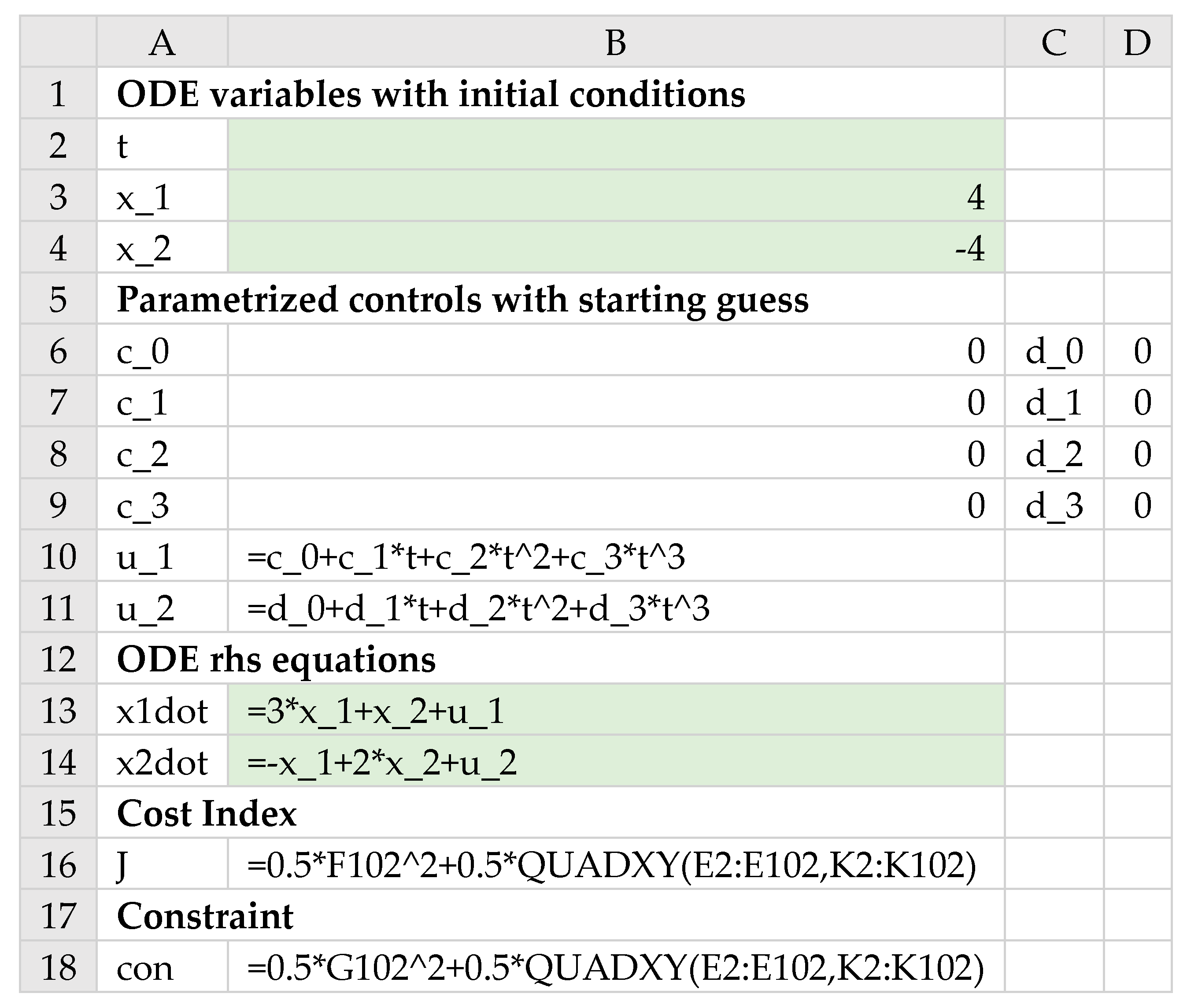
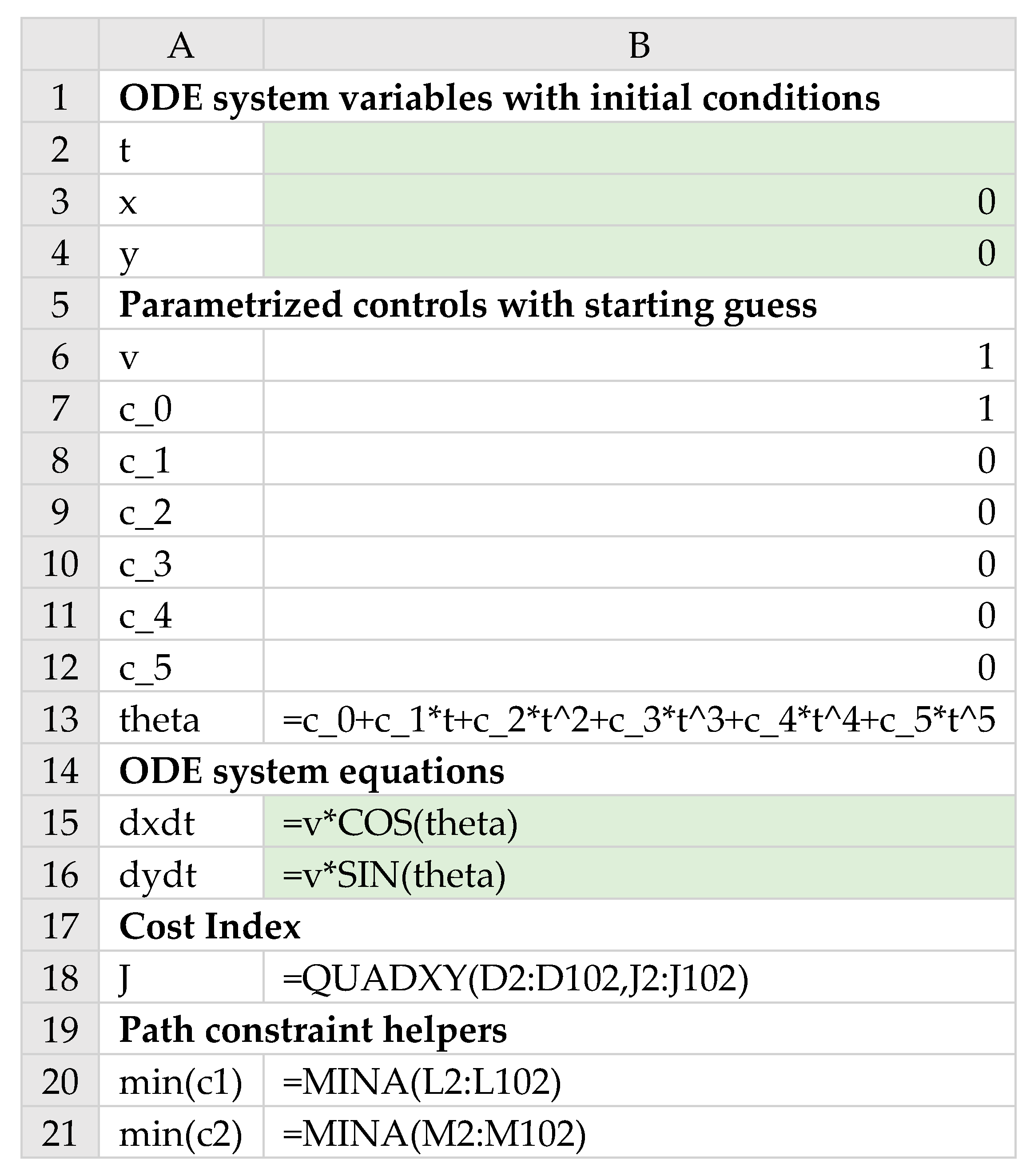
Figure 1 illustrates the aforementioned steps applied to an optimal control problem with one control and two state variables. An initial IVP solution, which is dependent on a decision parameters vector, is obtained with IVSOLVE in an array (
Figure 1a). Values for the control,
, and any needed state derivatives such as
, are generated in additional columns (
Figure 1b,c) at the time values of the IVP solution. Next, the cost index integrand expression is sampled at the IVP solution times (
Figure 1d), and the sample is then integrated to define the cost index formula (
Figure 1e). The generated values interdependence hierarchy ensures that any change to the decision parameters vector, such as by an outer NLP solver, will trigger reevaluation of the cost index formula in the proper order shown in the figure. The cost index formula thus fully encapsulates the inner IVP problem.
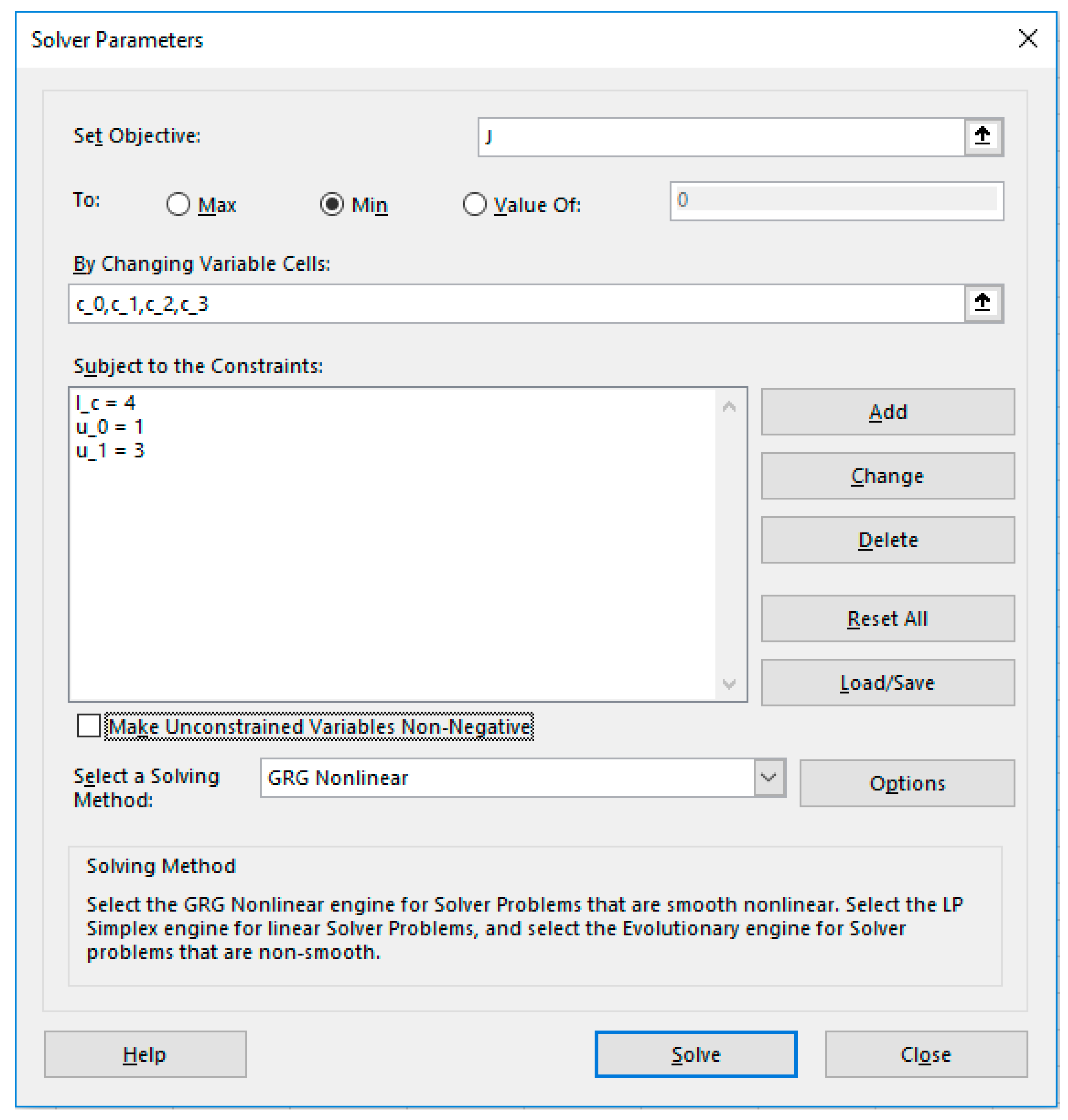
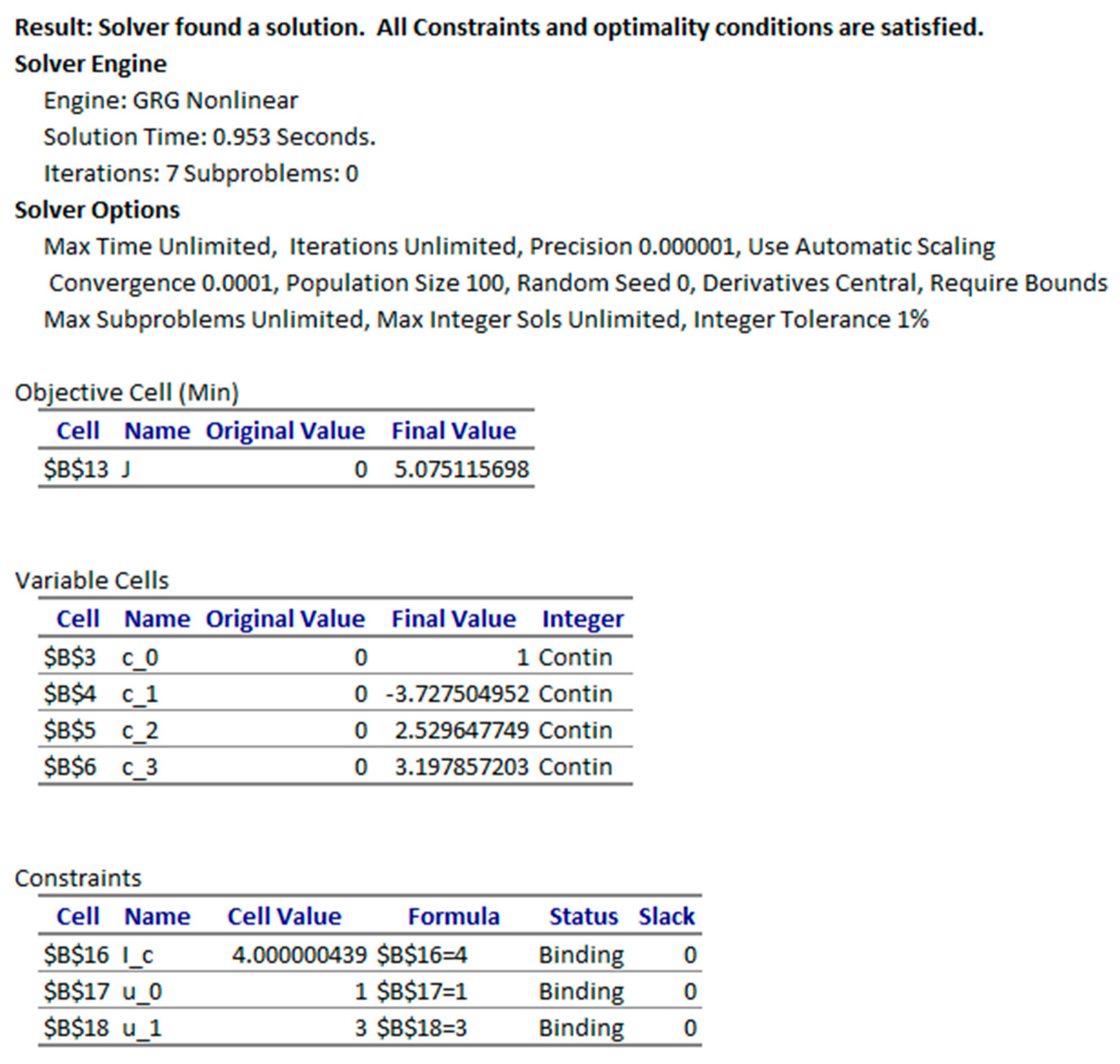
In the last step, we configure Excel NLP solver to minimize (or maximize) the cost index formula by varying the decision parameters vector subject to bounds, end conditions and other present constraints. Bound constraints on , as well as end point constraints on , are imposed directly on the corresponding values in the IVP solution array. More general constraints are imposed on additional formulas constructed in step 2 as needed. The three steps are demonstrated on several examples in the next section.
2.2. Convergence and Error Control
Two sources of errors are introduced by the spreadsheet method with respect to the original problem. The first error is introduced by restricting the space of admissible control functions to a finite-dimensional space, for example, variable-order polynomials up to a fixed degree. For some problems, it may not be possible to find a solution if the optimal control, in fact, lies outside the admissible space. The second source of error is introduced by the calculus numerical algorithms. This error can be further split into two sources. The error associated with solution of the inner IVP, and the error associated with integration (or differentiation) of discrete data sets generated from the IVP solution. The first error is bounded by the tolerances specified for IVSOLVE algorithm. The second error impacts the accuracy of the computed integral for the cost index. Under the assumption that the discrete data describe a smooth curve, the computed integral by QUADXY using cubic splines is generally quite accurate. However, it may be further improved by any of the following acts.
Increasing the size of the data set by increasing the number of rows of the allocated IVP solution array to output a finer time grid.
Supplying optional slopes at the end points of the curve to the calculus function when available. The slopes may be derived analytically from the integrand expression and can improve the accuracy of the spline fit near the curve edges.
Using nonuniform output time points clustered near rapidly-varying regions of the state trajectories. This can be controlled via optional arguments to IVSOLVE including supplying exact values for the output time points.
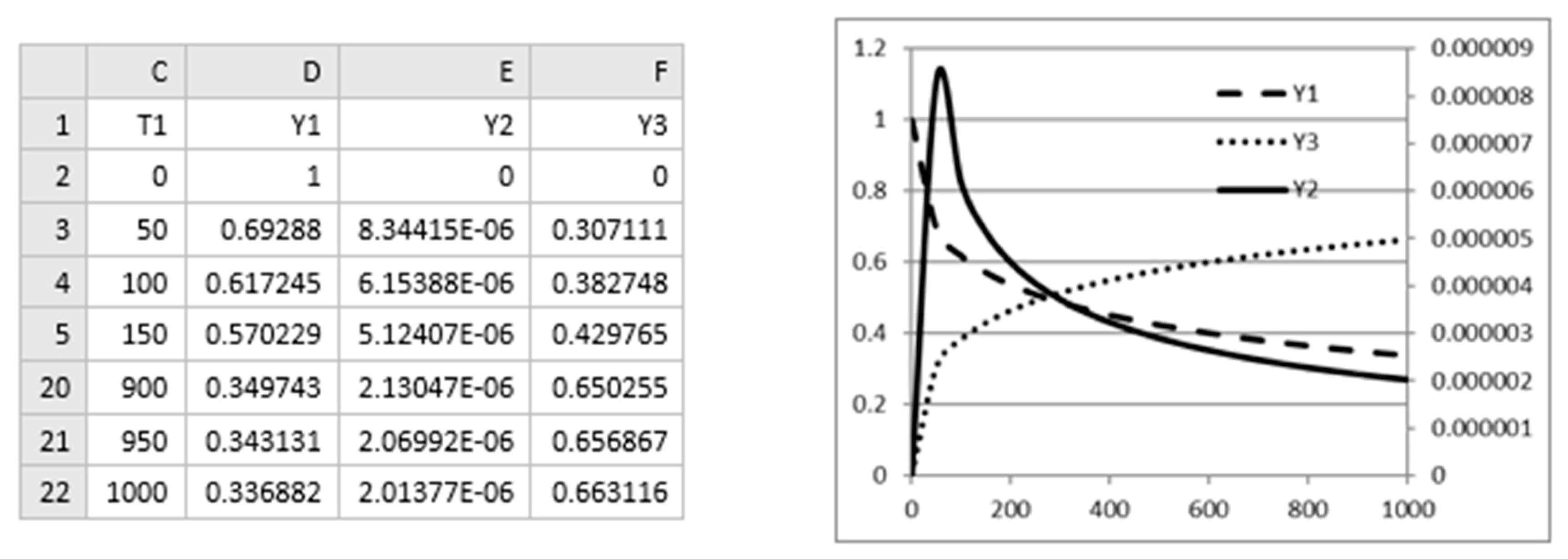
In practice, we have found that the parametrization order and the starting guess for unknown parameters to be the most important factors influencing convergence. We have generally used polynomials up to 5th order which have performed reasonably well. On the other hand, increasing the output array for IVP solution beyond a reasonable size, on the order of 100 uniform subdivisions for the time interval, has not generally resulted in a consistent or significant improvement of the result. In the examples in the next section, we shall demonstrate the effects of both increasing the parametrization order and reducing the output time interval.
4. Conclusions
We devised a practical and systematic spreadsheet solution strategy for solving general optimal control problems. The strategy is based on an adaptation of the partial-parametrization direct solution method which preserves the structure of the original mathematical optimization statement, but transforms it into a simplified NLP problem suitable for Excel NLP solver. The solution strategy is formulated by the aid of several elementary calculus functions from an available Excel calculus Add-in [
11] for solving differential equations, computing integrals and derivatives. The calculus functions are employed as building blocks in a hierarchical functional paradigm implemented by standard Excel formulas in conjunction with Excel built-in NLP solver to carry out a dynamic optimization program.
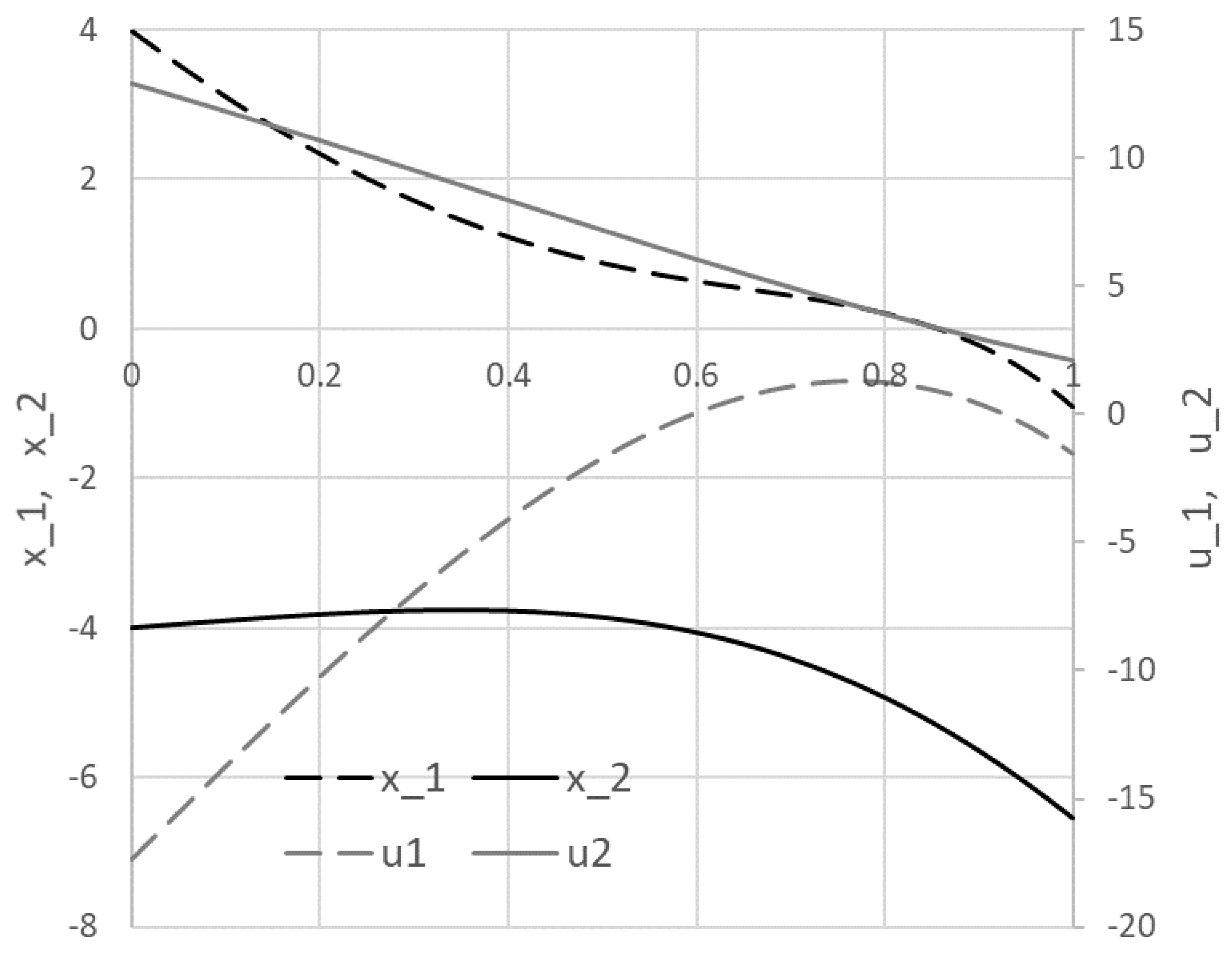
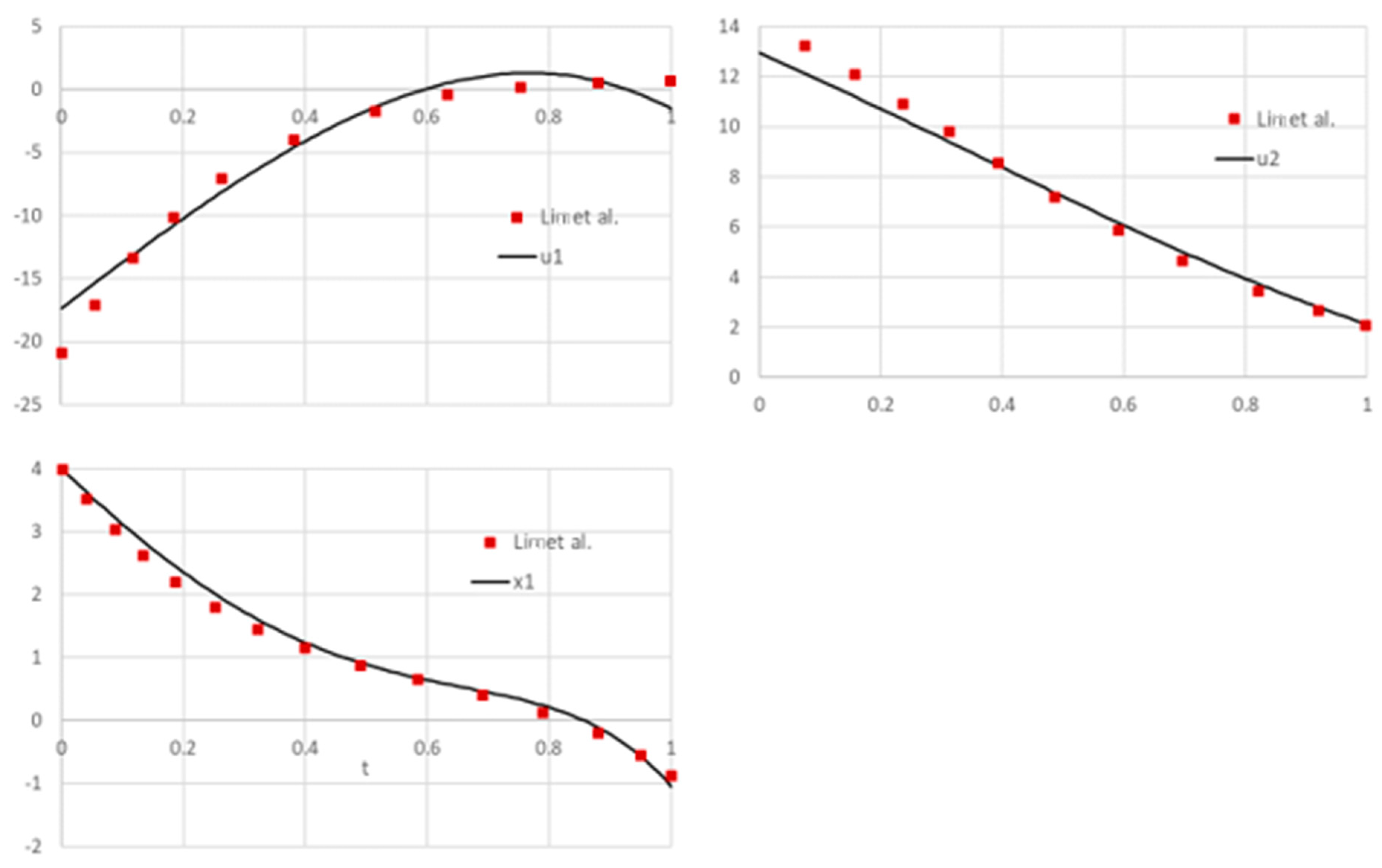
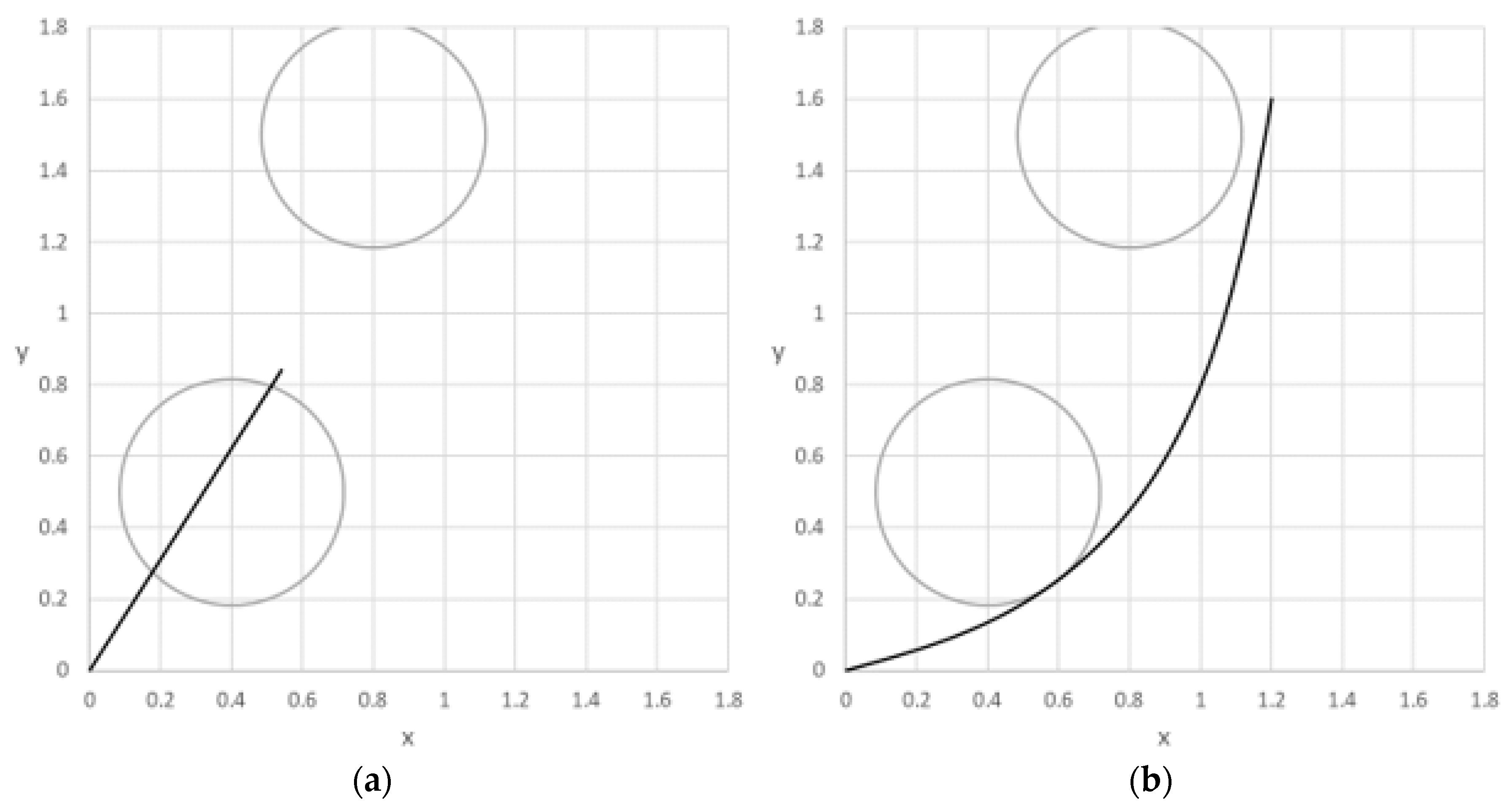
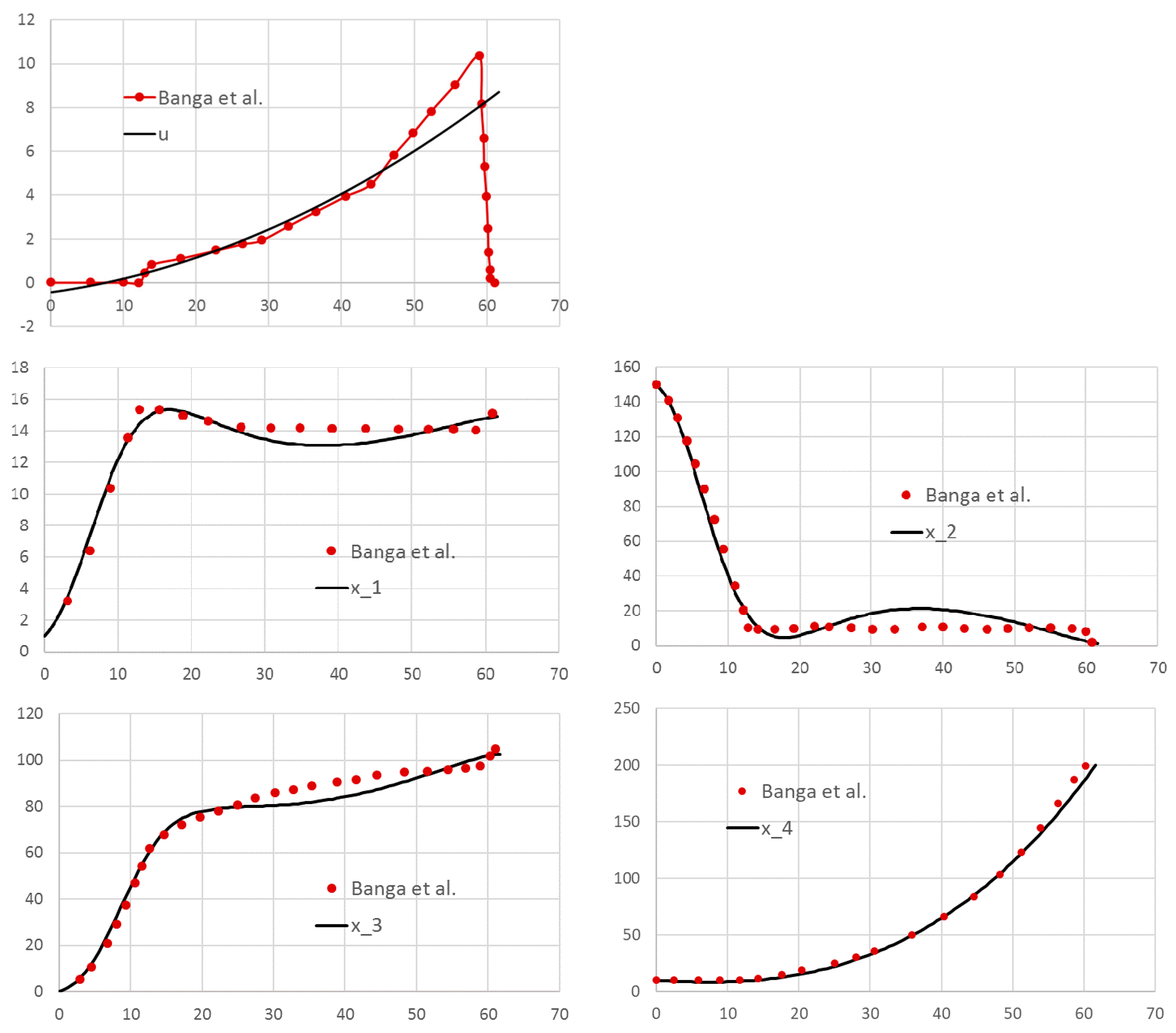
Results were obtained for four representative problems selected to illustrate modeling of several conditions including dependence on higher order derivatives of state and controls as well as implicit IVP problems and integral constraints. The results were compared with published solutions obtained by other methods, and in some cases, were shown to be better by the measure of the cost index. The performance of the method is also notable with computing times on the order of seconds to a minute on a standard laptop. As has been illustrated by the solution procedure, applying the technique involves no more than defining a few formulas that parallel the original mathematical equations. No special programming skill is needed beyond basic familiarity with the common spreadsheet operation. The minimal problem setup effort, in combination with the ubiquity of Excel spreadsheet, present reasons to explore the method as an alternative, simpler educational tool for rather complex problems.
The success of the devised strategy for optimal control of ordinary differential equations supports future research for extending the strategy to optimal control of partial differential equations. In [
22], the author demonstrated an analogous formulation combing the NLP solver with a PDE solver from the same Add-in [
11] for parameter estimation of partial differential algebraic equations, and it may be feasible that certain formulations of optimal control of partial differential equations are solvable in the spreadsheet by a similar strategy. On the other hand, it is worth investigating devising an alternative strategy based on the indirect solution method [
4,
5] for optimal control problems. The indirect method requires solving a boundary value problem which could be solved by the aid of a boundary value problem solver function also available in the Excel calculus Add-in [
11].