1. Introduction
More than 14% of the Thai GDP comes from the transportation and logistics sector. More than 60% of the transportation cost incurred in Thailand is by one actor: the agricultural supply chain. This is because Thailand is known as an agricultural country. The major agricultural industry is the rubber industry. More than 80% of rubber is produced in the southern part of Thailand, with the remaining part of rubber production mainly in the northeastern part of Thailand. The rubber industry in the South has a long history, and much suitable infrastructure has been developed. Aside from the northeastern part of Thailand, the infrastructure and knowledge, including technology, knowledge, instruments and so forth, are not yet sufficient for the high growth of the rubber industry. The transportation costs in the rubber industry are not paid by the government or the person who takes care of this issue; farmers still deliver latex themselves to sell at the rubber collecting points. This activity generates a very high transportation cost for the whole country. Our research team is engaged in a project to design the latex collection system. This system comprises of finding the location of the collection points and the transportation route of the vehicles. This problem is actually similar to the vehicle routing problem which was first proposed by Dantzig and Ramser [
1] and has been proven to be an NP-hard problem [
2]. Apart from the vehicle routing problem (VRP), this problem must also decide the collection point of the latex; thus, the VRP turns out to be a location routing problem (LRP). Location routing [
3].
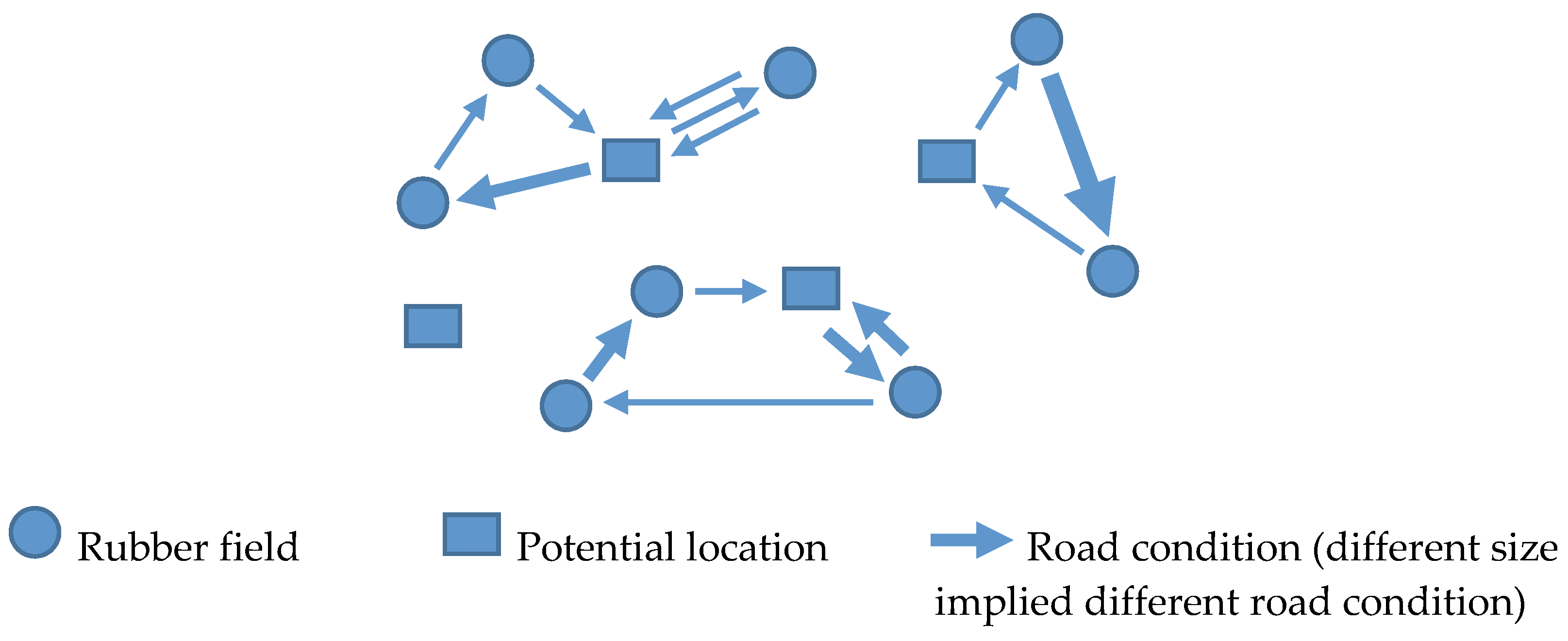
The proposed problem is not the general LRP that we found in the literature but has a few characteristics that make it a special case of LRP. These characteristics are as follows:
- (1)
The volume of latex which is available in the rubber field can be more or less than the capacity of the vehicles;
- (2)
The potential location and the rubber fields have different attributes such as different road conditions which can affect the speed used and the fuel consumption rate of the truck.
- (3)
The maximum duration or distances used for each vehicle are limited due to the latex’s fast transformation to solid;
- (4)
We focus the objective function on minimizing the total fuel consumption instead of the total distance as we often see in the literature.
These four special attributes make this problem a special case of the LRP problem (SLRP). The SLRP has never been found in the literature due to its 4 special attributes explained above. This problem can be found in many real-world applications. Nakorn Panom Province is one of the cities that has the fastest growing rate of development in the agricultural industry. The rubber cultural area has increased by more than 150% in the last 5 years in Nakorn Panom Province. We will take Nakorn Panom Province as the case study. The method which is presented here is customized to the rubber field industry, and it is also applicable to other industries where it has the same attributes as mentioned above.
In this study, the effective modified differential evolution algorithm will be presented to solve the proposed problem. The article is organized as follows;
Section 2 is the literature review;
Section 3 is the problem definition, and current practice procedures will be presented;
Section 4 presents the proposed heuristics; and
Section 5 gives the conclusions and outlook of the article.
2. Literature Review
Dantzig and Ramser [
1] introduced the vehicle routing problem (VRP) and Lenstra and Rinnooy [
2] proved that it is an NP-hard problem. Various types of VRP have been presented in many research articles. Braekers and Ramaekers [
4] have given an overview of the scenario and the problem’s physical characteristics, extending the basic uncapacitated VRP. Besides the various types of VRP problems, there are also various types of methods for solving the VRP. The metaheuristic method is one of the solution methods that is very popular for solving VRP as it is fast and effective. The solution approaches presented in many articles are simulated annealing [
5].
The location routing problem (LRP) is one of many various types of VRP. This problem has two decision variables which need to be solved. These two decision variables are (1) the suitable location to be used and (2) the routing of the field or the clients that are assigned to that location [
6,
7]. The optimal value of the suitable location can be determined before or during the assignment of the clients to the locations.
There are many researchers that have presented a methodology to solve the LRP. Most of the algorithms proposed in the literature are two-phase heuristics, which are (1) cluster first, (2) route second or (1) route first, (2) cluster second [
8]. From the literature, both choices perform well in many test problems; thus, selecting one will not affect the solution quality. In our research, the proposed heuristics employ the idea of using two-phase heuristics. We select cluster first, route second as the starting point of our algorithm.
There are many researchers who have focused on developing metaheuristics to solve the problem such as tabu search [
9] and the simulated annealing (SA) technique [
10,
11].
In this research, the differential evolution algorithm (DE) is presented as it is a fast and effective algorithm.
The differential evolution (DE) algorithm is a branch of the evolutionary algorithm developed by Rainer Storn and Kenneth Price [
12] for optimization problems over continuous optimization. Thereafter, DE has been successfully used in combinatorial optimization such as in assembly line balancing [
13,
14], the location-allocation problem [
15], machine layout [
16,
17], and the manufacturing problem [
18].
The DE has been applied to VRP problem [
19,
20,
21,
22,
23,
24,
25]. The design of DE to solve VRP problem has both the traditional [
20] way or the slight modification of some mechanism to get a more effective algorithm. Key successes of DE are the good designing of vectors to represent the problem, the encoding and decoding methods, the setting of good predefined parameters in the DE mechanism and the effectiveness of the mutation, recombination, and selection procedure [
23,
24,
25]. Moreover, with DE, it is also easy to add some procedure to increase its performance such as add local search [
19], adjust decoding method [
21], and self-adaptive some parameters [
23]. Though there are many articles proposing DE to solve VRP, we cannot find an effective DE to solve the LRP [
22]. So it is our contribution to present the effective DE to solve the special case of LRP. When all key successes have been introduced to DE, DE will be very effective compared with other metaheuristics proposed in the literature. Moreover, DE has the advantage that it is fast and efficient; thus, in this article, we will present the modified version of it to solve the problem.
This article is organized as follows: in the next section, the problem definition and the current practice heuristics is presented.
Section 3 presents the proposed heuristics.
Section 4 proposes the computational results and
Section 5 is the conclusion of the article.
4. The Proposed Heuristic
The proposed heuristic is designed to solve the problem. Many metaheuristics are available in the literature. The differential evolution algorithm (DE) is selected to solve this problem because it is a fast and effective heuristic. Generally, DE is composed of four steps:
- (1)
Randomly generate the initial vector or solution;
- (2)
Use the mutation process;
- (3)
Use the recombination process;
- (4)
Use the selection process.
Steps (2) to (4) will be iteratively executed. Details of each step are explained in
Section 4.1.
4.1. Randomly Generated Vector or Solution
The solution can be obtained by generating a set of vectors. Each vector is composed of D positions, where D is the number of fields. The number of the population is 5 (or NP = 5).
Table 11 shows an example of the values in each position of five vectors which are randomly generated in the first iteration.
When the vectors are generated, obtaining the solution of the problem, the decoding method needs to be executed. There are five steps of decoding (transferring) the vector into the problem’s solution, which are explained in
Section 4.1.1,
Section 4.1.2,
Section 4.1.3 and
Section 4.1.4.
4.1.1. Finding the Order of the Fields
In this step, we need to sort the value of the position of each vector to get the order of the fields. The position’s value is sorted according to the increasing order. For example, for vector 4, the original value of positions 1, 2, 3, 4, 5, and 6 are 0.01, 0.57, 0.62, 0.17, 0.53, and 0.42. The order of the value in each position according to increasing order is 0.01, 0.17, 0.42, 0.53, 0.57, and 0.62. This order of value generates an order of position for vector 4 of 1, 4, 6, 5, 2, and 3.
4.1.2. Randomly Select the Location
The method of selecting the opened location is explained in the following example. The probability of selecting the location can be calculated using Formula (2):
where
pk is the probability of location
k and
Sk is the heuristics information as explained in
Section 3.2.
From the example, the probabilities pk of locations A, B, C, D, and E are 0.16, 0.11, 0.22, 0.25, and 0.26, respectively. In the next step, the cumulative probability of each location is 0.16, 0.27, 0.49, 0.74, and 1. If the random number is 0.57, then location D is selected to be the first opened location. We can apply this mechanism to get the order of the location. The order of the locations in this step is D, E, A, B, and C; then, the next step, the decoding method, will be executed.
4.1.3. Assigning the Field to the Location According to Their Place in the Order
For example, the field order is 1, 4, 6, 5, 2, and 3 and the location order is D, A, E, B, and C. We start to assign the field to the location by adding the field in the very first order until this location is full, and then we move forward to the next possible location and continue doing this until all fields are assigned to exactly one location.
In this example, field 1 will be assigned to location D, and the capacity of D is updated whenever an assignment has been done. The location will close when it loads a volume of latex in the field reaching the full capacity level. The result of the assignment is shown in
Table 12.
From
Table 12, locations D, A, and E will be in use while the remaining locations will be closed.
4.1.4. Routing All Fields in the Locations
In this step, we construct the route of the fields that are assigned to the locations according to the capacity of the truck per round, the longest distance or traveling time per round and the total distance or time that the truck can travel per day. The result of
Section 4.1.1 is the same as in
Table 10 because the routing phase (
Section 4.1.1) is the same as the routing phase of the current practice procedure and the order of the fields and locations are the same as in the current practice example.
4.2. Mutation Process
4.2.1. The Original Mutation Process
In this step, after we get the initial solution, we apply the mutation process formulas. In the proposed heuristic, the mutation formula is Formula (3):
where
= 1.5,
is a randomly selected target vector and
is the vector that has the best solution compared among all target vectors.
4.2.2. The Modified Mutation Process
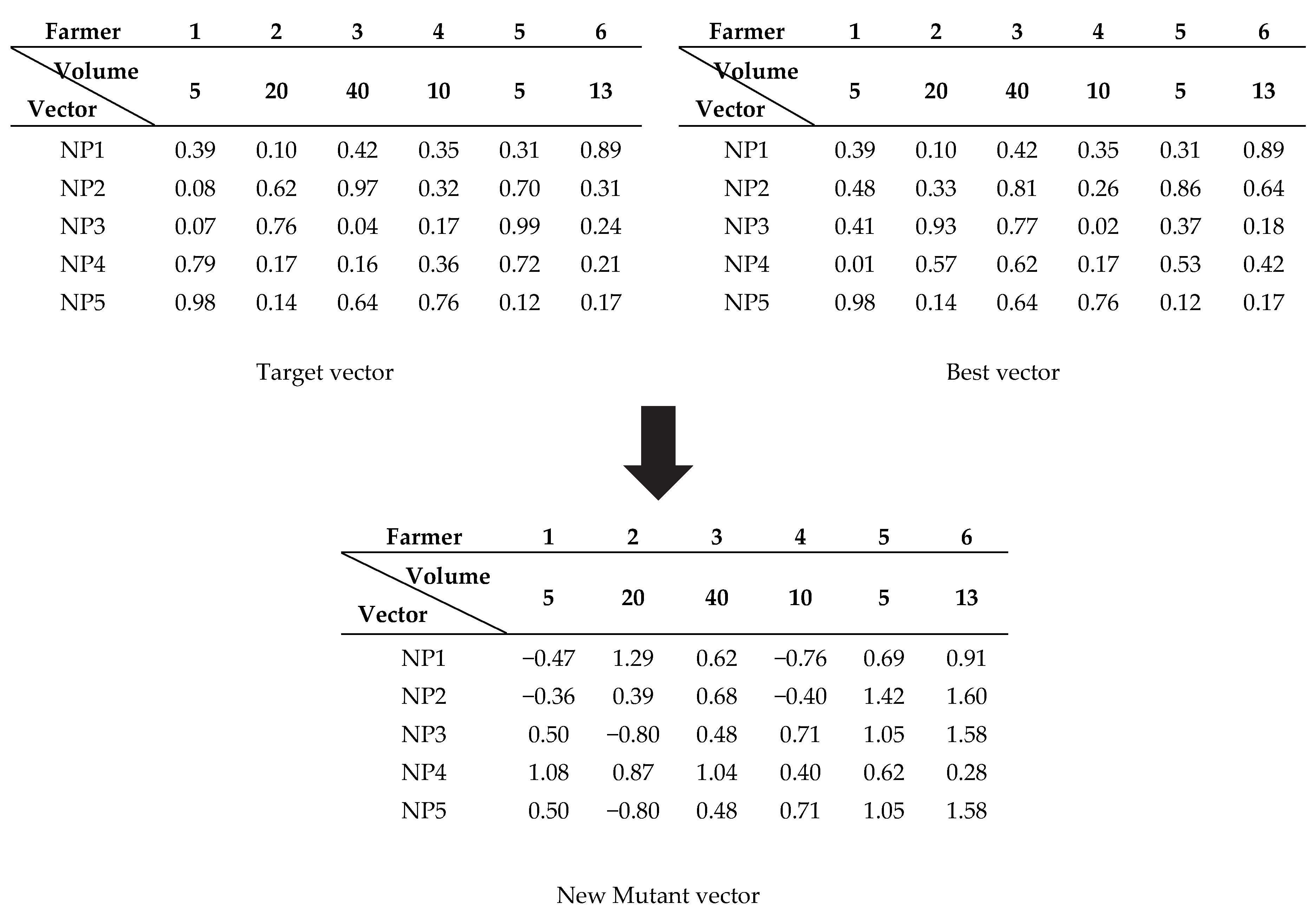
Originally, all vectors were random; we take them from the current iteration target vectors, and the best solution is the set of best vectors obtained from the best among all target vectors. The modified version of the mutation process is one in which we add one set of the best vectors. The number of the best vectors in this set is equal to the number of the population in the normal DE method. For example, if there are 10 target vectors (NP = 10), there will be 10 vectors in the best vectors set as well. The set of best vectors is obtained by collecting the best vectors that are found during the simulation. These vectors are not the same as the normal target vectors due to the collection of all good vectors, even if they come from the same vector number. The target vector of vector 1 at the current iteration is the best vector that obtains the best solution for vector 1. The second best for vector 1 is the vector from the last iteration if the current iteration found a new solution. This vector will forget the last best solution whenever it finds a better solution, even if the last best solution is better than that of the other vector in the set of target vectors. In the modified version of the mutation process, the second-best vector of a vector can be kept in the best vectors set if it is better than that of the other target vectors. The mutant vector used in the modified mutation process is generated from both the normal target vector and the set of best vectors, as shown in
Figure 2.
From
Figure 2, the mutant vector of vector 2 is generated from the best vector (assuming that vector 1 is the best vector) and the two random vectors are vector 3 (from the set of target vectors) and 5 (from the set of best vectors) and the result is given in
Figure 2. The switching between using the set of best vectors or the set of target vectors can be executed by randomly choosing the using probability. Each vector is randomly chosen before the mutant process is executed. The probability function of the use of the set of best vectors is shown in Formula (4):
If the random number is less than or equal to C, then the random vector used in the mutant process is drawn from the set of best vectors instead of the set of target vectors.
The updating of the set of best vectors can be done by getting rid of the worst vector in the set and putting the new best vector in if the new best vector is better than at least one vector in the set of best vectors. This is done whenever a new best vector (better than at least the worst vector in the set of best vectors) is found. The result of the mutant process is mutant vector , where i is the number of the vector, j is the position number, and G is the current iteration.
4.3. Recombination Process
The recombination process can be executed by randomly assigning one number for each position in a vector; if this random number is less than or equal to the predefined parameter
CR, then the value in position
j of vector
i is taken from the value of position
j in vector
i of the mutant vector. On the other hand, if the random number is higher than that of
CR, the value in that position is taken from the target vector. The formula of the original version of DE is shown in Formula (5):
When it is executed, the set of trial vectors () will be obtained.
In this article, a new recombination formula is presented in Formula (6).
Predefined parameters CR1 and CR2 have to be set first and lie between 0 and 1. If the random number randi,j is less than CR1, then the value in position j of vector i is drawn from the mutant vector. If it is greater than CR1 but less than CR2, the value in position j, vector i will be taken from the target vector. Finally, if the random number is higher than CR2, that position will take the value from the set of best vectors (). After the trial vector is obtained, the local search will be applied for all vectors.
4.4. The Local Search
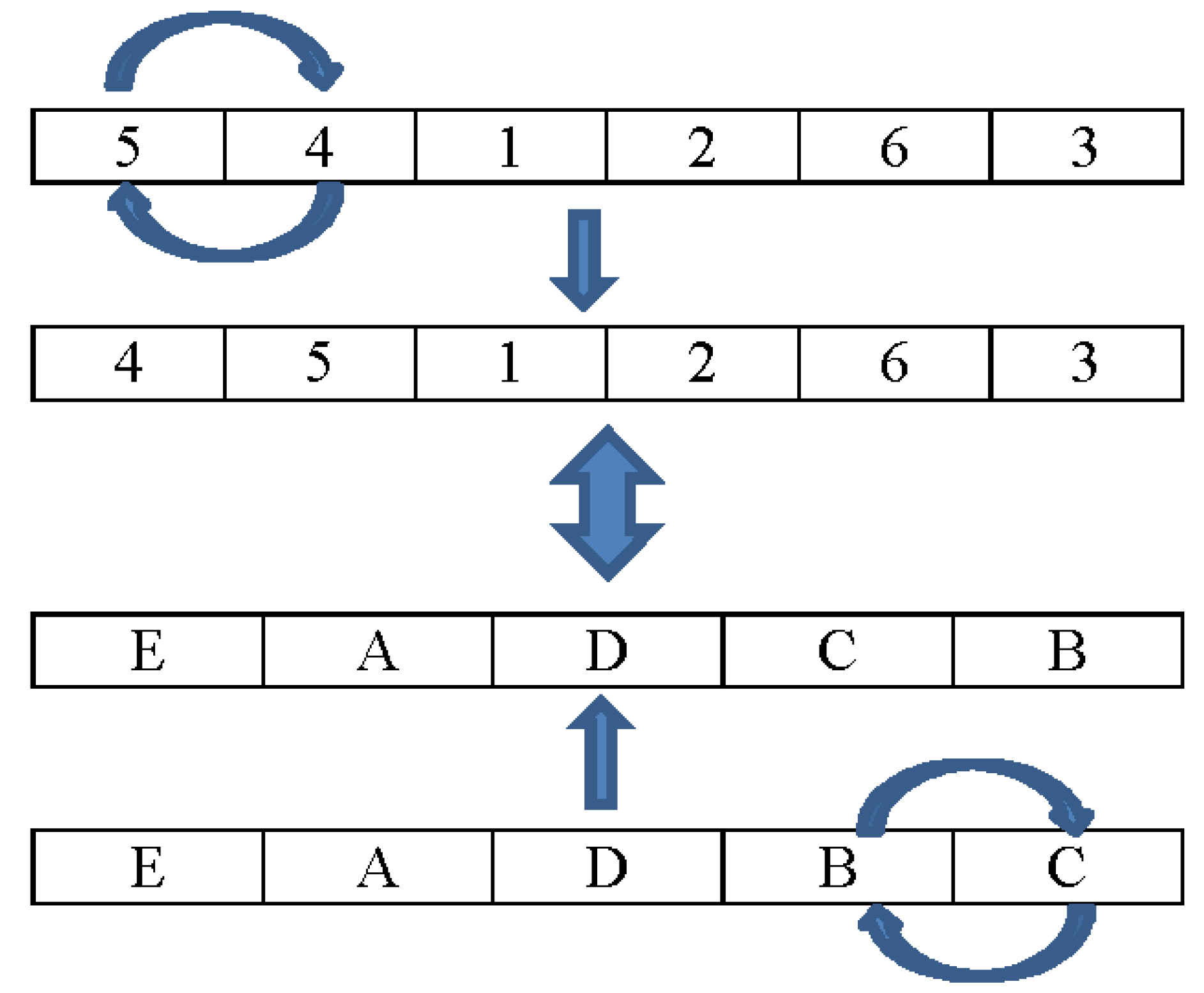
The local search that we use in the proposed heuristic is the SWAP algorithm. The swap algorithm will be executed in the order of the fields and the locations generated in the decoding method. For example, in
Figure 3, the current interchange of the fields is order 1 and 2, which is now fields 5 and 4. The exchange is performed and obtains the order of fields as 4, 5, 1, 2, 6, and 3, respectively. The new order will use the decoding method using the location order E, A, D, C, and B, which is the exchange order between the locations B and C. The order of location has to exchange all positions, such as E exchanging with A, D, C, and B. After the exchange, the new order will be used to decode with the current order of the fields being 4, 5, 1, 2, 6, and 3.
After all possible exchanges of location are performed with the current order of fields, then the new order of the fields is generated by exchanging the next position in the field order.
4.5. Selection Process
The selection process is according to Equation (7).
When the selection process is finished, we will get the target vectors of the next generation (iteration).
The procedure of the proposed heuristics is shown in
Figure 4.
5. Computational Results
The computational results are obtained by testing the DE (original version), the modified DE (MDE), and the current practice procedure with 10 test instances and one case study. The test instances are named N-1 to N-10 and the case study is named Case. The detail of the number of locations (#location) and the number of fields (#field) of each test instance is shown in
Table 13.
CR is set to 0.6, F is set to 2 [
13],
CR1 is set to 0.6, and
CR2 is set to 0.8. The simulation has been executed five times, and the best solutions among all five results are drawn to be representative of the algorithm. The simulation was performed in a Computer notebook Core™ i5-2467M CPU 1.6 GHz.
The stopping criterion which is used in the first test is the runtime limitation, which is set to 10 min. The computational result of the 11 test instances is shown in
Table 14.
From
Table 14, DE and MDE outperform the current practice procedure. To prove that they are outperforming it statistically, the result of the statistical test using the Wilcoxon signed-rank test with a 95% confident interval is shown in
Table 15.
From
Table 15, DE and MDE generate a significantly better solution than that of the current practice. The solution obtained from MDE is statistically better than that of DE.
Now, the performance of DE and MDE will be tested to draw the contribution of the proposed heuristics. The proposed heuristics are split into 4 sub-heuristics, which are DE (original DE), MDE-1 (DE + new mutation Formula (6)), MDE-2 (DE + local search), and MDE-3 (DE + new mutation Formula (6) + local search). The stopping criterion in this test is the runtime limitation, which is set to 10 min. The results of all proposed heuristics are shown in
Table 16.
The significance test has been executed for all results using the Wilcoxon signed-rank test with a 95% confident interval as shown in
Table 17.
From
Table 17, all MDE algorithms outperform the original version of DE, and MDE-3 outperforms MDE-1 and MDE-2. This means that both the local search and the new mutation formula should be combined to get a better solution. The local search alone can improve the solution better than that of DE using the new mutation formula. The new mutation formula works well in the DE due to it statistically improving the solution from the original DE. The percentage difference of each proposed heuristic to the best solution (MDE-3) is shown in
Table 18.
From
Table 18, we can see that the best heuristic (MDE-3) has a percentage difference of fuel usage less than that of MDE-2, MDE-1, and DE of 10.173%, 12.116%, and 16.056%, respectively.
6. Conclusions
This research presents solution approaches to solving a special case of the location routing problem (SLRP). The SLRP could have a volume of latex more or less than the capacity of the vehicle. The objective function of SLRP is to minimize the fuel usage, and the fuel usage depends on the road condition and the distance of the road.
We developed a differential evolution algorithm to solve the problem. The new mutation formula is presented in the article. The new rule of applying SWAP is presented and is used as the local search in the proposed heuristics.
The heuristics proposed in the article are split into four sub-heuristics, which are DE (original DE), MDE-1 (DE + new mutation Formula (6)), MDE-2 (DE + local search), MDE-3 (DE + new mutation Formula (6) + local search). The best heuristic is MDE-3, which has a 16.056% difference from the original version of DE and is 10.173 and 12.116 better than MDE-2 and MDE-1, respectively.
From the computational result, we can see that using the new mutation formula and the local search is beneficial to the original DE. The new mutation formula and the local search is designed based on the idea of increasing the intensification of DE. This makes MDE-1, MDE-2, and MDE-3 outperform the original DE.