A New Analytical Procedure to Solve Two Phase Flow in Tubes
Abstract
1. Introduction
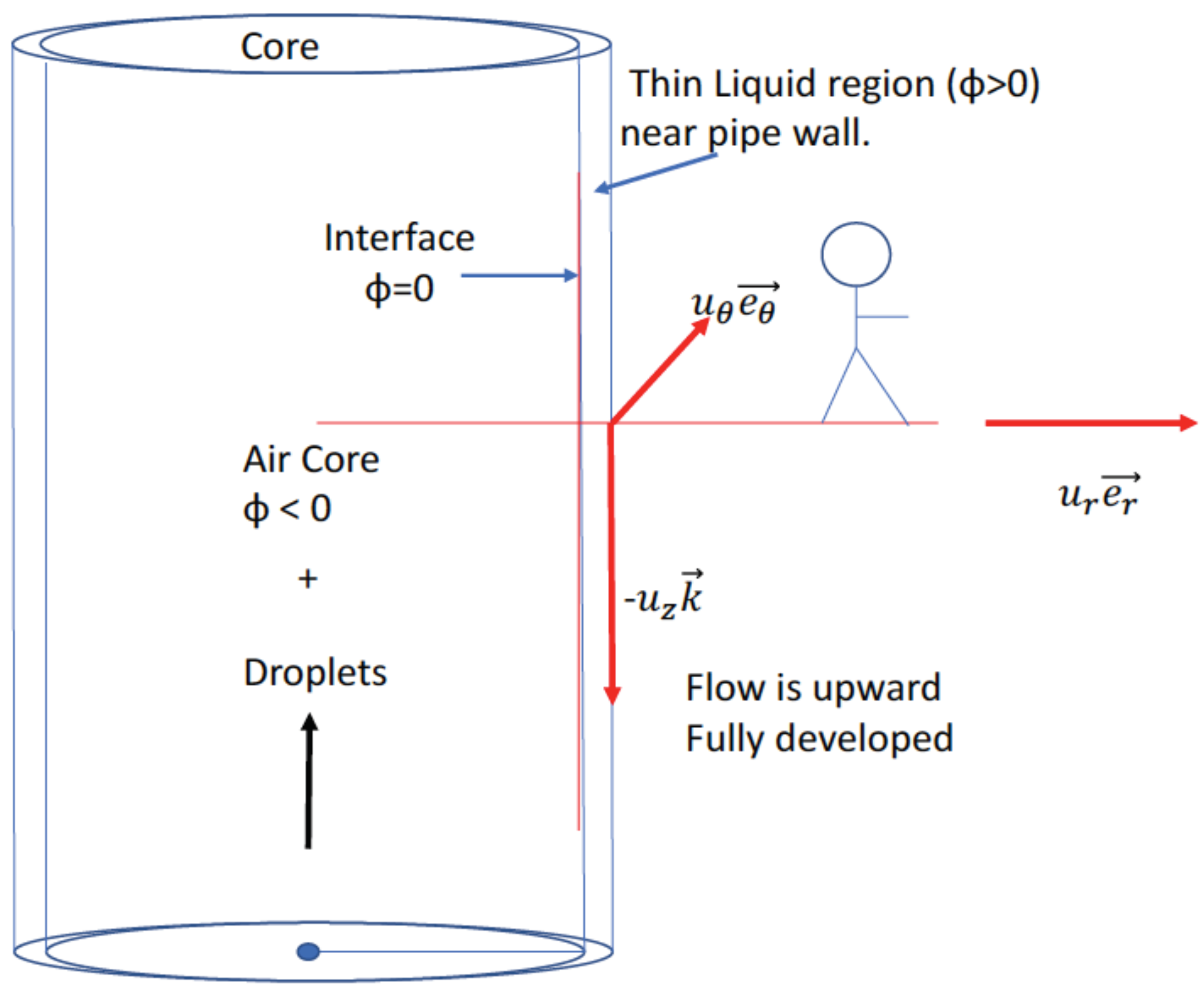
1.1. Level Sets in Cylindrical Co-Ordinates
1.2. A New Composite Velocity Formulation
1.3. Special Case Solution
Consideration of Curvature Alone
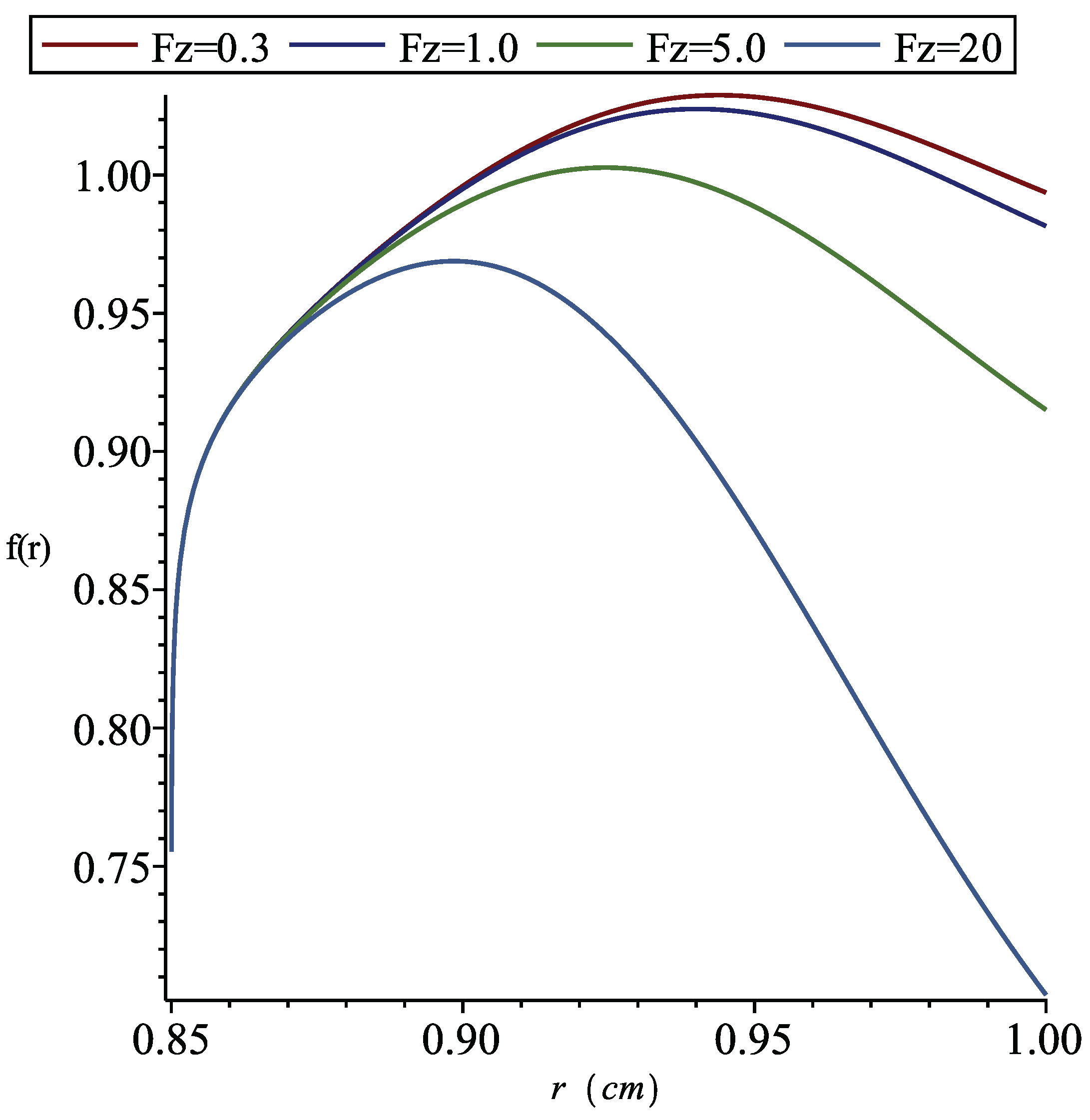
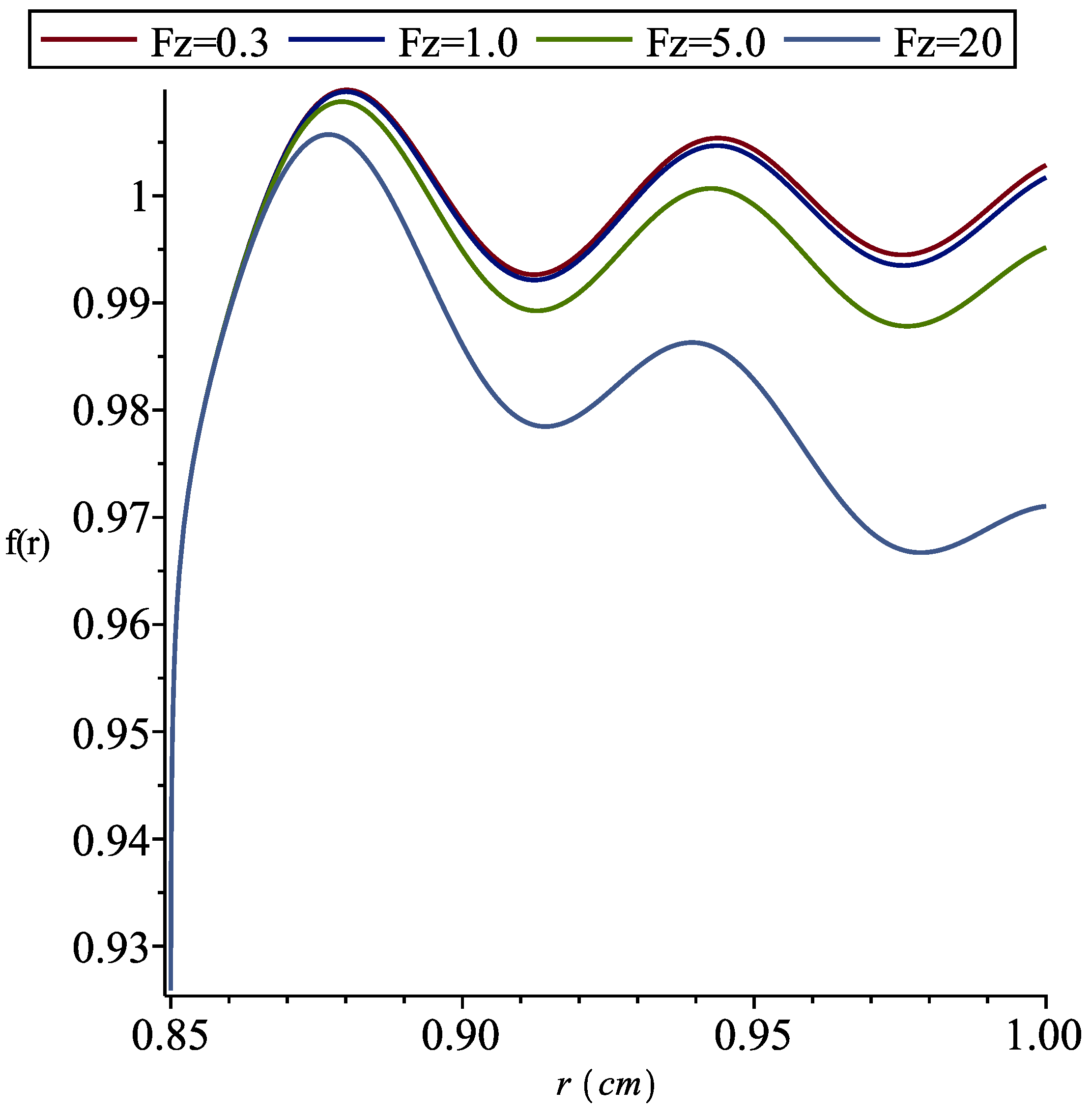
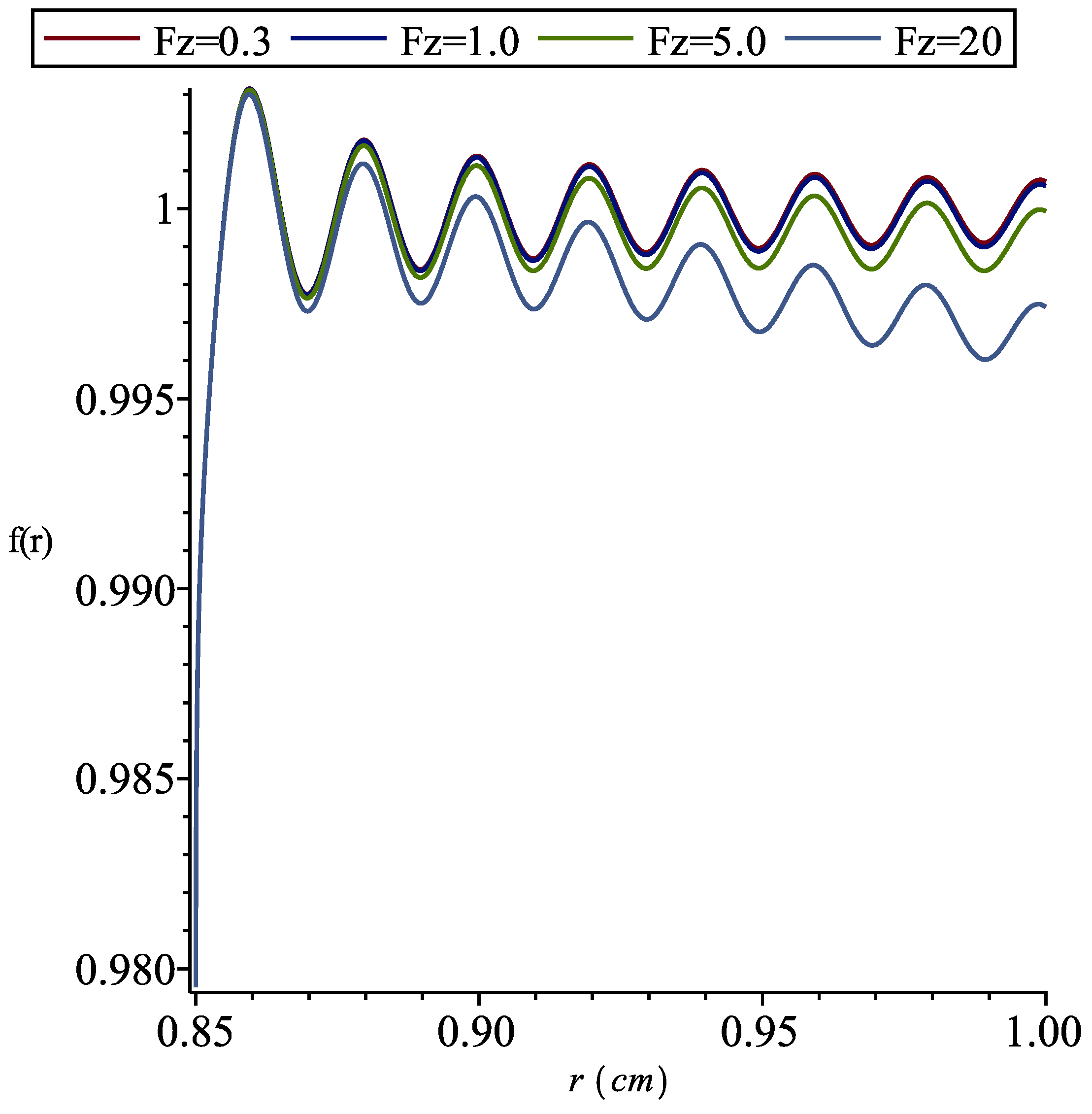
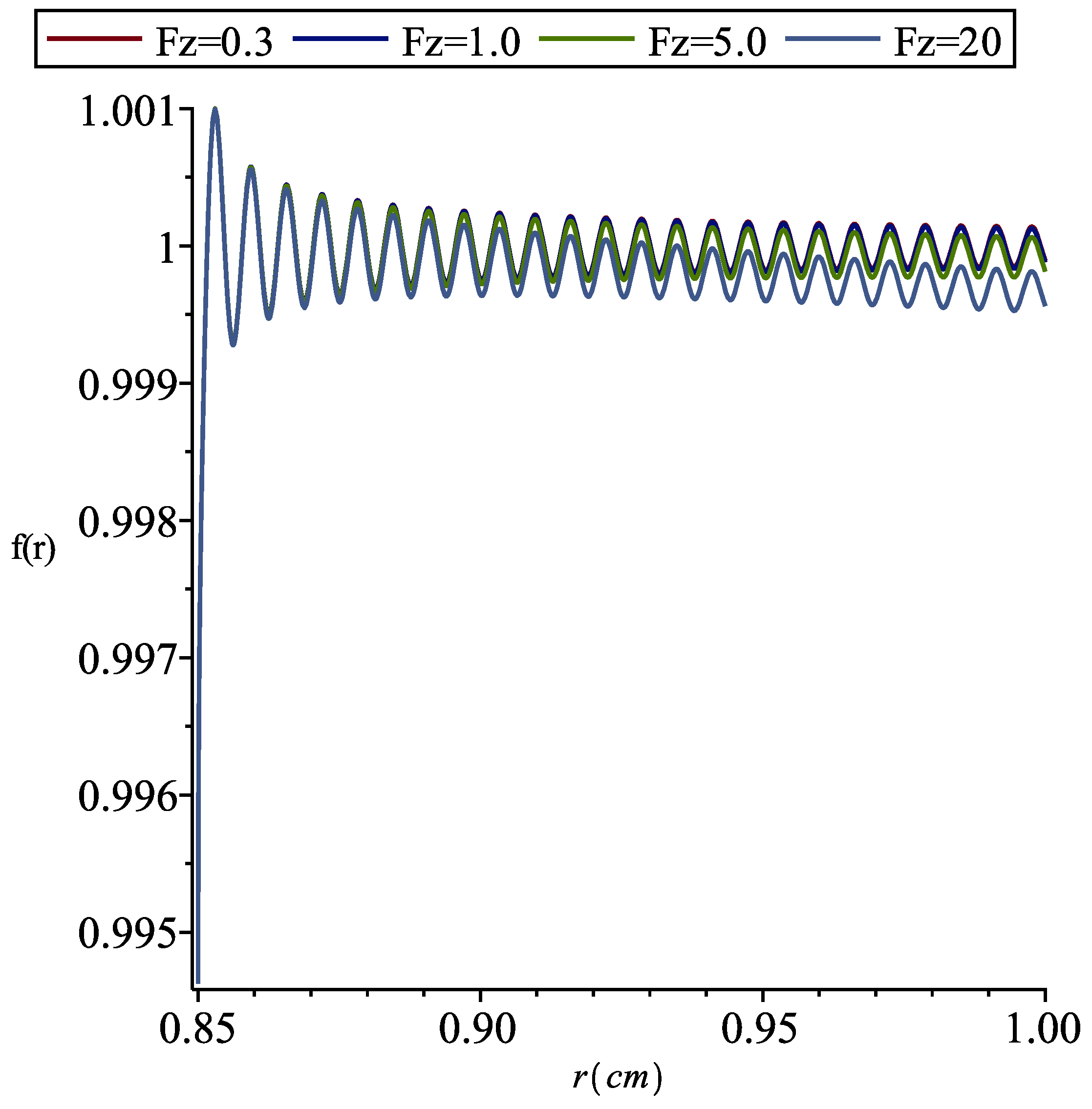
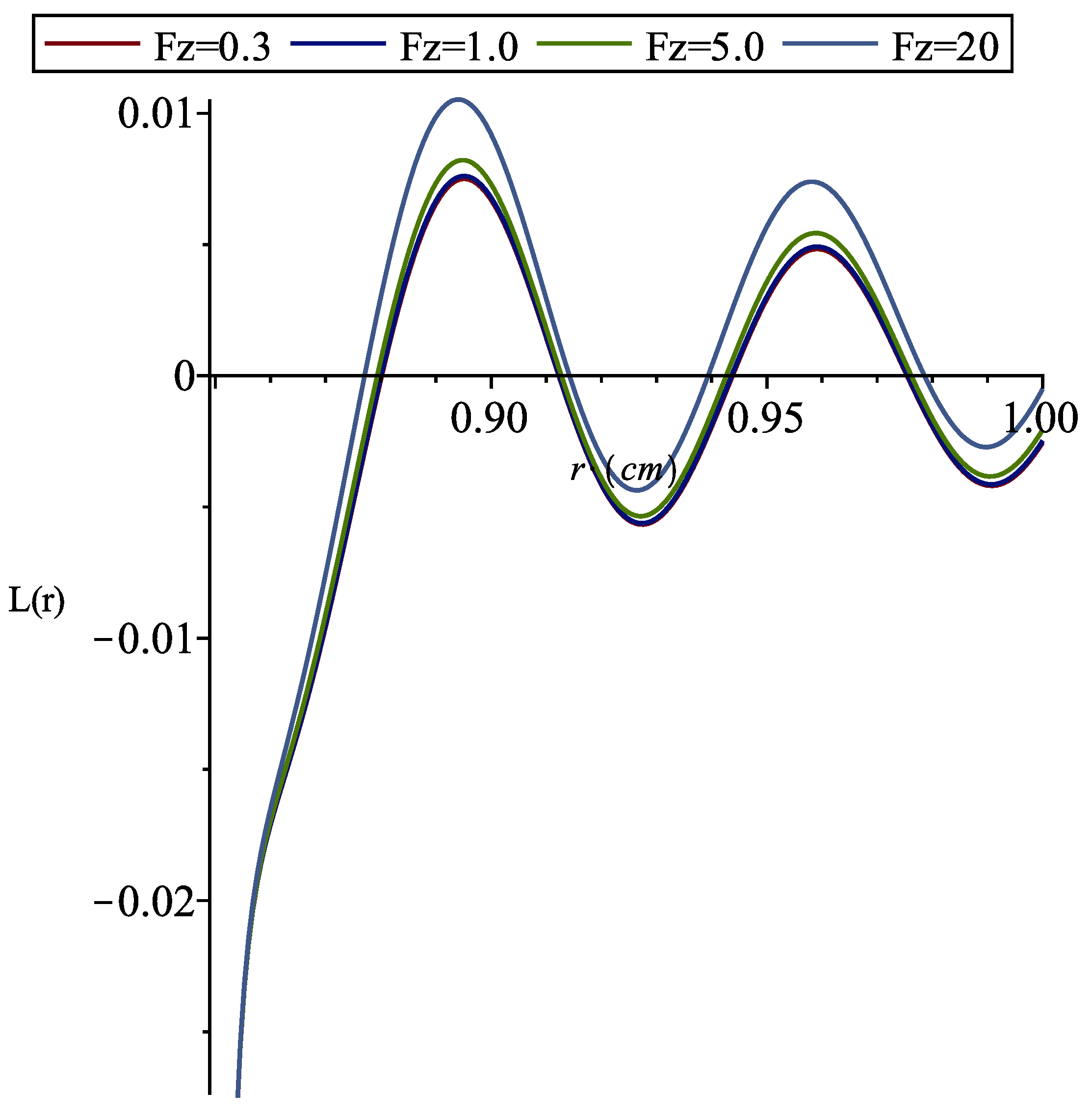
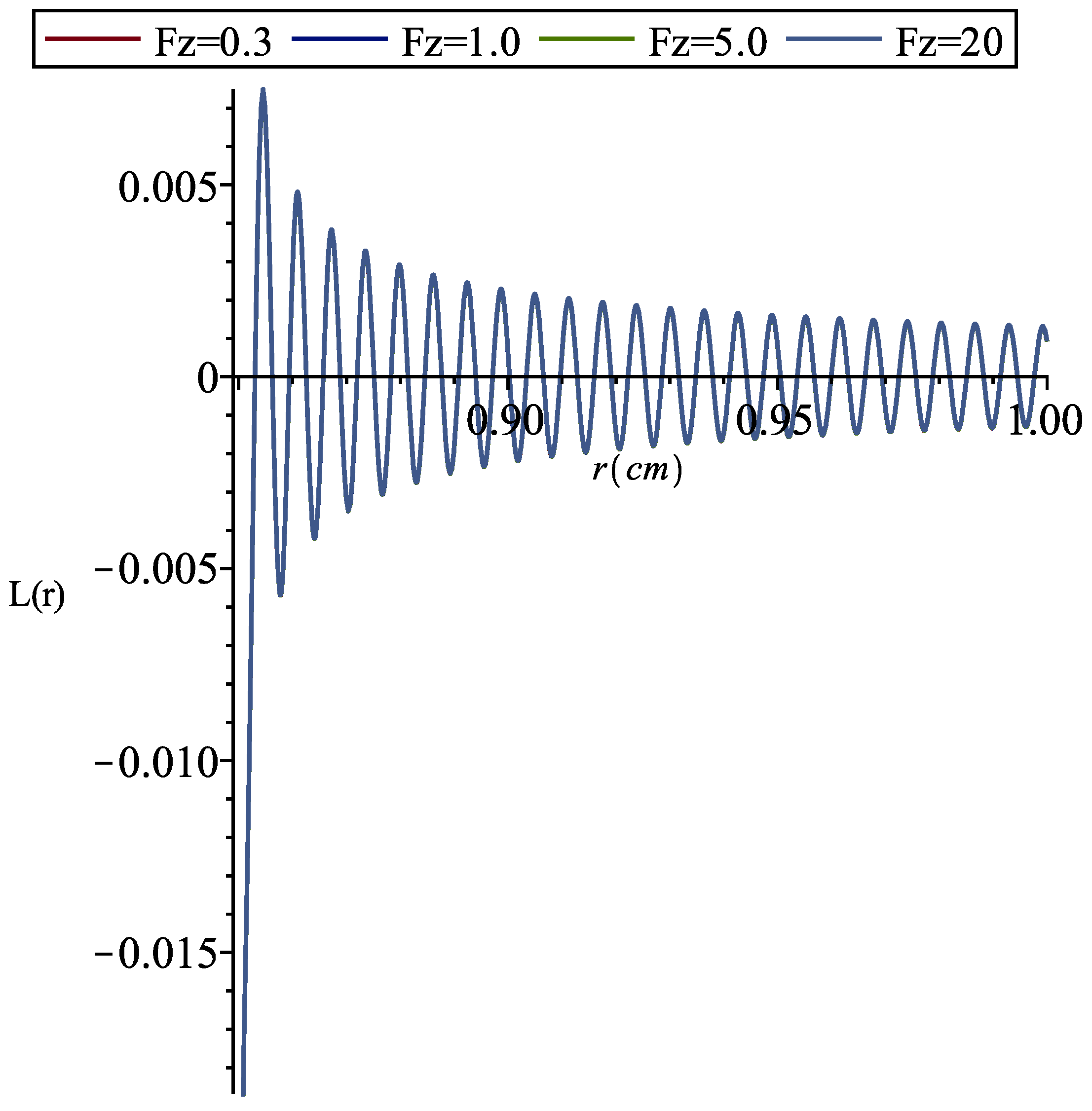
2. Results and Discussion
3. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Adanhounme, V.; Adomoub, A.; Codo, F.P. Analytical solutions for Navier-Stokes equations in the cylindrical coordinates. Bull. Soc. Math. Serv. Stand. 2012, 2, 16–23. [Google Scholar] [CrossRef]
- Pereira, L.M.; Guerrero, J.S.P.; Cotta, R.M. Integral transformation of the Navier-Stokes equations in cylindrical geometry. Comput. Mech. 1998, 21, 60–70. [Google Scholar] [CrossRef]
- Taylor, C.; Hood, P. A numerical solution of the Navier-Stokes equations using the finite element technique. Comput. Fluids 1973, 1, 73–100. [Google Scholar] [CrossRef]
- Chorin, A.J. The numerical solution of the Navier-Stokes equations for an incompressible fluid. Bull. Am. Math. Soc. 1967, 73, 928–931. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comp. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sethian, J. Level Set Methods and Fast Marching Methods; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Duflot, M. A study of the representation of cracks with level sets. Int. J. Numer. Methods Eng. 2007, 70, 1261–1302. [Google Scholar] [CrossRef]
- Caselles, V.; Catte, F.; Coll, T.; Dibos, F. A geometric model for active contours in image processing. Numer. Math. 1993, 66, 1–31. [Google Scholar] [CrossRef]
- Li, C.; Huang, R.; Ding, Z.; Gatenby, J.C.; Metaxas, D.N. A Level Set Method for Image Segmentation in the Presence of Intensity Inhomogeneities with Application to MRI. IEEE Trans. Image Process. 2011, 20, 2007–2016. [Google Scholar] [PubMed]
- Mitchell, I.; Tomlin, C.J. Level Set Methods for Computation in Hybrid Systems, International Workshop on Hybrid Systems: Computation and Control. In Proceedings of the International Workshop on Hybrid Systems: Computation and Control, Pittsburgh, PA, USA, 23–25 March 2000; pp. 310–323. [Google Scholar]
- Maitre, E.; Milcent, T.; Cottet, G.-H.; Raoult, A.; Usson, Y. Applications of level set methods in computational biophysics. Math. Comput. Model. 2009, 49, 2161–2169. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G. A conservative level set method for two phase flow. J. Comput. Phys. 2005, 210, 225–246. [Google Scholar] [CrossRef]
- Ayati, A.A.; Farias, P.S.C.; Azevedo, L.F.A.; de Paula, I.B. Characterization of linear interfacial waves in a turbulent gas-liquid pipe flow. Phys. Fluids 2017, 29, 062106. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R. Level Set Methods and Dynamic Implicit Surfaces; Springer: Berlin, Germany, 2003. [Google Scholar]
- Yaji, K.; Otomori, M.; Yamada, T.; Izui, K.; Nishiwaki, S.; Pironneau, O. Shape and topology optimization based on the convected level set method. Struct. Multidiscip. Optim. 2016, 54, 659–672. [Google Scholar] [CrossRef]
- Xie, F.; Zheng, X.; Triantafyllou, M.S.; Constantinides, Y.; Zheng, Y.; Karniadakis, G.E. Direct numerical simulations of two-phase flow in an inclined pipe. J. Fluid Mech. 2017, 825, 189–207. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moschandreou, T.E. A New Analytical Procedure to Solve Two Phase Flow in Tubes. Math. Comput. Appl. 2018, 23, 26. https://doi.org/10.3390/mca23020026
Moschandreou TE. A New Analytical Procedure to Solve Two Phase Flow in Tubes. Mathematical and Computational Applications. 2018; 23(2):26. https://doi.org/10.3390/mca23020026
Chicago/Turabian StyleMoschandreou, Terry E. 2018. "A New Analytical Procedure to Solve Two Phase Flow in Tubes" Mathematical and Computational Applications 23, no. 2: 26. https://doi.org/10.3390/mca23020026
APA StyleMoschandreou, T. E. (2018). A New Analytical Procedure to Solve Two Phase Flow in Tubes. Mathematical and Computational Applications, 23(2), 26. https://doi.org/10.3390/mca23020026




