The Construction of a Model-Robust IV-Optimal Mixture Designs Using a Genetic Algorithm
Abstract
:1. Introduction
2. The Mixture Model and Design Optimality
2.1. Notation and Models
2.2. Optimality Criteria
2.3. Weighted IV-Optimality
3. Genetic Algorithms and Constructing IV-Optimal Mixture Designs
3.1. Development of the Genetic Algorithm
- Step 1
- Specify the GA parameters: population size , number of iterations , selection method (elitism with random parent pairing), blending rate , crossover rates , and mutation rate .
- Step 2
- Generate an initial population of chromosomes (mixture designs). We use the real-value encoding with four decimal places to encode each chromosome. Assume is odd. To generate the initial population, a random sample is first taken in a hypercube. Then each sampled point in a hypercube is mapped to the constrained mixture space by applying the function used by Borkowski and Piepel [28]. Each experimental mixture is recorded to four-decimal place accuracy.
- Step 3
- Calculate the IV-efficiency objective function for each chromosome in the initial population.
- Step 4
- Find the elite chromosome which is the chromosome that has the largest weighted IV-efficiency . The remaining chromosomes are randomly paired for the reproduction process.
- Step 5
- Produce offspring of the next generation by using genetic operators: blending, between-parent crossover, within-parent crossover, and mutation. Larger values of genetic parameters are used for the early iterations and the smaller values of genetic parameters are used for the later.
- Step 6
- Calculate objective function for each parent/offspring pair. The fitter chromosome in the pair is retained for the next generation.
- Step 7
- Repeat Steps 5 and 6 for generations.
- Step 8
- Apply a local grid search to the best design to further improve objective function yielding the IV-optimal design. A local grid search searches designs in a small neighborhood of the best design. This is accomplished by perturbing the component proportions by small increments to search for further improvements in . This continues until no further improvement is found.
3.2. Illustration: A Genetic Algorithm for Constructing an Optimal Mixture Design
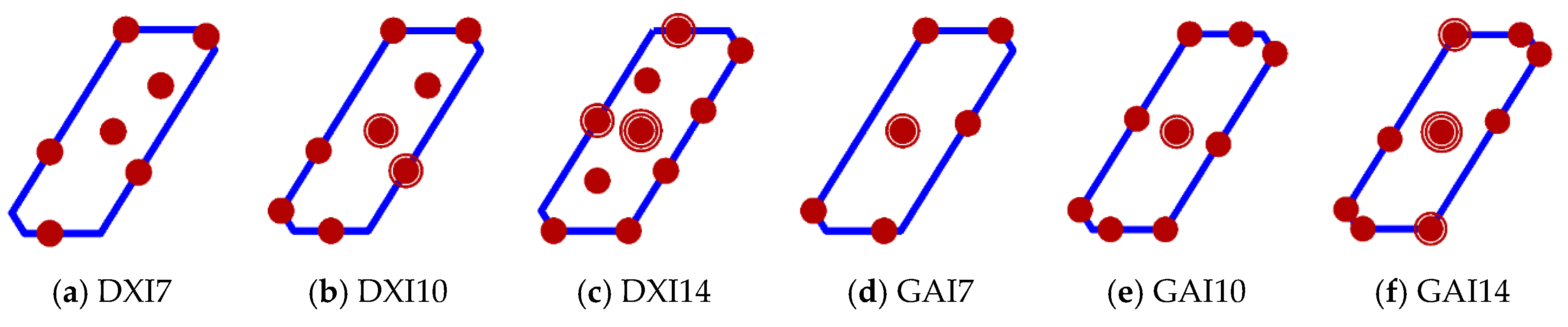
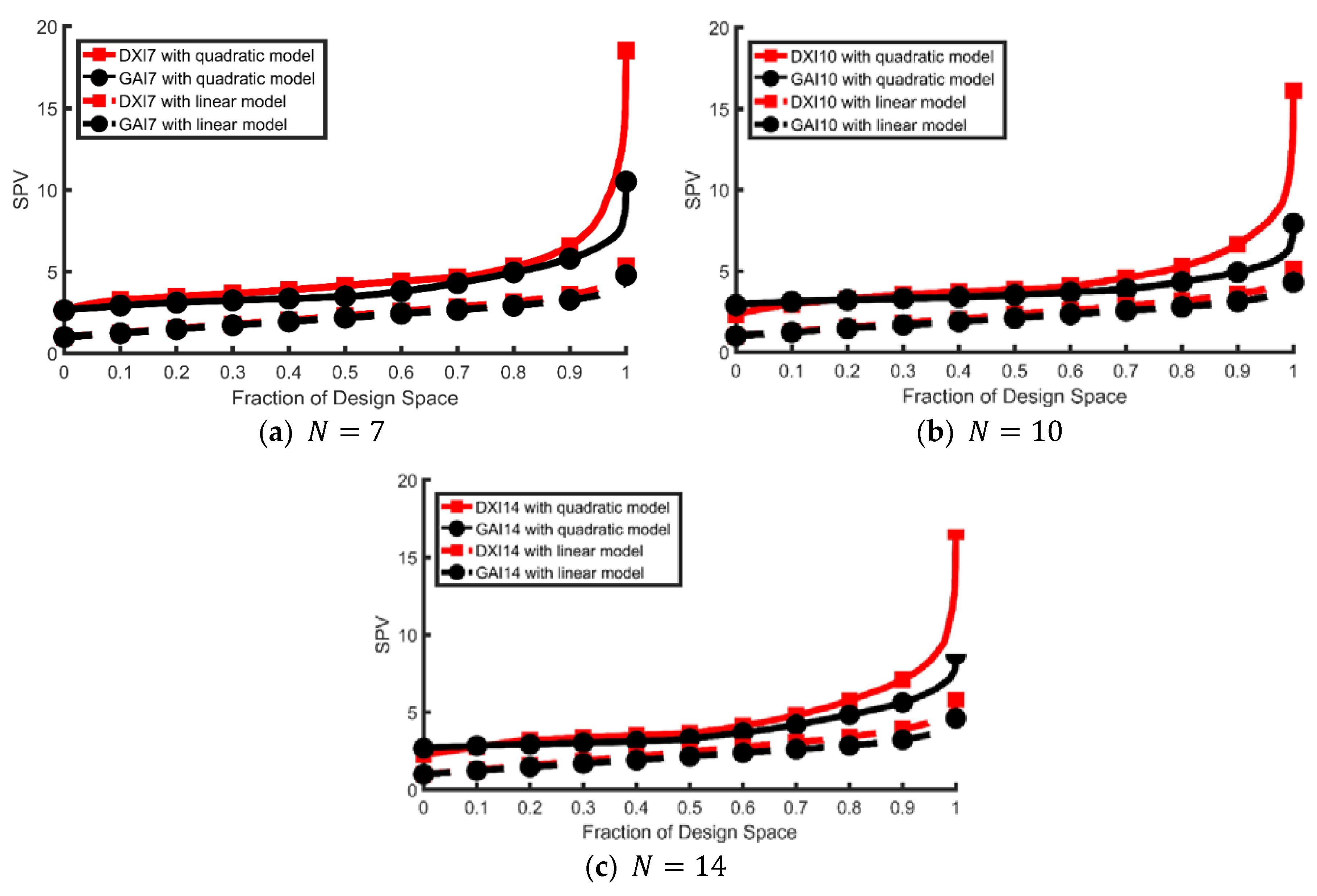
4. A Three-Component Mixture Example
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Cornell, J.A. Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Smith, W.F. Experimental Design for Formulation; The American Statistical Association and the Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- McLean, R.A.; Anderson, V.L. Extreme vertices designs of mixture experiments. Technometrics 1966, 8, 447–456. [Google Scholar] [CrossRef]
- Welch, W.J. ACED: Algorithm for the construction of experimental designs. Am. Stat. 1985, 39, 146–148. [Google Scholar] [CrossRef]
- Snee, R.D.; Marquardt, D.W. Extreme vertices designs for linear mixture model. Technometrics 1974, 16, 399–408. [Google Scholar] [CrossRef]
- Snee, R.D. Experiment design for mixture systems with multicomponent constraints. Commun. Stat. Theory Methods 1979, 17, 149–159. [Google Scholar]
- Fedorov, V.V. Theory of Optimal Experiments; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Mitchell, T.J. An algorithm for the construction of D-optimal experimental designs. Technometrics 1974, 16, 203–210. [Google Scholar]
- Huizenga, H.M.; Heslenfeld, D.J.; Molenaar, P.C.M. Optimal measurement conditions for spatiotemporal EEG/MEG source analysis. Psychometrika 2002, 67, 299–313. [Google Scholar] [CrossRef]
- Smucker, B.J.; Del Castillo, E.; Rosenberger, J.L. Exchange Algorithms for Constructing Model-Robust Experimental Designs. J. Qual. Technol. 2011, 43, 1–15. [Google Scholar] [CrossRef]
- Borkowski, J.J. Using Genetic Algorithm to Generate Small Exact Response Surface Designs. J. Probab. Stat. Sci. 2003, 1, 65–88. [Google Scholar]
- Heredia-Langner, A.; Carlyle, W.M.; Montgomery, D.C.; Borror, C.M.; Runger, G.C. Genetic algorithms for the construction of D-optimal designs. J. Qual. Technol. 2003, 35, 28–46. [Google Scholar] [CrossRef]
- Heredia-Langner, A.; Montgomery, D.C.; Carlyle, W.M.; Borror, C.M. Model-robust optimal designs: A genetic algorithm approach. J. Qual. Technol. 2004, 3, 263–279. [Google Scholar] [CrossRef]
- Juang, Y.; Lin, S.; Kao, H. An adaptive scheduling system with genetic algorithms for arranging employee training programs. Expert Syst. Appl. 2007, 33, 642–651. [Google Scholar] [CrossRef]
- Park, Y.; Montgomery, D.C.; Fowler, J.W.; Borror, C.M. Cost-constrained G-efficient response surface designs for cuboidal regions. Qual. Reliab. Eng. Int. 2006, 22, 121–139. [Google Scholar] [CrossRef]
- Limmun, W.; Borkowski, J.J.; Chomtee, B. Using a Genetic Algorithm to Generate D-optimal Designs for Mixture Experiments. Qual. Reliab. Eng. Int. 2013, 29, 1055–1068. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 3rd ed.; John Wiley & Sons Inc.: New York, NY, USA, 2009. [Google Scholar]
- Atkinson, A.C.; Donev, A.N.; Tobias, R.D. Optimal Experimental Design, with SAS; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Hardin, R.H.; Sloane, N.J.A. A new approach to construction of optimal designs. J. Stat. Plan. Inference 1993, 37, 339–369. [Google Scholar] [CrossRef]
- Syafitri, U.; Sartono, B.; Goos, P. I-optimal design of mixture experiments in the presence of ingredient availability constraints. J. Qual. Technol. 2015, 47, 220–234. [Google Scholar] [CrossRef]
- Borkowski, J.J. A comparison of Prediction Variance Criteria for Response Surface Designs. J. Qual. Technol. 2003, 35, 70–77. [Google Scholar] [CrossRef]
- Coetzer, R.; Haines, L.M. The construction of D- and I-optimal designs for mixture experiments with linear constraints on the components. Chemom. Intell. Lab. Syst. 2017, 171, 112–124. [Google Scholar] [CrossRef]
- Box, G.E.P.; Draper, N.R. A basis for the selection of a response surface design. J. Am. Stat. Assoc. 1959, 54, 622–654. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: New York, NY, USA, 1989. [Google Scholar]
- Bäck, T.; Hammel, U.; Schwefel, H.P. Evolutionary computation: Comments on the history and current state. IEEE Trans. Evol. Comput. 1997, 1, 3–17. [Google Scholar] [CrossRef]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer-Verlag: New York, NY, USA, 1996. [Google Scholar]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Borkowski, J.J.; Piepel, G.F. Uniform designs for highly constrained mixture experiments. J. Qual. Technol. 2009, 41, 1–13. [Google Scholar] [CrossRef]
- Crosier, R.D. Symmetry in mixture experiments. Commun. Stat.-Theory Methods 1991, 20, 1911–1935. [Google Scholar] [CrossRef]
- Ozol-Godfrey, A.; Anderson-Cook, C.M.; Montgomery, D.C. Fraction of design space plots for examining model robustness. J. Qual. Technol. 2005, 37, 223–235. [Google Scholar] [CrossRef]
| Model | Terms in Model | p | ψj | wi | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1st | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 0.4950 | 0.4950 |
| 2nd | 1 | 1 | 1 | 0 | 1 | 1 | 5 | 0.3318 | 0.1106 |
| 3rd | 1 | 1 | 1 | 1 | 0 | 1 | 5 | 0.1106 | |
| 4th | 1 | 1 | 1 | 1 | 1 | 0 | 5 | 0.1106 | |
| 5th | 1 | 1 | 1 | 0 | 0 | 1 | 4 | 0.1683 | 0.0561 |
| 6th | 1 | 1 | 1 | 0 | 1 | 0 | 4 | 0.0561 | |
| 7th | 1 | 1 | 1 | 1 | 0 | 0 | 4 | 0.0561 | |
| 8th | 1 | 1 | 1 | 0 | 0 | 0 | 3 | 0.0049 | 0.0049 |
| 0.6531 | 0.2958 | 0.0511 | 0.5242 | 0.2016 | 0.2742 | 0.5771 | 0.1605 | 0.2624 | 0.5160 | 0.1979 | 0.2861 | 0.6705 | 0.0536 | 0.2759 |
| 0.3612 | 0.2765 | 0.3623 | 0.5858 | 0.2007 | 0.2135 | 0.5229 | 0.1136 | 0.3635 | 0.6487 | 0.1443 | 0.2070 | 0.5256 | 0.0173 | 0.4571 |
| 0.5077 | 0.1156 | 0.3767 | 0.5367 | 0.2877 | 0.1756 | 0.7316 | 0.1828 | 0.0856 | 0.4404 | 0.0682 | 0.4914 | 0.4927 | 0.1614 | 0.3459 |
| 0.4479 | 0.1197 | 0.4324 | 0.5214 | 0.0236 | 0.455 | 0.4780 | 0.2241 | 0.2979 | 0.5488 | 0.2372 | 0.2140 | 0.4754 | 0.0946 | 0.4300 |
| 0.7274 | 0.0546 | 0.2180 | 0.3942 | 0.1999 | 0.4059 | 0.7514 | 0.2388 | 0.0098 | 0.6744 | 0.1869 | 0.1387 | 0.6723 | 0.0354 | 0.2923 |
| 0.6519 | 0.2764 | 0.0717 | 0.7271 | 0.1305 | 0.1424 | 0.7969 | 0.1201 | 0.0830 | 0.7693 | 0.2281 | 0.0026 | 0.5367 | 0.0700 | 0.3933 |
| 0.7612 | 0.2179 | 0.0209 | 0.7569 | 0.1026 | 0.1405 | 0.5422 | 0.2942 | 0.1636 | 0.5322 | 0.1513 | 0.3165 | 0.6342 | 0.1343 | 0.2315 |
| F = 0.2050 | F = 0.1344 | F = 0.0848 | F = 0.0400 | F = 0.0285 | ||||||||||
| Blending | Between-Parent Crossover | Within-Parent Crossover | Mutation | ||
|---|---|---|---|---|---|
| Parent 1 | Parent 1 | Parent 1 | Parent 2 | Parent 1 | Parent 2 |
| 0.9563 | 0.7198 | 0.2807 | 0.4561 | 0.8851 | 0.0049 |
| 0.5209 | 0.7448 | 0.5894 | 0.5453 | 0.9218 | 0.9710 |
| 0.0158 | 0.6830 | 0.0179 | 0.6338 | 0.1266 | 0.2420 |
| 0.6306 | 0.6609 | 0.1799 | 0.7857 | 0.0155 | 0.0400 |
| 0.1155 | 0.4510 | 0.6985 | 0.0769 | 0.3290 | 0.6497 |
| 0.6471 | 0.0017 | 0.6031 | 0.5732 | 0.8324 | 0.0840 |
| 0.8924 | 0.0509 | 0.9297 | 0.0095 | 0.6498 | 0.3173 |
| After Blending | After between-Parent Crossover | After within-Parent Crossover | After Mutation | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6705 | 0.0536 | 0.2759 | 0.5160 | 0.1979 | 0.2861 | 0.6705 | 0.0536 | 0.2759 | 0.5160 | 0.1979 | 0.2861 | 0.6705 | 0.0536 | 0.2759 | 0.5160 | 0.1979 | 0.2861 | 0.6705 | 0.0536 | 0.2759 | 0.4721 | 0.2999 | 0.2800 |
| 0.5256 | 0.0173 | 0.4571 | 0.6487 | 0.1443 | 0.2070 | 0.5256 | 0.0173 | 0.4571 | 0.6487 | 0.1443 | 0.2070 | 0.5256 | 0.0173 | 0.4571 | 0.6487 | 0.1443 | 0.2070 | 0.5256 | 0.0173 | 0.4571 | 0.6487 | 0.1443 | 0.2070 |
| 0.5239 | 0.2036 | 0.2725 | 0.4404 | 0.0682 | 0.4914 | 0.5239 | 0.2036 | 0.2725 | 0.4467 | 0.0600 | 0.4933 | 0.5225 | 0.2036 | 0.2739 | 0.4467 | 0.0600 | 0.4933 | 0.5225 | 0.2036 | 0.2739 | 0.4467 | 0.0600 | 0.4933 |
| 0.4754 | 0.0946 | 0.4300 | 0.5176 | 0.1950 | 0.2874 | 0.4754 | 0.0946 | 0.4300 | 0.5176 | 0.1950 | 0.2874 | 0.4754 | 0.0946 | 0.4300 | 0.5176 | 0.1950 | 0.2874 | 0.5534 | 0.2885 | 0.1581 | 0.5176 | 0.1950 | 0.2874 |
| 0.6723 | 0.0354 | 0.2923 | 0.6744 | 0.1869 | 0.1387 | 0.6723 | 0.0354 | 0.2923 | 0.6744 | 0.1869 | 0.1387 | 0.6723 | 0.0354 | 0.2923 | 0.6744 | 0.1869 | 0.1387 | 0.6723 | 0.0354 | 0.2923 | 0.6744 | 0.1869 | 0.1387 |
| 0.5367 | 0.0700 | 0.3933 | 0.7693 | 0.2281 | 0.0026 | 0.5304 | 0.0782 | 0.3914 | 0.7693 | 0.2281 | 0.0026 | 0.5304 | 0.0782 | 0.3914 | 0.7693 | 0.2281 | 0.0026 | 0.5304 | 0.0782 | 0.3914 | 0.7693 | 0.2281 | 0.0026 |
| 0.6342 | 0.1343 | 0.2315 | 0.5322 | 0.1513 | 0.3165 | 0.6342 | 0.1343 | 0.2315 | 0.5322 | 0.1513 | 0.3165 | 0.6342 | 0.1343 | 0.2315 | 0.5322 | 0.1565 | 0.3113 | 0.6342 | 0.1343 | 0.2315 | 0.5322 | 0.1565 | 0.3113 |
| Initial Population | Offspring | Next Generation | |||||
|---|---|---|---|---|---|---|---|
| Chromosome | F | Partner | Chromosome | F | Chromosome | F | |
| 0.2050 | elite | 0.2050 | 0.2050 | ||||
| 0.1344 | 0.0285 | 0.1344 | |||||
| 0.0848 | 0.3169 | 0.3169 | elite | ||||
| 0.0400 | 0.0827 | 0.0827 | |||||
| 0.0285 | 0.0486 | 0.0486 | |||||
| Design | D-Efficiency | A-Efficiency | G-Efficiency | IV-Efficiency | |
|---|---|---|---|---|---|
| 7 | DX7 | 0.2329 | 0.0036 | 32.4052 | 0.2152 |
| GA7 | 0.2729 | 0.0038 | 57.1217 | 0.2503 | |
| 10 | DX10 | 0.2443 | 0.0045 | 37.2507 | 0.2291 |
| GA10 | 0.2989 | 0.0057 | 75.7591 | 0.2642 | |
| 14 | DX14 | 0.2284 | 0.0039 | 36.0426 | 0.2226 |
| GA14 | 0.2900 | 0.0047 | 68.8525 | 0.2592 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Limmun, W.; Chomtee, B.; Borkowski, J.J. The Construction of a Model-Robust IV-Optimal Mixture Designs Using a Genetic Algorithm. Math. Comput. Appl. 2018, 23, 25. https://doi.org/10.3390/mca23020025
Limmun W, Chomtee B, Borkowski JJ. The Construction of a Model-Robust IV-Optimal Mixture Designs Using a Genetic Algorithm. Mathematical and Computational Applications. 2018; 23(2):25. https://doi.org/10.3390/mca23020025
Chicago/Turabian StyleLimmun, Wanida, Boonorm Chomtee, and John J. Borkowski. 2018. "The Construction of a Model-Robust IV-Optimal Mixture Designs Using a Genetic Algorithm" Mathematical and Computational Applications 23, no. 2: 25. https://doi.org/10.3390/mca23020025
APA StyleLimmun, W., Chomtee, B., & Borkowski, J. J. (2018). The Construction of a Model-Robust IV-Optimal Mixture Designs Using a Genetic Algorithm. Mathematical and Computational Applications, 23(2), 25. https://doi.org/10.3390/mca23020025





