Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface

Abstract

The main intention of this article is to examine the heat transmission of the flow of Eyring–Powell fluid over an unstable oscillatory porous stretching surface. The effect of thermal radiation on the fluid flow is investigated, where the flow is actuated by the unbounded flexible surface which is extended occasionally to and fro on its plane. The rudimentary leading equations are changed to differential equations through the use of applicable similarity variables. An optimal and numerical approach was used to find the solution to the modeled problems. The convergence of the homotopy analysis method (HAM) is shown numerically. The homotopy analysis method predictions of the structures formed are in close agreement with the obtained results from the numerical method. Comparisons between HAM and numerical methods are shown graphically as well as numerically. The convergence of this method is shown numerically. The impacts of the skin friction and heat flux are shown through a table. The influence of the porosity, oscillation, thermal radiation, and heat absorption/generation are the main focus of this work. The consequences of emerging parameters are demonstrated through graphs.

1. Introduction

Boundary layer fluid flow problems in different dimensions through a stretching sheet with heat transfer and magnetohydrodynamic effects have plentiful and inclusive applications in several engineering and industrial sectors. They include glass blowing melt spinning, heat exchanger design, fiber and wire coating, production of glass fibers, industrialization of rubber and plastic sheets, etc. In addition, the action of thermal radiation is vital to calculating heat transmission in the polymer treating industry. In investigations of all these applications, many investigators deliberate the flow of different fluid models over a stretching sheet. Sakiadis [1] studied boundary layer flow over a flat surface. Crane [2] obtained the closed-form solution for the flow instigated by the stretching of a flexible parallel sheet moving periodically. Gupta and Gupta [3] extended this work by considering suction/blowing at the surface of the sheet. The dissemination of chemically reactive species over a moving continuous sheet was studied by Anderson et al. [4]. Pop [5] studied time-dependent flow over a stretched surface. The impact of heat transmission on second-grade fluid over a stretching sheet was explored by Cortell et al. [6]. Areal [7] studied an asymmetric viscoelastic fluid flow past a stretching sheet for different purposes in the fluid field. Rashdi et al. [8,9] studied entropy generation in magneto hydrodynamic Eyring–Powell field and Carreau nanofluid through a permeable stretching surface. Hayat et al. [10,11,12,13] studied boundary layer flow using different phenomena.

There are no solitary constitutive equations for non-Newtonian fluid that clarify all the distinctive aspects of compound rheological fluids. The Eyring–Powell model [14], an important subclass of these, models from the kinetic theory of liquids instead of experimental relations. Recently, Prasad [15] studied heat transfer and momentum in Eyring–Powell fluid over a nonisothermal stretching sheet. Noreen et al. [16] examined the peristaltic flow of magnetohydrodynamic Eyring–Powell fluid in a channel. Ellahi [17] recently completed a numerical study of the magnetohydrodynamic generalized Couette flow of Eyring–Powell fluid with heat transfer and the slip condition. Ellahi et al. [18] examined the shape effects of spherical and nonspherical nanoparticles in mixed convection flow over a vertical stretching permeable sheet. Other related studies concerning Eyring–Powell fluid can be seen in [19,20,21,22,23,24,25].

Thermal radiation is the procedure in which energy is released in the form of electromagnetic radiation by a surface in all directions. Thermal radiation has numerous uses in the areas of engineering and heat transfer analysis. In the case of conduction and convection, energy transmission amongst objects depends almost entirely on the temperature. For natural free convection, or when variable property effects are included, the power of the temperature difference may be slightly larger than one, and can reach two. Tawade et al. [26] investigated a thin liquid flow through a stretching surface with the influence of thermal radiation and a magnetic field. A brief discussion was given on physical parameters in his work. Ellahi et al. [27] examined the boundary layer magnetic flow of nano-ferroliquid under the influence of low oscillation over a stretchable rotating disk. Zeeshan et al. [28] studied the effect of a magnetic dipole on viscous ferrofluid past a stretching surface with thermal radiation. The Hall effect on Falkner–Skan boundary layer fluid flow over a stretching sheet was examined by Maqbool et al. [29]. The enhancement of heat transfer and heat exchange effectiveness in a double-pipe heat exchanger filled with porous media was examined by Shirvan et al. [30]. Ramesh et al. [31] studied the Casson fluid flow near the stagnation point over a stretching sheet with variable thickness and radiation. Other related studies concerning stretching sheets can be seen in [32,33,34]. Bakier and Moradi et al. [35,36] studied the influence of thermal radiation on assorted convective flow on an upright surface in a permeable medium. Chaudhary et al. [37] investigated the thermal radiation effects of fluid on an exponentially extending surface.

The aim of the current research is to investigate the heat transmission of Eyring–Powell fluid over an unsteady oscillatory porous stretching surface. The homotopy analysis method (HAM) was used in the present work for the solution of modelled equations that are nonlinear and coupled. The homotopy analysis method is a substitute method and its main advantage is in its application to nonlinear differential equations without discretization and linearization. In 1992, Liao [38,39,40] was the first to investigate this technique for the solution of this type of problem and generally proved that this method is rapidly convergent to the approximated solutions. Solutions using this technique are significant because they involve all the physical parameters of the problem and we can easily discuss their behavior. Due to its fast convergence, many researchers [41,42,43,44] have used this procedure to solve highly nonlinear combined equations. The effects of all the embedding parameters have been studied graphically. Khan et al. [45] studied the flow and heat transfer of Eyring–Powell fluid over an oscillatory stretching sheet with thermal radiation. Shah et al. [46,47] studied the effects of a Hall current on three-dimensional non-Newtonian nanofluids and micropolar nanofluids in a rotating frame. Hameed et al. [48] investigated the combined magnetohydrodynamic and electric field effect on an unsteady Maxwell nanofluid flow over a stretching surface under the influence of variable heat and thermal radiation. Recently Muhammad et al. [49] studied the rotating flow of magneto hydrodynamic carbon nanotubes over a stretching sheet with the impact of non-linear thermal radiation and heat generation/absorption.

2. Formulation of the Problem

Consider a two-dimensional incompressible boundary layer flow of Eyring–Powell fluid over an oscillating stretched sheet concurring with plane $y$ (Figure 1). In the Cartesian coordinate system, $x$ is beside the sheet and $y$ is vertical to the sheet. The fluid flow is assumed to be in an unsteady state and the stretching sheet is kept porous. Let ${\mathrm{T}}_{\mathrm{w}}$ denote the surface temperature and ${\mathrm{T}}_{\infty }$ denote the temperature of the fluid as the distance from the surface tends to infinity. It is assumed that ${\mathrm{T}}_{\mathrm{w}}>{\mathrm{T}}_{\infty }$. The Cauchy stress tensor for Eyring–Powel fluid [15,16,17,18,19,20,21,22,23,24,25] is

$$\overrightarrow{\mathrm{T}}=-\overrightarrow{\mathrm{P}}\overrightarrow{\mathrm{I}}+{\overrightarrow{\tau }}_{ij},$$

(1)

where ${\overrightarrow{\tau }}_{ij}$ for the Eyring–Powel fluid is

$${\overrightarrow{\tau }}_{ij}=\mu \frac{\partial {\overrightarrow{u}}_i}{\partial x_j}+\frac{1}{\alpha }{\sinh }^{-1}\left(\frac{1}{c}\frac{\partial {\overrightarrow{u}}_i}{\partial x_j}\right).$$

(2)

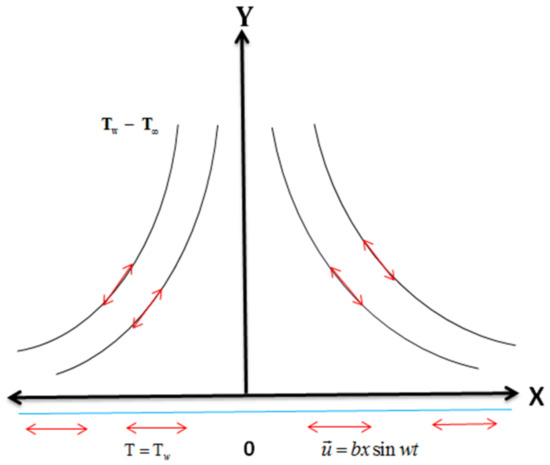
Figure 1. Geometrical figure of the problem.

Here, $\mathsf{\alpha }$ and c denote the Eyring–Powel fluid constants. We expand the term ${\sinh }^{-1}\left(\frac{1}{c}\frac{\partial {\overrightarrow{u}}_i}{\partial x_j}\right)$ as below:

$${\sinh }^{-1}\left(\frac{1}{c}\frac{\partial {\overrightarrow{u}}_i}{\partial x_j}\right)=\frac{1}{c}\frac{\partial {\overrightarrow{u}}_i}{\partial x_j}-\frac{1}{6}{\left(\frac{1}{c}\frac{\partial {\overrightarrow{u}}_i}{\partial x_j}\right)}^3,\left|\frac{1}{c}\frac{\partial {\overrightarrow{u}}_i}{\partial x_j}\right|<1.$$

(3)

Using the boundary layer approximations, the continuity, energy equations and momentum are as:

$$\frac{\partial \overrightarrow{u}}{\partial x}+\frac{\partial \overrightarrow{v}}{\partial y}=0$$

(4)

$$\frac{\partial \overrightarrow{u}}{\partial t}+\overrightarrow{u}\frac{\partial \overrightarrow{u}}{\partial x}+\overrightarrow{v}\frac{\partial \overrightarrow{u}}{\partial y}=\left(\upsilon +\frac{1}{\rho \mathsf{\Psi }\mathsf{\Upsilon }}\right)\frac{{\partial }^2\overrightarrow{u}}{\partial y^2}-\frac{1}{2\rho \mathsf{\Psi }{\mathsf{\Upsilon }}^3}{\left(\frac{\partial \overrightarrow{u}}{\partial y}\right)}^2\frac{{\partial }^2\overrightarrow{u}}{\partial y^2}-\frac{\upsilon }{k}\overrightarrow{u}$$

(5)

$$\rho C_p\left(\left(\frac{\partial \mathrm{T}}{\partial t}\right)+\overrightarrow{u}\left(\frac{\partial \mathrm{T}}{\partial x}\right)+\overrightarrow{v}\left(\frac{\partial \mathrm{T}}{\partial y}\right)\right)=k\left(\frac{{\partial }^2\mathrm{T}}{\partial y^2}\right)-\left(\frac{\partial Q_{rad}}{\partial y}\right)+\frac{Q_0}{\rho C_p}\left(\mathrm{T}-{\mathrm{T}}_{\infty }\right)$$

(6)

The terms $\overrightarrow{u}$ and $\overrightarrow{v}$ represent the velocity component in the directions of $x$ and $y$, respectively; $\upsilon$ indicates the kinematic viscosity; the symbol $\rho$ denotes the density; $\mathsf{\Psi }$ and $\mathsf{\Upsilon }$ are the fluid materials; $C_p$ indicates the specific heat; $Q_0$ is the heat source/sink; $k$ signifies thermal conductivity; and $Q_{rad}$ is the radiative heat flux is defined as

$$Q_{rad}=-\frac{4{\sigma }^{\prime }}{3k^{\prime }}\frac{\partial {\mathrm{T}}^4}{\partial y},$$

(7)

where ${\sigma }^{\prime }$ denotes the Stefan–Boltzmann constant and $k^{\prime }$ is the absorption coefficient.

Expanding Equation (7) by Taylor series, we obtain

$${\mathrm{T}}^4={{\mathrm{T}}_{\infty }}^4+4{{\mathrm{T}}_{\infty }}^3\left(\mathrm{T}-{\mathrm{T}}_{\infty }\right)+6{{\mathrm{T}}_{\infty }}^2{\left(\mathrm{T}-{\mathrm{T}}_{\infty }\right)}^2+\dots$$

(8)

By neglecting the higher terms from Equation (8), we get

$${\mathrm{T}}^4=4{\mathrm{T}}_{\infty }^3\mathrm{T}-3{\mathrm{T}}_{\infty }^4.$$

(9)

In observation of Equations (7) and (8), Equation (6) becomes

$$\rho C_p\left(\frac{\partial \mathrm{T}}{\partial t}+\overrightarrow{u}\frac{\partial \mathrm{T}}{\partial x}+\overrightarrow{v}\frac{\partial \mathrm{T}}{\partial y}\right)=\left(k+\frac{16{\sigma }^{\prime }{{\mathrm{T}}_{\infty }}^3}{3k^{\prime }}\right)\frac{{\partial }^2\mathrm{T}}{\partial y^2}+\frac{Q_0}{\rho C_p}\left(\mathrm{T}-{\mathrm{T}}_{\infty }\right).$$

(10)

The subjected boundary condition for the flow phenomena [45] is

$$\begin{array}{l}\overrightarrow{u}={\overrightarrow{u}}_w=bx\sin \omega t,\overrightarrow{v}=0,\mathrm{T}=\mathrm{T}w\mathrm{at}y=0,t>0,\\ \overrightarrow{u}\to 0,\mathrm{T}\to {\mathrm{T}}_{\infty }\mathrm{at}y\to \infty ,\end{array}$$

(11)

where the dimensionless variables are given as

$$y=\sqrt{\frac{b}{\upsilon }}y,\tau =t\omega ,\overrightarrow{u}=bx{F}_y\left(y,\tau \right),\overrightarrow{v}=-\sqrt{\upsilon b}F\left(y,\tau \right),G\left(y,\tau \right)=\frac{\mathrm{T}-{\mathrm{T}}_{\infty }}{{\mathrm{T}}_w-{\mathrm{T}}_{\infty }}.$$

(12)

In observation of the dimensionless variables defined above, Equations (5) and (10) reduce to

$$\left(1+\mathrm{K}\right)F^{‴}-A{F}^{″}-{\left(F^{\prime }\right)}^2+F{F}^{″}-\lambda \mathrm{K}{F^{″}}^2{F}^{‴}-\kappa F^{\prime }=0,$$

(13)

$$\left(1+Rd\right)G^{″}+\mathrm{Pr}\left(F{G}^{\prime }-A{G}^{\prime }\right)-\gamma G=0,$$

(14)

with the boundary conditions

$$F^{\prime }\left(0,\tau \right)=\sin \tau ,F(0,\tau )=0,G(0,\tau )=1,F^{\prime }\left(\infty ,\tau \right)=0,G(\infty ,\tau )=0.$$

(15)

In the above equations, $\mathrm{K}=\frac{1}{\mu \mathsf{\Psi }\mathsf{\Upsilon }}$ and $\lambda =\frac{x^2{b}^3}{2\upsilon {\mathsf{\Upsilon }}^2}$ are dimensionless material fluid parameters, $\kappa =\frac{\upsilon }{kb}$ indicates the porosity, $A=\frac{\omega }{b}$ represents the ratio of the oscillation frequency, $\gamma =\frac{\upsilon Q_0}{kb\rho C_p}\left(\frac{\mathrm{T}-{\mathrm{T}}_{\infty }}{{\mathrm{T}}_w-{\mathrm{T}}_{\infty }}\right)$ represents the heat source/sink, $\mathrm{Pr}=\frac{\mu C_p}{k}$ denotes the Prandtl number, and $Rd=\frac{16{\sigma }^{\prime }{\mathrm{T}}_{\infty }^3\mathrm{T}}{3k{k}^{\prime }}$ is the radiation parameter. According to Javed et al. [27], Equation (15) is subject to the constraint $\mathsf{\lambda }\mathrm{K}<<1$.

Physical Quantities of Interest

The physical quantities for interest to engineers, such as skin friction $C_f$ and the local Nusselt number $N{u}_x$, are defined as

$$C_f=\frac{{\tau }_w}{\rho u_w^2},N{u}_x=\frac{x{q}_w}{k({\mathrm{T}}_w-{\mathrm{T}}_{\infty })},q_w=-k{\left(\frac{\partial \mathrm{T}}{\partial y}\right)}_{y=0},$$

(16)

In observation of Equation (12), Equation (16) takes the following forms:

$${\mathrm{Re}}_x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}Cf=(1+\mathrm{K})F^{″}-\frac{\mathrm{K}}{3}\mathsf{\Psi }(F^{″}\left(0\right)),{\mathrm{Re}}_x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}N{u}_x=-\left(1+\frac{4}{3}Rd\right)G^{\prime }\left(0\right).$$

(17)

3. Solution by HAM

Liao was the first person who used the basic idea of a topology called homotopy and derived a new method known as the homotopy analysis method. He used two homotopic functions to derive this technique. Two functions are called homotopic functions when one of them can be continuously distorted into the other. Let $H_1,H_2$ be two functions that are continuous and ${\mathrm{X}}_1,{\mathrm{X}}_2$ be two topological spaces where $H_1$ and $H_2$ map from ${\mathrm{X}}_1$ to ${\mathrm{X}}_2$; then $H_1$ is said to be homotopic to $H_2$ if there is a continuous function $\overline{f}$,

$$\overline{f}:{\mathrm{X}}_1\times \left[0,1\right]\to {\mathrm{X}}_2,$$

(18)

such that, $\forall x\in {\mathrm{X}}_1$,

$$\overline{f}\left[x,0\right]=H_1\left(x\right)\mathrm{and}\overline{f}\left[x,0\right]=H_2\left(x\right).$$

(19)

This mapping $\overline{f}$ is then called homotopic.

In order to solve Equations (13) and (14) with the boundary Condition (15), we use the HAM according to the following process. The preliminary guesses are

$$F_0(\mathsf{\Gamma })=1-e^{-\mathsf{\Gamma }}\sin \mathsf{\Gamma },{\mathrm{G}}_0(\mathsf{\Gamma })=e^{-\mathsf{\Gamma }}.$$

(20)

The linear operators are taken as $L_F\mathrm{and}{\mathrm{L}}_G:$

$$L_F(F)=F^{‴}-F^{\prime },{\mathrm{L}}_G\left(\mathrm{G}\right)={\mathrm{G}}^{″}-G.$$

(21)

These operators have the following properties:

$$L_F({\psi }_1+{\psi }_2{e}^{-\mathsf{\Gamma }}+{\psi }_3{e}^{\mathsf{\Gamma }})=0,{\mathrm{L}}_G({\psi }_4{e}^{-\mathsf{\Gamma }}+{\psi }_5{e}^{\mathsf{\Gamma }})=0,$$

(22)

where ${\psi }_i(i=1-5)$ are constants.

The nonlinear operators $N_F$ and $N_G$ are specified as

$$\begin{array}{l}{\mathrm{N}}_{\mathrm{F}}\left[\mathrm{F}\left(\mathsf{\Gamma };\mho \right)\right]=\left(1+\mathrm{K}\right)\frac{{\partial }^3\mathrm{F}\left(\mathsf{\Gamma };\mho \right)}{\partial {\mathsf{\Gamma }}^3}-\mathrm{A}\frac{{\partial }^2\mathrm{F}\left(\mathsf{\Gamma };\mho \right)}{\partial {\mathsf{\Gamma }}^2}-{\left(\frac{\partial \mathrm{F}\left(\mathsf{\Gamma };\mho \right)}{\partial \mathsf{\Gamma }}\right)}^2\\ -\mathsf{\lambda }\mathrm{k}{\left(\frac{{\partial }^2\mathrm{F}\left(\mathsf{\Gamma };\mho \right)}{\partial {\mathsf{\Gamma }}^2}\right)}^2\frac{{\partial }^3\mathrm{F}\left(\mathsf{\Gamma };\mho \right)}{\partial {\mathsf{\Gamma }}^3}-\mathsf{\kappa }\frac{\partial \mathrm{F}\left(\mathsf{\Gamma };\mho \right)}{\partial \mathsf{\Gamma }},\end{array}$$

(23)

$$\left(1+\mathrm{Rd}\right)\frac{{\partial }^2\mathrm{G}\left(\mathsf{\Gamma };\mho \right)}{\partial {\mathsf{\Gamma }}^2}+\mathrm{Pr}\left(\mathrm{F}\left(\mathsf{\Gamma };\mho \right)\frac{\partial \mathrm{G}\left(\mathsf{\Gamma };\mho \right)}{\partial \mathsf{\Gamma }}-\mathrm{A}\frac{\partial \mathrm{G}\left(\mathsf{\Gamma };\mho \right)}{\partial \mathsf{\Gamma }}\right)-\mathsf{\gamma }\mathrm{G}\left(\mathsf{\Gamma };\mho \right)=0.$$

(24)

The zero-order problems from Equations (13) and (14) are

$$\begin{array}{c}\left(1-\mho \right){\mathrm{L}}_{\mathrm{F}}\left[\mathrm{F}\left(\mathsf{\Gamma };\mho \right)-{\mathrm{F}}_0\left(\mathsf{\Gamma }\right)\right]=\mho {\hslash }_{\mathrm{F}}{\mathrm{N}}_{\mathrm{F}}\left[\mathrm{F}\left(\mathsf{\Gamma };\mho \right)\right],\\ \left(1-\mho \right){\mathrm{L}}_{\mathrm{G}}\left[\mathrm{G}\left(\mathsf{\Gamma };\mho \right)-{\mathrm{G}}_0\left(\mathsf{\Gamma }\right)\right]=\mho {\hslash }_{\mathrm{G}}{\mathrm{N}}_{\mathrm{G}}[\mathrm{F}\left(\mathsf{\Gamma };\mho \right),\mathrm{G}\left(\mathsf{\Gamma };\mho \right)].\end{array}$$

(25)

The equivalent boundary conditions are

$$\begin{array}{l}{F(\mathsf{\Gamma };\mho )|}_{\mathsf{\Gamma }=0}=0,{\frac{\partial F(\mathsf{\Gamma };\mho )}{\partial \mathsf{\Gamma }}|}_{\mathsf{\Gamma }=0}=\sin \tau ,{\frac{\partial F(\mathsf{\Gamma };\mho )}{\partial \mathsf{\Gamma }}|}_{\mathsf{\Gamma }=\to \infty }=0,\\ {G(\mathsf{\Gamma };\mho )|}_{\mathsf{\Gamma }=0}=1,{G(\mathsf{\Gamma };\mho )|}_{\mathsf{\Gamma }\to \infty }=0,\end{array}$$

(26)

where $0\le \mho \le 1$ is the embedding parameter. When $\mho =0$ and $\mho =1,$ we have

$$F(\mathsf{\Gamma };1)=F(\mathsf{\Gamma })\mathrm{and}\mathrm{G}(\mathsf{\Gamma };1)=G(\mathsf{\Gamma }).$$

(27)

Expanding $F(\mathsf{\Gamma };\mho )$ and $\mathrm{G}(\mathsf{\Gamma };\mho )$ by Taylor series,

$$\begin{array}{l}F(\mathsf{\Gamma };\mho )=F_0(\mathsf{\Gamma })+{\displaystyle \sum _{q=1}^{\infty }{F}_q(\mathsf{\Gamma }){\mho }^q}\\ G(\mathsf{\Gamma };\mho )=G_0(\mathsf{\Gamma })+{\displaystyle \sum _{q=1}^{\infty }{G}_q(\mathsf{\Gamma }){\mho }^q}\end{array}$$

(28)

where

$$F_q(\mathsf{\Gamma })={\frac{1}{q!}\frac{\partial F(\mathsf{\Gamma };\mho )}{\partial \mathsf{\Gamma }}|}_{\mho =0}\mathrm{and}{\mathrm{G}}_q(\mathsf{\Gamma })={\frac{1}{q!}\frac{\partial G(\mathsf{\Gamma };\mho )}{\partial \mathsf{\Gamma }}|}_{\mho =0}.$$

(29)

Setting $\mho =1$ in (29), we obtain

$$\begin{array}{l}F(\mathsf{\Gamma })=F_0(\mathsf{\Gamma })+{\displaystyle \sum _{q=1}^{\infty }{F}_q(\mathsf{\Gamma })},\\ G(\mathsf{\Gamma })=G_0(\mathsf{\Gamma })+{\displaystyle \sum _{q=1}^{\infty }{G}_q(\mathsf{\Gamma })}.\end{array}$$

(30)

The $q$th-order problem satisfies the following:

$$\begin{array}{l}{L}_F\left[F_q(\mathsf{\Gamma })-{\chi }_q{F}_{q-1}(\mathsf{\Gamma })\right]={\hslash }_F{U}_q^F(\mathsf{\Gamma })\\ L_G\left[G_q(\mathsf{\Gamma })-{\chi }_q{G}_{q-1}(\mathsf{\Gamma })\right]={\hslash }_G{U}_q^G(\mathsf{\Gamma })\end{array}$$

(31)

with the conditions

$$\begin{array}{l}{F}_q(0)=F_q^{\prime }(0)=F_q^{\prime }(\infty )=0,\\ G_q(0)=G_q(\infty )=0.\end{array}$$

(32)

Here,

$$U_q^F(\mathsf{\Gamma })=(1+K)F_{q-1}^{‴}-A{F}_{q-1}^{″}-{\displaystyle \sum _{k=0}^{q-1}{F}_{q-1-k}^{\prime }}{F}_k^{\prime }+{\displaystyle \sum _{k=0}^{q-1}{F}_{q-1-k}}{F}_k^{″}-\lambda k{\displaystyle \sum _{k=0}^{q-1}{F}_{q-1-k}^{″}}{\displaystyle \sum _{j=0}^k{F}_{k-j}^{″}}{F}_j^{‴}-\kappa F_{q-1}^{\prime }$$

(33)

$$U_q^G(\mathsf{\Gamma })=\left(1+Rd\right)G_{q-1}^{″}+\mathrm{Pr}\left[{\displaystyle \sum _{k=0}^{q-1}{F}_{q-1-k}}{G}_k^{\prime }-A{G}_{q-1}^{\prime }\right]-\gamma G_{q-1}$$

(34)

where

$${\chi }_q=\{\begin{array}{ll}0,& \mathrm{if}\mho \le 1\\ 1,& \mathrm{if}\mho >1\end{array}$$

(35)

4. HAM Solution Convergence

When we compute the series solutions of the velocity and temperature functions in order to use HAM, the assisting parameters $h_f,h_{\theta }$ appear. These assisting parameters are responsible for adjusting the convergence of these solutions. The $\hslash$-curves of $f^{″}(0)$ and ${\theta }^{\prime }(0)$, at 12th-order approximations are plotted in Figure 2 and Figure 3 for dissimilar values of the embedding parameter. The $\hslash$-curves consecutively display the valid region.

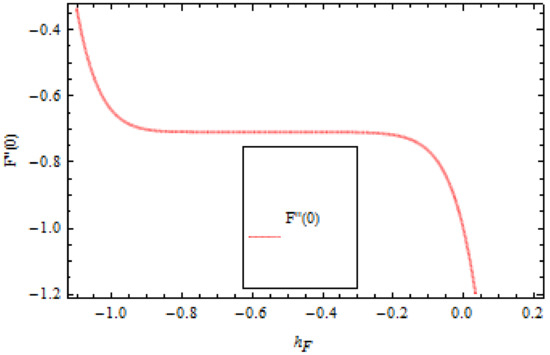
Figure 2. The $\hslash$-curve graph of velocity profile, when $Pr=0.5,K=0.5,Rd=0.5,\lambda =0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0,A=0.5$.

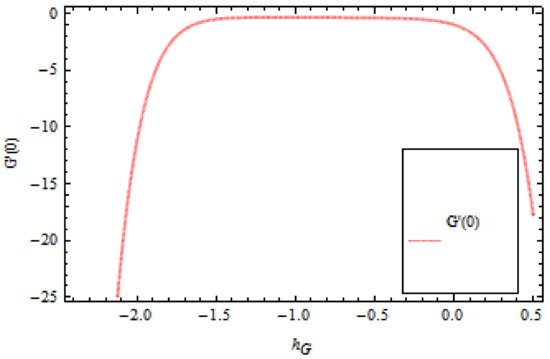
Figure 3. The $\hslash$-curve graph of temperature profile, when $Pr=0.5,K=0.5,Rd=0.5,\lambda =0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0,A=0.5$.

5. Results and Discussion

In this section, we present the special effects of the concerned parameters graphically. In all the graphs, the values of $K$ and $\lambda$ are chosen such that the product $\lambda K$ should be much smaller than one. Figure 4 shows the effect of the rate of the relative amplitude of frequency and the stretching rate $A$ on the time series of the velocity distribution. It is observed that the amplitude of the flow motion falls with large values of $A.$ Figure 5 demonstrates the effect of $A$ on the temperature profile. It is observed that the temperature profile $G$ decreases as $A$ increases. Actually, the amplitude of oscillation rises for large values of $A$ which, in turn, decreases the temperature. The influence of the Prandtl number ($Pr$) on the temperature distribution is shown in Figure 6. The temperature distribution varies inversely with $Pr$ It is clear that the temperature distribution decreases for a large $Pr$ and increases for small values of $Pr$. Physically, the fluids with a small $Pr$ have larger thermal diffusivity, and this effect is opposite for a higher Prandtl number. Due to this fact, a large $Pr$ causes the thermal boundary layer to decrease. The effect is even more distinct for a small $Pr$, since the thermal boundary layer thickness is relatively large. The impact of the thermal radiation parameter $Rd$ is presented in Figure 7. Thermal radiation has a dominating role in the comprehensive surface heat transmission, when the coefficient of convection heat transmission is small. When we increase the thermal radiation parameter $Rd,$ we see that it augments the temperature in the boundary layer area in the fluid layer. Figure 8 represents the influence of $\kappa$ on the velocity profile. It is noted that the increasing value of $\kappa$ increases the velocity of the fluid during oscillation. The features of the porosity parameter $\kappa$ on the velocity field are shown in Figure 9, and have an imperative character in terms of the flow motion. The higher values of $\kappa$ increase the porous space; this produces resistance in the flow path and reduces the flow motion. In fact, growing values of $\gamma$ show a large number of porous spaces, which create resistance in the flow path and reduce overall fluid motion. Figure 10 shows the influence of the dimensionless fluid parameter $\lambda$ on the velocity profile. Large values of $\lambda$ speed up the flow motion and increase its oscillation. Figure 11 presents the influence of the heat source/sink $\gamma$ on the temperature profile. It is obvious from the figure that increases in the value enhance the temperature profile $\gamma$ of the flow. This occurs due to the fact that the different values of $\gamma$ perform like a heat generator, releasing heat energy to the flow. This helps to develop the thermal boundary layer thickness. Figure 12 and Figure 13 show the effect of different values of $\tau$ on the velocity and temperature profiles. Greater values of $\tau$ increase the temperature and velocity profiles.

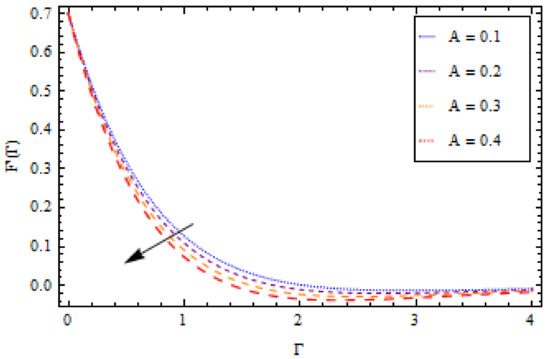
Figure 4. Impact of $A$ on velocity profile $F^{\prime }(\mathsf{\Gamma })$ when $Pr=0.5,K=0.5,Rd=0.5,\lambda =0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0$.

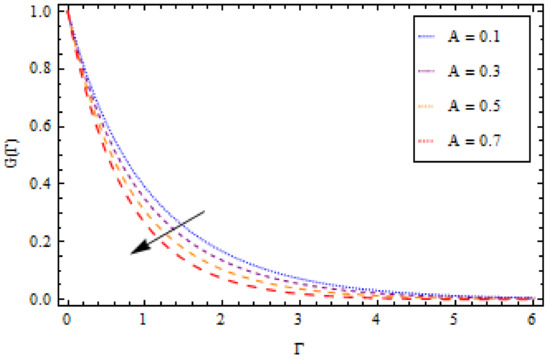
Figure 5. Impact of $A$ on temperature profile $G(\mathsf{\Gamma })$, when $Pr=0.5,K=0.5,Rd=0.5,\lambda =0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0$.

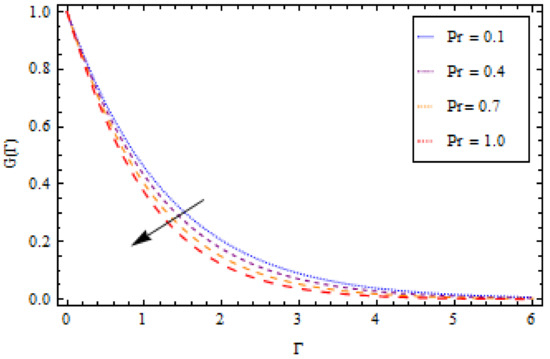
Figure 6. Impact of $Pr$ on temperature profile $G(\mathsf{\Gamma })$, when $A=0.5,K=0.5,Rd=0.5,\lambda =0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0$.

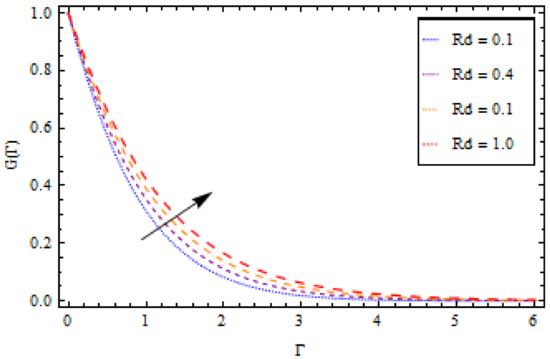
Figure 7. Impact of $Rd$ on temperature profile $G(\mathsf{\Gamma })$, when $K=0.5,Pr=0.5,\lambda =0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0,A=0.5$.

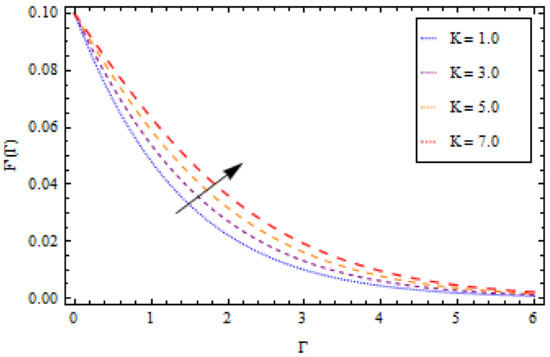
Figure 8. Impact of $K$ on velocity profile $F^{\prime }(\mathsf{\Gamma })$, when $Pr=0.5,Rd=0.5,\lambda =0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0,A=0.5$.

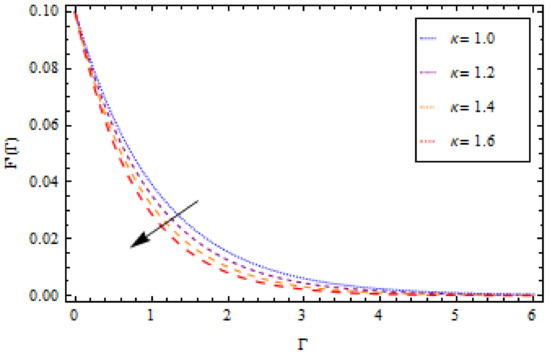
Figure 9. Impact of $\kappa$ on velocity profile $F^{\prime }(\mathsf{\Gamma })$, when $Pr=0.5,Rd=0.5,\lambda =0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0,A=0.5$.

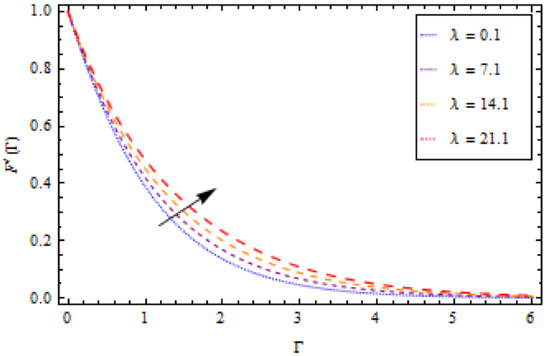
Figure 10. Impact of $\lambda$ on velocity profile $F^{\prime }(\mathsf{\Gamma })$ when $Pr=0.5,Rd=0.5,K=0.5,\kappa =0.5,\gamma =0.5,\mathrm{Sin}\tau =1.0,A=0.5$.

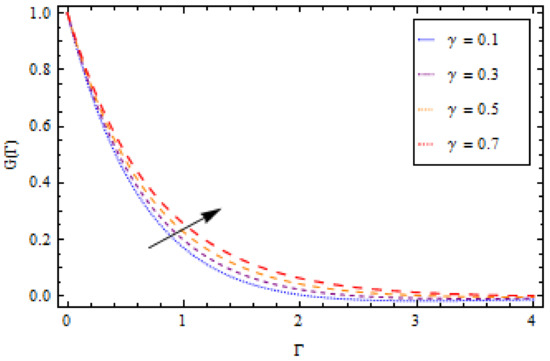
Figure 11. Impact of $\gamma$ on temperature profile $G(\mathsf{\Gamma })$, when $Pr=0.5,Rd=0.5,K=0.5,\kappa =0.5,\lambda =0.5,\mathrm{Sin}\tau =1.0,A=0.5$.

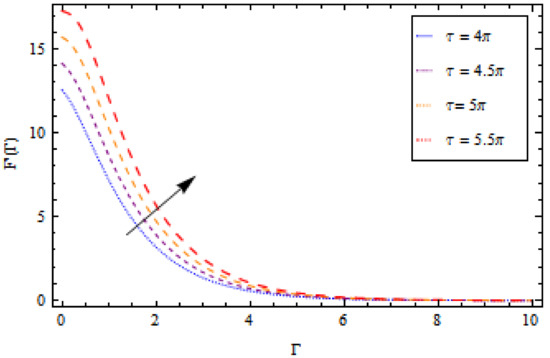
Figure 12. Impact of $\tau$ on velocity profile $F^{\prime }(\mathsf{\Gamma })$, when $Pr=0.5,Rd=0.5,K=0.5,\kappa =0.5,\gamma =0.5,\lambda =0.5,A=0.5$.

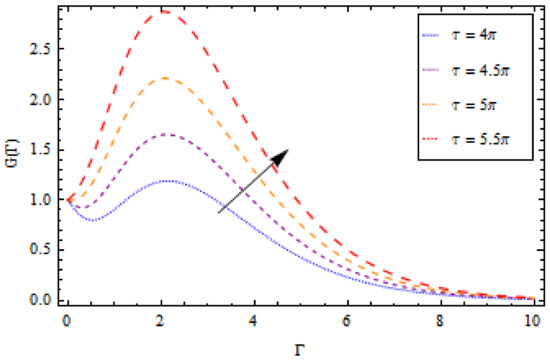
Figure 13. Impact of $\tau$ on temperature profile $G(\mathsf{\Gamma })$, when $Pr=0.5,Rd=0.5,K=0.5,\kappa =0.5,\gamma =0.5,\lambda =0.5,A=0.5$.

Figure 14 and Figure 15 show the comparison between HAM and numerical solutions using the ND-solve technique on velocity and temperature profiles, respectively. An excellent agreement was found between the homotopy analysis method and the ND-solve technique.

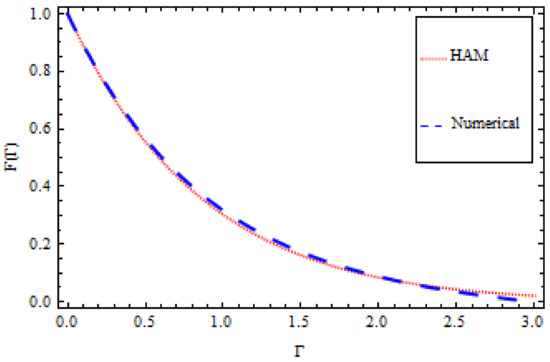
Figure 14. HAM and numerical comparison for velocity profile $F^{\prime }(\mathsf{\Gamma })$.

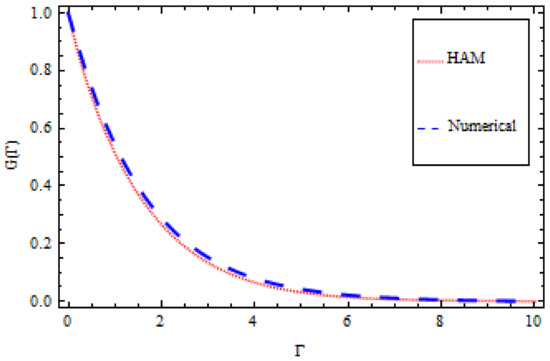
Figure 15. HAM and numerical comparison for temperature profile $G(\mathsf{\Gamma })$.

Table Discussion

The physical quantities such as the skin friction coefficient $C_f$ and heat flux $Nu$, which are of engineering interest, are calculated through Table 1 and Table 2. The impact of $\kappa ,K\mathrm{and}\lambda$ on the skin friction coefficient is shown in Table 1. It is observed that higher values of $\kappa ,K$ and $\lambda$ reduce the coefficient. The impact of $Pr,\gamma \mathrm{and}Rd$ on heat flux is shown in Table 2. It is observed that higher values of $Pr$ decrease the heat flux, while higher values of $\gamma \mathrm{and}Rd$ increase the heat flux. The comparison of HAM and the numerical solution and the absolute error are provided in Table 3 and Table 4. Table 3 shows the comparison of HAM and the numerical solution for the velocity profile, while Table 4 shows the comparison of HAM and the numerical solution for the temperature profile.

Table 1. The numerical values of skin fraction $(1+K)F^{″}(0)-\frac{K}{3}\mathsf{\Psi }(F^{″}(0)),$ when $A=0.5,\mathsf{\Psi }=1$ at time instant $\tau =\pi /2$.

$\mathit{\kappa }$	$\mathit{K}$	$\mathit{\lambda }$	${\mathit{C}}_{\mathit{f}}$
0.5	-	-	−1.29447
0.7	-	-	−1.39927
0.9	-	-	−1.50053
1.1	1.0	-	−1.59913
-	1.3	-	−1.68426
-	1.5	-	−1.73747
-	1.7	0.5	−1.78810
-	-	0.6	−1.81316
-	-	0.7	−1.84069

Table 2. The numerical values of heat flux $\left(1+\frac{4}{3}Rd\right)G^{\prime }(0),$ when $A=0.5,\mathsf{\Psi }=1$ at time instant $\tau =\pi /2$.

$\mathit{P}\mathit{r}$	$\mathit{\gamma }$	$\mathit{Rd}$	$\mathit{N}{\mathit{u}}_{\mathit{x}}$
1.0	-	-	1.82770
1.2	-	-	1.80574
1.4	-	-	1.78404
1.6	2.5	-	1.76259
-	2.6	-	1.79740
-	2.7	-	1.83133
-	2.8	0.3	1.85965
-	-	0.4	1.97571
-	-	0.5	2.08693

Table 3. The association between HAM and numerical solution for $F^{\prime }(\mathsf{\Gamma }),$ when $K=0,A=0.2,\kappa =0.5,Rd=1.0,\mathrm{Sin}\tau =1.0,\lambda =Pr=\gamma =0.6$.

$\mathsf{\Gamma }$	HAM Solution ${\mathit{F}}^{\mathbf{\prime }}(\mathsf{\Gamma })$	Numerical Solution ${\mathit{F}}^{\mathbf{\prime }}(\mathsf{\Gamma })$	Absolute Error AE
0.0	1.12757 × 10−17	0.000000	1.12757 × 10−17
0.5	0.378563	0.381439	0.002876
1.0	0.586888	0.596535	0.009647
1.5	0.699341	0.715829	0.016488
2.0	0.758826	0.779103	0.020276
2.5	0.789566	0.808656	0.019089
3.0	0.804988	0.816817	0.011828
3.5	0.812414	0.866641	0.054227
4.0	0.815772	0.873029	0.057257
4.5	0.817129	0.875971	0.058842
5.0	0.817552	0.876772	0.059220

Table 4. The association between HAM and numerical solution for $G(\mathsf{\Gamma })$, when $K=0,A=0.2,\kappa =0.5,Rd=1.0,\mathrm{Sin}\tau =1.0,\lambda =Pr=\gamma =0.6$.

$\mathsf{\Gamma }$	HAM Solution $\mathit{G}(\mathsf{\Gamma })$	Numerical Solution $\mathit{G}(\mathsf{\Gamma })$	Absolute Error AE
0	1.000000	1.000000	0.000000
1.0	0.513778	0.543757	0.029978
2.0	0.266242	0.288424	0.022182
3.0	0.133781	0.152038	0.018257
4.0	0.065247	0.080017	0.014769
5.0	0.030998	0.042041	0.011042
6.0	0.014391	0.021973	0.007582
7.0	0.006548	0.011297	0.004748
8.0	0.002927	0.005503	0.002575
9.0	0.001288	0.002181	0.000892
10.0	0.000559	2.093 × 10−6	0.000557

6. Conclusions

In this article, we analyzed an Eyring–Powell fluid over an oscillatory thermally conductive stretching sheet in the presence of thermal radiation and a heat source/sink. A coordinate transformation was used to transform the semi-infinite flow domain to a finite computational domain. The homotopy analysis method was used to solve the modeled problem. The main remarks from this study are as follows:

• The amplitude of the velocity decreased with an increase in $A$ and porosity $\kappa$, while it increased with an increase in the dimensionless fluid parameters $K$ and $\lambda .$
• The temperature increased with an increase in $A$, the radiation parameter $Rd$, and the heat source/sink $\gamma$, while it decreased with an increase in the Prandtl number $Pr$ and the ratio of the oscillation frequency of the sheet to its stretching rate $A$.
• The local Nusselt number increased with an increase in the Prandtl number $Pr$, the heat source/sink $\gamma$, the dimensionless fluid parameter $K$ and radiation parameter $Rd$, while it decreased with an increase in the porosity $\kappa$ and the dimensionless fluid parameter $\lambda$.