How Am I Driving? Using Genetic Programming to Generate Scoring Functions for Urban Driving Behavior
Abstract
:1. Introduction
2. Related Work
3. Methodology
3.1. The Dataset
3.2. Genetic Programming and Tested Flavors
| Algorithm 1 Genetic Programming pseudocode. |
| 1: for to (or until an acceptable solution is found) do |
| 2: if 1st generation then |
| 3: generate initial population with primitives (variables, constants and elements from the function set) |
| 4: end if |
| 5: Calculate fitness (minimize RMSE) of population members |
| 6: Select n parents from population (based on fitness) |
| 7: Stochastically apply Genetic operators to generate n offspring |
| 8: end for |
| 9: Return best individual (based on fitness) found during search |
3.2.1. GPTIPS V2
3.2.2. neatGP
3.2.3. neatGP-LS
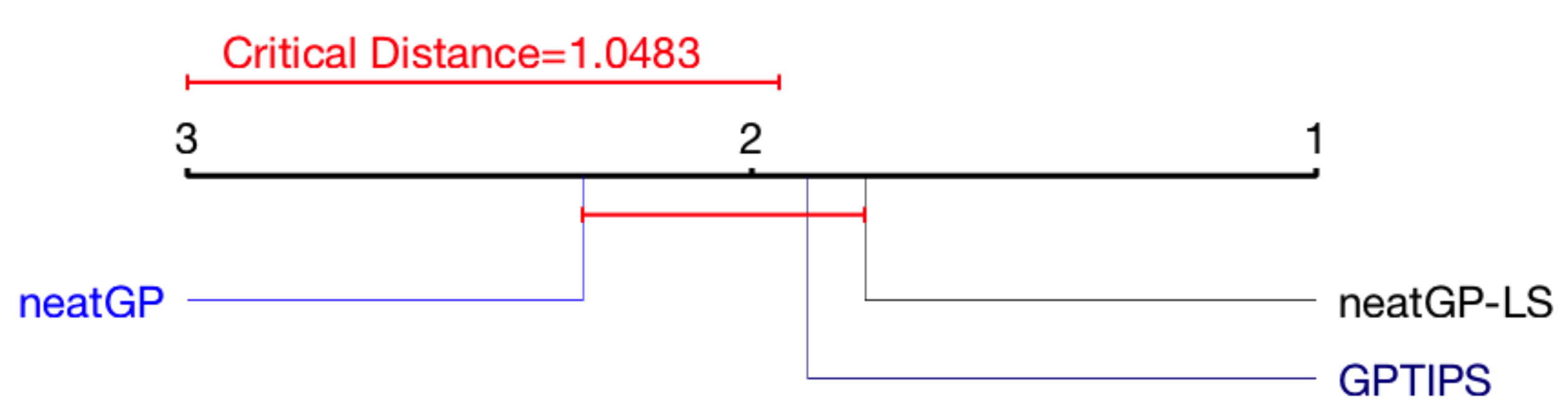
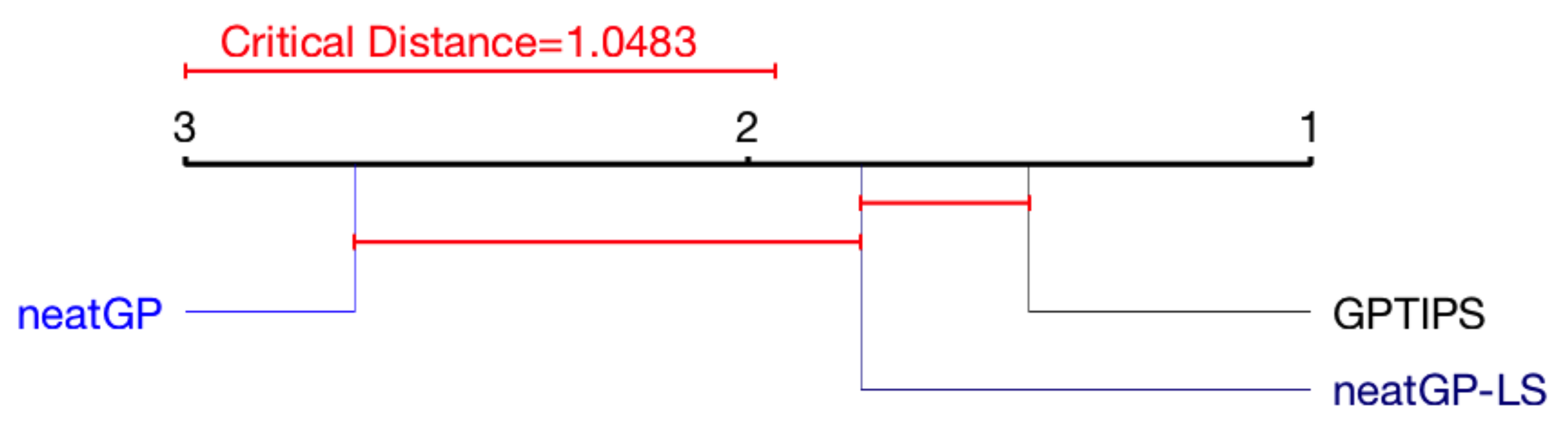
3.3. Statistical Analysis: Friedman Test and Critical Difference Diagram
4. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GP | Genetic Programming |
| ML | Machine Learning |
| SRM | Symbolic Regression Model |
| ANN | Artificial Neural Networks |
| SVM | Support Vector Machines |
| RF | Random Forest |
| BN | Bayesian Networks |
| FIS | Fuzzy Inference Systems |
| BRR | Bayesian Ridge Regression |
| SVR | Support Vector Regression |
| LS | Local Search |
| NEAT | NeuroEvolution of Augmenting Topologies algorithm |
| Flat-OE | Flat Operator Equalization |
| DE | Driving Event |
| RMSE | Root Mean Squared Error |
References
- Castignani, G.; Thierry, D.; Frank, R.; Engel, T. Smartphone-Based Adaptive Driving Maneuver Detection: A Large-Scale Evaluation Study. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2330–2339. [Google Scholar] [CrossRef]
- Handel, P.; Skog, I.; Wahlström, J.; Welch, R.; Ohlsson, J.; Ohlsson, M. Insurance telematics: Opportunities and challenges with the smartphone solution. IEEE Intell. Transp. Syst. Mag. 2014, 6, 57–70. [Google Scholar] [CrossRef]
- Saiprasert, C.; Thajchayapong, S.; Pholprasit, T.; Tanprasert, C. Driver Behaviour Profiling using Smartphone Sensory Data in a V2I Environment. In Proceedings of the International Conference on Connected Vehicles and Expo (ICCVE), Vienna, Austria, 3–7 November 2014. [Google Scholar]
- Aljaafreh, A.; Alshabatat, N.; Al-Din, N.S.M. Driving Style Recognition Using Fuzzy Logic. In Proceedings of the IEEE International Conference on Vehicular Electronics and Safety, Istanbul, Turkey, 24–27 July 2012. [Google Scholar]
- Eren, H.; Makinist, S.; Akin, E.; Yilmaz, A. Estimating Driving Behavior by a Smartphone. In Proceedings of the Intelligent Vehicles Symposium, Alcala de Henares, Spain, 3–7 June 2012. [Google Scholar]
- Al-Sultan, S.; Al-Bayatti, A.H.; Zedan, H. Context-aware driver behavior detection system in intelligent transportation systems. IEEE Trans. Veh. Technol. 2013, 62, 4264–4275. [Google Scholar] [CrossRef]
- López, J.R.; Gonzalez, L.C.; Gómez, M.M.; Trujillo, L.; Ramirez, G. A Genetic Programming Approach for Driving Score Calculation in the Context of Intelligent Transportation Systems. 2017; under review. [Google Scholar]
- Searson, D.P. Handbook of Genetic Programming Applications: Chapter 22-GPTIPS 2: An Open Source Software Platform for Symbolic Data Mining; Springer: Newcastle, UK, 2015. [Google Scholar]
- Trujillo, L.; Munoz, L.; Galvan-Lopez, E.; Silva, S. Neat Genetic Programming: Controlling Bloat Naturally. Inf. Sci. 2016, 333, 21–43. [Google Scholar] [CrossRef]
- Juárez-Smith, P.; Trujillo, L. Integrating Local Search Within neat-GP. In Proceedings of the 2016 on Genetic and Evolutionary Computation Conference Companion, Denver, CO, USA, 20–24 July 2016; pp. 993–996. [Google Scholar]
- Ali, N.A.; Abou-zeid, H. Driver Behavior Modeling: Developments and Future Directions. Int. J. Veh. Technol. 2016, 2016, 6952791. [Google Scholar]
- Dai, J.; Teng, J.; Bai, X.; Shen, Z.; Xuan, D. Mobile phone based drunk driving detection. In Proceedings of the 2010 4th International Conference on Pervasive Computing Technologies for Healthcare, Munich, Germany, 22–25 March 2010; pp. 1–8. [Google Scholar]
- Chaovalit, P.; Saiprasert, C.; Pholprasit, T. A method for driving event detection using SAX with resource usage exploration on smartphone platform. EURASIP J. Wirel. Commun. Netw. 2014, 2014, 135. [Google Scholar] [CrossRef]
- Zylius, G. Investigation of Route-Independent Aggressive and Safe Driving Features Obtained from Accelerometer Signals. IEEE Intell. Transp. Syst. Mag. 2017, 9, 103–113. [Google Scholar] [CrossRef]
- Davarynejad, M.; Vrancken, J. A survey of fuzzy set theory in intelligent transportation: State of the art and future trends. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 3952–3958. [Google Scholar]
- Engelbrecht, J.; Booysen, M.; van Rooyen, G.; Bruwer, F. Performance comparison of dynamic time warping (DTW) and a maximum likelihood (ML) classifier in measuring driver behavior with smartphones. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015; pp. 427–433. [Google Scholar]
- Johnson, D.; Trivedi, M.M. Driving style recognition using a smartphone as a sensor platform. In Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 1609–1615. [Google Scholar]
- Wahlström, J.; Skog, I.; Händel, P. Smartphone-Based Vehicle Telematics: A Ten-Year Anniversary. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2802–2825. [Google Scholar] [CrossRef]
- Stanley, K.O.; Miikkulainen, R. Evolving Neural Networks through Augmenting Topologies. Evolut. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
- Silva, S.; Dignum, S.; Vanneschi, L. Operator Equalisation for Bloat Free Genetic Programming and a Survey of Bloat Control Methods. Genet. Program. Evolvable Mach. 2012, 13, 197–238. [Google Scholar] [CrossRef]
- De Rainville, F.M.; Fortin, F.A.; Gardner, M.A.; Parizeau, M.; Gagné, C. DEAP: A Python Framework for Evolutionary Algorithms. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation GECCO’12, Philadelphia, PA, USA, 7–11 July 2012; pp. 85–92. [Google Scholar]
- Conover, W.J. Practical Nonparametric Statistics, 3rd ed.; John Wiley: New York, NY, USA, 1999. [Google Scholar]
- Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Carlos, M.R.; Gonzalez, L.C.; Ramirez, G. Unsupervised Feature Extraction for the Classification of Risky Driving Maneuvers. 2017; under review. [Google Scholar]
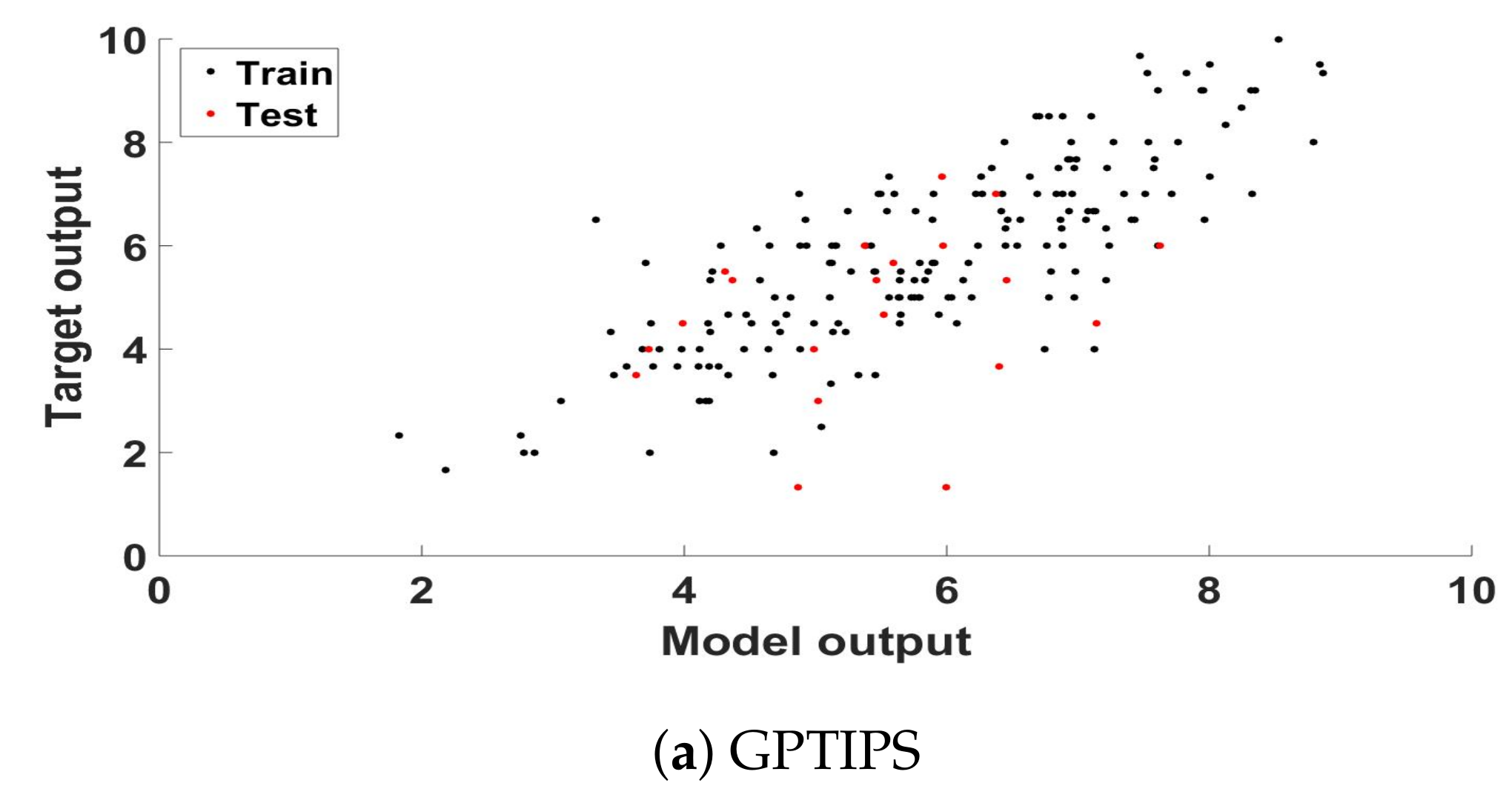
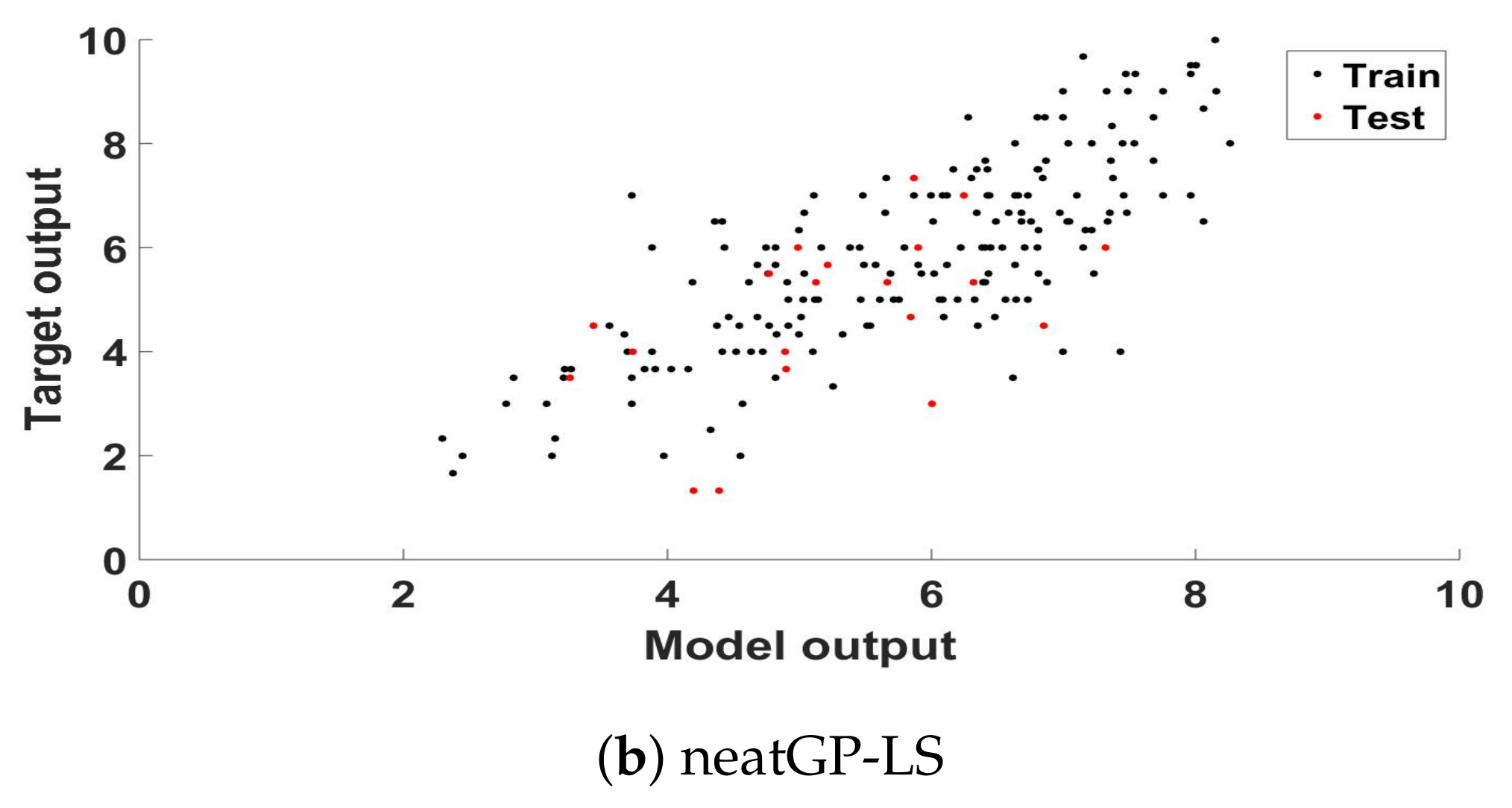
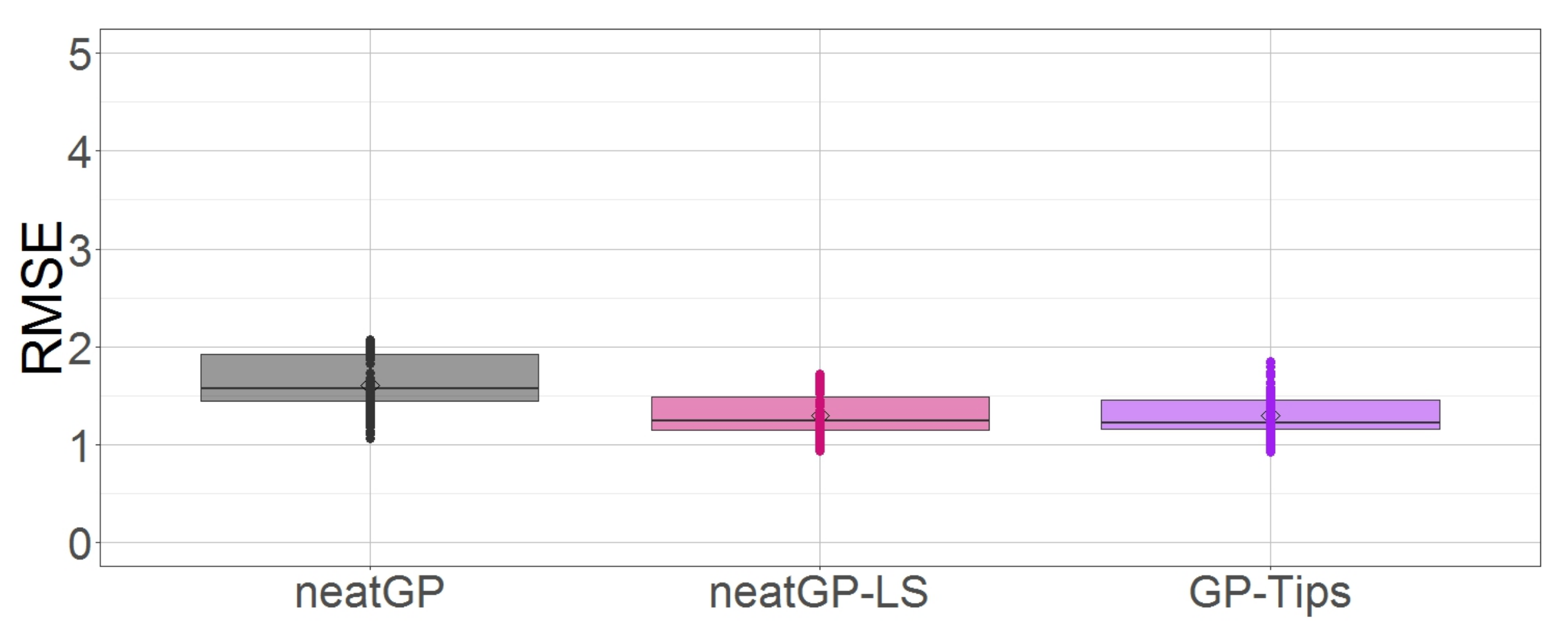
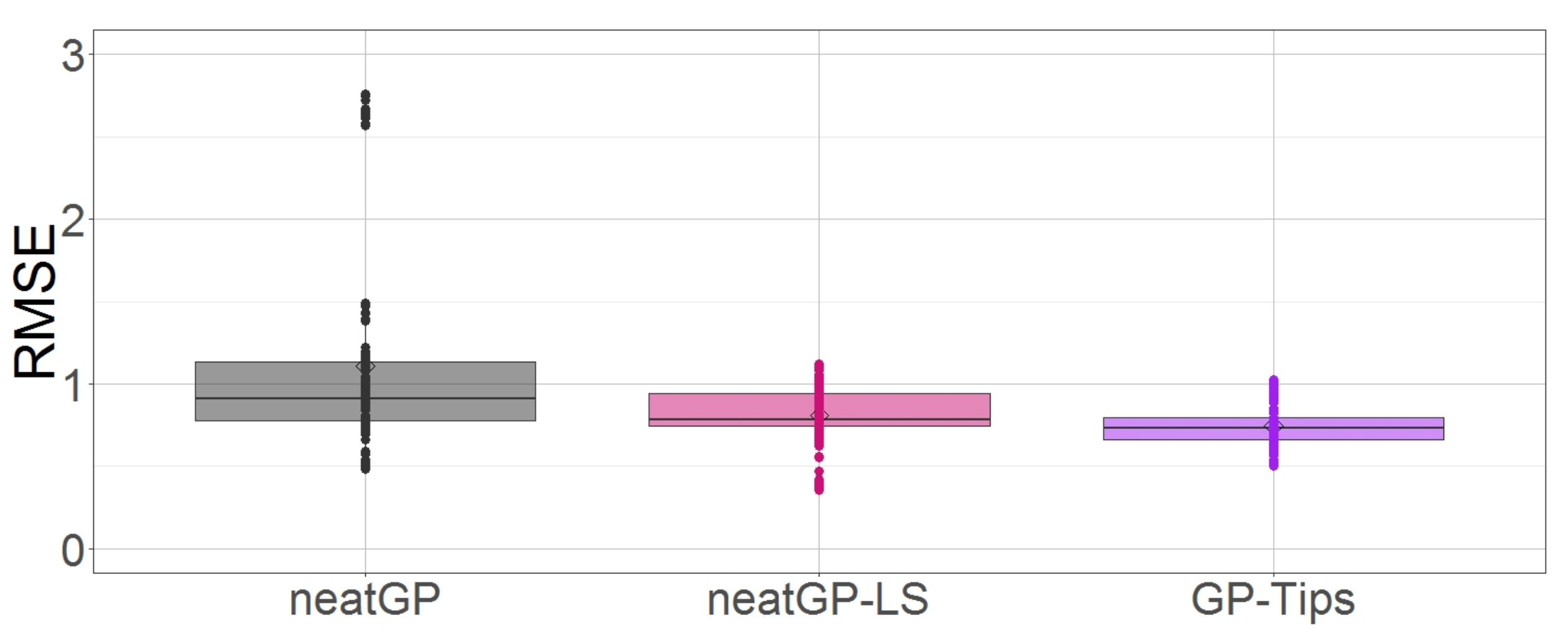
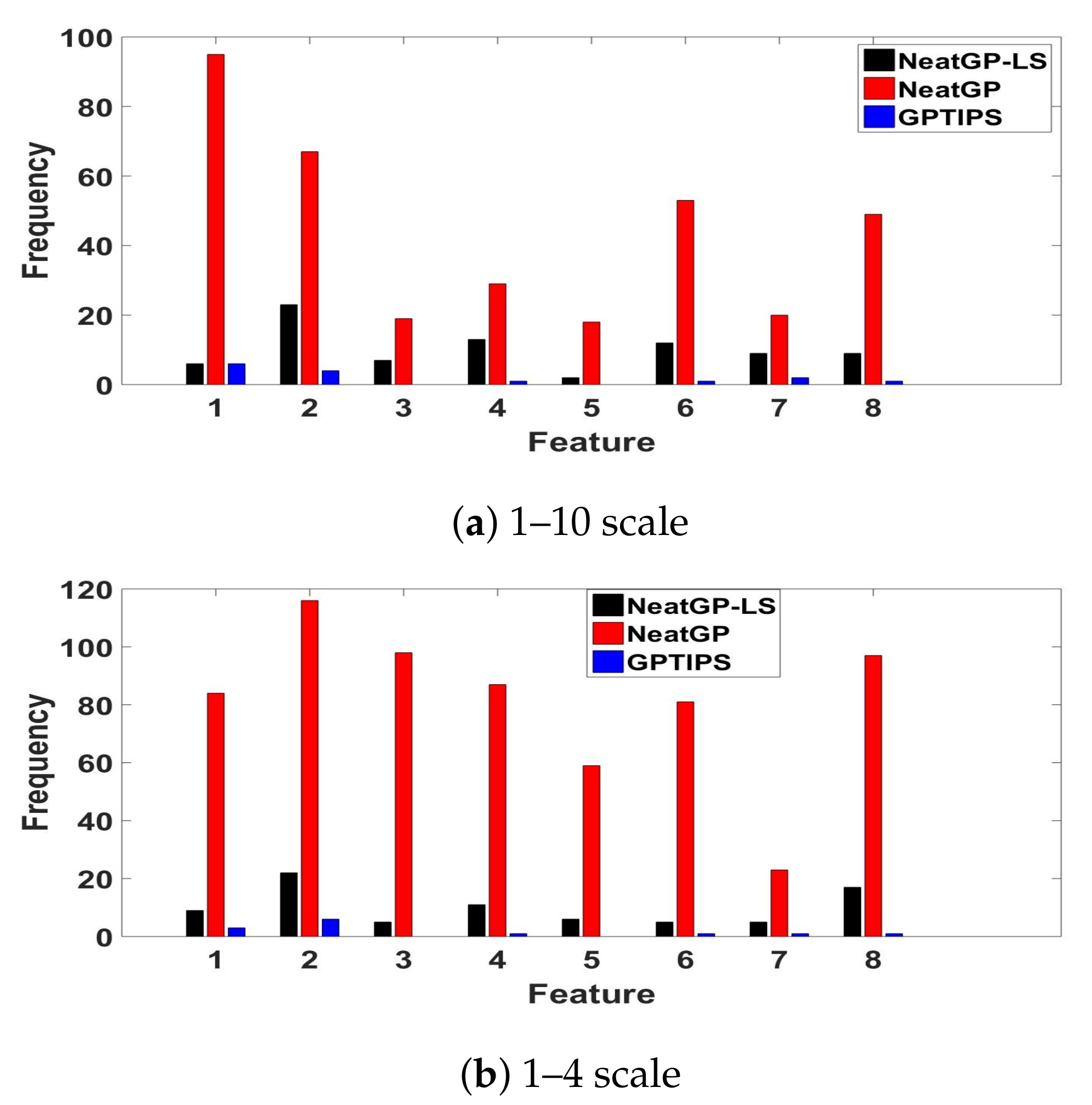
| Driving Event (id Number in the Feature Vector) | Value (Frequency) | Score for the Travel |
|---|---|---|
| Distance () | 7 | |
| Avg. Velocity () | 6 | |
| # of acceleration events () | 5 | |
| # of sudden starts () | 3 | 8 |
| # of abrupt lane changes () | 2 | |
| # of intense brakes () | 7 | |
| # of sudden stops () | 0 | |
| # of abrupt steerings () | 1 |
| Parameter | Value | Units |
|---|---|---|
| Population size | 100 | items |
| Max. # of generations | 100 | items |
| Input variables | 8 | items |
| Range of Constants | [−10, 10] | items |
| Training instances | 180 | road trips |
| Testing instances | 20 | road trips |
| Crossover probability | 85 | percentage (%) |
| Mutation probability | 15 | percentage (%) |
| Function set | functions | |
| GPTIPS | ||||
|---|---|---|---|---|
| Fold | Best Train | Best Test | Size Best Ind | Avg. Pop. Size |
| 1 | 1.1219 | 1.2211 | 22 | 21.1200 |
| 2 | 1.1168 | 1.2188 | 25 | 22.6067 |
| 3 | 1.1329 | 1.0482 | 22 | 20.0633 |
| 4 | 1.0978 | 1.4509 | 26 | 23.6000 |
| 5 | 1.1479 | 1.0034 | 25 | 22.7067 |
| 6 | 1.1296 | 1.1546 | 24 | 24.3533 |
| 7 | 1.1367 | 1.1857 | 24 | 23.2800 |
| 8 | 1.0650 | 1.7854 | 25 | 23.0167 |
| 9 | 1.1356 | 1.3130 | 23 | 22.2233 |
| 10 | 1.0595 | 1.5560 | 22 | 21.1667 |
| Minimum | 1.0595 | 1.0034 | 22 | 20.0633 |
| Maximum | 1.1479 | 1.7854 | 26 | 24.3533 |
| mean | 1.1144 | 1.2937 | 23.8000 | 22.4137 |
| SD | 0.0306 | 0.2408 | 1.4757 | 1.2994 |
| median | 1.1257 | 1.2199 | 24.0000 | 22.6567 |
| Correlation Coefficient | 0.8030 | 0.2868 | ||
| neatGP | ||||
|---|---|---|---|---|
| Fold | Best Train | Best Test | Size Best Ind | Avg. Pop. Size |
| 1 | 1.2093 | 1.5795 | 46 | 39.1850 |
| 2 | 1.2584 | 1.1488 | 64 | 45.9650 |
| 3 | 1.8291 | 1.9927 | 183 | 124.3400 |
| 4 | 1.3928 | 1.3015 | 132 | 100.0250 |
| 5 | 1.3064 | 1.5171 | 44 | 27.9500 |
| 6 | 1.2969 | 1.9753 | 61 | 44.3100 |
| 7 | 0.8505 | 1.5701 | 625 | 211.0900 |
| 8 | 1.2261 | 1.6290 | 69 | 54.6200 |
| 9 | 1.2496 | 1.9254 | 66 | 47.0100 |
| 10 | 1.2546 | 1.4381 | 44 | 29.5650 |
| Minimum | 0.8505 | 1.1488 | 44 | 27.9500 |
| Maximum | 1.8291 | 1.9927 | 625 | 211.0900 |
| mean | 1.2874 | 1.6077 | 133.4000 | 72.4060 |
| SD | 0.2378 | 0.2845 | 178.4204 | 57.7911 |
| median | 1.2565 | 1.5748 | 65.0000 | 46.4875 |
| Correlation Coefficient | 0.6432 | 0.6337 | ||
| neatGP-LS | ||||
|---|---|---|---|---|
| Fold | Best Train | Best Test | Size Best Ind | Avg. Pop. Size |
| 1 | 1.1690 | 1.6912 | 30 | 11.5900 |
| 2 | 1.2195 | 1.1623 | 40 | 11.9700 |
| 3 | 1.1622 | 1.2626 | 22 | 16.0000 |
| 4 | 1.2188 | 1.0513 | 31 | 18.8400 |
| 5 | 1.1756 | 1.5657 | 29 | 16.1750 |
| 6 | 1.1813 | 1.0310 | 36 | 20.1050 |
| 7 | 1.3758 | 1.3739 | 1 | 3.4200 |
| 8 | 1.1822 | 1.1456 | 18 | 18.5950 |
| 9 | 1.1326 | 1.4899 | 31 | 13.2200 |
| 10 | 1.1917 | 1.2202 | 35 | 16.5700 |
| Minimum | 1.1326 | 1.0310 | 1 | 3.4200 |
| Maximum | 1.3758 | 1.6912 | 40 | 20.1050 |
| mean | 1.2009 | 1.2994 | 27.3000 | 14.6485 |
| SD | 0.0666 | 0.2236 | 11.2551 | 4.8923 |
| median | 1.1818 | 1.2414 | 30.5000 | 16.0875 |
| Correlation Coefficient | 0.7735 | 0.5012 | ||
| GPTIPS | ||||
|---|---|---|---|---|
| Fold | Best Train | Best Test | Size Best Ind | Avg. Pop. Size |
| 1 | 0.6445 | 0.7347 | 22 | 22.0300 |
| 2 | 0.6567 | 0.6591 | 18 | 17.7833 |
| 3 | 0.6474 | 0.7408 | 21 | 21.8767 |
| 4 | 0.6215 | 0.9530 | 23 | 23.9733 |
| 5 | 0.6604 | 0.6833 | 29 | 24.4567 |
| 6 | 0.6491 | 0.7931 | 20 | 18.0233 |
| 7 | 0.6630 | 0.5913 | 22 | 20.8233 |
| 8 | 0.6524 | 0.6400 | 29 | 22.3667 |
| 9 | 0.6402 | 0.7241 | 21 | 19.9933 |
| 10 | 0.6176 | 0.9286 | 23 | 21.7733 |
| Minimum | 0.6176 | 0.5913 | 18 | 17.7833 |
| Maximum | 0.6630 | 0.9530 | 29 | 24.4567 |
| mean | 0.6453 | 0.7448 | 22.8000 | 21.3100 |
| SD | 0.0153 | 0.1182 | 3.5839 | 2.2205 |
| median | 0.6482 | 0.7294 | 22.0000 | 21.8250 |
| Correlation Coefficient | 0.7505 | 0.6219 | ||
| neatGP | ||||
|---|---|---|---|---|
| Fold | Best Train | Best Test | Size Best Ind | Avg. Pop. Size |
| 1 | 0.6070 | 2.6656 | 234 | 174.0650 |
| 2 | 0.5770 | 0.9034 | 276 | 169.5550 |
| 3 | 0.8056 | 0.8421 | 464 | 266.4800 |
| 4 | 0.6513 | 1.1010 | 176 | 118.1200 |
| 5 | 0.4705 | 0.5493 | 236 | 151.3600 |
| 6 | 0.5038 | 1.1317 | 245 | 160.8900 |
| 7 | 0.6748 | 0.7746 | 159 | 110.3400 |
| 8 | 0.7093 | 0.7463 | 55 | 42.1850 |
| 9 | 0.5284 | 0.9176 | 205 | 146.1850 |
| 10 | 0.5491 | 1.4260 | 139 | 65.5550 |
| Minimum | 0.4705 | 0.5493 | 55 | 42.1850 |
| Maximum | 0.8056 | 2.6656 | 464 | 266.4800 |
| mean | 0.6077 | 1.1058 | 218.9000 | 140.4735 |
| SD | 0.1034 | 0.5991 | 107.1888 | 62.4507 |
| median | 0.5920 | 0.9105 | 219.5000 | 148.7725 |
| Correlation Coefficient | 0.8805 | 0.5857 | ||
| neatGP-LS | ||||
|---|---|---|---|---|
| Fold | Best Train | Best Test | Size Best Ind | Avg. Pop. Size |
| 1 | 0.6387 | 0.9852 | 30 | 18.9650 |
| 2 | 0.7240 | 0.7477 | 29 | 16.7000 |
| 3 | 0.6675 | 0.7854 | 28 | 14.3150 |
| 4 | 0.6291 | 0.9384 | 37 | 20.5550 |
| 5 | 0.6321 | 0.7810 | 21 | 16.1550 |
| 6 | 0.6611 | 0.7851 | 41 | 24.1900 |
| 7 | 0.7217 | 0.4519 | 29 | 19.7950 |
| 8 | 0.6337 | 0.6387 | 34 | 19.5900 |
| 9 | 0.6622 | 0.9408 | 29 | 15.8750 |
| 10 | 0.6323 | 1.0198 | 17 | 14.0850 |
| Minimum | 0.6291 | 0.4519 | 17 | 14.0850 |
| Maximum | 0.7240 | 1.0198 | 41 | 24.1900 |
| mean | 0.6603 | 0.8074 | 29.5000 | 18.0225 |
| SD | 0.0359 | 0.1738 | 6.9960 | 3.1629 |
| median | 0.6499 | 0.7852 | 29.0000 | 17.8325 |
| Correlation Coefficient | 0.7598 | 0.3352 | ||
| RMSE Testing | Complexity (# of Nodes) | Model |
|---|---|---|
| 0.919 | 37 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López, R.; González Gurrola, L.C.; Trujillo, L.; Prieto, O.; Ramírez, G.; Posada, A.; Juárez-Smith, P.; Méndez, L. How Am I Driving? Using Genetic Programming to Generate Scoring Functions for Urban Driving Behavior. Math. Comput. Appl. 2018, 23, 19. https://doi.org/10.3390/mca23020019
López R, González Gurrola LC, Trujillo L, Prieto O, Ramírez G, Posada A, Juárez-Smith P, Méndez L. How Am I Driving? Using Genetic Programming to Generate Scoring Functions for Urban Driving Behavior. Mathematical and Computational Applications. 2018; 23(2):19. https://doi.org/10.3390/mca23020019
Chicago/Turabian StyleLópez, Roberto, Luis Carlos González Gurrola, Leonardo Trujillo, Olanda Prieto, Graciela Ramírez, Antonio Posada, Perla Juárez-Smith, and Leticia Méndez. 2018. "How Am I Driving? Using Genetic Programming to Generate Scoring Functions for Urban Driving Behavior" Mathematical and Computational Applications 23, no. 2: 19. https://doi.org/10.3390/mca23020019
APA StyleLópez, R., González Gurrola, L. C., Trujillo, L., Prieto, O., Ramírez, G., Posada, A., Juárez-Smith, P., & Méndez, L. (2018). How Am I Driving? Using Genetic Programming to Generate Scoring Functions for Urban Driving Behavior. Mathematical and Computational Applications, 23(2), 19. https://doi.org/10.3390/mca23020019







