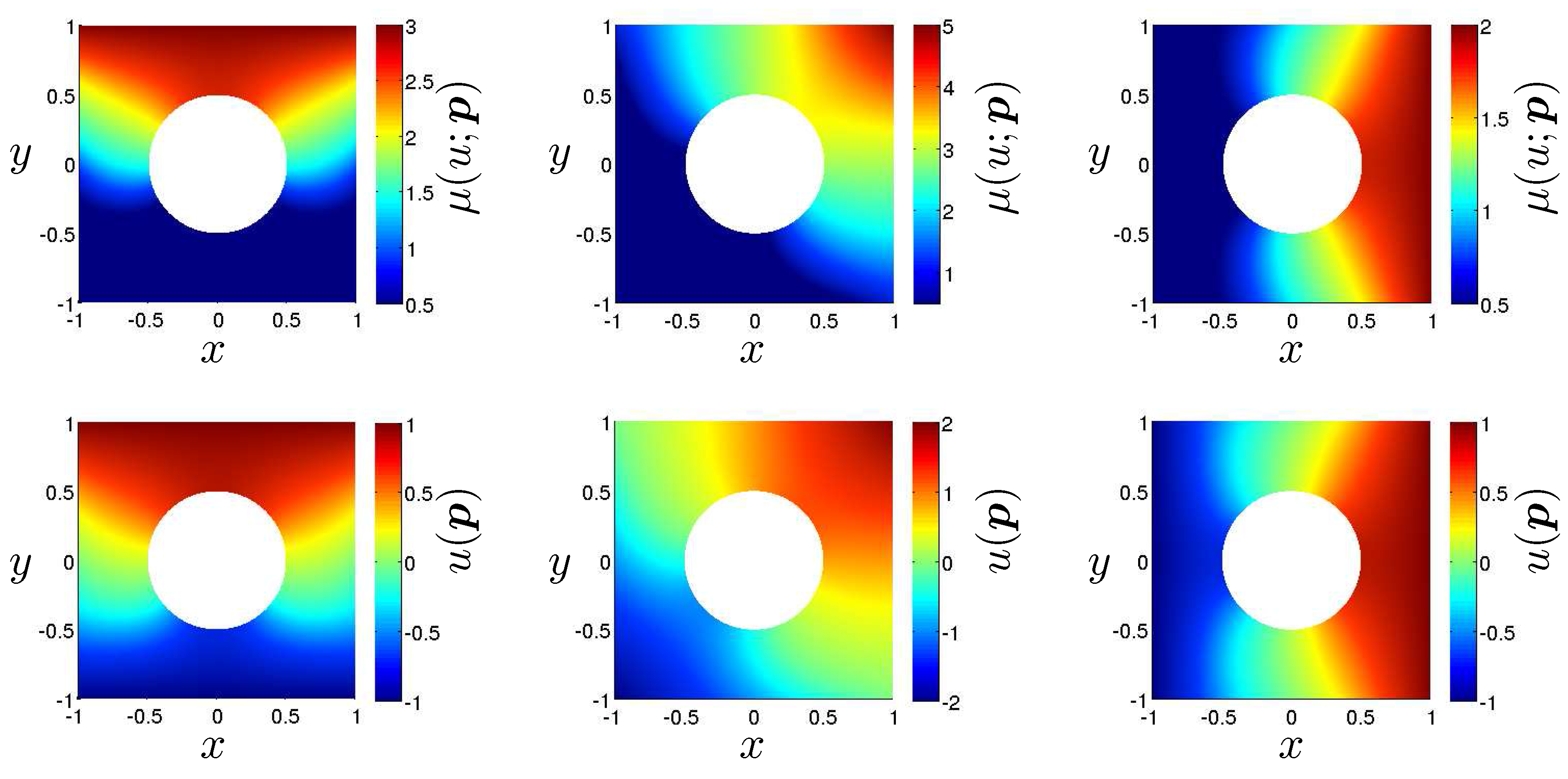
3.1. Galerkin Reduced Basis Approximation
A classical Galerkin projection on a POD space is used to provide reference solutions for the HR and the DEIM. In order to solve the weak form of the nonlinear problem for given parameters
,
, a successive substitution is performed in which the local conductivity
is computed using the previous iteration of the temperature
with
in the reduced setting, where
is the iteration number and
is the iterate of the reduced degrees of freedom in iteration
. As in a classical Galerkin approach, we assume the (reduced) test function
with arbitrary coefficients
(
) represented by the vector
. For convenience, we define the conductivity corresponding to the
-th iterate
of the reduced coefficient vector
Here,
can be interpreted as a constant parameter similar to
p during the subsequent iteration, which provides the new iterate
as the solution of
Rewriting (
26) using the approximated Jacobian
J and the residual
r leads to the linear system
The projection of the residual onto the reduced basis defines the reduced residual
In view of the definition of the reduced basis by
-orthogonal POD modes and with
one obtains
This gives rise to the simple convergence criterion , i.e., the iteration should stop upon sufficiently small changes of the temperature field. Algorithm 3 summarizes the online phase of the Galerkin RB method.
| Algorithm 3: Galerkin Reduced Basis Solution (Online Phase) |
![Mca 23 00008 i003 Mca 23 00008 i003]() |
The projected system can be interpreted as a finite element method with global, problem specific ansatz functions , whereas the classical finite element method uses local and rather general ansatz functions (e.g., piecewise defined polynomials).
Note that, the solution of (
26), (
27) is also a minimizer of the potential
Therefore, variational methods can directly be applied to solve the minimization problem and alternative numerical strategies are available. Such variational schemes are also used, e.g., in the context of solid mechanical problems involving internal variables (e.g., [
26]).
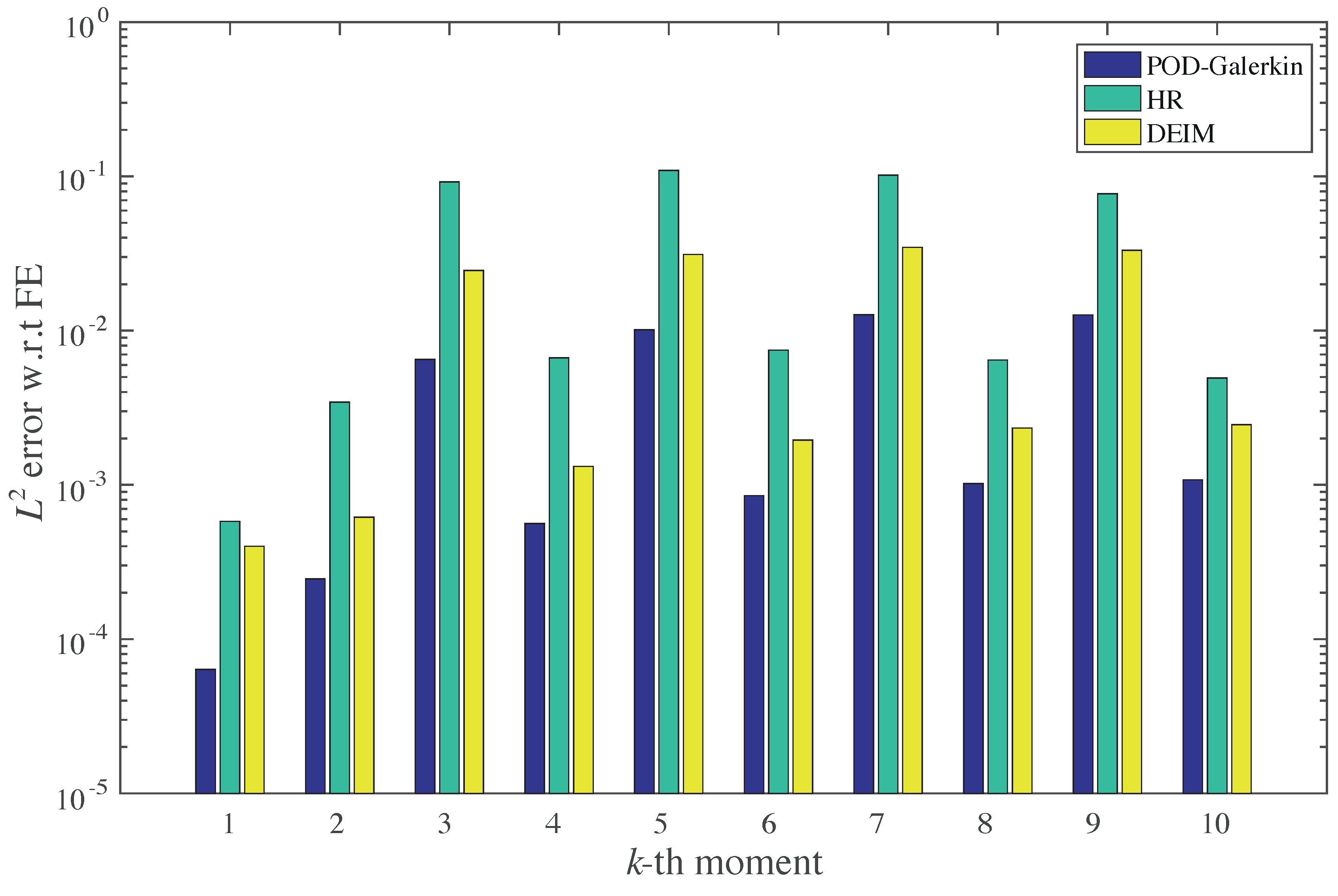
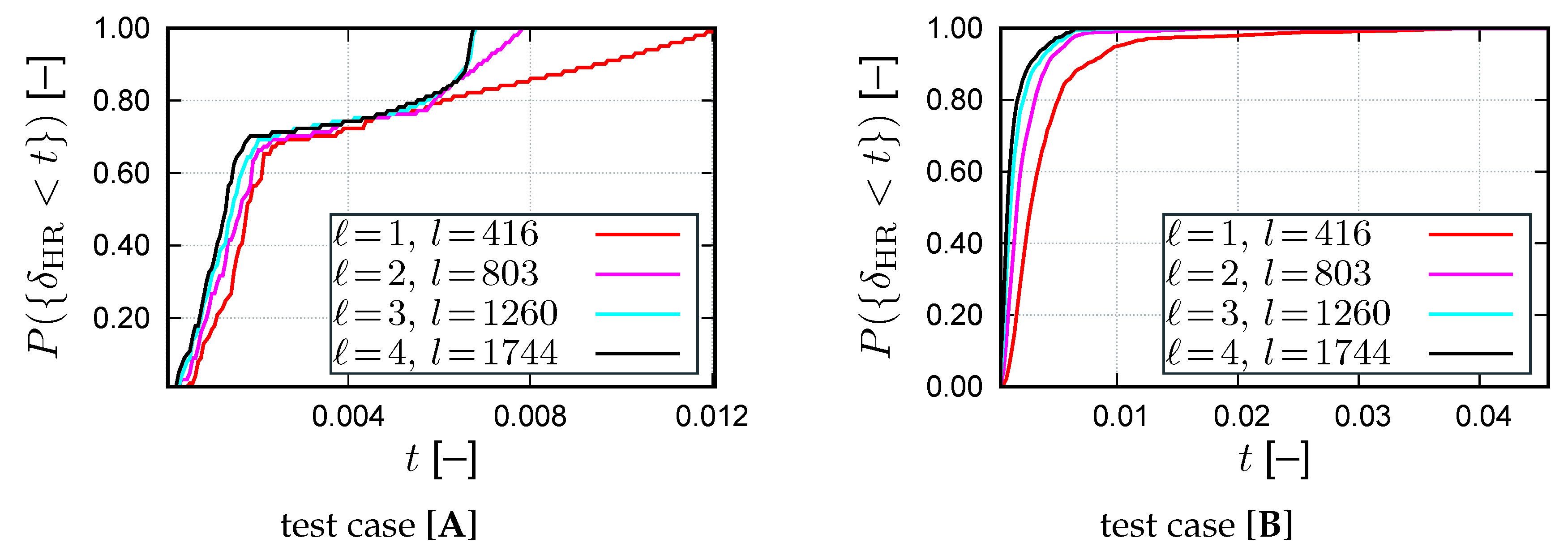
The Galerkin RB method with a well-chosen reduced basis functions
(represented via the matrix
V) can replicate the FEM solution to a high accuracy (see
Section 4). It also provides a significant reduction of the memory requirements: instead of
, only
needs to be stored. Despite the significant reduction of the number of unknowns from
n to
m, the Galerkin RB cannot attain substantial accelerations of the nonlinear simulation due to a computationally expensive assembly procedure with complexity
for the residual vector
r and for the fixed point operator
J (compare
and
in Algorithm 1 and Algorithm 3). Here,
is the number of quadrature points in the mesh. However, if the linear systems are not solved with optimal complexity, e.g., using sparse
or Cholesky decompositions with at least
, then a reduction of complexity can still be achieved. It shall be pointed out that, for very large
n (i.e., for millions of unknowns), the linear solver usually dominates the overall computational expense. Then, the Galerkin RB may provide good accelerations without further modifications.
In order to significantly improve on the computational efficiency while maintaining the reduced number of degrees of freedom (and thus the reduced storage requirements), the Hyper-Reduction [
11,
12] and the Discrete Empricial Interpolation Method (DEIM, [
7,
8,
9]) are used. Both methods are specifically designed for the computationally efficient approximation of the nonlinearity of PDEs.
3.2. Discrete Empirical Interpolation Method (DEIM)
The empirical interpolation method (EIM) was introduced by [
6] to approximate parametric or nonlinear functions by separable interpolants. This technique is meanwhile standard in the reduced basis methodology for parametric PDEs. Discrete versions of the EIM for instationary problems have been introduced as empirical operator interpolation [
7,
8,
27] or alternatively (and in some cases equivalently) as discrete empirical interpolation (DEIM) [
9,
10]. In particular, a posteriori [
8,
27,
28] and a priori [
10] error control is possible under certain assumptions (see also [
5]).
We present a formulation for the present stationary problem. Instead of approximating a continuous field variable, the goal of the discrete versions is to provide an approximation
for the vectorial nonlinearity of the nodal residual vector
r of the form
where the columns of
are called
collateral reduced basis and
is a sampling matrix with interpolation indices (also known as
magic points)
, with
being the
i-th unit vector. By multiplication of (
31) with
, we verify that
In this sense, the approximation acts as an interpolation within the set of magic points.
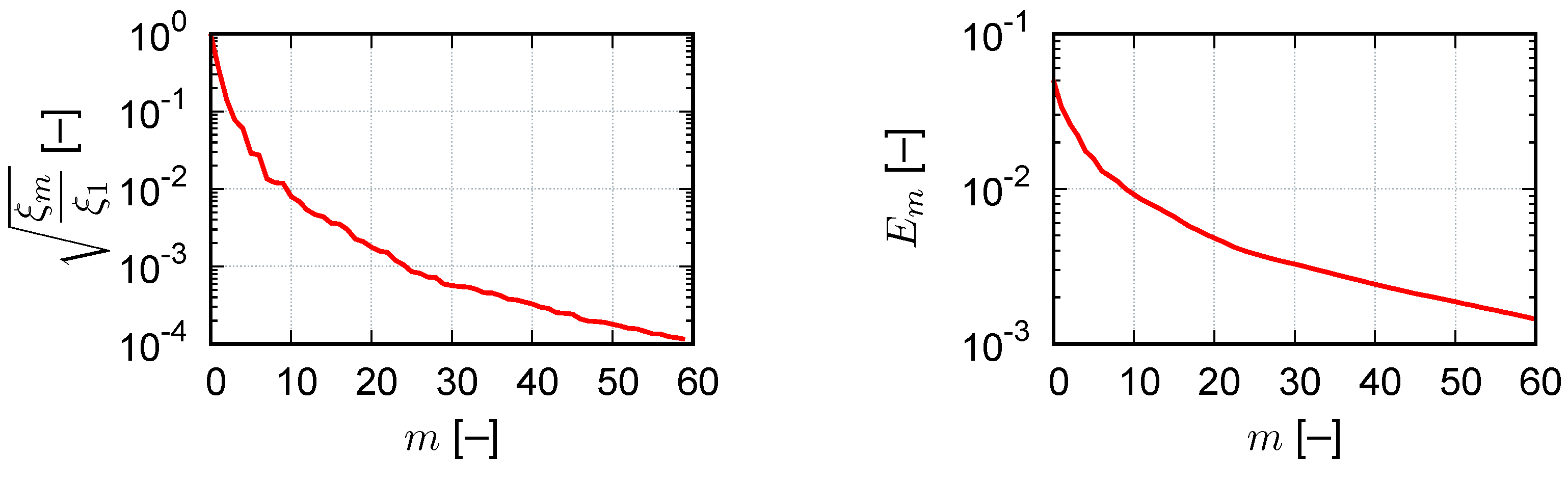
The identification of the interpolation points is an incremental procedure, which is performed during the offline phase. We assume the existence of a set of training snapshots with .
Then, a POD of these snapshots results, see e.g., [
10], in the collateral basis vectors
and we define
for
. The algorithm for the point selection is initialized with
,
,
and then computes for
Finally, we set
,
and
, which concludes the construction of
. Intuitively, in each iteration, the interpolation error
for the current POD basis vector
is determined and the vector entry
with maximum absolute value is identified, which gives the next index. Regularity of the matrix
is required for a well-defined interpolation. This condition is automatically satisfied under the aforementioned assumption of a sufficiently rich set of snapshots
. As training set
, one can either use samples of the nonlinearity [
8], or use snapshots of the state vector or combinations thereof. In contrast to the instationary case, we may not use only training snapshots of
r: As the residual
r is zero for all snapshots, we would try to find a basis for a zero-dimensional space
, which is not possible for
. However, the residual at the intermediate (non-equilibrium) iterates is non-zero and this is also a good target quantity for the (D)EIM, as these terms appear on the right-hand side of the linear system during the fixed point iteration. Hence, a reasonable set
is obtained via
where
, ...,
are the number of fixed point iterations of the full simulation scheme for parameters
.
Inserting
from (
31) for the nonlinearity into the full problem and projection by left-multiplication with a weight matrix
yields the POD-DEIM reduced
m-dimensional nonlinear system for the unknown
This low-dimensional nonlinear problem is iteratively solved by a fixed point procedure, i.e., at the current approximation
we solve the linearized problem for
and set
. As in the previous sections, if
, this linear system cannot be solved uniquely. In that case, an alternative would be to solve a residual least-squares problem, similar to the GNAT-procedure, cf. [
15]. Note that the assembly of this system does not involve any high-dimensional operations, as the product of the first four matrices on the left- and right-hand side can be precomputed as a small matrix
. Then, the terms
also do not require any high-dimensional operations, as the multiplication with
corresponds to evaluation of the “magic” rows of the Jacobian and right-hand side, respectively. Typically, in discretized PDEs, these
M rows only depend on few
entries of the unknown variable (e.g., the DOFs related to neighboring elements). This number
is typically bounded by a certain multiple of
M due to regularity constraints on the mesh [
8].
In (
38), what is required for the collateral basis
U can be recognized: If
and
then we are exactly solving the Galerkin–POD reduced linearized system
Hence, this gives a guideline for an alternative reasonable choice of the training set , namely consisting of snapshots of both (columns of) J or and r.
In the Galerkin projection case, one can choose . This is the choice that we pursue in the experiments to make the procedure more similar to the other reduction approaches. The offline phase of the DEIM is summarized in Algorithm 4 and an algorithm of the online phase is provided in Algorithm 5.
| Algorithm 4: Offline Phase of the Discrete Empirical Interpolation Method (DEIM) |
![Mca 23 00008 i004 Mca 23 00008 i004]() |
| Algorithm 5: Online Phase of the Discrete Empirical Interpolation Method (DEIM) |
Input : parameters reduced basis V, POD-DEIM sampling matrix and magic point index set I
Output: reduced vector and nodal temperatures (optional) |
| 1 set ; ; ; | // initialize |
| 2 ; | // ; evaluate M rows of right-projected Jacobian |
| 3 ; | // ; evaluate M rows of right hand side |
| 4 solve ; | // ; fixpoint iter. for |
| 5 update ; | // update |
| 6 compute and set ; | // |
| 7 converged ()? → end; else: goto 2 | |
3.3. Hyper-Reduction (HR)
In order to improve the numerical efficiency, the Hyper-Reduction method [
11] introduces a Reduced Integration Domain (RID) denoted
. The RID depends on the reduced basis. It is constructed by offline algebraic operations. The hyper-reduced equations are a Petrov–Galerkin formulation of the equilibrium equations, obtained by using truncated test functions having zero values outside the RID. The vector form of the reduced equations is similar to the one obtained by the Missing Point Estimation method [
14] proposed for the Finite Volume Method. The strength of the Hyper-Reduction is its ability to reduce mechanical models in material science while keeping the formulation of the constitutive equations unchanged [
12]. The smaller the RID, the lower the computational complexity and the higher the approximation errors. These points have been developed in previous papers dealing with various mechanical problems (e.g., [
29,
30]).
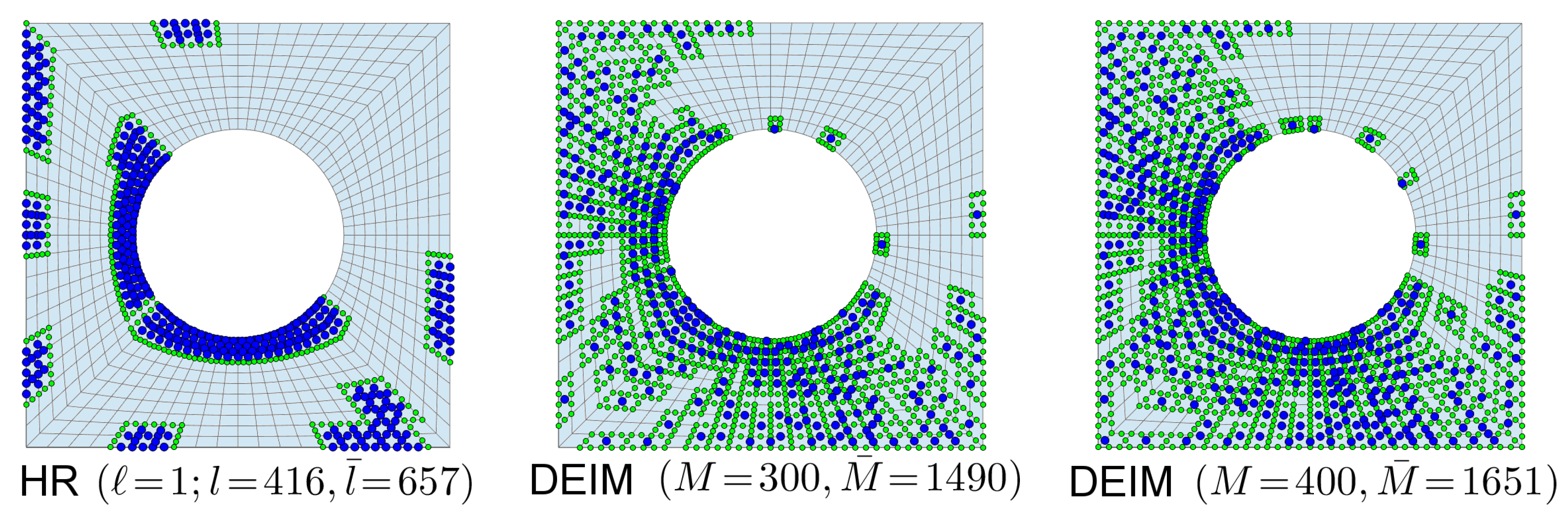
The offline procedure of the Hyper-Reduction method involves two steps. The first step is the construction of the Reduced Integration Domain
. For the present benchmark test, the RID is the union of a subdomain denoted by
generated from the reduced vector gradients
, and a domain denoted by
corresponding to a set of neighboring elements to the previous subdomain. Usually, in the Hyper-reduction method, the user can select an additional subdomain of
in order to extend the RID over a region of interest. This subdomain is denoted by
. In the sequel, to get small RIDs,
is empty. The set
consists of aggregated contributions
from all the reduced vectors:
To give the full details of the procedure, we introduce the domain partition in finite elements denoted
:
, where
is the number of elements in the mesh. The domain
is the element where the maximum
norm of the reduced vectors
is reached. In [
11],
was set equal to
. Here, when applying the DEIM to
, the interpolation residuals provide a new reduced basis
(cf. Algorithm 6) related to temperature gradients. In this paper,
is the output reduced basis produced by the DEIM, when it is applied to
. Other procedures, for the RID construction, are available in previous papers on hyper-reduction, e.g., [
11,
12]. The element selection reads for
:
where
is the
norm restricted to the element
. Several layers of surrounding elements denoted
can be added to
.
The second step of the offline Hyper-Reduction procedure is the generation of truncated test functions that are zero outside of the RID. The truncation operator is defined for all by
Here, is the set of indices of internal points, i.e., inner FE nodes, in , which are related to the available FE equilibrium for predictions, which are forecasted only over , i.e., for all holds with
The operator
can be represented by a truncated projector denoted
Z. More precisely, if
with
, then
with
the
i-th unit vector. Therefore, the hyper-reduced form of the linearized prediction step is: for a given
, find
such that,
where
J is given by (
15) and
.
In addition to Z, we introduce also the operator that is a truncated projection operator onto the points contained in the RID. In practice, the discrete unknowns are computed at these points in order to compute the residual at the inner points l. Note that often is significantly larger than l, especially if the RID consists of disconnected (scattered) regions.
The complexity of the products related to the fixed point operator
J on the left-hand side term scale with
, where
is the maximum number of non-zero entries per row of
J. For the right-hand side, the computational complexity is
. For both products, the complexity reduction factors are
. To obtain a well-posed hyper-reduced problem, one requires to fulfill the following condition
. If this condition is not fulfilled, the linear system of Equation (
45) is rank deficient. In case of rank deficiency, one has to add more surrounding elements to the RID. The closer
l to
m, and the lower
m, the less complex is the solution of the hyper-reduced formulation. The RID construction must generate a sufficiently large RID. If not, the convergence can be hampered, the number of correction steps can be increased and, moreover, the accuracy of the prediction can suffer. When
, then
Z is the identity matrix and the hyper-reduced formulation coincides with the usual system obtained by the Galerkin projection. An a posteriori error estimator for hyper-reduced approximations has recently been proposed in [
31] for generalized standard materials.
The offline phase of the hyper-reduction is summarized in Algorithm 6 and an algorithm of the online phase is provided in Algorithm 7.
3.4. Methodological Comparison
We comment on some formal commonalities and differences between the HR and the (D)EIM.
We first note that both methods reproduce the Galerkin–POD case, if
. For the HR, this means that the RID is the full domain, which implies that
Z is a square permutation matrix, hence being invertible and yielding
, thus (
45) reduces to the POD–Galerkin reduced system (
27). For the (D)EIM, this implies that the magic points consist of all grid points. We similarly obtain that
P and
U are invertible and thus
and (
38) also reproduces the POD–Galerkin reduced system (
27).
| Algorithm 6: Offline Phase of the Hyper-Reduction (HR) |
![Mca 23 00008 i005 Mca 23 00008 i005]() |
| Algorithm 7: Online Phase of the Hyper-Reduction (HR) |
![Mca 23 00008 i006 Mca 23 00008 i006]() |
Furthermore, we can state an equivalence of the DEIM and the HR under certain conditions, more precisely, the reduced system of the HR is a special case of the DEIM reduced system. Let us assume that the sampling matrices coincide and the collateral basis is also chosen as this sampling matrix, i.e., . Let us further assume that we have a Galerkin projection by choosing for the DEIM. Then, is the M-dimensional identity matrix, hence we obtain
Then, (
38) yields
which is exactly the HR reduced system (
45).
A common aspect of HR, and (D)EIM obviously is the point selection by a sampling matrix. The difference, however, is the selection criterion of the internal points. In case of the DEIM, these points are used as interpolation points, while, for the HR, they are used to specify the reduced integration domain.
A main difference of (D)EIM to HR is the way an additional collateral reduced-space is introduced in the reduced setting of the equations. The HR is more simple by not using an additional basis related to the residuals, but the implicit assumption, that
(which approximates
u) also approximates
r and
J well. This is a very reasonable assumption in symmetric elliptic problems and—in a certain way—it mimics the idea of having the same ansatz and test space as in any Galerkin formulation. However, from a mathematical point of view, it may not be valid in some more general cases, as in principle
U and
V are completely independent. For example, we can multiply the vectorial residual Equation (
11) by an arbitrary regular matrix, hence arbitrarily change
r (and thus
U for the DEIM), but not changing
u at all (i.e., not changing the POD-basis
U). Hence, the collateral basis in the (D)EIM is first an additional technical ingredient and difficulty, which in turn allows for adopting the approximation space to the quantities that needs to be approximated well.
Theoretically, the EIM is well founded by analytical convergence results [
32]. However, in addition, as a downside, the Lebesgue-constant, which essentially bounds the interpolation error to the best-approximation error, can grow exponentially. The DEIM is substantiated with a priori error estimates [
10]. In particular, the error bounds depend on the conditioning of the small matrix
. We are not aware of such a priori results for the HR, but also a posteriori error control has been presented in [
31].
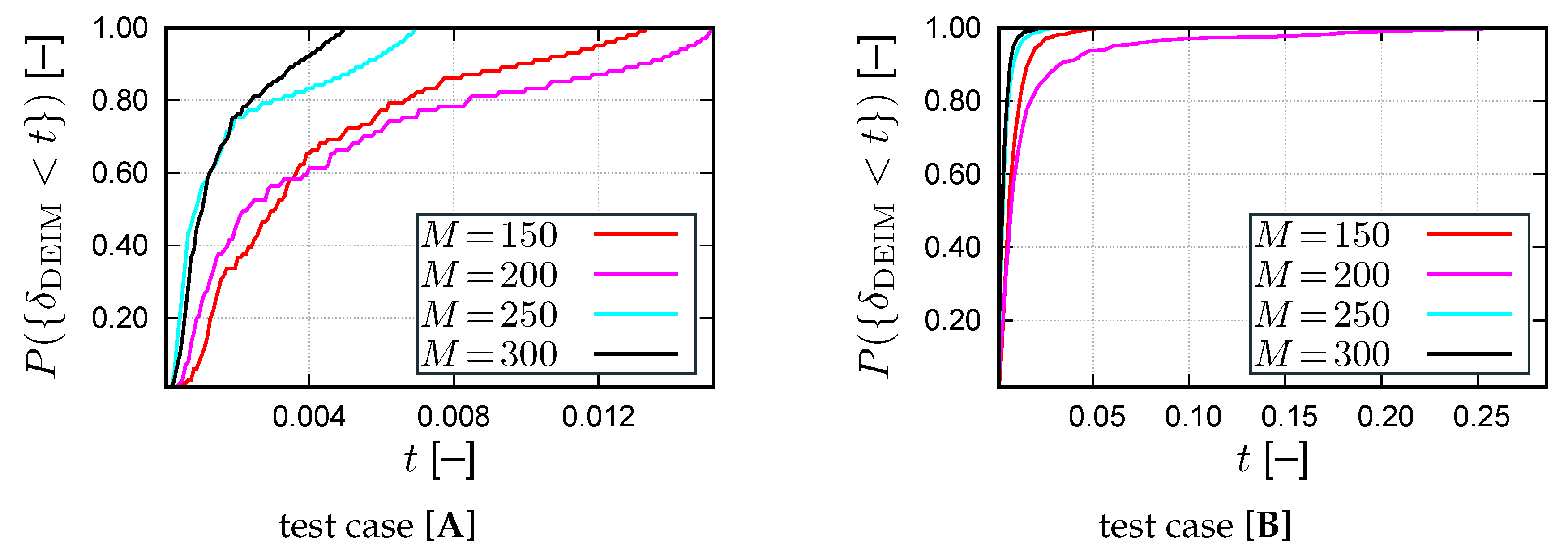
3.5. Computational Complexity
While the aim of model reduction is ultimately a reduction of the computing time, this quantity may heavily depend on the chosen implementation (see
Section 4.6). Generally, the computational effort can be decomposed into the following contributions:
the computation of the local unknowns and of their gradients (gradient/temperature computation),
the evaluations of the (nonlinear) constitutive model ,
the assembly of the residual and of the Jacobian ,
the solution of the (dense) reduced linear system .
From a theoretical point of view, the presented methods differ with respect to , , and :
From these considerations, the following conclusions can be drawn: First, the number of integration points (, , ) required for the residual and Jacobian evaluation enter linearly into the effort. Second, the reduced basis dimension m enters linearly into the residual assembly and both linearly and quadratically into the Jacobian assembly. Third, for the HR and the (D)EIM, the ratio and have a significant impact on the efficiency: for the considered 2D problem with quadratic ansatz functions, these ratios can range from 1 up to 21, i.e., for the same number of magic points pronounced variations in the runtime are in fact possible. The ratio is determined by the topology of the RID, i.e., for connected RIDs it is smaller than for a scatter RID (i.e., for many disconnected regions forming the RID). Similarly, the (D)EIM has much smaller computational complexity in the case of magic points belonging to connected elements. Fourth, the Galerkin-POD can be based on simplified algebraic operations as no nodal variables need to be computed. This is due to the fact that the reduced residual and Jacobian are directly assembled without recurse to nodal coordinates and to any standard FE routine.