Numerical Solution for Fuzzy Enzyme Kinetic Equations by the Runge–Kutta Method
Abstract
1. Introduction
2. Preliminaries
- (a)
- is upper semi-continuous on .
- (b)
- is fuzzy convex, i.e., for and any .
- (c)
- is normal, i.e., for which .
- (d)
- is the support of , and its closure is compact.
- (i)
- for all sufficiently small, , and the limits (in the metric D):or
- (ii)
- for all sufficiently small, , and the limits (in the metric D):or
- (iii)
- for all sufficiently small, , and the limits (in the metric D):or
- (iv)
- for all sufficiently small, , and the limits (in the metric D):
3. A System of Fuzzy Initial Value Problems
4. Fuzzy Runge–Kutta Method of Order Four for the Fuzzy Kinetic Enzyme Reaction
5. Convergence and Stability
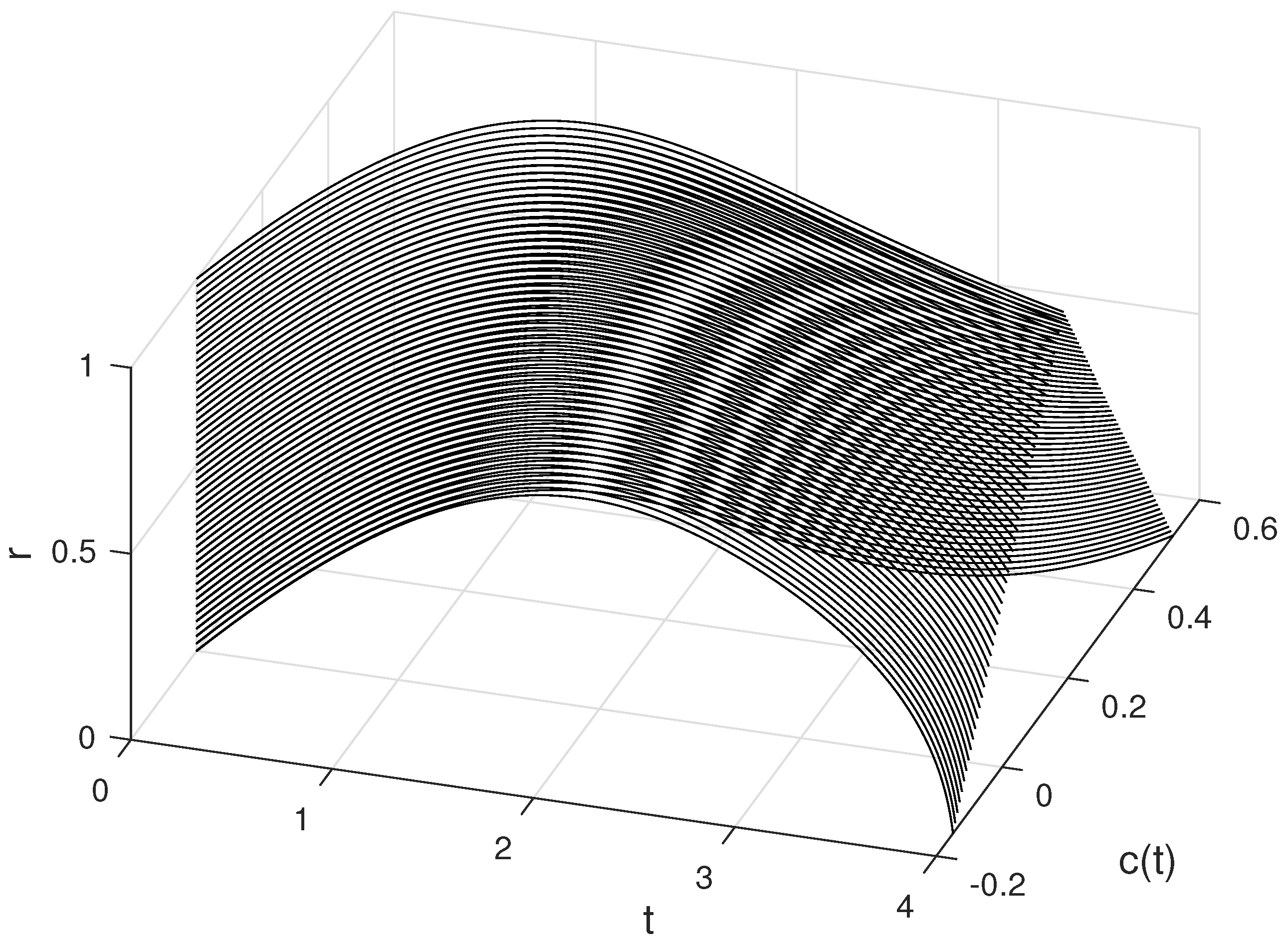
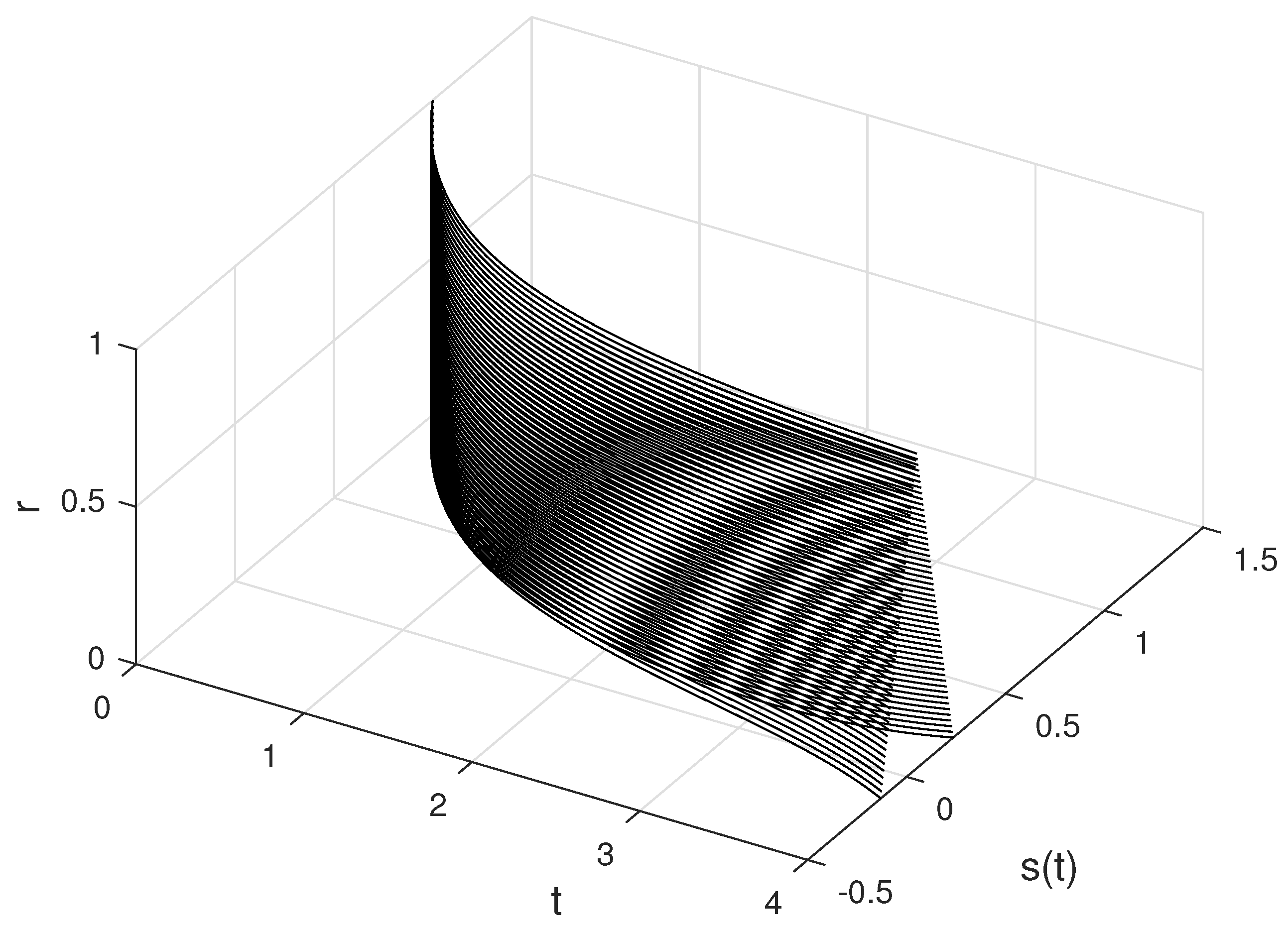
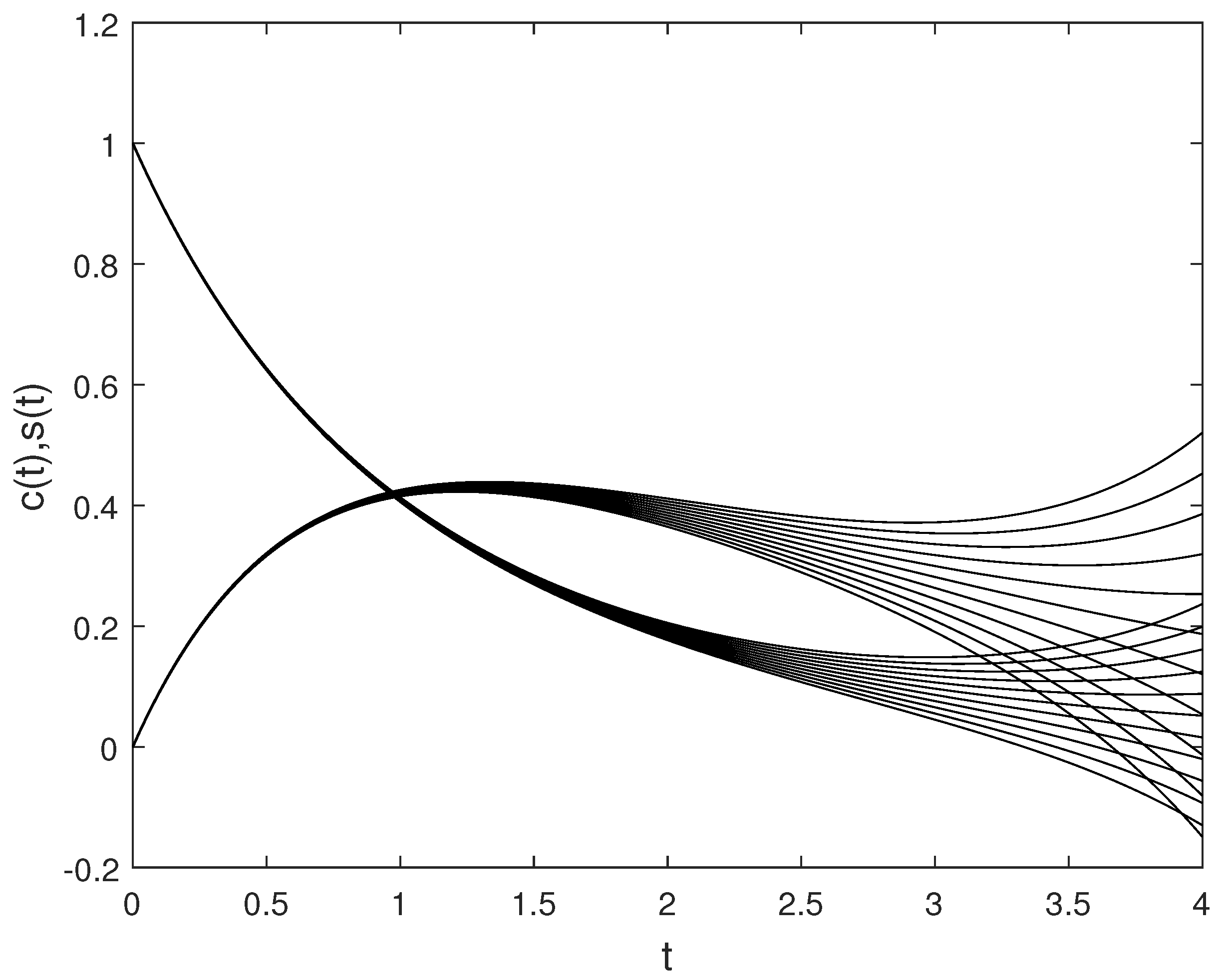
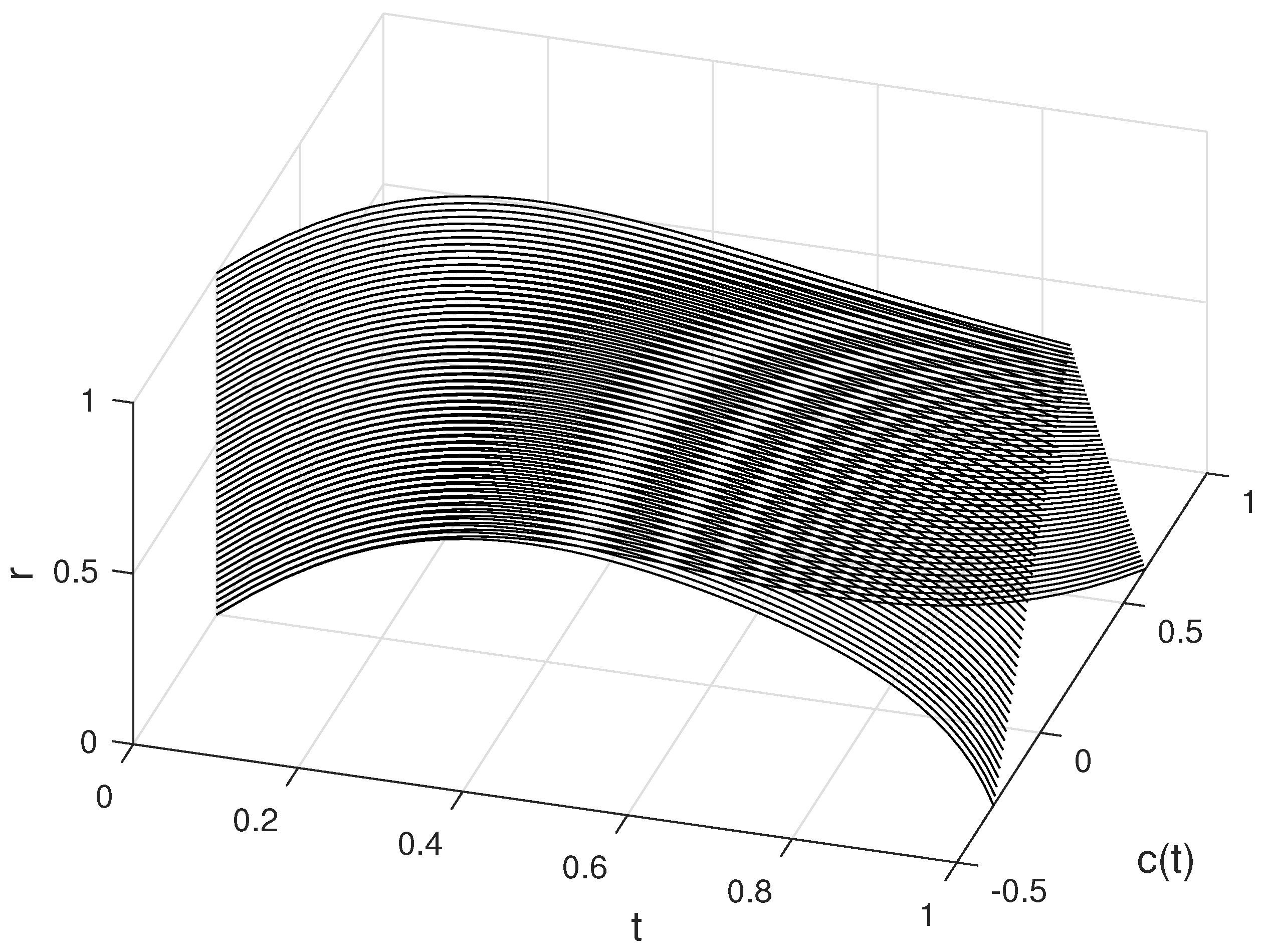
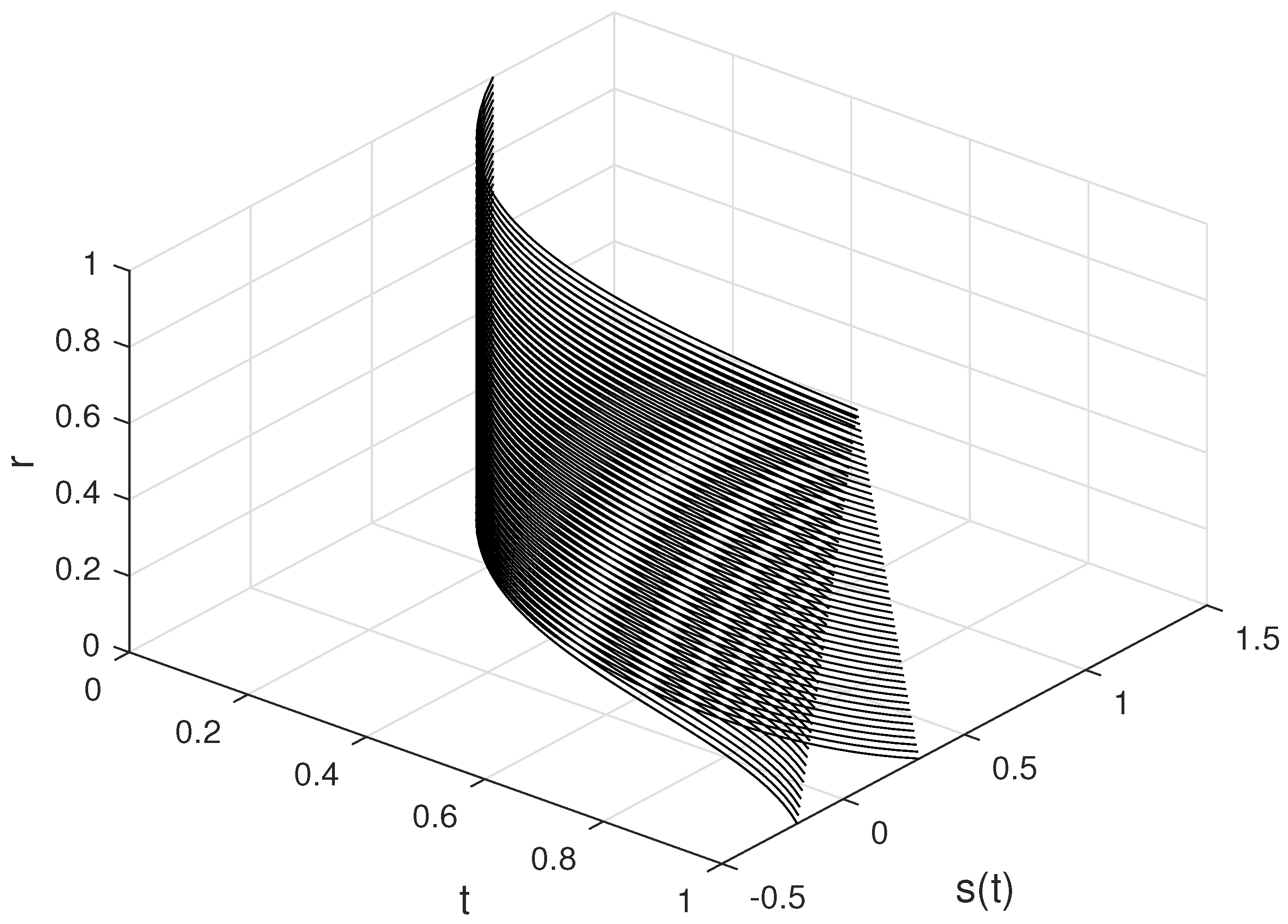
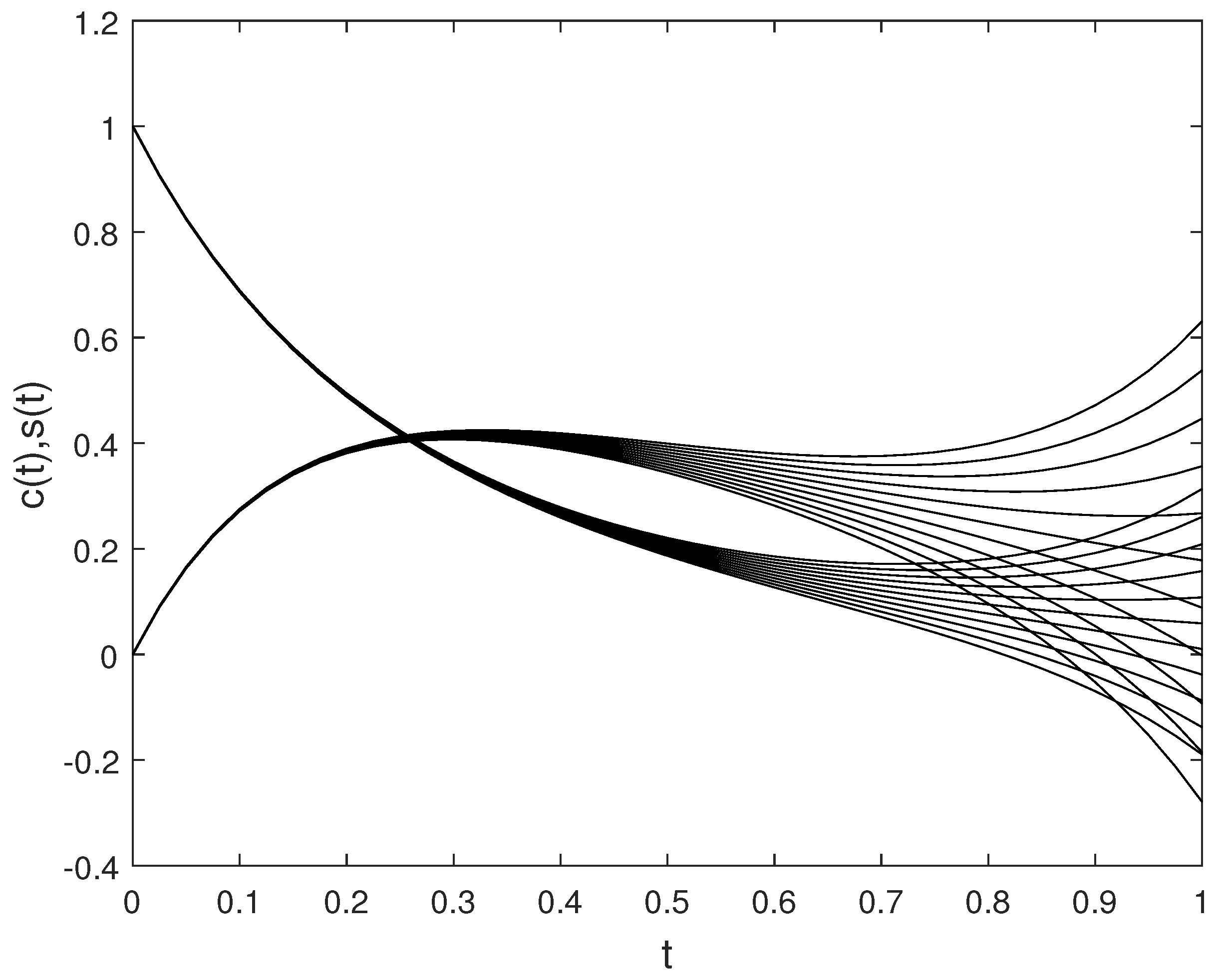
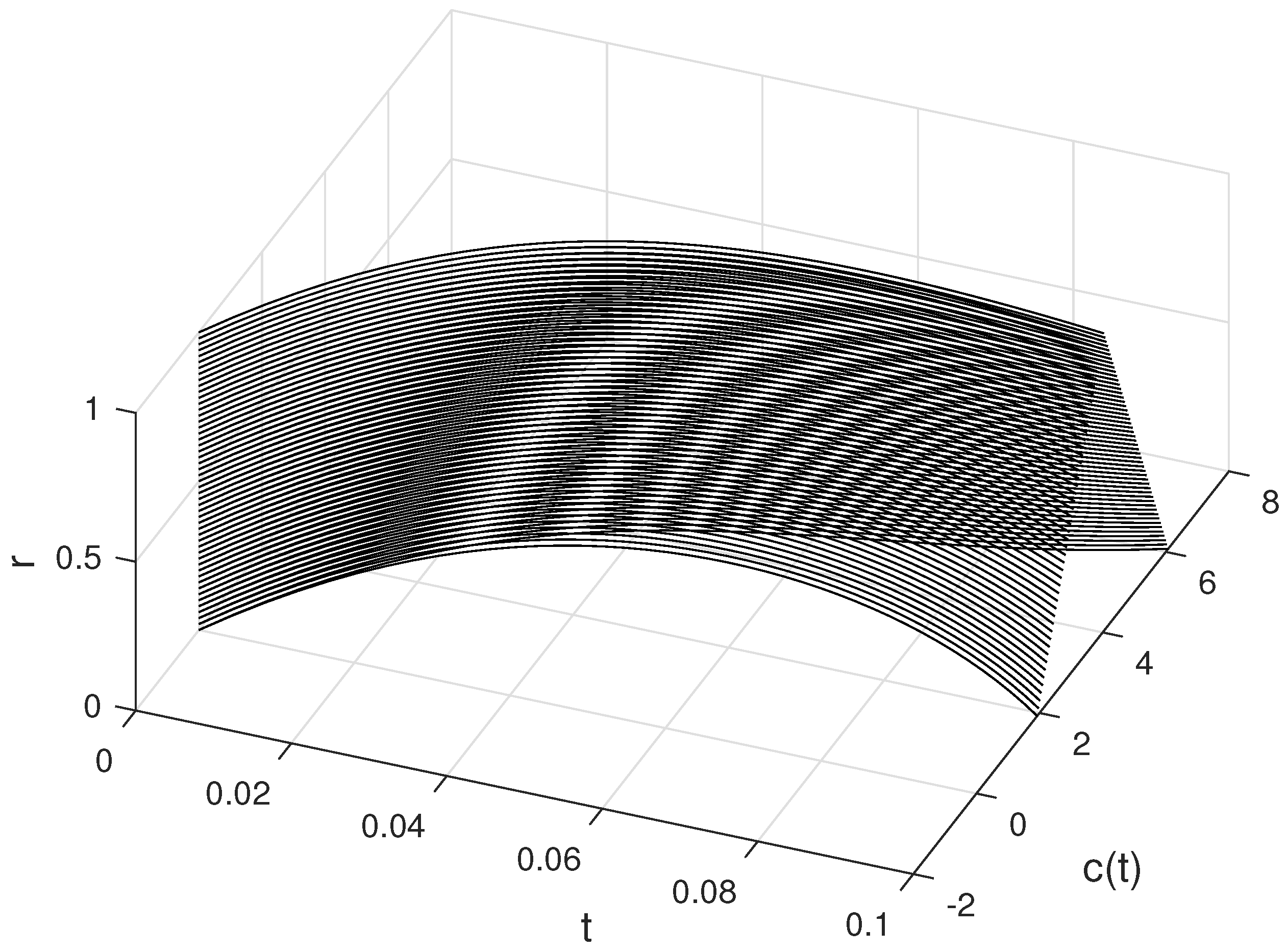
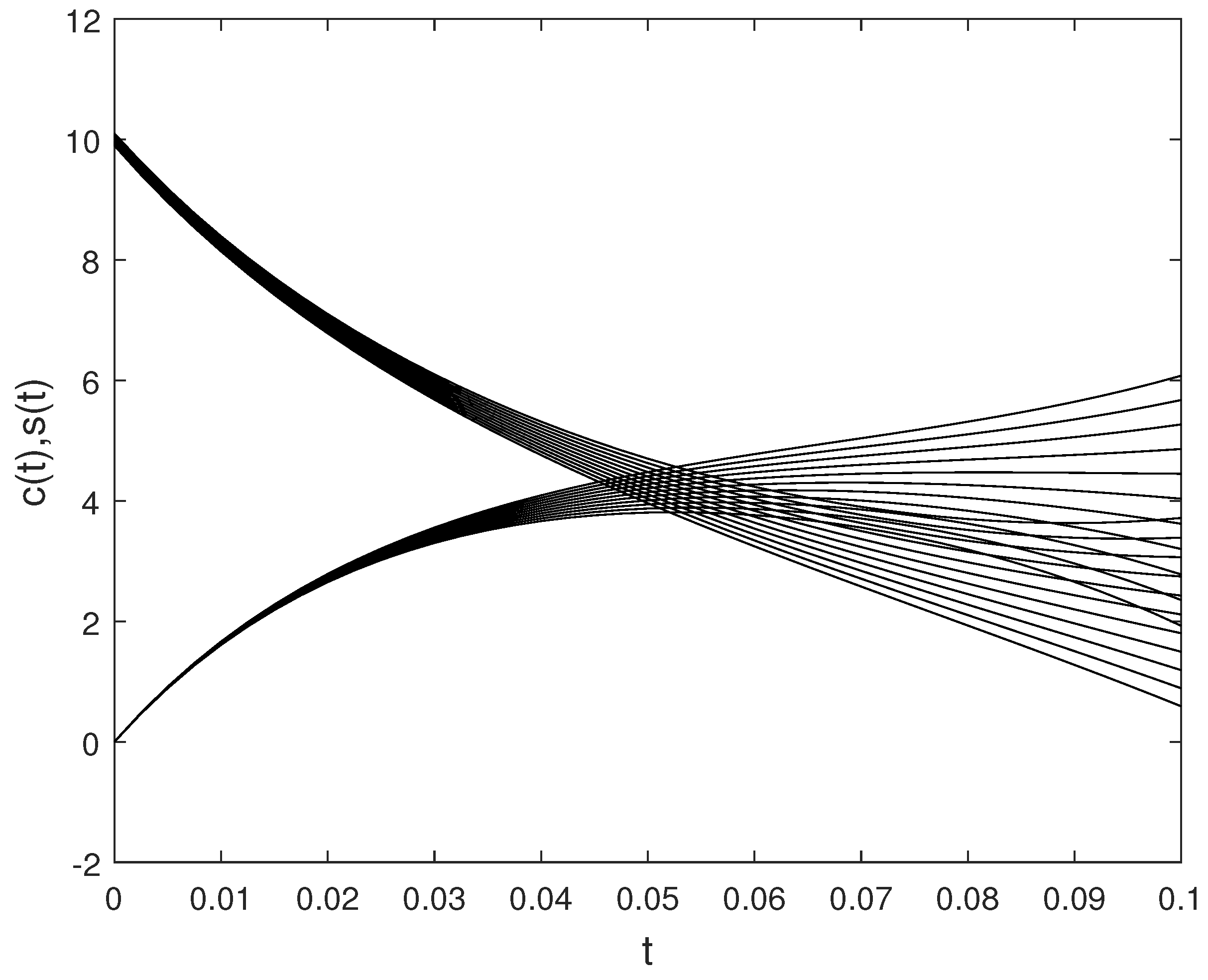
6. Examples
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Kirk, O.; Borchert, T.V.; Fuglasang, C.C. Industrial enzyme applications. Curr. Opin. Biotechnol. 2002, 13, 345–351. [Google Scholar] [CrossRef]
- Buxbaum, E. Fundamentals of Protein Structure and Function, 2nd ed.; Springer International Publishing: New York, NY, USA, 2015. [Google Scholar]
- Keener, J.; Sneyd, J. Mathematical Physiology; Springer: New York, NY, USA, 1978. [Google Scholar]
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Biochemistry, 5th ed.; W. H. Freeman: San Francisco, CA, USA, 2002. [Google Scholar]
- Chasnov, J.R. Mathematical Biology Lecture notes for MATH 365; The Hong Kong University of Science and Technology: Hongkong, China, 2009. [Google Scholar]
- Chapwanya, M.; Lubuma, J.M.; Mickens, R.E. From enzyme kinetics to epidemiological models with Michaelis–Menten contact rate: Design of nonstandard finite difference schemes. Comput. Math. Appl. 2012, 64, 201–213. [Google Scholar] [CrossRef]
- Sen, A.K. An Application of the Adomian decomposition method to the transient behaviour of a model biochemical reaction. J. Math. Anal. Appl. 1988, 131, 232–245. [Google Scholar] [CrossRef]
- Khader, M.M. On the numerical solutions to nonlinear biochemical reaction model using Picard-Pade technique. World J. Model. Simul. 2013, 9, 38–46. [Google Scholar]
- Batiha, A.M.; Batiha, B. Differential Transformation Method for a Reliable Treatment of the Nonlinear Biochemical Reaction Model. Adv. Stud. Biol. 2011, 3, 355–360. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Chang, S.L.; Zadeh, L.A. On fuzzy mapping and control. IEEE Trans. Syst. Man Cybern. 1972, 2, 30–34. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Toward fuzzy differential calculus: Part 3, differentiation. Fuzzy Sets Syst. 1982, 8, 225–233. [Google Scholar] [CrossRef]
- Seikkala, S. On the fuzzy initial value problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Kaleva, O. Fuzzy differential equations. Fuzzy Sets Syst. 1987, 24, 301–317. [Google Scholar] [CrossRef]
- Kaleva, O. The Cauchy problem for fuzzy differential equations. Fuzzy Sets Syst. 1990, 35, 389–396. [Google Scholar] [CrossRef]
- Buckley, J.J.; Feuring, T. Fuzzy differential equations. Fuzzy Sets Syst. 2000, 110, 43–54. [Google Scholar] [CrossRef]
- Goetschel, R.; Voxman, W. Elementary calculus. Fuzzy Sets Syst. 1986, 18, 31–43. [Google Scholar] [CrossRef]
- Ma, M.; Friedman, M.; Kandel, A. Numerical solution of fuzzy differential equations. Fuzzy Sets Syst. 1999, 105, 133–138. [Google Scholar] [CrossRef]
- Puri, M.L.; Ralescu, D. Differential for fuzzy function. J. Math. Anal. Appl. 1983, 91, 552–558. [Google Scholar] [CrossRef]
- Nieto, J.J. The Cauchy problem for continuous fuzzy differential equations. Fuzzy Sets Syst. 1999, 102, 259–262. [Google Scholar] [CrossRef]
- Stefanini, L.; Bede, B. Generalized fuzzy differentiability with LU-parametric reperesentation. Fuzzy Sets Syst. 2014, 257, 184–203. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Allahviranloo, T. Numerical solution of fuzzy differential equation by Runge–Kutta method. Nonlinear Stud. 2004, 11, 117–129. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Allahviranloo, T.; Darabi, P. Numerical solution of n-order fuzzy differential equation by Runge–Kutta method. Math. Comput. Appl. 2011, 16, 935–946. [Google Scholar] [CrossRef]
- Palligkinis, S.C.; Papageorgiou, G.; Famelis, I.T. Runge–Kutta methods for fuzzy differential equations. Appl. Math. Comput. 2009, 209, 97–105. [Google Scholar] [CrossRef]
- Gomes, L.T.; de Barros, L.C.L.; Bede, B. Fuzzy Differentiatial Equations in Various Approaches; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ralston, A.; Rabinowitz, P. First Course in Numerical Analysis, 2nd ed.; Dover Publications: New York, NY, USA, 2001. [Google Scholar]
- Bede, B.; Rudas, I.J.; Bencsik, A.L. First order linear fuzzy differential equations under generalized differentiability. Inf. Sci. 2007, 177, 1648–1662. [Google Scholar] [CrossRef]
- Chalco-Cano, Y.; Roman-Flores, H. On new solutions of fuzzy differential equations. Chaos Solitons Fractals 2008, 38, 112–119. [Google Scholar] [CrossRef]
- Gear, C.W. Numerical Initial Value Problem in Ordinary Differential Equations; Prentice Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barazandeh, Y.; Ghazanfari, B. Numerical Solution for Fuzzy Enzyme Kinetic Equations by the Runge–Kutta Method. Math. Comput. Appl. 2018, 23, 16. https://doi.org/10.3390/mca23010016
Barazandeh Y, Ghazanfari B. Numerical Solution for Fuzzy Enzyme Kinetic Equations by the Runge–Kutta Method. Mathematical and Computational Applications. 2018; 23(1):16. https://doi.org/10.3390/mca23010016
Chicago/Turabian StyleBarazandeh, Yousef, and Bahman Ghazanfari. 2018. "Numerical Solution for Fuzzy Enzyme Kinetic Equations by the Runge–Kutta Method" Mathematical and Computational Applications 23, no. 1: 16. https://doi.org/10.3390/mca23010016
APA StyleBarazandeh, Y., & Ghazanfari, B. (2018). Numerical Solution for Fuzzy Enzyme Kinetic Equations by the Runge–Kutta Method. Mathematical and Computational Applications, 23(1), 16. https://doi.org/10.3390/mca23010016




