Abstract
In wireless sensor networks (WSNs), users can use broadcast authentication mechanisms to connect to the target network and disseminate their messages within the network. Since data transfer for sensor networks is wireless, as a result, attackers can easily eavesdrop deployed sensor nodes and the data sent between them or modify the content of eavesdropped data and inject false data into the sensor network. Hence, the implementation of the message authentication mechanisms (in order to avoid changes and injecting messages into the network) of wireless sensor networks is essential. In this paper, we present an improved protocol based on elliptic curve cryptography (ECC) to accelerate authentication of multi-user message broadcasting. In comparison with previous ECC-based schemes, complexity and computational overhead of proposed scheme is significantly decreased. Also, the proposed scheme supports user anonymity, which is an important property in broadcast authentication schemes for WSNs to preserve user privacy and user untracking.
1. Introduction
Wireless sensor networks (WSNs) are composed of a few number of sensor nodes (SNs) which are named as sink or base station, and they have higher computing and processing power, but they need more energy consumption [1]. In addition, WSNs have a great number of resource-constrained SNs which are named as typical nodes [1]. WSNs are used in many industrial and critical applications such as monitoring in hospitals, national and international security centers, medical monitoring systems, electrical power plants, and environmental monitoring [2,3,4,5]. In most cases, the SNs are deployed in hostile environments and the data transmission between them takes place in wireless form. A hostile node can be deployed between nodes and easily take two different actions: (I) sniff and modify data packets and (II) inject bogus data packets into the sensor network [6]. Because of this reason, using a broadcast authentication mechanism in WSNs is very important and vital. In addition, another important factor in the multi-user broadcast authentication mechanism for sensor networks is scalability. In broadcast authentication process, which is multi-user-based, a large number of users join a WSN and, in order to obtain the required information, disseminate their requests in the SN [6,7,8].
Based on the cryptographic methods and techniques, proposed solutions for broadcast authentication in WSNs are distinguished in three different categories. WSNs in the first category use broadcast authentication process by the symmetric key cryptography [9,10,11,12]. The approaches of this category suffer from poor scalability and various breaches of the security [6,8,13,14]. WSNs in the second category use broadcast authentication process by one-time signature methods [15,16,17]. These methods provide high-speed, acceptable performance and high scalability architecture. However, the methods in this category have a series of limitations that cannot be ignored. For example, the security of data packages will be weak when a large number of signatures are generated to accomplish the authentication process [18]. WSNs in the third category use schemes based on asymmetric keys [6,8,18,19]. SNs are resource-constraint, and also public key cryptography (PKC) operations are very costly. Thus, if we employ the PKC method in WSNs, then extra computational overhead can be imposed on the SNs. As a consequence, many researchers and practitioners were following other techniques to deploy the multi-user broadcast authentication schemes. Nevertheless, the current significant progress in sensor technology showed that using the PKC method in WSNs is possible. Also, recent researches in various PKC methods have shown that Elliptic Curve Cryptography (ECC) is a suitable authentication method for WSNs [20,21]. In addition, ECC compared with the other PKC methods has smaller key size and lower time complexity. Because of this reason, we use the ECC method to secure multi-user broadcast authentication process in sensor networks.
Compared to symmetric-key-cryptography-based solutions, using solutions based on PKC for achieving broadcast authentication process in WSNs provides straightforward solutions, high scalability, and security. Nevertheless, PKC-based solutions to the broadcast authentication process in sensor networks have a common drawback: the signature verification phase in public-key-based digital signature is much slower than the signature verification phase of message authentication code (MAC) in symmetric-key-based solutions. As a consequence, a large number of packets may be waiting in the message queue of each SN in the signature verification phase when many users (or SNs) broadcast their requests into the WSNs simultaneously [22]. In order to solve this problem, we improve the time complexity of the signature verification phase in the ECC digital signature protocol.
The remainder of this paper is organized as follows: In Section 2, we review related works on broadcast authentication schemes for WSNs. In Section 3, an introduction about ECC is presented. In Section 4, the adversary model is explained. Then, in Section 5 we propose an efficient protocol with minimal time complexity for digital signature based on the elliptic curve discrete logarithm (ECDLP). In Section 6, the proposed protocol is used in broadcast authentication in WSN. In Section 7, security analysis of the proposed protocol is presented. In Section 8, the performance evaluation of our scheme compared to other schemes is presented. Finally, Section 9 concludes the paper.
2. Related Works
The first solution for multi-user broadcast authentication was proposed by Benenson et al. [23]. When the attacker through Node Capture Attack obtains full control of sensor nodes, she/he can send the authenticated query to other sensor networks. Their scheme was resistant and robust against these security problems. However, Benenson’s method was inefficient in terms of communication costs and energy consumption. In fact, Benenson’s method was ineffective because sensors, in addition to transfer of data, should also verify the user’s public key certificate, which is an expensive option in terms of energy consumption. After a while, Jiang et al. [24] improved Benenson’s method by using self-certified PKC. Since this method is based on symmetric key cryptography (SKC), it is very efficient in terms of energy and computing speed. On the other hand, in this way, each sensor node is forced to keep a private-key and public-key pair in the memory. If any sensor node is seized by an attacker all classified information within the embedded sensor nodes can be disclosed. As a result, this security problem in Jiang’s method led the sensor nodes to be vulnerable against capture attack. Hence, this method is not secure. Ren et al. suggested IDS, an ID-based scheme which is highly scalable and has robust security [6]. This scheme, by using an effective plan based on several PKC, provides quick authentication broadcast. Also, this scheme has removed the security issues of schemes belonging to the μTESLA family. In addition, scheme-based IDS are bilinear pairings. Since the cost of any action in bilinear pairing is about 20 times more than a scalar multiplication, therefore energy consumption in IDS is much higher compared to ECC-based schemes, in which scalar multiplication is one of the main operations [22]. Ren et al. [8] offered a strong multi-user broadcast authentication method that is called the hybrid authentication scheme (HAS), based on ECC. This method uses a hybrid encryption for broadcast authentication. In order to remove the transfer process of a user’s public key certificate in sensor nodes, in the HAS scheme, each sensor node initializes the public key information in advance by using the Bloom filter and Merkel hash tree. Due to the use of the Merkel hash tree, the total number of users must be fixed, thus HAS does not provide user scalability and a new user can be added to WSN only after the removal of an old user.
Cao et al. [18] have proposed an IMBAS scheme to a multi-user broadcast authentication method, which was based on IDs. IMBAS provides strong security, high scalability, and acceptable performance in terms of energy consumption at the same time, for wireless sensor networks. To secure multi-user broadcast authentication in WSNs with high scalability, IMBAS has employed public key cryptography (PKC). The performance analysis showed that IMBAS provides much better scalability and lower energy consumption compared to IDS [6] and HAS [8].
Design Goal
Most of the previous works which are mentioned above do not provide new protocols for broadcast authentication and only employ the traditional ECDLP in their schemes. In this paper, instead of proposing a new algorithm for broadcast authentication similar to other schemes, we focus on improving the digital signature for broadcast authentication in WSN using Elliptic Curve Cryptography. The main goal of this paper is to propose a protocol for broadcast authentication in WSN with strong security and efficiency. In the proposed protocol, we can easily broadcast an authenticated message, add a user, and revoke a compromised user. Also, the proposed protocol supports user anonymity, which is an important property in broadcast authentication schemes for WSNs in order to preserve the user privacy and the user untracking.
3. Preliminary Material
In this section, an introduction to elliptic curve cryptography is described briefly.
Binary Elliptic Curve Cryptography
Elliptic curve cryptography (ECC) is a type of public key encryption method. This encryption mechanism is based on elliptic curve discrete logarithm problem solving (ECDLP). Elliptic binary curves is defined over the Galois field GF(2m) by two parameters, b ≠ 0 and a, b ∈ GF(2m), where m is a positive integer. An elliptic curve over GF(2m) is the point at infinity, denoted as O, as well as all points (x, y) with the proviso that x, y ∈ GF(2m) and also satisfies Equation (1).
If the symbol Z denotes an elliptic curve over GF(2m), then the main points, in the encryption system, are the following:
- for all values of .
- for all values of and .
- Point addition operation in an Elliptic Curve
- Point Addition Operation uses two points P = (x1, y1) and Q = (x2, y2) on the elliptic curve, in order to obtain another point is L = (x3, y3) = P + Q on the same elliptic curve [25,26].
For all and where , perform as follows:
• Point doubling operation in an Elliptic Curve
Point Doubling Operation uses a point P = (x1, y1) on the elliptic curve to obtain another point L = (x2, y2) = 2P on the same elliptic curve [27,28].
For any , where , it is performed as follows:
• Point Multiplication Operation in an Elliptic Curve
By using the two basic elliptic curve operations, the point multiplication can be performed as follows: Point Addition Operation and Point Doubling Operation. For example, the scalar point multiplication method for calculating the point is kP = P + P + ... + P (k time), where n is a positive integer that is called scalar, and the P is the point on the elliptic curve.
We can compute through iterative point additions. For example, If k = 23; then . For more details about ECC, see [27].
4. Adversary Model
Many attacks have been proposed for WSNs as an adversary model in the literature [6,8,18,25,29,30] . However, only a few are about signature-based broadcast authentication schemes for WSNs. In this paper, we assume that the adversaries are able to launch various attacks on WSN against broadcast authentication schemes that have been proposed in the literature [6,8,18]. These attacks can be categorized as follows:
• Active Attack
The attacker simply sends captured data which was previously sent by some authenticated network users for deceiving sensor nodes to produce an unauthorized effect such as executing specific commands. In addition to packet eavesdropping, attackers can also modify or directly create forged messages and disseminate them into the network that leads to damage to the sensor network.
• Compromise Attack
Since WSN users usually are equipped with portable devices such as a smart card, this makes them vulnerable to a compromise attack. An attacker can compromise both the user devices and the sensor nodes in a WSN. However, we assume that the attackers cannot compromise all of the user devices and sensor nodes. When network users or sensor nodes are compromised, all embedded secret data such as the private keys can be stolen by the attacker.
• Denial-of-Service Attack (DoS)
An attacker can easily disseminate bogus messages into the WSN. This will waste the energy of sensor nodes and will also fill the buffer of sensor nodes. Since the adversaries can easily inject bogus messages into sensor networks, these two DoS attacks are very destructive in multi-user schemes.
• User Anonymity
User anonymity is an important property in broadcast authentication schemes for WSNs to preserve user privacy and user untracking. In other words, user anonymity involves two aspects: identity protection and user un-traceability [31,32]. Both of these aspects are needed to hide from attackers (e.g., eavesdropping attackers) rather than the sink, because the sink needs the real identity in order to evict and revoke a malicious user or add him/her. So, if any scheme does not provide this property, the attacker can easily find privacy information of each user, such as identity, and track them [29,31].
5. An Improved Proposed Protocol Based on Elliptic Curve Cryptography
According to other digital signature protocols based on the elliptic curve discrete logarithm problem (ECDLP), our proposed digital signature protocol consists of four phases. In the following section, we review each phase separately.
5.1. Pre-Distribution Phase
Suppose E is an elliptic curve defined over a finite field and the number of points on E is equal to q. Also, P is on and also suppose that P has prime order n and a point Q is a multiple of P. The point Q = kP where k ≤ n − 1. Given the point P and Q, estimating the value of k is computationally infeasible. A private key is an integer k that is selected uniformly at random from the interval [1, n − 1], and the corresponding public key is Q = k P [27].
Specify a suitable elliptic curve by selecting two parameters a and b of the elliptic curve E over finite field .
Choose a base point G = (Gx,Gy) on the elliptic curve with the proviso that G is a finite point on the elliptic curve and also has the largest order n.
The order n of base point G is a large prime number in E over finite field .
5.2. Key Generation Phase
In this phase, signer A provides public and private key by performing the following steps:
d, an integer in the range [1, n − 1], is selected as her/his private key.
Q = dG is calculated, and is considered as the public key.
5.3. Signed Production Phase
In this phase, signer A generates a signed message m as follows:
First, a random integer k in the interval [1, n − 1] is generated with the proviso that k ≠ d.
The and is calculated with the proviso r ≠ 0
Through hash function , abstract of message m is gained and it is named by the symbol e.
The expression is calculated.
is calculated, where r is the x-coordinate of F.
Finally, , in signed formed, is produced by the signatories of A for message m.
5.4. Signature Verification Phase
In this phase, confirming the signature, as follows, admits the validity of signature for message m:
First, through the hash function Hash (m*), the abstract of message m* is obtained and named with the symbol e*.
Then, and are calculated. If , the sign is approved, otherwise it is denied.
Note: We assumed that the received message and signature for the verification phase is and . Use of this new symbol (*) denotes that message and signature may have been altered by an attacker.
6. Proposed Scheme for Broadcast Authentication in Wireless Sensor Network
Our scheme consists of four parts: (1) System initialization, in which sensor nodes are initialized by the base station or sink; (2) User addition, in which the sink generates a public/private key pair for a user joining the sensor network; (3) Multi-user broadcast authentication, in which the users or the sink sign the message and broadcast it to the sensor network; (4) User revocation, in which the compromised users are revoked by the sink.
Our proposed scheme is explained as follows:
- (1)
- System initialization phase: Before deploying sensor nodes, each of them is preloaded with system parameters such as elliptic curve parameters and public key of sink and also for all users. ID denotes the identity and Q denotes the public key of a user.
- (2)
- User addition: A user chooses a unique identifier ID and sends it to the sink. Next, the sink generates a public key and private key in the key generation phase of the proposed protocol for . The sink delivers for and also broadcasts to sensor networks using secure channel.
- (3)
- Broadcast authentication message: In order to broadcast an authenticated message to the sensor networks, the with identifier sends the following message:, where M denotes the message, denotes the timestamp, and is the signature generation phase of proposed protocol over . When the message is received, the sensor node takes the following action:
- (a)
- Check whether the timestamp is fresh.
- (b)
- Verify the received signature using the proposed protocol if is fresh, otherwise drop the message.
- (c)
- If the signature verification on the received message succeeds, then disseminate the authenticated message to the adjacent sensor nodes, otherwise reject the message and report the potential attack to the sink immediately.
- (4)
- User revocation: When a user is compromised by an attacker, the sink may revoke her/him from the WSN. As a result, in order to revoke a user, the sink broadcasts a revoke message to the sensor network. Sensor nodes listen to the sink’s broadcast and remove the ID and the public key of the compromised user. After that, if each sensor node that received the broadcast message is from the same user, it will drop it and report the potential attack to the sink.
Let us consider a multi-user wireless sensor network. First, in order to allow the users to connect to the network, they must register. Thus, the target users through registration gain necessary validity in order to connect to a WSN. Sensor nodes that are located in their neighborhood run an authentication procedure to authenticate each other. Then, registered users start sending their requests (in order to obtain the required information from the network) into wireless sensor networks. As shown in Figure 1, the first user signs her/his request and sends it to the sensor nodes (e.g., Nodes A, B, and C). Then, nodes A, B, and C verify the signing of the first user. If the authentication is approved, they send out user requests locally. This process continues until all available nodes have received the user’s broadcast package. If during the broadcast process, one of the verification operations fails, sensor nodes drop the packet and will report to the base station. It should be noted that in the signature verification phase, all sensor nodes require the public key of registered users. Since the base station in sensor networks have more energy and are very powerful, they can easily broadcast the public key of users to sensor network and then they can fetch this public key from the base station. Also, the public key of registered users can be preloaded in sensor nodes at the initialization phase. For example, according to Figure 1, we assume that user 1 wants to send requests into the network. We also assume that the user has already registered in a WSN. The user generates the request m and signs it as with the condition that the d is private key and e is the abstract of the desired message.
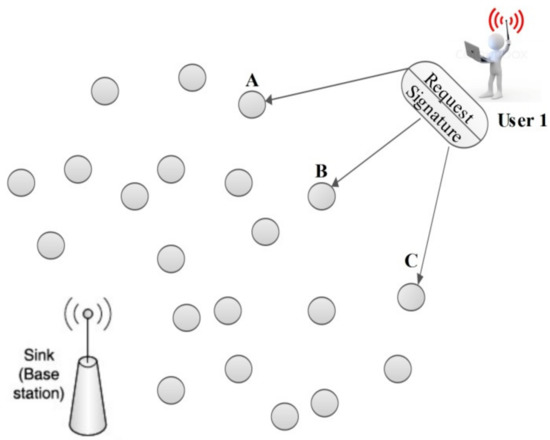
Figure 1.
Dissemination of a user message in wireless sensor networks.
It should be noted that in the process of broadcast authentication in WSNs, each user signs their messages only once. On the other hand, the user signature may be verified a thousand times by sensor nodes. Thus, by reducing the cost of operations (in terms of energy consumption) in the signature verification phase, the computational cost of each node will be reduced significantly. Consequently, the total energy consumption of the WSN will be reduced. As a result, in this paper, to reduce the computational cost of WSN, we focused more on the improvement of the signature verification phase.
However, our proposed scheme is very simple and efficient, but it is still vulnerable against the following attacks:
- First, the attacker creates a fake message .
- In this step, the potential attacker calculates (if can be divided by ).
- Also, the attacker calculates the .
- Finally, the attacker uses as the signature of the message and broadcasts the fake package into wireless sensor networks.
- Finally, the intended victim receives the fake package and calculates and compares the values and to each other. Since and are equal, as a result, the intended victim approves the fake message as a valid message.
It is obvious that the above attack occurs when is divisible (with zero remainder) by and also > .
In other words, these attacks occur when mod = 0 and also . It should be noted that and . In order to clarify the issue, consider the following four modes:
6.1. When Output mod = 0 with the Condition that
When the attacker intends to change message m (the generated message ), where e is bigger than e* and is also divisible into e*, then he/she can easily divide by . The result obtained (here ) is a positive integer. Then, multiplied by the value of X (a point on the elliptic curve), performing a scalar multiplication will obtain .
When is sent to the network by an attacker, each node receives it separately and and are calculated as follows:
Since is exactly the quotient of e on e* (with remainder zero), therefore, it is possible to calculate the amount of . Hence, the intended victim with the calculation of and can check their equality and verify the authenticity of the fake message.
6.2. When Output mod = 0 with the Condition that
In this case, e* is also divisible by e. Since e < e*, the attacker, in order to forge the message, should perform and then try to compute . X is a point on the elliptic curve and in the elliptic curve the operations ÷ is an undefined action. Therefore, an attacker cannot set the value X’ in such a way that the intended victim would not be able to recognize the forgery of the message.
6.3. When Output mod 0 with the Condition that
In this case, e is not divisible by e* and the quotient is not an integer (since e > e* the result of the division, will be a floating-point number). Since e > e*, the attacker, in order to the forge a message, has to multiply X by a floating-point number. Since X is a point on elliptic curves and in elliptic curve, multiplying a floating-point number by a point on the elliptic curve is an undefined operation. Therefore, an attacker cannot set the value X’ in such a way that the intended victim is unable to recognize the forgery of the message.
6.4. When Output mod ≠ 0 with the Condition that
In this case, is also not divisible by and since the quotient is not an integer (the result of the division, will be a floating-point number). Since e < e*, the attacker, in order to forge the message, has to divide X by a floating-point number. X is a point on elliptic curves, and in elliptic curve, dividing a point by a floating-point number is an undefined operation. Therefore, an attacker could not set value X’ in such a way that the intended victim is unable to recognize the forgery of the message.
With the improvement of the proposed protocol as above, we can guarantee that may not be divided by (assuming secure hash functions). Thus, security problems related to the proposed protocol will be resolved and the attacker will not be able to forge or inject messages into the wireless sensor network.
It is obvious that the above attack occurs when . is divisible (with zero remainder) by . Since the nature of cryptographic hash function is one-way, in the most optimistic state, the attacker can hardly generate a bogus message that can be divisible by ). As a result, the probability of occurrence of the above attack is very low, if not impossible. Nevertheless, we will solve this problem even if the probability of its occurrence is negligible. If we can prevent the divisibility of by , then the mentioned attack is thwarted. To thwart the mentioned attack in our main protocol, we amend the signature generation phase and signature verification phase as follows:
• Signature Generation
In this phase, the signature for message is generated by signer A, as follows:
- Selects an integer number k randomly in the range of 1 to n − 1, where .
- Computes .
- Extracts the integer from the message using a hash-function operation, and sets the most significant bit (MSB) of to 1.
- Computes .
- Finally, the generated signature for the message by the signer is .
• Signature Verification
After the signature is received, the verifier B confirms the validity of the signature for message , as follows:
- Computes and sets the most significant bit (MSB) of to 1.
- Computes and u=X + Q.
If v equals u, then the verifier B will validate the signature ; otherwise, she/he rejects it.
By altering our protocol, we can guarantee that will not be divisible by . As a result, the security problem of our proposed protocol will be solved. Moreover, for the sake of simplicity for our proposed protocol, we assume that the binary numbers are unsigned.
The following example clearly describes our solution.
Suppose and also ) = 8 bits.
The largest binary integer of 8 bits is . The smallest binary integer of 8 bits is . As a result, is always nonzero, as shown in Figure 2 below.

Figure 2.
Proof that is always nonzero.
It is noted that in the case of 255, 11111111 mod 11111111 is 0. It means that the content of message is not altered. Moreover, this example can be extended to N-bits. As a result, we can easily prevent the mentioned attack.
7. Security Analysis
7.1. Security Analysis of Proposed Protocol
Here, we demonstrate the impossibility of message forging in our proposed protocol. First, we suppose that the attacker easily forges the signature of message m. For example, the attacker alters the message and then the epsilon value will be added to the signature s: s + ε and then (s, X) is changed to (s*, X*) subsequently. We demonstrate that the attacker cannot find any value for ε and X* in such a way that satisfies Equation (6).
(kre + d + ε)G = e*X* + (dG)
When the attacker alters the message m, the hash (m) is changed subsequently. Also, the signature s is changed too. Normally, when the sensor node computes Equation (6), it can easily detect the bogus message and it would reports the potential attack to the sink. The value of s and X are dependent on each other. So, when the attacker alters the message m, then she/he tries to change the value of X in such a way that the sensor node does not detect the bogus message. However, even when the attacker selects the value of ε arbitrarily, based on ECDLP, he/she cannot find any valid value for X* that satisfies the Equation (6).
Since the value of X* is not available by the attacker, then r* and k will be unknown. As a result, after that the signature s is altered by the attacker, the attacker cannot find a valid value for X* in such a way that the two sides of the Equation (6) are equal.
From Equation (6) the relation Equation (7) can be obtained.
(kre + d)G − e*X* − dG = εG
The parameter on the left side of Equation (7) is available to the attacker, in other words, the attacker has the value of the product (εG) and he/she doesn’t know the value of ε itself. However, based on ECDLP, the attacker cannot estimate the value of ε correctly. Hence, even with an arbitrary value of X*, the value of ε cannot be estimated by the attacker.
Also, in rare circumstances, it is possible that the attacker can forge the message in the proposed protocol. We finally resolve this vulnerability as mentioned in Section 6.
7.2. Security Strength of Proposed Scheme
In this subsection, we investigate the security strength of proposed scheme as follows:
• Active Attack
Our scheme uses a proposed digital signature protocol for message broadcast authentication such that the forging message is not possible, and the attacker cannot modify or directly create forged messages and disseminate them into the sensor network as a real message. Also, the replay attack in multi-user broadcast authentication can be prevented by adding a time-stamp in the broadcast messages.
• Compromise Attack
Our scheme supports user revocation property, thus, when a user is compromised by an attacker, the sink will revoke the user by broadcasting a revocation message into the sensor network. On the other hand, an attacker can compromise both the user devices and the sensor nodes in WSN. To cope with a compromise attack for user device, we can use a password-based user private key protection and user revocation in our scheme, similar to the one in IMBAS literature [18].
• Denial-of-Service Attack (DoS)
In the DoS attack, the attackers try to waste energy on sensor nodes by disseminating bogus messages to the WSN. In our scheme the DoS attack are mitigated as follows:
Each sensor node is able to authenticate a broadcast message by executing signature verification phase immediately after receiving it. If the signature verification failed, the sensor node will be dropped rather than the forged message be stored or forwarded to the next hop. Then, it will report the potential attack to the sink immediately. After that, the sink will take further actions to limit the adversary from performing DoS attack and investigate any access to the WSN again.
• User Anonymity
User anonymity is an important property in broadcast authentication schemes for WSNs to preserve the user privacy. Thus, we have added the user anonymity property to the proposed scheme. Many types of techniques have been investigated in literature [31], such as the Pre-loading a pseudo-IDs pool method, Group and ring signatures method, and IND-CCA2 public-key encryption. However, none of them are for multi-user broadcast authentication in WSN. Nevertheless, we have added the user anonymity to our scheme. So, the proposed scheme achieves user anonymity and un-traceability as follows.
First, the with identifier , concatenates and then executes signature generation phase on it. After that, he/she broadcasts into the sensor networks. Since the user only sends and not the identity itself in message broadcasting, as a result his/her ID always remains anonymous and the attacker cannot find the user identity. On the other side, when the sensor node receives the message, it verifies it by executing the signature verification phase. If the verification phase fails, it will report the potential attack to the sink.
8. Results and Evaluations
To demonstrate that our proposed scheme is better (as compared to other proposed schemes) in terms of computational cost, we first give some definitions and then, based on these definitions, we present the comparison.
Naturally, by reducing the cost of computing nodes, each node life increases and prolonging the life of nodes the entire lifetime of wireless sensor network also becomes longer. In most cases, the researchers, in order to prove the efficiency of their method, first express the cost of all scalar operations based on modular multiplication and then, based on the number of multiplications, they evaluate their schemes against others.
For convenience, the following notation will be used for the complexity analysis and evaluation of proposed schemes:
- TMul: time complexity of implementing a modular multiplication.
- TAdd: time complexity for implementing a modular add operation.
- TEC Mul: time complexity for implementation of multiplying points in an elliptic curve.
- TEC Add: time complexity to implement the sum of two points of the elliptic curves.
- T Inv: time complexity for executing a reverse acting modular.
- THash: time complexity to run a one-way hash function.
Also, we can demonstrate the scalar multiplication operation based on modular multiplication. Koblitz et al. have shown the time complexity of each elliptic curve cryptography operator based on modular multiplication [33]. In Table 1 below, we can observe the time complexity of elliptic curve cryptography operators based on modular multiplication.

Table 1.
Unit conversion of various operations based on modular multiplication.
As shown in Table 2 below, the computation complexity of the signature generation phase in our proposed protocol is higher than other protocols. On the other hand, the computational complexity of the signature verification phase in our proposed protocol is less than other mentioned protocols in Table 2. As already mentioned, in WSNs the signature generation phase can be executed only once for each user at each communication round. However, the signature verification phase can possibly be executed more than 1000 times by the sensor network at each communication round. As a result, in special application of WSNs such as multi-user broadcast authentication schemes, the impact of reducing the computational complexity in the signature verification phase is far more than the signature generation phase. Consequently, compared with the previous proposed protocols [34,35,36,37,38,39,40], the time complexity of our proposed schemes is more efficient.

Table 2.
Comparing various protocols in term of time complexity.
After that, the proposed protocol is evaluated in terms of broadcast authentication in WSNs and is compared with other schemes. The results obtained from Table 3 below clearly show that our proposed scheme outperforms other schemes in terms of computational cost.

Table 3.
The Time Complexity of Schemes in Unit of .
Based on the above results, we demonstrate that the time complexity of our scheme is less than Cao et al.’s scheme and Ren et al.’s scheme. For example, let the symbol . denote the number of executions for signature generation phase, symbol . denote the number of executions for signature verification phase, and denote the time complexity of broadcast authentication in WSN. Now, if = 1 and = 1000, then is calculated next is less than both schemes.
- The Cao et al.’s time complexity scheme equals .
- The Ren et al.’s time complexity scheme equals .
- Time complexity of our proposed scheme equals .
9. Conclusions
In this paper, we presented an efficient protocol-based ECDLP. Compared with previous protocols, the complexity of our protocol is very efficient. Finally, we applied the proposed protocol authentication on wireless sensor network broadcast. By using the proposed protocol in wireless sensor networks, the authentication of wireless sensor networks broadcast is shown to be accelerated.
Finally, we evaluate the proposed scheme with other schemes previously presented in the field of broadcast authentication, and we have shown that our proposed scheme’s computational overhead is less than the rest of other schemes. Also, our proposed scheme has the user anonymity property that preserves user privacy and thus it prevents user untracking.
Author Contributions
Hamed Bashirpour and Saman Bashirpour designed the protocol and performed the comparisons and wrote the results. Shahaboddin Shamshirband and Anthony T. Chronopoulos contributed in directing the research and in writing the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y. A survey on Sensor Networks. IEEE Commun. Mag. 2002, 40, 102–116. [Google Scholar] [CrossRef]
- Mainwaring, A.; Polastre, J.; Szewczyk, R.; Culler, D.; Anderson, J. Wireless sensor networks for habitat monitoring. In Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications (WSNA ’02), Atlanta, GA, USA, 28 September 2002; pp. 88–97. [Google Scholar]
- Lorincz, K.; Malan, D.J.; Fulford-Jones, T.R.F.; Nawoj, A.; Clavel, A.; Shnayder, V.; Mainland, G.; Welsh, M.; Moulton, S. Sensor Networks for Emergency Response: Challenges and Opportunities. IEEE Pervasive Comput. 2004, 3, 16–23. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Kasimoglu, I.H. Wireless Sensor and Actor Networks: Research challenges. Ad Hoc Netw. 2004, 2, 351–367. [Google Scholar] [CrossRef]
- Ren, K.; Lou, W. Communication Security in Wireless Sensor Networks; VDM Ve: Saarbrücken, Germany, 2008. [Google Scholar]
- Ren, K.; Zeng, K.; Moran, J. On Broadcast Authentication in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2007, 6, 4136–4144. [Google Scholar] [CrossRef]
- Liu, D.; Ning, P.; Zhu, S.; Jajodia, S. Practical Broadcast Authentication in Sensor Networks. In Proceedings of the Second Annual International Conference on Mobile and Ubiquitous Systems: Networking and Services (MobiQuitous), San Diego, CA, USA, 17–21 July 2005; pp. 118–132. [Google Scholar]
- Ren, K.; Lou, W.; Zhang, Y. Multi-user Broadcast Authentication in Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2009, 58, 4554–4564. [Google Scholar] [CrossRef]
- Liu, D.; Ning, P. Multi-level μTESLA: Broadcast Authentication for Distributed Sensor Networks. ACM Trans. Embed. Comput. Syst. 2004, 3, 800–836. [Google Scholar] [CrossRef]
- Perrig, A.; Szewczyk, R.; Wen, V.; Culler, C.; Tygar, J.D. SPINS: Security Protocols for Sensor Networks. ACM Wirel. Netw. 2002, 8, 521–534. [Google Scholar] [CrossRef]
- Wu, T.; Cui, Y.; Kusy, B.; Ledeczi, A.; Sallai, J.; Skirvin, N.; Werner, J.; Xue, Y. A Fast and Efficient Source Authentication Solution for Broadcasting in Wireless Sensor Networks. In New Technologies, Mobility and Security; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Zhou, Y.; Fang, Y. Babra: Batch-Based Broadcast Authentication in Wireless Sensor Networks. In Proceedings of the IEEE GLOBECOM’06, San Francisco, CA, USA, 27 November–1 December 2006; pp. 1–5. [Google Scholar]
- Ning, P.; Liu, A.; Du, W. Mitigate DOS Attacks Against Broadcast Authentication in Wireless Sensor Networks. ACM Trans. Sens. Netw. 2008, 4, 1. [Google Scholar] [CrossRef]
- Hu, Y.; Perrig, A.; Johnson, D. Packet leashes: A Defense Against Wormhole Attacks in Wireless Ad Hoc networks. In Proceedings of the INFOCOM, Twenty-Second Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, CA, USA, 30 March–3 April 2003; pp. 1976–1986. [Google Scholar]
- Chang, S.; Shieh, S.; Hsieh, C. An Efficient Broadcast Authentication Scheme in Wireless Sensor Networks. In Proceedings of the ACM Symposium on Information, Computer and Communications Security (ASIACCS), Taipei, Taiwan, 21–24 March 2006; pp. 311–320. [Google Scholar]
- Lee, J.; Kim, S.; Cho, Y.; Chung, Y.; Park, Y. HORSIC: An Efficient One-Time Signature Scheme for Wireless Sensor networks. Inf. Process. Lett. 2012, 112, 783–787. [Google Scholar] [CrossRef]
- Reyzin, L.; Reyzin, N. Better than biba: Short One-Time Signatures with Fast Signing and Verifying. In Information Security and Privacy; Springer: Berlin/Heidelberg, Germany, 2002; pp. 1–47. [Google Scholar]
- Cao, X.; Kou, W.; Dang, L.; Zhao, B. IMBAS: Identity-Based Multi-User Broadcast Authentication in Wireless Sensor Networks. Comput. Commun. 2008, 31, 659–667. [Google Scholar] [CrossRef]
- Yamakawa, S.; Cui, Y.; Kobara, K.; Imai, H. Lightweight Broadcast Authentication Protocols Reconsidered. In Proceedings of the IEEE Wireless Communications & Networking Conference (WCNC), Budapest, Hungary, 5–8 April 2009; pp. 3076–3081. [Google Scholar]
- Gura, N.; Patel, A.; Wander, A. Comparing Elliptic Curve Cryptography and RSA on 8-bit CPUs. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems (CHES’04), Cambridge, MA, USA, 11–13 August 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 119–132. [Google Scholar]
- Du, W.; Wang, R.; Ning, P. An Efficient Scheme for Authenticating Public Keys in Sensor Networks. In Proceedings of the 6th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc’05), Urbana-Champaign, IL, USA, 25–27 May 2005; ACM: New York, NY, USA, 2005; pp. 58–67. [Google Scholar]
- Cao, X.; Kou, W.; Du, X. A Pairing-Free Identity-Based Authenticated Key Agreement Protocol with Minimal Message Exchanges. Inf. Sci. 2010, 180, 2895–2903. [Google Scholar] [CrossRef]
- Benenson, Z.; Gedicke, N.; Raivio, O. Realizing Robust User Authentication in Sensor Networks. In Proceedings of the First REALWSN 2005 Workshop on Real-World Wireless Sensor Networks, Stockholm, Sweden, 20–21 June 2005. [Google Scholar]
- Jiang, C.; Li, B.; Xu, H. An Efficient Scheme for User Authentication in Wireless Sensor Networks. In Proceedings of the 21st International Conference, Advanced Information Networking and Applications Workshops (AINAW ’07), Niagara Falls, ON, Canada, 21–23 May 2007; pp. 438–442. [Google Scholar]
- Wang, D.; Wang, P. Two Birds with One Stone: Two-Factor Authentication with Security beyond Conventional Bound. IEEE Trans. Dependable Secur. Comput. 2016. [Google Scholar] [CrossRef]
- Nyang, D.H.; Song, J.S. Knowledge-Proof Based Versatile Smart Card Verification Protocol. Comput. Commun. Rev. 2000, 30, 39–44. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer Professional Computing Series; Springer: New York, NY, USA; London, UK, 2004. [Google Scholar]
- Dormale, G.; Quisquater, J. Area and Time Trade-Offs for Iterative Modular Division Over GF(2(m)): Novel Algorithm and Implementations on FPGA. Int. J. Electron. 2007, 94, 515–529. [Google Scholar] [CrossRef]
- Wang, D.; He, D.; Wang, P.; Chu, C. Anonymous Two-Factor Authentication in Distributed Systems: Certain goals are Beyond Attainment. IEEE Trans. Depend. Secur. Comput. 2015, 12, 428–442. [Google Scholar] [CrossRef]
- Huang, X.; Chen, X.; Li, J.; Xiang, Y.; Xu, L. Further Observations on Smart-Card-Based Password-Authenticated Key Agreement in Distributed Systems. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1767–1775. [Google Scholar] [CrossRef]
- Wang, D.; Wang, P. On the Anonymity of Two-Factor Authentication Schemes for Wireless Sensor Networks: Attacks, principle and solutions. Comput. Netw. 2014, 73, 41–57. [Google Scholar] [CrossRef]
- Li, X.; Qiu, W.; Zheng, D.; Chen, K.F.; Li, J. Anonymity Enhancement on Robust and Efficient Password-Authenticated key Agreement Using Smart Cards. IEEE Trans. Ind. Electron. 2010, 57, 793–800. [Google Scholar]
- Koblitz, N.; Menezes, A.; Vanstone, S. The State of Elliptic Curve Cryptography. Des. Code Cryptogr. 2000, 19, 173–193. [Google Scholar] [CrossRef]
- Johnson, D.; Menezes, A.; Vanstone, S. The Elliptic Curve Digital Signature Algorithm (ECDSA). Int. J. Inf. Secur. 2001, 1, 36–63. [Google Scholar] [CrossRef]
- Nikooghadam, N.; Bonyadi, M.R.; Malekian, E.; Zakerolhosseini, A. A Protocol for Digital Signature Based on the Elliptic Curve Discrete Logarithm Problem. J. Appl. Sci. 2008, 8, 1919–1925. [Google Scholar]
- Li, L.H.; Tzeng, S.F.; Hwang, M.S. Improvement of Signature Scheme Based on Factoring and Discrete Logarithms. Appl. Math. Comput. 2005, 161, 49–54. [Google Scholar] [CrossRef]
- Rabah, K. Elliptic Curve Elgamal Encryption and Signature Scheme. Inf. Technol. 2005, 4, 299–306. [Google Scholar]
- Chung, Y.F.; Huang, K.H.; Lai, F.; Chen, T.S. ID-Based Digital Signature Scheme on the Elliptic Curve Cryptosystem. Comput. Stand. Interfaces 2007, 29, 601–604. [Google Scholar] [CrossRef]
- Junru, H. The Improved Elliptic Curve Digital Signature Algorithm. In Proceedings of the 2011 International Conference on Electronic & Mechanical Engineering and Information Technology, Harbin, China, 12–14 August 2011; Volume 1, pp. 12–14. [Google Scholar]
- Technical Guideline TR-0311 Elliptic Curve Cryptography Version 2.0. Available online: https://www.bsi.bund.de/SharedDocs/Downloads/EN/BSI/Publications/TechGuidelines/TR03111/BSI-TR-03111_pdf.html (accessed on 20 March 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).