1. Introduction
Recently, many metaheuristic algorithms have been developed by researchers and scientists in different fields. These include Differential Evolution (DE), Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Differential Evolution (DE), Ant Colony Optimization (ACO), Bat Algorithm (BA), Biogeographically Based Optimization (BBO), Firefly Algorithm (FA), Sine Cosine Algorithm (SCA), Robust Optimization (RO), Grey Wolf Optimizer (GWO), Whale Optimizer Algorithm (WOA), Mean Grey Wolf Optimizer (MGWO) and many others. The common goal of these algorithms is to improve quality of solutions, stability and convergence performance. In order to do this, nature-inspired techniques should be equipped with exploration and exploitation.
Exploitation is the convergence ability to the most excellent solution of the problem near a good optimal solution and exploration is the capability of an algorithm to locate whole parts of a problem search space. Finally, the goal of all metaheuristics is to balance the capability of exploration and exploitation in order to search for the best global optimal solution in the search space. The process continues over a number of generations (iterative process) till the solutions are found to be most suitable for the environment.
GWO has recently been developed and is metaheuristics-inspired from the hunting mechanism and leadership hierarchy of grey wolves in nature and has been successfully applied for solving optimizing key values in the cryptography algorithms [
1], feature subset selection [
2], time forecasting [
3], optimal power flow problem [
4], economic dispatch problems [
5], flow shop scheduling problem [
6] and optimal design of double later grids [
7]. Several algorithms have also been developed to improve the convergence performance of GWO that includes parallelized GWO [
8,
9], a hybrid version of GWO with PSO [
10] and binary GWO [
11].
The article is organized as follows. In
Section 1 and
Section 2 in this text, we introduce the introductory and related works of the old and new meta-heuristics.
Section 3 and
Section 4 describe the mathematical model of WOA and MGWO. A new hybrid approach is fully described in
Section 5. The details of parameter settings and tested benchmark functions are presented in
Section 6 and
Section 7. The performance of the new hybrid existing variant is verified in
Section 8.
Section 9 describes the analysis of the meta-heuristics. In order to show the performance of the developed variant, twenty three standard benchmarks, four bio-medical sciences, Welded Beam Design, Pressure Vessel Design problems are studied in
Section 10,
Section 11,
Section 12 and
Section 13. Finally, some conclusions are derived in
Section 14.
2. Related Works
Metaheuristic global optimization techniques are stochastic variants that have become the most popular solutions for solving real life applications and global optimization functions in the last few decades; they have the strong robustness, flexibility, characteristics of simplicity, and so on. Some of the most famous of these algorithms are BA [
12], GA [
13], Harmony Search (HS) [
14], ACO [
15], Cuckoo Search (CS) [
16], Bacterial Foraging Optimization (BFO) [
17], PSO [
18], Artificial Bee Colony (ABC) [
19], Black Hole (BH) [
20], One Half Personal Best Position Particle Swarm Optimizations (OHGBPPSO) [
21], Half Mean Particle Swarm Optimization algorithm (HMPSO) [
22], Personal Best Position Particle Swarm Optimization (PBPPSO) [
23], Hybrid Particle Swarm Optimization (HPSO) [
24], Hybrid MGBPSO-GSA [
25] and MGWO [
26], Gravitational Search Algorithm (GSA) [
27], Artificial Neural Network (ANN) [
28], SCA [
29], Adaptive Group Search Optimization (AGSO) [
30], Ant Lion Optimizer (ALO) [
31], Biogeography Based Optimization (BBO) [
32], Moth Flame Optimizer (MFO) [
33], Krill Herd Algorithm (KHA) [
34], Grasshopper Optimization Algorithm (GOA) [
35], Multi-Verse Optimizer (MVO) [
36], Black-Hole-Based Optimization (BHBO) [
37], Dragonfly Algorithm (DA) [
38], HPSOGWO [
39], MOSCA [
40] and so forth.
Bentouati et al. [
41] presented a new power system planning strategy by combining Pattern Search algorithm (PS) with WOA. The existing variant has been carried out on the IEEE 30-bus test system considering several objective functions, such as voltage profile improvement, generating fuel cost, emission reduction and minimization of total power losses which were also verified. The obtained numerical and statistical solutions are verified with recently published population-based metaheuristic variants. Simulation solutions clearly conceal the speed and effectiveness of the presented approach for solving the OPF function.
A new hybrid approach has been developed by [
42] called Hybrid GWOSCA which is a combination of GWO used for exploitation phase and SCA for the exploration phase in an uncertain environment. The position and convergence performance of the grey wolf (alpha) is improved using position update equations of SCA. Experimental solutions obtained with existing approaches are verified with other metaheuristics approaches. On the basis of the numerical and statistical experimental results, the proposed existing hybrid algorithm can highly be effective in solving standard test functions and recent real life problems with or without constrained and unknown search space.
Tawhid and Ali [
43] presented a new hybrid approach between the GWO and the GA variant in order to minimize a simplified model of the energy function of the molecule. This research used three different procedures: (i) they used the GWO variant to balance between the exploitation and the exploration process in the proposed variant; (ii) they used the dimensionality reduction and the population partitioning processes by dividing the population into sub-populations and using the arithmetical crossover operator in each sub-population in order to increase the diversity of the search in the algorithm; (iii) they used the GA operator in the whole population in order to refrain from premature convergence and trapping in local minima. The performance of the new hybrid algorithm has been tested on several standard test functions and performance of the algorithm has been compared with different metaheuristics. Experimental solutions prove that the hybrid approach is promising and competent for searching the near global optimal minimum value of the molecular energy function faster than other meta-heuristics.
Emary et al. [
44] used three modern techniques, namely Antlion Optimizer, MFO and GWO in domain of machine learning for feature selection. Solutions on a set of standard machine learning data using a set of assessment indicators proved advances in optimization approach performance when using variational repeated periods of declined exploration rates over using systematically decreased exploration rates.
Emary et al. [
45] proposed a variant of the recently introduced WOA based on adaptive switching of random walk per individual search agent. The basic approach stochastically switches amid the two random walks at each iteration regardless of the search member performance and regardless of the fitness of terrain around it and in which a newly existing approach called Adaptive Whale Optimization Algorithm (AWOA), an adaptive switching amid the two random walks is recommended based on the agent’s performance. The proposed AWOA was benchmarked using 29 standard test functions with uni-modal, multi-modal, and composite test functions. Performance over such functions proves that the capability of the proposed variant outperforms the original WOA. The performance has been tested on the 29 standard functions and its convergence performance over such functions proves the capability of the newly existing approach to outperform the basic Whale Optimizer Algorithm.
In this paper, we propose a new hybrid whale optimizer algorithm and mean grey wolf optimizer algorithm in order to solve the standard benchmark, XOR, Baloon, Iris, Breast Cancer, Welded Beam Design and Pressure Vessel Design functions. We call the proposed algorithm Whale Optimizer Algorithm and Mean Grey Wolf Optimizer (HAGWO). The proposed HAGWO algorithm is based on two procedures. In the first procedure, we used the spiral equation in GWO algorithm for balance between the exploitation and the exploration process in the new hybrid approach. In the second procedure, we also apply this equation in the whole population in order to refrain from the premature convergence and trapping in local minima. The partitioning idea can improve the diversity search of the proposed variant. The combination between these two procedures accelerates the search and helps the algorithm to reach the optimal or near optimal solution in reasonable time.
3. Whale Optimizer Algorithm (WOA)
Mirjalili and Lewis [
46] proposed a new nature-inspired technique, namely, Whale Optimizer Algorithm (WOA), which mimics the social behavior of humpback whales. The algorithm is inspired by the bubble-net hunting strategy.
The mathematical model for WOA is given as follows:
Encircling prey: Whale encircles the small fishes (prey) then modifies its position towards the global optimum solution over the course of increasing number of generation from start to a maximum number of generations.
The coefficient
and
are calculated as follows:
where
is the current time,
and
are coefficient vectors,
the position vector of the best solution obtained so far,
the position vector,
is random vector in [0, 1], “
” the absolute value and an element by element multiplication.
Bubble-net attacking method: In order to reach a mathematical equation for the bubble net behavior of whales, two separate methods are as follows:
where and indicates the distance of the ith whale to the prey, is a constant for defining the shape of the logarithmic spiral, is a random number in [−1, 1].
In addition, if probability is 50%, then positions of whales are calculated as follows:
where
is random number in [0, 1]. In addition to the bubble-net method, the humpback whales search for prey randomly.
In this mechanism, the whales search for small fishes (prey) randomly and change their positions according the position of other search agents.
In order to force the whale to move away from the reference whale, we use the or .
It is mathematically calculated as follows:
where
is a random position vector (a random whale) chosen from the current population.
4. Mean Grey Wolf Optimizer (MGWO)
A modified variant of Grey Wolf Optimization algorithm, namely Mean Grey Wolf Optimization algorithm has been developed by Singh and Singh [
26] by modifying the position updated (encircling behavior) equations of Grey Wolf Optimization algorithm. This variant has been developed for the purpose of improving the exploration and exploitation performance of the basic GWO algorithm. It is also inspired by the hunting mechanism and leadership hierarchy of grey wolves in nature.
The Mean Grey Wolf Optimization (MGWO) approach is outlined as:
The encircling behavior of each agent of the crowd is calculated by the following mathematical equations:
The vectors
and
are formulate as below:
where
indicates the current iteration,
and
are coefficient vectors,
are random vectors in [0, 1],
is the vector of the prey, and
indicates the position vector of a grey wolf.
Hunting: In order to mathematically simulate hunting behavior, we suppose that the alpha, beta and delta have better knowledge about the potential location of the prey. The following equations are developed in this regard.
Search for prey and attacking prey: The is random value in the gap . When random value the wolves are forced to attack the prey. Searching for prey is the exploration ability and attacking the prey is the exploitation ability. The arbitrary values of are utilized to force the search to move away from the prey.
When , the members of the population are enforced to diverge from the prey.
5. Hybrid Algorithm
Several scientists/researchers have been developing several hybrid nature-inspired approaches for improving the exploration and exploitation performance of existing algorithms. According to Talbi [
47], two variants can be hybridized in low-level or high-level with relay or coevolutionary techniques as heterogeneous or homogeneous.
In this text, we hybridize Whale Optimizer Algorithm with Mean Grey Wolf Optimizer algorithm using low-level coevolutionary mixed hybrid. The hybrid is low-level because we merge the functionality of both approaches. It is co-evolutionary because we do not use both variant one after another. In other words, they run in parallel. It is mixed because there are two different approaches that are involved to generate a final optimal solution of the test benchmark and real life problems. On behalf of this modification, we improve the capability of exploitation in Mean Grey Wolf Optimizer with the capability of exploration in Whale Optimizer Algorithm to show the strengths of both approaches.
Under this research, the Whale Optimizer Algorithm is used for the exploration phase as it uses logarithmic spiral problems, so it covers broader areas in uncertain search spaces. Since both of the variants are randomization approaches, we use unknown term search space during the computation over the course of iteration from starting to maximum iteration limit. Exploration phase means the ability of the variant to try out large numbers of feasible solutions. Position of grey wolf that is liable for finding the global optimum solution of the problem is replaced with the position of whale that is equivalent to position of grey wolf but highly efficient to move a solution towards an optimal one. Whale Optimizer Algorithm directs the wolves towards an optimal value and reduces computational time. We know that that Grey Wolf Optimizer is a recognized approach that exploits the best possible solution from its unknown search space. Therefore, mixture of best characteristic (exploitation with Mean Grey Wolf Optimizer and exploration with Whale Optimizer Algorithm) guarantees to obtain best possible global optimal solution of the real life and standard problems that also avoid local stagnation or local optima problems. Hybrid WOA-MGWO merges the best strength of both Mean Grey Wolf Optimizer in exploitation and Whale Optimizer Algorithm in the exploration phase towards the targeted optimum solution.
Mathematical model for HAGWO is given as follows:
In HAGWO variant, the position of alpha, beta and delta have been updated using spiral updating equation of whale optimizer algorithm for the purpose of improving the convergence performance of MGWO algorithm. The rest of the operations of Mean GWO and WOA algorithm are the same. The following spiral and hunting position update equations are developed in this regard.
where
and indicates the distance of the
ith whale to the prey,
is a constant for defining the shape of the logarithmic spiral,
,
and
are position of three best search agents,
is a mean and
is a random number in [−1, 1].
| Pseudo Code of HAGWO |
| Initialize the population |
| Find the fitness of each search member |
| is the best search member |
| While ( max. number of generations) |
| For every search member |
| Update and |
| if () |
| if () |
| update the position of the current search member by the Equation (1) |
| else if () |
| select a random search member () |
| update the position of the current search member by the Equation (8) |
| end if |
| else if () |
| update the position of the present search member by using Equations (16) and (17) |
| end if |
| end for |
| Find the fitness of all search members |
| Update ,, and |
|
| end while |
| return |
6. Parameter Setting
Computational Experiments were performed to fine tune the values of various parameters for its best performance. For that purpose, all measured values of parameters viz. number of search agents ~20 and number of generations ~[5, 5000], were tested.
7. Test Problems
It is often found that the evaluation of a newly developed approach is evaluated only on a standard benchmark function. However, in this article we consider a test of Unimodal, Multimodal and fixed dimension multimodal functions with varying difficulty levels and problem sizes. The capability of the newly hybrid variant, Particle Swarm Optimization, Grey Wolf Optimizer, Whale Optimizer algorithm and Mean Grey Wolf Optimizer has been verified on these three types of function sets. The exact details of these test problems are given in
Table 1,
Table 2 and
Table 3.
8. The Performance of the HAGWO Algorithm
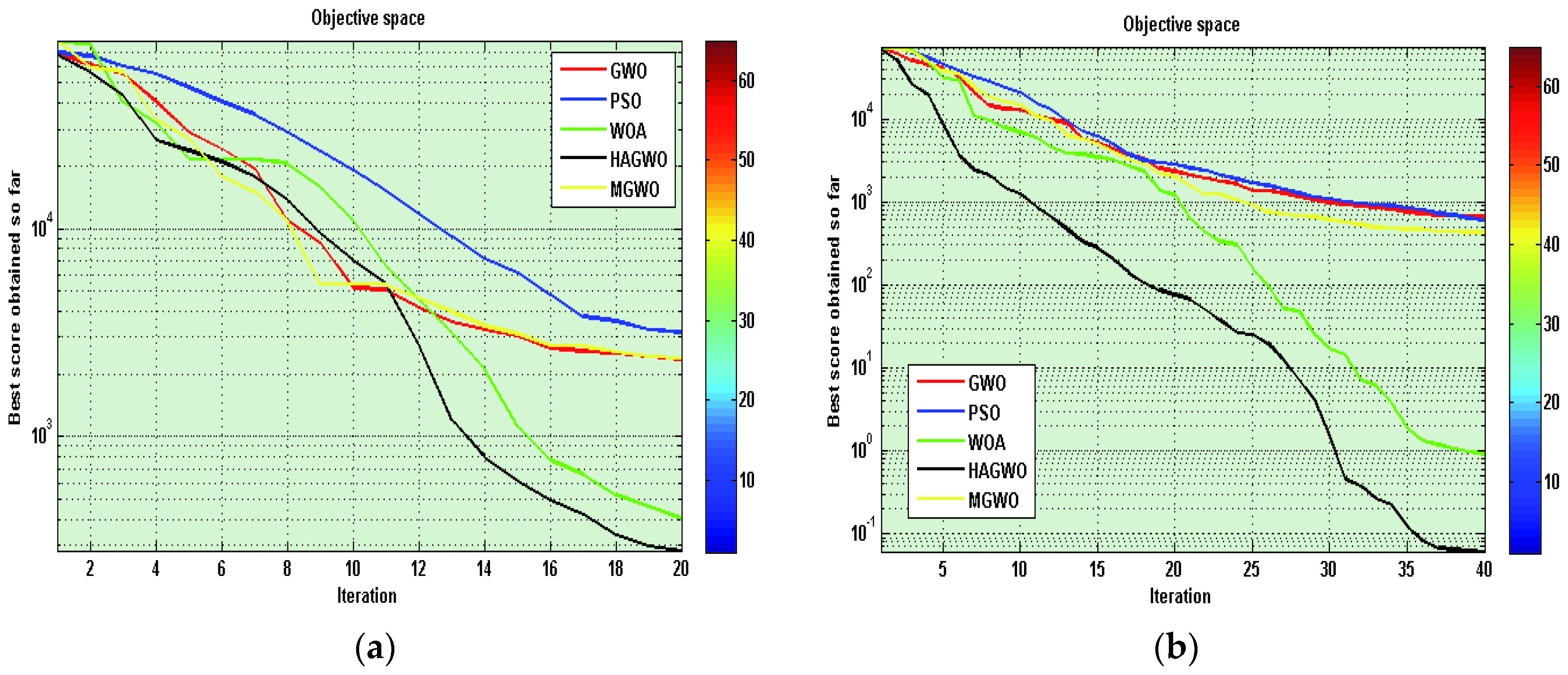
The performance of several population-based metaheuristics has been verify with the newly existing variant in order to test the stability, convergence rate and computational accuracy on the number of iterations in
Figure 1. We have taken the similar parameter constants (in
Section 6) for the entire variants to make a valid comparison. We illustrate the results in
Figure 1 by plotting the worst optimal values of problem values against the number of iterations for a simplified model of the molecule with a distinct size from 20 to 100 dimensions.
The figure shows that the standard test function values quickly decrease as the number of generations increase for newly existing variant solutions than those of the other metaheuristics. In
Figure 1, HAGWO, PSO, GWO, WOA and MGWO variants suffer from slow convergence and get stuck in the partitioning procedure; nevertheless, many local minima and invoking the Mean Grey Wolf variant in the newly existing hybrid algorithm avoid trapping in local minima and accelerate the search.
9. Analysis
The capability of improved metaheuristic has been tested on 29 benchmark functions. We have chosen these benchmark functions to be able to compare our numerical and statistical results to those of the recently nature-inspired techniques. These tested functions are shown in
Table 1,
Table 2 and
Table 3, where
dim represents the dimension of the objective function,
Range boundary of the objective function’s search space and
is the optimum.
The HAGWO variant was run 20 times on each standard function. The numerical and statistical solutions (standard deviation and average) are reported in
Table 1,
Table 2,
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8 and
Table 9. For verifying the solutions, the HAGWO variant is compared with PSO, GWO, WOA and MGWO algorithms. In WOA, MGWO and the newly developed approach HAGWO, the balance amid the local and global exploration abilities is mainly controlled by the mean. The numerical and statistical experimental solutions have been performed to illustrate this. By best parameter settings, it was found that the best global optimal solutions lie within a reasonable number of generations. A number of criteria have been used to evaluate the capability of GWO, PSO, WOA, MGWO with HAGWO. The mean and standard deviation statistical values are used to evaluate the reliability. The average computational time of the successful runs and the average number of problem evaluations of successful runs, are applied to estimate the cost of the standard problem.
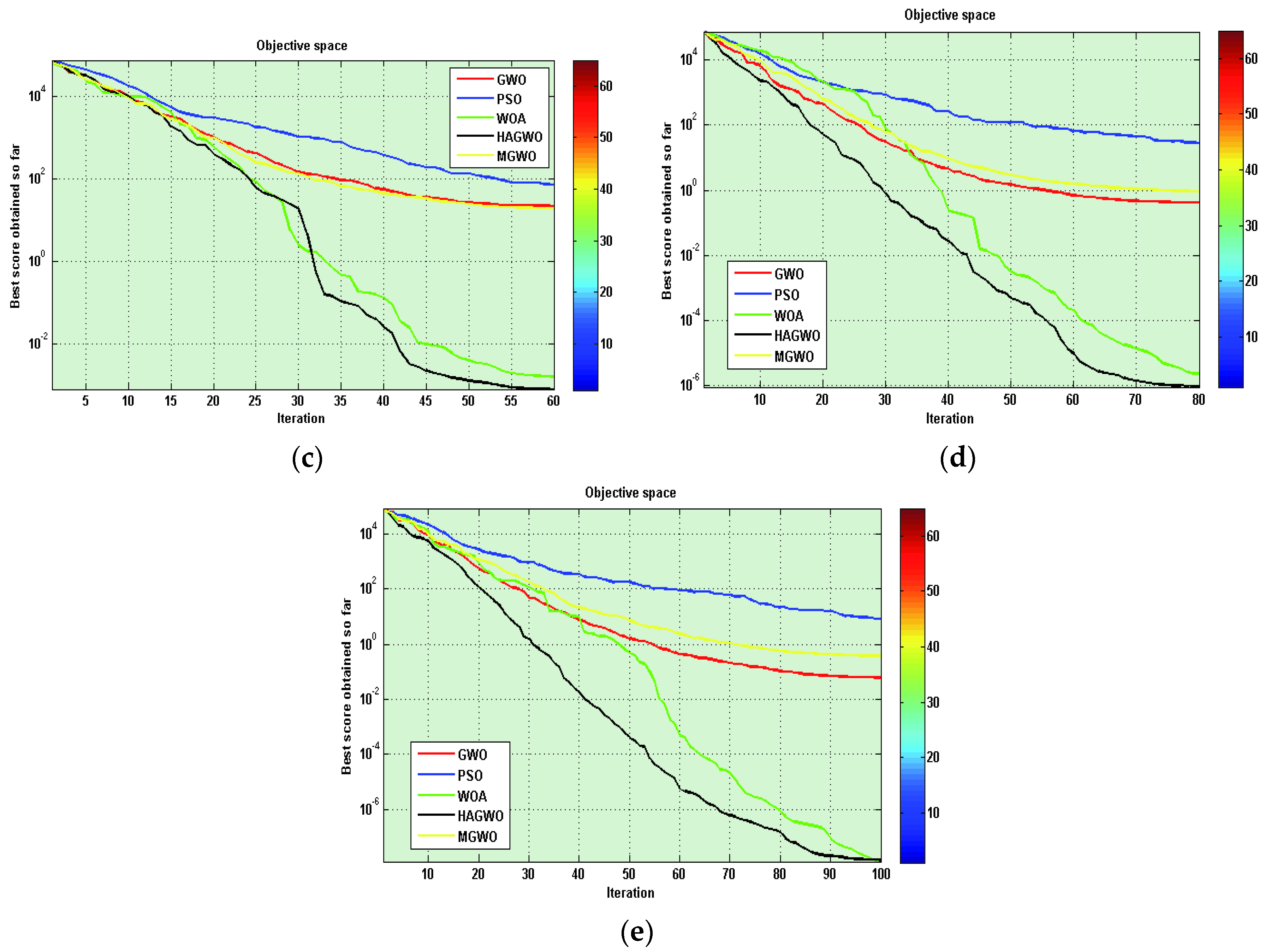
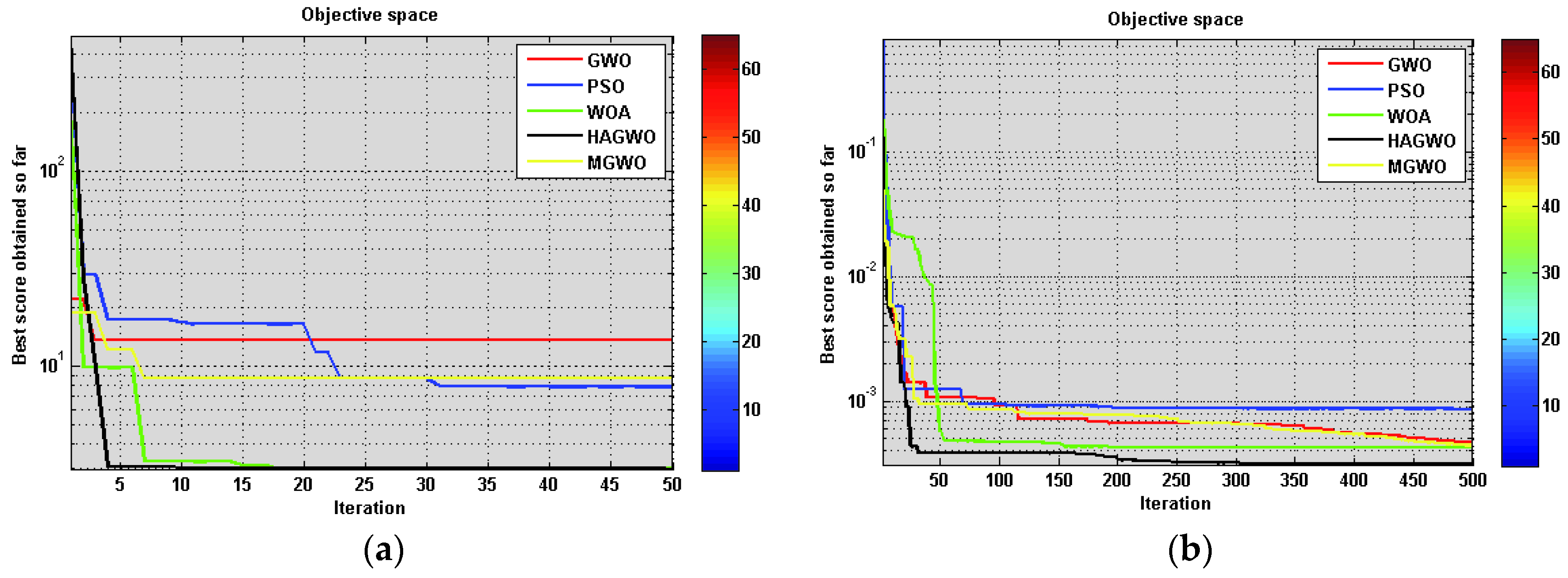
For Unimodal benchmark functions, the quality of the global optimal solution obtained is considered by the maximum, minimum, standard deviation and mean of the objective function values out of twenty runs. This is shown in
Table 4 and
Table 5 and convergence performance of PSO, GWO, WOA, MGWO and HAGWO algorithms are shown in
Figure 2.
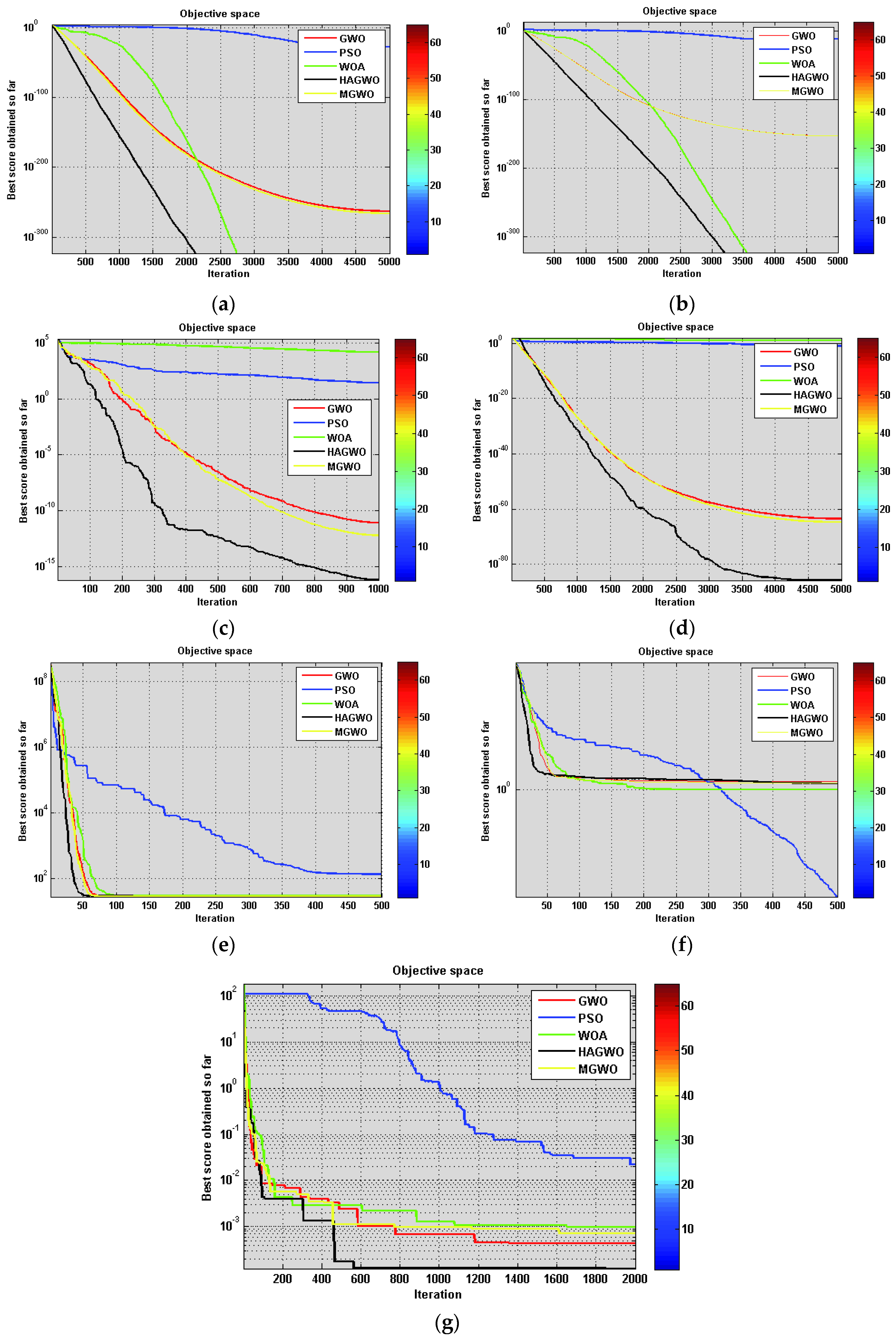
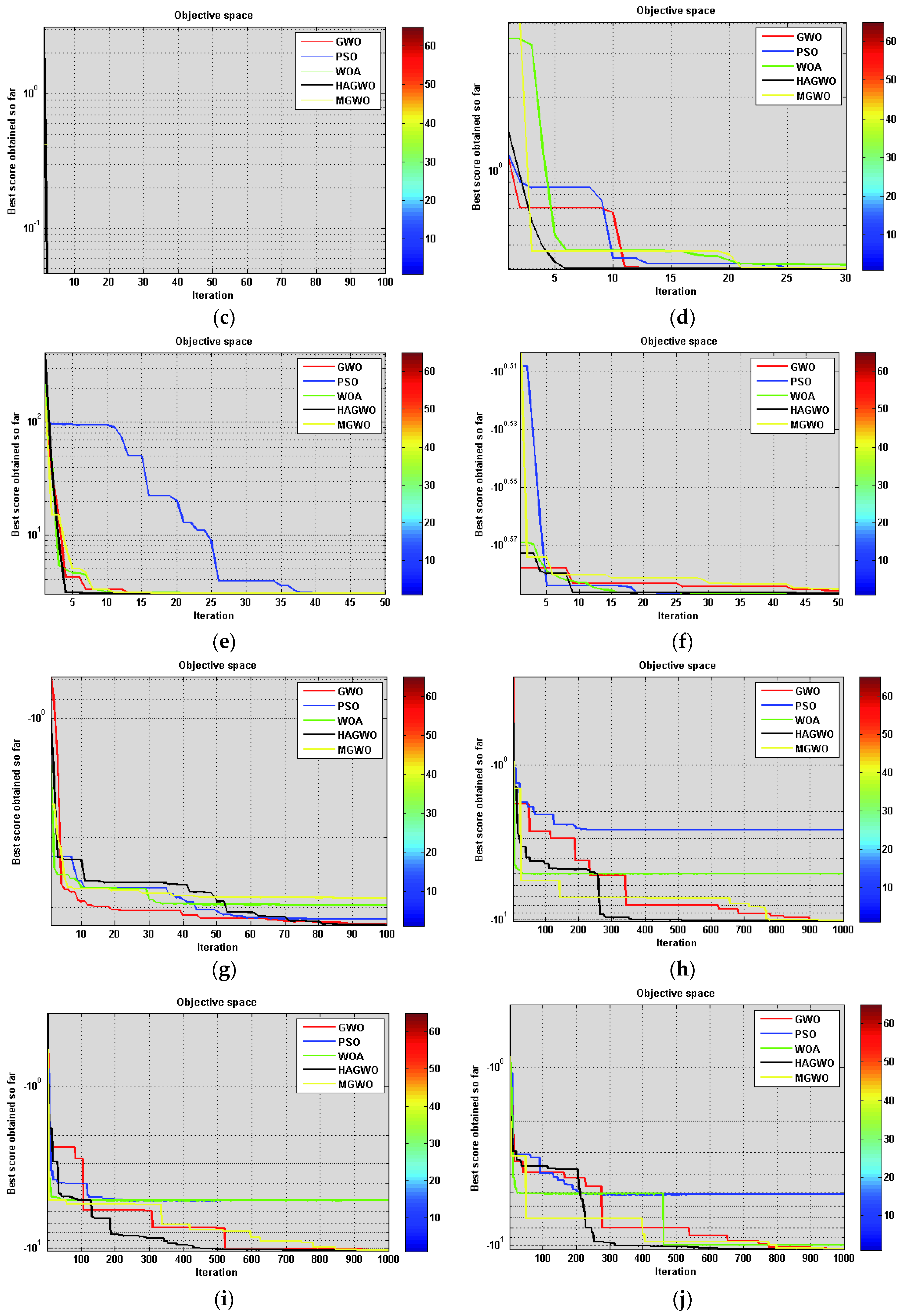
Furthermore, the performance of the algorithms in solving multimodal benchmark functions is shown in
Table 6,
Table 7 and the convergence curve is shown in
Figure 3, respectively.
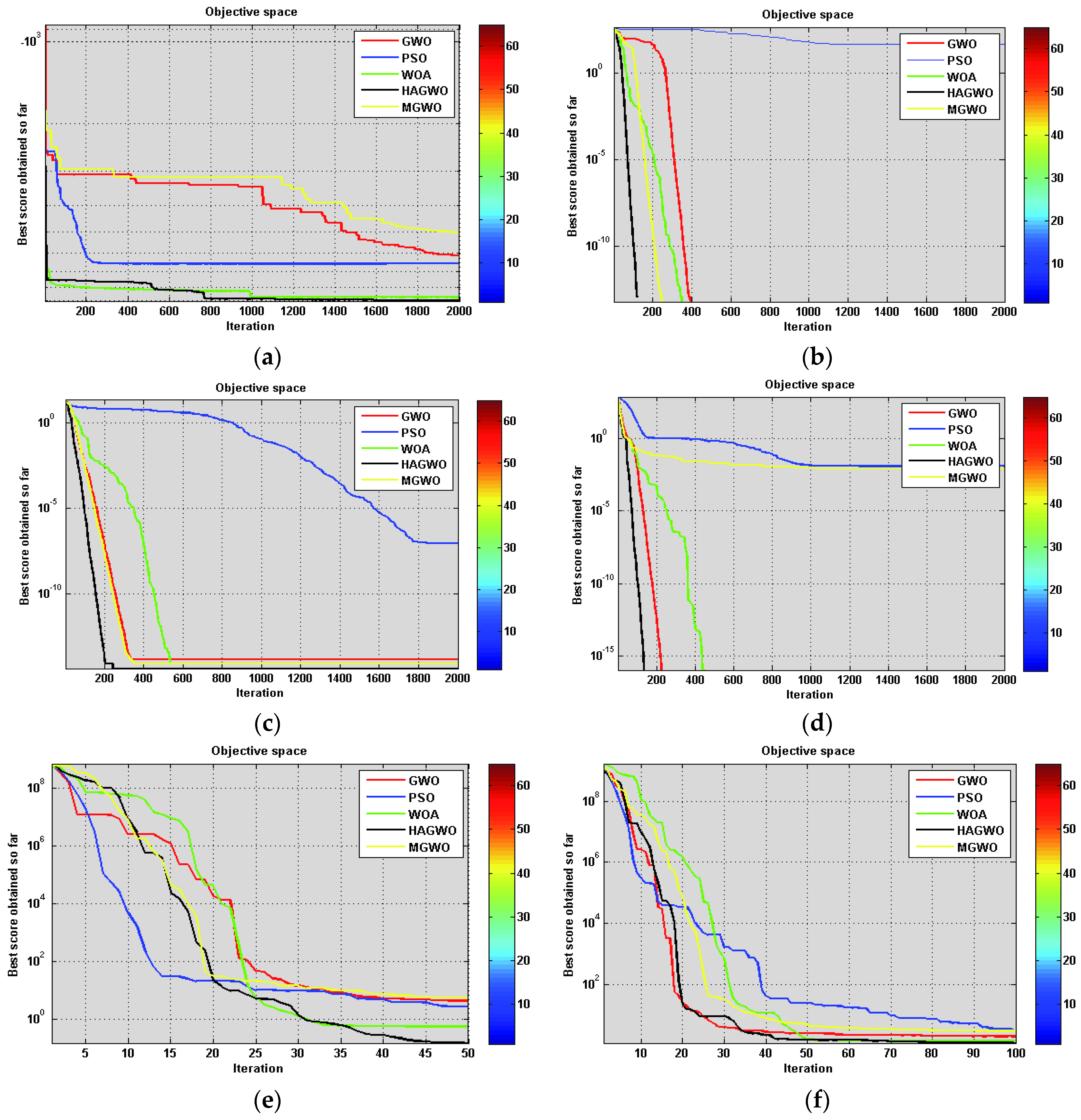
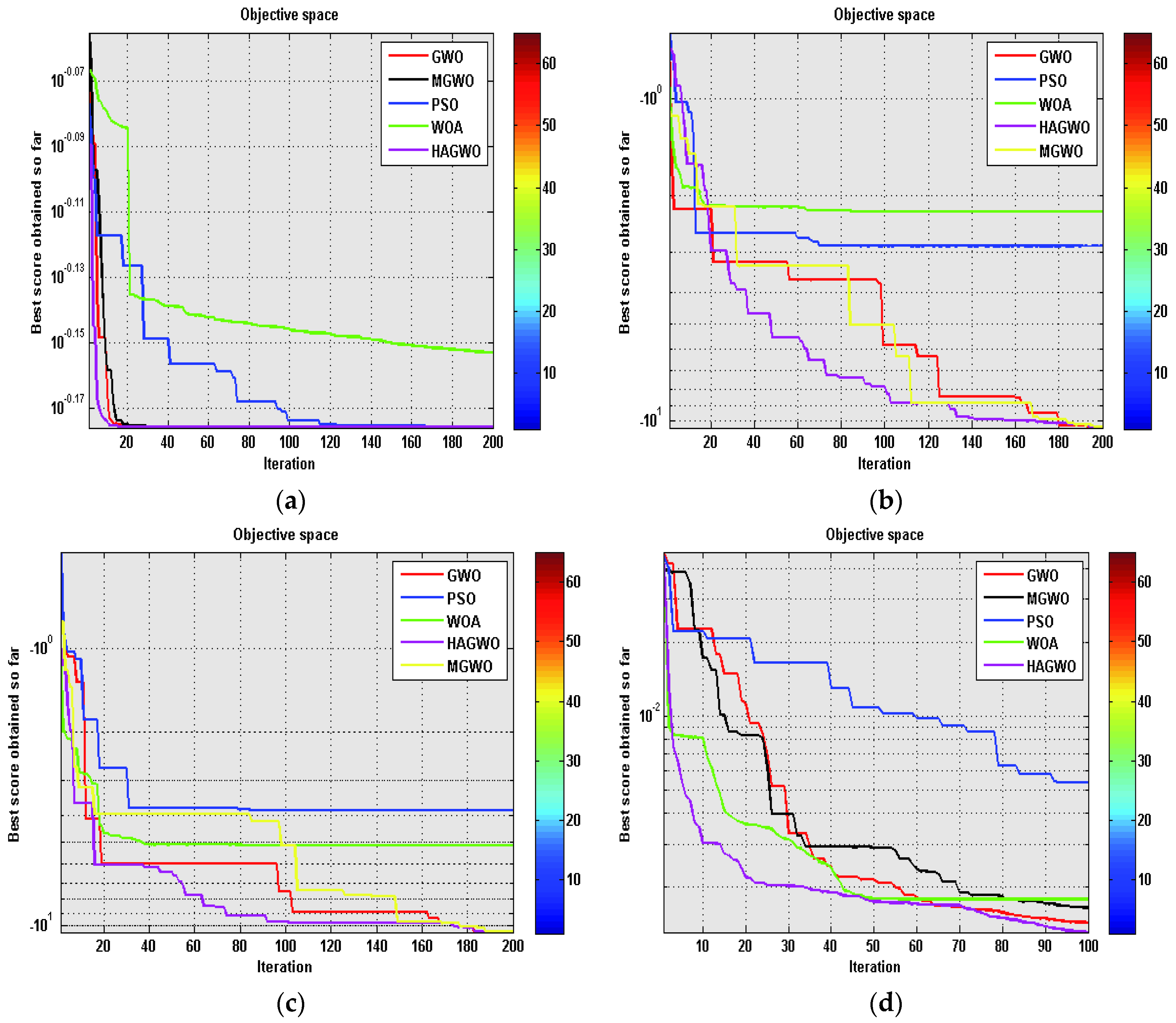
Furthermore, the statistical and numerical global optimal solutions using PSO, GWO, WOA, MGWO and HAGWO variants on fixed dimensional multimodal benchmark functions are given in
Table 8 and
Table 9. The performance of algorithms is shown in
Figure 4.
The performance of the newly existing variant has been tested on the standard, bio-medical and engineering real life functions in terms of minimum objective function values, maximum objective function values, mean and standard deviations (
Table 4,
Table 5,
Table 6,
Table 7,
Table 8 and
Table 9).
Here, the maximum and minimum values represent the best possible cost of the functions in the number of iterations. On the other sides, the mean and standard deviation statistical values are used to evaluate the reliability. Furthermore, the convergence graphs of the functions represent the convergence performance of the algorithms.
Summing up,
Table 4,
Table 6 and
Table 8 show that the newly hybrid approach provides the best possible optimal values of the functions in terms of minimum and maximum values of the functions as compared to others meta-heuristics, and
Table 5,
Table 7 and
Table 9 illustrate that the hybrid approach also gives superior quality of standard and mean values of the functions which outperforms others. At the end, the convergence of graphs (
Figure 2,
Figure 3 and
Figure 4) proves that, the existing approach finds the best possible optimal values of the standard functions in the least number of iterations in comparison to others.
10. Experiments and Discussion on the Results
Performance of the proposed variant was tested on a set of 23 standard functions (Unimodal, Multimodal and Fixed dimension multimodal). These functions were chosen as the test functions. Computer programs for solving the numerical problems using PSO, WOA, GWO, MGWO and HAGWO pseudo code were coded in MATLAB R2013a and implemented on Intel HD Graphics, i5 Processor 430 M, 15.6” 3GB Memory, 320 GB HDD, 16.9 HD LCD and Pentium-Intel Core (TM). The maximum number of generations~5000; all this parameter setting is used to test the ability of meta-heuristics.
As per the numerical results of
Table 4, improved hybrid variant is capable to give very competitive global optimal solutions. This variant outperforms all other metaheuristics in all unimodal functions. It may be noted that these test problems are suitable for benchmarking exploitation. These numerical and statistical global optimal solutions indicate that the improved hybrid variant is more reliable in giving superior quality of solutions in terms of exploiting the global optimum.
While observing
Table 6, the superiority of the result obtained is measured by the minimum and maximum objective function value, average and standard deviation and the objective function values out of 20 runs. It can be seen that HAGWO gives a better quality of results as compared to other metaheuristics. Thus, for the multimodal benchmark functions, HAGWO outperforms PSO, GWO, WOA, MGWO with respect to efficiency, reliability, cost and robustness.
Fixed-dimension multimodal functions have many local optima with the number growing exponentially with dimension. This makes them fitting for benchmarking the exploration capacity of a variant. As per the results shown in
Table 8, the HAGWO variant is competent to provide very competitive solutions to these problems as well. This variant outperforms PSO, WOA, GWO and MGWO on the majority of these test functions. Hence, HAGWO variant has merit in terms of exploration.
A number of criteria have been applied to find out the performance of PSO, GWO, WOA, MGWO and the new hybrid approach of GWO variants. The mean and standard deviation statistical values are used to evaluate the reliability in
Table 5,
Table 7 and
Table 9. The average computational time of the successful runs and the average number of function evaluations of successful runs, are applied to estimate the cost of the standard function.
In
Figure 2,
Figure 3 and
Figure 4, the convergence performance of PSO, GWO, WOA, MGWO and HAGWO variants in solving unimodal benchmark functions is compared; obtained convergence solutions prove that the HAGWO variant is more able to find the best optimal solution in minimum number of iterations. Hence, the HAGWO variant avoids premature convergence of the search process to local optimal points and provides superior exploration of the search course.
To sum up, all simulation solutions assert that the new hybrid existing approach is very helpful in improving the efficiency of the Whale Optimizer Algorithm and Mean Grey Wolf Optimizer Algorithm in terms of result quality as well as computational efforts.
11. Bio-Medical Science Real Life Applications
In this section, four dataset problems: (i) Iris (ii) XOR (iii) Baloon and (iv) Breast Cancer are employed (Mirjalili, S. [
48]). These real-life problems have been solved using the new hybrid variant and compared with PSO, WOA, GWO and MGWO meta-heuristics. Different parameter settings have been used for running the code of meta-heuristics and these parameter settings are described in
Appendix Table A1. The capability of the variants has been compared in terms of minimum objective function value, maximum objective function value, average, standard deviation, classification rate and convergence rate of the algorithms in
Table 10. All these real-life applications are discussed step by step in this section:
The performance of the metaheuristics has been tested on different parameter settings as shown in
Appendix Table A2. The experimental numerical and statistical results of HAGWO, PSO, WOA, GWO and MGWO on these datasets have been given in
Table 10 and convergence performance of the algorithms is shown
Figure 5. In
Table 10, we show that HAGWO algorithm gives superior quality of numerical and statistical solutions in comparison to other meta-heuristics. The results of the HAGWO algorithm indicate that it has the highest capability to avoid the local optima and is considerably superior to other algorithms like PSO, WOA, GWO and MGWO.
Secondly, the performance of meta-heuristics has been compared in terms of average, standard deviation classification rate (in
Table 10) and convergence rate (in
Figure 5). The low average and standard deviation shows the superior local optima avoidance of the algorithm. On the basis of the obtained solutions, we have concluded that the new hybrid algorithm gives highly competitive results as compared to other metaheuristics and the convergence graph shows that HAGWO gives better solutions than PSO, WOA, GWO and MGWO variants.
12. Welded Beam Design
This function is designed for the minimum cost subject to constraints on side constraints, buckling load on the bar (
), shear stress (
), end deflection of the beam (
) and bending stress in the beam (
). There are four design variables:
and
. The WBD function can be mathematical formulated as below [
49]:
where
During last few years, many scientists and researchers have used several types of nature-inspired metaheuristics to locate the best optimal results of the Welded Beam Design (WBD) problem in the literature, such as Genetic Algorithm (GA) [
50,
51,
52], Unified Particle Swarm Optimization (UPSO) [
53], Artificial Bee Colony algorithm (ABC) [
54], Co-evolutionary Differential Evolution (CDE) [
55], Co-evolutionary Particle Swarm Optimization (CPSO) [
56], Harmony Search algorithm (IHS) [
57], Moth-Flame Optimization algorithm (MFO) [
33], Adaptive Firefly Algorithm (AFA) [
58], Charged System Search (CSS) [
59] and Lightning Search Algorithm-Simplex Method (LSA-SM) [
49].
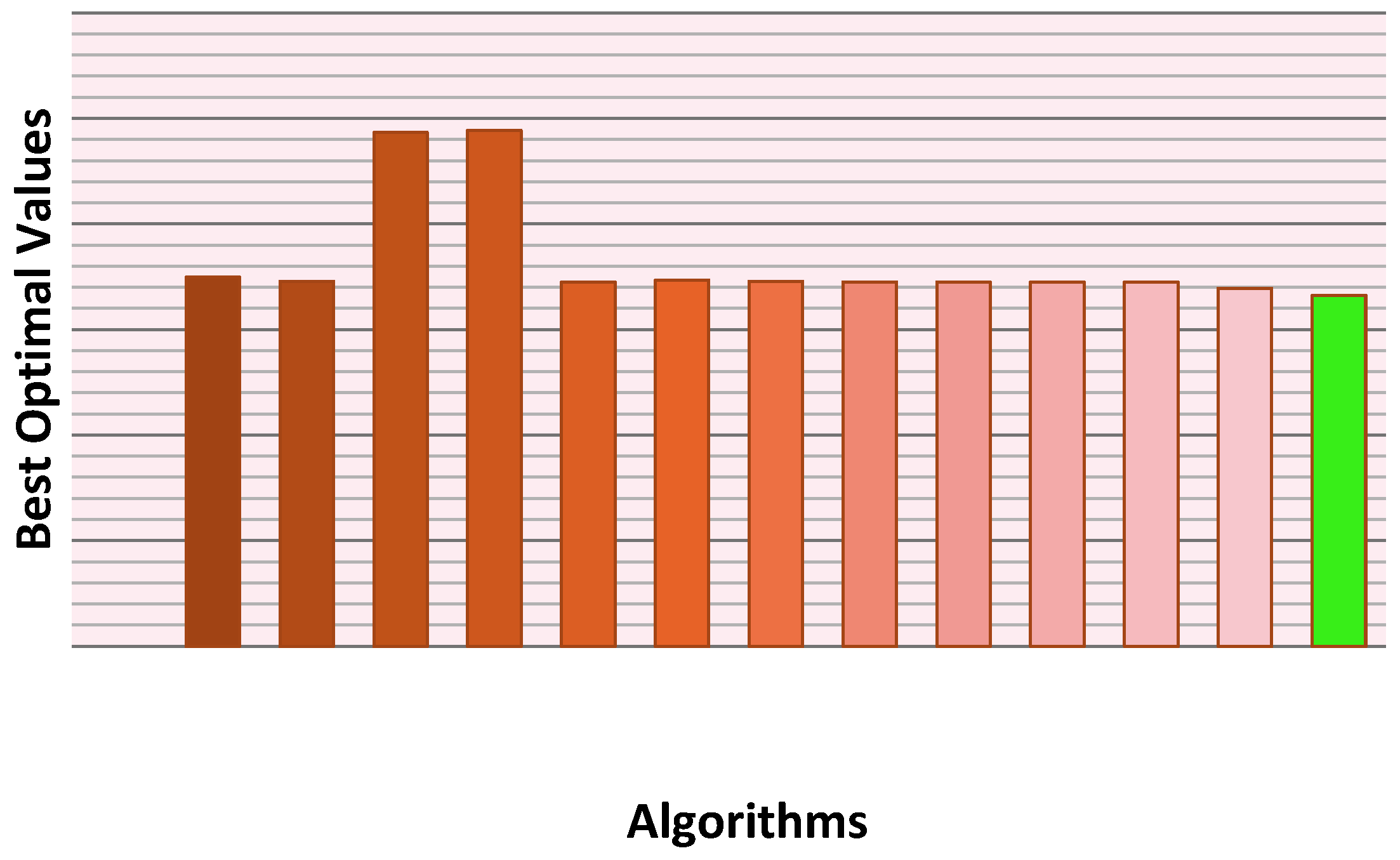
In
Table 11 and
Figure 6, we compare the optimal solutions of the new hybrid approach (HAGWO) and other metaheuristics found in the literature, where the newly existing variant achieves better quality of solutions that are better than several latest metaheuristics with minimum cost of 1.661258 for the welded beam design problem.
13. Pressure Vessel Design
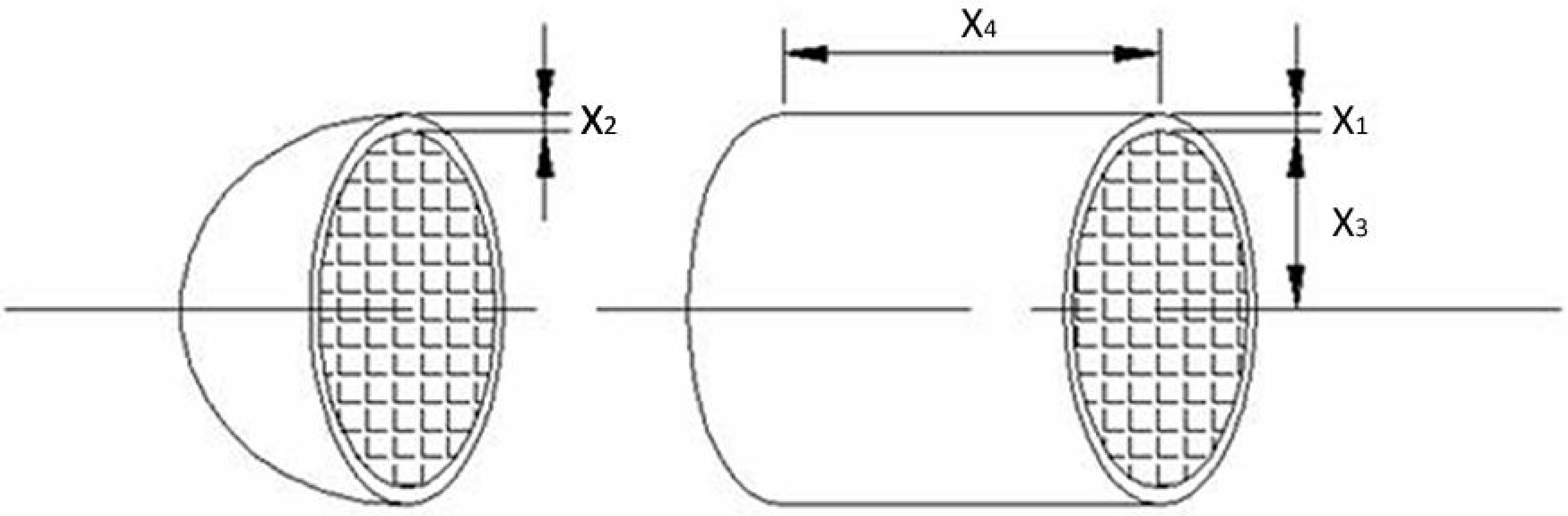
This problem is a cylindrical vessel whose ends are capped by a hemispherical head as shown in
Figure 7. The main objective is to minimize the total cost. The pressure vessel design problem can be mathematically formulated as below [
49]:
where
is the thickness of the shell,
is thickness of the head,
is inner radius and
length of the cylindrical section of the vessel [
57].
During the last few decades, several researchers have used different types of metaheuristics to find the best possible optimal solutions of the Pressure Vessel Design Problem in the literature such as Genetic Algorithm (GA) [
50,
51,
52], Artificial Bee Colony algorithm (ABC) [
54], Co-evolutionary Differential Evolution (CDE) [
55], Co-evolutionary Particle Swarm Optimization (CPSO) [
56], Improved Harmony Search algorithm (IHS) [
57], Moth-Flame Optimization algorithm (MFO) [
33], Adaptive Firefly Algorithm (AFA) [
58], Bat Algorithm (BA) [
60], Cuckoo Search algorithm (CS) [
61], Evolution Strategies (ES) [
62], Ant Colony Optimization (ACO) [
63], Teaching-Learning-Based Optimization (TLBO) [
64] and Lightning Search Algorithm-Simplex Method (LSA-SM) [
49].
The experimental solutions of the different metaheuristics pressure vessel design are represented in
Table 12. It can be seen that the best optimal value of the pressure vessel design problem by HAGWO is 5924.2536. Hence HAGWO algorithm provides the superior quality of the solutions in comparison to others.
14. Conclusions and Future Work
In the current study, we have developed an improved hybrid algorithm utilizing the strengths of Whale Optimizer Algorithm and Grey Wolf Optimizer algorithm. The global optimal solution quality of benchmark function has been improved with Hybrid WOA–MGWO as it extracts quality characteristics of both WOA and MGWO. Whale Optimizer Algorithm (WOA) is used for the exploration phase as it uses a spiral function, hence, it covers a broader area in an uncertain search space. Hence, Whale Optimizer algorithm directs the members more rapidly towards global optimal value and reduces computational time. Twenty three benchmark functions are utilized to test the quality of the hybrid variant compared to PSO, WOA, GWO and MGWO. The experimental numerical and statistical solutions have shown that an improved hybrid strategy is most suitable for giving the superior quality of solutions with a minimum number of iterations, therefore, the HAGWO variant avoids premature convergence of the search process to local optima and gives superior exploration due to the search procedure.
This article also considers solving bio-medical science dataset (XOR, Baloon, Iris, and Breast Cancer) and engineering (Welded Beam Design and Pressure Vessel Design) problems. The solutions of these problems indicate that the proposed approach is applicable to solve challenging problems with unknown search spaces.
Future work will focus on two parts: (i) Structural Damage Detection, composite functions, aircraft wings, feature selection, the gear train design problem, bionic car problem, cantilever beam, and mechanical engineering functions; and (ii) Developing new variants based on nature-inspired algorithms for these tasks. Finally, we expect that this work will encourage young researchers who are working on recent evolutionary metaheuristics concepts.