An Algorithm Based on GSVD for Image Encryption
Abstract
:1. Introduction
2. Basic Theory
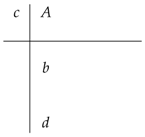

- if ,
- if
- if and repeat the step,
3. Derivation of the Proposed Method
4. Algebraic Order and Error Analysis
Absolute Stability Analysis of the New Embedded Pair
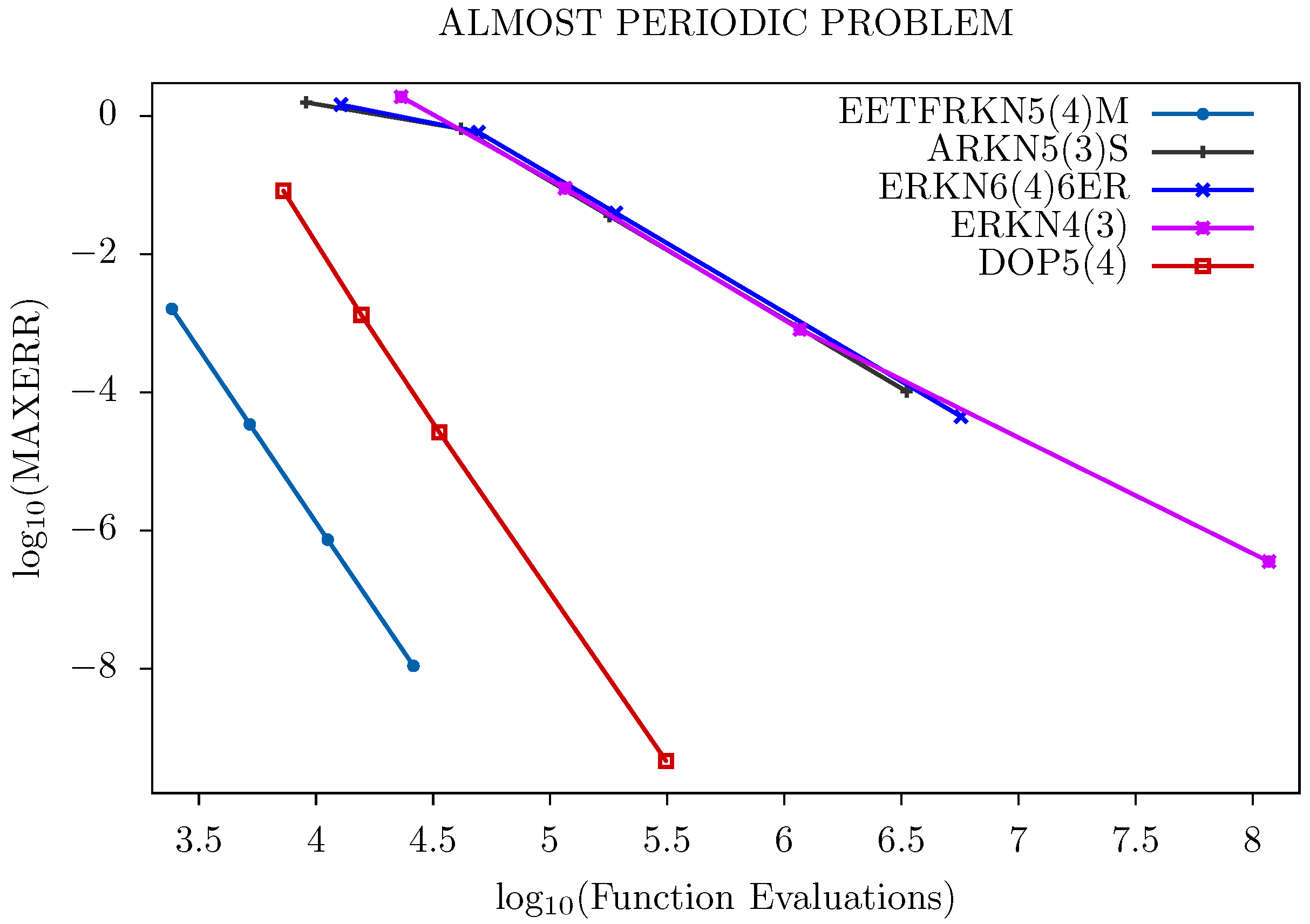
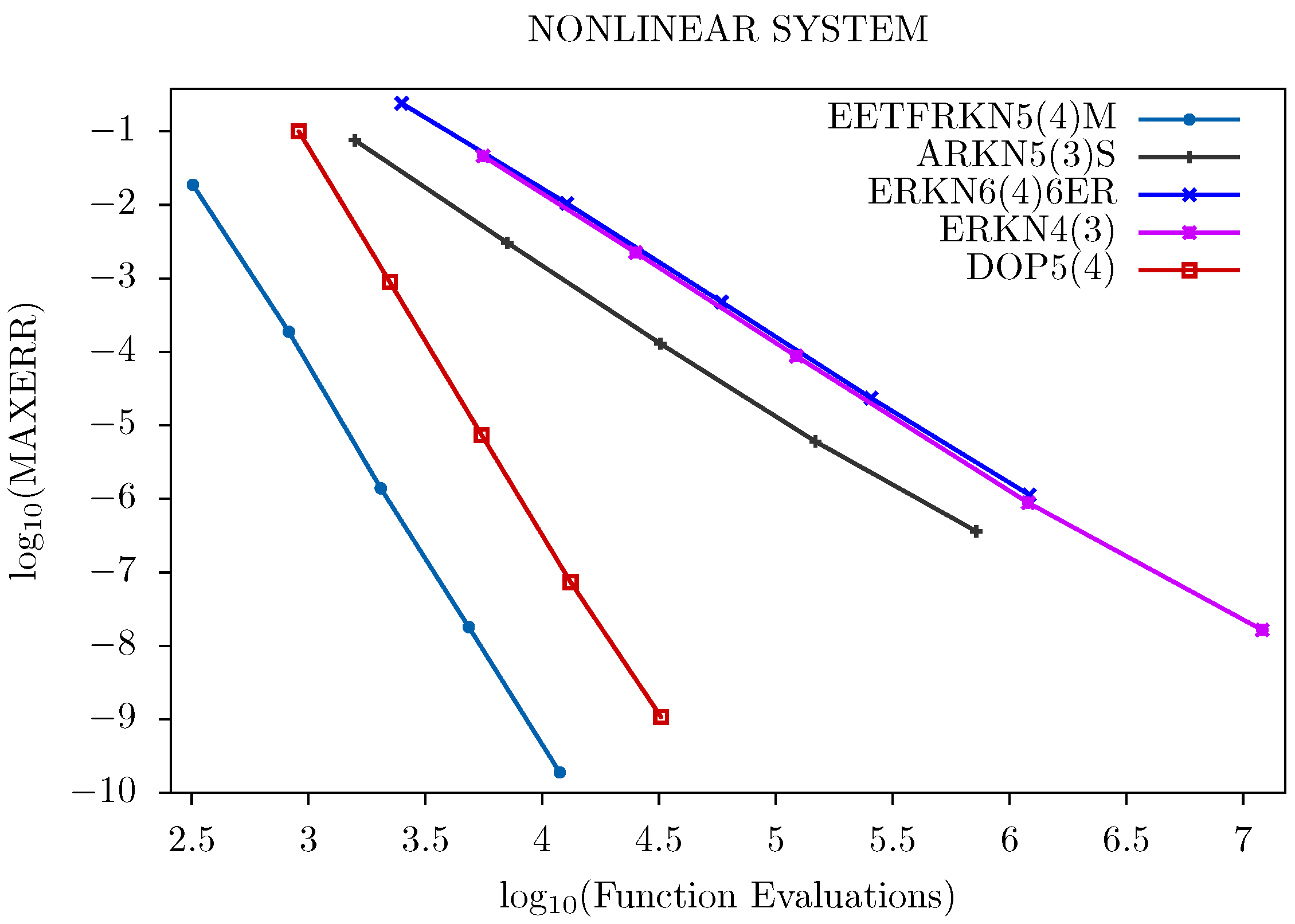
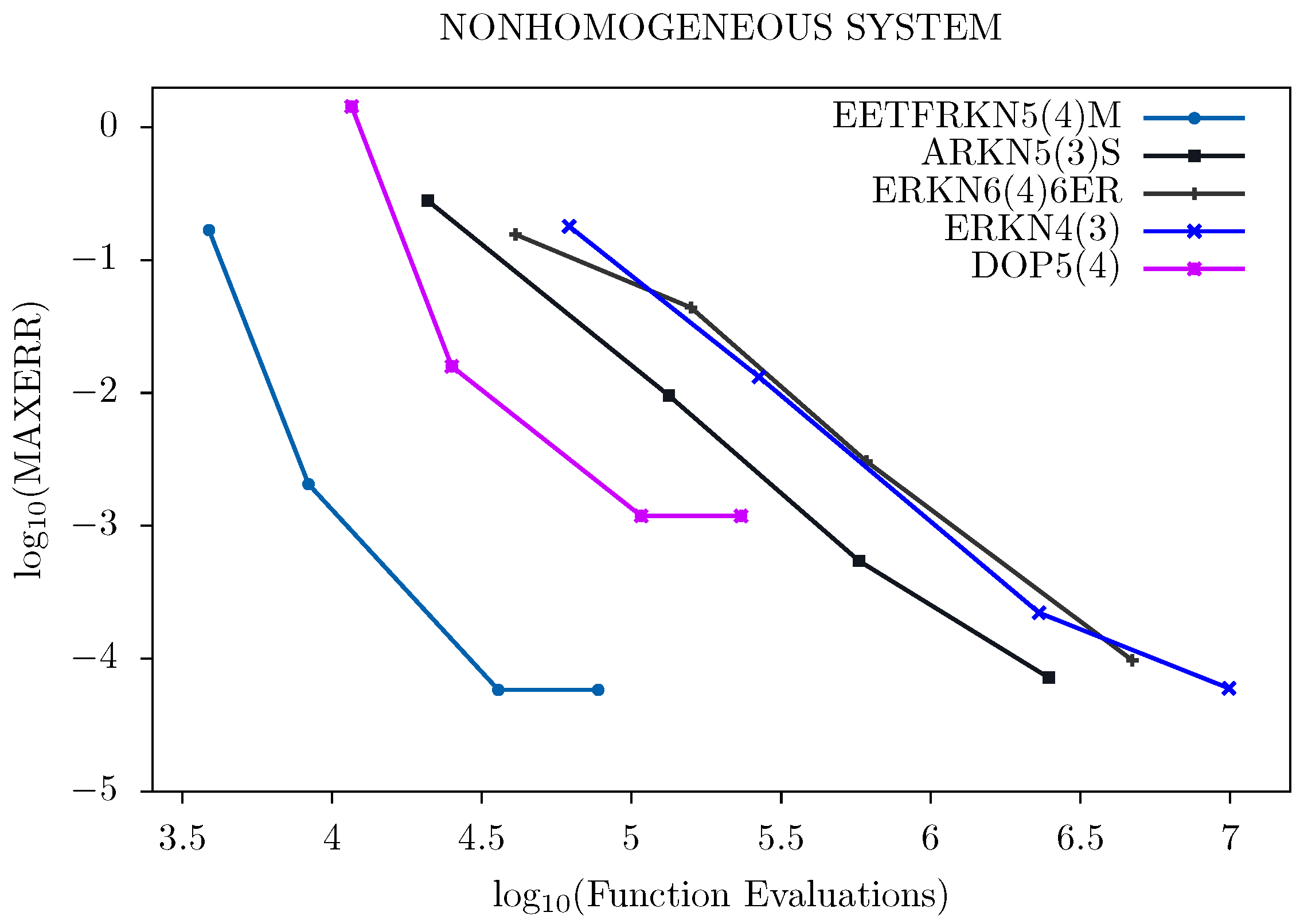
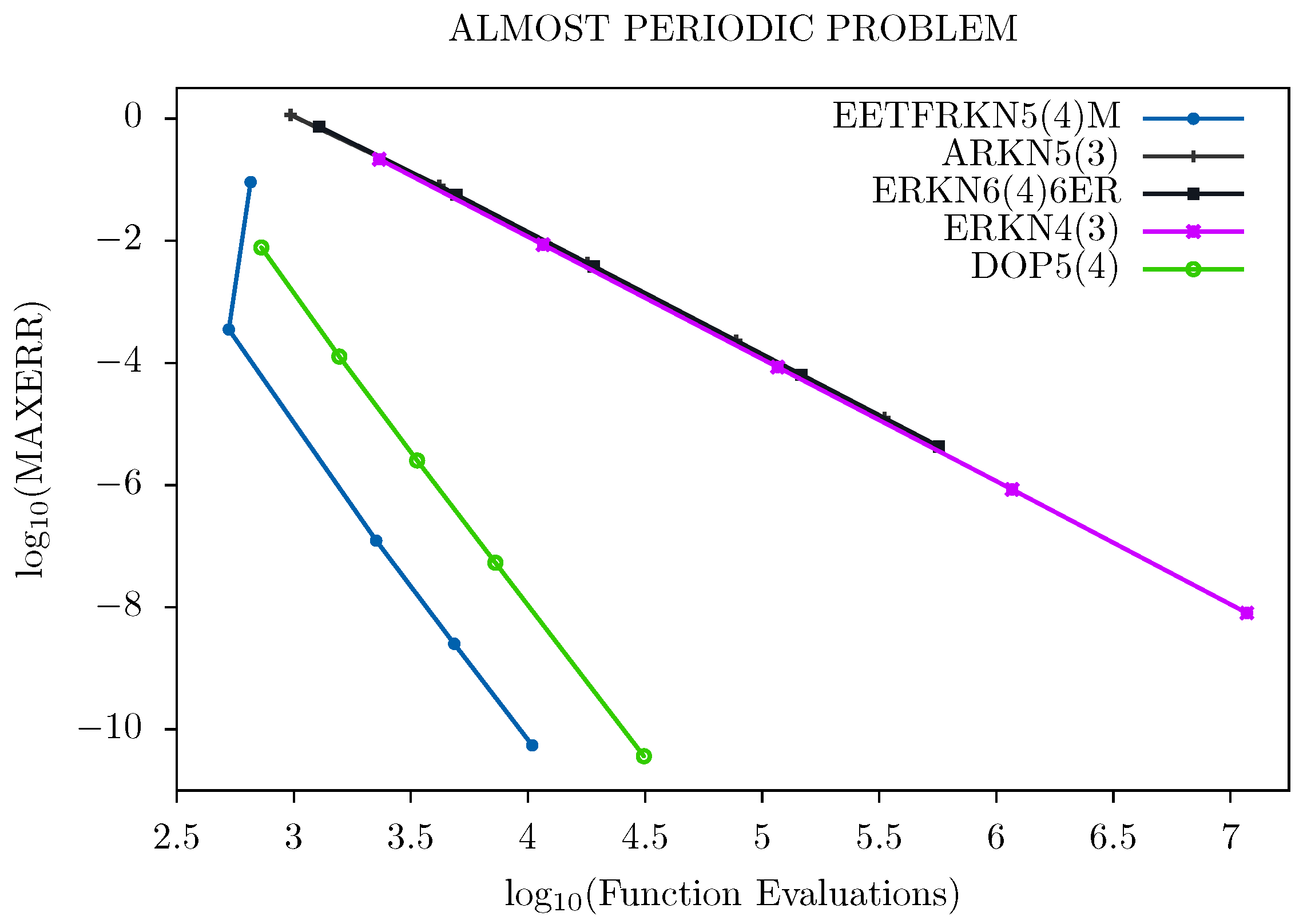
5. Numerical Results
- EETFRKN5(4)M: The new embedded explicit trigonometrically-fitted Runge–Kutta–Nyström pair (EETFRKN5(4)) derived in this paper,
- ERKN6(4)6ER: A 6(4) optimized embedded Runge–Kutta–Nyström pair derived by Anastassi and Kosti in [11],
- ERKN4(3): The embedded Runge–Kutta–Nyström method obtained by Van de Vyver in [6],
- ARKN5(3)S: A 5(3) pair of explicit adapted Runge–Kutta–Nyström method derived by Franco in [5],
- DOP5(4): A 5(4) Dormand and Prince embedded Runge–Kutta method given by Butcher in [15],
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Simos, T.E. Exponentially fitted modified Runge–Kutta–Nyström method for the numerical solution of initial-value problems with oscillating solutions. Appl. Math. Lett. 2002, 15, 217–225. [Google Scholar] [CrossRef]
- Van de Vyver, H. An embedded exponentially-fitted Runge–Kutta–Nyström method for the numerical solution of orbital problems. New Astron. 2006, 11, 577–587. [Google Scholar] [CrossRef]
- Kalogiratou, Z.; Simos, T.E. Construction of trigonometrically-fitted and exponentially-fitted Runge–Kutta–Nyström methods for the numerical solution of schrödinger equation and related problems-a method of 8th algebraic order. J. Math. Chem. 2002, 31, 211–232. [Google Scholar] [CrossRef]
- Liu, S.; Zheng, J.; Fang, Y. A new modified embedded 5(4) pair of explicit Runge-Kutta methods for the numerical solution of schrödinger equation. J. Math. Chem. 2002, 15, 217–225. [Google Scholar] [CrossRef]
- Franco, J. A 5(3) pair of explicit ARKN methods for the numerical integration of pertubed oscillators. J. Comput. Appl. Math. 2003, 161, 283–293. [Google Scholar] [CrossRef]
- Vande Vyver, H. A Runge–Kutta–Nyström pair for the numerical integration of pertubed oscillators. Comput. Phys. Commun. 2002, 15, 217–225. [Google Scholar]
- Vande Vyver, H. A 5(3) pair of explicit Runge–Kutta–Nyström methods for oscillatory problems. Comput. Phys. Commun. 2002, 15, 217–225. [Google Scholar] [CrossRef]
- Senu, N.; Suleiman, M.; Ismail, F. An embedded explicit Runge–Kutta–Nyström method for solving oscillatory problems. Phys. Scr. 2009, 80, 015005. [Google Scholar] [CrossRef]
- Tsitouras, C. On fitted modifications of Runge–Kutta–Nyström pairs. Appl. Math. Comput. 2014, 232, 416–423. [Google Scholar] [CrossRef]
- Franco, J.; Khiar, Y.; Randez, L. Two new embedded pairs of explicit Runge-Kutta methods adapted to the numerical solution of oscillatory problems. Appl. Math. Comput. 2014, 232, 416–423. [Google Scholar] [CrossRef]
- Anastassi, Z.; Kosti, A. A 6(4) optimized embedded Runge-Kutta Nyström pair for the numerical solution of periodic problems. J. Comput. Appl. Math. 2015, 275, 311–320. [Google Scholar] [CrossRef]
- Simos, T.E. An exponentially-fitted Runge-Kutta method for the numerical solution of initial-value problem with periodic or oscillating solutions. Comput. Phys. Commun. 1998, 115, 1–8. [Google Scholar] [CrossRef]
- Senu, N. Runge-Kutta Nyström Methods for Solving Oscillatory Problems. Ph.D. Thesis, Department of Mathematics, Faculty of Science, Serdang, Malaysia, 25th April 2009. [Google Scholar]
- Van der Houwen, P.; Sommeijer, B. Diagonaly implicit Runge-Kutta Nyström methods for oscillatory problems. SIAM J. Numer. Anal. 1989, 26, 414–429. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; Wiley & Sons LTD.: England, UK, 2008. [Google Scholar]
- Fang, Y.; You, X.; Ming, Q. Trigonometrically-fitted two derivative Runge-Kutta methods for solving oscillatory differential equations. Numer. Algorithms 2014, 65, 651–667. [Google Scholar] [CrossRef]
| TOL | METHOD | STEP | FCN | FSTEP | MAXE | TIME (s) |
|---|---|---|---|---|---|---|
| EETFRKN5(4)M | 63 | 252 | 0 | 1.589499(-4) | 0.312 | |
| ARKN5(3)S | 242 | 968 | 0 | 9.829659(-1) | 0.812 | |
| ERKN6(4)6ER | 215 | 1290 | 0 | 7.375736(-1) | 1.063 | |
| ERKN4(3) | 578 | 2315 | 1 | 2.175738(-1) | 1.031 | |
| DOP5(4) | 121 | 726 | 0 | 7.747317(-3) | 0.531 | |
| EETFRKN5(4)M | 132 | 528 | 0 | 3.336685(-6) | 0.359 | |
| ARKN5(3)S | 1044 | 4179 | 1 | 6.406274(-2) | 1.547 | |
| ERKN6(4)6ER | 825 | 4955 | 0 | 5.685758(-2) | 1.531 | |
| ERKN4(3) | 2901 | 11,610 | 2 | 8.650517(-3) | 2.000 | |
| DOP5(4) | 262 | 1572 | 0 | 1.273632(-4) | 1.531 | |
| EETFRKN5(4)M | 283 | 1132 | 0 | 7.329552(-8) | 1.230 | |
| ARKN5(3)S | 4491 | 17,970 | 2 | 3.460856(-3) | 3.044 | |
| ERKN6(4)6ER | 3180 | 19,090 | 2 | 3.817832(-3) | 2.904 | |
| ERKN4(3) | 29,131 | 116,536 | 4 | 8.569318(-5) | 14.371 | |
| DOP5(4) | 561 | 3366 | 0 | 2.521377(-6) | 2.531 | |
| EETFRKN5(4)M | 654 | 2616 | 0 | 1.089911(-9) | 1.250 | |
| ARKN5(3)S | 83,362 | 333,460 | 4 | 1.003239(-5) | 41.557 | |
| ERKN6(4)6ER | 94,782 | 568,717 | 5 | 4.291853(-6) | 41.977 | |
| ERKN4(3) | 2,940,668 | 11,762,696 | 8 | 8.077835(-9) | 1347.362 | |
| DOP5(4) | 5210 | 31,260 | 0 | 3.630829(-11) | 4.531 |
| TOL | METHOD | STEP | FCN | FSTEP | MAXE | TIME (s) |
|---|---|---|---|---|---|---|
| EETFRKN5(4)M | 77 | 320 | 4 | 1.868952(-2) | 0.500 | |
| ARKN5(3)S | 391 | 1579 | 5 | 7.585297(-2) | 1.297 | |
| ERKN6(4)6ER | 412 | 2502 | 6 | 2.409650(-1) | 1.685 | |
| ERKN4(3) | 1391 | 5585 | 7 | 4.620804(-2) | 1.984 | |
| DOP5(4) | 148 | 908 | 4 | 1.003445(-1) | 0.703 | |
| EETFRKN5(4)M | 203 | 824 | 4 | 1.883175(-4) | 0.844 | |
| ARKN5(3)S | 1768 | 7090 | 6 | 3.050204(-3) | 2.250 | |
| ERKN6(4)6ER | 2119 | 12,749 | 7 | 1.047787(-2) | 2.188 | |
| ERKN4(3) | 6278 | 25,136 | 8 | 2.250399(-3) | 5.234 | |
| DOP5(4) | 369 | 2234 | 4 | 8.921876(-4) | 1.020 | |
| EETFRKN5(4)M | 507 | 2040 | 4 | 1.389967(-6) | 1.609 | |
| ARKN5(3)S | 8001 | 32,025 | 7 | 1.295624(-4) | 5.636 | |
| ERKN6(4)6ER | 9744 | 58,504 | 8 | 4.798031(-4) | 6.125 | |
| ERKN4(3) | 30,571 | 122,311 | 9 | 8.727528(-5) | 15.296 | |
| DOP5(4) | 915 | 5510 | 4 | 7.372093(-6) | 2.703 | |
| EETFRKN5(4)M | 1208 | 4844 | 4 | 1.809555(-8) | 1.844 | |
| ARKN5(3)S | 36,949 | 147,823 | 9 | 6.030980(-6) | 19.549 | |
| ERKN6(4)6ER | 42,606 | 255,681 | 9 | 2.359393(-5) | 20.213 | |
| ERKN4(3) | 300,521 | 120,214 | 10 | 8.837019(-7) | 134.762 | |
| DOP5(4) | 2202 | 13,232 | 4 | 7.347484(-8) | 3.124 | |
| EETFRKN5(4)M | 2968 | 11,887 | 5 | 1.891552(-10) | 3.584 | |
| ARKN5(3)S | 180,503 | 722,042 | 10 | 3.607369(-7) | 86.196 | |
| ERKN6(4)6ER | 202,603 | 1,215,673 | 11 | 1.132031(-6) | 86.814 | |
| ERKN4(3) | 3,017,354 | 12,069,452 | 12 | 1.646494(-8) | 1620.306 | |
| DOP5(4) | 5378 | 32,293 | 5 | 1.071751(-9) | 5.223 |
| TOL | METHOD | STEP | FCN | FSTEP | MAXE | TIME (s) |
|---|---|---|---|---|---|---|
| EETFRKN5(4)M | 65 | 263 | 1 | 2.665158(-3) | 0.250 | |
| ARKN5(3)S | 133 | 541 | 3 | 1.336913(-1) | 0.328 | |
| ERKN6(4)6ER | 219 | 1324 | 2 | 6.973318(-2) | 0.422 | |
| ERKN4(3) | 588 | 2361 | 3 | 2.107025(-2) | 0.719 | |
| DOP5(4) | 127 | 772 | 2 | 1.107309(+1) | 0.344 | |
| EETFRKN5(4)M | 138 | 555 | 1 | 7.897400(-5) | 0.359 | |
| ARKN5(3)S | 551 | 2213 | 3 | 2.752336(-2) | 0.828 | |
| ERKN6(4)6ER | 429 | 2589 | 3 | 2.187558(-2) | 0.609 | |
| ERKN4(3) | 3005 | 12,035 | 5 | 8.461092(-4) | 1.703 | |
| DOP5(4) | 529 | 3184 | 2 | 1.1000002(+1) | 1.030 | |
| EETFRKN5(4)M | 164 | 662 | 2 | 5.757119(-7) | 0.422 | |
| ARKN5(3)S | 4523 | 18,137 | 15 | 9.530356(-4) | 2.188 | |
| ERKN6(4)6ER | 1688 | 10,153 | 5 | 1.495030(-3) | 1.047 | |
| ERKN4(3) | 15,709 | 62,857 | 7 | 3.359187(-5) | 6.748 | |
| DOP5(4) | 1143 | 6868 | 2 | 1.099999(+1) | 2.344 | |
| EETFRKN5(4)M | 355 | 1426 | 2 | 8.919276(-9) | 0.625 | |
| ARKN5(3)S | 9943 | 39,796 | 8 | 1.652088(-4) | 4.453 | |
| ERKN6(4)6ER | 6550 | 39,330 | 6 | 1.003134(-4) | 3.069 | |
| ERKN4(3) | 85,151 | 340,631 | 9 | 1.337546(-6) | 36.152 | |
| DOP5(4) | 2483 | 14,913 | 3 | 1.100000(+1) | 3.031 | |
| EETFRKN5(4)M | 774 | 3102 | 2 | 1.223295(-10) | 0.781 | |
| ARKN5(3)S | 43,042 | 172,186 | 6 | 4.372055(-6) | 17.310 | |
| ERKN6(4)6ER | 48,932 | 293,632 | 8 | 1.680967(-6) | 20.141 | |
| ERKN4(3) | 855,349 | 3,421,429 | 11 | 1.314822(-8) | 356.970 | |
| DOP5(4) | 5379 | 32,289 | 3 | 1.100000(+1) | 4.344 |
| TOL | METHOD | STEP | FCN | FSTEP | MAXE | TIME (s) |
|---|---|---|---|---|---|---|
| EETFRKN5(4)M | 122 | 488 | 0 | 5.791290(-4) | 0.424 | |
| ARKN5(3)S | 242 | 968 | 0 | 2.111440(-1) | 0.453 | |
| ERKN6(4)6ER | 215 | 1290 | 0 | 7.335990(-1) | 0.453 | |
| ERKN4(3) | 578 | 2315 | 1 | 2.168852(-1) | 0.844 | |
| DOP5(4) | 121 | 726 | 0 | 7.766793(-3) | 0.429 | |
| EETFRKN5(4)M | 262 | 1048 | 0 | 1.294696(-5) | 0.578 | |
| ARKN5(3)S | 1044 | 4179 | 1 | 1.141697(-2) | 1.109 | |
| ERKN6(4)6ER | 825 | 4955 | 1 | 5.673723(-2) | 0.781 | |
| ERKN4(3) | 2901 | 11,610 | 2 | 8.642825(-3) | 1.547 | |
| DOP5(4) | 262 | 1572 | 0 | 1.275701(-4) | 1.422 | |
| EETFRKN5(4)M | 562 | 2248 | 0 | 2.671335(-7) | 0.656 | |
| ARKN5(3)S | 4491 | 17,970 | 2 | 6.156293(-4) | 2.219 | |
| ERKN6(4)6ER | 3180 | 19,090 | 2 | 3.814429(-3) | 1.656 | |
| ERKN4(3) | 29,131 | 116,536 | 4 | 8.562316(-5) | 12.500 | |
| DOP5(4) | 561 | 3366 | 0 | 2.521051(-6) | 2.422 | |
| EETFRKN5(4)M | 1211 | 4844 | 0 | 5.680715(-9) | 0.859 | |
| ARKN5(3)S | 19347 | 77,397 | 3 | 3.316106(-5) | 8.094 | |
| ERKN6(4)6ER | 24,548 | 147,308 | 4 | 6.394316(-5) | 10.047 | |
| ERKN4(3) | 292,676 | 1,170,722 | 6 | 8.477710(-7) | 123.098 | |
| DOP5(4) | 1210 | 7260 | 0 | 5.343219(-8) | 3.422 | |
| EETFRKN5(4)M | 2622 | 10488 | 0 | 1.301748(-10) | 1.500 | |
| ARKN5(3)S | 83,362 | 333,460 | 4 | 1.785978(-6) | 34.359 | |
| ERKN6(4)6ER | 94,782 | 568,717 | 5 | 4.2883486(-6) | 37.406 | |
| ERKN4(3) | 2,940,668 | 11,762,696 | 8 | 8.074738(-9) | 1164.595 | |
| DOP5(4) | 5210 | 31,260 | 0 | 3.620826(-11) | 4.422 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Kufi, M.A.H.J.; Hashim, H.R.; Hussein, A.M.; Mohammed, H.R. An Algorithm Based on GSVD for Image Encryption. Math. Comput. Appl. 2017, 22, 28. https://doi.org/10.3390/mca22020028
Al-Kufi MAHJ, Hashim HR, Hussein AM, Mohammed HR. An Algorithm Based on GSVD for Image Encryption. Mathematical and Computational Applications. 2017; 22(2):28. https://doi.org/10.3390/mca22020028
Chicago/Turabian StyleAl-Kufi, Mohammed Abdul Hameed Jassim, Hayder Raheem Hashim, Ameer Mohammed Hussein, and Hind Rustum Mohammed. 2017. "An Algorithm Based on GSVD for Image Encryption" Mathematical and Computational Applications 22, no. 2: 28. https://doi.org/10.3390/mca22020028
APA StyleAl-Kufi, M. A. H. J., Hashim, H. R., Hussein, A. M., & Mohammed, H. R. (2017). An Algorithm Based on GSVD for Image Encryption. Mathematical and Computational Applications, 22(2), 28. https://doi.org/10.3390/mca22020028





