Damping Characteristics of Viscoelastic Damping Structure under Coupled Condition
Abstract
:1. Introduction
2. Simulation Method
2.1. Hyper-Viscoelastic Model
2.2. Finite Element Method (FEM) Implementation
3. Results and Discussion
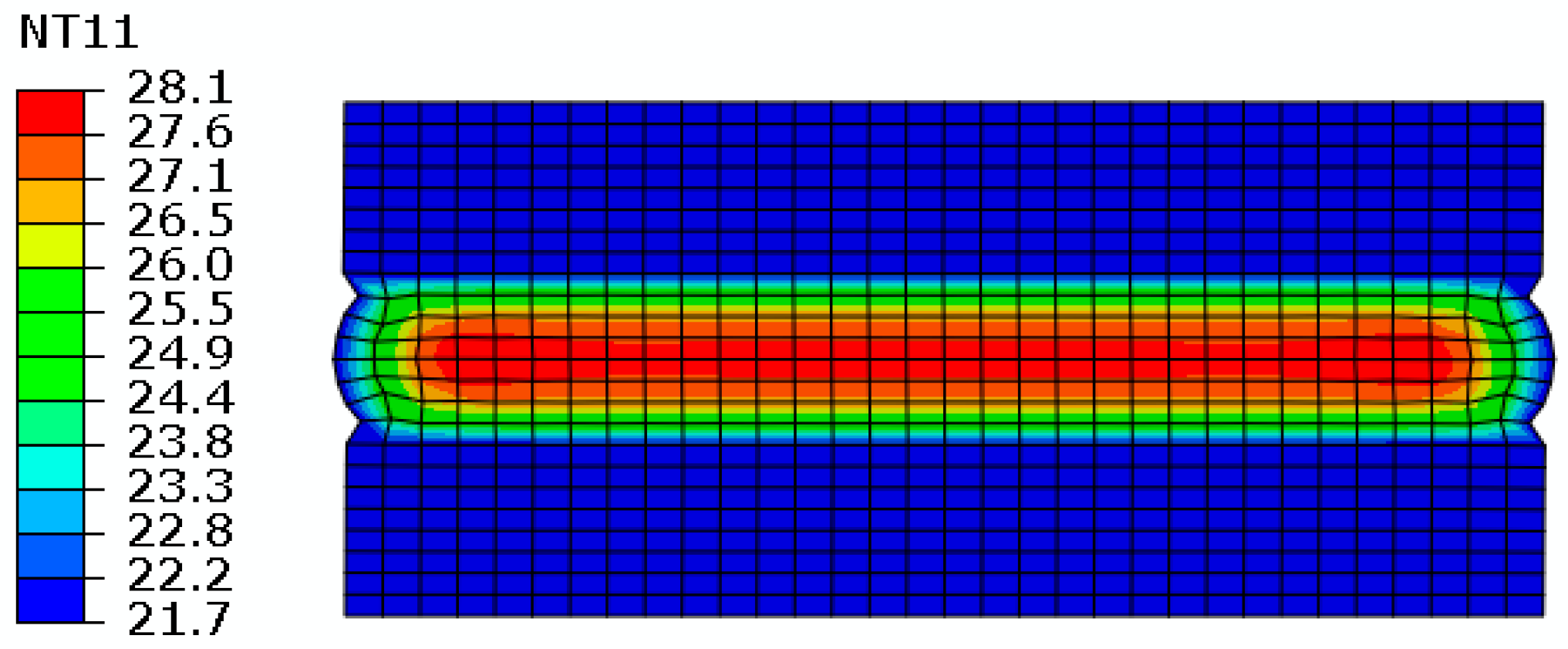
3.1. Temperature Distribution
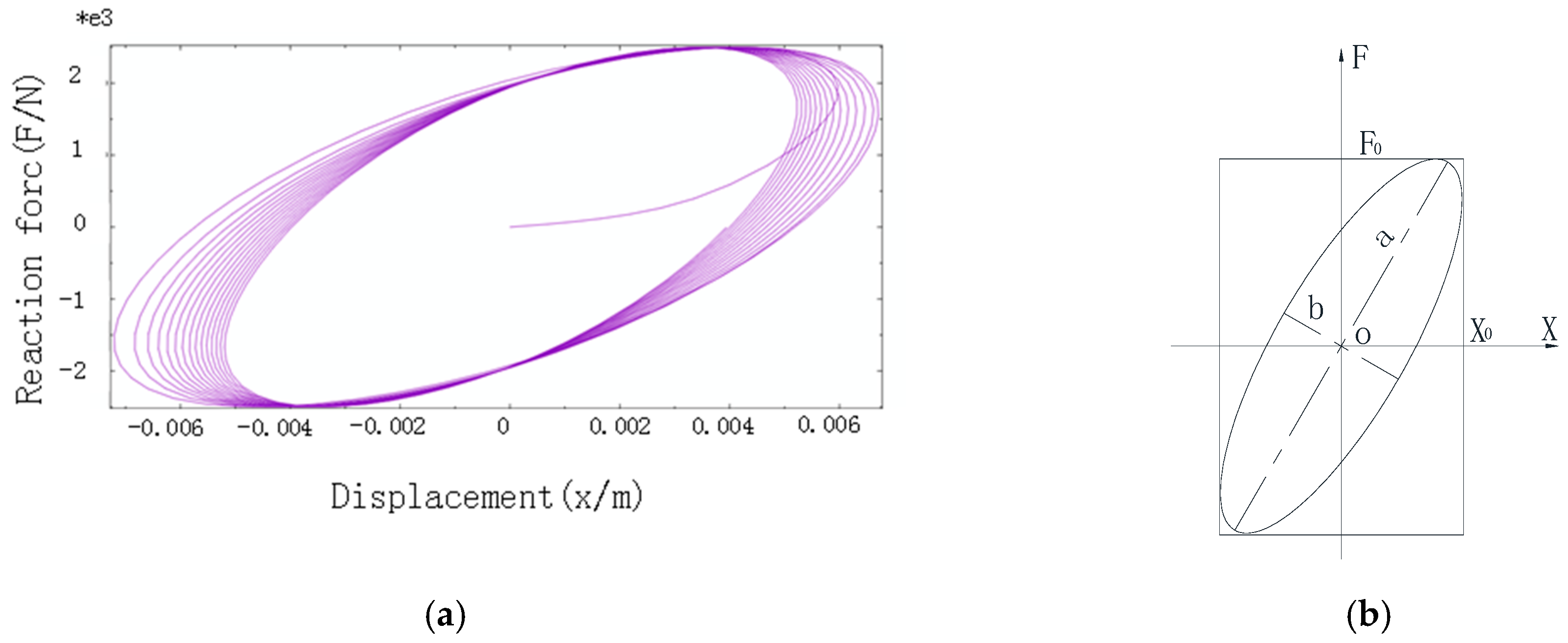
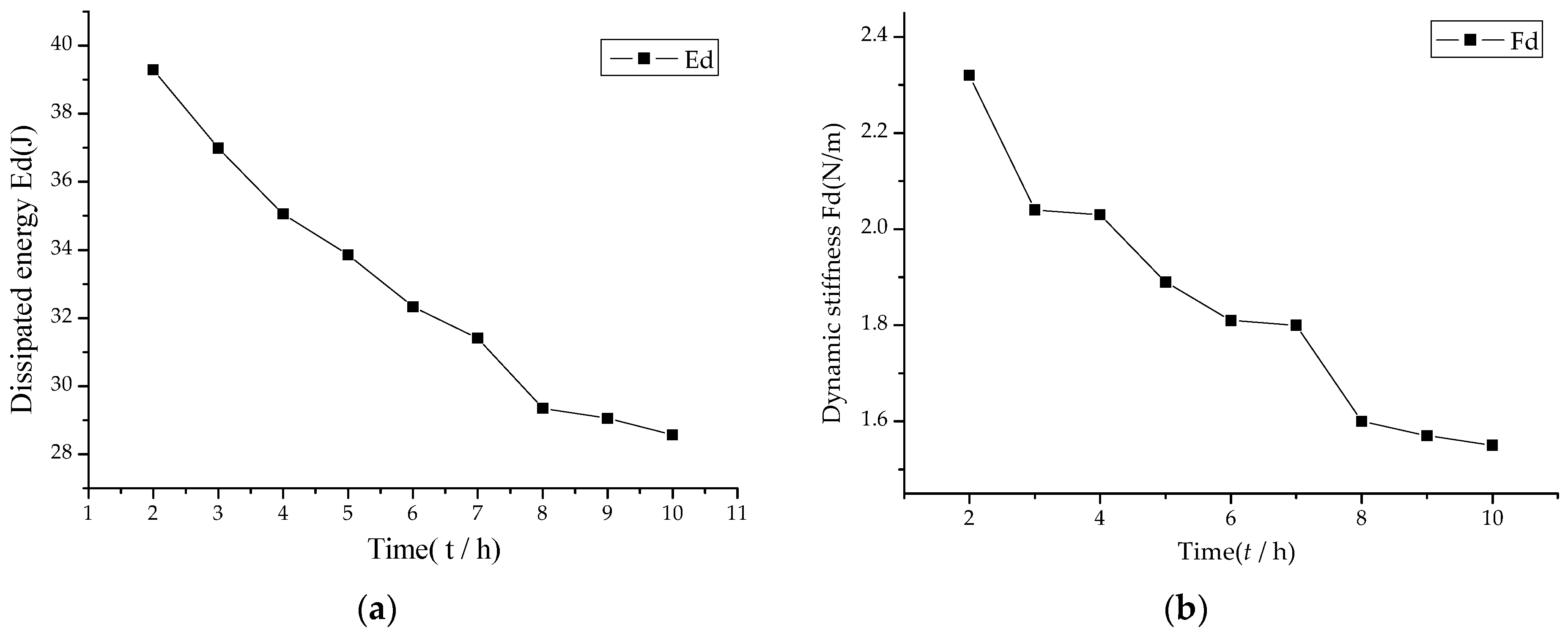
3.2. Dynamic Damping Characteristics
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ward, I.M.; Sweeney, J. Chapter 2 The mechanical properties of polymers: General considerations. In Mechanical Properties of Solid Polymers, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Christensen, R. Chapter 3 Thermoviscoelasticity. In Theory of Viscoelasticity, 2nd ed.; Academic Press: Waltham, MA, USA, 1982. [Google Scholar]
- Ferry, J.D. Chapter 11 Dependence of viscoelastic behavior on temperature and pressure. In Viscoelastic Properties of Polymers; Wiley: Hoboken, NJ, USA, 1970. [Google Scholar]
- Chang, K.C.; Soong, T.T.; Oh, S.; Lai, M.L. Effect of Ambient Temperature on Viscoelastically Damped Structure. J. Struct. Eng. 1992, 118, 1955–1973. [Google Scholar] [CrossRef]
- Fang, Q.H.; Zhang, F.P.; Huang, B.Z. Study on Extension Characteristics of Vulcanized Rubber at Different Temperatures. J. Build. Mater. 2005, 8, 383–386. [Google Scholar] [CrossRef]
- Liu, D.H.; Fan, D.; Ouyang, Y.F.; Wu, C.P. Temperature Effect on Mechanical Properties of Rubber Isolators. Noise Vib. Control 2014, 3, 203–206. [Google Scholar] [CrossRef]
- Boukamel, A.; Méo, S.; Débordes, O.; Jaeger, M. A Thermo-viscoelastic Model for Elastomeric Behaviour and Its Numerical Application. Arch. Appl. Mech. 2001, 71, 785–801. [Google Scholar] [CrossRef]
- Rodas, C.O.; Zaïri, F.; Naït-abdelaziz, M. A Finite Strain Thermo-viscoelastic Constitutive Model to Describe the Self-heating in Elastomeric Materials during Low-cycle Fatigue. J. Mech. Phys. Solids 2013, 64, 396–410. [Google Scholar] [CrossRef]
- Stefanie, R. A Micromechanically Motivated Material Model for the Thermo-viscoelastic Material Behaviour of Rubber-like Polymers. Int. J. Plast. 2003, 19, 909–940. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Simo, J.C. A New Viscoelastic Constitutive Model for Continuous Media at Finite Thermomechanical Changes. Int. J. Solids Struct. 1996, 33, 3019–3034. [Google Scholar] [CrossRef]
- Habibi, M.K.; Tam, L.H.; Lau, D.; Yang, L. Viscoelastic Damping Behavior of Structural Bamboo Material and Its Microstructural Origins. Mech. Mater. 2016, 97, 184–198. [Google Scholar] [CrossRef]
- Jones, D.I.G. Handbook of Viscoelastic Vibration Damping, 1st ed.; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Johnson, A.R.; Chen, T.K. Approximating Thermo-viscoelastic Heating of Largely Strained Solid Rubber Components. Comput. Methods Appl. Mech. Engrg. 2005, 194, 313–325. [Google Scholar] [CrossRef]
- Shah, S.; Muliana, A.; Rajagopal, K.R. Coupled Heat Conduction and Deformation in a viscoelastic Composite Cylinder. Mech. Time-Depend. Mater. 2009, 13, 121–147. [Google Scholar] [CrossRef]
- Pešek, L.; Půst, L.; Šulc, P. FEM Modeling of Thermo-Mechanical Interaction in Pre-pressed Rubber Block. Eng. Mech. 2007, 14, 3–11. Available online: http://www.im.fme.vutbr.cz/pdf/14_1_003.pdf (accessed on 13 March 2017). [Google Scholar]
- Banic, M.S.; Stamenkovic, D.S.; Miltenovic, V.D.; Milosevi, M.S.; Miltenovi, A.V.; Djeki, P.S.; Rackov, M.J. Prediction of Heat Generation in Rubber or Rubber-metal Springs. Therm. Sci. 2012, 16, 527–539. [Google Scholar] [CrossRef]
- Luo, R.K.; Wu, W.X. A Method to Predict the Heat Generation in a Rubber Spring Used in the Railway Industry. Proc. Inst. Mech. Eng. Part F. J. Rail Rapid Transit 2005, 219, 239–244. [Google Scholar] [CrossRef]
- Khan, A.M. Fully Coupled Heat Conduction and Deformation Analyses of Nonlinear Viscoelastic Composites. Mech. Time Depend. Mater. 2012, 16, 461–489. [Google Scholar] [CrossRef]
- Lin, Y.J.; Hwang, S.J. Temperature Prediction of Rolling Tires by Computer Simulation. Math. Comput. Simul. 2004, 67, 235–249. [Google Scholar] [CrossRef]
- Fenza, A.D.; Monaco, E.; Amoroso, F.; Lecce, L. Experimental Approach in Studying Temperature Effects on Composite Material Structures Realized with Viscoelastic Damping Treatments. J. Vib. Control 2014, 22, 358–370. [Google Scholar] [CrossRef]
- Kerchman, V.; Cheng, S. Experimental Study and Finite Element Simulation of Heat Build-up in Rubber Compounds with Application to Fracture. Rubber Chem. Technol. 2003, 76, 386–405. [Google Scholar] [CrossRef]
- Zghal, S.; Bouazizi, M.L.; Bouhaddi, N.; Nasri, R. Model Reduction Methods for Viscoelastic Sandwich Structures in Frequency and Time Domains. Finite Elements Anal. Des. 2015, 93, 12–29. [Google Scholar] [CrossRef]
- Failla, G. An Exact Generalised Function Approach to Frequency Response Analysis of Beams and Plane Frames with the Inclusion of Viscoelastic Damping. J. Sound Vib. 2016, 360, 171–202. [Google Scholar] [CrossRef]
- Johnson, A.R.; Quigley, C.J.; Mead, J.L. Large Strain Viscoelastic Constitutive Models for Rubber, Part I: Formulations. Rubber Chem. Technol. 1994, 67, 904–917. [Google Scholar] [CrossRef]
- Quigley, C.J.; Mead, J.; Johnson, A.R. Large Strain Viscoelastic Constitutive Models for Rubber, Part II: Determination of Material Constants. Rubber Chem. Technol. 1995, 68, 230–247. [Google Scholar] [CrossRef]
- Systèmes, D. ABAQUS 6.14. Available online: http://abaqus.software.polimi.it/v6.14/index.html (accessed on 10 March 2017).
- Ghazaly, N.M. ABAQUS Analysis User’s Manual, Vol 2-abaqus 6.10.
- Holzapfel, G.A.; Reiter, G. Fully Coupled Thermomechanical Behaviour of Viscoelastic Solids Treated with Finite Elements. Int. J. Eng. Sci. 1995, 33, 1037–1058. [Google Scholar] [CrossRef]
- Rittel, D. On the Conversion of Plastic Work to Heat during High Strain Rate Deformation of Glassy Polymers. Mech. Mater. 1999, 31, 131–139. [Google Scholar] [CrossRef]
- Gent, A.N.; Hertz, D.L.; Hamed, G.R. Chapter 4 Dynamic mechanical properties. In Engineering with Rubber—How to Design Rubber Components, 2nd ed.; Hanser Gardner Publications, Carl Hanser Publishers: Cincinnati, OH, USA, 2001. [Google Scholar]
- GB/T 15168-2013. Vibration and shock isolators measuring method for its static and dynamic characteristics. Available online: http://www.sac.gov.cn/was5/web/search?channelid=97779&templet=gjcxjg_detail.jsp&searchword=STANDARD_CODE='GB/T 15168-2013'&XZ=T&STANDARD_CODE=GB/T 15168-2013 (accessed on 10 March 2017).

| Property | Elastic Constrained Layer | Viscoelastic Damping Layer |
|---|---|---|
| Density (kg/m3) | 7850 | 1130 |
| Modulus of elasticity (Pa) | 2.1 × 1011 | - |
| Poisson ratio | 0.3 | - |
| Thermal expansion coefficient (10−6(m/m·K)) | 10.8 | 220 |
| Specific heat capacity (J/kg·°C) | 502 | 1900 |
| Heat conduction(W/(m·°C) | 70 | 0.14 |
| Non-elastic thermal friction coefficient | - | 1.071 × 10−4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Sun, D.; Liu, S.; Zhang, X. Damping Characteristics of Viscoelastic Damping Structure under Coupled Condition. Math. Comput. Appl. 2017, 22, 27. https://doi.org/10.3390/mca22010027
Wang J, Sun D, Liu S, Zhang X. Damping Characteristics of Viscoelastic Damping Structure under Coupled Condition. Mathematical and Computational Applications. 2017; 22(1):27. https://doi.org/10.3390/mca22010027
Chicago/Turabian StyleWang, Jun, Dagang Sun, Shizhong Liu, and Xin Zhang. 2017. "Damping Characteristics of Viscoelastic Damping Structure under Coupled Condition" Mathematical and Computational Applications 22, no. 1: 27. https://doi.org/10.3390/mca22010027
APA StyleWang, J., Sun, D., Liu, S., & Zhang, X. (2017). Damping Characteristics of Viscoelastic Damping Structure under Coupled Condition. Mathematical and Computational Applications, 22(1), 27. https://doi.org/10.3390/mca22010027





