Modeling Sound Propagation Using the Corrective Smoothed Particle Method with an Acoustic Boundary Treatment Technique
Abstract
:1. Introduction
2. CSPM Formulations for Sound Waves
2.1. Basic Concepts of SPH
2.2. Acoustic Wave Equations in Lagrangian Form
2.3. CSPM Formulations for Acoustic Waves
2.3.1. Particle Approximation of the Continuity Equation
2.3.2. Particle Approximation of the Momentum Equation
2.3.3. Particle Approximation of the Equation of State
2.3.4. Corrective Smoothed Particle Method
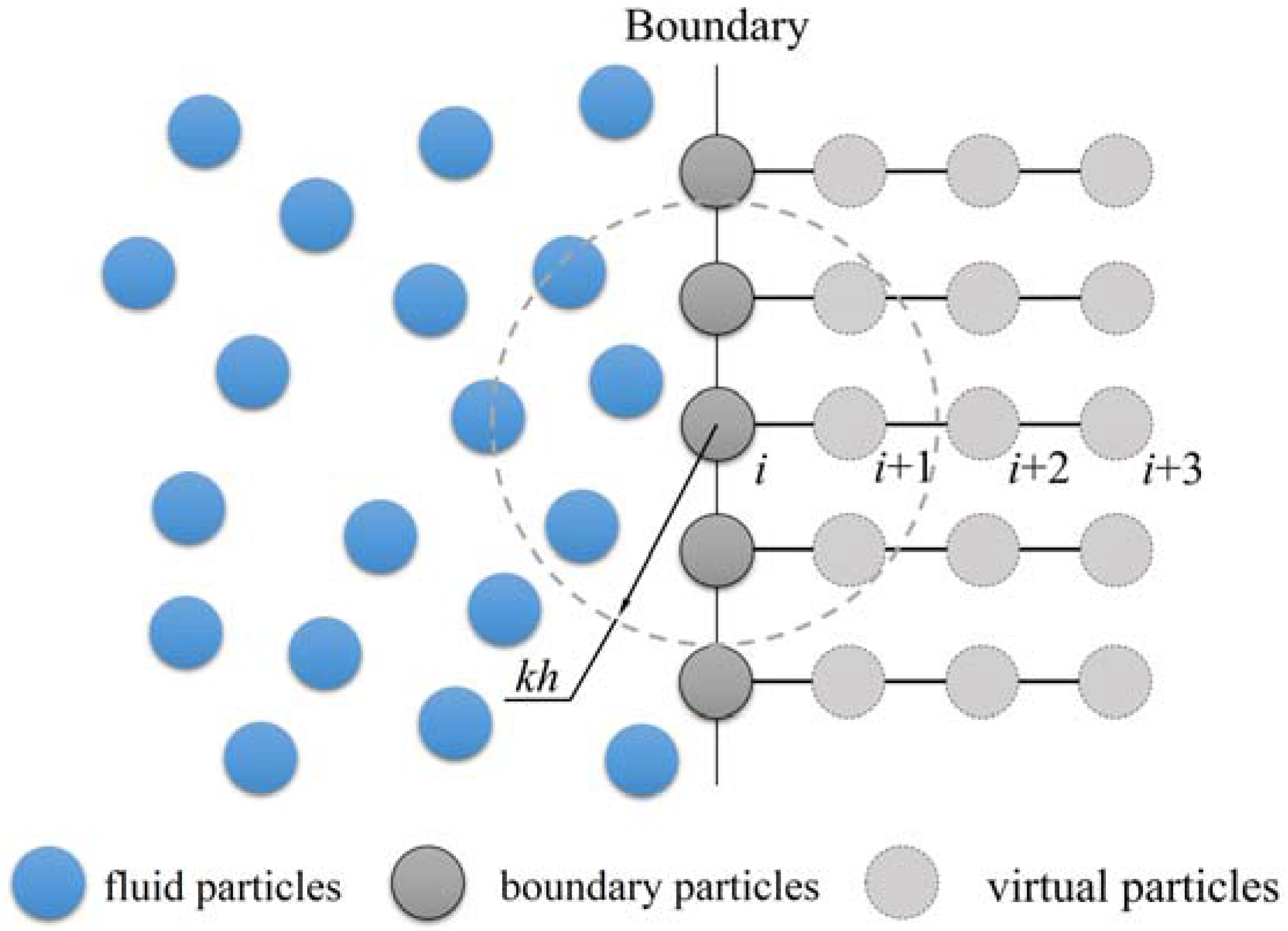
3. Hybrid Meshfree-FDTD Method for Boundary Treatment
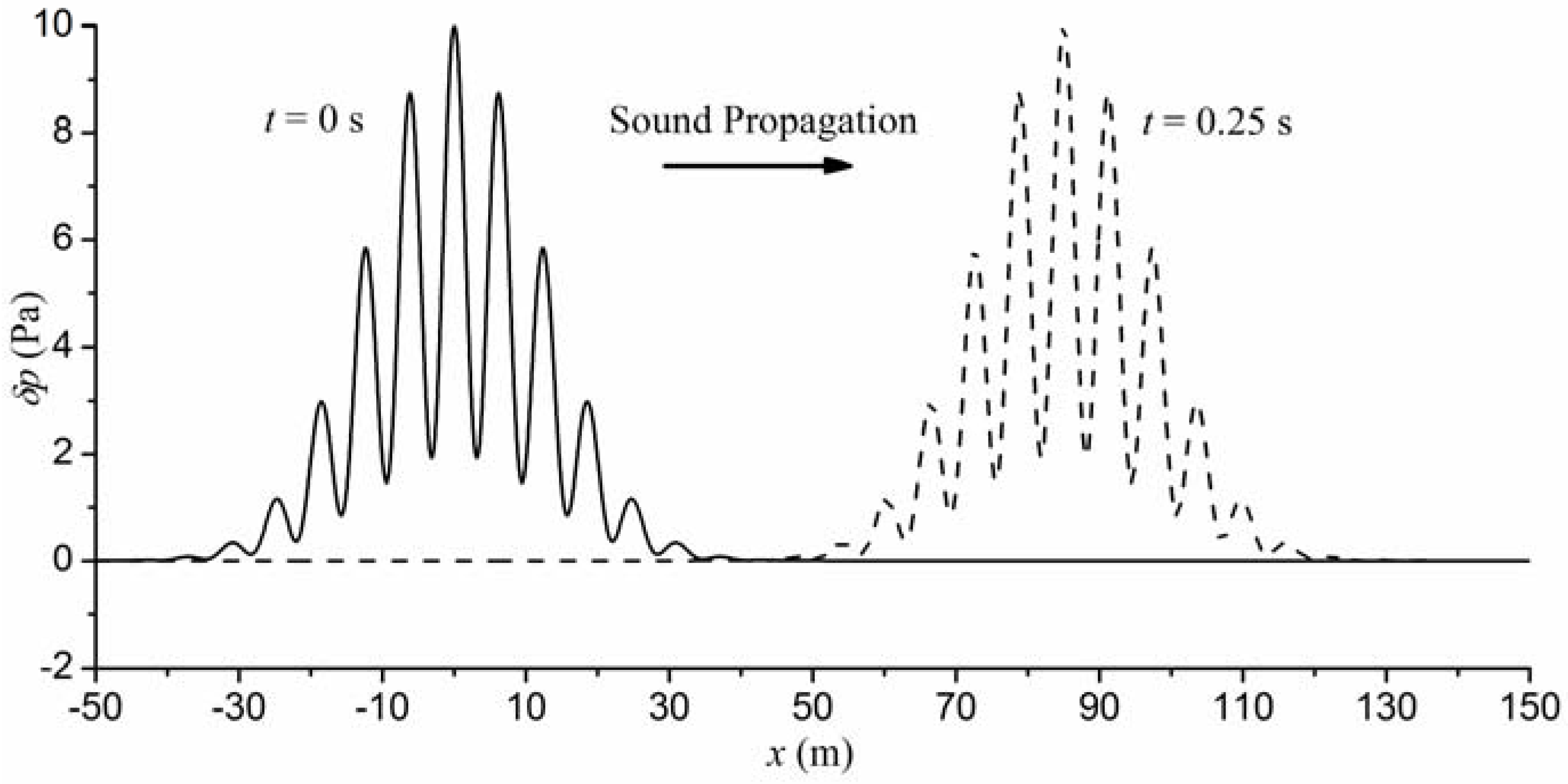
4. Sound Propagation Simulation with CSPM
4.1. Sound Propagation Model
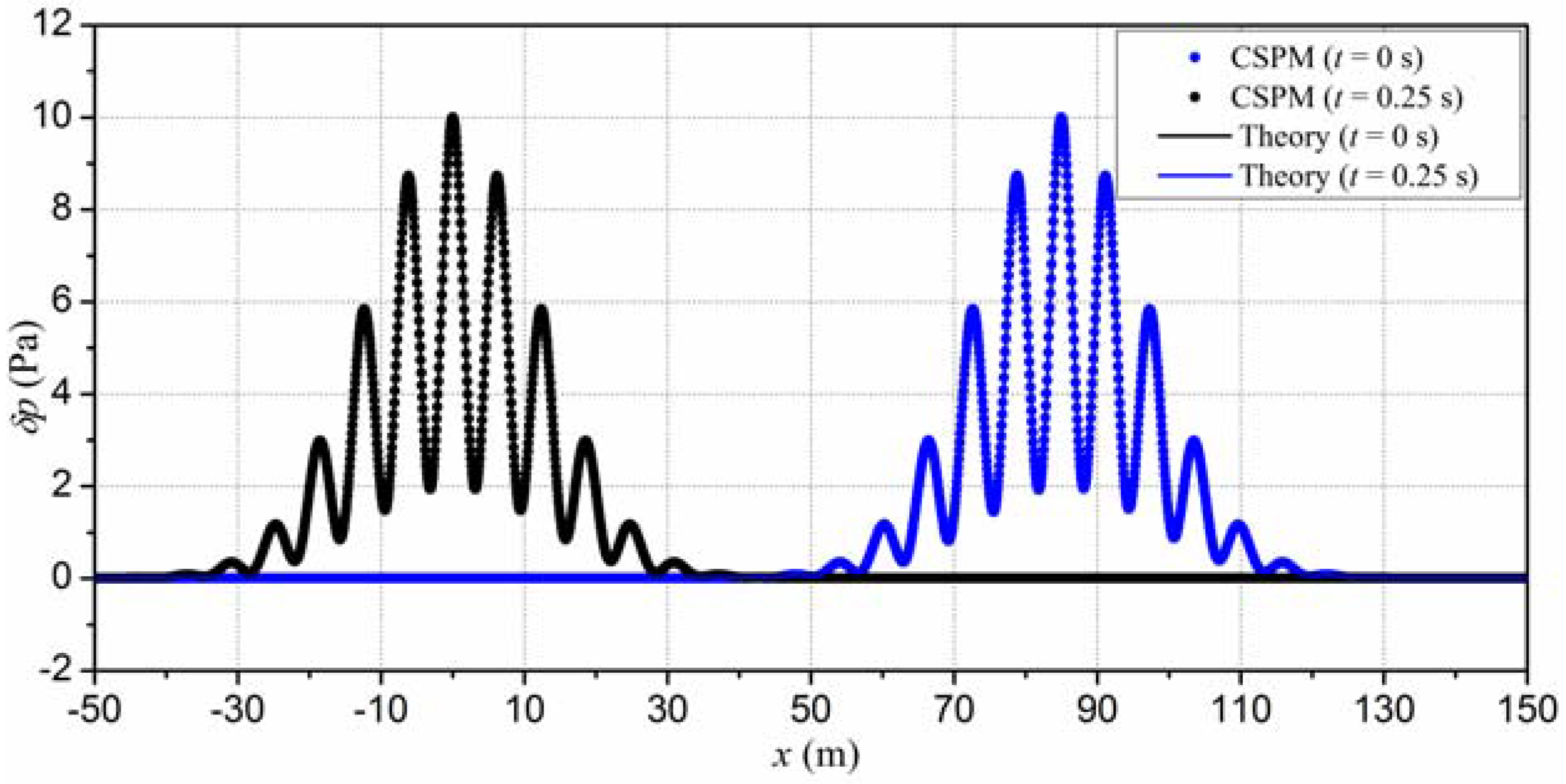
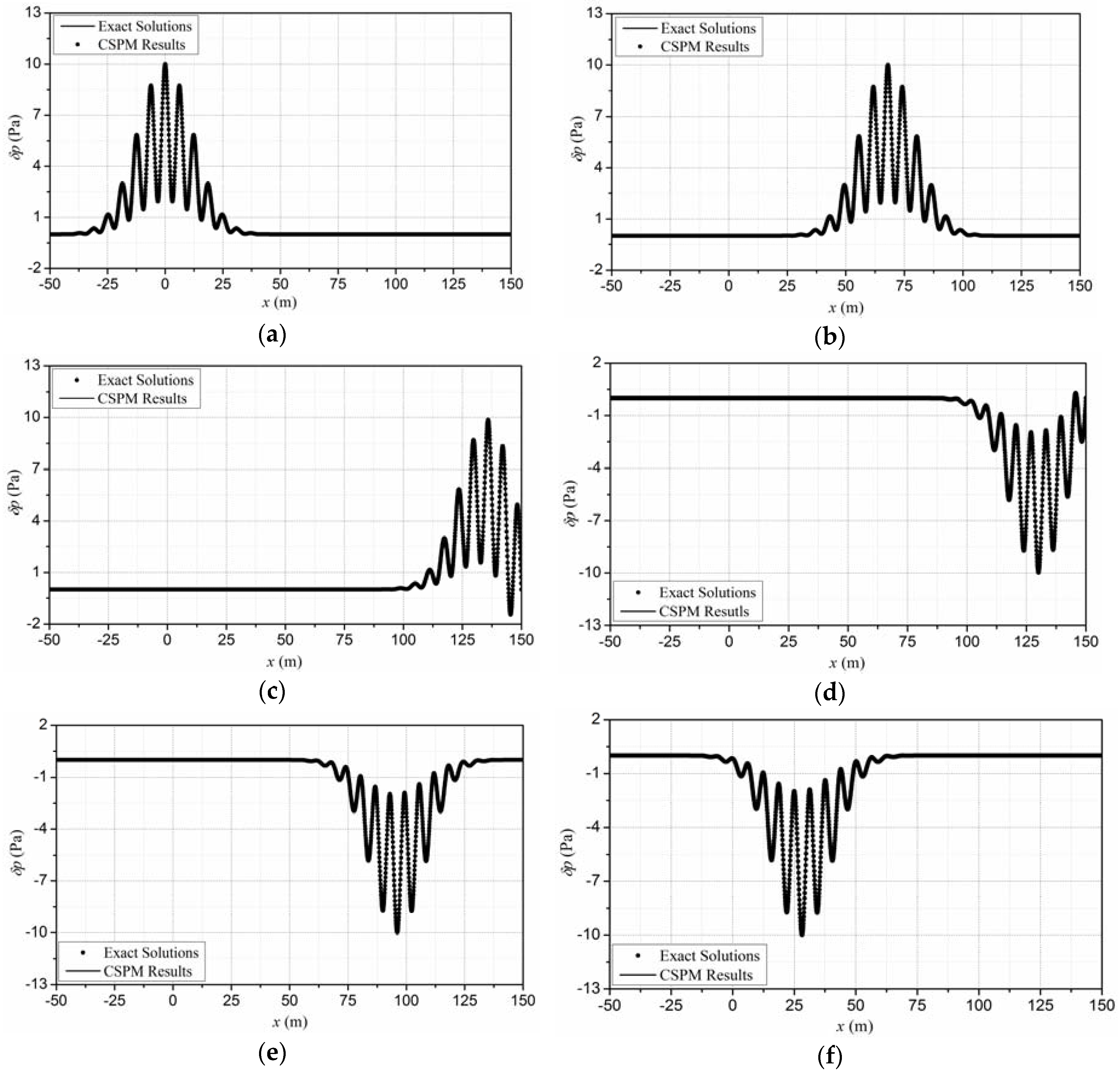
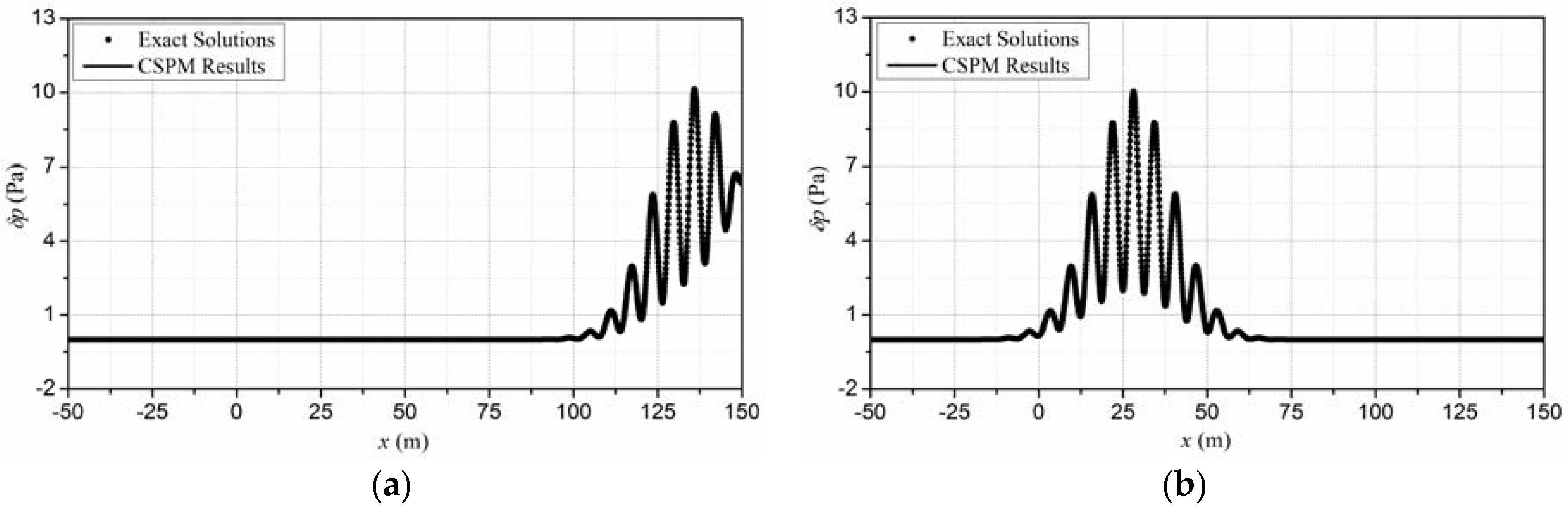
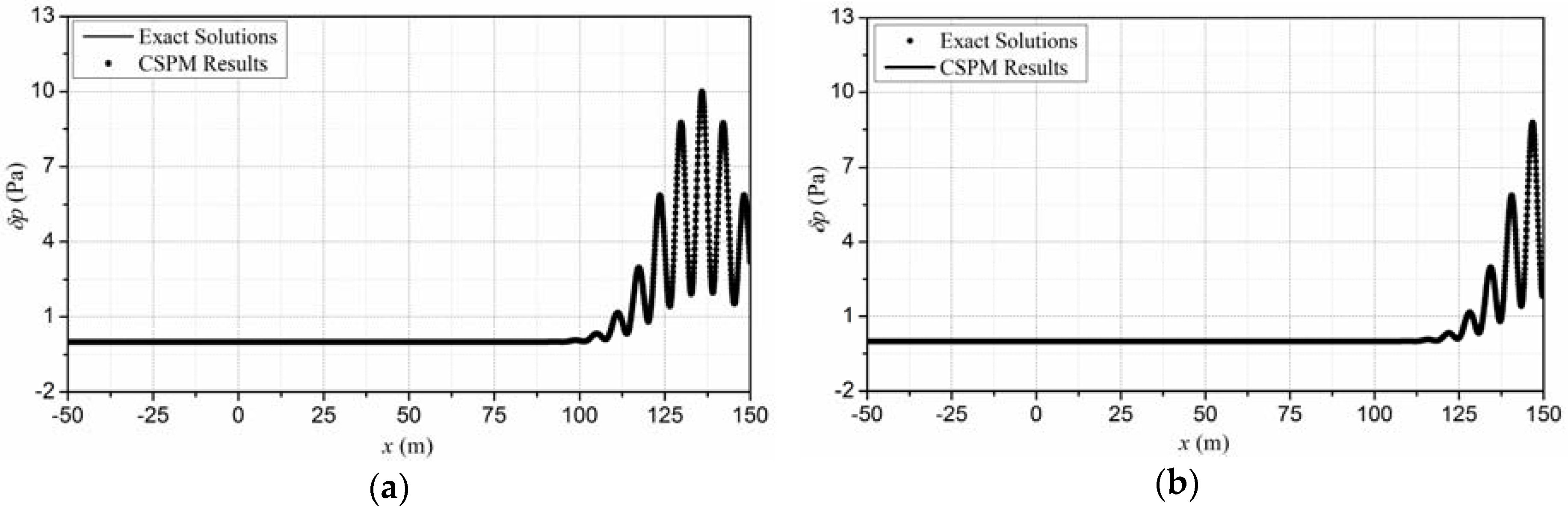
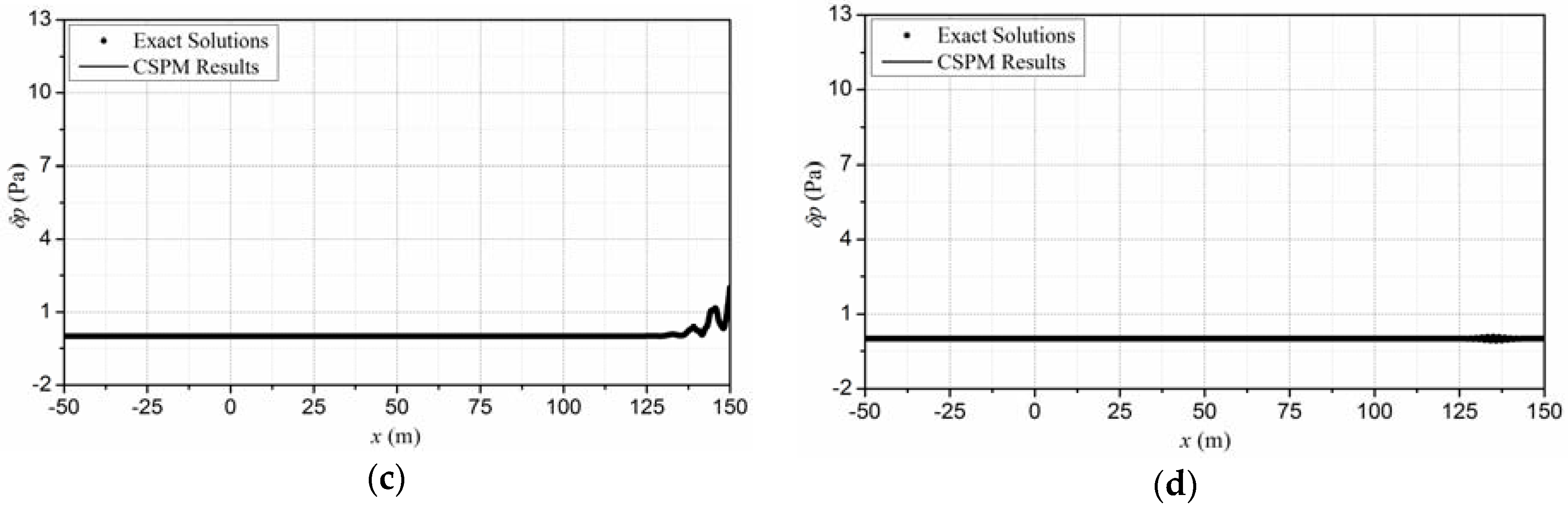
4.2. Verification of the Meshfree Algorithm
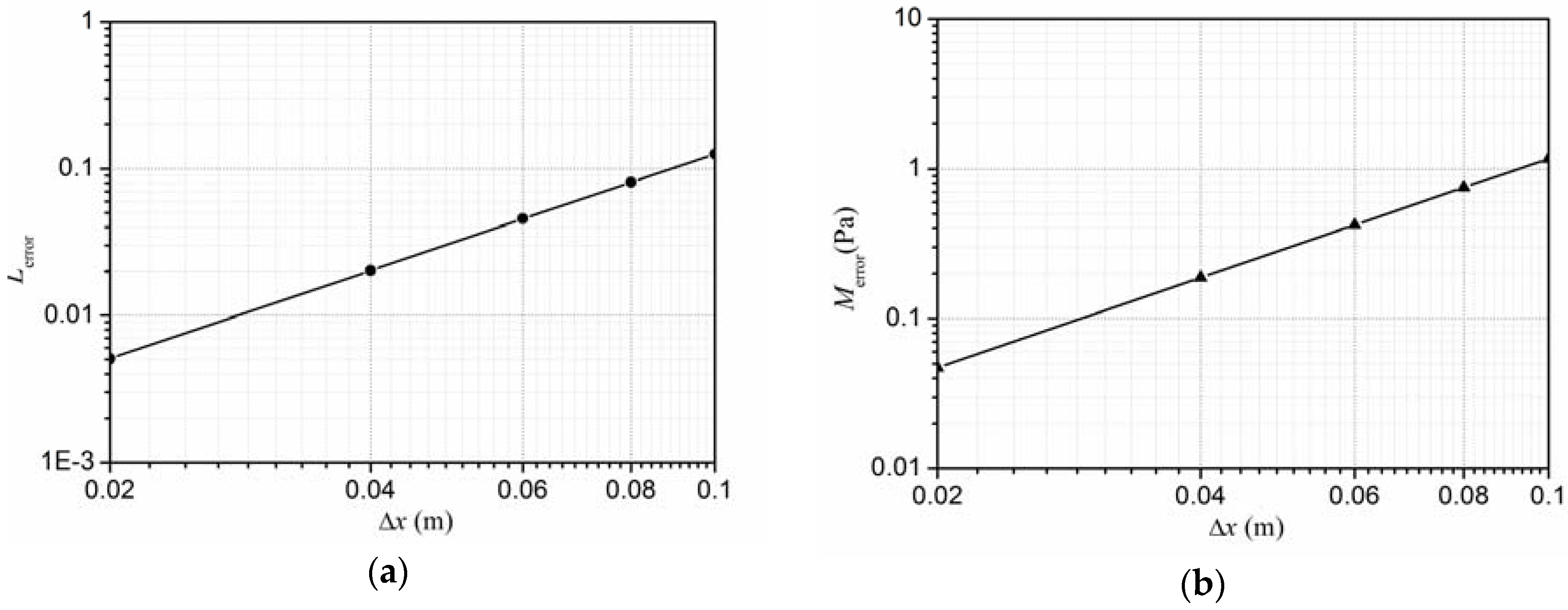
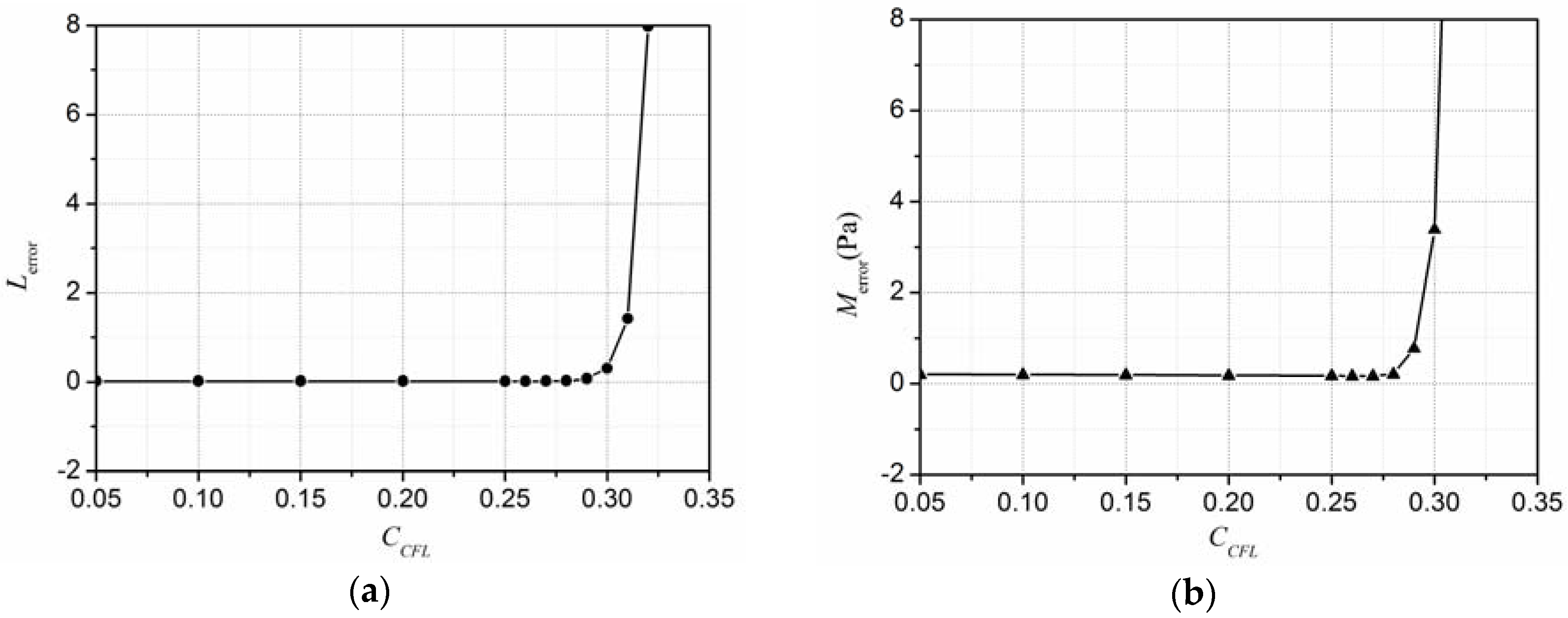
4.3. Discussion on Computational Parameters
5. Application of Different Acoustic Boundaries
5.1. Soft Boundary
5.2. Rigid Boundary
5.3. Absorbing Boundary
6. Conclusions
- The CSPM method is proposed to simulate sound propagation in the time domain by solving acoustic wave equations. Numerical results agree well with theoretical solutions in the modeling of sound propagation in pipes.
- The CSPM method exhibits good convergence, while maintaining a constant ratio of the particle spacing to the smoothing length. According to the present work, the convergence rate is about 1.998 and the CCFL is suggested to be under 0.28.
- A hybrid meshfree-FDTD method is developed and used as an acoustic boundary treatment technique for the meshfree method, and different boundaries are built for virtual particles by using this technique.
- The sound propagation and reflection computed with soft, rigid, and absorbing boundaries, agree well with theoretical solutions for modeling sound propagation.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lee, D.; McDaniel, S.T. Ocean Acoustic Propagation by Finite Difference Methods; Pergamon Press: Oxford, UK, 2014. [Google Scholar]
- Harari, I. A survey of finite element methods for time-harmonic acoustics. Comput. Methods Appl. Mech. Eng. 2006, 195, 1594–1607. [Google Scholar] [CrossRef]
- Kythe, P.K. An Introduction to Boundary Element Methods; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Li, W.; Chai, Y.B.; Lei, M.; Liu, G.R. Analysis of coupled structural-acoustic problems based on the smoothed finite element method (S-FEM). Eng. Anal. Bound. Elem. 2014, 42, 84–91. [Google Scholar] [CrossRef]
- Tadeu, A.; Stanak, P.; Sladek, J.; Sladek, V. Coupled BEM-MLPG acoustic analysis for non-homogeneous media. Eng. Anal. Bound. Elem. 2014, 44, 161–169. [Google Scholar] [CrossRef]
- Fairweather, G.; Karageorghis, A.; Martin, P.A. The method of fundamental solutions for scattering and radiation problems. Eng. Anal. Bound. Elem. 2003, 27, 759–769. [Google Scholar] [CrossRef]
- Uras, R.A.; Chang, C.T.; Chen, Y.; Liu, W.K. Multiresolution reproducing kernel particle methods in acoustics. J. Comput. Acoust. 1997, 5, 71–94. [Google Scholar] [CrossRef]
- Bouillard, P.; Suleau, S. Element-free Galerkin solutions for Helmholtz problems: Formulation and numerical assessment of the pollution effect. Comput. Methods Appl. Mech. Eng. 1998, 162, 317–335. [Google Scholar] [CrossRef]
- Fu, Z.J.; Chen, W.; Gu, Y. Burton-Miller-type singular boundary method for acoustic radiation and scattering. J. Sound Vib. 2014, 333, 3776–3793. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, J.Y.; Fu, Z.J. Singular boundary method for modified Helmholtz equations. Eng. Anal. Bound. Elem. 2014, 44, 112–119. [Google Scholar] [CrossRef]
- Godinho, L.; Amado-Mendes, P.; Carbajo, J.; Ramis-Soriano, J. 3D numerical modelling of acoustic horns using the method of fundamental solutions. Eng. Anal. Bound. Elem. 2015, 51, 64–73. [Google Scholar] [CrossRef]
- Godinho, L.; Soares, D.; Santos, P.G. Efficient analysis of sound propagation in sonic crystals using an ACA–MFS approach. Eng. Anal. Bound. Elem. 2016, 69, 72–85. [Google Scholar] [CrossRef]
- Lee, S. Review: The use of equivalent source method in computational acoustics. J. Comput. Acoust. 2016, 24, 1630001. [Google Scholar] [CrossRef]
- Lee, S.; Brentner, K.S.; Morris, P.J. Assessment of time-domain equivalent source method for acoustic scattering. AIAA J. 2011, 49, 1897–1906. [Google Scholar] [CrossRef]
- Lee, S.; Brentner, K.S.; Morris, P.J. Acoustic scattering in the time domain using an equivalent source method. AIAA J. 2010, 48, 2772–2780. [Google Scholar] [CrossRef]
- Li, J.; Chen, W.; Fu, Z.; Sun, L. Explicit empirical formula evaluating original intensity factors of singular boundary method for potential and Helmholtz problems. Eng. Anal. Bound. Elem. 2016, 73, 161–169. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.; Fu, Z. Singular boundary method using time-dependent fundamental solution for scalar wave equations. Comput. Mech. 2016, 58, 717–730. [Google Scholar] [CrossRef]
- Li, J.; Chen, W.; Fu, Z. Numerical investigation on convergence rate of singular boundary method. Math. Probl. Eng. 2016, 2016, 3564632. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics-theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R.; Zong, Z. An overview on smoothed particle hydrodynamics. Int. J. Comput. Methods 2008, 5, 135–188. [Google Scholar] [CrossRef]
- Springel, V. Smoothed particle hydrodynamics in astrophysics. Annu. Rev. Astron. Astrophys. 2010, 48, 391–430. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Fan, H.; Bergel, G.L.; Li, S. A hybrid peridynamics-SPH simulation of soil fragmentation by blast loads of buried explosive. Int. J. Impact Eng. 2016, 87, 14–27. [Google Scholar] [CrossRef]
- Wolfe, C.T. Acoustic Modeling of Reverberation Using Smoothed Particle Hydrodynamics. Master’s Thesis, University of Colorado, Denver, CO, USA, 2007. [Google Scholar]
- Hahn, P. On the Use of Meshfree Methods in Acoustic Simulations. Master’s Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2009. [Google Scholar]
- Bruneau, M. Chapter 1: Equations of Motion in Non-Dissipative Fluid. In Fundamentals of Acoustics; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Zhang, Y.O.; Zhang, T.; Ouyang, H.; Li, T.Y. Smoothed particle hydrodynamics simulation of sound reflection and transmission. J. Acoust. Soc. Am. 2014, 136, 2224. [Google Scholar] [CrossRef]
- Zhang, Y.O.; Zhang, T.; Ouyang, H.; Li, T.Y. SPH simulation of sound propagation and interference. In Proceedings of the 5th International Conference of Computational Method, Cambridge, UK, 28–30 July 2014.
- Zhang, Y.O.; Zhang, T.; Ouyang, H.; Li, T.Y. Efficient SPH simulation of time-domain acoustic propagation. Eng. Anal. Bound. Elem. 2016, 62, 112–122. [Google Scholar] [CrossRef]
- Zhang, Y.O.; Zhang, T.; Ouyang, H.; Li, T.Y. SPH simulation of acoustic waves: Effects of frequency, sound pressure, and particle spacing. Math. Probl. Eng. 2015, 348314. [Google Scholar] [CrossRef]
- Chen, J.K.; Beraun, J.E.; Carney, T.C. A corrective smoothed particle method for boundary value problems in heat conduction. Int. J. Numer. Methods Eng. 1999, 46, 231–252. [Google Scholar] [CrossRef]
- Chen, J.K.; Beraun, J.E.; Jih, C.J. Completeness of corrective smoothed particle method for linear elastodynamics. Comput. Mech. 1999, 24, 273–285. [Google Scholar] [CrossRef]
- Chen, J.K.; Beraun, J.E.; Jih, C.J. An improvement for tensile instability in smoothed particle hydrodynamics. Comput. Mech. 1999, 23, 279–287. [Google Scholar] [CrossRef]
- Chen, J.K.; Beraun, J.E.; Jih, C.J. A corrective smoothed particle method for transient elastoplastic dynamics. Comput. Mech. 2001, 27, 177–187. [Google Scholar] [CrossRef]
- Liu, W.K.; Chen, Y. Wavelet and multiple scale reproducing kernel methods. Int. J. Numer. Methods Fluids 1995, 21, 901–931. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Liu, M.B.; Xie, W.P.; Liu, G.R. Modeling incompressible flows using a finite particle method. Appl. Math. Model. 2005, 29, 1252–1270. [Google Scholar] [CrossRef]
- Dilts, G.A. Moving-Least-Squares-particle hydrodynamics I: Consistency and stability. Int. J. Numer. Methods Eng. 1999, 44, 1115–1155. [Google Scholar] [CrossRef]
- Dilts, G.A. Moving least square particle hydrodynamics II: Conservation and boundaries. Int. J. Numer. Methods Eng. 2000, 48, 1503–1524. [Google Scholar] [CrossRef]
- Zhang, G.M.; Batra, R.C. Modified smoothed particle hydrodynamics method and its application to transient problems. Comput. Mech. 2004, 34, 137–146. [Google Scholar] [CrossRef]
- Schussler, M.; Schmitt, D. Comments on smoothed particle hydrodynamics. Astron. Astrophys. 1981, 97, 373–379. [Google Scholar]
- Agertz, O.; Moore, B.; Stadel, J.; Potter, D.; Miniati, F.; Read, J.; Mayer, L.; Gawryszczak, A.; Kravtosov, A.; Nordlund, A.; et al. Fundamental differences between SPH and grid methods. Mon. Not. R. Astron. Soc. 2007, 380, 963–978. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulation free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Randles, P.W.; Libersky, L.D. Smoothed particle hydrodynamics: Some recent improvements and applications. Comput. Methods Appl. Mech. Eng. 1996, 138, 375–408. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R.; Lam, K.Y. Investigation into water mitigations using a meshfree particle method. Shock Waves 2002, 12, 181–195. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Lattanzio, J.C. A refined particle method for astrophysical problems. Astron. Astrophys. 1985, 149, 135–143. [Google Scholar]
- Liu, G.R.; Liu, M.B. Chapter 1.4: Meshfree Particle Methods. In Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Kelager, M. Lagrangian Fluid Dynamics Using Smoothed Particle Hydrodynamics; Technical Report; University of Copenhagen: Copenhagen, Denmark, 2006. [Google Scholar]
- Li, X.; Zhang, T.; Zhang, Y.O. Time domain simulation of sound waves using smoothed particle hydrodynamics algorithm with artificial viscosity. Algorithms 2015, 8, 321–335. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Wang, S. Finite-difference time-domain approach to underwater acoustic scattering problems. J. Acoust. Soc. Am. 1996, 99, 1924–1931. [Google Scholar] [CrossRef]
- Li, K.; Huang, Q.B.; Wang, J.L.; Lin, L.G. An improved localized redial basis function meshfree method for computational aeroacoustics. Eng. Anal. Bound. Elem. 2011, 35, 47–55. [Google Scholar] [CrossRef]
| Computational Parameters | Values |
|---|---|
| ∆x | 0.04 m |
| h | 0.058 m |
| Kernel Type | Cubic Spline |
| CCFL | 0.10 |
| c0 | 340 m/s |
| ρ0 | 1.0 kg/m3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.O.; Li, X.; Zhang, T. Modeling Sound Propagation Using the Corrective Smoothed Particle Method with an Acoustic Boundary Treatment Technique. Math. Comput. Appl. 2017, 22, 26. https://doi.org/10.3390/mca22010026
Zhang YO, Li X, Zhang T. Modeling Sound Propagation Using the Corrective Smoothed Particle Method with an Acoustic Boundary Treatment Technique. Mathematical and Computational Applications. 2017; 22(1):26. https://doi.org/10.3390/mca22010026
Chicago/Turabian StyleZhang, Yong Ou, Xu Li, and Tao Zhang. 2017. "Modeling Sound Propagation Using the Corrective Smoothed Particle Method with an Acoustic Boundary Treatment Technique" Mathematical and Computational Applications 22, no. 1: 26. https://doi.org/10.3390/mca22010026
APA StyleZhang, Y. O., Li, X., & Zhang, T. (2017). Modeling Sound Propagation Using the Corrective Smoothed Particle Method with an Acoustic Boundary Treatment Technique. Mathematical and Computational Applications, 22(1), 26. https://doi.org/10.3390/mca22010026





